Abstract
The complex q-rung orthopair fuzzy set (Cq-ROFS) is the extension of complex Pythagorean fuzzy set (CPFS) in which the sum of the q-power of the real part (imaginary part) of the support for and the q-power of the real part (imaginary part) of the support against is limited by one; however, it is difficult to express the hesitant information. In this study, the conception of complex q-rung orthopair hesitant fuzzy set (Cq-ROHFS) by combining the Cq-ROFS and hesitant fuzzy set (HFS) is proposed, and its properties are discussed, obviously, Cq-ROHFS can reflect the uncertainties in structure and in detailed evaluations. Further, some distance measures (DMs) and cross-entropy measures (CEMs) are developed based on complex multiple fuzzy sets. Moreover, these proposed measures are utilized to solve a multi-criteria decision-making problem based on TOPSIS (technique for order preference by similarity to ideal solution) method. Then, the advantages and superiority of the proposed measures are explained by the experimental results and comparisons with some existing methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Multi-criteria decision-making (MCDM), as an essential framework for comparison, has always been used to select the most desirable one from a set of alternatives, which are evaluated by some finite and predefined attributes. Universally, because of complexity and uncertainty of decision-making environment, the decision information cannot always be expressed by crisp numbers. To overcome this drawback, Zadeh [1] presented the theory of fuzzy set (FS), which is an essential tool to deal with fuzzy information. Since it was proposed, FS has received more and more attention and many scholars have utilized it in the different field [2]. However, because there is only membership grade, the FS failed to solve some complex uncertain real-life problems. In this situation, Atanassov [3] presented intuitionistic FS (IFS) which can be successfully applied in different awkward fields because it is characterized by the values of positive grade and negative grade and their sum must be restricted to [0,1]. Then, IFS becomes an essential tool to cope with awkward and difficult fuzzy information, and since it was established, it has received the attention of many researchers and it is utilized in the environments of different fields [4, 5]. However, there are some practical cases, if the decision-maker gives 0.9 for positive grade and o.3 for negative, and now their sum is greater than 1, IFS cannot deal with it. Therefore, Yager [6] proposed Pythagorean FS (PFS) in which the sum of the square of positive grade and square of negative grade is restricted to [0,1], then PFS becomes an essential tool to cope with awkward and difficult fuzzy information, and many researchers utilized it to solve the decision-making problems [7, 8]. However, there are also some practical cases, when the decision-maker gives 0.9 for positive grade and o.8 for negative, and their sum of squares is greater than 1, PFS cannot express it. Then Yager [9] presented q-rung orthopair FS (q-ROFS) in which the sum of the q-power of positive grade and the q-power of negative grade is restricted to [0,1], where q is greater than 1. Since it was established, it has received the attention of many researchers and it is utilized in the environments of aggregation operators, similarity measures, hybrid aggregation operators and so on. The various existing works based on QROFS are elaborated as follow as:
-
1.
General operators Many scholars have successfully developed some aggregation operators in the environment of QROFS. For instance, Liu and Wang [10] developed some aggregation operators using the QROFSs. Garg and Chen [11] explored the neutrality aggregation operators for QROFSs. Using the new score function, Peng et al. [12] presented the exponential operations and aggregation operators based on QROFSs. Xing et al. [13] established point weighted aggregation operators based on QROFSs.
-
2.
Similarity measures (SMs) SM is a proficient technique to accurately examine the degree between any two objects. Many scholars have developed some SMs in different notions. For example, Wang et al. [14] used the cosine function to explore the SMs for QROFSs. Du [15] established makowski-type distance measures based on generalized QROFSs. Liu et al. [16] presented the cosine SMs for QROFSs. Peng and Liu [17] explored information measures for QROFSs.
-
3.
Hybrid operators To find the interrelationships between two objects, the hybrid aggregation operators play an essential role in the environment of realistic decision-making. Many scholars explored different hybrid aggregation operators using the QROFSs, such as Archimedean Bonferroni mean (BM) operators [18], Maclaurin symmetric mean (MSM) operators [19], Muirhead mean operators [20], and the others [21, 22].
The improvement of the above different FSs is not restricted to the real numbers but generalized to the complex numbers. Ramot et al. [23] presented complex FS (CFS) which is characterized by a complex positive grade, which is not limited to [0,1], but generalized to the unit circle in the complex plane. The CFS gives a mathematical framework for describing positive grades in a set in terms of a complex number. Now the CFS has received more attention and many researchers have applied it to decision-making problems [24]. Further, Alkouri and Salleh [25] established the complex IFS (CIFS), which characterized the objective world more comprehensively from three perspectives, such as positive, negative, and neutral degrees. In CIFS, the positive, negative, and neutral degrees are the form of complex-valued with conditions: the sum of the real part (similarly for imaginary part) of the positive degree and real part (similarly for imaginary part) of the negative degree is limited to [0,1]. Since it was established, it has been used to solve the decision-making problem [26, 27]. Moreover, Ullah et al. [28] established the complex PFS (CPFS) in which the positive, negative, and neutral degrees are the form of polar coordinates with conditions: sum of the square of the real part (similarly for imaginary part) of the positive degree and the square of the real part (similarly for imaginary part) of the negative degree is limited to [0,1]. Since it was established, it has received more attention from scholars and is used in different areas [29]. But there was still a problem when a decision-maker gives \(0.9{e}^{{\mathbbm{i}}2\pi \left(0.8\right)}\) for complex-valued positive grade and \(0.8{e}^{{\mathbbm{i}}2\pi \left(0.7\right)}\) for complex-valued negative, and their sum of squares is greater than 1, i.e., \({0.9}^{2}+{0.8}^{2}>1,{0.8}^{2}+{0.7}^{2}>1\), the CPFS canoe describes it. In that situation, Liu et al. [30, 31] proposed complex q-ROFS (Cq-ROFS) in which the positive, negative, and neutral degrees are the form of polar coordinates with conditions: sum of the q-power of the real part (similarly for imaginary part) of the positive degree and the q-power of the real part (similarly for imaginary part) of the negative degree is limited to [0,1]. The innovative concept of Cq-ROFS is an effective tool to solve the above problem i.e., \({0.9}^{6}+{0.8}^{6}=0.7936\le 1,{0.8}^{6}+{0.7}^{6}=0.3798\le 1\).
There are some practical cases, the fuzzy set theory has been neglected. For instance, when an individual provides information by a group for a truth grade, such as \(\left\{\mathrm{0.4,0.3,0.1}\right\}\), then the theory of FS has failed to solve the above issues. Therefore, to tackle this situation, the hesitant fuzzy set (HFS) was established by Torra [32], which can express the hesitation by a few different values. Thus, compared to the FS and its many classical extensions, the HFS can more accurately reflect the people’s hesitancy in stating their preferences over objects. Because HFS is a modification of FS which contains the number of values in [0,1], since it was established, it has received the attention of many researchers. Zhang et al. [33] explored a novel model based on HFS and sentiment word framework. Kumar et al. [34] presented the intuitionistic fuzzy time series for dual HFS. Ren et al. [35] established the minority opinions for social networks based on hesitant fuzzy linguistic sets. Ma et al. [36] explored the three-ways group decisions based on hesitant fuzzy linguistic information. Beg and Rashid [37] explored the intuitionistic HFS (IHFS).
Entropy measure (EM) is one of the most useful and proficient techniques to describe the relation between two objects. Zadeh [38] presented the EM based on FS. Maassen and Uffink [39] improved the EM and proposed the cross EM (CEM). Shang and Jiang [40] explored the notion of fuzzy ECM, which is the mixture of CEM and fuzzy set to cope with unreliable and awkward information in realistic decision-making. Further, Vlachos and Sergiadis [41] improved the fuzzy CEM to explore the intuitionistic fuzzy CEM using the De Luca-Termini non-probabilistic entropy. Zhang and Jiang [42] developed the CEM for vague sets. Ye [43] explored the intuitionistic fuzzy CEM. Currently, Liu et al. [44] established the entropy-based GODs methods using QROFS.
Distance and similarity are important concepts in human cognition and decision-making. Similarity plays an essential role in taxonomy, recognition, case-based reasoning, and many other fields [45]. Chen et al. [46] explored the similarity and distance measures based on IHFS. Peng et al. [47] established the cross-entropy measure based on IHFS. Liu et al. [48] explored some distance measures based on q-rung orthopair HFS (QROHFS) and their application in the MADM problem. In classical MADM problems, TOPSIS (technique for order preference by similarity to ideal solution) method is an effective technique to cope with inconsistent and awkward information, which is proposed by Hwang and Yoon [45]. Due to the complexity of realistic decision problems, many scholars [48] explored the TOPSIS method based on PFSs. When decision-makers face two kinds of opinions like yes and no, some new extended TOPSIS methods are developed to be suitable for these decision environments, for example, many researchers established some extensions of the TOPSIS method based on IFS [3], PFS [6], and QROFS [9]. The IHFS [37], PHFS [49], and QROHFS [50] are the mixtures of HFS and IFS, PFS, QROFS, and QROHFS is the most generalized form with a condition that the sum of the q-power of the maximum of the support and support against grades is not exceeded form unit interval. Obviously, The FS [1], IFS [3], HFS [32], IHFS [37], and PHFS [49] are the special cases of QROHFS [50].
To easily explain the meaning of the CQROHFS, we delineate it with a real example. Assume an organization X needs to buy vehicles from a carmaker Y who gives the organization X data in regard to (1) models of vehicles, (2) production dates of vehicles. Since the carmakers consistently produce similar models of vehicles with slight upgrades and contrasts, the creation date of a vehicle is a central point to be considered while buying it. Thus, the issue considered here is two-dimensional, to be specific, the model of vehicles and the creation date of vehicles. This issue cannot be demonstrated precisely utilizing the conventional QROHFS, as it cannot handle both the measurements all the while. In general, they can be expressed by two QROHFSs, However, this process is complex, and the best choice is to use a single set. Obviously, we can express all data given by the carmaker by CQROHFS. The sufficiency terms in CQROHFS might be utilized to give the organization's choice in regard to the model of vehicles and the creation date of vehicles. For instance, when an intellectual provides \(\left\{0.7{e}^{{\mathbbm{i}}2\pi \left(0.4\right)},0.6{e}^{{\mathbbm{i}}2\pi \left(0.5\right)},0.5{e}^{{\mathbbm{i}}2\pi \left(0.2\right)}\right\}\) for truth grade and \(\left\{0.4{e}^{{\mathbbm{i}}2\pi \left(0.3\right)},0.1{e}^{{\mathbbm{i}}2\pi \left(0.4\right)},0.1{e}^{{\mathbbm{i}}2\pi \left(0.1\right)}\right\}\) for falsity grade, then the IFSs, PFSs, QROFSs, CIFSs, CPFSs, CQROFSs, QROHFSs are not express them, and are only described by CQROHFS, so we develop the concept of CQROHFSs and their algebraic laws. Their advantages are discussed below:
-
1.
When we choose the value of truth and falsity grades in the shape of a singleton set, then the CQROHFS is converted into complex q-rung orthopair fuzzy set.
-
2.
When we choose the value of \(q=1\), then the CQROHFS is converted into complex intuitionistic hesitant fuzzy set.
-
3.
When we choose the value of \(q=2\), then the CQROHFS is converted into t complex Pythagorean hesitant fuzzy set.
-
4.
When we choose the value of truth and falsity grades in the shape of a singleton set for \(q=1\), then the CQROHFS is converted into a complex intuitionistic fuzzy set.
-
5.
When we choose the value of truth and falsity grades in the shape of a singleton set for \(q=2\), then the CQROHFS is converted into complex Pythagorean fuzzy set.
-
6.
When we choose the imaginary parts of the truth and falsity grades are equal to zero, then the CQROHFS is converted into q-rung orthopair hesitant fuzzy set.
-
7.
When we choose the imaginary parts of the truth and falsity grades are equal to zero for \(q=1\), then the CQROHFS is converted into intuitionistic hesitant fuzzy set.
-
8.
When we choose the imaginary parts of the truth and falsity grades are equal to zero for \(q=2\), then the CQROHFS is converted into Pythagorean hesitant fuzzy set.
In a word, the CQROHFS is a generalization of some existing fuzzy sets. For keeping the advantages of the CQROHFS, motivated by these approaches, first, we establish the concept of a complex q-rung orthopair hesitant fuzzy set (Cq-ROHFS) and discuss its properties. Then we also establish the cross-entropy and distance measures using Cq-ROHFS, the contributions of the article are explained as follows:
-
1.
The conception of Cq-ROHFS and their properties are pioneered to resolve multiple complications in the environment of fuzzy set, which combines the Cq-ROFS and HFS, and reflects both uncertainty in structure and the uncertainty in detailed evaluations.
-
2.
Further, some distance measures (DMs) and cross-entropy measures (CEMs) are initiated based on Cq-ROHFS, and their properties are also discussed.
-
3.
Moreover, these initiated measures are utilized to solve the multi-criteria decision-making (MCDM) problem. Then, the advantages and superiority of the proposed measures are explained by the experimental results and comparisons with some existing methods.
The structure of this article is developed as follows: section “Preliminaries” reviews some basic notions such as q-ROFSs, Cq-ROFSs, HFSs, and their properties. In section “Complex q-rung orthopair hesitant fuzzy sets”, Cq-ROHFS and its properties are proposed. In section “Distance measures and improved distance measures between Cq-ROHFNs”, some distance measures (DMs) and cross-entropy measures (CEMs) are initiated based on a complex multiple fuzzy set (CMFS). In section “Multi-criteria decision-making with distance measures based on TOPSIS method”, the initiated measures are utilized to solve multi-criteria decision-making (MCDM) problems. In section “Conclusion”, we concluded.
Preliminaries
In this study, some basic notions related to established works are discussed such as Cq-ROFSs, HFSs, and their basic properties.
Definition 1
[30, 31] A Cq-ROFS is represented as
The symbols \(\mathfrak{Q}\left(x\right)= \fancyscript{f}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{ \fancyscript{f}}\left(x\right)}\) and \(\mathfrak{R}\left(x\right)= \fancyscript{g}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{ \fancyscript{g}}\left(x\right)}\) represent the values of complex-valued positive degree and complex-valued negative degree and they hold the following conditions: \(0\le {\left( \fancyscript{f}\left(x\right)\right)}^{q}+{\left( \fancyscript{g}\left(x\right)\right)}^{q}\le \mathrm{1,0}\le {\left({\Delta }_{ \fancyscript{f}}\left(x\right)\right)}^{q}+{\left({\Delta }_{ \fancyscript{g}}\left(x\right)\right)}^{q}\le 1\). The refusal or neutral grade of q-ROFS is represented as \(\mathfrak{S}\left(x\right)={\left(1-{\fancyscript{f}}^{q}\left(x\right)-{ \fancyscript{g}}^{q}\left(x\right)\right)}^{\frac{1}{q}}{e}^{{\mathbbm{i}}2\pi {\left(1-{\left({\Delta }_{ \fancyscript{f}}\left(x\right)\right)}^{q}-{\left({\Delta }_{ \fancyscript{g}}\left(x\right)\right)}^{q}\right)}^{\frac{1}{q}}}\). The pair \(\left( \fancyscript{f}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{ \fancyscript{f}}\left(x\right)}, \fancyscript{g}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{ \fancyscript{g}}\left(x\right)}\right)\) expresses the complex q-rung orthopair fuzzy number (q-ROFN).
Definition 2
[30, 31] For any three Cq-ROFNs \(H=\left( \fancyscript{f}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{ \fancyscript{f}}\left(x\right)}, \fancyscript{g}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{ \fancyscript{g}}\left(x\right)}\right),{H}_{1}=\left({ \fancyscript{f}}_{1}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{{ \fancyscript{f}}_{1}}\left(x\right)},{ \fancyscript{g}}_{1}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{{ \fancyscript{g}}_{1}}\left(x\right)}\right)\) and \({H}_{2}=\left({ \fancyscript{f}}_{2}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{{ \fancyscript{f}}_{2}}\left(x\right)},{ \fancyscript{g}}_{2}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{{ \fancyscript{g}}_{2}}\left(x\right)}\right)\) with \(\Gamma >0,q\ge 1\), the operational laws are established as follows:
Definition 3
[32] A hesitant fuzzy set (HFS) on \(X\) is in terms of a function that when applied to \(X\) returns a subset of [0, 1], which can be represented as
where \( \fancyscript{f}\left(x\right)\) is a set of values in [0, 1], denoting the possible membership degrees of the element \(x\in X\) to the set \(H\). For convenience, we call \( \fancyscript{f}\left(x\right)\) a hesitant fuzzy element (HFE) and \(H\) the set of all HFSs.
Complex q-rung orthopair hesitant fuzzy sets
In this study, the innovative concept of Cq-ROHFS is established, which is the mixture of Cq-ROFS and HFS. The basic properties and their examples of Cq-ROHFS are also described. In this article, the symbol \(X\) represents a finite fixed set.
Definition 4
A Cq-ROHFS is represented as
The symbols \(\mathfrak{Q}\left(x\right)=\Big\{{ \fancyscript{f}}_{i}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{{ \fancyscript{f}}_{i}}\left(x\right)},i=\mathrm{1,2},3,\ldots ,n\big\}\) and \(\mathfrak{R}\left(x\right)=\left\{{ \fancyscript{g}}_{i}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{{ \fancyscript{g}}_{i}}\left(x\right)},i=\mathrm{1,2},3,\ldots ,n\right\}\) are two sets that contain the finite families of complex-valued positive degrees and complex-valued negative degrees and they hold the following conditions:
\(0\le {\left(\underset{i=\mathrm{1,2},\ldots ,n}{\mathrm{max}}\left({ \fancyscript{f}}_{i}\left(x\right)\right)\right)}^{q}+{\left(\underset{i=\mathrm{1,2},\ldots ,n}{\mathrm{max}}\left({ \fancyscript{g}}_{i}\left(x\right)\right)\right)}^{q}\le 1\) and \(0\le {\left(\underset{i=\mathrm{1,2},\ldots ,n}{\mathrm{max}}\left({\Delta }_{{ \fancyscript{f}}_{i}}\left(x\right)\right)\right)}^{q}+{\left(\underset{i=\mathrm{1,2},\ldots ,n}{\mathrm{max}}\left({\Delta }_{{ \fancyscript{g}}_{i}}\left(x\right)\right)\right)}^{q}\le 1,\) where \({ \fancyscript{f}}_{i}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{{ \fancyscript{f}}_{i}}\left(x\right)}\in \mathfrak{Q}\left(x\right),{ \fancyscript{g}}_{i}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{{ \fancyscript{g}}_{i}}\left(x\right)}\in \mathfrak{R}\left(x\right)\). The refusal or neutral grade of Cq-ROHFS is represented as
The symbol \(\left(\mathfrak{Q}\left(x\right),\mathfrak{R}\left(x\right)\right)\) expresses the complex q-rung orthopair hesitant fuzzy number (Cq-ROHFN).
Definition 5
For any three Cq-ROHFNs \(H=\left({\mathfrak{Q}}_{H}\left(x\right),{\mathfrak{R}}_{H}\left(x\right)\right),{H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left(x\right),{\mathfrak{R}}_{{H}_{1}}\left(x\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left(x\right),{\mathfrak{R}}_{{H}_{2}}\left(x\right)\right)\) with \(\Gamma >0,q\ge 1\), the operational laws are established as follows:
Theorem 1
For any three Cq-ROHFNs \(H=\left({\mathfrak{Q}}_{H}\left(x\right),{\mathfrak{R}}_{H}\left(x\right)\right),{H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left(x\right),{\mathfrak{R}}_{{H}_{1}}\left(x\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left(x\right),{\mathfrak{R}}_{{H}_{2}}\left(x\right)\right)\) with \(\Gamma >0,q\ge 1\), then.
-
1.
\({H}_{1}\oplus {H}_{2}={H}_{2}\oplus {H}_{1}\);
-
2.
\({H}_{1}\otimes {H}_{2}={H}_{2}\otimes {H}_{1}\);
-
3.
\(\Gamma \left({H}_{1}\oplus {H}_{2}\right)=\Gamma {H}_{1}\oplus\Gamma {H}_{2}\);
-
4.
\({\left({H}_{1}\otimes {H}_{2}\right)}^{\Gamma }={H}_{1}^{\Gamma }\otimes {H}_{2}^{\Gamma }\).
Proof
The proof of 3 is given as follows, and the others are omitted.
Definition 6
For any Cq-ROHFN \(H=\left({\mathfrak{Q}}_{H}\left(x\right),{\mathfrak{R}}_{H}\left(x\right)\right)=\left\{\left({ \fancyscript{f}}_{i}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{{ \fancyscript{f}}_{i}}\left(x\right)},{ \fancyscript{g}}_{i}\left(x\right){e}^{{\mathbbm{i}}2\pi {\Delta }_{{ \fancyscript{g}}_{i}}\left(x\right)}\right),i=\mathrm{1,2},3,..,n\right\}\), the score function (SF) \(S\left(H\right)\) and accuracy function (SF) \(A\left(H\right)\) are established as follows:
Taking the advantages of the SF and AF, we define the relation for comparison between two Cq-ROHFNs.
Definition 7
An order relation between two Cq-ROHFNs \({H}_{1}\) and \({H}_{2}\) can be defined as
1. If \(S\left({H}_{1}\right)>S\left({H}_{2}\right)\) then \({H}_{1}>{H}_{2}\),
2. If \(S\left({H}_{1}\right)=S\left({H}_{2}\right)\) and
1. If \(A\left({H}_{1}\right)>A\left({H}_{2}\right)\) then \({H}_{1}>{H}_{2}\).
2. If \(A\left({H}_{1}\right)=A\left({H}_{2}\right)\) then \({H}_{1}={H}_{2}\).
Distance measures and improved distance measures between Cq-ROHFNs
This section aims to explore some distance and similarity measures for Cq-ROHFSs, and further to explore the improved distance and similarity measures that are more superior to existing measures [14,15,16,17]. Because the constraint of Cq-ROHFS is that the sum of the q power of the maximum of the real part (imaginary part) of the support for and the q power of the maximum of the real part (imaginary part) of the support against is limited by one, Cq-ROHFS is more powerful and more reliable than existing notions [25, 28], due to its conditions. The established measures based on Cq-ROHFS are shown as follows:
Definition 8
For any two Cq-ROHFSs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{1}}\left({x}_{i}\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{2}}\left({x}_{i}\right)\right), i=\mathrm{1,2},\ldots ,n\) and their weight vector \(\sum_{i=1}^{n}{\Psi }_{i}=1,{\Psi }_{i}\in [\mathrm{0,1}]\), the complex q-rung orthopair hesitant fuzzy generalized distance measure is established as follows:
Definition 9
For any two Cq-ROHFSs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{1}}\left({x}_{i}\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{2}}\left({x}_{i}\right)\right), i=\mathrm{1,2},\ldots ,n\) and their weight vector \(\sum_{i=1}^{n}{\Psi }_{i}=1,{\Psi }_{i}\in [\mathrm{0,1}]\), the complex q-rung orthopair hesitant fuzzy weighted generalized distance measure is established as follows:
Remark 1
In Eq’s. (6, 7), if we choose the value of parameter \(\Gamma =1\), then the Eqs. (6, 7) is called hamming distance measures. In Eq’s. (6, 7), if we choose the value of parameter \(\Gamma =2\), then the Eqs. (6, 7) is called Euclidean distance measures.
Theorem 2
For any two Cq-ROHFSs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{1}}\left({x}_{i}\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{2}}\left({x}_{i}\right)\right), i=\mathrm{1,2},\ldots ,n\), the distance measures \({{\bar{\rm d}}}_{Cq-ROHFGDM}\left({H}_{1},{H}_{2}\right)\) and \({{\bar{\rm d}}}_{Cq-ROHFWGDM}\left({H}_{1},{H}_{2}\right)\) hold the following conditions:
1. \(0\le {{\bar{\rm d}}}_{Cq-ROHFGDM}\left({H}_{1},{H}_{2}\right),{{\bar{\rm d}}}_{Cq-ROHFWGDM}\left({H}_{1},{H}_{2}\right)\le 1\);
2. \({{\bar{\rm d}}}_{Cq-ROHFGDM}\left({H}_{1},{H}_{2}\right)={{\bar{\rm d}}}_{Cq-ROHFGDM}\left({H}_{2},{H}_{1}\right),{{\bar{\rm d}}}_{Cq-ROHFWGDM}\left({H}_{1},{H}_{2}\right)={{\bar{\rm d}}}_{Cq-ROHFWGDM}\left({H}_{2},{H}_{1}\right)\);
3. \({{\bar{\rm d}}}_{Cq-ROHFGDM}\left({H}_{1},{H}_{2}\right),{{\bar{\rm d}}}_{Cq-ROHFWGDM}\left({H}_{1},{H}_{2}\right)=0\) iff \({H}_{1}={H}_{2}\) i.e. \({ \fancyscript{f}}_{{H}_{1}}^{j}\left({x}_{i}\right)={ \fancyscript{f}}_{{H}_{2}}^{j}\left({x}_{i}\right),{ \fancyscript{g}}_{{H}_{1}}^{j}\left({x}_{i}\right)={ \fancyscript{g}}_{{H}_{2}}^{j}\left({x}_{i}\right),{{\Delta }_{ \fancyscript{f}}}_{{H}_{1}}^{j}\left({x}_{i}\right)={{\Delta }_{ \fancyscript{f}}}_{{H}_{2}}^{j}\left({x}_{i}\right)\) and \({{\Delta }_{ \fancyscript{g}}}_{{H}_{1}}^{j}\left({x}_{i}\right)={{\Delta }_{ \fancyscript{g}}}_{{H}_{2}}^{j}\left({x}_{i}\right)\).
Proof: Straightforward
Definition 10
For any two Cq-ROHFSs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{1}}\left({x}_{i}\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{2}}\left({x}_{i}\right)\right), i=\mathrm{1,2},\ldots ,n\) and their weight vector \(\sum_{i=1}^{n}{\Psi }_{i}=1,{\Psi }_{i}\in [\mathrm{0,1}]\), the improved complex q-rung orthopair hesitant fuzzy generalized distance measure is established as follows:
Definition 11
For any two Cq-ROHFNs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{1}}\left({x}_{i}\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{2}}\left({x}_{i}\right)\right), i=\mathrm{1,2},\ldots ,n\) and their weight vector \(\sum_{i=1}^{n}{\Psi }_{i}=1,{\Psi }_{i}\in [\mathrm{0,1}]\), the improved complex q-rung orthopair hesitant fuzzy weighted generalized distance measure is established as follows:
Remark 2
In Eq’s. (8, 9), if we choose the value of parameter \(\Gamma =1\), then the Eq’s. (8, 9) is called hamming distance measures. In Eq’s. (8, 9), if we choose the value of parameter \(\Gamma =2\), then the Eq’s. (8, 9) is called Euclidean distance measures.
Theorem 3
For any two Cq-ROHFSs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left(x\right),{\mathfrak{R}}_{{H}_{1}}\left(x\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left(x\right),{\mathfrak{R}}_{{H}_{2}}\left(x\right)\right)\), the distance measures \({{\bar{\rm d}}}_{ICq-ROHFGDM}\left({H}_{1},{H}_{2}\right)\) and \({{\bar{\rm d}}}_{ICq-ROHFWGDM}\left({H}_{1},{H}_{2}\right)\) hold the following conditions:
1. \(0\le {{\bar{\rm d}}}_{ICq-ROHFGDM}\left({H}_{1},{H}_{2}\right),{{\bar{\rm d}}}_{ICq-ROHFWGDM}\left({H}_{1},{H}_{2}\right)\le 1\);
2. \({{\bar{\rm d}}}_{ICq-ROHFGDM}\left({H}_{1},{H}_{2}\right)={{\bar{\rm d}}}_{ICq-ROHFGDM}\left({H}_{2},{H}_{1}\right),{{\bar{\rm d}}}_{ICq-ROHFWGDM}\left({H}_{1},{H}_{2}\right)={{\bar{\rm d}}}_{ICq-ROHFWGDM}\left({H}_{2},{H}_{1}\right)\);
3. \({{\bar{\rm d}}}_{ICq-ROHFGDM}\left({H}_{1},{H}_{2}\right),{{\bar{\rm d}}}_{ICq-ROHFWGDM}\left({H}_{1},{H}_{2}\right)=0\) iff \({H}_{1}={H}_{2}\) i.e. \({ \fancyscript{f}}_{{H}_{1}}^{j}\left({x}_{i}\right)={ \fancyscript{f}}_{{H}_{2}}^{j}\left({x}_{i}\right),{ \fancyscript{g}}_{{H}_{1}}^{j}\left({x}_{i}\right)={ \fancyscript{g}}_{{H}_{2}}^{j}\left({x}_{i}\right),{{\Delta }_{ \fancyscript{f}}}_{{H}_{1}}^{j}\left({x}_{i}\right)={{\Delta }_{ \fancyscript{f}}}_{{H}_{2}}^{j}\left({x}_{i}\right)\) and \({{\Delta }_{ \fancyscript{g}}}_{{H}_{1}}^{j}\left({x}_{i}\right)={{\Delta }_{ \fancyscript{g}}}_{{H}_{2}}^{j}\left({x}_{i}\right)\).
Proof: Straightforward
The cross-entropy measures of Cq-ROHFSs
Entropy measure (EM), as one of the most useful and proficient techniques, is important to examine the relation between two objects. Zadeh [38] presented the EM based on FS. Maassen and Uffink [39] improved the EM to explore the cross EM (CEM) as the starting point in the information theory. Shang and Jiang [40] explored the notion of fuzzy ECM, which is the mixture of CEM and FS to cope with unreliable and awkward information in realistic decision-making. Further, Vlachos and Sergiadis [41] improved the fuzzy CEM to explore the intuitionistic fuzzy CEM using the De Luca-Termini non-probabilistic entropy. Zhang and Jiang [42] established the CEM for vague sets. Ye [43] explored the intuitionistic fuzzy CEM. Currently, Liu et al. [44] established the entropy-based GODs methods using QROFS. The purpose of this sub-section is to examine the different kinds of CEMs based on CQROHFSs. The special properties of the explored work are also justified.
Definition 12
For any two Cq-ROHFSs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{1}}\left({x}_{i}\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{2}}\left({x}_{i}\right)\right), i=\mathrm{1,2},\ldots ,n\) and their weight vector \(\sum_{i=1}^{n}{\Psi }_{i}=1,{\Psi }_{i}\in [\mathrm{0,1}]\), the cross-entropy measure is established as follows:
which holds the following conditions:
1. \(C{E}_{1}\left({H}_{1},{H}_{2}\right)\ge 0\);
2. \(C{E}_{1}\left({H}_{1},{H}_{2}\right)=0\) iff \({H}_{1}={H}_{2}\);
3. \(C{E}_{1}\left({H}_{1}^{C},{H}_{2}^{C}\right)=C{E}_{1}\left({H}_{1},{H}_{2}\right)\), where \({H}_{1}^{C}=\left({\mathfrak{R}}_{{H}_{1}}\left(x\right),{\mathfrak{Q}}_{{H}_{1}}\left(x\right)\right)\).
Definition 13
For any two Cq-ROHFSs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{1}}\left({x}_{i}\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{2}}\left({x}_{i}\right)\right), i=\mathrm{1,2},\ldots ,n\) and their weight vector \(\sum_{i=1}^{n}{\Psi }_{i}=1,{\Psi }_{i}\in [\mathrm{0,1}]\), the cross-entropy measure is established as follows:
Which holds the following conditions:
1.\(C{E}_{2}\left({H}_{1},{H}_{2}\right)\ge 0\);
2. \(C{E}_{2}\left({H}_{1},{H}_{2}\right)=0\) iff \({H}_{1}={H}_{2}\);
3. \(C{E}_{3}\left({H}_{1}^{C},{H}_{2}^{C}\right)=C{E}_{3}\left({H}_{1},{H}_{2}\right)\), where \({H}_{1}^{C}=\left({\mathfrak{R}}_{{H}_{1}}\left(x\right),{\mathfrak{Q}}_{{H}_{1}}\left(x\right)\right)\).
Definition 14
For any two Cq-ROHFSs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{1}}\left({x}_{i}\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{2}}\left({x}_{i}\right)\right), i=\mathrm{1,2},\ldots ,n\) and their weight vectors \(\sum_{i=1}^{n}{\Psi }_{i}=1,{\Psi }_{i}\in [\mathrm{0,1}]\), the cross-entropy measure is established as follows:
which holds the following conditions:
1. \(C{E}_{3}\left({H}_{1},{H}_{2}\right)\ge 0\);
2. \(C{E}_{3}\left({H}_{1},{H}_{2}\right)=0\) iff \({H}_{1}={H}_{2}\);
3. \(C{E}_{3}\left({H}_{1}^{C},{H}_{2}^{C}\right)=C{E}_{3}\left({H}_{1},{H}_{2}\right)\), where \({H}_{1}^{C}=\left({\mathfrak{R}}_{{H}_{1}}\left(x\right),{\mathfrak{Q}}_{{H}_{1}}\left(x\right)\right)\).
Definition 15
For any two Cq-ROHFSs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{1}}\left({x}_{i}\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{2}}\left({x}_{i}\right)\right), i=\mathrm{1,2},\ldots ,n\) and their weight vector \(\sum_{i=1}^{n}{\Psi }_{i}=1,{\Psi }_{i}\in [\mathrm{0,1}]\), the cross-entropy measure is established as follows:
which holds the following conditions:
1. \(C{E}_{4}\left({H}_{1},{H}_{2}\right)\ge 0\);
2. \(C{E}_{4}\left({H}_{1},{H}_{2}\right)=0\) iff \({H}_{1}={H}_{2}\);
3. \(C{E}_{4}\left({H}_{1}^{C},{H}_{2}^{C}\right)=C{E}_{4}\left({H}_{1},{H}_{2}\right)\), where \({H}_{1}^{C}=\left({\mathfrak{R}}_{{H}_{1}}\left(x\right),{\mathfrak{Q}}_{{H}_{1}}\left(x\right)\right)\).
Definition 16
For any two Cq-ROHFSs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{1}}\left({x}_{i}\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{2}}\left({x}_{i}\right)\right), i=\mathrm{1,2},\ldots ,n\) and their weight vector \(\sum_{i=1}^{n}{\Psi }_{i}=1,{\Psi }_{i}\in [\mathrm{0,1}]\), the cross-entropy measure is established as follows:
which holds the following conditions:
1. \(C{E}_{5}\left({H}_{1},{H}_{2}\right)\ge 0\);
2. \(C{E}_{5}\left({H}_{1},{H}_{2}\right)=0\) iff \({H}_{1}={H}_{2}\);
3. \(C{E}_{5}\left({H}_{1}^{C},{H}_{2}^{C}\right)=C{E}_{5}\left({H}_{1},{H}_{2}\right)\), where \({H}_{1}^{C}=\left({\mathfrak{R}}_{{H}_{1}}\left(x\right),{\mathfrak{Q}}_{{H}_{1}}\left(x\right)\right)\).
Definition 17
For any two Cq-ROHFSs \({H}_{1}=\left({\mathfrak{Q}}_{{H}_{1}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{1}}\left({x}_{i}\right)\right)\) and \({H}_{2}=\left({\mathfrak{Q}}_{{H}_{2}}\left({x}_{i}\right),{\mathfrak{R}}_{{H}_{2}}\left({x}_{i}\right)\right), i=\mathrm{1,2},\ldots ,n\) and their weight vector \(\sum_{i=1}^{n}{\Psi }_{i}=1,{\Psi }_{i}\in [\mathrm{0,1}]\), the cross-entropy measure is established as follows:
which holds the following conditions:
1. \(C{E}_{6}\left({H}_{1},{H}_{2}\right)\ge 0\);
2. \(C{E}_{6}\left({H}_{1},{H}_{2}\right)=0\) iff \({H}_{1}={H}_{2}\);
3. \(C{E}_{6}\left({H}_{1}^{C},{H}_{2}^{C}\right)=C{E}_{6}\left({H}_{1},{H}_{2}\right)\), where \({H}_{1}^{C}=\left({\mathfrak{R}}_{{H}_{1}}\left(x\right),{\mathfrak{Q}}_{{H}_{1}}\left(x\right)\right)\).
Theorem 4
The proposed measures defined in Definition (10) to Definition (15) are a picture hesitant fuzzy cross-entropy, and satisfy the three conditions given in all definitions.
Proof: Straightforward
Remark 3
In Eqs. (10)–(15), if we choose the value of parameter \(p=1\), then the Eqs. (10)–(15) are called hamming CE measures, and if we choose the value of parameter \(p=2\), then Eqs. (10)–(15) are called Euclidean CE measures.
Multi-criteria decision-making with distance measures based on TOPSIS method
TOPSIS (technique for order preference by similarity to ideal solution) method is one of the most powerful and effective methods in solving the multi-attribute decision-making problem. Hwang and Yoon [45] firstly explored the TOPSIS method.
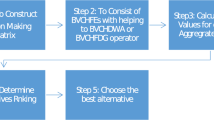
The steps of the TOPSIS method for CQROHFS are shown as follows:
Step 1 Because there are benefits and cost types we must normalize the decision matrix, and have
Step 2 Based on the following formula, we examine the weight vector of the attributes
where the \({\mathcal{H}}_{k}\in \left[\mathrm{0,1}\right],k=\mathrm{1,2},3,\ldots ,t\) is defined as
or
Step 3 Based on the following formulas, we get the PIS and NIS.
Step 4 Using Eq. (43), we get the closeness of each alternative
Step 5 Ranking all alternatives and get the best optimal one.
Step 6 The end.
The proposed method can easily solve the MADM problems with unknown attribute weight.
Example 1
The energy development strategy project is one of the most common issues which are discussed in various countries. To choose the best alternative from the family of alternates, which are evaluated by some attributes, suppose that \(H=\left\{{H}_{1},{H}_{2},{H}_{3},{H}_{4},{H}_{5}\right\},\) is the set of alternates and \(\mathcal{H}=\left\{{\mathcal{H}}_{1},{\mathcal{H}}_{2},{\mathcal{H}}_{3},{\mathcal{H}}_{4}\right\}\) is the set of attributes which are described as follows: \({\mathcal{H}}_{1}\): Economic Strategy; \({\mathcal{H}}_{2}\): Technological Strategy; \({\mathcal{H}}_{3}\): Environmental Strategy; \({\mathcal{H}}_{4}\): Sociopolitical Strategy.
For solving this issue, we construct the decision matrix in the formed complex q-rung orthopair hesitant fuzzy numbers, which is stated in the form of Table 1.
The steps of the proposed TOPSIS method for CQROHFS are shown as follow:
Step 1 This MADM problem contains only one kind of information, i.e., benefits type. So, this step is omitted.
Step 2 Based on the Eqs. (17)–(19), we get the weight vector of the attributes shown as:
Step 3 Based on Eq. (20) and Eq. (21), we get the PIS and NIS as follows:
Step 4 First, we can calculate the distances between PIS, NIS, and each alternative, which are shown in Table 2. Then using Eq. (43), we get the closeness of each alternative, we have
Step 5 We rank all the alternatives and get the best optimal one, such that
i.e., the best alternative is \({H}_{3}\).
Step 6 The end.
Next, we can compare the proposed method with some existing methods based on example 1, and the results are shown in Table 3.
From Table 1, we obtain that all methods get the same ranking result, and the best alternative is \({H}_{3}\). This has shown the validity of the proposed method. The graphical interpretation is shown in Fig. 1.
Graphical representations for the information’s in Table 3
In Fig. 1, we discuss five different series, which denotes the graphical interpretation of the alternatives \({H}_{1}\) to H5. From Fig. 1, it is clear that series 3 gives the biggest values compared to other values in different series.
Advantages and comparative analysis with graphical representations
The advantage of the CQROHFS is that it contains the truth and falsity grades with the conditions that the sum of q-power of the supremum of the real parts (also for imaginary parts) of the truth grade and the q-power of the supremum of the real parts (also for imaginary parts) falsity grade is not exceeded from unit interval. Further, to explore the validities of the established method based on the novel CQROHFS, we choose some existing measures based on IHFSs [37, 46, 47], PHFSs [49], QROHFSs [50], complex intuitionistic hesitant fuzzy sets (Special case of CQROHFSs), complex Pythagorean hesitant fuzzy sets (Special case of CQROHFSs), and CQROHFSs. Further, we choose the complex Pythagorean hesitant fuzzy information shown in Table 4 and solve it using some existing measures [14,15,16,17].
The results are shown in Table 5.
Form Table 5, we obtain that the best alternative is \({H}_{1}\), and it also shows the advantage of CQROHFSs. In addition, the graphical interpretation is shown in Fig. 2.
Graphical representation for the information’s in Table 5
In Fig. 2, we discuss five different series, which denotes the graphical interpretation of the alternatives \({H}_{1}\) to H5. From Fig. 2, it is clear that series 1 gives the biggest value compared to other values in different series.
Example 2
We consider another example from Ref. [37] in which the decision information is given in intuitionistic hesitant fuzzy information shown in Table 6.
We know that about the value of the exponential function \({e}^{{\mathbbm{i}}2\pi \left(0.0\right)}={e}^{0}=1\), then we give a modified version of Table 6 shown in Table 7.
The results are shown in Table 8.
From Table 8, we obtain that the best alternative is \({H}_{3}\). The graphical interpretation is shown in Fig. 3.
Geometrical representation for the information’s in Table 8
In Fig. 3, we discuss five different series, which denotes the graphical interpretation of the alternatives \({H}_{1}\) to H5. From Fig. 3, it is clear that series 3 gives the biggest value compared to other values in different series.
From the above examples and comparisons with some existing methods, the proposed method based on CQROHFSs is more general than the methods based on Ifs, IFSs, CIFS, CPFS, CQROFS, and so on, at the same time, they can also verify the validity of this method.
Conclusion
Some complex fuzzy sets have received massive attention from different scholars. The notion of CQROFS is the extension of CPFS in which the sum of the q power of the real part (imaginary part) of the support for and the q power of the real part (imaginary part) of the support against is limited by one. In this study, by combining the CQROFS and HFS, The main purpose of this study is discussed below.
-
1.
The conception of CQROHFS and their properties are firstly proposed which could reflect both the uncertainty in structure and the uncertainty in detailed evaluations.
-
2.
Some DMs and CEMs are developed based on CMFS, and an MCDM approach is presented based on the TOPSIS method and CEMs.
-
3.
These initiated measures are utilized to examine the dominance and effectiveness.
-
4.
The experimental results are compared with some existing methods to show the advantages and superiority of the proposed measures.
In the future, we will try to develop the complex spherical hesitant fuzzy sets, complex T-spherical hesitant fuzzy sets, complex linear Diophantine hesitant fuzzy sets, and complex bipolar soft sets using the ideas of complex spherical and complex T-spherical fuzzy sets [52], linear Diophantine fuzzy sets [53,54,55], and bipolar soft sets [56]. We will also use the proposed DMs and CEMs to develop some decision-making methods, and then apply them to solve some real decision-making problems.
Data availability statement
The data used to support the findings of this study are included within the article.
References
Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353
Van Amerongen J, van Nauta Lemke HR, Van der Veen JCT (1977) An autopilot for ships designed with fuzzy sets. IFAC Proc Vol 10(16):479–487
Atanassov KT (1999) Intuitionistic fuzzy sets. In: Intuitionistic fuzzy sets (pp 1–137). Physica, Heidelberg
Hung WL, Yang MS (2004) Similarity measures of intuitionistic fuzzy sets based on Hausdorff distance. Pattern Recogn Lett 25(14):1603–1611
Ansari MD, Mishra AR, Ansari FT (2018) New divergence and entropy measures for intuitionistic fuzzy sets on edge detection. Int J Fuzzy Syst 20(2):474–487
Yager RR (2013) Pythagorean fuzzy subsets. In: 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS) (pp 57–61), IEEE
Zhou Q, Mo H, Deng Y (2020) A new divergence measure of pythagorean fuzzy sets based on belief function and its application in medical diagnosis. Mathematics 8(1):142
Song P, Li L, Huang D, Wei Q, Chen X (2020) Loan risk assessment based on Pythagorean fuzzy analytic hierarchy process. In: Journal of Physics: Conference Series (Vol. 1437, No. 1, p. 012101). IOP Publishing
Yager RR (2016) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222–1230
Liu P, Wang P (2018) Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int J Intell Syst 33(2):259–280
Garg H, Chen SM (2020) Multiattribute group decision making based on neutrality aggregation operators of q-rung orthopair fuzzy sets. Inf Sci 517:427–447
Peng X, Dai J, Garg H (2018) Exponential operation and aggregation operator for q-rung orthopair fuzzy set and their decision-making method with a new score function. Int J Intell Syst 33(11):2255–2282
Xing Y, Zhang R, Zhou Z, Wang J (2019) Some q-rung orthopair fuzzy point weighted aggregation operators for multi-attribute decision making. Soft Comput 23(22):11627–11649
Wang P, Wang J, Wei G, Wei C (2019) Similarity measures of q-rung orthopair fuzzy sets based on cosine function and their applications. Mathematics 7(4):340
Du WS (2018) Minkowski-type distance measures for generalized orthopair fuzzy sets. Int J Intell Syst 33(4):802–817
Liu D, Chen X, Peng D (2019) Some cosine similarity measures and distance measures between q-rung orthopair fuzzy sets. Int J Intell Syst 34(7):1572–1587
Peng X, Liu L (2019) Information measures for q-rung orthopair fuzzy sets. Int J Intell Syst 34(8):1795–1834
Liu P, Wang P (2018) Multiple-attribute decision-making based on Archimedean Bonferroni Operators of q-rung orthopair fuzzy numbers. IEEE Trans Fuzzy Syst 27(5):834–848
Wei G, Wei C, Wang J, Gao H, Wei Y (2019) Some q-rung orthopair fuzzy maclaurin symmetric mean operators and their applications to potential evaluation of emerging technology commercialization. Int J Intell Syst 34(1):50–81
Wang J, Wei G, Wei C, Wei Y (2019) Dual hesitant q-Rung Orthopair fuzzy Muirhead mean operators in multiple attribute decision making. IEEE Access 7:67139–67166
Liu P, Chen SM, Wang P (2018) Multiple-attribute group decision-making based on q-rung orthopair fuzzy power maclaurin symmetric mean operators. IEEE Trans Syst Man Cybern Syst 50:3741–3756
Wei G, Gao H, Wei Y (2018) Some q-rung orthopair fuzzy Heronian mean operators in multiple attribute decision making. Int J Intell Syst 33(7):1426–1458
Ramot D, Milo R, Friedman M, Kandel A (2002) Complex fuzzy sets. IEEE Trans Fuzzy Syst 10(2):171–186
Ramot D, Friedman M, Langholz G, Kandel A (2003) Complex fuzzy logic. IEEE Trans Fuzzy Syst 11(4):450–461
Alkouri AMDJS, Salleh AR (2012) Complex intuitionistic fuzzy sets. In: AIP conference proceedings (Vol. 1482, No. 1, pp. 464–470). American Institute of Physics
Garg H, Rani D (2020) New generalised Bonferroni mean aggregation operators of complex intuitionistic fuzzy information based on Archimedean t-norm and t-conorm. J Exp Theor Artif Intell 32(1):81–109
Ngan RT, Ali M, Tamir DE, Rishe ND, Kandel A (2020) Representing complex intuitionistic fuzzy set by quaternion numbers and applications to decision making. Appl Soft Comput 87:105961
Ullah K, Mahmood T, Ali Z, Jan N (2019) On some distance measures of complex Pythagorean fuzzy sets and their applications in pattern recognition. Complex Intell Syst 2019:1–13
Akram M, Naz S (2019) A novel decision-making approach under complex Pythagorean fuzzy environment. Math Comput Appl 24(3):73
Liu P, Ali Z, Mahmood T (2019) A method to multi-attribute group decision-making problem with complex q-Rung orthopair linguistic information based on Heronian mean operators. Int J Comput Intell Syst 12(2):1465–1496
Liu P, Mahmood T, Ali Z (2020) Complex q-Rung orthopair fuzzy aggregation operators and their applications in multi-attribute group decision making. Information 11(1):5
Torra V (2010) Hesitant fuzzy sets. Int J Intell Syst 25(6):529–539
Zhang D, Wu C, Liu J (2020) Ranking products with online reviews: a novel method based on hesitant fuzzy set and sentiment word framework. J Oper Res Soc 71(3):528–542
Kumar S, Bisht K, Gupta KK (2019) Intuitionistic Fuzzy time series forecasting based on dual hesitant fuzzy set for stock market: DHFS-Based IFTS model for stock market. In: Exploring critical approaches of evolutionary computation (pp. 37–57). IGI Global
Ren R, Tang M, Liao H (2020) Managing minority opinions in micro-grid planning by a social network analysis-based large scale group decision making method with hesitant fuzzy linguistic information. Knowl Based Syst 189:105060
Ma W, Lei W, Sun B (2020) Three-way group decisions under hesitant fuzzy linguistic environment for green supplier selection. Kybernetes
Beg I, Rashid T (2014) Group decision making using intuitionistic hesitant fuzzy sets. Int J Fuzzy Logic Intell Syst 14(3):181–187
Zadeh LA (1965) Fuzzy sets and systems. In: Proc. symp. on systems theory, Polytechnic Institute of Brooklyn, New York, pp 29–37
Maassen H, Uffink JB (1988) Generalized entropic uncertainty relations. Phys Rev Lett 60(12):1103
Shang XG, Jiang WS (1997) A note on fuzzy information measures. Pattern Recogn Lett 18(5):425–432
Vlachos IK, Sergiadis GD (2007) Intuitionistic fuzzy information–applications to pattern recognition. Pattern Recogn Lett 28(2):197–206
Zhang QS, Jiang SY (2008) A note on information entropy measures for vague sets and its applications. Inf Sci 178(21):4184–4191
Ye J (2009) Multicriteria fuzzy decision-making method based on the intuitionistic fuzzy cross-entropy. In: 2009 international conference on intelligent human-machine systems and cybernetics (Vol. 1, pp. 59–61), IEEE.
Liu L, Wu J, Wei G, Wei C, Wang J, Wei Y (2020) Entropy-based GLDS method for social capital selection of a PPP project with q-Rung orthopair fuzzy information. Entropy 22(4):414
Hwang CL, Yoon K (1981) Multiple attribute decision making-methods and applications. Springer, Berlin Heidelberg New York
Chen X, Li J, Qian L, Hu X (2016) Distance and similarity measures for intuitionistic hesitant fuzzy sets. In: 2016 international conference on artificial intelligence: technologies and applications. Atlantis Press
Peng JJ, Wang JQ, Wu XH, Zhang HY, Chen XH (2015) The fuzzy cross-entropy for intuitionistic hesitant fuzzy sets and their application in multi-criteria decision-making. Int J Syst Sci 46(13):2335–2350
Sajjad-Ali-Khan M, Ali A, Abdullah S, Amin F, Hussain F (2018) New extension of TOPSIS method based on Pythagorean hesitant fuzzy sets with incomplete weight information. J Intell Fuzzy Syst 35(5):5435–5448
Ullah K, Ali Z, Jan N, Mahmood T, Maqsood S (2018) Multi-attribute decision making based on averaging aggregation operators for picture hesitant fuzzy sets. Tech J 23(04):84–95
Liu D, Peng D, Liu Z (2019) The distance measures between q-rung orthopair hesitant fuzzy sets and their application in multiple criteria decision making. Int J Intell Syst 34(9):2104–2121
Khan MSA, Abdullah S, Ali A, Amin F (2019) An extension of VIKOR method for multi-attribute decision-making under Pythagorean hesitant fuzzy setting. Granul Comput 4(3):421–434
Ali Z, Mahmood T, Yang MS (2020) TOPSIS method based on complex spherical fuzzy sets with Bonferroni mean operators. Mathematics 8(10):1739–1778
Riaz M, Hashmi MR (2019) Linear Diophantine fuzzy set and its applications towards multi-attribute decision-making problems. J Intell Fuzzy Syst 37(4):5417–5439
Riaz M, Hashmi MR, Pamucar D, Chu YM (2021) Spherical linear Diophantine fuzzy sets with modeling uncertainties in MCDM. Comput Model Eng Sci 126(3):1125–1164
Ayub S, Shabir M, Riaz M, Aslam M, Chinram R (2021) Linear diophantine fuzzy relations and their algebraic properties with decision making. Symmetry 13(6):945–967
Mahmood T (2020) A novel approach towards bipolar soft sets and their applications. J Math 2020:4690808
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
We declare that we do have no commercial or associative interests that represent a conflict of interests in connection with this manuscript. There are no professional or other personal interests that can inappropriately influence our submitted work.
Research involving human participants and/or animals
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, P., Mahmood, T. & Ali, Z. The cross-entropy and improved distance measures for complex q-rung orthopair hesitant fuzzy sets and their applications in multi-criteria decision-making. Complex Intell. Syst. 8, 1167–1186 (2022). https://doi.org/10.1007/s40747-021-00551-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-021-00551-2