Correlation coefficients of credibility interval-valued neutrosophic sets and their group decision-making method in single- and interval-valued hybrid neutrosophic multi-valued environment

Abstract

Although a single-valued neutrosophic multi-valued set (SVNMVS) can reasonably and perfectly express group evaluation information and make up for the flaw of multi-valued/hesitant neutrosophic sets in group decision-making problems, its information expression and group decision-making methods still lack the ability to express and process single- and interval-valued hybrid neutrosophic multi-valued information. To overcome the drawbacks, this study needs to propose single- and interval-valued hybrid neutrosophic multi-valued sets (SIVHNMVSs), correlation coefficients of consistency interval-valued neutrosophic sets (CIVNSs), and their multi-attribute group decision-making (MAGDM) method in the setting of SIVHNMVSs. First, we propose SIVHNMVSs and a transformation method for converting SIVHNMVSs into CIVNSs based on the mean and consistency degree (the complement of standard deviation) of truth, falsity and indeterminacy sequences. Then, we present two correlation coefficients between CIVNSs based on the multiplication of both the correlation coefficient of interval-valued neutrosophic sets and the correlation coefficient of neutrosophic consistency sets and two weighted correlation coefficients of CIVNSs. Next, a MAGDM method is developed based on the proposed two weighted correlation coefficients of CIVNSs for performing MAGDM problems under the environment of SIVHNMVSs. At last, a selection case of landslide treatment schemes demonstrates the application of the proposed MAGDM method under the environment of SIVHNMVSs. By comparative analysis, our new method not only overcomes the drawbacks of the existing method, but also is more extensive and more useful than the existing method when tackling MAGDM problems in the setting of SIVHNMVSs.

Introduction

In recent decades, neutrosophic decision-making theories and methods [1, 2] have aroused general interest in indeterminate and inconsistent situations. Then, simplified neutrosophic sets (SNSs), including single-valued neutrosophic sets (SVNSs) and interval-valued neutrosophic sets (IVNS), and their various multiple attribute (group) decision-making (MADM/MAGDM) methods have been effectively applied in many decision-making problems [3,4,5,6,7,8,9]. Under neutrosophic hesitant situations, various neutrosophic hesitant fuzzy sets (NHFSs), such as single-valued and interval-valued NHFSs, and their MADM/MAGDM methods have been proposed to resolve neutrosophic hesitant decision-making problems [10,11,12,13,14,15]. Further, multi-valued/hesitant neutrosophic sets (MVNSs) and their MADM/MAGDM methods have been also introduced and applied in MADM/MAGDM problems [16,17,18,19,20]. Since there is the loss of some identical neutrosophic values/elements in NHFSs and MVNSs, single-valued neutrosophic multisets were proposed to make up for the shortcomings of NHFSs and MVNSs, and then their MADM/MAGDM methods were developed and applied in MADM/MAGDM problems [21,22,23]. Especially in the current literature [24], single-valued neutrosophic multi-valued sets/elements (SVNMVSs/SVNMVEs) were presented based on the truth, falsity and indeterminacy sequences with the same and/or different fuzzy values, and then a transformation method was introduced to convert SVNMVSs/SVNMVEs into consistency single-valued neutrosophic sets/elements (CSVNSs/CSVNEs) by the average value and consistency degree (the complement of standard deviation) of truth, falsity and indeterminacy sequences. However, CSVNSs can simplify the information expression and difficult operation problems of SVNMVSs with different truth, falsity and indeterminacy sequence lengths, which indicate the outstanding advantages. Then, a MAGDM method [24] was developed by the proposed correlation coefficients of CSVNSs to tackle MAGDM problems with the information of SVNMVSs. Although the proposed techniques [24] can overcome the drawbacks of existing techniques and provide more extensive information representation and decision-making method in performing MAGDM problems with the information of SVNMVSs, the existing techniques still lack the single- and interval-valued hybrid neutrosophic (multi-valued) information expression and operational processing capabilities in real group decision-making problems.

In the neutrosophic multi-valued decision-making problem, because decision-makers have certainty and uncertainty in the judgment/cognition of some evaluated object, they possibly give single-valued/exact fuzzy values and interval-valued fuzzy values (IVFVs) of the truth, falsity and indeterminacy simultaneously in the evaluation process. For example, decision-makers give the single- and interval-valued hybrid neutrosophic evaluation information <(0.8, [0.6, 0.7], [0.5, 0.6]), (0.2, [0.2, 0.3], [0.2, 0.3]), (0.3, 0.1, [0.3, 0.4])> . Thus, the aforementioned NHFSs, MVNSs and SVNMVSs cannot express the single- and interval-valued hybrid neutrosophic multi-valued information, and then various MADM/MAGDM methods presented in existing literature cannot also perform the single- and interval-valued hybrid neutrosophic multi-valued decision-making problem. To our best knowledge, none of the existing studies focused on the expression, correlation coefficient, and decision-making problems of the single- and interval-valued hybrid neutrosophic multi-valued information. Therefore, it is necessary to propose the hybrid neutrosophic multi-valued information expression form, correlation coefficient, and decision-making method to solve the aforementioned challenges. Motivated by the new challenging ideas, the targets of this study are (1) to propose a single- and interval-valued hybrid neutrosophic multi-valued set/element (SIVHNMVS/(SIVHNMVE) and a transformation method that converts SIVHNMVS/SIVHNMVE into a consistency interval-valued neutrosophic set/element (CIVNS/CIVNE) based on the average value and consistency degree (the complement of standard deviation) of the truth, falsity and indeterminacy sequences, (2) to present two correlation coefficients between CIVNSs based on the multiplication of both the correlation coefficient of IVNSs and the correlation coefficient of neutrosophic consistency sets (NCSs) in the setting of SIVHNMVSs and then two weighted correlation coefficients of CIVNSs, and (3) to develop a MAGDM method by the proposed two weighted correlation coefficients of CIVNSs for performing MAGDM problems under the environment of SIVHNMVSs.

To indicate the application of the proposed MAGDM method under the environment of SIVHNMVSs, a selection case of landslide treatment schemes demonstrates the validity of the proposed MAGDM method. By comparative analysis, our new method not only overcomes the drawbacks of the existing method [24], but also is more extensive and more useful than the existing method when tackling MAGDM problems in the setting of SIVHNMVSs.

In this study, the advantages of the proposed new techniques are summarized as follows:

• 1. The proposed SIVHNMVS can overcome the single information expression defect of existing SVNMVS.

• 2. The proposed transformation method that converts SIVHNMVS/SIVHNMVE into CIVNS/CIVNE based on the average value and consistency degree of the truth, falsity and indeterminacy sequences can extend the existing conversion method and solve operational problems between different hybrid information forms.

• 3. The proposed correlation coefficients of CIVNSs based on the multiplication of two correlation coefficients of IVNSs and NCSs can obviously reflect that the correlation coefficients of IVNSs are special cases of the proposed correlation coefficients of CIVNSs when the correlation coefficients of NCSs are equal to one, while the existing correlation coefficients [24] cannot reflect the cases. Hence, the proposed correlation coefficients of CIVNSs are more extensive and more useful than the existing correlation coefficients of CSVNSs [24] under the environment of SIVHNMVSs.

• 4. The developed MAGDM method can solve the MAGDM problems with the SIVHNMVS information, which the existing MAGDM methods cannot do, and make the decision results more reasonable and more effective.

However, the proposed hybrid neutrosophic multi-valued information expression, correlation coefficients of CIVNSs, and MAGDM method in this article show the contributions of these new techniques.

The remainder of this article consists of the parts. The next section introduces basic concepts of SVNMVSs and their drawbacks. In the subsequent section, we propose SIVHNMVS for representing the hybrid information of SVNMVS and an interval-valued neutrosophic multi-valued set (IVNMVS) simultaneously and then introduce a transformation method for converting SIVHNMVS into CIVNS based on the mean and consistency degree of the truth, falsity and indeterminacy sequences in SIVHNMVS. Following this, two correlation coefficients of CIVNSs and two weighted correlation coefficients of CIVNSs in the setting of SIVHNMVSs are put forward. Then a MAGDM method is developed using the proposed two weighted correlation coefficients of CIVNSs in the SIVHNMVS setting. Before the last section, a selection case of landslide treatment schemes and comparison with existing relative method to indicate the validity of the new method are introduced. The final section summarizes conclusions and further research.

Basic concepts of SVNMVSs and drawbacks

A SVNMVS S on a universe set X = {x₁, x₂, …, x_n} is defined as the following form [24]:

$$ S = \left\{ {\left\langle {x_{j} ,{\text{TM}}_{S} (x_{j} ),{\text{IM}}_{S} (x_{j} ),{\text{FM}}_{S} (x_{j} )} \right\rangle |x_{j} \in X} \right\}, $$

where TM_S(x_j), IM_S(x_j) and FM_S(x_j) are the truth, indeterminacy and falsity membership functions in [0, 1], which are depicted by the three decreasing single-valued sequences with the same and/or different fuzzy values $TM_{S} (x_{j} ) = (\mu_{H}^{1} (x_{j} ),\mu_{H}^{2} (x_{j} ),...,\mu_{H}^{{p_{j} }} (x_{j} ))$, $IM_{S} (x_{j} ) = (\rho_{S}^{1} (x_{j} ),\rho_{S}^{2} (x_{j} ),...,\rho_{S}^{{p_{j} }} (x_{j} ))$, and $FM_{S} (x_{j} ) = (\nu_{S}^{1} (x_{j} ),\nu_{S}^{2} (x_{j} ),...,\nu_{S}^{{p_{j} }} (x_{j} ))$, such that $\mu_{S}^{k} (x_{j} ),\rho_{S}^{k} (x_{j} ),\nu_{S}^{k} (x_{j} ) \in [0,1]$ (k = 1, 2, …, p_j; j = 1, 2, …, n) and $0 \le \mu_{{\text{S}}}^{1} (x_{j} ) + \rho_{S}^{1} (x_{j} ) + \nu_{S}^{1} (x_{j} ) \le 3$ for x_j ∈ X and j = 1, 2, …, n. Then, each element $\left\langle {x_{j} ,TM_{S} (x_{j} ),IM_{S} (x_{j} ),FM_{S} (x_{j} )} \right\rangle$ in S can be simply denoted as the SVNMVE $s_{j} = \left\langle {TM_{j} ,IM_{j} ,FM_{j} } \right\rangle = \left\langle {(\mu_{j}^{1} ,\mu_{j}^{2} ,...,\mu_{j}^{{p_{j} }} ),(\rho_{j}^{1} ,\rho_{j}^{2} ,...,\rho_{j}^{{p_{j} }} ),(\nu_{j}^{1} ,\nu_{j}^{2} ,...,\nu_{j}^{{p_{j} }} )} \right\rangle$ (j = 1, 2, …, n).

Set S₁ = {s₁₁, s₁₂, …, s_1n} and S₂ = {s₂₁, s₂₂, …, s_2n} as two SVNMVSs, where $s_{ij} = \left\langle {{\text{TM}}_{ij} ,{\text{IM}}_{ij} ,{\text{FM}}_{ij} } \right\rangle = \left\langle {(\mu_{ij}^{1} ,\mu_{ij}^{2} ,...,\mu_{ij}^{{p_{ij} }} ),(\rho_{ij}^{1} ,\rho_{ij}^{2} ,...,\rho_{ij}^{{p_{ij} }} ),(\nu_{ij}^{1} ,\nu_{ij}^{2} ,...,\nu_{ij}^{{p_{ij} }} )} \right\rangle$ (i = 1, 2; j = 1, 2, …, n) are SVNMVEs. Then, the weight of s_ij is ω_j with ω_j ≥ 0 and $\sum\nolimits_{j = 1}^{n} {\omega_{j} } = 1$. Based on the mean and consistency degree (the complement of standard deviation) of TM_ij, IM_ij and FM_ij, two weighted correlation coefficients between CSVNSs are defined as follows [24]:

$$ M_{W1} (S_{1} ,S_{2} ) = \frac{{\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\mu_{m1j} \mu_{m2j} + \rho_{m1j} \rho_{m2j} + \nu_{m1j} \nu_{m2j} } \right]} + \sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {c_{\mu 1j} c_{\mu 2j} + c_{\rho 1j} c_{\rho 2j} + c_{\nu 1j} c_{\nu 2j} } \right]} }}{{\left( \begin{gathered} \sqrt {\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {\mu_{m1j} } \right)^{2} + \left( {\rho_{m1j} } \right)^{2} + \left( {\nu_{m1j} } \right)^{2} + \left( {c_{\mu 1j} } \right)^{2} + \left( {c_{\rho 1j} } \right)^{2} + \left( {c_{\nu 1j} } \right)^{2} } \right]} } \hfill \\ \times \sqrt {\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {\mu_{m2j} } \right)^{2} + \left( {\rho_{m2j} } \right)^{2} + \left( {\nu_{m2j} } \right)^{2} + \left( {c_{\mu 2j} } \right)^{2} + \left( {c_{\rho 2j} } \right)^{2} + \left( {c_{\nu 2j} } \right)^{2} } \right]} } \hfill \\ \end{gathered} \right)}}, $$

(1)

$$ M_{W2} (S_{1} ,S_{2} ) = \frac{{\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\mu_{m1j} \mu_{m2j} + \rho_{m1j} \rho_{m2j} + \nu_{m1j} \nu_{m2j} } \right]} + \sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {c_{\mu 1j} c_{\mu 2j} + c_{\rho 1j} c_{\rho 2j} + c_{\nu 1j} c_{\nu 2j} } \right]} }}{{\max \left( \begin{gathered} \sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {\mu_{m1j} } \right)^{2} + \left( {\rho_{m1j} } \right)^{2} + \left( {\nu_{m1j} } \right)^{2} + \left( {c_{\mu 1j} } \right)^{2} + \left( {c_{\rho 1j} } \right)^{2} + \left( {c_{\nu 1j} } \right)^{2} } \right]} , \hfill \\ \sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {\mu_{m2j} } \right)^{2} + \left( {\rho_{m2j} } \right)^{2} + \left( {\nu_{m2j} } \right)^{2} + \left( {c_{\mu 2j} } \right)^{2} + \left( {c_{\rho 2j} } \right)^{2} + \left( {c_{\nu 2j} } \right)^{2} } \right]} \hfill \\ \end{gathered} \right)}}, $$

(2)

where μ_mij, ρ_mij, ν_mji, c_μij, c_ρij and c_νij are the average values and consistency degrees of TM_ij, IM_ij and FM_ij, which are yielded by the following Eqs. (3)–(8):

$$ \mu_{mij} = \frac{1}{{p_{ij} }}\sum\limits_{k = 1}^{{p_{ij} }} {\mu_{ij}^{k} } , $$

(3)

$$ \rho_{mij} = \frac{1}{{p_{ij} }}\sum\limits_{k = 1}^{{p_{ij} }} {\rho_{ij}^{k} } , $$

(4)

$$ \nu_{mij} = \frac{1}{{p_{ij} }}\sum\limits_{k = 1}^{{p_{ij} }} {\nu_{ij}^{k} } , $$

(5)

$$ c_{\mu ij} = 1 - \sigma_{\mu ij} = 1 - \sqrt {\frac{1}{{p_{ij} - {1}}}\sum\limits_{k = 1}^{{p_{ij} }} {\left( {\mu_{ij}^{k} - \mu_{mij} } \right)^{2} } } , $$

(6)

$$ c_{\rho ij} = 1 - \sigma_{\rho ij} = 1 - \sqrt {\frac{1}{{p_{ij} - {1}}}\sum\limits_{k = 1}^{{p_{ij} }} {\left( {\rho_{ij}^{k} - \rho_{mij} } \right)^{2} } } , $$

(7)

$$ c_{\nu ij} = 1 - \sigma_{\nu ij} = 1 - \sqrt {\frac{1}{{p_{ij} - {1}}}\sum\limits_{k = 1}^{{p_{ij} }} {\left( {\nu_{ij}^{k} - \nu_{mij} } \right)^{2} } } , $$

(8)

where σ_μij, σ_ρij, σ_νij ∈ [0, 1] are the standard deviations corresponding to TM_ij, IM_ij and FM_ij (i = 1, 2; j = 1, 2, …, n), respectively, and p_ij is the number of fuzzy values in TM_ij, IM_ij and FM_ij.

Then, the weighted correlation coefficients M_W1(S₁, S₂) and M_W2(S₁, S₂) imply the following properties [24]:

(p1) M_W1(S₁, S₂) = M_W2(S₁, S₂) = 1 if S₁ = S₂;

(p2) M_W1(S₁, S₂) = M_W1(S₂, S₁) and M_W2(S₁, S₂) = M_W2(S₂, S₁);

(p3) 0 ≤ M_W1(S₁, S₂), M_W2(S₁, S₂) ≤ 1.

However, the above information expression and correlation coefficients of SVNMVSs cannot perform either IVNMVS or SIVHNMVS information expression and processing capabilities in real decision-making problems, which show main drawbacks of the existing techniques [24].

SIVHNMVSs and CIVNSs

Based on the extension of the SVNMVS and CSVNS concepts [24], this section proposes SIVHNMVSs, then introduces a transformation method for converting SIVHNMVSs into CIVNSs based on the average values and credibility degrees of the truth, falsity and indeterminacy sequences so as to reasonably simplify the information expression and operation of different lengths/information types of the truth, falsity and indeterminacy sequences in the setting of SIVHNMVSs.

Definition 1

Set X = {x₁, x₂, …, x_n} as a universe set. A SIVHNMVS H on X is defined as the following form:

$$ H = \left\{ {\left\langle {x_{j} ,TS_{H} (x_{j} ),IS_{H} (x_{j} ),FS_{H} (x_{j} )} \right\rangle |x_{j} \in X} \right\}, $$

where TS_H(x_j), IS_H(x_j) and FS_H(x_j) are the truth membership function, the indeterminacy membership function and the falsity membership function in [0, 1] respectively, which are described by the three single- and interval-valued fuzzy sequences including decreasing subsequences with the same and/or different p_αj/p_βj/p_γj single-valued/exact fuzzy values and decreasing subsequences with the same and/or different q_αj/q_βj/q_γj interval-valued fuzzy values: ${\text{TS}}_{H} (x_{j} ) = (\alpha_{H}^{1} (x_{j} ),\alpha_{H}^{2} (x_{j} ),...,\alpha_{H}^{{p_{\alpha j} }} (x_{j} ),\alpha_{H}^{{p_{\alpha j} { + 1}}} (x_{j} ),\alpha_{H}^{{p_{\alpha j} { + }2}} (x_{j} ),...,\alpha_{H}^{{p_{\alpha j} { + }q_{\alpha j} }} (x_{j} ))$, ${\text{IS}}_{H} (x_{j} ) = (\beta_{H}^{1} (x_{j} ),\beta_{H}^{2} (x_{j} ),...,\beta_{H}^{{p_{\beta j} }} (x_{j} ),\beta_{H}^{{p_{\beta j} + 1}} (x_{j} ),\beta_{H}^{{p_{\beta j} + 2}} (x_{j} ),...,\beta_{H}^{{p_{\beta j} + q_{\beta j} }} (x_{j} ))$, ${\text{FS}}_{H} (x_{j} ) = (\gamma_{H}^{1} (x_{j} ),\gamma_{H}^{2} (x_{j} ),...,\gamma_{H}^{{p_{\gamma j} }} (x_{j} ),\gamma_{H}^{{p_{\gamma j} + 1}} (x_{j} ),\gamma_{H}^{{p_{\gamma j} + 2}} (x_{j} ),...,\gamma_{H}^{{p_{\gamma j} + q_{\gamma j} }} (x_{j} ))$, such that $\alpha_{H}^{k} (x_{j} ),\beta_{H}^{k} (x_{j} ),\gamma_{H}^{k} (x_{j} ) \in [0,1]$ (k = 1, 2, …, p_αj/p_βj/p_γj; j = 1, 2, …, n) and $\alpha_{H}^{k} (x_{j} ),\beta_{H}^{k} (x_{j} ),\gamma_{H}^{k} (x_{j} ) \subseteq [0,1]$ (k = p_αj + 1/p_βj + 1/p_γj + 1, p_αj + 2/p_βj + 2/p_γj + 2, …, p_αj + q_αj/p_βj + q_βj/p_γj + q_γj; j = 1, 2, …, n) for x_j ∈ X.

Then, the basic element $\left\langle {x_{j} ,{\text{TS}}_{H} (x_{j} ),{\text{IS}}_{H} (x_{j} ),{\text{FS}}_{H} (x_{j} )} \right\rangle$ (j = 1, 2, …, n) in H is denoted as the following simple form:

$$ h_{j} = \left\langle {{\text{TS}}_{j} ,{\text{IS}}_{j} ,{\text{FS}}_{j} } \right\rangle = \left\langle \begin{gathered} (\alpha_{j}^{1} ,\alpha_{j}^{2} ,...,\alpha_{j}^{{p_{\alpha j} }} ,\alpha_{j}^{{p_{\alpha j} + 1}} ,\alpha_{j}^{{p_{\alpha j} + 2}} ,...,\alpha_{j}^{{p_{\alpha j} + q_{\alpha j} }} ), \hfill \\ (\beta_{j}^{1} ,\beta_{j}^{2} ,...,\beta_{j}^{{p_{\beta j} }} ,\beta_{j}^{{p_{\beta j} + 1}} ,\beta_{j}^{{p_{\beta j} + 2}} ,...,\beta_{j}^{{p_{\beta j} + q_{\beta j} }} ), \hfill \\ (\gamma_{j}^{1} ,\gamma_{j}^{2} ,...,\gamma_{j}^{{p_{\gamma j} }} ,\gamma_{j}^{{p_{\gamma j} + 1}} ,\gamma_{j}^{{p_{\gamma j} + 2}} ,...,\gamma_{j}^{{p_{\gamma j} + q_{\gamma j} }} ) \hfill \\ \end{gathered} \right\rangle , $$

which is called SIVHNMVE.

Especially when p_αj = p_βj = p_γj = 0 or q_αj = q_βj = q_γj = 0 (j = 1, 2, …, n), SIVHNMVS is reduced to IVNMVS or SVNMVS. It is clear that SIVHNMVS contains SVNS, IVNS, SVNMVS, and IVNMVS as its special cases.

Based on the average values and consistency degrees of TS_j, IS_j and FS_j (j = 1, 2, …, s) in each SIVHNMVE h_j, the SIVHNMVS H can be converted into CIVNS, which is defined below.

Definition 2

Assume there is the SIVHNMVS H = {h₁, h₂, …, h_n}, where $h_{j} = \left\langle {TS_{j} ,IS_{j} ,FS_{j} } \right\rangle = \left\langle \begin{gathered} (\alpha_{j}^{1} ,\alpha_{j}^{2} ,...,\alpha_{j}^{{p_{j} }} ,\alpha_{j}^{{p_{j} + 1}} ,\alpha_{j}^{{p_{j} + 2}} ,...,\alpha_{j}^{{p_{j} + q_{j} }} ), \hfill \\ (\beta_{j}^{1} ,\beta_{j}^{2} ,...,\beta_{j}^{{p_{j} }} ,\beta_{j}^{{p_{j} + 1}} ,\beta_{j}^{{p_{j} + 2}} ,...,\beta_{j}^{{p_{j} + q_{j} }} ), \hfill \\ (\gamma_{j}^{1} ,\gamma_{j}^{2} ,...,\gamma_{j}^{{p_{j} }} ,\gamma_{j}^{{p_{j} + 1}} ,\gamma_{j}^{{p_{j} + 2}} ,...,\gamma_{j}^{{p_{j} + q_{j} }} ) \hfill \\ \end{gathered} \right\rangle$ (j = 1, 2, …, n) is the jth SIVHNMVE. Based on the average values and consistency degrees of TS_j, IS_j and FS_j (j = 1, 2, …, n), the SIVHNMVS H can be converted into the CIVNS R = {r₁, r₂, …, r_n} including the n SIVHNMVEs $r_{j} = \left\langle ([\alpha_{mj}^{ - } ,\alpha_{mj}^{ + } ],[c_{\alpha j}^{ - } ,c_{\alpha j}^{ + } ]),([\beta_{mj}^{ - } ,\beta_{mj}^{ + } ],[c_{\beta j}^{ - } ,c_{\beta j}^{ + } ]),\right.\break\left. ([\gamma_{mj}^{ - } ,\gamma_{mj}^{ + } ],[c_{\gamma j}^{ - } ,c_{\gamma j}^{ + } ]) \right\rangle$ (j = 1, 2, …, n), where $[\alpha_{mj}^{ - } ,\alpha_{mj}^{ + } ] \subseteq [0,1]$, $[\beta_{mj}^{ - } ,\beta_{mj}^{ + } ] \subseteq [0,1]$, and $[\gamma_{mj}^{ - } ,\gamma_{mj}^{ + } ] \subseteq [0,1]$ are the interval-valued fuzzy average values of TS_j, IS_j and FS_j and then $[c_{\alpha j}^{ - } ,c_{\alpha j}^{ + } ] \subseteq [0,1]$, $[c_{\beta j}^{ - } ,c_{\beta j}^{ + } ] \subseteq [0,1]$, and $[c_{\gamma j}^{ - } ,c_{\gamma j}^{ + } ] \subseteq [0,1]$ are the interval-valued consistency degrees of TS_j, IS_j and FS_j. Then, these interval-valued fuzzy average values and consistency degrees are given by the following equations:

$$ \left[ {\alpha_{mj}^{ - } ,\alpha_{mj}^{ - } } \right] = \left[ {\frac{1}{{p_{\alpha j} + q_{\alpha j} }}\left( {\sum\limits_{k = 1}^{{p_{\alpha j} }} {\alpha_{j}^{k} } + \sum\limits_{{k = p_{\alpha j} + 1}}^{{p_{\alpha j} + q_{\alpha j} }} {\inf \alpha_{j}^{k} } } \right),\frac{1}{{p_{\alpha j} + q_{\alpha j} }}\left( {\sum\limits_{k = 1}^{{p_{\alpha j} }} {\alpha_{j}^{k} } + \sum\limits_{{k = p_{\alpha j} + 1}}^{{p_{\alpha j} + q_{\alpha j} }} {\sup \alpha_{j}^{k} } } \right)} \right], $$

(9)

$$ \left[ {\beta_{mj}^{ - } ,\beta_{mj}^{ + } } \right] = \left[ {\frac{1}{{p_{\beta j} + q_{\beta j} }}\left( {\sum\limits_{k = 1}^{{p_{\beta j} }} {\beta_{j}^{k} } + \sum\limits_{{k = p_{\beta j} + 1}}^{{p_{\beta j} + q_{\beta j} }} {\inf \beta_{j}^{k} } } \right),\frac{1}{{p_{\beta j} + q_{\beta j} }}\left( {\sum\limits_{k = 1}^{{p_{\beta j} }} {\beta_{j}^{k} } + \sum\limits_{{k = p_{\beta j} + 1}}^{{p_{\beta j} + q_{\beta j} }} {\sup \beta_{j}^{k} } } \right)} \right], $$

(10)

$$ \left[ {\gamma_{mj}^{ - } ,\gamma_{mj}^{ + } } \right] = \left[ {\frac{1}{{p_{\gamma j} + q_{\gamma j} }}\left( {\sum\limits_{k = 1}^{{p_{\gamma j} }} {\gamma_{j}^{k} } + \sum\limits_{{k = p_{\gamma j} + 1}}^{{p_{\gamma j} + q_{\gamma j} }} {\inf \gamma_{j}^{k} } } \right),\frac{1}{{p_{\gamma j} + q_{\gamma j} }}\left( {\sum\limits_{k = 1}^{{p_{\gamma j} }} {\gamma_{j}^{k} } + \sum\limits_{{k = p_{\gamma j} + 1}}^{{p_{\gamma j} + q_{\gamma j} }} {\sup \gamma_{j}^{k} } } \right)} \right], $$

(11)

$$ \left[ {c_{\alpha j}^{ - } ,c_{\alpha j}^{ + } } \right] = \left[ {1 - \sigma_{\alpha j}^{ + } ,1 - \sigma_{\alpha j}^{ - } } \right] = \left[ \begin{gathered} 1 - \max \left( \begin{gathered} \sqrt {\frac{1}{{p_{\alpha j} + q_{\alpha j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\alpha j} }} {\left( {\alpha_{j}^{k} - \alpha_{mj}^{ - } } \right)^{2} } + \sum\limits_{{k = p_{\alpha j} + 1}}^{{p_{\alpha j} + q_{\alpha j} }} {\left( {\inf \alpha_{j}^{k} - \alpha_{mj}^{ - } } \right)^{2} } } \right)} , \hfill \\ \sqrt {\frac{1}{{p_{\alpha j} + q_{\alpha j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\alpha j} }} {\left( {\alpha_{j}^{k} - \alpha_{mj}^{ + } } \right)^{2} } + \sum\limits_{{k = p_{\alpha j} + 1}}^{{p_{\alpha j} + q_{\alpha j} }} {\left( {\sup \alpha_{j}^{k} - \alpha_{mj}^{ + } } \right)^{2} } } \right)} \hfill \\ \end{gathered} \right), \hfill \\ 1 - \min \left( \begin{gathered} \sqrt {\frac{1}{{p_{\alpha j} + q_{\alpha j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\alpha j} }} {\left( {\alpha_{j}^{k} - \alpha_{mj}^{ - } } \right)^{2} } + \sum\limits_{{k = p_{\alpha j} + 1}}^{{p_{\alpha j} + q_{\alpha j} }} {\left( {\inf \alpha_{j}^{k} - \alpha_{mj}^{ - } } \right)^{2} } } \right)} , \hfill \\ \sqrt {\frac{1}{{p_{\alpha j} + q_{\alpha j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\alpha j} }} {\left( {\alpha_{j}^{k} - \alpha_{mj}^{ + } } \right)^{2} } + \sum\limits_{{k = p_{\alpha j} + 1}}^{{p_{\alpha j} + q_{\alpha j} }} {\left( {\sup \alpha_{j}^{k} - \alpha_{mj}^{ + } } \right)^{2} } } \right)} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right], $$

(12)

$$ \left[ {c_{\beta j}^{ - } ,c_{\beta j}^{ + } } \right] = \left[ {1 - \sigma_{\beta j}^{ + } ,1 - \sigma_{\beta j}^{ - } } \right] = \left[ \begin{gathered} 1 - \max \left( \begin{gathered} \sqrt {\frac{1}{{p_{\beta j} + q_{\beta j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\beta j} }} {\left( {\beta_{j}^{k} - \beta_{mj}^{ - } } \right)^{2} } + \sum\limits_{{k = p_{\beta j} + 1}}^{{p_{\beta j} + q_{\beta j} }} {\left( {\inf \beta_{j}^{k} - \beta_{mj}^{ - } } \right)^{2} } } \right)} , \hfill \\ \sqrt {\frac{1}{{p_{\beta j} + q_{\beta j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\beta j} }} {\left( {\beta_{j}^{k} - \beta_{mj}^{ + } } \right)^{2} } + \sum\limits_{{k = p_{\beta j} + 1}}^{{p_{\beta j} + q_{\beta j} }} {\left( {\sup \beta_{j}^{k} - \beta_{mj}^{ + } } \right)^{2} } } \right)} \hfill \\ \end{gathered} \right), \hfill \\ 1 - \min \left( \begin{gathered} \sqrt {\frac{1}{{p_{\beta j} + q_{\beta j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\beta j} }} {\left( {\beta_{j}^{k} - \beta_{mj}^{ - } } \right)^{2} } + \sum\limits_{{k = p_{\beta j} + 1}}^{{p_{\beta j} + q_{\beta j} }} {\left( {\inf \beta_{j}^{k} - \beta_{mj}^{ - } } \right)^{2} } } \right)} , \hfill \\ \sqrt {\frac{1}{{p_{\beta j} + q_{\beta j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\beta j} }} {\left( {\beta_{j}^{k} - \beta_{mj}^{ + } } \right)^{2} } + \sum\limits_{{k = p_{\beta j} + 1}}^{{p_{\beta j} + q_{\beta j} }} {\left( {\sup \beta_{j}^{k} - \beta_{mj}^{ + } } \right)^{2} } } \right)} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right], $$

(13)

$$ \left[ {c_{\gamma j}^{ - } ,c_{\gamma j}^{ + } } \right] = \left[ {1 - \sigma_{\gamma j}^{ + } ,1 - \sigma_{\gamma j}^{ - } } \right] = \left[ \begin{gathered} 1 - \max \left( \begin{gathered} 1 - \sqrt {\frac{1}{{p_{\gamma j} + q_{\gamma j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\gamma j} }} {\left( {\gamma_{j}^{k} - \gamma_{mj}^{ - } } \right)^{2} } + \sum\limits_{{k = p_{\gamma j} + 1}}^{{p_{\gamma j} + q_{\gamma j} }} {\left( {\inf \gamma_{j}^{k} - \gamma_{mj}^{ - } } \right)^{2} } } \right)} , \hfill \\ 1 - \sqrt {\frac{1}{{p_{\gamma j} + q_{\gamma j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\gamma j} }} {\left( {\gamma_{j}^{k} - \gamma_{mj}^{ + } } \right)^{2} } + \sum\limits_{{k = p_{\gamma j} + 1}}^{{p_{\gamma j} + q_{\gamma j} }} {\left( {\sup \gamma_{j}^{k} - \gamma_{mj}^{ + } } \right)^{2} } } \right)} \hfill \\ \end{gathered} \right), \hfill \\ 1 - \min \left( \begin{gathered} 1 - \sqrt {\frac{1}{{p_{\gamma j} + q_{\gamma j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\gamma j} }} {\left( {\gamma_{j}^{k} - \gamma_{mj}^{ - } } \right)^{2} } + \sum\limits_{{k = p_{\gamma j} + 1}}^{{p_{\gamma j} + q_{\gamma j} }} {\left( {\inf \gamma_{j}^{k} - \gamma_{mj}^{ - } } \right)^{2} } } \right)} , \hfill \\ 1 - \sqrt {\frac{1}{{p_{\gamma j} + q_{\gamma j} - 1}}\left( {\sum\limits_{k = 1}^{{p_{\gamma j} }} {\left( {\gamma_{j}^{k} - \gamma_{mj}^{ + } } \right)^{2} } + \sum\limits_{{k = p_{\gamma j} + 1}}^{{p_{\gamma j} + q_{\gamma j} }} {\left( {\sup \gamma_{j}^{k} - \gamma_{mj}^{ + } } \right)^{2} } } \right)} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right], $$

(14)

where p_αj/p_βj/p_γj is the number of single-valued fuzzy values and q_αj/q_βj/q_γj is the number of IVFVs in TS_j, IS_j and FS_j and then $\left[ {c_{\alpha j}^{ - } ,c_{\alpha j}^{ + } } \right] = \left[ {1 - \sigma_{\alpha j}^{ + } ,1 - \sigma_{\alpha j}^{ - } } \right] \subseteq [0,1]$, $\left[ {c_{\beta j}^{ - } ,c_{\beta j}^{ + } } \right] = \left[ {1 - \sigma_{\beta j}^{ + } ,1 - \sigma_{\beta j}^{ - } } \right] \subseteq [0,1]$ and $\left[ {c_{\gamma j}^{ - } ,c_{\gamma j}^{ + } } \right] = \left[ {1 - \sigma_{\gamma j}^{ + } ,1 - \sigma_{\gamma j}^{ - } } \right]$ are the interval-valued consistency degrees (the complements of the standard deviations $\left[ {\sigma_{\alpha j}^{ - } ,\sigma_{\alpha j}^{ + } } \right] \subseteq [0,1]$, $\left[ {\sigma_{\beta j}^{ - } ,\sigma_{\beta j}^{ + } } \right] \subseteq [0,1]$ and $\left[ {\sigma_{\gamma j}^{ - } ,\sigma_{\gamma j}^{ + } } \right] \subseteq [0,1]$) of TS_j, IS_j and FS_j.

Remarks

• 1. The consistency degree indicates a measure of how close the fuzzy values in TS_j, IS_j and FS_j are to their average values. The closer the fuzzy values are to the average value, the better the consistency and consensus of group fuzzy judgments.

• 2. The fuzzy values in TS_j, IS_j and FS_j are identical when $\left[ {c_{\alpha j}^{ - } ,c_{\alpha j}^{ + } } \right] = \left[ {c_{\beta j}^{ - } ,c_{\beta j}^{ + } } \right]{ = }\left[ {c_{\gamma j}^{ - } ,c_{\gamma j}^{ + } } \right]{ = [1,1]}$, which can indicate the complete consensus of group fuzzy judgments.

• 3. From the viewpoint of standard deviation, the closer the fuzzy values are to the average value, the smaller the dispersion degree of the fuzzy values relative to the average value and the higher the consistency and consensus of group fuzzy judgments.

Example 1.

Set SIVHNMVS as H = {< (0.8, 0.6, [0.6, 0.7], [0.5, 0.6]), (0.3, 0.2, [0.2, 0.3], [0.1, 0.2]), (0.4, 0.2, [0.3, 0.4], [0.3, 0.4]) > , < (0.7, 0.5, 0.4, [0.4, 0.6]), (0.2, 0.2, 0.2, [0.3, 0.5]), (0.4, 0.2, 0.1, [0.2, 0.4]) >} in X = {x₁, x₂}. Thus, using Eqs. (9)–(14) the SIVHNMVS H can be converted into the CIVNS R = {< ([0.625, 0.675], [0.8742, 0.9043]), ([0.25, 0.8], [0.9184, 0.9423]), ([0.25, 0.8], [0.9184, 0.9423]) > , < ([0.3, 0.65], [0.9, 0.9184]), ([0.225, 0.275], [0.85, 0.95]), ([0.2250, 0.275], [0.85, 0.8742]) >}.

In this example, it is clear that existing various fuzzy concepts cannot express and process SIVHNMVS information, while the proposed expression and transformation techniques of SIVHNMVS demonstrate their advantages.

Correlation coefficients between CIVNSs

Under the environment of SIVHNMVSs, two correlation coefficients between CIVNSs are defined below.

Definition 3

Set $r_{1j} = \left\langle ([\alpha_{m1j}^{ - } ,\alpha_{m1j}^{ + } ],[c_{\alpha 1j}^{ - } ,c_{\alpha 1j}^{ + } ]),\right.\break\left. ([\beta_{m1j}^{ - } ,\beta_{m1j}^{ + } ],[c_{\beta 1j}^{ - } ,c_{\beta 1j}^{ + } ]),([\gamma_{m1j}^{ - } ,\gamma_{m1j}^{ + } ],[c_{\gamma 1j}^{ - } ,c_{\gamma 1j}^{ + } ]) \right\rangle$ and $r_{2j} = \left\langle ([\alpha_{m2j}^{ - } ,\alpha_{m2j}^{ + } ],[c_{\alpha 2j}^{ - } ,c_{\alpha 2j}^{ + } ]),([\beta_{m2j}^{ - } ,\beta_{m2j}^{ + } ],\right.\break\left. [c_{\beta 2j}^{ - } ,c_{\beta 2j}^{ + } ]),([\gamma_{m2j}^{ - } ,\gamma_{m2j}^{ + } ],[c_{\gamma 2j}^{ - } ,c_{\gamma 2j}^{ + } ]) \right\rangle$(j = 1, 2, …, n) as two groups of CIVNEs in two CIVNSs R₁ = {r₁₁, r₁₂, …, r_1n} and R₂ = {r₂₁, r₂₂, …, r_2n} regarding the SIVHNMVSs H₁ and H₂. Thus, two correlation coefficients between CIVNSs are defined as follows:

$$ \begin{gathered} N_{1} (H_{1} ,H_{2} ) = N_{1} (R_{1} ,R_{2} ) \hfill \\ \quad = \frac{{\sum\nolimits_{j = 1}^{n} {\left[ {\alpha_{m1j}^{ - } \alpha_{m2j}^{ - } + \beta_{m1j}^{ - } \beta_{m2j}^{ - } + \gamma_{m1j}^{ - } \gamma_{m2j}^{ - } + \alpha_{m1j}^{ + } \alpha_{m2j}^{ + } + \beta_{m1j}^{ + } \beta_{m2j}^{ + } + \gamma_{m1j}^{ + } \gamma_{m2j}^{ + } } \right]} }}{{\left( \begin{gathered} \sqrt {\sum\nolimits_{j = 1}^{n} {\left[ {\left( {\alpha_{m1j}^{ - } } \right)^{2} + \left( {\beta_{m1j}^{ - } } \right)^{2} + \left( {\gamma_{m1j}^{ - } } \right)^{2} + \left( {\alpha_{m1j}^{ + } } \right)^{2} + \left( {\beta_{m1j}^{ + } } \right)^{2} + \left( {\gamma_{m1j}^{ + } } \right)^{2} } \right]} } \hfill \\ \times \sqrt {\sum\nolimits_{j = 1}^{n} {\left[ {\left( {\alpha_{m2j}^{ - } } \right)^{2} + \left( {\beta_{m2j}^{ - } } \right)^{2} + \left( {\gamma_{m2j}^{ - } } \right)^{2} + \left( {\alpha_{m2j}^{ + } } \right)^{2} + \left( {\beta_{m2j}^{ + } } \right)^{2} + \left( {\gamma_{m2j}^{ + } } \right)^{2} } \right]} } \hfill \\ \end{gathered} \right)}} \hfill \\ \quad \times \frac{{\sum\nolimits_{j = 1}^{n} {\left[ {c_{\alpha 1j}^{ - } c_{\alpha 2j}^{ - } + c_{\beta 1j}^{ - } c_{\beta 2j}^{ - } + c_{\gamma 1j}^{ - } c_{\gamma 2j}^{ - } + c_{\alpha 1j}^{ + } c_{\alpha 2j}^{ + } + c_{\beta 1j}^{ + } c_{\beta 2j}^{ + } + c_{\gamma 1j}^{ + } c_{\gamma 2j}^{ + } } \right]} }}{{\left( \begin{gathered} \sqrt {\sum\nolimits_{j = 1}^{n} {\left[ {\left( {c_{\alpha 1j}^{ - } } \right)^{2} + \left( {c_{\beta 1j}^{ - } } \right)^{2} + \left( {c_{\gamma 1j}^{ - } } \right)^{2} + \left( {c_{\alpha 1j}^{ + } } \right)^{2} + \left( {c_{\beta 1j}^{ + } } \right)^{2} + \left( {c_{\gamma 1j}^{ + } } \right)^{2} } \right]} } \hfill \\ \times \sqrt {\sum\nolimits_{j = 1}^{n} {\left[ {\left( {c_{\alpha 2j}^{ - } } \right)^{2} + \left( {c_{\beta 2j}^{ - } } \right)^{2} + \left( {c_{\gamma 2j}^{ - } } \right)^{2} + \left( {c_{\alpha 2j}^{ + } } \right)^{2} + \left( {c_{\beta 2j}^{ + } } \right)^{2} + \left( {c_{\gamma 2j}^{ + } } \right)^{2} } \right]} } \hfill \\ \end{gathered} \right)}}, \hfill \\ \end{gathered} $$

(15)

$$ \begin{gathered} N_{2} (H_{1} ,H_{2} ) = N_{2} (R_{1} ,R_{2} ) \hfill \\ = \frac{{\sum\nolimits_{j = 1}^{n} {\left[ {\alpha_{m1j}^{ - } \alpha_{m2j}^{ - } + \beta_{m1j}^{ - } \beta_{m2j}^{ - } + \gamma_{m1j}^{ - } \gamma_{m2j}^{ - } + \alpha_{m1j}^{ + } \alpha_{m2j}^{ + } + \beta_{m1j}^{ + } \beta_{m2j}^{ + } + \gamma_{m1j}^{ + } \gamma_{m2j}^{ + } } \right]} }}{{\frac{1}{2}\sum\nolimits_{j = 1}^{n} {\left[ {\alpha_{m1j}^{ - } + \alpha_{m2j}^{ - } + \beta_{m1j}^{ - } + \beta_{m2j}^{ - } + \gamma_{m1j}^{ - } + \gamma_{m2j}^{ - } + \alpha_{m1j}^{ + } + \alpha_{m2j}^{ + } + \beta_{m1j}^{ + } + \beta_{m2j}^{ + } + \gamma_{m1j}^{ + } + \gamma_{m2j}^{ + } } \right]} }} \hfill \\ \times \frac{{\sum\nolimits_{j = 1}^{n} {\left[ {c_{\alpha 1j}^{ - } c_{\alpha 2j}^{ - } + c_{\beta 1j}^{ - } c_{\beta 2j}^{ - } + c_{\gamma 1j}^{ - } c_{\gamma 2j}^{ - } + c_{\alpha 1j}^{ + } c_{\alpha 2j}^{ + } + c_{\beta 1j}^{ + } c_{\beta 2j}^{ + } + c_{\gamma 1j}^{ + } c_{\gamma 2j}^{ + } } \right]} }}{{\frac{1}{2}\sum\nolimits_{j = 1}^{n} {\left[ {c_{\alpha 1j}^{ - } + c_{\alpha 2j}^{ - } + c_{\beta 1j}^{ - } + c_{\beta 2j}^{ - } + c_{\gamma 1j}^{ - } + c_{\gamma 2j}^{ - } + c_{\alpha 1j}^{ + } + c_{\alpha 2j}^{ + } + c_{\beta 1j}^{ + } + c_{\beta 2j}^{ + } + c_{\gamma 1j}^{ + } + c_{\gamma 2j}^{ + } } \right]} }}, \hfill \\ \end{gathered} $$

(16)

where $[\alpha_{m1j}^{ - } ,\alpha_{m1j}^{ + } ],[\alpha_{m2j}^{ - } ,\alpha_{m2j}^{ + } ],[\beta_{m1j}^{ - } ,\beta_{m1j}^{ + } ],[\beta_{m2j}^{ - } ,\beta_{m2j}^{ + } ],[\gamma_{m1j}^{ - } ,\gamma_{m1j}^{ + } ],[\gamma_{m2j}^{ - } ,\gamma_{m2j}^{ + } ]$ and $[c_{\alpha 1j}^{ - } ,c_{\alpha 1j}^{ + } ],[c_{\alpha 2j}^{ - } ,c_{\alpha 2j}^{ + } ],[c_{\beta 1j}^{ - } ,c_{\beta 1j}^{ + } ],[c_{\beta 2j}^{ - } ,c_{\beta 2j}^{ + } ],[c_{\gamma 1j}^{ - } ,c_{\gamma 1j}^{ + } ],[c_{\gamma 2j}^{ - } ,c_{\gamma 2j}^{ + } ]$ are the interval-valued fuzzy average values and consistency degrees of TS_ij, IS_ij and FS_ij (i = 1, 2; j = 1, 2, …, n), which are obtained by Eqs. (9)–(14).

Clearly, Eqs. (15) and (16) can be viewed as the multiplication of both the correlation coefficient between IVNSs and the correlation coefficient between NCSs regarding CIVNSs. Especially when the correlation coefficients of NCSs in Eqs. (15) and (16) are equal to one, Eq. (15) is reduced to a traditional correlation coefficient of IVNSs [25] and Eq. (16) is reduced to another correlation coefficient of IVNSs.

Then, the two correlation coefficients contain the following proposition:

Proposition 1.

The correlation coefficients N₁(H₁, H₂) and N₂(H₁, H₂) contain the following properties:

(p1) N₁(H₁, H₂) and N₂(H₁, H₂) = 1 if H₁ = H₂;

(p2) N₁(H₁, H₂) = N₁(H₂, H₁) and N₂(H₁, H₂) = N₂(H₂, H₁);

(p3) 0 ≤ N₁(H₁, H₂), N₂(H₁, H₂) ≤ 1.

Proof:

According to Eqs. (15) and (16), the two properties (p1) and (p2) are straightforward. Then, the property (p3) can be verified below.

There is the inequality $\sqrt {\sum\nolimits_{j = 1}^{n} {a_{j}^{2} } } \sqrt {\sum\nolimits_{j = 1}^{n} {b_{j}^{2} } } \ge \sum\nolimits_{j = 1}^{n} {a_{j} b_{j}^{{}} }$ based on the Cauchy–Schwarz inequality $\sum\nolimits_{j = 1}^{n} {a_{j}^{2} } \sum\nolimits_{j = 1}^{n} {b_{j}^{2} } \ge \left( {\sum\nolimits_{j = 1}^{n} {a_{j} b_{j}^{{}} } } \right)^{2}$. Thus, there also exist the following inequalities:

$$ \begin{gathered} \sum\limits_{j = 1}^{n} {\left[ {\alpha_{m1j}^{ - } \alpha_{m2j}^{ - } + \beta_{m1j}^{ - } \beta_{m2j}^{ - } + \gamma_{m1j}^{ - } \gamma_{m2j}^{ - } + \alpha_{m1j}^{ + } \alpha_{m2j}^{ + } + \beta_{m1j}^{ + } \beta_{m2j}^{ + } + \gamma_{m1j}^{ + } \gamma_{m2j}^{ + } } \right]} \hfill \\ \le \left( \begin{gathered} \sqrt {\sum\limits_{j = 1}^{n} {\left[ {\left( {\alpha_{m1j}^{ - } } \right)^{2} + \left( {\beta_{m1j}^{ - } } \right)^{2} + \left( {\gamma_{m1j}^{ - } } \right)^{2} + \left( {\alpha_{m1j}^{ + } } \right)^{2} + \left( {\beta_{m1j}^{ + } } \right)^{2} + \left( {\gamma_{m1j}^{ + } } \right)^{2} } \right]} } \hfill \\ \times \sqrt {\sum\limits_{j = 1}^{n} {\left[ {\left( {\alpha_{m2j}^{ - } } \right)^{2} + \left( {\beta_{m2j}^{ - } } \right)^{2} + \left( {\gamma_{m2j}^{ - } } \right)^{2} + \left( {\alpha_{m2j}^{ + } } \right)^{2} + \left( {\beta_{m2j}^{ + } } \right)^{2} + \left( {\gamma_{m2j}^{ + } } \right)^{2} } \right]} } \hfill \\ \end{gathered} \right), \hfill \\ \end{gathered} $$

$$ \begin{gathered} \sum\limits_{j = 1}^{n} {\left[ {c_{\alpha 1j}^{ - } c_{\alpha 2j}^{ - } + c_{\beta 1j}^{ - } c_{\beta 2j}^{ - } + c_{\gamma 1j}^{ - } c_{\gamma 2j}^{ - } + c_{\alpha 1j}^{ + } c_{\alpha 2j}^{ + } + c_{\beta 1j}^{ + } c_{\beta 2j}^{ + } + c_{\gamma 1j}^{ + } c_{\gamma 2j}^{ + } } \right]} \hfill \\ \le \left( \begin{gathered} \sqrt {\sum\limits_{j = 1}^{n} {\left[ {\left( {c_{\alpha 1j}^{ - } } \right)^{2} + \left( {c_{\beta 1j}^{ - } } \right)^{2} + \left( {c_{\gamma 1j}^{ - } } \right)^{2} + \left( {c_{\alpha 1j}^{ + } } \right)^{2} + \left( {c_{\beta 1j}^{ + } } \right)^{2} + \left( {c_{\gamma 1j}^{ + } } \right)^{2} } \right]} } \hfill \\ \times \sqrt {\sum\limits_{j = 1}^{n} {\left[ {\left( {c_{\alpha 2j}^{ - } } \right)^{2} + \left( {c_{\beta 2j}^{ - } } \right)^{2} + \left( {c_{\gamma 2j}^{ - } } \right)^{2} + \left( {c_{\alpha 2j}^{ + } } \right)^{2} + \left( {c_{\beta 2j}^{ + } } \right)^{2} + \left( {c_{\gamma 2j}^{ + } } \right)^{2} } \right]} } \hfill \\ \end{gathered} \right). \hfill \\ \end{gathered} $$

Regarding the above inequalities, there is 0 ≤ N₁(H₁, H₂) ≤ 1.

Based on $a \times b \le (a + b)/2$ for a, b ∈ [0, 1], there are also the inequalities:

$$ \begin{gathered} \sum\limits_{j = 1}^{n} {\left[ {\alpha_{m1j}^{ - } \alpha_{m2j}^{ - } + \beta_{m1j}^{ - } \beta_{m2j}^{ - } + \gamma_{m1j}^{ - } \gamma_{m2j}^{ - } + \alpha_{m1j}^{ + } \alpha_{m2j}^{ + } + \beta_{m1j}^{ + } \beta_{m2j}^{ + } + \gamma_{m1j}^{ + } \gamma_{m2j}^{ + } } \right]} \hfill \\ \le \frac{1}{2}\sum\limits_{j = 1}^{n} \left[ \alpha_{m1j}^{ - } + \alpha_{m2j}^{ - } + \beta_{m1j}^{ - } + \beta_{m2j}^{ - } + \gamma_{m1j}^{ - } + \gamma_{m2j}^{ - } + \alpha_{m1j}^{ + } + \alpha_{m2j}^{ + } + \beta_{m1j}^{ + } \right.\\ \left.+\,\beta_{m2j}^{ + } + \gamma_{m1j}^{ + } + \gamma_{m2j}^{ + } \right] \hfill \\ \end{gathered}$$

$$\begin{gathered} \sum\limits_{j = 1}^{n} {\left[ {c_{\alpha 1j}^{ - } c_{\alpha 2j}^{ - } + c_{\beta 1j}^{ - } c_{\beta 2j}^{ - } + c_{\gamma 1j}^{ - } c_{\gamma 2j}^{ - } + c_{\alpha 1j}^{ + } c_{\alpha 2j}^{ + } + c_{\beta 1j}^{ + } c_{\beta 2j}^{ + } + c_{\gamma 1j}^{ + } c_{\gamma 2j}^{ + } } \right]} \hfill \\ \le \frac{1}{2}\sum\limits_{j = 1}^{n} \left[ c_{\alpha 1j}^{ - } + c_{\alpha 2j}^{ - } + c_{\beta 1j}^{ - } + c_{\beta 2j}^{ - } + c_{\gamma 1j}^{ - } + c_{\gamma 2j}^{ - } + c_{\alpha 1j}^{ + } + c_{\alpha 2j}^{ + } + c_{\beta 1j}^{ + }\right.\\ \left.+\, c_{\beta 2j}^{ + } + c_{\gamma 1j}^{ + } + c_{\gamma 2j}^{ + } \right] \hfill \\ \end{gathered}$$

Based on the above inequalities, there is 0 ≤ N₂(H₁, H₂) ≤ 1.

In actual problems, the importance of the SIVHNMVEs h_1j and h_2j (j = 1, 2, …, n) is reflected by the weight ω_j ≥ 0 for $\sum\nolimits_{j = 1}^{n} {\omega_{j} } = 1$. Thus, we can give the weighted correlation coefficients:

$$ \begin{gathered} N_{W1} (H_{1} ,H_{2} ) = N_{W1} (R_{1} ,R_{2} ) \hfill \\ = \frac{{\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\alpha_{m1j}^{ - } \alpha_{m2j}^{ - } + \beta_{m1j}^{ - } \beta_{m2j}^{ - } + \gamma_{m1j}^{ - } \gamma_{m2j}^{ - } + \alpha_{m1j}^{ + } \alpha_{m2j}^{ + } + \beta_{m1j}^{ + } \beta_{m2j}^{ + } + \gamma_{m1j}^{ + } \gamma_{m2j}^{ + } } \right]} }}{{\left( \begin{gathered} \sqrt {\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {\alpha_{m1j}^{ - } } \right)^{2} + \left( {\beta_{m1j}^{ - } } \right)^{2} + \left( {\gamma_{m1j}^{ - } } \right)^{2} + \left( {\alpha_{m1j}^{ + } } \right)^{2} + \left( {\beta_{m1j}^{ + } } \right)^{2} + \left( {\gamma_{m1j}^{ + } } \right)^{2} } \right]} } \hfill \\ \times \sqrt {\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {\alpha_{m2j}^{ - } } \right)^{2} + \left( {\beta_{m2j}^{ - } } \right)^{2} + \left( {\gamma_{m2j}^{ - } } \right)^{2} + \left( {\alpha_{m2j}^{ + } } \right)^{2} + \left( {\beta_{m2j}^{ + } } \right)^{2} + \left( {\gamma_{m2j}^{ + } } \right)^{2} } \right]} } \hfill \\ \end{gathered} \right)}} \hfill \\ \quad \times \frac{{\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {c_{\alpha 1j}^{ - } c_{\alpha 2j}^{ - } + c_{\beta 1j}^{ - } c_{\beta 2j}^{ - } + c_{\gamma 1j}^{ - } c_{\gamma 2j}^{ - } + c_{\alpha 1j}^{ + } c_{\alpha 2j}^{ + } + c_{\beta 1j}^{ + } c_{\beta 2j}^{ + } + c_{\gamma 1j}^{ + } c_{\gamma 2j}^{ + } } \right]} }}{{\left( \begin{gathered} \sqrt {\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {c_{\alpha 1j}^{ - } } \right)^{2} + \left( {c_{\beta 1j}^{ - } } \right)^{2} + \left( {c_{\gamma 1j}^{ - } } \right)^{2} + \left( {c_{\alpha 1j}^{ + } } \right)^{2} + \left( {c_{\beta 1j}^{ + } } \right)^{2} + \left( {c_{\gamma 1j}^{ + } } \right)^{2} } \right]} } \hfill \\ \times \sqrt {\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {c_{\alpha 2j}^{ - } } \right)^{2} + \left( {c_{\beta 2j}^{ - } } \right)^{2} + \left( {c_{\gamma 2j}^{ - } } \right)^{2} + \left( {c_{\alpha 2j}^{ + } } \right)^{2} + \left( {c_{\beta 2j}^{ + } } \right)^{2} + \left( {c_{\gamma 2j}^{ + } } \right)^{2} } \right]} } \hfill \\ \end{gathered} \right)}}, \hfill \\ \end{gathered} $$

(17)

$$ \begin{gathered} N_{W2} (H_{1} ,H_{2} ) = N_{W2} (R_{1} ,R_{2} ) \hfill \\ = \frac{{\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\alpha_{m1j}^{ - } \alpha_{m2j}^{ - } + \beta_{m1j}^{ - } \beta_{m2j}^{ - } + \gamma_{m1j}^{ - } \gamma_{m2j}^{ - } + \alpha_{m1j}^{ + } \alpha_{m2j}^{ + } + \beta_{m1j}^{ + } \beta_{m2j}^{ + } + \gamma_{m1j}^{ + } \gamma_{m2j}^{ + } } \right]} }}{{\frac{1}{2}\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\alpha_{m1j}^{ - } + \alpha_{m2j}^{ - } + \beta_{m1j}^{ - } + \beta_{m2j}^{ - } + \gamma_{m1j}^{ - } + \gamma_{m2j}^{ - } + \alpha_{m1j}^{ + } + \alpha_{m2j}^{ + } + \beta_{m1j}^{ + } + \beta_{m2j}^{ + } + \gamma_{m1j}^{ + } + \gamma_{m2j}^{ + } } \right]} }} \hfill \\ \times \frac{{\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {c_{\alpha 1j}^{ - } c_{\alpha 2j}^{ - } + c_{\beta 1j}^{ - } c_{\beta 2j}^{ - } + c_{\gamma 1j}^{ - } c_{\gamma 2j}^{ - } + c_{\alpha 1j}^{ + } c_{\alpha 2j}^{ + } + c_{\beta 1j}^{ + } c_{\beta 2j}^{ + } + c_{\gamma 1j}^{ + } c_{\gamma 2j}^{ + } } \right]} }}{{\frac{1}{2}\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {c_{\alpha 1j}^{ - } + c_{\alpha 2j}^{ - } + c_{\beta 1j}^{ - } + c_{\beta 2j}^{ - } + c_{\gamma 1j}^{ - } + c_{\gamma 2j}^{ - } + c_{\alpha 1j}^{ + } + c_{\alpha 2j}^{ + } + c_{\beta 1j}^{ + } + c_{\beta 2j}^{ + } + c_{\gamma 1j}^{ + } + c_{\gamma 2j}^{ + } } \right]} }}. \hfill \\ \end{gathered} $$

(18)

Similarly, the above weighted correlation coefficients also contain the following proposition.

Proposition 2.

The two weighted correlation coefficients N_W1(H₁, H₂) and N_W2(H₁, H₂) contain the following properties:

(p1) N_W1(H₁, H₂) = N_W2(H₁, H₂) = 1 if H₁ = H₂;

(p2) N_W1(H₁, H₂) = N_W1(H₂, H₁) and N_W2(H₁, H₂) = N_W2(H₂, H₁);

(p3) 0 ≤ N_W1(H₁, H₂), N_W2(H₁, H₂) ≤ 1.

Proof:

Obviously, the above properties of the two weighted correlation coefficients can be easily verified corresponding to the similar proof manner of Proposition 1, which is omitted here.

MAGDM method based on the weighted correlation coefficients of CIVNSs

In this section, we propose a MADGM method using the weighted correlation coefficients of CIVNSs to resolve group decision-making problems under the environment of SIVHNMVSs.

In a MAGDM problem under the environment of SIVHNMVSs, t alternatives are preliminarily provided and denoted as a set of them K = {K₁, K₂, …, K_t}, then they must satisfy the requirements of n attributes, denoted by a set of n attributes L = {L₁, L₂, …, L_n}. However, the importance of n attributes is reflected by their weight vector ω = (ω₁, ω₂, …, ω_n) with ω_j ∈ [0, 1] and $\sum\nolimits_{j = 1}^{n} {\omega_{j} = 1}$. Then, the t alternatives are satisfactorily assessed over the n attributes by a group of decision-makers, and then their assessed truth, falsity and indeterminacy sequences are expressed as the following SIVHNMVEs:

$$ h_{ij} = \left\langle {TS_{ij} ,IS_{ij} ,FS_{ij} } \right\rangle = \left\langle \begin{gathered} (\alpha_{ij}^{1} ,\alpha_{ij}^{2} ,...,\alpha_{ij}^{{p_{\alpha ij} }} ,\alpha_{ij}^{{p_{\alpha ij} + 1}} ,\alpha_{ij}^{{p_{\alpha ij} + 2}} ,...,\alpha_{ij}^{{p_{\alpha ij} + q_{\alpha ij} }} ), \hfill \\ (\beta_{ij}^{1} ,\beta_{ij}^{2} ,...,\beta_{ij}^{{p_{\beta ij} }} ,\beta_{ij}^{{p_{\beta ij} + 1}} ,\beta_{ij}^{{p_{\beta ij} + 2}} ,...,\beta_{ij}^{{p_{\beta ij} + q_{\beta ij} }} ), \hfill \\ (\gamma_{ij}^{1} ,\gamma_{ij}^{2} ,...,\gamma_{ij}^{{p_{\gamma ij} }} ,\gamma_{ij}^{{p_{\gamma ij} + 1}} ,\gamma_{ij}^{{p_{\gamma ij} + 2}} ,...,\gamma_{ij}^{{p_{\gamma ij} + q_{\gamma ij} }} ) \hfill \\ \end{gathered} \right\rangle , $$

where $\alpha_{ij}^{k} ,\beta_{ij}^{k} ,\gamma_{ij}^{k} \in [0,1]$(i = 1, 2, …, t; j = 1, 2, …, n) for k = 1, 2, …, p_αij/p_βij/p_γij and $\alpha_{ij}^{k} ,\beta_{ij}^{k} ,\gamma_{ij}^{k} \subseteq [0,1]$ for k = p_αij + 1/p_βij + 1/p_γij + 1, p_αij + 2/p_βij + 2/p_γij + 2, …, p_αij + q_αij/p_βij + q_βij/p_γij + q_γij. Thus, all the assessed values can be constructed as the decision matrix of SIVHNMVEs D = (h_ij )_t×n (i = 1, 2, …, t; j = 1, 2, …, n).

In this MAGDM problem, a MAGDM method is presented by using the weighted correlation coefficients of CIVNSs to resolve group decision-making problems under the environment of SIVHNMVSs, then its decision process is detailed below:

Step 1: Based on Eqs. (9)–(14), we can convert SIVHNMVEs into CIVNEs, then CIVNEs are constructed as the CIVNE matrix R = (r_ij )_t×n, where $r_{ij} = \left\langle ([\alpha_{mij}^{ - } ,\alpha_{mij}^{ + } ],[c_{\alpha ij}^{ - } ,c_{\alpha ij}^{ + } ]),([\beta_{mij}^{ - } ,\beta_{mij}^{ + } ],[c_{\beta ij}^{ - } ,c_{\beta ij}^{ + } ]),\right.\break\left. ([\gamma_{mij}^{ - } ,\gamma_{mij}^{ + } ],[c_{\gamma ij}^{ - } ,c_{\gamma ij}^{ + } ]) \right\rangle$ (j = 1, 2, …, n; i = 1, 2, …, t) are CIVNEs.

Step 2: Based on the CIVNE matrix R, we give an ideal solution composed of ideal CIVNEs $r_{j}^{*}$ (j = 1, 2, …, n), namely the ideal CIVNS $R_{{}}^{*} = \{ r_{1}^{*} ,r_{2}^{*} ,...,r_{n}^{*} \}$, where $r_{j}^{*}$ (j = 1, 2, …, n) are yielded by the formula:

$$ \begin{gathered} r_{j}^{*} = \left\langle ([\alpha_{mj}^{* - } ,\alpha_{mj}^{* + } ],[c_{\alpha j}^{* - } ,c_{\alpha j}^{* + } ]), ([\beta_{mj}^{* - } ,\beta_{mj}^{* + } ],[c_{\beta j}^{* - } ,c_{\beta j}^{* + } ]),\right.\\ \quad \left. ([\gamma_{mj}^{* - } ,\gamma_{mj}^{* + } ],[c_{\gamma j}^{* - } ,c_{\gamma j}^{* + } ]) \right\rangle \hfill \\ \quad = \left\langle \begin{gathered} ([\mathop {\max }\limits_{i} (\alpha_{mij}^{ - } ),\mathop {\max }\limits_{i} (\alpha_{mij}^{ + } )],[\mathop {\max }\limits_{i} (c_{\alpha ij}^{ - } ),\mathop {\max }\limits_{i} (c_{\alpha ij}^{ + } )]), \hfill \\ ([\mathop {\min }\limits_{i} (\beta_{mij}^{ - } ),\mathop {\min }\limits_{i} (\beta_{mij}^{ + } )],[\mathop {\min }\limits_{i} (c_{\beta ij}^{ - } ),\mathop {\min }\limits_{i} (c_{\beta ij}^{ + } )]), \hfill \\ ([\mathop {\min }\limits_{i} (\gamma_{mij}^{ - } ),\mathop {\min }\limits_{i} (\gamma_{mij}^{ + } )],[\mathop {\min }\limits_{i} (c_{\gamma ij}^{ - } ),\mathop {\min }\limits_{i} (c_{\gamma ij}^{ + } )]) \hfill \\ \end{gathered} \right\rangle . \hfill \\ \end{gathered} $$

Step 3: Using Eq. (17) or (18), the weighted correlation coefficient values between R_i (i = 1, 2, …, t) and R^* for K_i are obtained by the following formula:

$$ \begin{gathered} N_{W1} (R_{i} ,R^{*} ) = \frac{{\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\alpha_{mij}^{ - } \alpha_{mj}^{* - } + \beta_{mij}^{ - } \beta_{mj}^{* - } + \gamma_{mij}^{ - } \gamma_{mj}^{* - } + \alpha_{mij}^{ + } \alpha_{mj}^{* + } + \beta_{mij}^{ + } \beta_{mj}^{* + } + \gamma_{mij}^{ + } \gamma_{mj}^{* + } } \right]} }}{{\left( \begin{gathered} \sqrt {\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {\alpha_{mij}^{ - } } \right)^{2} + \left( {\beta_{mij}^{ - } } \right)^{2} + \left( {\gamma_{mij}^{ - } } \right)^{2} + \left( {\alpha_{mij}^{ + } } \right)^{2} + \left( {\beta_{mij}^{ + } } \right)^{2} + \left( {\gamma_{mij}^{ + } } \right)^{2} } \right]} } \hfill \\ \quad \quad \times \sqrt {\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {\alpha_{mj}^{* - } } \right)^{2} + \left( {\beta_{mj}^{* - } } \right)^{2} + \left( {\gamma_{mj}^{* - } } \right)^{2} + \left( {\alpha_{mj}^{* + } } \right)^{2} + \left( {\beta_{mj}^{* + } } \right)^{2} + \left( {\gamma_{mj}^{* + } } \right)^{2} } \right]} } \hfill \\ \end{gathered} \right)}} \hfill \\ \quad \quad \quad \quad \quad \times \frac{{\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {c_{\alpha ij}^{ - } c_{\alpha j}^{* - } + c_{\beta ij}^{ - } c_{\beta j}^{* - } + c_{\gamma ij}^{ - } c_{\gamma j}^{* - } + c_{\alpha ij}^{ + } c_{\alpha j}^{* + } + c_{\beta ij}^{ + } c_{\beta j}^{* + } + c_{\gamma ij}^{ + } c_{\gamma j}^{* + } } \right]} }}{{\left( \begin{gathered} \sqrt {\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {c_{\alpha ij}^{ - } } \right)^{2} + \left( {c_{\beta ij}^{ - } } \right)^{2} + \left( {c_{\gamma ij}^{ - } } \right)^{2} + \left( {c_{\alpha ij}^{ + } } \right)^{2} + \left( {c_{\beta ij}^{ + } } \right)^{2} + \left( {c_{\gamma ij}^{ + } } \right)^{2} } \right]} } \hfill \\ \times \sqrt {\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\left( {c_{\alpha j}^{* - } } \right)^{2} + \left( {c_{\beta j}^{* - } } \right)^{2} + \left( {c_{\gamma j}^{* - } } \right)^{2} + \left( {c_{\alpha j}^{* + } } \right)^{2} + \left( {c_{\beta j}^{* + } } \right)^{2} + \left( {c_{\gamma j}^{* + } } \right)^{2} } \right]} } \hfill \\ \end{gathered} \right)}} \hfill \\ \end{gathered} $$

(19)

or

$$ \begin{gathered} N_{W2} (R_{i} ,R^{*} ) = \frac{{\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\alpha_{mij}^{ - } \alpha_{mj}^{* - } + \beta_{mij}^{ - } \beta_{mj}^{* - } + \gamma_{mij}^{ - } \gamma_{mj}^{* - } + \alpha_{mij}^{ + } \alpha_{mj}^{* + } + \beta_{mij}^{ + } \beta_{mj}^{* + } + \gamma_{mij}^{ + } \gamma_{mj}^{* + } } \right]} }}{{\frac{1}{2}\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {\alpha_{mij}^{ - } + \alpha_{mj}^{* - } + \beta_{mij}^{ - } + \beta_{mj}^{* - } + \gamma_{mij}^{ - } + \gamma_{mj}^{* - } + \alpha_{mij}^{ + } + \alpha_{mj}^{* + } + \beta_{mij}^{ + } + \beta_{mj}^{* + } + \gamma_{mij}^{ + } + \gamma_{mj}^{* + } } \right]} }} \hfill \\ \quad \quad \quad \quad \quad \quad\quad \quad \times \frac{{\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {c_{\alpha ij}^{ - } c_{\alpha j}^{* - } + c_{\beta ij}^{ - } c_{\beta j}^{* - } + c_{\gamma ij}^{ - } c_{\gamma j}^{* - } + c_{\alpha ij}^{ + } c_{\alpha j}^{* + } + c_{\beta ij}^{ + } c_{\beta j}^{* + } + c_{\gamma ij}^{ + } c_{\gamma j}^{* + } } \right]} }}{{\frac{1}{2}\sum\nolimits_{j = 1}^{n} {\omega_{j} \left[ {c_{\alpha ij}^{ - } + c_{\alpha j}^{* - } + c_{\beta ij}^{ - } + c_{\beta j}^{* - } + c_{\gamma ij}^{ - } + c_{\gamma j}^{* - } + c_{\alpha ij}^{ + } + c_{\alpha j}^{* + } + c_{\beta ij}^{ + } + c_{\beta j}^{* + } + c_{\gamma ij}^{ + } + c_{\gamma j}^{* + } } \right]} }}. \hfill \\ \end{gathered} $$

(20)

Step 4: We rank the alternatives in a descending order based on the weighted correlation coefficient values, then the first one is the best choice.

Step 5: End.

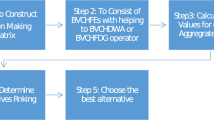
Generally, the above decision process of the proposed MAGDM method is shown in Fig. 1.

Fig. 1

The flowchart of the proposed MAGDM method

Actual case and relative comparative analysis

A selection case of landslide treatment schemes

In the construction of a city, the excavation projects will greatly affect the stability of the landslide and threaten the construction of infrastructures and safety of people's lives and property. Therefore, it is very important that treatment issues of the relative landslides. This section applies the proposed MAGDM method to a selection case of landslide treatment schemes as a MAGDM example to illustrate its applicability and validity under the environment of SIVHNMVSs.

Some construction company wants to choose the best landslide treatment scheme from six potential treatment schemes/alternatives: the scheme K₁ (the scheme retaining walls, mortar rubble masonry pavements and surface water treatment), the scheme K₂ (grid beams, surface-drainage works and monitoring system), the scheme K₃ (anchor anti-slide pile, cut-off drain treatment and monitoring system), the scheme K₄ (anchor anti-slide piles, cantilever piles and slope protection), the scheme K₅ (anti-slide piles, retaining walls and cut-off drain treatment), and the scheme K₆ (reduce-loading works, anti-slide piles and surface-drainage works), which are denoted by a set of them K = {K₁, K₂, K₃, K₄, K₅, K₆}. Then, they must satisfy four requirements/attributes: the treatment cost (L₁), the difficulty of construction (L₂), the technical risk (L₃), and the environmental impact (L₄). Regarding the importance of the attributes, their weight vector is specified as ω = (0.3,0.22,0.25,0.23).

In this selection case of landslide treatment schemes, three experts/decision-makers are requested to satisfactorily evaluate each alternative over the four attributes by their truth, falsity and indeterminacy judgments. Thus, each expert/decision-maker gives fuzzy values/interval-valued fuzzy values of the truth, falsity, and indeterminacy in the evaluation process, and then the evaluation values of the three experts/decision-makers can form the truth, falsity and indeterminacy sequences with the different and/or same fuzzy values and interval-valued fuzzy values to be expressed as the evaluation information of the SIVHNMVEs $h_{ij} = \left\langle {TS_{ij} ,IS_{ij} ,FS_{ij} } \right\rangle = \left\langle {(\alpha_{ij}^{1} ,\alpha_{ij}^{2} ,\alpha_{ij}^{3} ),(\beta_{ij}^{1} ,\beta_{ij}^{2} ,\beta_{ij}^{3} ),(\gamma_{ij}^{1} ,\gamma_{ij}^{2} ,\gamma_{ij}^{3} )} \right\rangle$ for i = 1, 2, …, 6; j = 1, 2, 3, 4, where $\alpha_{ij}^{k} ,\beta_{ij}^{k} ,\gamma_{ij}^{k} \in [0,1]$ or $\alpha_{ij}^{k} ,\beta_{ij}^{k} ,\gamma_{ij}^{k} \subseteq [0,1]$ for k = 1, 2, 3. Thus, all the evaluated SIVHNMVEs can be constructed as their decision matrix D, as shown in Table 1.

Table 1 The decision matrix D of SIVHNMVEs

In this MAGDM problem, the proposed MAGDM method is applied to the selection case of landslide treatment schemes under the environment of SIVHNMVSs. Then, its decision process is detailed below:

Step 1: Based on Eqs. (9)–(14), we can convert SIVHNMVEs in Table 1 into CIVNEs, which are constructed as the CIVNE matrix R in Table 2.

Table 2 The CIVNE matrix R

Step 2: Based on the CIVNE matrix R, we give an ideal CIVNS $R_{{}}^{*} = \{ r_{1}^{*} ,r_{2}^{*} ,...,r_{s}^{*} \}$ composed of ideal CIVNEs $r_{j}^{*}$ (j = 1, 2, …, n) by the following ideal solution:

R^* = {< ([0.7333, 0.8], [0.9423, 1]), ([0.1333, 0.1667], [0.9, 0.9423]), ([0.1, 0.1333], [0.8472, 0.9]) > , < ([0.7333, 0.8333], [0.9423, 1]), ([0.1667, 0.2], [0.9, 0.9423]), ([0.1, 0.1333], [0.9, 0.9423]) > , < ([0.7667, 0.8333], [0.9423, 0.9423]), ([0.1667, 0.2], [0.9, 0.9423]), ([0.1, 0.1667], [0.8845, 0.9423]) > , < ([0.7667, 0.8333], [0.9423, 1]), ([0.1333, 0.2], [0.7918, 0.9]), ([0.1333, 0.2], [0.8472, 0.9]) >} .

Step 3: Using Eqs. (19) or (20), the weighted correlation coefficient values between R_i (i = 1, 2, …, 6) and R^* for K_i are obtained as follows:

N_W1(R₁, R^*) = 0.9930, N_W1(R₂, R^*) = 0.9947, N_W1(R₃, R^*) = 0.9924, N_W1(R₄, R^*) = 0.9776, N_W1(R₅, R^*) = 0.9792, and N_W1(R₆, R^*) = 0.9738.

Or N_W2(R₁, R^*) = 0.5546, N_W2(R₂, R^*) = 0.5481, N_W2(R₃, R^*) = 0.5317, N_W2(R₄, R^*) = 0.5151, N_W2(R₅, R^*) = 0.4997, and N_W2(R₆, R^*) = 0.5146.

Step 4: The ranking order of the six alternatives is K₂ > K₁ > K₃ > K₅ > K₄ > K₆ or K₁ > K₂ > K₃ > K₄ > K₆ > K₅. Although the different weighted correlation coefficients cause the ranking difference of the alternatives, the best scheme is K₁ or K₂, which depends on the decision-makers’ preference selection or the actual requirement.

Comparison with existing MAGDM method based on the correlation coefficients of CSVNSs

Under the application environments of SIVHNMVSs and SVNMVSs, this section compares our new MAGDM method with existing MAGDM method [24] to show the superiority of the new method over the existing method.

First, the characteristic comparison between our new method and the existing method [24] is indicated in Table 3.

Table 3 Characteristic comparison between our new method and the existing method

From the comparative results of Table 3, we see that our new method contains much more information (SIVHNMVSs, SVNMVSs, IVNMVSs) than the existing method when handling MAGDM problems in the environment of SIVHNMVSs. Furthermore, the expression forms of the correlation coefficients of CSVNSs and CIVNSs are different. Then, our new method uses SIVHNMVE information to carry out neutrosophic MAGDM problems, while the existing method [24] only uses SVNMVE information to perform neutrosophic MAGDM problems. Clearly, the existing method [24] is only a special case of our new method. Therefore, our new method is more extensive and more useful than the existing method [24].

Since the existing MAGDM method based on the correlation coefficients of CSVNSs [24] cannot deal with the selection problem of landslide treatment schemes under the environment of SIVHNMVSs, we can convert SIVHNMVEs into SVNMVEs by taking the average values of IVFVs in the decision matrix D as their special case to conveniently apply the existing MAGDM method [24] to the selection problem of landslide treatment schemes in the setting of SVNMVSs. In this case, the decision matrix D of SIVHNMVEs in Table 1 is reduced to the decision matrix D’ of SVNMVEs in Table 4. Therefore, the existing MAGDM method [24] can be applied to the special case to select the best landslide treatment scheme under the environment of SVNMVSs. Thus, its decision process is detailed below:

Table 4 The decision matrix D’ of SVNMVEs

By Eqs. (3)–(8) [24], we converse SVNMVEs into CSVNEs, then the CSVNE matrix R’ are shown in Table 5.

Table 5 The CSVNE matrix R’

From Table 5, we obtain the ideal solution R’* = {<(0.7667, 0.9711), (0.1500, 0.9236), (0.1167, 0.8742)>, <(0.7833, 0.9711), (0.1833, 0.9236), (0.1167, 0.9236)>, <(0.7833, 0.9711), (0.1833, 0.9236), (0.1333, 0.9134)>, <(0.7833, 0.9711), (0.1833, 0.8472), (0.1667, 0.8742)>}.

By Eqs. (1) and (2), the values of the weighted correlation coefficients between R_i’ (i = 1, 2, …, 6) and R’^* are obtained in the special case, and then all decision results of our new MAGDM method and the existing MAGDM method [24] are shown in Table 6 for the convenient comparison.

Table 6 All decision results of our new method and the existing method

In Table 6, there is the same best scheme K₂ corresponding to the weighted correlation coefficients of Eq. (1) and Eq. (19), then the best ones K₁ and K₄ reflect the difference regarding the weighted correlation coefficients of Eq. (20) and Eq. (2). However, there is also the ranking difference between our new method and the existing method under different information environments. Therefore, the different evaluation information of SIVHNMVSs and SVNMVSs can impact on the ranking order of alternatives in the selection case of landslide treatment schemes. Since the existing method [24] only contains the information of SVNMVSs without the interval-valued fuzzy information, it is only a special case of our new method when SIVHNMVSs are reduced to SVNMVSs. Obviously, our new method is broader and more useful than the existing method in terms of decision-making capability.

Generally, our new method reflects the following new contributions:

• 1. The proposed SIVHNMVS can resolve the expression problem of the single- and interval-valued hybrid neutrosophic multi-valued information which existing SVNMVS cannot do.

• 2. The proposed correlation coefficients of CIVNSs provide necessary modeling tools for handling MAGDM problems in the SIVHNMVS setting.

• 3. Our new MAGDM method is more extensive and more useful than the existing MAGDM method [24] in the decision-making capability.

• 4. The new techniques show the superiorities of the hybrid neutrosophic multi-valued information expression, correlation coefficients, and MAGDM method over the existing techniques in the SVNMVS setting.

Conclusion

Due to the lack of single- and interval-valued hybrid neutrosophic (multi-valued) information expression, correlation coefficients, and decision-making methods in existing neutrosophic theories and decision-making applications, this study first proposed SIVHNMVS to solve the hybrid information expression problem of both SVNMVS and IVNMVS. Then, we introduced a transformation method that converts SIVHNMVSs into CIVNSs based on the average value and consistency degree of the truth, falsity and indeterminacy sequences to reasonably simplify the hybrid information expression and operation problems of different lengths/information types of the truth, falsity and indeterminacy sequences in the setting of SIVHNMVSs. Next, the proposed correlation coefficients of CIVNSs provided necessary modeling tools for performing MAGDM problems with SIVHNMVSs. The developed MAGDM method resolved single- and interval-valued hybrid neutrosophic multi-valued decision-making problems. At last, a selection case of landslide treatment schemes and comparison with existing method were given to indicate the applicability and validity of the new method. Furthermore, our new techniques not only overcome the drawbacks of the existing techniques, but also are more extensive and more useful than the existing techniques when performing MAGDM problems in the setting of SIVHNMVSs. Moreover, the new techniques demonstrated the outstanding superiorities of the hybrid information expression, the correlation coefficients of CIVNSs, and the developed MAGDM method over the existing techniques.

However, the new contributions of this study will be further extended to other areas, such as clustering analysis and evaluation of slope risk/stability, risk assessment and investment analysis of engineering projects, evaluation of high-speed rail system in China [26] under the environment of SIVHNMVSs.

Furthermore, existing Pythagorean fuzzy sets [27, 28] or hesitant fuzzy linguistic sets [29] also cannot express the hybrid information of both single-valued Pythagorean fuzzy sets and interval-valued Pythagorean fuzzy sets or both hesitant fuzzy linguistic sets and uncertain hesitant fuzzy linguistic sets. Hence, the new techniques in this study will be also extended to the Pythagorean fuzzy set or hesitant fuzzy linguistic set as a future research direction.