Abstract
The aim of this paper is to propose a new multi-attribute decision-making (MADM) method to rank all feasible alternatives in complex decision-making scenarios and determine the optimal one. To this end, we first propose the notion of interval-valued q-rung dual hesitant linguistic sets (IVq-RDHLSs) by combining interval-valued q-rung dual hesitant fuzzy (IVq-RDHF) sets with linguistic terms set. The proposed IVq-RDHLSs utilize IVq-RDHF membership and non-membership degrees to assess linguistic terms, so that they can fully express decision-makers’ evaluation information. Additionally, some related concepts such as the operational rules, score and accuracy functions, and ranking method of IVq-RDHLSs are presented. Considering the good performance of the classical Maclaurin symmetric mean (MSM) in integrating fuzzy information, we further generalize MSM into IVq-RDHLSs to propose the interval-valued q-rung dual hesitant linguistic MSM operator, the interval-valued q-rung dual hesitant linguistic dual MSM operator, as well as their weighted forms. Afterwards, we study the applications of IVq-RDHLSs and their aggregation operators in decision-making and propose a new MADM method. Some real decision-making problems in daily life are employed to prove the rightness of the proposed method. We also attempt to demonstrate the advantages and superiorities of our proposed method through comparing with some other methods in this paper.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The past years have witnessed the great success of the study on Pythagorean fuzzy sets (PFSs) based multi-attribute decision-making (MADM) methods [1,2,3,4,5,6,7,8,9,10,11]. PFSs were proposed by Prof. Yager [12] to overcome the shortcoming of intuitionistic fuzzy sets (IFSs) [13], which they fail to describe decision-making situations in which the sum of membership grade (MG) and non-membership grade (NMG) is greater than one. Hence, PFSs have been regarded as an effective tool to comprehensively express decision-makers’ (DMs’) complex evaluation information. Recently, Yager [14] generalized PFSs by relaxing their constraint and proposed the notion of q-rung orthopair fuzzy sets (q-ROFSs). Due to their high efficiency in expressing fuzzy and complex DMs’ assessment information, q-ROFS-based MADM models and methods have been a new research topic in operational research. Recent publications focused on q-ROFSs based decision-making can be roughly divided into three types. The first type is q-rung orthopair fuzzy (q-ROF) aggregation operators (AOs)-based MADM methods. Liu and Wang [15] proposed basic q-ROF operational rules and simple weighted average/geometric AOs, which are the foundation of q-rung orthopair fuzzy AO theory. On the basis of Liu and Wang’s [15] pioneering works, some other powerful AOs have been proposed, such as the q-ROF Bonferroni mean [16], q-ROF Heronian mean [17], q-ROF Hamy mean [18], q-ROF Maclaurin symmetric mean (MSM) [19], q-ROF Muirhead mean [20], and q-ROF power MSM [21]. Some other scholars also investigated the existence of heterogeneous interrelationship among q-ROF numbers (q-ROFNs) and proposed some partitioned AOs of q-ROFNs [22,23,24]. It is noted that the AOs proposed in [15,16,17,18,19,20,21,22,23,24] are based on the algebraic t-norm and t-conorm. In addition, some scholars investigated the operation theory of q-ROFNs and proposed novel q-ROF operational laws. For instance, Peng et al. [25] proposed exponential operations and corresponding AOs of q-ROFNs. Xing and her colleagues [26] studied the interaction operations of q-ROFNs, which take the relationship among MGs and NMGs into consideration. Besides, scholars also investigated Hamacher operations [27], Dombi operations [28], and Archimedean operations of q-ROFNs [29], respectively. The second type is information measures of q-ROFSs. Du [30] introduced Minkowski-type distance measures of q-ROFSs. Peng and Liu [31] studied distance measure, similarity measure, entropy, and inclusion measure for q-ROFSs, and invested their application in MADM. Liu et al. [32] discussed the cosine similarity measure and a Euclidean distance measure of q-ROFSs, and investigated their properties and applications. Peng and Dai [33] proposed multi-parametric similarity measure of q-ROFSs and applied it in the assessment of classroom teaching quality. The third type focuses on extensions of classical q-ROFSs and studies their corresponding MADM methods. For example, Liu and Liu [34, 35] employed linguistic terms to represent the MGs and NMGs to propose the linguistics q-ROFSs and investigated their applications in MADM. Li et al. [36] and Wang et al. [37] utilized q-rung orthopair fuzzy MGs and NMGs to portray linguistic variables and proposed the q-rung orthopair linguistic sets (q-ROLSs). Similarly, Wang et al. [38], Xing et al. [39], and Liu et al. [40, 41] proposed the q-rung orthopair uncertain linguistic sets and discussed their applications in MADM, respectively.
Recently, Xu et al. [42, 43] proposed the q-rung dual hesitant fuzzy sets (q-RDHFSs) and interval-valued q-RDHFSs (IVq-RDHFSs) which are powerful to deal with DMs’ high hesitancy in giving MGs and NMGs in q-ROFSs context. In addition, Xu et al. [42, 43] introduced the AOs of q-RDHFSs and IVq-RDHFSs to propose novel MADM methods. Numerical examples have proved the effectiveness advantages of these MADM approaches. However, Xu et al.’s [43] method still has shortcomings, owing to its information expression capability. In most practical decision-making situations, it is almost impossible for DMs to comprehensively provide their evaluation values by quantitative methods, due to the high complexity of real decision-making problems. As a matter of fact, more and more scientists and scholars have realized the importance and necessity of depicting DMs’ evaluations both quantificationally and qualitatively [44,45,46,47]. For example, Liu and Jin [48] generalized intuitionistic fuzzy sets to intuitionistic uncertain linguistic sets, which employ intuitionistic fuzzy sets and uncertain linguistic to express DMs’ quantitative and qualitative evaluation values, respectively. Similarly, Du et al.’s [49] combined interval-valued PFSs with linguistic terms set (LST) and proposed the interval-valued Pythagorean linguistic sets. In light of this, Xu et al.’s [43] method is flawed as it only considers DMs’ quantitative assessment information.
Based on the above analysis, the motivation of this paper is to propose a new MADM method, which overcomes the drawback of Xu et al.’s [43] method. To do so, we first propose the concept of interval-valued q-rung dual hesitant linguistic sets (IVq-RDHLSs) to portray fuzzy decision-making information. The IVq-RDHLS can be regarded as a combination of IVq-ROFS with LTS. The IVq-RDHFLSs are parallel to the interval-valued dual hesitant fuzzy linguistic sets (IVDHFLSs) proposed by Wei et al. [50], but are more powerful and flexible as they have relaxer constraint, which provides DMs more freedom to fully express their evaluation opinions. In addition, IVq-RDHFLSs are also stronger than q-ROLSs as they can effectively deal with DMs’ hesitancy and indeterminacy in expressing their decision information. When considering to integrate attribute values in interval-valued q-rung dual hesitant linguistic (IVq-RDHL) MADM problems, the MSM operator has deeply impressed us, due to its flexibility of reflecting the interrelationship among multiple input variables. Because of this characteristic, MSM has been extensively applied to fuse IFSs [51, 52], interval-valued IFSs [53], hesitant fuzzy sets [54], neutrosophic sets [55]. Therefore, this paper utilizes MSM to aggregate IVq-RDHFL information and proposes a series of AOs of IVq-RDHFL variables (IVq-RDHLVs). Finally, based on the newly proposed AOs, we investigate MADM problems with IVq-RDHL information and present a new method to select the optimal alternative. The new method is applied to practical MADM problems to verify its validity and effectiveness. We also illustrate the advantages of the new through comparative analysis.
The rest of this paper is organized as follows. In section “Preliminaries”, we review the existing basic notions and propose the concept if IVq-RDHLSs. The operations and comparison method are also presented in section “Preliminaries”. Section “Aggregation operators for IVq-RDHL information” proposes some AOs of IVq-RDHL information and discusses their properties in detail. Section “A novel method to MADM with IVq-RDHL information” gives the main steps of a novel MADM based on the proposed AOs. Numerical examples are investigated in section “Application of the proposed method in medical equipment selection”. Conclusion remarks are provided in “Conclusions”.
Preliminaries
In this section, we briefly review the basic notions that will be used in the following parts. In addition, we also propose the concept of IVq-RDHLSs as well as their operations and comparison method.
IVq-RDHFSs, IVq-RDHLSs, and their related notions
To comprehensively express DMs’ fuzzy judgements over alternatives with high hesitancy, Xu et al. [43] introduced the IVq-RDHFSs. The remarkable feature of IVq-RDHFS is that its MG and NMG are denoted by a set of interval values, satisfying the sum of qth power of MG and qth power of NMG is less than or equal to one \( \left( {q \ge 1} \right) \). The definition of IVq-RDHFS is given as follows.
Definition 1
[43] Let \( X \) be a fixed set, and then, an interval-valued q-rung dual hesitant fuzzy set (IVq-RDHFS) \( D \) defined on \( X \) is expressed as:
where \( h_{D} \left( x \right) = \cup_{{\left[ {r_{D}^{\text{l}} ,r_{D}^{\text{u}} } \right] \in h_{D} \left( x \right)}} \left\{ {\left[ {r_{D}^{\text{l}} ,r_{D}^{\text{u}} } \right]} \right\} \) and \( g_{D} \left( x \right) = \cup_{{\left[ {\eta_{D}^{\text{l}} ,\eta_{D}^{\text{u}} } \right] \in g_{D} \left( x \right)}} \left\{ {\left[ {\eta_{D}^{\text{l}} ,\eta_{D}^{\text{u}} } \right]} \right\} \) are two sets of some interval values in [0, 1], denoting the possible MG and NMG of the element \( x \in X \) to the set \( D \), respectively, such that \( \left[ {r_{D}^{\text{l}} ,r_{D}^{\text{u}} } \right],\left[ {\eta_{D}^{\text{l}} ,\eta_{D}^{\text{u}} } \right] \subset \left[ {0,1} \right] \), and \( 0 \le \left( {\left( {r_{\text{D}}^{\text{u}} } \right)^{ + } } \right)^{q} + \left( {\left( {\eta_{\text{D}}^{\text{u}} } \right)^{ + } } \right)^{q} \le 1 \),\( q \ge 1 \), where \( \left[ {r_{\text{D}}^{\text{l}} ,r_{\text{D}}^{\text{u}} } \right] \in h_{\text{D}} \left( x \right) \),\( \left[ {\eta_{D}^{l} ,\eta_{D}^{u} } \right] \in g_{D} \left( x \right) \),\( \left( {r_{D}^{u} } \right)^{ + } \in h_{D}^{ + } \left( x \right) = \cup_{{\left[ {r_{D}^{l} ,r_{D}^{u} } \right] \in h_{D} \left( x \right)}} \hbox{max} \left\{ {r_{D}^{u} } \right\} \), and \( \left( {\eta_{D}^{u} } \right)^{ + } \in g_{D}^{ + } \left( x \right) = \cup_{{\left[ {\eta_{D}^{l} ,\eta_{D}^{u} } \right] \in g_{D} \left( x \right)}} \hbox{max} \left\{ {\eta_{D}^{u} } \right\} \). For convenience, we call the pair \( d\left( x \right) = \left( {h_{D} \left( x \right),g_{D} \left( x \right)} \right) \) an interval-valued q-rung dual hesitant fuzzy element (IVq-RDHFE), which can be denoted by \( d = \left( {h,g} \right) \) for simplicity. Especially, if \( r^{l} = r^{u} \) and \( \eta^{l} = \eta^{u} \), then \( D \) reduces to the q-rung dual hesitant fuzzy set [42]; if \( q = 1 \), then \( D \) reduces to interval-valued dual hesitant fuzzy set [56]; if \( q = 2 \), then \( D \) reduces to hesitant interval-valued Pythagorean fuzzy set [57].
Similar to nature language, the LTS is an effective tool proposed by Zadeh [58] to depict DMs’ fuzzy evaluations, and, in addition, to more comprehensively and accurately portray DMs’ judgements, scholars, and scientists combined LTS with fuzzy set theories to propose new hybrid tools. The typical representatives are the intuitionistic linguistic sets [59], Pythagorean fuzzy linguistic sets [60], hesitant fuzzy linguistic sets [61], q-rung orthopair linguistic sets [36, 37], etc. Similarly, we employ IVq-RDHFSs to denote the possible MGs and NMGs of linguistic terms to propose the IVq-RDHLSs. To this end, we first briefly review the concept of LTS.
Definition 2
[58] Let \( S = \left\{ {s_{i} \left| {i = 1,2, \ldots ,t} \right.} \right\} \) be a linguistic term set (LTS) with odd cardinality. Any label \( s_{i} \) represents a possible value for a linguistic variable, and it should satisfy the following characteristics [62]: (1) the set is ordered: \( s_{i} > s_{j} \) if \( i > j \); (2) there is the negation operator: \( {\text{neg}}\left( {s_{i} } \right) = s_{j} \), such that \( i + j = t + 1 \). For example, an LTS \( S \) can be defined as:
In the following, we combine IVq-RDHLSs with LTS and propose the IVq-RDHLSs.
Definition 3
Let \( X \) be a fixed set and \( \tilde{S} \) be a continuous LTS of \( S = \left\{ {s_{i} \left| {i = 1,2, \ldots ,t} \right.} \right\} \), and then, an interval-valued q-rung dual hesitant linguistic set (IVq-RDHLS) D defined on X is expressed as:
where \( s_{\theta \left( x \right)} \in \tilde{S} \), \( h_{D} \left( x \right) = \cup_{{\left[ {r_{D}^{l} ,r_{D}^{u} } \right] \in h_{D} \left( x \right)}} \left\{ {\left[ {r_{D}^{l} ,r_{D}^{u} } \right]} \right\} \) and \( g_{D} \left( x \right) = \cup_{{\left[ {\eta_{D}^{l} ,\eta_{D}^{u} } \right] \in g_{D} \left( x \right)}} \left\{ {\left[ {\eta_{D}^{l} ,\eta_{D}^{u} } \right]} \right\} \) are two sets of interval values in [0,1], denoting the possible MG and NMG of the element \( x \in X \) to the set \( D \), respectively, such that \( \left[ {r_{D}^{l} ,r_{D}^{u} } \right],\left[ {\eta_{D}^{l} ,\eta_{D}^{u} } \right] \in \left[ {0,1} \right] \), and \( 0 \le \left( {\left( {r_{D}^{u} } \right)^{ + } } \right)^{q} + \left( {\left( {\eta_{D}^{u} } \right)^{ + } } \right)^{q} \le 1 \),\( q \ge 1 \), where \( \left[ {r_{D}^{l} ,r_{D}^{u} } \right] \in h_{D} \left( x \right) \),\( \left[ {\eta_{D}^{l} ,\eta_{D}^{u} } \right] \in g_{D} \left( x \right) \),\( \left( {r_{D}^{u} } \right)^{ + } \in h_{D}^{ + } \left( x \right) = \cup_{{\left[ {r_{D}^{l} ,r_{D}^{u} } \right] \in h_{D} \left( x \right)}} \hbox{max} \left\{ {r_{D}^{u} } \right\} \), and \( \left( {\eta_{D}^{u} } \right)^{ + } \in g_{D}^{ + } \left( x \right) = \cup_{{\left[ {\eta_{D}^{l} ,\eta_{D}^{u} } \right] \in g_{D} \left( x \right)}} \hbox{max} \left\{ {\eta_{D}^{u} } \right\} \) for all \( x \in X \). For convenience, we call \( d = \left\langle {s_{\theta \left( x \right)} ,\left\{ {\left\{ {\left[ {r_{D}^{l} ,r_{D}^{u} } \right]} \right\},\left\{ {\left[ {\eta_{D}^{l} ,\eta_{D}^{u} } \right]} \right\}} \right\}} \right\rangle \) an interval-valued q-rung dual hesitant linguistic variable (IVq-RDHLV), which can be denoted as \( d = \left\langle {s_{\theta } ,\left( {h,g} \right)} \right\rangle \) for simplicity. In addition, if \( r^{l} = r^{u} \) and \( \eta^{l} = \eta^{u} \), then D is a q-rung dual hesitant linguistic set; if \( q = 2 \), then D is a hesitant interval-valued Pythagorean linguistic set; if \( q = 1 \) then D is IVDHFLS [50].
The operational laws of IVq-RDHLVs are proposed as follows.
Definition 4
Let \( d = \left\langle {s_{\theta } ,\left( {h,g} \right)} \right\rangle \), \( d_{1} = \left\langle {s_{{\theta_{1} }} ,\left( {h_{1} ,g_{1} } \right)} \right\rangle \), and \( d_{2} = \left\langle {s_{{\theta_{2} }} ,\left( {h_{2} ,g_{2} } \right)} \right\rangle \) be any three IVq-RDHLVs, and then:
-
1.
\(\begin{aligned} & d_{1} \oplus d_{2} = \left\langle {s_{{\theta_{1} + \theta_{2} }} , \cup_{{r_{1} \in h_{1} ,r_{2} \in h_{2} ,\eta_{1} \in g_{1} ,\eta_{2} \in g_{2} }} } \right. \hfill \\ & \left. {\quad \quad \quad \quad \left\{ {\left\{ {\left[ {\left( {\left( {r_{1}^{\text{l}} } \right)^{q} + \left( {r_{2}^{\text{l}} } \right)^{q} - \left( {r_{1}^{\text{l}} r_{2}^{\text{l}} } \right)^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\left( {\left( {r_{1}^{\text{u}} } \right)^{q} + \left( {r_{2}^{\text{u}} } \right)^{q} - \left( {r_{1}^{\text{u}} r_{2}^{\text{u}} } \right)^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right]} \right\},\left\{ {\left[ {\eta_{1}^{\text{l}} \eta_{2}^{\text{l}} ,\eta_{1}^{\text{u}} \eta_{2}^{\text{u}} } \right]} \right\}} \right\}} \right\rangle ; \hfill \\ \end{aligned} \)
-
2.
\( \begin{aligned} & d_{1} \otimes d_{2} = \left\langle {s_{{\theta_{1} \times \theta_{2} }} , \cup_{{r_{1} \in h_{1} ,r_{2} \in h_{2} ,\eta_{1} \in g_{1} ,\eta_{2} \in g_{2} }} } \right. \hfill \\ & \left. {\quad \quad \quad \left\{ {\left\{ {\left[ {r_{1}^{\text{l}} r_{2}^{\text{l}} ,r_{1}^{\text{u}} r_{2}^{\text{u}} } \right]} \right\},\left\{ {\left[ {\left( {\left( {\eta_{1}^{\text{l}} } \right)^{q} + \left( {\eta_{2}^{\text{l}} } \right)^{q} - \left( {\eta_{1}^{\text{l}} \eta_{2}^{\text{l}} } \right)^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\left( {\left( {\eta_{1}^{\text{u}} } \right)^{q} + \left( {\eta_{2}^{\text{u}} } \right)^{q} - \left( {\eta_{1}^{\text{u}} \eta_{2}^{\text{u}} } \right)^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right]} \right\}} \right\}} \right\rangle ; \hfill \\ \end{aligned} \)
-
3.
\( \lambda d = \left\langle {s_{\lambda \theta } , \cup_{r \in h,\eta \in g} \left\{ {\left\{ {\left[ {\left( {1 - \left( {1 - \left( {r^{\text{l}} } \right)^{q} } \right)^{\lambda } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\left( {1 - \left( {1 - \left( {r^{\text{u}} } \right)^{q} } \right)^{\lambda } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right]} \right\},\left\{ {\left( {\eta^{\text{l}} } \right)^{\lambda } ,\left( {\eta^{\text{u}} } \right)^{\lambda } } \right\}} \right\}} \right\rangle \)
-
4.
\( d^{\lambda } = \left\langle {s_{{\theta^{\lambda } }} , \cup_{r \in h,\eta \in g} \left\{ {\left\{ {\left( {r^{\text{l}} } \right)^{\lambda } ,\left( {r^{\text{u}} } \right)^{\lambda } } \right\},\left\{ {\left[ {\left( {1 - \left( {1 - \left( {\eta^{\text{l}} } \right)^{\text{q}} } \right)^{\lambda } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\left( {1 - \left( {1 - \left( {\eta^{\text{u}} } \right)^{\text{q}} } \right)^{\lambda } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right]} \right\}} \right\}} \right\rangle . \)
According to Definition 4, the following theorem can be easily obtained.
Theorem 1
Let \( d = \left\langle {s_{\theta } ,\left( {h,g} \right)} \right\rangle \), \( d_{1} = \left\langle {s_{{\theta_{1} }} ,\left( {h_{1} ,g_{1} } \right)} \right\rangle \)and \( d_{2} = \left\langle {s_{{\theta_{2} }} ,\left( {h_{2} ,g_{2} } \right)} \right\rangle \)be any three IVq-RDHLVs, and then:
-
1.
\( d_{1} \oplus d_{2} = d_{2} \oplus d_{1} ; \)
-
2.
\( d_{1} \otimes d_{2} = d_{2} \otimes d_{1} ; \)
-
3.
\( \lambda \left( {d_{1} \oplus d_{2} } \right) = \lambda d_{1} \oplus \lambda d_{2} \;\left( {\lambda_{1} ,\lambda_{2} } \right) \ge 0; \)
-
4.
\( \lambda_{1} d \oplus \lambda_{2} d = \left( {\lambda_{1} \oplus \lambda_{2} } \right)d\;\left( {\lambda_{1} ,\lambda_{2} } \right) \ge 0; \)
-
5.
\( d_{1}^{\lambda } \otimes d_{2}^{\lambda } = \left( {d_{1} \otimes d_{2} } \right)^{\lambda } \;\left( {\lambda \ge 0} \right); \)
-
6.
\( d_{1}^{\lambda } \otimes d_{2}^{\lambda } = \left( {d_{1} \otimes d_{2} } \right)^{\lambda } \;\left( {\lambda_{1} ,\lambda_{2} \ge 0} \right). \)
We present the following comparison method to rank any two IVq-RDHLVs.
Definition 5
Let \( d = \left\langle {s_{\theta } ,\left( {h,g} \right)} \right\rangle \) be an IVq-RDHLV, and then, the score function of d is defined as:
and the accuracy function of d is defined as:
where \( \# h \) and \( \# g \) represent the numbers of interval values in \( h \) and \( g \), respectively. Let \( d_{1} = \left\langle {s_{{\theta_{1} }} ,\left( {h_{1} ,g_{1} } \right)} \right\rangle \) and \( d_{2} = \left\langle {s_{{\theta_{2} }} ,\left( {h_{2} ,g_{2} } \right)} \right\rangle \) be any two IVq-RDHLVs, and then:
-
1.
If \( S\left( {d_{1} } \right) > S\left( {d_{2} } \right) \), then \( d_{1} \) is superior to \( d_{2} \), denoted by \( d_{1} > d_{2} \);
-
2.
If \( S\left( {d_{1} } \right) = S\left( {d_{2} } \right) \), then
if \( p\left( {d_{1} } \right) = p\left( {d_{2} } \right) \), then \( d_{1} \) is equivalent to \( d_{2} \), denoted by \( d_{1} = d_{2} \);
if \( p\left( {d_{1} } \right) > p\left( {d_{2} } \right) \), then \( d_{1} \) is superior to \( d_{2} \), denoted by \( d_{1} > d_{2} \).
Maclaurin symmetric mean
Definition 6
[63] Let \( \alpha_{i} \left( {i = 1,2, \ldots ,n} \right) \) be a collection of crisp numbers, and \( k = 1,2, \ldots ,n \). If
and then, \( {\text{MSM}}^{\left( k \right)} \) is called the MSM, where \( \left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right) \) traversals all the k-tuple combination of \( \left( {1,2, \ldots ,n} \right) \) and \( C_{n}^{k} \) is the binomial coefficient.
In addition, Qin and Liu [51] proposed the dual Maclaurin symmetric mean.
Definition 7
[51]. Let \( \alpha_{i} \left( {i = 1,2, \ldots ,n} \right) \) be a collection of crisp numbers, and \( k = 1,2, \ldots ,n \). If
then \( {\text{DMSM}}^{\left( k \right)} \) is called dual Maclaurin symmetric mean (DMSM), where \( \left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right) \) traversals all the k-tuple combination of \( \left( {1,2, \ldots ,n} \right) \) and \( C_{n}^{k} \) is the binomial coefficient.
Aggregation operators for IVq-RDHL information
In this section, we extend MSM and DMSM to IVq-RDHL environment and propose a family of interval-valued q-rung dual hesitant linguistic Maclaurin symmetric mean operators. Moreover, some desirable properties of the proposed AOs are presented and discussed.
Interval-valued q-rung dual hesitant linguistic Maclaurin symmetric mean operator
Definition 8
Let \( d_{i} = \left\langle {s_{{\theta_{i} }} ,\,\left( {h_{i} ,g_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \) be a collection of IVq-RDHLVs and \( k = 1,2, \ldots ,n \), then the interval-valued q-rung dual hesitant linguistic Maclaurin symmetric mean (IVq-RDHLMSM) operator is defined as:
where \( \left( {i_{1} ,i_{2} , \ldots ,i_{n} } \right) \) traversals all the k-tuple combination of \( \left( {1,2, \ldots ,n} \right) \), and \( C_{n}^{k} \) is the binomial coefficient.
Based on the operations for IVq-RDHLVs, the following theorem can be obtained.
Theorem 2
Let \( d_{i} = \left\langle {s_{{\theta_{i} }} ,\,\left( {h_{i} ,g_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \)be a collection of IVq-RDHLVs, and then, the aggregated value by the IVq-RDHLMSM operator is also an IVq-RDHLV and:
Proof
Based on the operations of IVq-RDHLVs introduced in Definition 4, we have:
and
Furthermore:
Hence:
In the following, we discuss some desirable properties of the IVq-RDHLMSM operator.
Theorem 3
(Idempotency) Let \( d_{i} = \left\langle {s_{{\theta_{i} }} ,\left( {h_{i} ,g_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \) be a collection of IVq-RDHLVs, if all the IVq-RDHLVs are equal, i.e., \( d_{i} = d \) for all \( i \), and d only has one MG and one NMG, then:
Proof
Since \( d_{i} = d \) for \( i = 1,2, \ldots ,n \), we can get:
Theorem 4
(Monotonicity) Let \( d_{i} = \left\langle {s_{{\theta_{i} }} ,\left( {h_{i} ,g_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \)and \( d_{i}^{\prime } = \left\langle {s_{{\theta^{\prime}_{i} }} ,\left( {h_{i}^{\prime } ,g^{\prime}_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \)be two collections of IVq-RDHLVs, if \( s_{{\theta_{i} }} \ge s^{\prime}_{{\theta_{i} }} \), \( r_{i} \ge r_{i}^{\prime } \)and \( \eta_{i} \le \eta_{i}^{\prime } \)holds for all \( i = 1,2,\ldots,n \), where \( r_{i} \in h_{i} \),\( r^{\prime}_{i} \in h_{i}^{\prime } \),\( \eta_{i} \in g_{i} \)and \( \eta^{\prime}_{i} \in g^{\prime}_{i} \), then:
Proof
For easy description, we assume that:
and
Since \( s_{{\theta_{i} }} \ge s^{\prime}_{{\theta_{i} }} \) hold for all \( i = 1,2, \ldots ,n \), it is easy to prove that:
i.e., \( s_{\theta } \ge s_{\xi } \).
Since \( d_{i} \ge d_{i}^{\prime } \), we can get \( r_{i} \ge \left( {r_{i} } \right)^{\prime } \) and \( \left( {\prod\nolimits_{j = 1}^{k} {r_{{i_{j} }}^{l} } } \right)^{q} \ge \left( {\prod\nolimits_{j = 1}^{k} {\left( {r_{{i_{j} }}^{l} } \right)^{\prime } } } \right)^{q} \). Then:
and
Therefore,
i.e., \( g \ge k \).
Similarly, we also have \( t \ge l \),\( p \le m \) and \( q \le n \).
In the following, we will discuss three situations as follows.
If \( g > k \) and \( t > l \), we can get \( p \le m \) and \( q \le n \). Then:
If \( g = k \) and \( t = l \), we can get \( p < m \) and \( q < n \). Then:
If \( g = k \) and \( t = l \), we can get \( p = m \) and \( q = n \). Then:
Therefore, Theorem 4 is kept.
Theorem 5
(Boundedness) Let \( d_{i} = \left\langle {s_{{\theta_{i} }} ,\left( {h_{i} ,g_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \) be a collection of IVq-RDHLVs, if
and
then
Proof
According to Theorem 3 and Theorem 4, we have:
and
In addition, both \( d^{ - } \) and \( d^{ + } \) only have one MG and NMG. Therefore:
Therefore, we have \( d^{ - } \le {\text{IVq}} - {\text{RDHFLMSM}}^{\left( k \right)} \left( {d_{1} ,d_{2} , \ldots ,d_{n} } \right) \le d^{ + } \).
In the following, we discuss some special cases of the proposed IVq-RDHLMSM operator with respect to parameters k and q.
Case 1
If \( k = 1 \), then the IVq-RDHLMSM operator reduces to the interval-valued q-rung dual hesitant linguistic average (IVq-RDHLA) operator, that is:
Case 2
If \( k = 2 \), then the IVq-RDHLMSM operator reduces to the interval-valued q-rung dual hesitant linguistic Bonferroni mean (IVq-RDHLBM) operator; that is:
Case 3
If \( k = n \), then the IVq-RDHLMSM operator reduces to the interval-valued q-rung dual hesitant linguistic geometric (IVq-DHLG) operator:
Case 4
If \( q = 1 \), then the IVq-RDHLMSM operator reduces to interval-valued dual hesitant linguistic Maclaurin symmetric mean (IVDHLMSM) operator; that is:
Case 5
If \( q = 2 \), then the IVq-RDHLMSM operator reduces to the hesitant interval-valued Pythagorean linguistic Maclaurin symmetric mean (HIVPLMSM) operator; that is:
Interval-valued q-rung dual hesitant linguistic weighted Maclaurin symmetric mean operator
Definition 9
Let \( d_{i} = \left\langle {s_{{\theta_{i} }} ,\left( {h_{i} ,g_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \) be a collection of IVq-RDHFLVs and \( k = 1,2, \ldots ,n \). Let \( w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{\text{T}} \) be the weight vector, such that \( w_{i} \in \left[ {0,1} \right] \) and \( \sum\nolimits_{i = 1}^{n} {w_{i} } = 1 \). The interval-valued q-rung dual hesitant linguistic weighted Maclaurin symmetric mean (IVq-RDHLWMSM) operator is defined as:
where \( \left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right) \) traversals all the k-tuple combination of \( \left( {1,2, \ldots ,n} \right) \), and \( C_{n}^{k} \) is the binomial coefficient.
Theorem 6
Let \( d_{i} = \left\langle {s_{{\theta_{i} }} ,\left( {h_{i} ,g_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \)be a collection of IVq-RDHLVs, and then, the aggregated value by the IVq-RDHLWMSM operator is still an IVq-RDHLV and:
The proof of Theorem 6 is similar to that of Theorem 2, which is omitted here. In addition, it is easy to prove that the IVq-RDHLWMSM operator has the properties of monotonicity and boundedness.
Interval-valued q-rung dual hesitant linguistic dual Maclaurin symmetric mean operator
Definition 10
Let \( d_{i} = \left\langle {s_{{\theta_{i} }} ,\left( {h_{i} ,g_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \) be a collection of IVq-RDHLVs, and \( k = 1,2, \ldots ,n \), and then, the interval-valued q-rung dual hesitant linguistic dual Maclaurin symmetric mean (IVq-RDHLDMSM) operator:
where \( \left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right) \) traversals all the k-tuple combination of \( \left( {1,2, \ldots ,n} \right) \) and \( C_{n}^{k} \) is the binomial coefficient.
Theorem 7
Let \( d_{i} = \left\langle {s_{{\theta_{i} }} ,\left( {h_{i} ,g_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \)be a collection of IVq-RDHLVs, and then, the aggregated value by the IVq-RDHLDMSM operator is still an IVq-RDHLV and:
The proof of Theorem 7 is similar to that of Theorem 2, which is omitted here. Similar to the IVq-RDHLMSM operator, the IVq-RDHLDMSM operator also has the properties of idempotency, monotonicity, and boundedness.
In the followings, we are to investigate the special cases of the IVq-RDHLDMSM operator with respect to the parameters k and q.
Case 1
If \( k = 1 \), the IVq-RDHLDMSM operator reduces to the IVq-DHLG operator, which is shown as Eq. (14).
Case 2
If \( k = 2 \), the IVq-RDHLDMSM operator reduces to the interval-valued q-rung dual hesitant linguistic geometric Bonferroni mean (IVq-RDHLGBM) operator; that is:
Case 3
If \( k = n \), the IVq-RDHLDMSM operator reduces to the IVq-RDHLA operator, which is shown as Eq. (12).
Case 4
If \( q = 1 \), the IVq-RDHLDMSM operator reduces to the interval-valued dual hesitant linguistic dual Maclaurin symmetric mean (IVDHLDMSM) operator; that is:
Case 5
If \( q = 2 \), the IVq-RDHLDMSM operator reduces to the hesitant interval-valued Pythagorean linguistic dual Maclaurin symmetric mean (HIVPLDMSM) operator; that is:
Interval-valued q-rung dual hesitant linguistic weighted dual Maclaurin symmetric mean operator
Definition 11
Let \( d_{i} = \left\langle {s_{{\theta_{i} }} ,\left( {h_{i} ,g_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \) be a collection of IVq-RDHLVs and \( k = 1,2, \ldots ,n \). Let \( w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{\text{T}} \) be the weight vector, such that \( w_{i} \in \left[ {0,1} \right] \) and \( \sum\nolimits_{i = 1}^{n} {w_{i} } = 1 \). The interval-valued q-rung dual hesitant linguistic weighted dual Maclaurin symmetric mean (IVq-RDHLWDMSM) operator is defined as:
where \( \left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right) \) traversals all the k-tuple combination of \( \left( {1,2, \ldots ,n} \right) \), and \( C_{n}^{k} \) is the binomial coefficient.
Theorem 8
Let \( d_{i} = \left\langle {s_{{\theta_{i} }} ,\left( {h_{i} ,g_{i} } \right)} \right\rangle \left( {i = 1,2, \ldots ,n} \right) \)be a collection of IVq-RDHLVs, and then, the aggregated value by the IVq-RDHLWDMSM operator is still an IVq-RDHLV and:
The proof of Theorem 8 is similar to that of Theorem 2, which is omitted. In addition, it is easy to prove that the IVq-RDHLWDMSM operator has the properties of monotonicity and boundedness.
A novel method to MADM with IVq-RDHL information
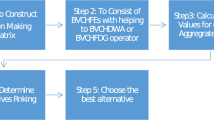
In the above sections, we have demonstrated the powerfulness and robustness of the IVq-RDHLVs and their AOs. In this section, we investigate the applications of IVq-RDHLVs and their AOs in MADM. Let us consider a MADM problem in which DMs express their evaluations in the form of IVq-RDHL information. Suppose that there are m alternatives that to be evaluated, which can be denoted as \( \left\{ {A_{1} ,A_{2} , \ldots ,A_{m} } \right\} \). Let \( \left\{ {C_{1} ,C_{2} , \ldots ,C_{n} } \right\} \) be a set of attributes, whose weight vector is \( w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{\text{T}} \), such that \( \sum\nolimits_{i = 1}^{n} {w_{i} } = 1 \) and \( 0 \le w_{i} \le 1 \). For the attribute \( C_{j} \left( {j = 1,2, \ldots ,n} \right) \) of \( A_{i} \left( {i = 1,2, \ldots ,m} \right) \), DMs use an IVq-RDHLV \( d_{ij} = \left\langle {s_{{\theta_{ij} }} ,\left\{ {\left\{ {\left[ {r_{ij}^{l} ,r_{ij}^{u} } \right]} \right\},\left\{ {\left[ {\eta_{ij}^{l} ,\eta_{ij}^{u} } \right]} \right\}} \right\}} \right\rangle \) to denote their evaluation value. Hence, finally, an IVq-RDHL decision matrix can be obtained, which can be denoted as \( R = \left( {d_{ij} } \right)_{m \times n} \). If we utilize the proposed IVq-RDHL aggregation operators to solve this MADM problem, the main steps are shown as follows.
-
Step 1.
Standardize the original decision matrix according to the following formula:
-
Step 2.
Calculate the overall evaluation value of each alternative by the IVq-RDHLWMSM operator:
or the IVq-RDHLWDMSM operator:
Hence, a set of overall evaluation values are derived.
-
Step 3.
Compute scores of the overall evaluations.
-
Step 4.
Rank the alternatives according to their corresponding scores.
Application of the proposed method in medical equipment selection
The former section introduces a novel MADM method. To better illustrate the procedure of the propose method, we apply it in a real decision-making problem. Furthermore, we also conduct comparative analysis to show the advantages and superiorities of the proposed method.
Example 1
Medical equipment is an important infrastructure for a hospital, which is directly related to the medical service content and service capacity. The choice of medical equipment is influenced by many factors, including the hospitals’ budget, whether the fund is sufficient, whether the hospital has the conditions to utilize the equipment, the degree of equipment demand, the technical evaluation of the equipment, the selection of equipment, the maintainability, etc. In this context, medical equipment selection is a problem with high dimension and high complexity. Thus, fuzzy theory is very suitable for the solving the medical equipment purchasing problem. In this paper, we assume that there are four medical equipment with different brands. Let \( A_{i} \left( {i = 1,2,3,4} \right) \) denote the brand of equipment i. DMs assess each of them under attribute \( C_{j} \left( {j = 1,2,3,4} \right) \), where C1 represents equipment quality; C2 represents equipment price; C3 represents after-sale service; and C4 represents user evaluation, whose weight vector is \( w = \left( {0.25,0.35,0.20,0.20} \right)^{\text{T}} \). Based on the procurement principle, DMs usually express their evaluation information on the medical equipment and mainly focus on 5 levels {unqualified, qualified, medium, good, excellent}. To comprehensively express the evaluation information over the performance of the feasible alternatives under attributes, DMs are requested to evaluate the four alternatives \( A_{i} \left( {i = 1,2,3,4} \right) \) with respect to the four attributes \( C_{j} \left( {j = 1,2,3,4} \right) \) by IVq-RDHLVs and an IVq-RDHL decision matrix \( d_{ij} = \left\langle {s_{{\theta_{ij} }} ,\left\{ {\left\{ {\left[ {r_{ij}^{\text{l}} ,r_{ij}^{\text{u}} } \right]} \right\},\left\{ {\left[ {\eta_{ij}^{\text{l}} ,\eta_{ij}^{\text{u}} } \right]} \right\}} \right\}} \right\rangle \) is obtained, which is shown in Table 1.
The decision-making procedure
-
Step 1.
As all attributes are benefit type, the original decision matrix does not need to be standardized.
-
Step 2.
Utilize the IVq-RDHFLWMSM operator to aggregate DMs’ assessments, so that the overall assessments of alternatives can be derived (suppose that k = 3, q = 3). As the aggregation results are so complicated, we omit them here.
-
Step 3.
Compute the scores of the overall assessments and we can obtain:
-
Step 4.
Based on the score values, the ranking order of alternatives is derived, i.e.,\( A_{4} \succ A_{3} \succ A_{1} \succ A_{2} \). Hence, the optimal choice is equipment is A4.
In step 3, if we utilize the IVq-RDHFLWDMSM operator to aggregate attribute values (suppose that k = 3, q = 3), then the scores of alternatives are:
Accordingly, the ranking order is \( A_{4} \succ A_{3} \succ A_{1} \succ A_{2} \) and \( A_{4} \) is the optimal alternative.
Sensitivity analysis
It is noted that our proposed method has two important parameters, i.e., k and q. It is obvious that the two parameters have a significant impact on the final decision results. This section aims to investigate the influence of the parameters on the decision results.
The influence of parameter k on the final results
In this subsection, we assign different values to k in the IVq-RDHLWMSM and IVq-RDHLWDMSM operators and present the decision results in Tables 2 and 3. As we can see from Tables 2 and 3, different score values are obtained with different parameter values of k; however, the ranking orders are the same, i.e., \( A_{4} \succ A_{3} \succ A_{1} \succ A_{2} \) and A4 is the optimal alternative. This characteristic demonstrates the robustness of our proposed method. In addition, it is noted that the score value of each alternative derived by the IVq-RDHLWMSM operator becomes smaller with the increase of parameter k. However, in the IVq-RDHLWDMSM operator, the increase of parameter values k leads to the increase of the score value of each alternative. Therefore, the parameter k can be regarded as DMs’ attitude to performance of alternatives. If DMs are optimistic about the alternatives, they can select a smaller value of k in the IVq-RDHLWMSM operator, or a larger value of k in the IVq-RDHLWDMSM operator. If DMs are pessimistic about the alternatives, they can choose a larger value of k in the IVq-RDHLWMSM operator and a smaller value of k in the IVq-RDHLWDMSM. If DMs do not have special preference, they choose the value of k can be taken as \( k = \left[ {{k \mathord{\left/ {\vphantom {k 2}} \right. \kern-0pt} 2}} \right] \), where [] is the round function and n is the number of attributes.
The influence of parameter q on the final results
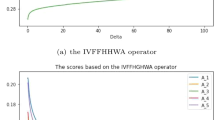
To investigate the influence of parameter q on the final decision results, we assign different values of q in the IVq-RDHLWMSM and IVq-RDHLWDMSM operators, and score values of alternatives are shown as Figs. 1 and 2. As seen from Fig. 1, different values of q lead to different score values of alternatives. Moreover, the score values of each alternative become greater with the increase of values of q in the IVq-RDHLWMSM operator. However, the ranking order is always \( A_{4} \succ A_{3} \succ A_{1} \succ A_{2} \) and A4 is the optimal alternative. Similarly, from Fig. 2, we find out that the increase of the value q in the IVq-RDHFLWDMSM operator also results in the increase of score value of each alternative. Although the ranking orders are slightly different, the best alternative is always A4. In our proposed method, how to select an appropriate value of q is an important issue. Liu [48] and his colleagues proposed a method to determine the value of q properly in q-rung orthopair fuzzy decision context, i.e., the value of q should be taken as the smallest integer that makes \( \mu^{q} + v^{q} \le 1\left( {q \ge 1} \right) \), where \( \mu \) and v denote the MG and NMG. For instance, a DM employs a q-ROFN \( \left( {0.75,0.95} \right) \) as his/her judgement over a certain alternative. As 0.755 + 0.955 = 1.0111 > 1 and 0.756 + 0.956 = 0.9131 < 1, the value of q can be taken as 6. In our proposed method, the value of q should be taken as the smallest integer that makes \( 0 \le \left( {\left( {r_{D}^{u} } \right)^{ + } } \right)^{q} + \left( {\left( {\eta_{D}^{u} } \right)^{ + } } \right)^{q} \le 1 \). For example, an IVq-RDHLV \( \left\langle s_{3} ,\big\{ \big\{ {\left[ {0.1,0.2} \right],\left[ {0.3,0.4} \right],\left[ {0.5,0.8} \right]} \big\},\big\{ \left[ {0.2,0.6} \right], [ 0.7, 0.8 ] \right. \left. \big\} \big\} \right\rangle \) is employed to express a DM’s evaluation over an alternative. As 0.83 + 0.83 = 1.024 > 1 and 0.84 + 0.84 = 0.8192 < 1, then the value of q should be taken as 4.
Validation analysis
In this subsection, we utilize our proposed method and some existing MADM methods to solve practical examples and discuss their decision results to demonstrate the validity of our proposed method. These methods involve that presented by Wei et al. [50] based on interval-valued dual hesitant fuzzy linguistic weighted average (IVDHFLWA) operator, and that introduced by Wei [64] based on interval-valued dual hesitant fuzzy uncertain linguistic weighted average (IVDHFULWA) operator.
Example 2
Suppose that there is a panel with three possible logistics outsourcing service providers in the engineering material procurement \( A_{i} \left( {i = 1,2,3} \right) \) to select with respect to four attributes, i.e.,\( C_{1} \) is the external environment; \( C_{2} \) is the enterprise management risk; \( C_{3} \) the logistics business risk; and \( C_{4} \) is the internal environment risk. The weight vector of the attributes is \( w = \left( {0.20,0.30,0.30,0.20} \right)^{T} \). DMs employed the interval-valued dual hesitant fuzzy linguistic variables (IVDHFLVs) to express their evaluations of alternatives and a normalized decision matrix is listed in Table 4. We utilize our proposed method based on the IVq-RDHLWMSM operator, and Wei et al.’s [50] and Wei’s [64] methods to solve Example 2.
It is noted that Wei’s [64] method is based on interval-valued dual hesitant fuzzy uncertain linguistic sets (IVDHFULSs). Actually, the interval-valued dual hesitant fuzzy linguistic set (IVDHFLS) is a special case of IVDHFULS, where the upper bound and lower bound of linguistic part are equal. Hence, we can transform an IVDHFLV into an interval-valued dual hesitant fuzzy uncertain linguistic variable (IVDHFULV). For instance, let \( \alpha = \left\langle {s_{4} ,\left\{ {\left\{ {0.3,0.4} \right\},\left\{ {0.5,0.6} \right\}} \right\}} \right\rangle \) be an IVDHFLV and we can transform \( \alpha \) into an IVDHFULV, i.e. \( \alpha = \left\langle {\left[ {s_{4} ,s_{4} } \right],\left\{ {\left\{ {0.3,0.4} \right\},\left\{ {0.5,0.6} \right\}} \right\}} \right\rangle \). Therefore, we can transform Table 4 into Table 5, which is an interval-valued dual hesitant fuzzy uncertain linguistic decision matrix. We list the decision results obtained by our proposed method and those introduced by Wei et al. [50] and Wei [64] in Table 6. As seen from Table 6, although the ranking orders are slightly different, the best alternative is always \( A_{2} \), which indicates the feasibility and correctness of our method.
Advantages of the proposed method
In this subsection, we further demonstrate the advantages and superiorities of our proposed method through comparative analysis.
Its powerfulness of expressing DMs’ judgements comprehensively
Our proposed method employs IVq-RDHLSs to depict DMs’ evaluation values over the performance of alternatives. As we know, the IVq-RDHLS should satisfy the constraint that the sum of qth power of MG and qth power of NMG is less than or equal to one. In practical decision-making situations, DMs adjust the parameter value q to make DMs’ evaluation values to meet this constraint. Hence, our method can comprehensively describe DMs’ assessment values in complicated decision-making problems. To better explain this advantage, we provide the following example.
Example 3
In Example 2, DMs employ IVDHFLSs to express their decision preference. The constraint of IVDHFLSs is that the sum of MG and NMG should be not greater than one. Nevertheless, this constraint cannot be always satisfied. For example, we replace the evaluation value of attribute C1 of A1 with \( \left\langle {s_{2} ,\left\{ {\left\{ {\left[ {0.1,0.2} \right],\left[ {0.2,0.8} \right]} \right\},\left\{ {\left[ {0.3,0.9} \right]} \right\}} \right\}} \right\rangle \)(The other evaluation values keep unchanged.). If we utilize the Wei et al.’s [50] and Wei’s [64] MADM method and our proposed method to solve Example 3, then the decision results are obtained (listed in Table 7).
As we can see from Table 7, the methods proposed by Wei et al. [50] and Wei [64] fail to deal with Example 3, whereas our proposed method can still handle this case and the ranking order is \( A_{2} \succ A_{3} \succ A_{1} \). This is because in the revised example, the evaluation value of the attribute C1 of alternative A1 cannot be represented by IVDHFLSs and IVDHFULSs as 0.8 + 0.9 = 1.7 > 1. Our proposed method can still deal with this case, and if we set q = 5, then 0.85 + 0.95 = 0.9182 < 1 (The method to appropriately determine the value of q is presented in section “The influence of parameter q on the final results”). Hence, our propose method can deal with more complicated decision information, give DMs more freedom to provide their evaluations, and comprehensively express DMs’ judgements.
Its ability of capturing the interrelationship among attributes
In practical decision-making problems, there exists weak or strong interrelationship among attributes. To make the final decision results more reliable, it is necessary to take such interrelationship into consideration when determining the optimal alternative. As we can see, our method and those proposed by Wei et al. [50] and Wei [64] can effectively solve Example 2. In addition, our proposed method is based on the IVq-RDHLWMSM operator, which has an important parameter k, making the decision-making procedure flexible. If we assign different values to k when dealing with Example 2 by our proposed method, we can obtain the following results (listed in Table 8).
It is noted that the methods proposed by Wei et al. [50] and Wei [64] are based on simple weighted average operator. Hence, the two MADM methods take the evaluation values and the weight information of attributes into account when calculating the overall preference of DMs over alternatives. However, Wei et al.’s [50] and Wei’s [64] methods do not consider the interrelationship among attributes. That is to say, Wei et al.’s [50] and Wei’s [64] methods assume that the attributes are independent, which is not always consistent with the reality. Our method based on the IVq-RDHLWMSM operator can effectively deal with the correlation among attributes. For example, when we set k = 2, then the interrelationship between any attributes is reflected. If any three attributes are interacted, we can set k = 3. If there is no interrelationship among attributes, we can let k = 1. Hence, as in the most practical MADM problems, the attributes are usually dependent, our proposed method is more powerful and suitable than those proposed by Wei et al. [50] and Wei [64].
The ability of portraying DMs’ evaluation information both quantificationally and qualitatively
Our proposed method employs IVq-RDHLSs to denote DMs’ evaluation information over the performance of alternatives. Basically, the IVq-RDHLS is a hybrid tool that can describe fuzzy decision information from both quantitative and qualitative aspects. When we utilize IVq-RDHLSs to express decision-making information, we first provide DMs a predefined LTS, and DMs can choose proper linguistic terms to express their qualitative decision information. In addition, the IVq-RDHFSs are employed for DMs to express the MG and NMG of a linguistic term, so that their quantitative decision ideas are expressed. Hence, via the LTS and IVq-RDHFSs, we can denote DMs’ evaluation information more accurately, so that the final decision results are more reliable. Compared with our proposed MADM method, the decision method proposed by Xu et al. [43] uses the IVq-RDHFSs to denote the DMs’ fuzzy judgements, which only concerns the quantitative information and neglects DMs’ qualitative evaluation information. In other words, the method of Xu et al. [43] cannot fully express DMs’ evaluation values in complicated decision-making context, so that the decision results obtained are insufficient. Hence, compared with Xu et al.’s [43] method, our proposed method is more sufficient to deal with complex decision-making problems and the final ranking orders of alternatives are more reliable. We list the characteristics of all the above-mentioned MADM methods in Table 9 to better illustrate the advantages and superiorities of our proposed method.
Conclusions
The IVq-RDHFSs are a good tool in describing fuzzy information. However, the main shortcoming of IVq-RDHFSs is that they only express DMs’ quantitative decision information. To overcome such drawback, we proposed the notion of IVq-RDHLSs by combining IVq-RDHFSs with TLS. The IVq-RDHLSs not only portray DMs’ quantitative and qualitative evaluation values, but also effectively deal with DMs’ hesitancy in MADM procedures. In addition, due to its laxer constraint, the IVq-RDHLS also give DMs great freedom to comprehensively express their judgements. To effectively handle MADM under IVq-RDHLSs, we have proposed the IVq-RDHLMSM, IVq-RDHLWMSM, IVq-RDHLDMSM, and IVq-RDHLWDMSM operators. Besides, we have also introduced a method to determine the optimal alternative based on the IVq-RDHLWMSM and IVq-RDHLWDMSM operators. From the numerical examples, the feasibility and effectiveness of our proposed method have been clearly illustrated. In addition, advantages and superiorities of the new MADM method have been presented through comparative analysis. For future research, we will investigate new AOs of IVq-RDHLs information and propose novel powerful MADM methods.
References
Abdullah L, Goh P (2019) Decision making method based on Pythagorean fuzzy sets and its application to solid waste management. Complex Intell Syst 5(2):185–198
Rahman K, Abdullah S (2019) Some induced generalized interval-valued Pythagorean fuzzy Einstein geometric aggregation operators and their application to group decision-making. Comput Appl Math 38(3):139
Rahman K, Abdullah S, Ali A, Amin F (2019) Interval-valued Pythagorean fuzzy Einstein hybrid weighted averaging aggregation operator and their application to group decision making. Complex Intell Syst 5(1):41–52
Peng X, Selvachandran G (2019) Pythagorean fuzzy set: state of the art and future directions. Artif Intell Rev 52(3):1873–1927
Khan MSA (2019) The Pythagorean fuzzy Einstein Choquet integral operators and their application in group decision making. Comput Appl Math 38(3):128
Kumar K, Edalatpanah SA, Jha S, Singh R (2019) A Pythagorean fuzzy approach to the transportation problem. Complex Intell Syst 5(2):255–263
Mandal P, Ranadive AS (2019) Multi-granulation Pythagorean fuzzy decision-theoretic rough sets based on inclusion measure and their application in incomplete multi-source information systems. Complex Intell Syst 5(2):145–163
Zhang R, Wang J, Zhu X, Xia M (2017) Some generalized Pythagorean fuzzy Bonferroni mean aggregation operators with their application to multi-attribute group decision-making. Complexity 2017:5937376
Zhu X, Bai K, Wang J, Zhang R, Xing Y (2019) Pythagorean fuzzy interaction power partitioned Bonferroni means with applications to multi-attribute group decision making. J Intell Fuzzy Syst 36(4):3423–3438
Yang W, Pang Y (2018) Hesitant interval-valued Pythagorean fuzzy VIKOR method. Int J Intell Syst 34(5):754–789
Yang W, Wang C, Liu Y, Sun Y (2019) Hesitant Pythagorean fuzzy interaction aggregation operators and their application in multiple attribute decision-making. Complex Intell Syst 5(2):199–216
Yager RR (2013) Pythagorean membership grades in multicriteria decision making. IEEE T Fuzzy Syst 22(4):958–965
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96
Yager RR (2017) Generalized orthopair fuzzy Sets. IEEE T Fuzzy Syst 25(5):1222–1230
Liu P, Wang P (2018) Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int J Intell Syst 33(2):259–280
Liu P, Liu J (2018) Some q-rung orthopair fuzzy Bonferroni mean operators and their application to multi-attribute group decision making. Int J Intell Syst 33(2):315–347
Wei G, Gao H, Wei Y (2018) Some q-rung orthopair fuzzy Heronian mean operators in multiple attribute decision making. Int J Intell Syst 33(7):1426–1458
Wang J, Wei G, Lu J, Alsaadi FE, Hayat T, Wei C, Zhang Y (2019) Some q-rung orthopair fuzzy Hamy mean operators in multiple attribute decision-making and their application to enterprise resource planning systems selection. Int J Intell Syst 34(10):2429–2458
Wei G, Wei C, Wang J, Gao H, Wei Y (2019) Some q-rung orthopair fuzzy Maclaurin symmetric mean operators and their applications to potential evaluation of emerging technology commercialization. Int J Intell Syst 34(1):50–81
Wang J, Zhang R, Zhu X, Zhou Z, Shang X, Li W (2019) Some q-rung orthopair fuzzy Muirhead means with their application to multi-attribute group decision making. J Intell Fuzzy Syst 36(2):1599–1614
Liu P, Chen S, Wang P (2018) Multiple-attribute group decision-making based on q-rung orthopair fuzzy power Maclaurin symmetric mean operators. IEEE T Syst Man CY. https://doi.org/10.1109/TSMC.2018.2852948
Bai K, Zhu X, Wang J, Zhang R (2018) Some partitioned Maclaurin symmetric mean based on q-rung orthopair fuzzy information for dealing with multi-attribute group decision making. Symmetry 10(9):383
Liu Z, Liu P, Liang X (2018) Multiple attribute decision-making method for dealing with heterogeneous relationship among attributes and unknown attribute weight information under q-rung orthopair fuzzy environment. Int J Intell Syst 33(9):1900–1928
Yang W, Pang Y (2019) New q-rung orthopair fuzzy partitioned Bonferroni mean operators and their application in multiple attribute decision making. Int J Intell Syst 34(3):439–476
Peng X, Dai J, Garg H (2018) Exponential operation and aggregation operator for q-rung orthopair fuzzy set and their decision-making method with a new score function. Int J Intell Syst 33(11):2255–2282
Xing Y, Zhang R, Wang J, Bai K, Xue J (2019) A new multi-criteria group decision-making approach based on q-rung orthopair fuzzy interaction Hamy mean operators. Neural Comput Appl. https://doi.org/10.1007/s00521-019-04269-8
Darko AP, Liang D (2020) Some q-rung orthopair fuzzy Hamacher aggregation operators and their application to multiple attribute group decision making with modified EDAS method. Eng Appl Artif Intell 87:103259
Jana C, Muhiuddin G, Pal M (2019) Some Dombi aggregation of Q-rung orthopair fuzzy numbers in multiple-attribute decision making. Int J Intell Syst 34(12):3220–3240
Liu P, Wang P (2018) Multiple-attribute decision-making based on Archimedean Bonferroni operators of q-rung orthopair fuzzy numbers. IEEE T Fuzzy Syst 27(5):834–848
Du WS (2018) Minkowski-type distance measures for generalized orthopair fuzzy sets. Int J Intell Syst 33(4):802–817
Peng X, Liu L (2019) Information measures for q-rung orthopair fuzzy sets. Int J Intell Syst 34(8):1795–1834
Liu D, Chen X, Peng D (2019) Some cosine similarity measures and distance measures between q-rung orthopair fuzzy sets. Int J Intell Syst 34(7):1572–1587
Peng X, Dai J (2019) Research on the assessment of classroom teaching quality with q-rung orthopair fuzzy information based on multiparametric similarity measure and combinative distance-based assessment. Int J Intell Syst 34(7):1588–1630
Liu P, Liu W (2019) Multiple-attribute group decision-making based on power Bonferroni operators of linguistic q-rung orthopair fuzzy numbers. Int J Intell Syst 34(4):652–689
Liu P, Liu W (2019) Multiple-attribute group decision-making method of linguistic q-rung orthopair fuzzy power Muirhead mean operators based on entropy weight. Int J Intell Syst 34(8):1755–1794
Li L, Zhang R, Shang X (2018) Some q-rung orthopair linguistic Heronian mean operators with their application to multi-attribute group decision making. Arch Control Sci 28(4):551–583
Wang H, Ju Y, Liu P (2019) Multi-attribute group decision-making methods based on q-rung orthopair fuzzy linguistic sets. Int J Intell Syst 34(6):1129–1157
Wang J, Zhang R, Li L, Zhu X, Shang X (2019) A novel approach to multi-attribute group decision making based on q-rung orthopair uncertain linguistic information. J Intell Fuzzy Syst 36(6):5565–5581
Xing Y, Zhang R, Zhu X, Bai K (2019) q-Rung orthopair fuzzy uncertain linguistic choquet integral operators and their application to multi-attribute decision making. J Intell Fuzzy Syst 37(1):1123–1139
Liu Z, Li L, Li J (2019) q-Rung orthopair uncertain linguistic partitioned Bonferroni mean operators and its application to multiple attribute decision-making method. Int J Intell Syst 34(10):2490–2520
Liu Z, Xu H, Yu Y, Li J (2019) Some q-rung orthopair uncertain linguistic aggregation operators and their application to multiple attribute group decision making. Int J Intell Syst 34(10):2521–2555
Xu Y, Shang X, Wang J, Wu W, Huang H (2018) Some q-rung dual hesitant fuzzy Heronian mean operators with their application to multiple attribute group decision-making. Symmetry 10(10):472
Xu Y, Shang X, Wang J, Zhao H, Zhang R, Bai K (2019) Some interval-valued q-rung dual hesitant fuzzy Muirhead mean operators with their application to multi-attribute decision-making. IEEE Access 7:54724–54745
Liu P, Xu H, Geng Y (2020) Normal wiggly hesitant fuzzy linguistic power Hamy mean aggregation operators and their application to multi-attribute decision-making. Comput Chem Eng 140:106224
Wang J, Zhang R, Zhu X, Buchmeister B (2018) Some hesitant fuzzy linguistic Muirhead means with their application to multi-attribute group decision-making. Complexity 2018:5087851
Liu P, Zhang X (2020) A new hesitant fuzzy linguistic approach for multiple attribute decision making based on Dempster-Shafer evidence theory. Appl Soft Comput 86:105897
Cao H, Zhang R, Wang J (2019) Some spherical linguistic Muirhead mean operators with their application to multi-attribute decision making. J Intell Fuzzy Syst 37(6):8097–8111
Liu P, Jin F (2012) Methods for aggregating intuitionistic uncertain linguistic variables and their application to group decision making. Inf Sci 205:58–71
Du Y, Hou F, Zafar W, Yu Q, Zhai Y (2017) A novel method for multi-attribute decision making with interval-valued Pythagorean fuzzy linguistic information. Int J Intell Syst 32(10):1085–1112
Wei G, Lin R, Wang H, Ran LG (2015) Interval-valued dual hesitant fuzzy linguistic arithmetic aggregation operators in multiple attribute decision making. Int Core J Eng 1(6):212–222
Qin J, Liu X (2014) An approach to intuitionistic fuzzy multiple attribute decision making based on Maclaurin symmetric mean operators. J Intell Fuzzy Syst 27(5):2177–2190
Liu P, Chen S, Wang Y (2020) Multi-attribute group decision making based on intuitionistic fuzzy partitioned Maclaurin symmetric mean operators. Inf Sci 512:830–854
Liu Z, Teng F, Liu P, Ge Q (2018) Interval-valued intuitionistic fuzzy power Maclaurin symmetric mean aggregation operators and their application to multiple attribute group decision-making. Int J Uncertain Quan 8(3):211–232
Qin J, Liu X, Pedrycz W (2015) Hesitant fuzzy Maclaurin symmetric mean operators and its application to multiple-attribute decision making. Int J Intell Syst 17(4):509–520
Liu P, Zhang X (2018) Some Maclaurin symmetric mean operators for single-valued trapezoidal neutrosophic numbers and their applications to group decision making. Int J Intell Syst 20(1):45–61
Ju Y, Liu X, Yang S (2014) Interval-valued dual hesitant fuzzy aggregation operators and their applications to multiple attribute decision making. J Intell Fuzzy Syst 27(3):1203–1218
Yang W, Pang Y (2019) Hesitant interval-valued Pythagorean fuzzy VIKOR method. Int J Intell Syst 34(5):754–789
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning—Part II. Inf Sci 8(4):301–357
Wang J, Li J (2009) The multi-criteria group decision making method based on multi-granularity intuitionistic two semantics. Sci Trans Inf 33(1):8–9
Peng X, Yang Y (2016) Multiple attribute group decision making methods based on Pythagorean fuzzy linguistic set. Comput Eng Appl 52(23):50–54
Lin R, Zhang F, Wang H, Wei G (2014) Hesitant fuzzy linguistic aggregation operators and their application to multiple attribute decision making. J Intell Fuzzy Syst 27(1):49–63
Herrera VE, Martinez L, Mata F, Chiclana F (2005) A consensus support system model for group decision-making problems with multigranular linguistic preference relations. IEEE T Fuzzy Syst 13(5):44–658
Maclaurin C (1729) A second letter to Martin Folkes, Esq concerning the roots of equations, with demonstration of other rules of algebra. Philos Trans 36:59–96
Wei G (2017) Interval-valued dual hesitant fuzzy uncertain linguistic aggregation operators in multiple attribute decision making. J Intell Fuzzy Syst 33(3):1881–1893
Acknowledgements
This work was supported by National Natural Science Foundation of China (61702023), Humanities and Social Science Foundation of Ministry of Education of China (17YJC870015), Beijing Natural Science Foundation (7192107), and the Beijing Social Science Foundation (19JDGLB022).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Feng, X., Shang, X., Xu, Y. et al. A method to multi-attribute decision-making based on interval-valued q-rung dual hesitant linguistic Maclaurin symmetric mean operators. Complex Intell. Syst. 6, 447–468 (2020). https://doi.org/10.1007/s40747-020-00141-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-020-00141-8