Abstract
One of the methods of studying on two sets is to calculate the similarity of two sets. Triangular norms and conorms generalize the basic connectives between fuzzy sets, intuitionistic fuzzy sets, Pythagorean fuzzy sets. In this paper we used triangular conorms (S-norm). The advantage of using S-norm is that the similarity order does not change using different norms. In fact, we are looking for a new definition for calculating the similarity of two Pythagorean fuzzy sets. To achieve this goal, using an S-norm, we first present a formula for calculating the similarity of two Pythagorean fuzzy values, so that they are truthful in similarity properties. Following that, we generalize a formula for calculating the similarity of the two Pythagorean fuzzy sets which prove truthful in similarity conditions. Finally, we give some examples of this method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Atanassov [1] initiated the concept of intuitionistic fuzzy set (IFS), which is a generalization of Zadeh’s fuzzy sets. Another generalization of fuzzy sets is Pythagorean fuzzy sets (PFSs), which was introduced by Yager [2] as an efficient expansion of the intuitionistic fuzzy sets. A intuitionistic fuzzy sets and Pythagorean fuzzy set has emerged as an effective tool for depicting uncertainty of the multiple attribute decision-making (MADM) problems [3,4,5,6]. The PFS is also characterized by the membership degree and the non-membership degree, whose sum of squares is less than or equal to 1. The Pythagorean fuzzy sets, more comprehensive than IFS, provides a new method for modeling uncertainty and vagueness. PFSs have meaningful applications in many different fields. For example, extension of TOPSIS to multiple criteria decision making (Zhang and Xu [4], Yang et al. [7], Liang and Xu [8]); Pythagorean fuzzy Choquet integral based MABAC method (Peng and Yang [9]); the multiobjective optimization on the basis of ratio analysis (MOORA) method (Perez-Dominguez et al. [10]); Pythagorean fuzzy analytic hierarchy process (Mohd and Abdullah [11], Ilbahar et al. [12]); application of Pythagorean fuzzy AHP and VIKOR methods in occupational health and safety risk assessment (Gul [13]).
Peng and Yang [14] developed a Pythagorean fuzzy superiority and inferiority ranking method to solve uncertainty multiple attribute group decision-making problem. Ren et al. [15] extended the TODIM approach to solve the MCDM problems with Pythagorean fuzzy information. Garg [16] proposed a novel correlation coefficient, and weighted correlation coefficient formulation to measure the relationship between two PFSs. Peng and Selvachandran [17] provided two novel algorithms in decision-making problems under Pythagorean fuzzy environment. Garg [18] presented a new decision-making model with probabilistic information and using the concept of immediate probabilities has been developed to aggregate the information under the Pythagorean fuzzy set environment. Xue et al. [19] studied the linear programming technique for multidimensional analysis of preference method under the Pythagorean fuzzy circumstance to solve MAGDM problems and so on [20,21,22,23,24,25,26,27,28,29].
The similarity measures are important and useful tools for determining the degree of similarity between two objects. The definition of similarity measure between PFSs is one of the most important topics in PFSs theory and it compares the information carried by PFSs. Measures of similarity between PFSs is an important tool for MADM Problem, medical diagnosis, decision making, pattern recognition, machine learning, image processing, and in other real-world problems. Recently, some researchers have been engaged in the development of similarity measure of PFSs and its applications . For example, Zhang [31] developed a new decision method based on similarity measure to address multiple criteria group decision-making problems within Pythagorean fuzzy environment. Recently, Peng [32] defined novel Pythagorean fuzzy distance measure and similarity measure. Furthermore, Wei and Wei [33] presented similarity measures of Pythagorean fuzzy sets based on the cosine function for dealing with the decision-making problems. Mohd and Abdullah [34] investigated similarity measures of Pythagorean fuzzy sets based on a combination of cosine similarity measure and Euclidean distance measure. Ejegwa [35] presented axiomatic definitions of distance and similarity measures for Pythagorean fuzzy sets, taking into account the three parameters, namely, membership degree, non-membership degree, and indeterminate degree, and so on [36,37,38]. In this paper, our aim is to propose similarity measures based on norms for PFSs, and some of the basic properties of the new similarity measures were discussed. The motivation for writing this paper is that we introduced triangular conorms (S-norm) as a new similarity measure for Pythagorean fuzzy sets. The advantage of using S-norm is that the similarity order does not change using different norms. In addition, we propose a multi-criteria group decision-making method based on the new similarity measures.
The rest of the presented paper is outlined as the following: In “Definitions and some properties” section, we review some definitions and properties. In “S-similarity measure of Pythagorean fuzzy sets” section, we propose several new similarity measures for Pythagorean fuzzy based on norms. In “Applications” section, we present examples. This paper is concluded in “Conclusions”.
Definitions and some properties
In sets theory, ambiguity in membership can be viewed from two perspectives: truth membership and false membership. Hence, these notions can be defined as follows.
Definition 2.1
[1, 40] Let \(U=\{u_1,u_2,u_3, \ldots ,u_n\}\) ndenote the discourse set. A intuitionistic fuzzy set A in U is characterized by a membership function \(\mu _A: U \rightarrow [0, 1]\) nand a non-membership function \(\nu _A: U \rightarrow [0, 1]\), where \(\mu _A(u_i)+ \nu _A(u_i)\le 1\).
Recently, Yager [2] introduced Pythagorean fuzzy set (PFS) characterized by a membership degree and a non-membership degree satisfying the condition that the square sum of its membership degree and non-membership degree is equal to or less than 1, which is a generalization of IFS.
Definition 2.2
[4] Let \(U=\{u_1,u_2,u_3, \ldots ,u_n\}\) denote the discourse set. A Pythagorean fuzzy set A in U is characterized by a truth-membership function \(\mu _A: U \rightarrow [0, 1]\) and a false-membership function \(\nu _A: U \rightarrow [0, 1]\), where \(\mu _A(u_i)\) are grades of the membership of \(u_i\) in A and \(\nu _A(u_i)\) are the negation of \(u_i\) in A, and \(\mu ^2_A(u_i)+ \nu ^2_A(u_i)\le 1\). Simply expressed, \(\mu _{A_i}:=\mu _{A}(u_i)\) and \(\nu _{A_i}:=\nu _{A}(u_i)\), \(i=1, \ldots ,n\). P(U) stands for the set of all Pythagorean fuzzy subsets in U and for \(A\in P(U)\), it can be we written as
where \(P_A(u_i)=(\mu _{A_i},\nu _{A_i})\) is Pythagorean fuzzy value.
For two Pythagorean fuzzy values \((\mu _1,\nu _1)\) and \((\mu _2,\nu _2)\), we have
and
and
In addition
Definition 2.3
[14] For two Pythagorean fuzzy sets \(A,B\in P(U)\), we can claim \(A\subseteq B\) if and only if \(\mu _{A_i}\le \mu _{B_i}\) and \(\nu _{A_i}\ge \nu _{B_i}\) for each \(u_i\in U;~~i=1, \ldots ,n\).
Decision making is the process of selecting a possible course from all of the possible alternatives. An effective approach to select an eligible alternative based on our opinion is its similarity to ideal point. In addition, in our study, we employ S-norm as an instrument for employing similarity measure. Hence, we give the following definitions.
Definition 2.4
Let A, B, and C be three sets. A real function s(., .) is called the similarity measure if s satisfies the following properties:
- (1)
\(0\le s(A,B)\le 1\).
- (2)
\(s(A,B)=s(B,A)\).
- (3)
\(s(A,B)=1~~ \leftrightarrow ~~ A=B\).
- (4)
If \(A\subseteq B\), and \(B\subseteq C\), then \(s(A,C) \le \mathrm{{min}}\{s(A,B), s(B,C)\}\).
Definition 2.5
[39] A binary operation \(S:[0,1]\times [0,1]\mapsto [0,1]\) is a continuous S-norm if it satisfies the following conditions:
- (S-1)
S is associative and commutative.
- (S-2)
\(S(a,0)=a\) for all \(a \in [0,1]\).
- (S-3)
\(S(a,b) \le S(c,d)\) whenever \(a \le c\) and \(b \le d\), for each \(a, b, c, d \in [0,1]\).
Some of the basic S-norm are as follows:
S-similarity measure of Pythagorean fuzzy sets
In this section, in order to determine a similar measure between two Pythagorean fuzzy sets, it is necessary that we first present the method for calculating a similar measure for two Pythagorean fuzzy values and then extended it for two Pythagorean fuzzy sets.
In [4], Zhang and Xu introduced a similar measure between Pythagorean fuzzy values as follows: Let \(x=(\mu _x,\nu _x)\), \(y=(\mu _y,\nu _y)\) be two Pythagorean fuzzy values, the similarity measure between x and y is defined as
where \(y^c=(\nu _y,\mu _y)\) and
Definition 3.1
Let x and y be two Pythagorean fuzzy values, such that \(x=(\mu _x,\nu _x)\) and \(y=(\mu _y,\nu _y)\), where \({\mu _x}^2+{\nu _x}^2\le 1\) and \({\mu _y}^2+{\nu _y}^2\le 1\). The s-similarity measure for the Pythagorean fuzzy values x and y denoted by \(s(x,y)_S\) is defined by
where S(., .) is a continuous S-norm.
Notation 3.2
The similar measure between Pythagorean fuzzy values by Zhang and Xu [4] in Eq. (3.1) does not give a suitable similar measure for \(\mu _y=\nu _y\). The similar measure by Eq. (3.1) is \(\frac{1}{2} \), but the similar measure between Pythagorean fuzzy values by Eq. (3.3) has a suitable similar measure.
Theorem 3.3
Let \(x=(\mu _x,\nu _x)\), \(y=(\mu _y,\nu _y)\) and \(z=(\mu _z,\nu _z)\) be three Pythagorean fuzzy values. Therefore, \(s(.,.)_S\) corresponding to the formula (3.3) is satisfied in the following property.
- (1)
\(0\le s(x,y)_S\le 1\).
- (2)
\(s(x,y)_S=s(y,x)_S\).
- (3)
\(s(x,y)_S=1~~ \leftrightarrow ~~ x=y\).
- (4)
If \(\mu _x \le \mu _y \le \mu _z\), and \(\nu _x \ge \nu _y \ge \nu _z\), then \(s(x,z)_S\le \mathrm{{min}}\{s(x,y)_S, s(y,z)_S\}\).
Proof
Simply we can obtain 1, 2 and 3. For 4:
If \(\mu _x \le \mu _y \le \mu _z\), and \(\nu _x \ge \nu _y \ge \nu _z\), then
Regarding (S-3) of Definition 2.5
Hence
With Definition 3.1
then
and the proof is completed. \(\square \)
Remark 3.4
\(s(x,y)_{S_2} \le s(x,y)_{S_3} \le s(x,y)_{S_1}\).
It can be easily shown that
Let \(c=(\mu _x-\mu _y)^2\) and \(d= (\nu _x-\nu _y)^2\), then we have \(0\le c \le 1\), \(0\le d \le 1\) and \(0\le c+d-cd \le 1 \), \( c+d-cd \le c+d\). Finally, we have \(c+d-cd \le \mathrm{{min}}\left\{ c+d,1\right\} \), that is \(s(x,y)_{S_2} \le s(x,y)_{S_3}\).
In addition, it is clear that \(c \le c+d-cd\) and \(d \le c+d-cd\), than \(\max \left\{ c,d\right\} \le c+d-cd\), that is \(s(x,y)_{S_3} \le s(x,y)_{S_1} \).
We find S-similarity measures for some Pythagorean fuzzy values with various S-norms presented in Definition 2.5. If \(x=(0.9,0.3), y=(0.7,0.4)\), then with regard to S-similarity measures in [4] \(sm(x,y)=0.67 \).
With regard to our S-similarity measures, the results are
In [33], Wei and Wei have presented:
- 1.:
A weighted cosine similarity measure between Pythagorean fuzzy sets A and B is as follows:
$$\begin{aligned}&WPFC^1\left( A,B\right) \nonumber \\&\quad =\sum _{j=1}^{n}w_j\frac{\mu _A^2(x_j)\mu _B^2(x_j)+\nu _A^2(x_j)\nu _B^2(x_j)}{\sqrt{\mu _A(x_j)^4+\nu _A(x_j)^4}\sqrt{\mu _B(x_j)^4+\nu _B(x_j)^4}}\nonumber \\ \end{aligned}$$(3.4)- 2.:
Two weighted cosine similarity measures between Pythagorean fuzzy sets A and B are as follows:
$$\begin{aligned}&WPFCS^1\left( A,B\right) \nonumber \\&\quad =\sum _{j=1}^{n}w_j\, \cos \left[ \frac{\pi }{2}\left( \left| \mu _{A}^{2}\left( x_j\right) -\mu _{B}^{2}\left( x_j\right) \right| \vee \right. \right. \nonumber \\&\qquad \left. \left. \left| \nu _{A}^{2}\left( x_j\right) -\nu _{B}^{2}\left( x_j\right) \right| \right) \right] \end{aligned}$$(3.5)$$\begin{aligned}&WPFCS^2\left( A,B\right) \nonumber \\&\quad =\sum _{j=1}^{n}w_j\, \cos \left[ \frac{\pi }{4}\left( \left| \mu _{A}^{2}\left( x_j\right) -\mu _{B}^{2}\left( x_j\right) \right| \right. \right. \nonumber \\&\qquad \left. \left. + \,\left| \nu _{A}^{2}\left( x_j\right) -\nu _{B}^{2}\left( x_j\right) \right| \right) \right] \end{aligned}$$(3.6)- 3.:
Two weighted cotangent similarity measures between Pythagorean fuzzy sets A and B are as follows:
$$\begin{aligned}&WPFCT^1\left( A,B\right) \nonumber \\&=\sum _{j=1}^{n}w_j\, \cot \left[ \frac{\pi }{4}+\frac{\pi }{4}\left( \left| \mu _{A}^{2}\left( x_j\right) -\mu _{B}^{2}\left( x_j\right) \right| \right. \right. \nonumber \\&\qquad \left. \left. \vee \left| \nu _{A}^{2}\left( x_j\right) -\nu _{B}^{2}\left( x_j\right) \right| \right) \right] \end{aligned}$$(3.7)$$\begin{aligned}&WPFCT^2\left( A,B\right) \nonumber \\&\quad =\sum _{j=1}^{n}w_j\, \cot \left[ \frac{\pi }{4}+\frac{\pi }{8}\left( \left| \mu _{A}^{2}\left( x_j\right) -\mu _{B}^{2}\left( x_j\right) \right| \right. \right. \nonumber \\&\qquad \left. \left. + \left| \nu _{A}^{2}\left( x_j\right) -\nu _{B}^{2}\left( x_j\right) \right. \right) \right] , \end{aligned}$$(3.8)
where \(w=\left( w_1,w2,\ldots ,w_n\right) ^{T}\) is the weight vector of \(x_j\)\((j=1,2,\ldots ,n)\), with \(w_j\in \left[ 0,\,1\right] \)\((j=1,2,\ldots ,n)\), \(\sum \nolimits _{j=1}^{n}w_j=1\) and the symbol “\(\vee \)” is the maximum operation.
Definition 3.5
Let \(U=\{u_1,u_2,u_3, \ldots ,u_n\}\) denote discourse set and \(A, B\in P(U)\) be two Pythagorean fuzzy sets. The s-similarity measure for the Pythagorean fuzzy sets A and B denoted by \(s(A,B)_S\) is defined by
where \(w_i>0\) is the weight of the element \(u_i\in U,~i=1,2, \ldots ,n\), where \(\sum \nolimits _{i=1}^{n}w_i=1\) and it depends on what decision maker and \(s(.,.)_S\) is defined in Eq. (3.3).
Theorem 3.6
Let \(A, B, C\in P(U)\) be three Pythagorean fuzzy sets. Therefore, \(s(.,.)_S\) corresponding to the formula (3.9) is satisfied in the following properties:
- (1)
\(0\le s(A,B)_S\le 1\).
- (2)
\(s(A,B)_S=s(B,A)_S\).
- (3)
\(s(A,B)_S=1~~ \leftrightarrow ~~ A=B\).
- (4)
If \(A\subseteq B\subseteq C\), then \(s(A,C)_S \le \mathrm{{min}}\{s(A,B)_S, s(B,C)_S\}\).
Proof
Simply we can obtain 1, 2 and 3. For 4:
If \(A\subseteq B\subseteq C\) then \(P_A(u_i)\le P_B(u_i)\le P_C(u_i)\); then, with case 4 of Theorem 3.3
Then
In addition, we have
Finally
Therefore, \(s(A,C)_S \le \mathrm{{min}}\{s(A,B)_S, s(B,C)_S\}\) and the proof is completed. \(\square \)
Corollary 3.7
For two Pythagorean fuzzy sets \(A,B\in P(U)\), for \(i (i=1,2,3) \), we have
Proof
Regarding \(A\cap B\subset A\subset A\cup B\) and case 4 of Theorem 3.6, the proof will be complete. Let

We have two corollaries in the following part. \(\square \)
Corollary 3.8
For two Pythagorean fuzzy sets \(A,B\in P(U)\), for \(i (i=1,2,3) \), we have

Proof
Regarding to  and case 4 of Theorem 3.6, the proof will be complete. \(\square \)
and case 4 of Theorem 3.6, the proof will be complete. \(\square \)
Corollary 3.9
Let \(A=\left( \mu , \nu \right) \). Then, for \(s_i(i=1,2,3)\), we have
- (i)
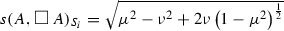 .
. - (ii)
 .
.
Proof
(i) Since  , then we have
, then we have  . Finally, we have
. Finally, we have

Since  .
.
Proof for (ii) is similar to that of (i). \(\square \)
Remark 3.10
\(s(A,B)_{S_2} \le s(A,B)_{S_3} \le s(A,B)_{S_1}\).
The similarity measure defined in this paper according to different choices \(s_i\) includes a set of similarity measures that the decision maker can use appropriately.
Notation 3.11
The similar measure between Pythagorean fuzzy sets by Wei and Wei [33] in Eq. (3.4) does not give a suitable similar measure for \(x=(\mu _x,\nu _x)\) and \(y=(0,0)\), but the similar measure between Pythagorean fuzzy sets by Eq. (3.9) has a suitable similar measure for these x and y.
Notation 3.12
The similar measure between Pythagorean fuzzy sets by Wei and Wei [33] in Eqs. (3.6) and (3.8) does not give a suitable similar measure for \(x=(1,0)\) and \(y=(0,0)\), but the similar measure between Pythagorean fuzzy sets by Eq. (3.9) has a suitable similar measure for these x and y.
Applications
In this section, we present two numerical examples in order to give more insights for the similarity measure for Pythagorean fuzzy sets.
Example 4.1
Let us consider a three known patterns \(A_i\ (i=1,2,3)\) which are represented by the Pythagorean fuzzy sets (PFSs) \(A_i \ (i=1,2,3)\) in the feature space as \(X=\left\{ x_1,x_2,x_3\right\} \):
Consider an unknown pattern \(A\in PFSs(X)\) that will be recognized, where
If we consider the weight of \(x_i\)\((i=1,2,3)\), to be 0.5, 0.33, and 0.17, respectively. Then, the proposed weighted similarity measures which have been computed from A to \(A_i\)\((i=1,2,3)\) are given in Table 1.
From the numerical results presented in Table 1, we know that the weighted similarity measures between \(A_2 \) and A are the largest.
Example 4.2
(Pattern recognition) [16, 33] Let us consider a three known patterns \(A_i \ (i=1,2,3) \) which are represented by the Pythagorean fuzzy sets (PFSs) \(A_i \ (i=1,2,3) \) in the feature space as \(X=\left\{ x_1,x_2,x_3\right\} \)
Consider an unknown pattern \(A\in PFSs(X) \) that will be recognized, where
If we consider the weight of \(x_i \)\((i=1,2,3) \), to be 0.5, 0.3, and 0.2, respectively, then we use the proposed weighted similarity measures which have been computed from A to \(A_i \)\((i=1,2,3) \) and are given in Table 2.
From the numerical results presented in Table 2, we know that the weighted similarity measures between \(A_3 \) and A are the largest ones as derived by 5 similarity measures in [33], and the results are similar to our similarity measures.
Example 4.3
(Medical diagnosis) [16, 33] Let us consider a set of diagnoses
in which \(A_1= \) viral fever, \(A_2= \) Malaria, \(A_3= \) typhoid, \(A_4 =\) stomach Problem and \(A_5= \) chest problem and a set of symptoms
in which \(x_1= \) temperature, \(x_2= \) headache, \(x_3= \) stomachache, \(x_4 =\) cough and \(x_5= \) chest Pain.
Suppose that a patient, with respect to all symptoms, can be depicted by the following PFS:
In addition, each diagnosis \(A_i(i = 1, 2, 3, 4, 5) \) can be viewed as PFSs with respect to all the symptoms as follows:
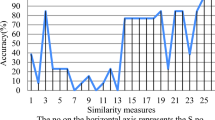
Our purpose is to classify the pattern A in one of classes \(A_i(i=1, 2, 3, 4, 5)\). For this, the proposed similarity measures which have been computed from A to \(A_i(i=1, 2, 3, 4, 5)\) are given in Table 3. We consider the weight of \(x_i\)\((i=1,2,3,4,5)\) to be 0.15, 0.25, 0.20, 0.15, and 0.25, respectively.
To provide a better view of the comparison results, they have been presented in Table 3. The numbers are bold in Table 3 refers to most appropriate diagnosis. According to the results obtained in Table 3, we can see that ranking for similarity measures with different S-norm is as follows
Meanwhile, similarity measure the based on the cosine function between PFSs does not the same order for ranking.
Conclusions
In this article, we have proposed some similarity measures for PFSs based on S-norms by considering the degree of membership and degree of non-membership. Then, we applied our similarity measures between PFSs to pattern recognition and medical diagnosis using numerical examples. The results show that the proposed similarity measures in PFS environment can suitably handle the real-life decision-making problem.
In the future, the application of our proposed similarity measures of PFSs needs to be explored in complex decision making, risk analysis, and many other fields under uncertain environments.
References
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96
Yager RR (2013) Pythagorean fuzzy subsets. The 9th joint world congress on fuzzy systems and NAFIPS annual meeting, IFSA/NAFIPS 2013, pp. 57-61, Edmonton, Canada, June 2013
Xu Z, Hu H (2010) Projection models for intuitionistic fuzzy multiple attribute decision making. Int J Inf Technol Decis Making 9(02):267–280
Zhang X, Xu Z (2014) Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst 29(12):1061–1078
Wei G, Lu M (2018) Pythagorean fuzzy power aggregation operators in multiple attribute decision making. Int J Intell Syst 33(1):169–186
Lu M, Wei G, Alsaadi FE, Hayat T, Alsaedi A (2017) Hesitant pythagorean fuzzy hamacher aggregation operators and their application to multiple attribute decision making. J Intell Fuzzy Syst 33(2):1105–1117
Yang Y, Ding H, Chen ZS, Li YL (2016) A Note on extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst 31(1):68–72
Liang D, Xu Z (2017) The new extension of TOPSIS method for multiple criteria decision making with hesitant Pythagorean fuzzy sets. Appl Soft Comput 60(C):167–179
Peng X, Yang Y (2016) Pythagorean fuzzy Choquet integral based MABAC method for multiple attribute group decision making. Int J Intell Syst 31(10):989–1020
Perez-Dominguez L, Rodriguez-Picon LA, Alvarado-Iniesta A, Luviano Cruz D, Xu Z (2018) MOORA under Pythagorean fuzzy set for multiple criteria decision making. Complexity, 2018
Mohd WRW, Abdullah L (2017) Pythagorean fuzzy analytic hierarchy process to multi-criteria decision making. In: AIP conference proceedings, vol. 1905, No. 1. AIP Publishing, p 040020
Ilbahar E, Karasan A, Cebi S, Kahraman C (2018) A novel approach to risk assessment for occupational health and safety using Pythagorean fuzzy AHP & fuzzy inference system. Saf Sci 103:124–136
Gul M (2018) Application of Pythagorean fuzzy AHP and VIKOR methods in occupational health and safety risk assessment: the case of a gun and rifle barrel external surface oxidation and colouring unit. Int J Occup saf Ergon. https://doi.org/10.1080/10803548.2018.1492251
Peng X, Yang Y (2015) Some results for Pythagorean fuzzy sets. Int J Intell Syst 30(11):1133–1160
Ren P, Xu Z, Gou X (2016) Pythagorean fuzzy TODIM approach to multi-criteria decision making. Appl Soft Comput 42:246–259
Garg H (2016) A novel correlation coefficients between Pythagorean fuzzy sets and its applications to decision-making processes. Int J Intell Syst 31(12):1234–1253
Peng X, Selvachandran G (2017) Pythagorean fuzzy set: state of the art and future directions. Artif Intell Rev. https://doi.org/10.1007/s10462-017-9596-9
Garg H (2018) Some methods for strategic decision-making problems with immediate probabilities in Pythagorean fuzzy environment. Int J Intell Syst 33(4):687–712
Xue W, Xu Z, Zhang X, Tian X (2018) Pythagorean fuzzy LINMAP method based on the entropy theory for railway project investment decision making. Int J Intell Syst 33(1):93–125
Enayattabar M, Ebrahimnejad A, Motameni H (2018) Dijkstra algorithm for shortest path problem under interval-valued Pythagorean fuzzy environment. Complex Intell Syst 5(2):93–100
Garg H (2016) A novel accuracy function under interval-valued Pythagorean fuzzy environment for solving multicriteria decision making problem. J Intell Fuzzy Syst 31(1):529–540
Garg H (2018) A linear programming method based on an improved score function for interval-valued pythagorean fuzzy numbers and its application to decision-making. Int J Uncertain Fuzziness Knowl Based Syst 26(01):67–80
Garg H (2018) Generalised Pythagorean fuzzy geometric interactive aggregation operators using Einstein operations and their application to decision making. J Exp Theor Artif Intell 30(6):763–794
Garg H (2018) Linguistic Pythagorean fuzzy sets and its applications in multiattribute decision-making process. Int J Intell Syst 33(6):1234–1263
Garg H (2018) Hesitant Pythagorean fuzzy sets and their aggregation operators in multiple attribute decision-making. Int J Uncertain Quantif 8:267–289
Garg H (2018) New exponential operational laws and their aggregation operators for interval-valued Pythagorean fuzzy multicriteria decision-making. Int J Intell Syst 33(3):653–683
Garg H (2017) Confidence levels based Pythagorean fuzzy aggregation operators and its application to decision-making process. Comput Math Organ Theory 23(4):546–571
Garg H (2017) A novel improved accuracy function for interval valued Pythagorean fuzzy sets and its applications in the decision-making process. Int J Intell Syst 32(12):1247–1260
Garg H (2016) A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int J Intell Syst 31(9):886–920
Garg H (2017) Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int J Intell Syst 32(6):597–630
Zhang X (2016) A novel approach based on similarity measure for Pythagorean fuzzy multiple criteria group decision making. Int J Intell Syst 31(6):593–611
Peng X (2019) New similarity measure and distance measure for Pythagorean fuzzy set. Complex Intell Syst 5(2):101–111
Wei G, Wei Y (2018) Similarity measures of Pythagorean fuzzy sets based on the cosine function and their applications. Int J Intell Syst 33(3):634–652
Abdullah L (2018) Similarity measures of Pythagorean fuzzy sets based on combination of cosine similarity measure and Euclidean distance measure. AIP Conf Proc 1974:030017. https://doi.org/10.1063/1.5041661
Ejegwa PA (2018) Distance and similarity measures for Pythagorean fuzzy sets. Granul Comput :1–14
Garg H, Kumar K (2018) An advanced study on the similarity measures of intuitionistic fuzzy sets based on the set pair analysis theory and their application in decision making. Soft Comput 22:4959–4970
Garg H (2018) An improved cosine similarity measure for intuitionistic fuzzy sets and their applications to decision-making process. Hacet J Math Stat 47:1585–1601
Garg H, Arora R (2017) Distance and similarity measures for dual hesitant fuzzy soft sets and their applications in multicriteria decision making problem. Int J Uncertain Quantif 7(3):
Fuller R (1995) Neural fuzzy systems, Abo Akademis tryckeri, Abo ESF Series A:443
Atanassov KT (1989) More on intuitionistic fuzzy sets. Fuzzy Sets Syst 33(1):37–45
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Firozja, M.A., Agheli, B. & Jamkhaneh, E.B. A new similarity measure for Pythagorean fuzzy sets. Complex Intell. Syst. 6, 67–74 (2020). https://doi.org/10.1007/s40747-019-0114-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-019-0114-3



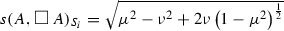 .
. .
.