Introduction

Pythagorean fuzzy sets (PFSs) [2], initiatively introduced by Yager, have regarded as an efficient tool to describe the vagueness of the MADM issues. PFSs are also denoted by the degrees of membership and nonmembership, which their sum of squares is equal or less than one. In some special cases, PFSs can deal with issues in which IFSs fail. For instance, if a DM or expert presents the degree of nonmembership and membership as 0.5 and 0.7, respectively, it is just efficacious for the PFSs. That is to say, all the IFSs are a part of the PFSs, which reveals that the PFSs are more forceful for solving the indeterminate issues. Zhang and Xu [3] presented the particular mathematical language expression for PFSs and defined notion of PFN. Besides, they continued to propose a revised Pythagorean fuzzy TOPSIS (PF-TOPSIS) for dealing with the MCDM issue with PFNs. Peng and Yang [4] explored the subtraction and division operations for PFNs and initiated a Pythagorean fuzzy SIR (PF-SIR) algorithm to handle multi-criteria group decision-making (MCGDM) issue. Moreover, some extension models [5,6,7,8] of PFSs are rapidly developed. Meanwhile, some research hotspots are concentrated on the aggregation operators [9,10,11,12,13,14,15,16,17,18,19,20,21,22], decision-making methods [3, 23,24,25,26,27,28,29,30,31].

Similarity measure (distance measure) is a significant means for measuring the uncertain information. The fuzzy similarity measure (distance measure) is a measure that depicts the closeness (difference) among fuzzy sets. Zhang [33] proposed the Pythagorean fuzzy similarity measures for dealing the multi-attribute decision-making problems. Peng et al. [23] proposed the many new distance measures and similarity measures for dealing the issues of pattern recognition, medical diagnosis and clustering analysis, and discussed their transformation relations. Wei and Wei [32] presented some Pythagorean fuzzy cosine function for dealing with the decision-making problems. However, some existing similarity measures/distance measures cannot the obey third or fourth axiom, and also have no power to differentiate positive difference and negative difference or deal with the division by the zero problem. Due to the above counterintuitive phenomena [32,33,34, 36,37,38,39,40,41,42,43,44,45,46] of the existing similarity measures of PFSs, they may be hard for DMs to choose convincible or optimal alternatives. As a consequence, the goal of this paper is to deal with the above issue by proposing a novel similarity measure and distance measure for Pythagorean fuzzy set, which can be without counterintuitive phenomena.

For counting the distance measure and similarity measure of the two PFSs, we introduce a novel method to build the distance measure and similarity measure which rely on four parameters, i.e., a, b, t and p, where p is the \(L_p\) norm and a, b, t identify the level of vagueness. Meanwhile, their relation with the similarity measures for PFSs are discussed in detail.

The rest of the presented paper is listed in the following. In Sect. 2, the fundamental notions of PFSs and IFSs are shortly retrospected, which will be employed in the analysis in each section. In Sect. 3, some new distance measures and similarity measures are proposed and proved. In Sect. 4, some counterintuitive examples are given to show the effectiveness of Pythagorean fuzzy similarity measure. The paper is concluded in Sect. 5.

Preliminaries

In this section, we briefly review the fundamental concepts related to IFS and PFS.

Definition 1

[1] Let X be a universe of discourse. An IFS I in X is given by

$$\begin{aligned} I=\{\langle x,\mu _{I}(x),\nu _{I}(x)\rangle \mid x\in X\}, \end{aligned}$$
(1)

where \(\mu _{I}:X\rightarrow [0,1]\) denotes the degree of membership and \(\nu _{I}:X\rightarrow [0,1]\) denotes the degree of nonmembership of the element \(x\in X\) to the set I, respectively, with the condition that \(0\le \mu _{I}(x)+\nu _{I}(x)\le 1\). The degree of indeterminacy \(\pi _{I}(x)=1-\mu _{I}(x)-\nu _{I}(x)\). For convenience, Xu and Yager [35] called \((\mu _I(x),\nu _I(x))\) an intuitionistc fuzzy number (IFN) denoted by \(i=(\mu _I,\nu _I)\).

Definition 2

[2] Let X be a universe of discourse. A PFS P in X is given by

$$\begin{aligned} P=\{\langle x,\mu _P(x),\nu _P(x)\rangle \mid x\in X\}, \end{aligned}$$
(2)

where \(\mu _P:X\rightarrow [0,1]\) denotes the degree of membership and \(\nu _P:X\rightarrow [0,1]\) denotes the degree of nonmembership of the element \(x\in X\) to the set P, respectively, with the condition that \(0\le (\mu _P(x))^2+(\nu _P(x))^2\le 1\). The degree of indeterminacy \(\pi _P(x)=\sqrt{1-(\mu _P(x))^2-(\nu _P(x))^2}\). For convenience, Zhang and Xu [3] called \((\mu _P(x),\nu _P(x))\) a Pythagorean fuzzy number (PFN) denoted by \(p=(\mu _P,\nu _P)\).

Definition 3

[3] For any PFN \(p=(\mu ,\nu )\), the score function of p is defined as follows:

$$\begin{aligned} s(p)=\mu ^2-\nu ^2, \end{aligned}$$
(3)

where \(s(p)\in [-1,1]\).

Definition 4

[5] For any PFN \(p=(\mu ,\nu )\), the accuracy function of p is defined as follows:

$$\begin{aligned} a(p)=\mu ^2+\nu ^2, \end{aligned}$$
(4)

where \(a(p)\in [0,1]\).

For any two PFNs \(p_1,p_2\),

(1) if \(s(p_1)>s(p_2)\), then \(p_1\succ p_2\);

(2) if \(s(p_1)=s(p_2)\), then

         (a) if \(a(p_1)>a(p_2)\), then \(p_1\succ p_2\);

         (b) if \(a(p_1)=a(p_2)\), then \(p_1\sim p_2\).

Definition 5

[3, 4] If \(M,N\in \) PFSs, then the operations can be defined as follows:

\((1)~M^c=\left\{ \langle x,\nu _M(x),\mu _M(x)\rangle |x\in X\right\} \);

\((2)~M\subseteq N~~~\) iff \(~\forall x\in X, \mu _M(x)\le \mu _N(x)\) and \(\nu _M(x)\ge \nu _N(x)\);

\((3)~M=N~~~\) iff \(~\forall x\in X, \mu _M(x)=\mu _N(x)\) and \(\nu _M(x)=\nu _N(x)\);

\((4)~\varPhi _M=\left\{ \langle x,1,0\rangle |x\in X\right\} \);

\((5)~\emptyset _M=\left\{ \langle x,0,1\rangle |x\in X\right\} \);

\((6)~M\bigcap N=\Big \{\langle x,\mu _M(x)\bigwedge \mu _N(x),\nu _M(x)\bigvee \nu _N(x)\rangle |x\in X\Big \}\);

\((7)~M\bigcup N=\Big \{\langle x,\mu _M(x)\bigvee \mu _N(x),\nu _M(x)\bigwedge \nu _N(x)\rangle |x\in X\Big \}\);

\((8)~M\oplus N=\Big \{\langle x,\sqrt{\mu _M^2(x)+\mu _N^2(x)-\mu _M^2(x)\mu _N^2(x)},\nu _M(x)\nu _N(x)\rangle |x\in X\Big \}\);

\((9)~M\otimes N=\Bigg \{\langle x,\mu _M(x)\mu _N(x),\sqrt{\nu _M^2(x)+\nu _N^2(x)-\nu _M^2(x)\nu _N^2(x)}|x\in X\Bigg \}\);

\((10)~M\ominus N=\left\{ \langle x,\sqrt{\frac{\mu _M^2(x)-\mu _N^2(x)}{1-\mu _N^2(x)}},\frac{\nu _M(x)}{\nu _N(x)}\rangle |x\in X\right\} ,~ \text {if} \) \(\mu _M(x)\ge \mu _N(x),\) \(\nu _M(x)\le \text {min}\left\{ \nu _N(x),\frac{\nu _N(x)\pi _M(x)}{\pi _N(x)}\right\} \);

\((11)~M\oslash N=\left\{ \langle x,\frac{\mu _M(x)}{\mu _N(x)},\sqrt{\frac{\nu _M^2(x)-\nu _N^2(x)}{1-\nu _N^2(x)}}\rangle |x\in X\right\} ,~\text {if} \nu _M(x)\ge \nu _N(x)\), \(\mu _M(x)\le \text {min}\left\{ \mu _N(x),\frac{\mu _N(x)\pi _M(x)}{\pi _N(x)}\right\} \).

Definition 6

[34] Let M, N and O be three PFSs on X. A distance measure D(M, N) is a mapping \(D:PFS(X)\times PFS(X)\rightarrow [0,1]\), possessing the following properties:

\((D1)~0\le D(M,N)\le 1\);

\((D2)~D(M,N)=D(N,M)\);

\((D3)~D(M,N)=0\) iff \(M=N\);

\((D4)~D(M,M^c)=1\) iff M is a crisp set;

(D5)  If \(M\subseteq N\subseteq O\), then \(D(M,N)\le D(M,O)\) and \(D(N,O)\le D(M,O)\).

Definition 7

[34] Let M, N and O be three PFSs on X. A similarity measure S(M, N) is a mapping \(S:PFS(X)\times PFS(X)\rightarrow [0,1]\), possessing the following properties:

\((S1)~0\le S(M,N)\le 1\);

\((S2)~S(M,N)=S(N,M)\);

\((S3)~S(M,N)=1\) iff \(M=N\);

\((S4)~S(M,M^c)=0\) iff M is a crisp set;

(S5)  If \(M\subseteq N\subseteq O\), then \(S(M,O)\le S(M,N)\) and \(S(M,O)\le S(N,O)\).

Distance measure and similarity measure of PFSs

Theorem 1

Let M and N be two PFSs in X where \(X=\{x_1,x_2,\cdots ,x_n\}\), then D(M, N) is the distance measure between two PFSs M and N in X.

$$\begin{aligned} D(M,N)= & {} \root p \of {\frac{1}{2n(t+1)^p}\sum \nolimits _{i=1}^n\bigg (|(t+1-a)(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))-a(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))|^p}\nonumber \\&\overline{+\;|(t+1-b)(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))-b(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))|^p \bigg ) } \end{aligned}$$
(5)

where p is the \(L_p\) norm, and t, a and b denote the level of uncertainty with the condition \(a+b\le t+1, 0<a,b\le t+1,t>0\).

Proof

For two PFSs M and N, we have

(D1) \(|(t+1-a)(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))-a(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))| =|((t+1-a)(\mu _{M}^2(x_i)-a\nu _{M}^2(x_i))-((t+1-a)\mu _{N}^2(x_i)-a\nu _{N}^2(x_i))|\),

\(|(t+1-b)(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))-b(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))| =|((t+1-b)(\nu _{M}^2(x_i)-b\mu _{M}^2(x_i))-((t+1-b)\nu _{N}^2(x_i)-b\mu _{N}^2(x_i))|\).

Since \(0\le \mu _M(x_i),\mu _N(x_i), \nu _M(x_i),\nu _N(x_i) \le 1\), we can have

\(-a\le (t+1-a)(\mu _{M}^2(x_i)-a\nu _{M}^2(x_i) \le t+1-a\), \(-(t+1-a)\le -((t+1-a)\mu _{N}^2(x_i)-a\nu _{N}^2(x_i)) \le a\).

Therefore, we have \(-(t+1)\le ((t+1-a)(\mu _{M}^2(x_i)-a\nu _{M}^2(x_i))-((t+1-a)\mu _{N}^2(x_i)-a\nu _{N}^2(x_i)) \le t+1\).

It means that \(0\le |((t+1-a)(\mu _{M}^2(x_i)-a\nu _{M}^2(x_i))-((t+1-a)\mu _{N}^2(x_i)-a\nu _{N}^2(x_i))|^p\le (t+1)^p\).

Similarly, we can have \(0\le |((t+1-b)(\nu _{M}^2(x_i)-b\mu _{M}^2(x_i))-((t+1-b)\nu _{N}^2(x_i)-b\mu _{N}^2(x_i))|^p\le (t+1)^p\).

Hence, by the above Eq. (5), we can obtain \(0\le D(M,N)\le 1\).

(D2) This is straightforward from Eq. (5).

(D3) Firstly, we suppose that \(M=N\), which implies that \(\mu _M(x_i)=\mu _N(x_i)\) and \(\nu _M(x_i)=\nu _N(x_i)\) for \(i=1,2,\cdots ,n\). Thus, by Eq. (5), we can have \(D(M,N)=0\).

Conversely, assuming that \(D(M,N)=0\) for two PFSs M and N, this implies that

$$\begin{aligned} |(t+1-a)(\mu _{M}^2(x_i){-}\mu _{N}^2(x_i)){-}a(\nu _{M}^2(x_i){-}\nu _{N}^2(x_i))|^p=0 \end{aligned}$$

and

$$\begin{aligned} |(t+1-b)(\nu _{M}^2(x_i){-}\nu _{N}^2(x_i)){-}b(\mu _{M}^2(x_i){-}\mu _{N}^2(x_i))|^p=0. \end{aligned}$$

After solving, we can obtain

\(\mu _M^2(x_i)-\mu _N^2(x_i)=0,\nu _M^2(x_i)-\nu _N^2(x_i)=0\), which implies \(\mu _M(x_i)=\mu _N(x_i)\), \(\nu _M(x_i)=\nu _N(x_i)\).

Consequently, \(M=N\). Hence \(D(M,N)=0\) iff \(M=N\).

(D4) \(D(M, M^c)=1\Leftrightarrow \root p \of {\frac{1}{n}\sum \nolimits _{i=1}^n |\mu _M^2(x_i)-\nu _M^2(x_i)|^p}=1 \Leftrightarrow |\mu _M^2(x_i)-\nu _M^2(x_i)|=1\Leftrightarrow \mu _M(x_i)=1,\nu _M(x_i)=0\) or \(\mu _M(x_i)=0,\nu _M(x_i)=1\) \(\Leftrightarrow M\) is a crisp set.

(D5) According to the formula of the distance measure, we have

$$\begin{aligned}&D(M,N)=\\&\root p \of {\frac{1}{2n(t{+}1)^p}\sum \nolimits _{i=1}^n(|(t{+}1-a)(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))-a(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))|^p{+}}\\&\quad \overline{|(t+1-b)(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))-b(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))|^p ) },\\&D(M,O)=\\&\root p \of {\frac{1}{2n(t{+}1)^p}\sum \nolimits _{i=1}^n(|(t{+}1-a)(\mu _{M}^2(x_i)-\mu _{O}^2(x_i))-a(\nu _{M}^2(x_i)-\nu _{O}^2(x_i))|^p{+}}\\&\quad \overline{|(t+1-b)(\nu _{M}^2(x_i)-\nu _{O}^2(x_i))-b(\mu _{M}^2(x_i)-\mu _{O}^2(x_i))|^p ) }. \end{aligned}$$

Since \(|(t+1-a)(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))-a(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))| =|((t+1-a)(\mu _{M}^2(x_i)-a\nu _{M}^2(x_i))-((t+1-a)\mu _{N}^2(x_i)-a\nu _{N}^2(x_i))|\),

\(|(t+1-b)(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))-b(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))| =|((t+1-b)(\nu _{M}^2(x_i)-b\mu _{M}^2(x_i))-((t+1-b)\nu _{N}^2(x_i)-b\mu _{N}^2(x_i))|\),

\(|(t+1-a)(\mu _{M}^2(x_i)-\mu _{O}^2(x_i))-a(\nu _{M}^2(x_i)-\nu _{O}^2(x_i))| =|((t+1-a)(\mu _{M}^2(x_i)-a\nu _{M}^2(x_i))-((t+1-a)\mu _{O}^2(x_i)-a\nu _{O}^2(x_i))|\),

\(|(t+1-b)(\nu _{M}^2(x_i)-\nu _{O}^2(x_i))-b(\mu _{M}^2(x_i)-\mu _{O}^2(x_i))| =|((t+1-b)(\nu _{M}^2(x_i)-b\mu _{M}^2(x_i))-((t+1-b)\nu _{O}^2(x_i)-b\mu _{O}^2(x_i))|\).

If \(M\subseteq N\subseteq O\), we have \(\mu _O\ge \mu _N(x_i) \ge \mu _M(x_i), \nu _O\le \nu _N(x_i) \le \nu _M(x_i).\)

Hence, \((t+1-a)\mu _{M}^2(x_i)-a\nu _{M}^2(x_i)\le (t+1-a)\mu _{N}^2(x_i)-a\nu _{N}^2(x_i) \le (t+1-a)\mu _{O}^2(x_i)-a\nu _{O}^2(x_i)\),

\((t+1-b)\nu _{O}^2(x_i)-a\mu _{O}^2(x_i)\le (t+1-b)\nu _{N}^2(x_i)-a\mu _{N}^2(x_i) \le (t+1-b)\nu _{M}^2(x_i)-a\mu _{M}^2(x_i)\).

Consequently,

$$\begin{aligned}&|((t+1-a)(\mu _{M}^2(x_i)-a\nu _{M}^2(x_i))-((t+1-a)\mu _{O}^2(x_i)\\&\quad -a\nu _{O}^2(x_i))| \le |((t+1-a)(\mu _{M}^2(x_i)-a\nu _{M}^2(x_i))\\&\quad -((t+1-a)\mu _{N}^2(x_i)-a\nu _{N}^2(x_i))|,\\&|((t+1-b)(\nu _{M}^2(x_i)-b\mu _{M}^2(x_i))\\&\quad -((t+1-b)\nu _{N}^2(x_i)-b\mu _{N}^2(x_i))|\\&\le |((t+1-b)(\nu _{M}^2(x_i)-b\mu _{M}^2(x_i))\\&\quad -((t+1-b)\nu _{O}^2(x_i)-b\mu _{O}^2(x_i))|. \end{aligned}$$

Therefore, \(D(M,O)\ge D(N,O)\) and \(D(M,O)\ge D(M,N)\). \(\square \)

However, in most real environment, the diverse sets may possess diverse weights. Therefore, the weight \(w_i(i = 1, 2,\dots , n)\) of the alternative \(x_i\in X\) should be taken into consideration. We present a weighted distance measure \(D^w(M,N)\) between PFSs in the following.

$$\begin{aligned}&D^w(M,N)= \root p \of {\frac{1}{2(t+1)^p}\sum \nolimits _{i=1}^nw_i\bigg (|(t+1-a)(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))-a(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))|^p+}\nonumber \\&\quad \overline{|(t+1-b)(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))-b(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))|^p \bigg ) }, \end{aligned}$$
(6)

where \(a+b\le t+1, 0<a,b\le t+1,t>0\), and \(w_i\) is the weights of the element \(x_i\) with \(\sum _{i=1}^n w_i=1\).

Theorem 2

\(D^w(M,N)\) is the distance measure between two PFSs M and N in X.

Proof

(D1) If we obtain the product of the inequality defined above with \(w_i\), then we can easily have

$$\begin{aligned}&0\le w_i|(t+1-a)(\mu _{M}^2(x_i)-\mu _{N}^2(x_i)) -a(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))|^p \le w_i(t+1)^p,\\&0\le w_i|(t+1-b)(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))-b(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))|^p \le w_i(t+1)^p. \end{aligned}$$

Furthermore, we can write the following inequality:

$$\begin{aligned}&0\le \sum \limits _{i=1}^n w_i|(t+1-a)(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))\\&\qquad -a(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))|^p \le \sum \limits _{i=1}^n w_i(t+1)^p,\\&0\le \sum \limits _{i=1}^n w_i|(t+1-b)(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))\\&\qquad -b(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))|^p \le \sum \limits _{i=1}^n w_i(t+1)^p. \end{aligned}$$

It is easy to know that \(\sum \limits _{i=1}^n w_i(t+1)^p\) is equal to \((t+1)^p\) since \(\sum \nolimits _{i=1}^n w_i=1\).

Hence, \(0\le \sum \nolimits _{i=1}^n w_i|(t+1-a)(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))-a(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))|^p \le (t+1)^p\),

\(0\le \sum \nolimits _{i=1}^n w_i|(t+1-b)(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))-b(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))|^p \le (t+1)^p\).

Hence, by Eq. (6), we can obtain \(0\le D^w(M,N)\le 1\).

(D2)–(D5) It is straightforward. \(\square \)

Theorem 3

If D(M, N) and \(D^w(M,N)\) are distance measures between PFSs M and N, then \(S(M,N)=1-D(M,N)\) and \(S^w(M,N)=1-D^w(M,N)\) are similarity measures between M and N,  respectively.

$$\begin{aligned} S(M,N)=1-D(M,N)= & {} 1-\root p \of {\frac{1}{2n(t+1)^p}\sum \limits _{i=1}^n(|(t+1-a)(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))-a(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))|^p}\nonumber \\&\quad \overline{+|(t+1-b)(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))-b(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))|^p) } \end{aligned}$$
(7)
$$\begin{aligned} S^w(M,N)=1-D(M,N)= & {} 1-\root p \of {\frac{1}{2(t+1)^p}\sum \limits _{i=1}^nw_i(|(t+1-a)(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))-a(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))|^p+}\nonumber \\&\quad \overline{|(t+1-b)(\nu _{M}^2(x_i)-\nu _{N}^2(x_i))-b(\mu _{M}^2(x_i)-\mu _{N}^2(x_i))|^p) }. \end{aligned}$$
(8)

Theorem 4

Let M and N be two PFSs, then we have

(1) \(D(M,M\otimes N)=D(N,M\oplus N)\);

(2) \(D(M,M\oplus N)=D(N,M\otimes N)\);

(3) \(S(M,M\otimes N)=S(N,M\oplus N)\);

(4) \(S(M,M\oplus N)=S(N,M\otimes N)\).

Proof

We only prove the (1), and (2)–(2) can be proved in a homologous way.

(1) According to Definition 5 and Eq. (5), and for \(D(M, M\bigotimes N)\) with \(\forall x_i\in X\), we can have

$$\begin{aligned}&|(t+1-a)(\mu _M^2(x_i)-\mu _M^2(x_i)\mu _N^2(x_i))- a(\nu _M^2(x_i)\\&\quad -(\nu _M^2(x_i)+\nu _N^2(x_i)-\nu _M^2(x_i)\nu _N^2(x_i)))|^p \\&\quad +|(t+1-b)( \nu _M^2(x_i)\\&\quad -(\nu _M^2(x_i)+\nu _N^2(x_i)-\nu _M^2(x_i)\nu _N^2(x_i)))\\&\quad -b( \mu _M^2(x_i)-\mu _M^2(x_i)\mu _N^2(x_i))|^p\\&=|(t+1-a)(\mu _M^2(x_i)-\mu _M^2(x_i)\mu _N^2(x_i))\\&\quad - a(\nu _M^2(x_i)\nu _N^2(x_i)-\nu _N^2(x_i))|^p \\&\quad +|(t+1-b)( \nu _M^2(x_i)\nu _N^2(x_i)\\&\quad -\nu _N^2(x_i))-b( \mu _M^2(x_i)-\mu _M^2(x_i)\mu _N^2(x_i))|^p. \end{aligned}$$

For \(D(N, M\bigoplus N)\) with \(\forall x_i\in X\), we can have

$$\begin{aligned}&|(t+1-a)(\mu _N^2(x_i)-(\mu _M^2(x_i)\\&\quad +\mu _N^2(x_i) -\mu _M^2(x_i)\mu _N^2(x_i)))\\&\quad - a(\nu _N^2(x_i)-\nu _M^2(x_i)\nu _N^2(x_i))|^p \\&\quad +|(t+1-b)(\nu _M^2(x_i)-\nu _M^2(x_i)\nu _N^2(x_i))\\&\quad -b( \mu _N^2(x_i)-(\mu _M^2(x_i)+\mu _N^2(x_i)\\&\quad -\mu _M^2(x_i)\mu _N^2(x_i)))|^p\\&=|(t+1-a)(\mu _M^2(x_i)\mu _N^2(x_i)-\mu _M^2(x_i))\\&\quad - a(\nu _N^2(x_i)-\nu _M^2(x_i)\nu _N^2(x_i))|^p \\&\quad +|(t+1-b)(\nu _N^2(x_i)-\nu _M^2(x_i)\nu _N^2(x_i))\\&\quad -b(\mu _M^2(x_i)\mu _N^2(x_i)-\mu _M^2(x_i))|^p\\&=|(t+1-a)(\mu _M^2(x_i)-\mu _M^2(x_i)\mu _N^2(x_i))\\&\quad - a(\nu _M^2(x_i)\nu _N^2(x_i)-\nu _N^2(x_i))|^p \\&\quad +|(t+1-b)(\nu _M^2(x_i)\nu _N^2(x_i)\\&\quad -\nu _N^2(x_i))-b(\mu _M^2(x_i)-\mu _M^2(x_i)\mu _N^2(x_i))|^p. \end{aligned}$$

Consequently, we can obtain \(D_1(M,M\otimes N)=D_1(N,M\oplus N)\). \(\square \)

Theorem 5

Let M and N be two PFSs, and \(x_i\in X, \mu _M^2(x_i)+\mu _N^2(x_i)=1,\) \(\nu _M^2(x_i)+\nu _N^2(x_i)=1\), then we have

(1) \(D(M,M\oslash N)=D(N,N\ominus M),\mu _M(x_i)\le \mu _N(x_i),\nu _M(x_i)\ge \nu _N(x_i)\);

(2) \(D(M,M\ominus N)=D(N,N\oslash M),\mu _M(x_i)\ge \mu _N(x_i),\nu _M(x_i)\le \nu _N(x_i)\);

(3) \(S(M,M\oslash N)=S(N,N\ominus M),\mu _M(x_i)\le \mu _N(x_i),\nu _M(x_i)\ge \nu _N(x_i)\);

(4) \(S(M,M\ominus N)=S(N,N\oslash M),\mu _M(x_i)\ge \mu _N(x_i),\nu _M(x_i)\le \nu _N(x_i)\).

Proof

We only prove (1), and (2)–(2) can be proved in a homologous way.

(1) According to Definition 5 and Eq. (5), and for \(D(M, M\oslash N)\) with \(\forall x_i\in X\), we can have

$$\begin{aligned}&\left| (t+1-a)(\mu _M^2(x_i)-\frac{\mu _M^2(x_i)}{\mu _N^2(x_i)})\right. \\&\left. \quad - a\left( \nu _M^2(x_i)-\frac{\nu _M^2(x_i)-\nu _N^2(x_i)}{1-\nu _N^2(x_i)}\right) \right| ^p \\&\quad +\left| (t+1-b)\left( \nu _M^2(x_i)-\frac{\nu _M^2(x_i)-\nu _N^2(x_i)}{1-\nu _N^2(x_i)} \right) \right. \\&\left. \quad -b\left( \mu _M^2(x_i)-\frac{\mu _M^2(x_i)}{\mu _N^2(x_i)}\right) \right| ^p\\&=\left| (t+1-a)\frac{\mu _M^2(x_i)(1-\mu _N^2(x_i))}{\mu _N^2(x_i)}\right. \\&\left. \quad - a\left( \frac{\nu _N^2(x_i)(1-\nu _M^2(x_i))}{1-\nu _N^2(x_i)}\right) \right| ^p \\&\quad +\left| (t+1-b)\frac{\nu _N^2(x_i)(1-\nu _M^2(x_i))}{1-\nu _N^2(x_i)}\right. \\&\left. \quad -b\frac{\mu _M^2(x_i)(1-\mu _N^2(x_i))}{\mu _N^2(x_i)}\right| ^p. \end{aligned}$$
Table 1 Existing similarity measures
Full size table
Table 2 The comparison of similarity measures adopted from [45]
Full size table
Table 3 The comparison of similarity measures adopted from [38]
Full size table
Table 4 The comparison of similarity measures
Full size table

For \(D(N, M\ominus N)\) with \(\forall x_i\in X\) and \(\mu _M^2(x_i)+\mu _N^2(x_i)=1, \nu _M^2(x_i)+\nu _N^2(x_i)=1\), we can have

$$\begin{aligned}&\left| (t+1-a)\left( \mu _N^2(x_i)-\frac{\mu _N^2(x_i)-\mu _M^2(x_i)}{1-\mu _M^2(x_i)}\right) \right. \\&\quad \left. - a\left( \nu _N^2(x_i)-\frac{\nu _N^2(x_i)}{\nu _M^2(x_i)}\right) \right| ^p\\&\quad +\left| (t+1-b)\left( \nu _N^2(x_i)-\frac{\nu _N^2(x_i)}{\nu _M^2(x_i)} \right) \right. \\&\left. \quad -b(\mu _N^2(x_i)-\frac{\mu _N^2(x_i)-\mu _M^2(x_i)}{1-\mu _M^2(x_i)})\right| ^p\\&=\left| (t+1-a)\frac{\mu _M^2(x_i)(1-\mu _N^2(x_i))}{1-\mu _M^2(x_i)}\right. \\&\left. \quad - a\frac{\nu _N^2(x_i)(1-\nu _M^2(x_i))}{\nu _M^2(x_i)}\right| ^p\\&\quad +\left| (t+1-b)\frac{\nu _N^2(x_i)(\nu _M^2(x_i))}{\nu _M^2(x_i)}- b\frac{\mu _M^2(x_i)(1-\mu _N^2(x_i))}{1-\mu _M^2(x_i)} \right| ^p\\&=|(t+1-a)\frac{\mu _M^2(x_i)(1-\mu _N^2(x_i))}{\mu _N^2(x_i)}\\&\quad - a\left( \frac{\nu _N^2(x_i)(1-\nu _M^2(x_i))}{1-\nu _N^2(x_i)}\right) |^p \\&\quad +\left| (t+1-b)\frac{\nu _N^2(x_i)(1-\nu _M^2(x_i))}{1-\nu _N^2(x_i)} -b \frac{\mu _M^2(x_i)(1-\mu _N^2(x_i))}{\mu _N^2(x_i)}\right| ^p. \end{aligned}$$

Consequently, we can obtain \(D(M,M\oslash N)=D(N,M\ominus N)\). \(\square \)

Apply the similarity measure between PFSs to pattern recognition

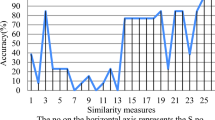
For stating the advantage of the explored similarity measure S, a comparison among the initiated similarity measure with the current similarity measures is established. Some existing similarity measures are presented in Table 1.

Next, we utilize six series of PFSs originally adopted from [45] to compare the decision results of the initiated similarity measure S with the existing similarity measures [32,33,34, 36,37,38,39,40,41,42,43,44,45,46] shown in Table 2. From Table 2, it is clear that the proposed similarity measure S, \(S_{BA}\) [46] and \(S_{CC}\) [38] can conquer the shortcomings of obtaining the illogical results of the existing similarity measures (\(S_{C}\) [37], \(S_{HY1}\) [39], \(S_{HY2}\) [39], \(S_{HY3}\) [39], \(S_{HK}\) [40], \(S_{LC}\) [41], \(S_{LX}\) [42], \(S_{L}\) [36], \(S_{LS1}\) [43], \(S_{LS2}\) [43], \(S_{LS3}\) [43], \(S_{M}\) [44], \(S_{Y}\) [45], \(S_{P1}\) [34], \(S_{P2}\) [34], \(S_{P3}\) [34], \(S_{Z}\) [33] and \(S_W\) [33]). We will state the five major shortcomings in detail in the following.

(1) It is easily seen that the third axiom of similarity measure (S3) is not satisfied by \(S_C, S_{LC},S_Y,S_W,S_{P1}\) since \(S_C(M,N)=S_{LC}(M,N)=S_Y(M,N)=S_W(M,N)=S_{P1}(M,N)=1\) when \(M= (0.3,0.3)\) and \(N=(0.4,0.4)\) (Case 1), which are indeed not equal to each other. Similarly, the third axiom of similarity measure (S3) is also not satisfied by \(S_C(M,N), S_{LC}(M,N)\) when \(M=(0.5,0.5), N= (0,0)\) and \(M= (0.4,0.2), N= (0.5,0.3)\). Moreover, we also can find that the fourth axiom of similarity measure (S4) is not satisfied by \(S_Z\) when \(M= (0.3,0.4)\) and \(N=(0.4,0.3)\)(Case 3) since \(S_Z(M,N)=0,\) which are indeed not a crisp number. Similarly, the fourth axiom of similarity measure (S4) is also not satisfied by \(S_{HY1}, S_{HY2}, S_{HY3}, S_{P2}\) when \(M=(1,0), N= (0,0)\) (Case 3) and \(S_{P2}\) when \(M=(0.5,0.5), N= (0,0)\) (Case 4).

(2) Some similarity measures [34, 36, 39, 40, 43, 44] have no power to differentiate positive and negative difference. For example, \(S_L(M,N)=S_L(M1, N2)=0.9\) when \(M= (0.3,0.3), N= (0.4,0.4)\) (Case 1), \(M1= (0.3,0.4)\) and \(N1= (0.4, 0.3)\) (Case 2). The same counter-intuitive example exists for \(S_{HY1},S_{HY2},S_{HY3}, S_{HK},S_{LS1}, S_{LS3},S_{M},S_{P2},S_{P3}\). Another type of counter-intuitive case occurs when \(M= (1, 0), N= (0, 0)\) (Case 3) and \(M1= (0.5, 0.5), N1= (0, 0)\) (Case 4). In this case, \(S_{HK}(M,N)=S_{HK}(M1,N1)=0.5\). The same counter-intuitive example exists for \(S_{LS1}, S_M, S_Z, S_{P2}\).

(3) The similarity measures have no power to deal with the division by zero problem. For example, \(S_Y\) and \(S_W\) when \(M=(1,0),N=(0,0)\) (Case 3) or \(M=(0.5,0.5), N=(0,0)\) (Case 4).

(4) Another kind of counter-intuitive example can be provided for the case where the similarity measures are \(S_{HY1}(M,N)=S_{HY1}(M1,N1)=0.9\) when \(M=(0.4,0.2), N=(0.5,0.3)\) (Case 5), \(M1=(0.4,0.2), N1=(0.5,0.2)\) (Case 6). The same counter-intuitive example also exists for \(S_{HY2},S_{HY3},S_{LX},S_{LS2}\).

(5) Another charming counter-intuitive issue happens when \(M=(0.4, 0.2), N= (0.5, 0.3)\) (Case 5), \(M= (0.4, 0.2),N1= (0.5, 0.2)\) (Case 6). In such case, it is expected that the degree of similarity between M and N is bigger than or equal to the degree of similarity between M and N1,  since they are ranked as \(N1\succ N\succ M\) by means of score function shown in Definition 3. However, the degree of similarity between M and N1 is bigger than the degree of similarity between M and N when \(S_{L},S_{HY1},S_{HY2},S_{HY3},S_{HK},S_{LC},S_{LX},S_{LS1},S_{LS2},S_C,S_{LS3},S_{M},S_{W},S_{Z},S_{P2}, S_{P3}\) are used, which does not seem to be reasonable. On the other hand, our proposed similarity measures \(S(M,N)=0.9625\) and \(S(M,N1)=0.9438\). Therefore, the developed similarity measure is the same as score function. The presented similarity measure S and the existing similarity measures (\(S_{CC}\) and \(S_{BA}\)) are the similarity measures that have no such counter-intuitive issues as stated in Table 2. To continue digging the defects of the existing similarity measures (\(S_{CC}\) and \(S_{BA}\)), we give the following tables for further discussion.

Meanwhile, \(S_{BA}\) [46] has the defects of obtaining unconscionable results in some special conditions which is shown in Table 3. In Table 3, we explore six sets of PFSs which are adopted from [38] to compare the decision results of the presented similarity measure S with the developed similarity measures [32,33,34, 36,37,38,39,40,41,42,43,44,45,46] shown in Table 3. From Table 3, we can conclude that the presented similarity measure S and \(S_{CC}\) [38], \(S_{P3}\) [34] can conquer the defects of obtaining the unconscionable results of the existing similarity measures \(S_{BA}\) [46], \(S_{C}\) [37], \(S_{HY1}\) [39], \(S_{HY2}\) [39], \(S_{HY3}\) [39], \(S_{HK}\) [40], \(S_{LC}\) [41], \(S_{LX}\) [42], \(S_{L}\) [36] , \(S_{LS1}\) [43], \(S_{LS2}\) [43], \(S_{LS3}\) [43], \(S_{M}\) [44], \(S_{Y}\) [45], \(S_{P1}\) [34], \(S_{P2}\) [34], \(S_Z\) [33] and \(S_W\) [32].

Nevertheless, \(S_{CC}\) [38] also has the defects of obtaining fallacious results in some special cases, which is shown in Table 4. In Table 4, we explore six series of PFSs to compare the results of the proposed similarity measure S and the existing similarity measures [32,33,34, 36,37,38,39,40,41,42,43,44,45,46] as shown in Table 4. From Table 4, we can see that the proposed similarity measure S with \(S_{P3}\) [34] can overcome the drawbacks of getting the unreasonable results of the existing similarity measures \(S_{BA}\) [46], \(S_{C}\) [37], \(S_{HY1}\) [39], \(S_{HY2}\) [39], \(S_{HY3}\) [39], \(S_{HK}\) [40], \(S_{LC}\) [41], \(S_{LX}\) [42], \(S_{L}\) [36] , \(S_{LS1}\) [43], \(S_{LS2}\) [43], \(S_{LS3}\) [43], \(S_{M}\) [44], \(S_{Y}\) [45], \(S_{P1}\) [34], \(S_{P2}\) [34], \(S_Z\) [33] and \(S_W\) [32].

Conclusion

The main contributions can be illustrated and reviewed in the following.

(1) The formulae of Pythagorean fuzzy similarity measures and distance measures are proposed, and their properties are proved. Meanwhile, the diverse desirable relations between the developed similarity measures and distance measures have also been elicited.

(2) A comparison with some existing literature [32,33,34, 36,37,38,39,40,41,42,43,44,45,46] is constructed in Tables 2, 3, 4 to state the availability of the proposed similarity measure.

In future, we will employ some similarity measures in other domains, such as medical diagnosis and machine learning. Besides, as this paper is just an applied research focusing on the similarity measures of PFSs, we will attempt to design some softwares to preferably realize the initiated information measure in daily life. Meanwhile, we also will take them into diverse fuzzy environment [47,48,49,50,51,52,53,54].