1 Introduction

Due to its interesting characteristics, the beta distribution is one of the well-known continuous distribution, that has a wide range of application in various filed, such as reliability applications and production quality control. It has a flexible shape, that reflects a wide range of natural and empirical phenomena in nature and reality that can be modelling with this distribution. Its domain, the interval from zero to one, add another interesting characteristic to this distribution by allowing it to consider as a probability distribution of probabilities, such as fraction of time, measurements whose values (or relative values) all lie between zero and one, or the random behavior of percentages and fractions, especially, in the cases when we have no idea about the probability, and therefore, it can be used to represents all probabilities. Another area that used beta distribution for representing possible values of probabilities or a distribution of the probabilities is the Bayesian studies, as being the prior distribution, that is widely used. In fact, it is one of the three common distributions, with the rectangular/uniform and normal distributions, that are employed to represents within the framework Bayesian analysis of continuous variables, Sheskin [1, p. 397]. Data mining methods and techniques need to use information about the prior probability knowledge, hence the beta distribution is representing a candidate for such situations, see Shi [2], and Olson and Shi [3] for further details. For an intensive reference of the beta distribution see Johnson et al. [4, p. 210–275].

The probability density function (pdf) of the four parameters beta distribution, Johnson et al. [5, p. 210], is given by;

$$f\left( t \right) = \frac{{\left( {t - a} \right)^{\alpha - 1} \left( {b - t} \right)^{\beta - 1} }}{{B\left( {\alpha , \beta } \right) \left( {b - a} \right)^{\alpha + \beta - 1} }}, \quad a < t < b,$$
(1)

where, the parameters \(\alpha ,\) \(\beta ,\) \(a\) and b satisfy that \(\alpha > 0,\) \(\beta > 0,\) \(a\) and \(b\) are real number such that \(a < b\), \(B\left( {\alpha , \beta } \right)\) is the beta function, Abramowitz and Stegun [6, p. 258], defined by;

$$B\left( {\alpha , \beta } \right) = \mathop \int \limits_{0}^{1} t^{\alpha - 1} \left( {1 - t} \right)^{\beta - 1} dt = \frac{{\varGamma \left( \alpha \right)\varGamma \left( { \beta } \right)}}{{\varGamma \left( {\alpha + \beta } \right)}}$$
(2)

and \(\varGamma \left( \alpha \right),\) the gamma function, Abramowitz and Stegun [6, p. 255], defined by;

$$\varGamma \left( \alpha \right) = \mathop \int \limits_{0}^{1} t^{\alpha - 1} e^{ - t} dt$$
(3)

The common widely used form of beta distribution in the literature, is the pdf given by;

$$f\left( x \right) = \frac{{x^{\alpha - 1} \left( {1 - x} \right)^{\beta - 1} }}{{B\left( {\alpha , \beta } \right)}},\quad 0 < x < 1,$$
(4)

This two parameters form is called sometimes, the standard beta distribution, which is obtained from (1) by making the transformation; \(x = \frac{t - a}{b - a}\).

One direction of the research employing the beta distribution is the generalization of the form given by (4), in order to be even more flexible and cover a lot of shapes.

Armero and Bayarri [7] introduced the Gauss hypergeometric distribution, with parameters \(p\), \(q, r\) and \(\delta ,\) as a generalization to the beta distribution when they studied a Bayesian queuing theory problem, with the following pdf;

$$f\left( x \right) = \frac{{x^{p - 1} \left( {1 - x} \right)^{q - 1} \left( {1 + \delta x} \right)^{ - r} }}{{B\left( {p,q} \right) F_{{\left( {2,1} \right)}} \left( {r, p;p + q; - \delta } \right)}},\quad 0 < x < 1,$$
(5)

where \(p > 0,\) \(q > 0,\) \(- \infty < r < \infty\), \(\delta > - 1,\) and \(F_{{\left( {2,1} \right)}}\) is the generalized hypergeometric function defined for non-negative integers n and m by;

$$F_{{\left( {n,m} \right)}} \left( {a_{1} , \ldots ,a_{n} ;b_{1} , \ldots ,b_{m} ;z} \right) = \mathop \sum \limits_{k = 0}^{\infty } \frac{{\left( {a_{1} } \right)_{k } \ldots \left( {a_{n} } \right)_{k } }}{{\left( {b_{1} } \right)_{k } \ldots \left( {b_{m} } \right)_{k } }}\frac{{z^{k} }}{k!}$$
(6)

and \(\left( a \right)_{k}\) is defined by;

$$\left( a \right)_{k} = \left\{ {\begin{array}{*{20}l} 0 \hfill &\quad {if\, k = 0} \hfill \\ {a\left( {a + 1} \right) \ldots \left( {a + k - 1} \right),} \hfill &\quad {k = 1,2,3, \ldots } \hfill \\ \end{array} } \right.$$
(7)

Gordy [8] introduced the confluent hypergeometric distribution, with parameters \(p\), \(q\) and s, with pdf given by;

$$f\left( x \right) = \frac{{x^{p - 1} \left( {1 - x} \right)^{q - 1} { \exp }\left( { - sx} \right)}}{{B\left( {p,q} \right) F_{{\left( {1,1} \right)}} \left( {p,p + q, - s} \right)}},\quad 0 < x < 1,$$

where \(p > 0,\) \(q > 0\) and \(- \infty < s < \infty\).

Pathan et al. [9] introduced a five parameters distribution as a generalization beta distribution, called it generalized beta distribution, with pdf given by;

$$f\left( x \right) = \frac{{x^{\alpha - 1} \left( {1 - x} \right)^{\beta - 1} \left( {1 - \sigma x} \right)^{\rho - 1} { \exp }\left( { - \gamma x} \right)}}{{B\left( {\alpha , \beta } \right){\Phi }_{1} \left( {\alpha ,\rho ;\alpha + \beta ;\sigma , - \gamma } \right)}}, \quad 0 < x < 1,$$

where the parameters \(\alpha ,\) \(\beta ,\) \(\sigma ,\) \(\rho\) and \(\gamma\) satisfy that \(\alpha > 0,\) \(\beta > 0,\) \(0 \le \sigma < 1,\) \(\rho\) and \(\gamma\) are real numbers and \(\Phi _{1} \left( . \right)\) is the Humbert’s confluent hypergeometric function given in Srivastava and Manocha [10, p. 58, Eq. (36)], and derive expressions for its distribution function moments.

Ng et al. [11] study the properties and evaluate the prediction level of a 6 parameters generalized beta distribution model with pdf given by;

$$f\left( x \right) = \frac{{\frac{{\varGamma \left( {\gamma + \rho - \alpha } \right)\varGamma \left( { \gamma + \rho - \beta } \right)}}{{\varGamma \left( {\gamma + \rho } \right)\varGamma \left( {\gamma + \rho - \alpha - \beta } \right)}}\left( {1 - z} \right)^{\sigma } x^{\gamma - 1} \left( {1 - x} \right)^{\rho - 1} \left( {1 - \sigma x} \right)^{\rho - 1} \left( {1 - zx} \right)^{ - \sigma } F_{{\left( {2,1} \right)}} \left( {\alpha ,\beta ;\gamma ;x} \right)}}{{F_{{\left( {3,2} \right)}} \left( {\rho ,\sigma ;\gamma + \rho - \alpha - \beta ;\gamma + \rho - \alpha ,\gamma + \rho - \beta ;\frac{z}{z - 1}} \right) B\left( {\gamma ,\rho } \right)}}\quad 0 < x < 1,$$
(8)

where the parameters \(\alpha ,\) \(\beta ,\) \(\gamma ,\) \(\sigma ,\) \(z\) and \(\rho\) satisfy that \(\alpha > 0,\) \(\beta > 0,\) \(\gamma > 0,\) \(\sigma > 0,\) \(z < 0.5\) and \(\rho > \alpha + \beta - \gamma .\)

Although Ng et al. [11], who provided a nice literature review for the beta family, showed interesting advances of this distribution with pdf given by (8) for fitting many different types of data, as well as that of Armero and Bayarri [7], Gordy [8] and Pathan et al. [9], but it is not easy to work with empirically. Finally, Gómez-Déniz and Sarabia [12] introduced a generalization of the standard beta distribution with bounded support, and study some of its basic properties, the behavior of its maximum likelihood estimators through simulation and derive its multivariate version.

The rest of the paper is organized as follows. Section 2 defines the six parameters beta distribution (SPBD). Section 3 gives some properties of this distribution, these properties are; boundaries and some limits of the pdf of SPBD, series expansion of its pdf, its mode, quantile function, reliability function, hazard function, special cases of SPBD, some transformation of the SPBD, its scaling, exponentiation and reflection symmetry properties, generation of its random variates, its order statistics distribution, moments about the origin, mean and variance, moment generating function, harmonic mean, incomplete moments, mean deviations, probability weighted moments, Renyi entropy, and Lorenz and Bonferroni curves. Section 4 introduces estimation of its parameters using the method of maximum likelihood estimation (MLE). Section 5 gives six miscellaneous simulation study of the SPBD to check the performance of the MLE. Section 6 uses the SPBD and other nested and related distributions to fit two different real-life data. Finally, Sect. 7 ends with conclusions.

2 The Six Parameters Beta Distribution

Let \(0 < a, b, \alpha , \beta ,A,B < \infty\), such that \(A < B\), and define the function \(f\) by:

$$f\left( {x;a, b, \alpha , \beta ,A,B} \right) = \left\{ {\begin{array}{*{20}l} {\frac{{bx^{b - 1} }}{{a^{b} \left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\left[ {\left( {\frac{x}{a}} \right)^{b} - A} \right]^{\alpha - 1} \left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]^{ \beta - 1} ,} \hfill & { aA^{{\frac{1}{b}}} < x < aB^{{\frac{1}{b}}} } \hfill \\ 0 \hfill & {otherwise, } \hfill \\ \end{array} } \right.$$
(9)

where \(B\left( {\alpha , \beta } \right)\) is the beta function defined by (2). We will write \(f\left( x \right)\) instead of \(f\left( {x;a, b, \alpha , \beta ,A,B} \right)\) for simplicity. We have the following proposition;

Proposition 1

The function \(f\) defined by (9) is a pdf with its cumulative distribution function (CDF) F given by;

$$F_{X} \left( {x;a, b, c, \alpha , \beta } \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {x \le a\alpha^{{\frac{1}{b}}} } \hfill \\ {\frac{1}{{B\left( {\alpha , \beta } \right)}}B\left( {\frac{{\left( {\frac{x}{a}} \right)^{b} -A}}{B - A};\alpha , \beta } \right),} \hfill & {aA^{{\frac{1}{b}}} < x < aB^{{\frac{1}{b}}} } \hfill \\ {1,} \hfill & {x \ge a\beta^{{\frac{1}{b}}} } \hfill \\ \end{array} } \right.$$
(10)

where \(B\left( {z;\alpha , \beta } \right)\) is the incomplete beta function, Abramowitz and Stegun [6, p. 263], defined by;

$$B\left( {z;\alpha , \beta } \right) = \mathop \int \limits_{0}^{z} t^{\alpha - 1} \left( {1 - t} \right)^{ \beta - 1} dt.$$
(11)

Proof

Since \(0 < a, b, \alpha , \beta ,A,B < \infty\), and \(aA^{{\frac{1}{b}}} < x < aB^{{\frac{1}{b}}}\), then \(A < \left( {\frac{x}{a}} \right)^{b} < B\), hence \(\left( {\frac{x}{a}} \right)^{b} - A > 0\) and also \(B - \left( {\frac{x}{a}} \right)^{b} > 0\), implying that f given in (9) is non-negative. Now;

$$\begin{aligned} \mathop \int \limits_{ - \infty }^{ + \infty } f\left( x \right)dx & = \mathop \int \limits_{{aA^{{\frac{1}{b}}} }}^{{aB^{{\frac{1}{b}}} }} \frac{{bx^{b - 1} }}{{a^{b} \left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\left[ {\left( {\frac{x}{a}} \right)^{b} - A} \right]^{\alpha - 1} \left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]^{ \beta - 1} dx \\ & = \frac{b}{{a^{b} \left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\mathop \int \limits_{{aA^{{\frac{1}{b}}} }}^{{aB^{{\frac{1}{b}}} }} x^{b - 1} \left[ {\left( {\frac{x}{a}} \right)^{b} - A} \right]^{\alpha - 1} \left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]^{ \beta - 1} dx \\ \end{aligned}$$

Let \(\left( {\frac{x}{a}} \right)^{b} - A = \left( {B - A} \right)t\), then \(x = a\left[ {\left( {B - A} \right)t + A} \right]^{{\frac{1}{b}}}\), and \(dx = \frac{{a\left( {B - A} \right)}}{b}\left[ {\left( {B - A} \right)t + A} \right]^{{\frac{1}{b} - 1}} dt\), then;

$$\begin{aligned} \mathop \int \limits_{{aA^{{\frac{1}{b}}} }}^{{aB^{{\frac{1}{b}}} }} x^{b - 1} \left[ {\left( {\frac{x}{a}} \right)^{b} - A} \right]^{\alpha - 1} \left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]^{ \beta - 1} dx & = \frac{{ a^{b} }}{b}\left( {B - A} \right)^{\alpha + \beta - 1} \mathop \int \limits_{0}^{1} t^{\alpha - 1} e^{ - t} dt \\ & = \frac{{ a^{b} }}{b}\left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right) \\ \end{aligned}$$

Hence, \(\mathop \int \limits_{ - \infty }^{ + \infty } f\left( x \right)dx = 1\). It follows that, for any x such that, \(a\alpha^{{\frac{1}{b}}} < x < a\beta^{{\frac{1}{b}}}\);

$$\begin{aligned} F_{X} \left( x \right) & = \mathop \int \limits_{ - \infty }^{x} f\left( t \right)dt \\ & = \mathop \int \limits_{{aA^{{\frac{1}{b}}} }}^{x} \frac{{bt^{b - 1} }}{{a^{b} \left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\left[ {\left( {\frac{t}{a}} \right)^{b} - A} \right]^{\alpha - 1} \left[ {B - \left( {\frac{t}{a}} \right)^{b} } \right]^{ \beta - 1} dt \\ \end{aligned}$$
(12)

Now by using the transformation \(z = \frac{{\left( {\frac{t}{a}} \right)^{b} - A}}{B - A}\), (12) reduces to;

$$= \frac{1}{{B\left( {\alpha , \beta } \right)}}\mathop \int \limits_{0}^{{\frac{{\left( {\frac{x}{a}} \right)^{b} - A}}{B - A}}} z^{\alpha - 1} e^{ - t} dz$$

from which we get (10).

We note that the \(F_{X}\) can be written, for \(aA^{{\frac{1}{b}}} < x < aB^{{\frac{1}{b}}}\), in the form;

$$F_{X} \left( x \right) = I\left( {\frac{{\left( {\frac{x}{a}} \right)^{b} - A}}{B - A}; \,\alpha , \beta } \right)$$
(13)

where \(I\left( {z;\alpha , \beta } \right)\) is the regularized incomplete beta function, Abramowitz and Stegun [6, p. 263], defined by;

$$I\left( {z;\alpha , \beta } \right) = \frac{1}{{B\left( {\alpha , \beta } \right)}}\mathop \int \limits_{0}^{z} t^{\alpha - 1} \left( {1 - t} \right)^{ \beta - 1} dt = \frac{{B\left( {z;\alpha , \beta } \right)}}{{B\left( {\alpha , \beta } \right)}}$$
(14)

□

Definition of the SPBD

The rv X is said to have a SPBD with parameters \(a, b, \alpha , \beta ,A\, {\text{and}}\,B\) written as \(X\sim {\text{SPBD}}(a, b, \alpha , \beta ,A,B\)), if its pdf is given by (9), or equivalently, its CDF is given by (10) or (13).

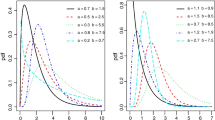
Figure 1 shows some plots of the pdf of the SPBD for some of its parameter’s values, inducting that this distribution has a lot of different flexible shapes.

Fig. 1
figure 1

Different pdf plots of the SPBD models

Full size image

3 Some Characteristics of the SPBD

3.1 Boundaries and Some Limits of the pdf

Let us study the behavior of the pdf of the \({\text{SPBD}}(a, b, \alpha , \beta ,A,B\)) at certain points. At the boundary’s points, we have from (9) for \(0 < \beta < \infty\), that;

$$f\left( {aA^{{\frac{1}{b}}} } \right) = \left\{ {\begin{array}{*{20}l} \infty ,&\quad 0 < \alpha < 1 \\ \frac{{\beta bA^{{1 - \frac{1}{b}}} }}{{a\left( {B - A} \right)}},&\quad \alpha = 1 \\ 0, &\quad \alpha > 1 \\ \end{array} } \right.$$

Therefore;

$$\begin{aligned} \mathop {\lim }\limits_{{a \to 0^{ + } }} f\left( {aA^{{\frac{1}{b}}} } \right) & = \mathop {\lim }\limits_{b \to \infty } f\left( {aA^{{\frac{1}{b}}} } \right) = \mathop {\lim }\limits_{\beta \to \infty } f\left( {aA^{{\frac{1}{b}}} } \right) = \infty , \\ \mathop {\lim }\limits_{a \to \infty } f\left( {aA^{{\frac{1}{b}}} } \right) & = \mathop {\lim }\limits_{{b \to 0^{ + } }} f\left( {aA^{{\frac{1}{b}}} } \right) = \mathop {\lim }\limits_{{\beta \to 0^{ + } }} f\left( {aA^{{\frac{1}{b}}} } \right) = \mathop {\lim }\limits_{B \to \infty } f\left( {aA^{{\frac{1}{b}}} } \right) = 0, \\ \mathop {\lim }\limits_{{A \to 0^{ + } }} f\left( {aA^{{\frac{1}{b}}} } \right) & = 0\quad {\text{if }}\,b \ne 1,\quad {\text{and}}\quad \mathop {\lim }\limits_{{A \to 0^{ + } }} f\left( {aA^{{\frac{1}{b}}} } \right) = \frac{\beta b }{aB}\quad {\text{if }}\, b = 1 \\ \end{aligned}$$

Similarly;

$$f\left( {aA^{{\frac{1}{b}}} } \right) = \left\{ {\begin{array}{*{20}l} {\infty , } \hfill &\quad {0 < \beta < 1} \hfill \\ {\frac{{\alpha bB^{{1 - \frac{1}{b}}} }}{{a\left( {B - A} \right)}},} \hfill &\quad {\beta = 1} \hfill \\ {0,} \hfill &\quad {\beta > 1} \hfill \\ \end{array} } \right.$$

Therefore;

$$\begin{aligned} & \mathop {\lim }\limits_{{a \to 0^{ + } }} f\left( {aB^{{\frac{1}{b}}} } \right) = \mathop {\lim }\limits_{b \to \infty } f\left( {aB^{{\frac{1}{b}}} } \right) = \mathop {\lim }\limits_{\alpha \to \infty } f\left( {aB^{{\frac{1}{b}}} } \right) = \mathop {\lim }\limits_{{\beta \to 0^{ + } }} f\left( {aB^{{\frac{1}{b}}} } \right) = \infty , \\ & \mathop {\lim }\limits_{a \to \infty } f\left( {aB^{{\frac{1}{b}}} } \right) = \mathop {\lim }\limits_{{b \to 0^{ + } }} f\left( {aB^{{\frac{1}{b}}} } \right) = \mathop {\lim }\limits_{{\alpha \to 0^{ + } }} f\left( {aB^{{\frac{1}{b}}} } \right) = \mathop {\lim }\limits_{\beta \to \infty } f\left( {aB^{{\frac{1}{b}}} } \right) = 0, \\ & {\text{ and}}\quad \mathop {\lim }\limits_{{A \to 0^{ + } }} f\left( {aB^{{\frac{1}{b}}} } \right) = \frac{\alpha b }{a}B^{{ - \frac{1}{b}}} \\ \end{aligned}$$

3.2 Series Expansion

Proposition 2

The function \(f\) given by (9) can be written in the following expansion series.

$$f\left( {x;a, b, \alpha , \beta ,A,B} \right) = \frac{{bB^{\beta - 1} }}{{\left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\mathop \sum \limits_{i = 0}^{\infty } \mathop \sum \limits_{j = 0}^{\infty } C\left( {i,j;a, b, \alpha , \beta ,A,B} \right)x^{{b\left( {\alpha + j - i} \right) - 1}}$$
(15)

where

$$C\left( {i,j;a, b, \alpha , \beta ,A,B} \right) = \left( { - 1} \right)^{i + j} \left( {\begin{array}{*{20}c} { \alpha - 1} \\ i \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\beta - 1} \\ j \\ \end{array} } \right)\frac{{A^{i} }}{{a^{{b\left( {\alpha + j - i} \right)}} B^{j} }}$$

Proof

Since \(0 < a\) and \(aA^{{\frac{1}{b}}} < x\), then \(A < \left( {\frac{x}{a}} \right)^{b}\), that is \(\frac{A}{{\left( {\frac{x}{a}} \right)^{b} }} < 1\), we can write

$$\left[ {\left( {\frac{x}{a}} \right)^{b} - A} \right]^{\alpha - 1} = \left( {\frac{x}{a}} \right)^{{b\left( {\alpha - 1} \right)}} \left[ {1 - \frac{A}{{\left( {\frac{x}{a}} \right)^{b} }}} \right]^{\alpha - 1}$$

Therefore, using the binomial series expansion, Abramowitz and Stegun [6, p. 14], we can write;

$$\left[ {\left( {\frac{x}{a}} \right)^{b} - A} \right]^{\alpha - 1} = \left( {\frac{x}{a}} \right)^{{b\left( {\alpha - 1} \right)}} \mathop \sum \limits_{i = 0}^{\infty } \left( { - 1} \right)^{i} \left( {\begin{array}{*{20}c} { \alpha - 1} \\ i \\ \end{array} } \right)\left[ {\frac{A}{{\left( {\frac{x}{a}} \right)^{b} }}} \right]^{i}$$
(16)

Similarly, we have that;

$$\left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]^{ \beta - 1} = B^{\beta - 1} \mathop \sum \limits_{j = 0}^{\infty } \left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} { \beta - 1} \\ j \\ \end{array} } \right)\left[ {\frac{{\left( {\frac{x}{a}} \right)^{b} }}{B}} \right]^{j}$$
(17)

Hence, using (16) and (17) into the function \(f\) given by (9) we get (15).□

3.3 The Mode

For \(aA^{{\frac{1}{b}}} < x < aB^{{\frac{1}{b}}}\), we can see that the pdf of the SPBD satisfies the following;

$$\frac{\partial }{\partial x}f\left( x \right) = \left\{ {\frac{{\frac{b}{a}\left( {\alpha - 1} \right)\left( {\frac{x}{a}} \right)^{b - 1} }}{{\left( {\frac{x}{a}} \right)^{b} - A}} - \frac{{b\left( {\beta - 1} \right)\left( {\frac{x}{a}} \right)^{b - 1} }}{{a\left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]}} + \frac{b - 1}{x}} \right\}f\left( x \right)$$
(18)

Therefore, \(\frac{\partial }{\partial x}f\left( x \right) = 0,\) is equivalent to either \(f\left( x \right) = 0,\) which is discussed in Sect. 3.1 above, or

$$\frac{{\frac{b}{a}\left( {\alpha - 1} \right)\left( {\frac{x}{a}} \right)^{b - 1} }}{{\left( {\frac{x}{a}} \right)^{b} - A}} - \frac{{b\left( {\beta - 1} \right)\left( {\frac{x}{a}} \right)^{b - 1} }}{{a\left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]}} + \frac{b - 1}{x} = 0$$
(19)

Multiplying (19) by \(ax\left[ {\left( {\frac{x}{a}} \right)^{b} - A} \right]\left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]\), and setting \(y = \left( {\frac{x}{a}} \right)^{b}\), it reduces to;

$$c_{1 } y^{2} + c_{2 } {\text{y }} + c_{3 } = 0$$
(20)

where

$$\begin{aligned} c_{1 } & = b\left( {\alpha + \beta - 1} \right) - 1 \\ c_{2 } & = \left( {1 - b\alpha } \right)B + b\left( {1 - b\beta } \right)A \\ c_{3 } & = \left( {b - 1} \right)AB \\ \end{aligned}$$

Let discuss the real roots of (20), according to the following cases.

Case 1

If \(\alpha + \beta \ne 1\), \(b = \frac{1}{\alpha + \beta - 1}\), and \(\left( {1 - b\alpha } \right)B \ne b\left( {1 - b\beta } \right)A\), that is when \(c_{1 } = 0\) and \(c_{2 } \ne 0\), then (20) has a single root given by;

$$y = \frac{{ - \left( {b - 1} \right)AB}}{{\left( {1 - b\alpha } \right)B + b\left( {1 - b\beta } \right)A}}$$

Hence; the root in term of x is given by;

$$x_{1 } = a\left[ {\frac{{\left( {1 - b} \right)AB}}{{\left( {1 - b\alpha } \right)B + b\left( {1 - b\beta } \right)A}}} \right]^{{\frac{1}{b}}}$$

Case 2

If \(b \ne \frac{1}{\alpha + \beta - 1}\), that is \(c_{1 } \ne 0\), then the real roots of (20) in terms of x, that is when \(c_{2 }^{2} - 4c_{1 } c_{3 } \ge 0\), are given by;

$$\begin{aligned} x_{2 } & = a\left[ {\frac{{\left( {b\alpha - 1} \right)B + b\left( {b\beta - 1} \right)A - \sqrt {\left( {\left( {1 - b\alpha } \right)B + b\left( {1 - b\beta } \right)A} \right)^{2} - 4\left( {b - 1} \right)AB\left[ {b\left( {\alpha + \beta - 1} \right) - 1} \right]} }}{{2b\left( {\alpha + \beta - 1} \right) - 2}}} \right]^{{\frac{1}{b}}} \\ x_{3 } & = a\left[ {\frac{{\left( {b\alpha - 1} \right)B + b\left( {b\beta - 1} \right)A + \sqrt {\left( {\left( {1 - b\alpha } \right)B + b\left( {1 - b\beta } \right)A} \right)^{2} - 4\left( {b - 1} \right)AB\left[ {b\left( {\alpha + \beta - 1} \right) - 1} \right]} }}{{2b\left( {\alpha + \beta - 1} \right) - 2}}} \right]^{{\frac{1}{b}}} \\ \end{aligned}$$

Since \(\frac{{\partial^{2} }}{{\partial x^{2} }}f\left( {x_{i} } \right), {\text{for }}i = 1, 2,\, {\text{and }}\,3\) is not easy to be evaluated, an empirical evaluation has to be studied to see at which point \(x_{i}\) we have a local maximum in order to determined the mode of the SPBD.

3.4 Quantile Function

Let \(0 < p < 1\), then the quantile function of the rv \(X\sim {\text{SPBD}}(a, b, \alpha , \beta ,A,B\)), \(Q\), is defined by;

$$Q\left( u \right) = { \inf }\left\{ {x \in {\mathbb{R}};p \le F\left( x \right)} \right\}$$

can be found using (13), to be;

$$Q\left( p \right) = a\left[ {A + \left( {B - A} \right) I^{ - 1} \left( {p; \alpha , \beta } \right)} \right]^{{\frac{1}{b}}}$$
(21)

where \(I^{ - 1}\) is the inverse of regularized incomplete beta function.

In particular, the median of X, \(Med\left( X \right)\); is given by;

$$Med\left( X \right) = a\left[ {A + \left( {B - A} \right) I^{ - 1} \left( {0.5; \alpha , \beta } \right)} \right]^{{\frac{1}{b}}}$$

Table 1 represents parameters values and domain ranges of the some selected SPBD data sets, which has different shapes and domain range, that will use for our simulation study in Sect. 5, as well as, will be used for computing of certain statistics of SPBD later in this section, while Fig. 2 represents the plots of the quantile functions of these SPBD data sets.

Table 1 Parameters values of the some selected SPBD data sets
Full size table
Fig. 2
figure 2

Plots of the quantile function of the six selected SPBD data sets

Full size image

3.5 Reliability Function

The reliability (survival) function of \(X\sim {\text{SPBD}}(a, b,\alpha , \beta ,A,B\)) using (13), is given by;

$$R\left( x \right) = 1 - F\left( x \right) = 1 - I\left( {\frac{{\left( {\frac{x}{a}} \right)^{b} - A}}{B - A}; \alpha , \beta } \right), \quad aA^{{\frac{1}{b}}} < x < aB^{{\frac{1}{b}}} ,$$
(22)

3.6 Hazard Function

The hazard function \(, h\left( x \right),\) of the rv \(X\sim {\text{SPBD}}(a, b, \alpha , \beta ,A,B\)), using (9) and (13), is given for \(aA^{{\frac{1}{b}}} < x < aB^{{\frac{1}{b}}}\), by;

$$h\left( x \right) = \frac{{{\text{f}}\left( {\text{x}} \right)}}{1 - F\left( x \right)} = \frac{{\frac{{bx^{b - 1} }}{{a^{b} \left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\left[ {\left( {\frac{x}{a}} \right)^{b} - A} \right]^{\alpha - 1} \left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]^{ \beta - 1} }}{{1 - I\left( {\frac{{\left( {\frac{x}{a}} \right)^{b} - A}}{B - A}; \alpha , \beta } \right)}}$$

3.7 Special Cases of SPBD

  1. 1.

    \({\text{The}} \,{\text{SPBD}}(1,1,p, q,a,b\)) is the 4 parameters Beta distribution, Johnson et al. [4, p. 210], with pdf;

    $$f\left( x \right) = \frac{1}{{B\left( {p,q} \right)}} \frac{{\left( {x - a} \right)^{p - 1} \left( {b - x} \right)^{q - 1} }}{{\left( {b - a} \right)^{p + q - 1} }},\quad a < x < b$$
  2. 2.

    \({\text{The}} \,{\text{SPBD}}(a, b,1, c,\alpha , \beta )\) is the generalized modification of the Kumaraswamy distribution, Alshkaki [13], with pdf;

    $$f\left( x \right) = \frac{bc}{a} \left( {\beta - \alpha } \right)^{ - c} \left( {\frac{x}{a}} \right)^{b - 1} \left[ {\beta - \left( {\frac{x}{a}} \right)^{b} } \right]^{c - 1} ,\quad a\alpha^{{\frac{1}{b}}} < x < a\beta^{{\frac{1}{b}}}$$
  3. 3.

    \({\text{The}}\, {\text{SPBD}}(1, a,1,b,0,1\) is the Kumaraswamy distribution, Kumaraswamy [14], with pdf;

    $$f\left( x \right) = ab x^{a - 1} \left[ {1 - x^{a} } \right]^{b - 1} ,\quad 0 < x < 1$$
  4. 4.

    \({\text{The}} \,{\text{SPBD}}\left( {a,b,p.q,0,1} \right)\) is the generalized beta of the first kind distribution, McDonald [15], with pdf;

    $$f\left( x \right) = \frac{\left| a \right|}{{b^{ap} B\left( {p,q} \right)}}x^{ap - 1} \left[ {1 - \left( {\frac{x}{a}} \right)^{b} } \right]^{ q - 1} ,\quad 0 < x < 1$$
  5. 5.

    \({\text{The}} \,{\text{SPBD}}\left( {1,1,1,1,0,1} \right)\) is the standard uniform distribution with pdf;

    $$f\left( x \right) = 1,\quad 0 < x < 1$$
  6. 6.

    \({\text{The}} \,{\text{SPBD}}\left( {1,2,1,1,0,1} \right)\) is the triangular distribution with pdf;

    $$f\left( x \right) = 2 x,\quad 0 < x < 1$$
  7. 7.

    \({\text{The}} \,{\text{SPBD}}(1, 1, 1, \delta , \alpha , \beta )\) is the power function distribution with pdf;

    $$f\left( x \right) = \frac{\delta }{{\left( {\beta - \alpha } \right)}} \left[ {\frac{\beta - x}{\beta - \alpha }} \right]^{\delta - 1} ,\quad \alpha < x < \beta$$
  8. 8.

    \({\text{The}} \,{\text{SPBD}}(\lambda , a\theta , 1, b, 0, 1)\) is the Kumaraswamy power function distribution, Abdul-Moniem [16], with pdf;

    $$f\left( x \right) = \frac{ab\theta }{\lambda } \left( {\frac{x}{\lambda }} \right)^{a\theta - 1} \left[ {1 - \left( {\frac{x}{\lambda }} \right)^{a\theta } } \right]^{b - 1} ,\quad 0 < x < \lambda$$
  9. 9.

    \({\text{The}}\, {\text{SPBD}}(1, \beta , 1, \gamma , 0, 1)\) is the Minimax distribution, McDonald [15], with pdf;

    $$f\left( x \right) = \beta \gamma x^{\beta - 1} \left[ {1 - x^{\beta } } \right]^{\gamma - 1} ,\quad 0 < x < 1$$
  10. 10.

    \({\text{The}}\,{\text{SPBD}}(c, - \,\upalpha, 1,\uptheta, 0, 1)\) is the exponentiated Pareto distribution, Gupta et al. [17], with pdf;

    $$f\left( x \right) = \theta \alpha c^{\alpha } x^{{ - \left( {a + 1} \right)}} \left[ {1 - \left( {\frac{x}{c}} \right)^{ - a} } \right]^{\theta - 1} ,\quad 0 < c < x$$
  11. 11.

    \({\text{The}}\, {\text{SPBD}}(\alpha , \beta , 1, 1, 0, 1)\) is the generalized uniform distribution, Tiwari et al. [18], with pdf;

    $$f\left( x \right) = \frac{\beta }{\alpha } \left( {\frac{x}{\alpha }} \right)^{\beta - 1} ,\quad 0 < x < \alpha$$

    We may note that the Kumaraswamy (Case 4), standard uniform (Case 5), triangular (Case 6), Kumaraswamy power function (Case 8), minimax (Case 9), Pareto (Case 10), and the generalized uniform (Case 11) distribution are all special cases of the generalized beta of the first kind distribution (Case 4).

3.8 Transformations

Lemma 2

  1. 1.

    Let the rv \({\text{U}}\) has the standard uniform distribution, \({\text{U}}(0,1\)), and the rv \({\text{X}}\) defined by \(X = a\left[ {A + \left( {B - A} \right)I^{ - 1} \left( {U,\alpha , \beta } \right)} \right]^{{\frac{1}{b}}}\), then \({\text{X}}\sim {\text{SPBD}}(a, b, \alpha , \beta ,A,B\)).

  2. 2.

    Let the rv \({\text{X}}\sim {\text{SPBD}}(1, 1, 1,1, 0, 1\)), then the rv \({\text{Y}}\) defined by \({\text{Y}} = \left( {\frac{{1 - {\text{X}}}}{\text{X}}} \right)^{{\frac{1}{\updelta}}} \cdot {\text{e}}^{{ - \frac{\upgamma}{\updelta}}}\) has a log-logistic distribution with parameters \({\updelta }\) and \({\upgamma }\), Johnson et al. [4, p. 151], with CDF given by;

    $$F_{Y} \left( y \right) = 1 - \left[ {1 + y^{\delta } e^{\gamma } } \right]^{ - 1} ,\quad y \ge 0$$
  3. 3.

    Let the rv \({\text{X}}\sim {\text{SPBD}}(a, b, 1,c,A,B\)), then the rv \({\text{Y}}\) defined by \({\text{Y}} = B - \left( {\frac{x}{a}} \right)^{b}\) has the generalized uniform distribution, Tiwari et al. [18], with CDF given by;

    $$F_{Y} \left( y \right) = \left[ {\frac{y}{B - A}} \right]^{c} ,\quad 0 \le y \le B - A$$
  4. 4.

    Let the rv \({\text{X}}\sim {\text{SPBD}}(a, b, 1,c,A,B)\) then the rv \({\text{Y}}\) defined by \({\text{Y}} = \left( {B - A} \right)^{ - 1} \left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]\) has the beta distribution with parameters 1 and \(c\), with CDF given by;

    $$F_{Y} \left( y \right) = y^{c} ,\quad 0 \le y \le 1$$
  5. 5.

    Let the rv \(X\sim {\text{SPBD}}(1, {\text{b}}, 1,1, 0, 1\)), then the rv \(Y\) defined by \(Y = \theta - b^{2} log\left( X \right)\) has an exponential distribution with parameters \(\theta\) and \(b\), Johnson et al. [5, p. 494], with CDF given by;

    $$F_{Y} \left( y \right) = 1 - e^{{ - \left( {\frac{y - \theta }{b}} \right)}} ,\quad x > \theta$$
  6. 6.

    Let the rv \(X\sim {\text{SPBD}}(1, {\text{b}}, 1,1, 0, 1\)), then the rv \(Y\) defined by \(Y = \mu - \beta log\left[ { - blog\left( {X^{b} } \right)} \right]\) has a Gumbel (generalized extreme value type-I) distribution with parameters \(\mu\) and \(\beta\), Forbes et al. [19, p. 98], with CDF given by;

    $$F_{Y} \left( y \right) = e^{{ - e^{{ - \left( {\frac{y - \mu }{\beta }} \right)}} }}$$
  7. 7.

    Let the rv \(X\sim {\text{SPBD}}(1, {\text{b}}, 1,1, 0, 1\)), then the rv \(Y\) defined by \(Y = \alpha + \beta log\left( {\frac{{X^{b} }}{{1 - X^{b} }}} \right)\) has a logistic distribution with parameters \(\alpha\) and \(\beta\), Johnson et al. [4, p. 115], with CDF given by;

    $$F_{Y} \left( y \right) = \left[ {1 + e^{{ - \left( {\frac{y - \alpha }{\beta }} \right)}} } \right]^{ - 1}$$
  8. 8.

    Let the rv \(X\sim {\text{SPBD}}(1, {\text{b}}, 1,1, 0, 1)\), then the rv \(Y\) defined by \(Y = \frac{k}{X}\), where k is a positive constant, has a Pareto distribution with parameters \(k\) and \(b\), Johnson et al. [4, p. 574], with CDF given by;

    $$F_{Y} \left( y \right) = 1 - \left( {\frac{k}{y}} \right)^{b}$$
  9. 9.

    Let the rv \(X\sim {\text{SPBD}}(1, {\text{b}}, 1,1, 0, 1)\), then the rv \(Y\) defined by \(Y = \xi + \alpha \left[ { - log\left( {X^{b} } \right)} \right]^{{\frac{1}{\theta }}}\) has a Weibull distribution with parameters \(\xi\), \(\alpha ,\) and \(\theta\), Johnson et al. [4, p. 629], with its CDF given by;

    $$F_{Y} \left( y \right) = 1 - e^{{ - \left( {\frac{y - \xi }{\alpha }} \right)^{\theta } }}$$

Proof

For case (1), we have;

$$\begin{aligned} F_{X} \left( x \right) & = P\left( {X \le x} \right) = P\left( {a\left[ {A + \left( {B - A} \right)I^{ - 1} \left( {U;\alpha , \beta } \right)} \right]^{{\frac{1}{b}}} \le x} \right) \\ & = P\left( {I^{ - 1} \left( {U;\alpha , \beta } \right) \le \frac{{\left( {\frac{x}{a}} \right)^{b} - A}}{B - A}} \right) = P\left( {U \le I\left( {\frac{{\left( {\frac{x}{a}} \right)^{b} - A}}{B - A};\alpha , \beta } \right)} \right) = I\left( {\frac{{\left( {\frac{x}{a}} \right)^{b} - A}}{B - A};\alpha , \beta } \right) \\ \end{aligned}$$

Therefore, the rv \({\text{X}}\sim {\text{SPBD}}(a, b, \alpha , \beta ,A,B\)).

Proof of cases (2) through (9) can be shown on the same lines as the proof of (1).

We may note that the SPBDs stated in Cases 2, 5, 6, 8, and 9 are all special cases of the generalized beta of the first kind distribution (see Case 4 of Sect. 3.7).□

3.9 Scaling Property

Proposition 3

(The SPBD is closed under scaling) Let the rv \(X\sim {\text{SPBD}}(a, b, \alpha , \beta ,A,B\)) and let the rv \(Y = cX\), where \(0 < c < \infty\), then \(Y\sim {\text{SPBD}}(ca, b, \alpha , \beta ,A,B).\)

Proof

$$F_{Y} \left( y \right) = P\left( {Y \le y} \right) = P\left( {cX \le y} \right) = P\left( {X \le \frac{y}{c}} \right) = F_{X} \left( {\frac{y}{c};a, b, \alpha , \beta ,A,B} \right)$$

Therefore, using (13), we have that;

$$F_{Y} \left( y \right) = I\left( {\frac{{\left( {\frac{{\frac{y}{c}}}{a}} \right)^{b} - A}}{B - A}; \alpha , \beta } \right) = I\left( {\frac{{\left( {\frac{y}{ca}} \right)^{b} - A}}{B - A}; \alpha , \beta } \right) = F_{X} \left( {y;ca, b, \alpha , \beta ,A,B} \right)$$

On the same lines as the proof of Proposition 3, we can prove the following Propositions 4 and 5.□

3.10 Exponentiation Property

Proposition 4

(The SPBD is closed under exponentiation) Let the rv \(X\sim {\text{SPBD}}(a, b, \alpha , \beta ,A,B\)) and let the rv \(Y = X^{c}\), where \(0 < c < \infty\), then \(Y\sim {\text{SPBD}}\left( {a^{c} ,\frac{b}{c}, \alpha , \beta ,A,B} \right).\)

3.11 Reflection Symmetry Property

Proposition 5

Let the rv \(X\sim {\text{SPBD}}(a, 1, \alpha , \beta ,A,B)\) and let the rv \(Y = a\left( {B + A} \right) - X\), then \(Y\sim {\text{SPBD}}(a,1, \beta ,\alpha ,A,B).\)

3.12 Generate SPBD Random Variates

Using result Lemma 2(1), we can generate \({\text{SPBD}}\left( {a, b, \alpha , \beta ,A,B} \right)\) random variates as follows;

  1. 1.

    Generate \(u \sim U\left( {0,1} \right).\)

  2. 2.

    Compute y = \(I^{ - 1} \left( {U,\alpha , \beta } \right).\)

  3. 3.

    Set \(x = a\left[ {A + \left( {B - A} \right)y} \right]^{{\frac{1}{b}}} .\)

3.13 Order Statistics

Let \(X_{1}\), \(X_{2}\), …, \(X_{n}\) be a random sample of size n from \({\text{SPBD}}(a, b, \alpha , \beta ,A,B\)), with pdf f and CDF F, and let \(X_{1:n}\), \(X_{2:n}\), …, \(X_{n:n}\) be their order statistics, then for \(i = 1, 2, 3, \ldots ,n\), the pdf of i-th order statistics \(X_{i:n}\), \(f_{i:n} \left( x \right),\) is given for by;

$$f_{i:n} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\frac{n!}{{\left( {i - 1} \right)!\left( {n - i} \right)!}} f\left( x \right)\left[ {F\left( x \right)} \right]^{i - 1} \left[ {1 - F\left( x \right)} \right]^{n - i} ,} \hfill & {a\alpha^{{\frac{1}{b}}} < x < a\beta^{{\frac{1}{b}}} } \hfill \\ 0 \hfill & {otherwise,} \hfill \\ \end{array} } \right.$$

Hence, for \(a\alpha^{{\frac{1}{b}}} < x < a\beta^{{\frac{1}{b}}}\), and using the fact that;

$$\left[ {1 - F\left( x \right)} \right]^{n - 1} = \mathop \sum \limits_{j = 0}^{n - 1} \left( {\begin{array}{*{20}c} {n - 1} \\ j \\ \end{array} } \right)\left( { - 1} \right)^{j} \left[ {F\left( x \right)} \right]^{j}$$

we have that;

$$\begin{aligned} f_{i:n} \left( x \right) & = \frac{n!}{{\left( {i - 1} \right)!\left( {n - i} \right)!}}f\left( x \right)\left[ {F\left( x \right)} \right]^{i - 1} \mathop \sum \limits_{j = 0}^{n - 1} \left( {\begin{array}{*{20}c} {n - 1} \\ j \\ \end{array} } \right)\left( { - 1} \right)^{j} \left[ {F\left( x \right)} \right]^{j} \\ & = \frac{n!}{{\left( {i - 1} \right)!\left( {n - i} \right)!}}f\left( x \right)\mathop \sum \limits_{j = 0}^{n - 1} \left( {\begin{array}{*{20}c} {n - 1} \\ j \\ \end{array} } \right)\left( { - 1} \right)^{j} \left[ {I\left( {\frac{{\left( {\frac{x}{a}} \right)^{b} - A}}{B - A};\alpha , \beta } \right)} \right]^{i + j - 1} \\ \end{aligned}$$

Then the pdf of the rv \(X_{i:n}\), \(f_{i:n}\), can be written as;

$$f_{i:n} \left( x \right) = f\left( x \right)\mathop \sum \limits_{j = 0}^{i - 1} A\left( {i,j;n} \right)\left[ {I\left( {\frac{{\left( {\frac{x}{a}} \right)^{b} - A}}{B - A};\alpha , \beta } \right)} \right]^{i + j - 1}$$
(23)

where

$$A\left( {i,j;n} \right) = \left( { - 1} \right)^{j} \frac{n!}{{\left( {i - 1} \right)!\left( {n - i - j} \right)!j!}}.$$

3.14 Moments about the Origin

Let \(k = 1, 2, 3, \ldots\), then the moment of the rv \(X\sim {\text{SPBD}}\left( {a, b, \alpha , \beta ,A,B} \right)\) of order k about zero is given by;

$$E\left( {X^{k} } \right) = \mathop \int \limits_{ - \infty }^{ + \infty } x^{k} f\left( x \right)dx = \mathop \int \limits_{{aA^{{\frac{1}{b}}} }}^{{aB^{{\frac{1}{b}}} }} \frac{{bx^{k + p - 1} }}{{a^{b} \left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\left[ {\left( {\frac{x}{a}} \right)^{b} - A} \right]^{\alpha - 1} \left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]^{ \beta - 1} dx$$

and by using the transformation \(y = \left( {\frac{x}{a}} \right)^{b}\), it reduces to;

$$E\left( {X^{k} } \right) = \frac{{a^{k} }}{{\left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\mathop \int \limits_{A}^{B} y^{{\frac{k}{b}}} \left( {y - A} \right)^{\alpha - 1} \left( {B - y} \right)^{ \beta - 1} dy$$

from which we have that;

$$E\left( {X^{k} } \right) = a^{k} A^{{\frac{k}{b}}} \varGamma \left( {\alpha + \beta } \right) \tilde{F}_{{\left( {2,1} \right)}} \left( { - \frac{k}{b}, \alpha ;\alpha + \beta ;1 - \frac{B}{A}} \right)$$
(24)

where \(\tilde{F}_{{\left( {2,1} \right)}}\) is the regularized hypergeometric function, Virchenko et al. [20], defined by;

$$\tilde{F}_{{\left( {2,1} \right)}} \left( {a, b;c;z} \right) = \mathop \sum \limits_{m = 0}^{\infty } \frac{{\left( a \right)_{m } \left( b \right)_{m} }}{{\varGamma \left( {c + m} \right) m!}}z^{i}$$

and \(\left( a \right)_{m}\) is as defined by (7).

Note that, in case that \(A = 0\) then;

$$E\left( {X^{k} } \right) = a^{k} B^{{\frac{k}{b}}} \frac{{ \varGamma \left( {\alpha + \frac{k}{b}} \right) \varGamma \left( {\alpha + \beta } \right)}}{{ \varGamma \left( \alpha \right) \varGamma \left( {\alpha + \beta + \frac{k}{b}} \right)}} .$$

3.15 Mean and Variance

Using (24), the mean of \(X \sim {\text{SPBD}}\left( {a, b, \alpha , \beta ,A,B} \right)\) is given by;

$$E\left( X \right) = a A^{{\frac{1}{b}}} \varGamma \left( {\alpha + \beta } \right) \tilde{F}_{{\left( {2,1} \right)}} \left( { - \frac{1}{b}, \alpha ,\alpha + \beta ;1 - \frac{B}{A}} \right)$$
(25)

And the variance;

$$Var\left( X \right) = a^{2} A^{{\frac{2}{b}}} \varGamma \left( {\alpha + \beta } \right)\left\{ {\tilde{F}_{{\left( {2,1} \right)}} \left( { - \frac{2}{b}, \alpha ,\alpha + \beta ;1 - \frac{B}{A}} \right) - \varGamma \left( {\alpha + \beta } \right)\left[ { \tilde{F}_{{\left( {2,1} \right)}} \left( { - \frac{1}{b}, \alpha ,\alpha + \beta ;1 - \frac{B}{A}} \right)} \right]^{2} } \right\}$$

Table 2 represents the mean, median, mode and variance of the selected SPBD data sets that are given in Table 1.

Table 2 Mean, median, mode and variance of the selected SPBD data sets
Full size table

3.16 The Moment Generating Function

Similarly, the moment generating function of the rv \(X\sim {\text{SPBD}}\left( {a, b, \alpha , \beta ,A,B} \right)\), \(M_{X} \left( t \right)\), can be found to be;

$$M_{X} \left( t \right) = E\left( {e^{tX} } \right) = \varGamma \left( {\alpha + \beta } \right)\mathop \sum \limits_{i = 0}^{\infty } \frac{{a^{i} A^{{\frac{i}{b}}} }}{i!}\tilde{F}_{{\left( {2,1} \right)}} \left( { - \frac{i}{b}, \alpha ,\alpha + \beta ;1 - \frac{B}{A}} \right)t^{i} .$$

3.17 Harmonic Mean

The harmonic mean of \(X\sim {\text{SPBD}}\left( {a, b, \alpha , \beta ,A,B} \right)\), on the same lines as that of the moment of X, is given by;

$$E\left( {\frac{1}{X}} \right) = \frac{{\varGamma \left( {\alpha + \beta } \right)}}{{aA^{{\frac{1}{b}}} }}\tilde{F}_{{\left( {2,1} \right)}} \left( {\frac{1}{b}, \alpha ,\alpha + \beta ;1 - \frac{B}{A}} \right).$$

3.18 Incomplete Moments

The k-th incomplete moment of \(X\sim {\text{SPBD}}\left( {a, b, \alpha , \beta ,A,B} \right)\), \(I\left( {z,k} \right)\), is defined by;

$$I\left( {z,k} \right) = \mathop \int \limits_{ - \infty }^{z} x^{k} f\left( x \right)dx$$

Using the form of the pdf of \(X\) given in (15), then;

$$I\left( {z,k} \right) = \mathop \int \limits_{{aA^{{\frac{1}{b}}} }}^{z} x^{k} \frac{{bB^{\beta - 1} }}{{\left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\mathop \sum \limits_{i = 0}^{\infty } \mathop \sum \limits_{j = 0}^{\infty } C\left( {i,j;a, b, \alpha , \beta ,A,B} \right)x^{{b\left( {\alpha + j - i} \right) - 1}} dx$$

from which we have that;

$$I\left( {z,k} \right) = \frac{{bB^{\beta - 1} }}{{\left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\mathop \sum \limits_{i = 0}^{\infty } \mathop \sum \limits_{j = 0}^{\infty } \frac{{C\left( {i,j;a, b, \alpha , \beta ,A,B} \right)}}{{k + b\left( {\alpha + j - i} \right)}}\left[ {z^{{k + b\left( {\alpha + j - i} \right)}} - (aA^{{\frac{1}{b}}} )^{{k + b\left( {\alpha + j - i} \right)}} } \right].$$
(26)

3.19 Mean Deviations

The mean deviation of \(X\sim {\text{SPBD}}\left( {a, b, \alpha , \beta ,A,B} \right)\) about its mean \(\mu = E\left( X \right)\), \(MD\left( \mu \right)\), is given by;

$$MD\left( \mu \right) = E\left| {X - \mu } \right|$$

which can be found, Cordeiro et al. [21], to be;

$$MD\left( \mu \right) = 2\left[ {\mu F\left( \mu \right) - I\left( {\mu ,1} \right)} \right]$$

Hence, using (13) and (26), for the rv \(X\sim {\text{SPBD}}\left( {a, b, \alpha , \beta ,A,B} \right)\), we have that;

$$MD\left( \mu \right) = 2\left[ {\mu I\left( {\frac{{\left( {\frac{\mu }{a}} \right)^{b} - A}}{B - A};\alpha , \beta } \right) - \frac{{bB^{\beta - 1} }}{{\left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\mathop \sum \limits_{i = 0}^{\infty } \mathop \sum \limits_{j = 0}^{\infty } \frac{{C\left( {i,j;a, b, \alpha , \beta ,A,B} \right)}}{{k + b\left( {\alpha + j - i} \right)}}\left[ {\mu^{{k + b\left( {\alpha + j - i} \right)}} - (aA^{{\frac{1}{b}}} )^{{k + b\left( {\alpha + j - i} \right)}} } \right]} \right]$$

where \(\mu\) is given from (25).

Similarly, the mean deviation of X about its median \(m\), \(MD\left( m \right)\), is given by;

$$MD\left( m \right) = a A^{{\frac{1}{b}}} \varGamma \left( {\alpha + \beta } \right) \tilde{F}_{{\left( {2,1} \right)}} \left( { - \frac{1}{b}, \alpha ,\alpha + \beta ;1 - \frac{B}{A}} \right) - 2 I\left( {\frac{{\left( {\frac{m}{a}} \right)^{b} - A}}{B - A};\alpha , \beta } \right).$$

3.20 Probability Weighted Moments

The probability weighted moments of order s and r of \(X\sim {\text{SPBD}}(a, b, \alpha , \beta ,A,B)\), \(\rho_{s,r}\), is given by;

$$\rho_{s,r} = E\left( {X^{s} \left[ {f\left( X \right)} \right]^{r} } \right)$$

Using the fact that;

$$\left[ {f\left( {x;a, b, \alpha , \beta ,A,B} \right)} \right]^{r} = \frac{{x^{{\left( {b - 1} \right)\left( {r - 1} \right)}} B\left( {\left( {\alpha - 1} \right)r + 1, \left( {\beta - 1} \right)r + 1} \right)}}{{a^{{b\left( {r - 1} \right)}} b^{{\left( {1 - r} \right)}} \left[ {B\left( {\alpha , \beta } \right)} \right]^{r} \left( {B - A} \right)^{r - 1} }}f\left( {x;a, b, \left( {\alpha - 1} \right)r + 1,\left( {\beta - 1} \right)r + 1,A,B} \right)$$

with the use of (24), we have that;

$$\rho_{s,r} = \frac{{b^{r} (aA^{{\frac{1}{b}}} )^{{\frac{{s + r\left( {b - 1} \right)}}{b}}} \varGamma \left[ {\left( {\alpha - 1)(r + 1} \right) + 1} \right] \varGamma \left[ {\left( {\beta - 1)(r + 1} \right) + 1} \right]}}{{a^{r - s } \left[ {B\left( {\alpha , \beta } \right)} \right]^{r + 1} \left( {B - A} \right)^{r} }} \tilde{F}_{{\left( {2,1} \right)}} \left( { - \frac{{s + r\left( {b - 1} \right)}}{b}, \left( {\alpha - 1} \right)\left( {{\text{r}} + 1} \right) + 1,\left( {{\text{r}} + 1} \right)\left( {\alpha + \beta - 2} \right) + 2;1 - \frac{B}{A}} \right).$$

3.21 Renyi Entropy

Let us compute the Renyi entropy as a measure of variation of the uncertainty of the rv \(X\sim {\text{SPBD}}(a, b, \alpha , \beta ,A,B\)). For \(\theta > 0\) such that \(\theta \ne 1\), we have for the rv \(X\sim {\text{SPBD}}(a, b, \alpha , \beta ,A,B\)) that;

$$I_{X} \left( \theta \right) = \frac{1}{1 - \theta }log\mathop \int \limits_{ - \infty }^{ + \infty } \left[ {f\left( x \right)} \right]^{\theta } dx$$
(27)

First, we note that;

$$\begin{aligned} \left[ {f\left( {x;a, b, \alpha , \beta ,A,B} \right)} \right]^{\theta } & = \left\{ {\frac{{bx^{b - 1} }}{{a^{b} \left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}\left[ {\left( {\frac{x}{a}} \right)^{b} - A} \right]^{\alpha - 1} \left[ {B - \left( {\frac{x}{a}} \right)^{b} } \right]^{ \beta - 1} } \right\}^{\theta } \\ & = \frac{{x^{{\left( {b - 1} \right)\left( {\theta - 1} \right)}} B\left( {\left( {\alpha - 1} \right)\theta + 1, \left( {\beta - 1} \right)\theta + 1} \right)}}{{a^{{b\left( {\theta - 1} \right)}} b^{{\left( {1 - \theta } \right)}} \left[ {B\left( {\alpha , \beta } \right)} \right]^{\theta } \left( {B - A} \right)^{\theta - 1} }}f\left( {x;a, b, \left( {\alpha - 1} \right)\theta + 1,\left( {\beta - 1} \right)\theta + 1,A,B} \right) \\ \end{aligned}$$

Therefore,

$$I_{X} \left( \theta \right) = \frac{1}{1 - \theta }log\left\{ {\left[ {\frac{{B\left( {\left( {\alpha - 1} \right)\theta + 1, \left( {\beta - 1} \right)\theta + 1} \right)}}{{a^{{b\left( {\theta - 1} \right)}} b^{{\left( {1 - \theta } \right)}} \left[ {B\left( {\alpha , \beta } \right)} \right]^{\theta } \left( {B - A} \right)^{\theta - 1} }} } \right]E\left[ {Y^{{\left( {b - 1} \right)\left( {\theta - 1} \right)}} } \right]} \right\}$$

where \(Y\sim {\text{SPBD}}(a, b, \left( {\alpha - 1} \right)\theta + 1,\left( {\beta - 1} \right)\theta + 1,A,B\)). It follows, using (24) that;

$$I_{X} \left( \theta \right) = \frac{1}{1 - \theta }log\left\{ {\frac{{B\left( {\left( {\alpha - 1} \right)\theta + 1, \left( {\beta - 1} \right)\theta + 1} \right)}}{{a^{\theta - 1 } \left[ {B\left( {\alpha , \beta } \right)} \right]^{\theta } \left( {B - A} \right)^{\theta - 1} }}\varGamma \left[ {\left( {\alpha + \beta - 1} \right)\theta + 2} \right] \tilde{F}_{{\left( {2,1} \right)}} \left( { - \frac{{\left( {b - 1} \right)\left( {\theta - 1} \right)}}{b}, \left( {\alpha - 1} \right)\theta + 1,\left( {\alpha - 1} \right)\theta + \left( {\beta - 1} \right)\theta + 2;1 - \frac{B}{A}} \right)} \right\}.$$

3.22 Lorenz and Bonferroni Curves

For \(0 < \pi < 1\), the Lorenz curve, \(L\left( \pi \right)\), and Bonferroni curves, \(B\left( \pi \right)\), for the rv \(X\sim {\text{SPBD}}(a, b, \alpha , \beta ,A,B\)), are given by, respectively;

$$L\left( \pi \right) = \frac{{I\left( {Q\left( \pi \right),1} \right)}}{\mu }$$

and

$$B\left( \pi \right) = \frac{{I\left( {Q\left( \pi \right),1} \right)}}{\pi \mu }$$

where \(Q\left( \pi \right)\) is the quantile function of the rv X at \(\pi\), and \(I\left( {z,k} \right)\) is the incomplete moment of the rv X. Therefore, using (25) and (26), we have that;

$$L\left( \pi \right) = \frac{{bB^{\beta - 1} \mathop \sum \nolimits_{i = 0}^{\infty } \mathop \sum \nolimits_{j = 0}^{\infty } \frac{{C\left( {i,j;a, b, \alpha , \beta ,A,B} \right)}}{{b\left( {\alpha + j - i} \right) + 1}}\left[ {\left( {Q\left( \pi \right)} \right)^{{b\left( {\alpha + j - i} \right) + 1}} - (aA^{{\frac{1}{b}}} )^{{b\left( {\alpha + j - i} \right) + 1}} } \right]}}{{a A^{{\frac{1}{b}}} \left( {B - A} \right)^{\alpha + \beta - 1} \varGamma \left( \alpha \right) \varGamma \left( \beta \right) \tilde{F}_{{\left( {2,1} \right)}} \left( { - \frac{1}{b}, \alpha ,\alpha + \beta ;1 - \frac{B}{A}} \right)}}$$

And similarly, that;

$$B\left( \pi \right) = \frac{{bB^{\beta - 1} \mathop \sum \nolimits_{i = 0}^{\infty } \mathop \sum \nolimits_{j = 0}^{\infty } \frac{{C\left( {i,j;a, b, \alpha , \beta ,A,B} \right)}}{{b\left( {\alpha + j - i} \right) + 1}}\left[ {\left( {Q\left( \pi \right)} \right)^{{b\left( {\alpha + j - i} \right) + 1}} - \left( {aA^{{\frac{1}{b}}} } \right)^{{b\left( {\alpha + j - i} \right) + 1}} } \right]}}{{a \pi A^{{\frac{1}{b}}} \left( {B - A} \right)^{\alpha + \beta - 1} \varGamma \left( \alpha \right) \varGamma \left( \beta \right) \tilde{F}_{{\left( {2,1} \right)}} \left( { - \frac{1}{b}, \alpha ,\alpha + \beta ;1 - \frac{B}{A}} \right)}}.$$

4 Parameters Estimation of the SPBD

The maximum likelihood estimation (MLE) method will be used for estimating the parameters of the SPBD. Let \(x_{1} ,x_{2} , \ldots ,x_{n}\) be a random sample from \({\text{SPBD}}(a, b, \alpha , \beta ,A,B\)), as given by (9), then we want to estimates the parameters \(a, b, \alpha , \beta ,A, \,{\text{and}}\,B\) by maximizing the log-likelihood function, where the likelihood function L = L (\(a, b, \alpha , \beta ,A,B;x_{1} ,x_{2} , \ldots ,x_{n} )\) can be written as;

$$L = \mathop \prod \limits_{i = 1}^{n} f\left( {x_{i} } \right) = \left[ {\frac{b}{{a^{b} \left( {B - A} \right)^{\alpha + \beta - 1} B\left( {\alpha , \beta } \right)}}} \right]^{n} \mathop \prod \limits_{i = 1}^{n} \left\{ { x_{i}^{b - 1} \left[ {\left( {\frac{{x_{i} }}{a}} \right)^{b} - A} \right]^{\alpha - 1} \left[ {B - \left( {\frac{{x_{i} }}{a}} \right)^{b} } \right]^{ \beta - 1} } \right\}$$

Let us inspect the normal equations \(\frac{\partial }{\partial a}\log L = 0, \frac{\partial }{\partial b}\log L = 0, \ldots , \frac{\partial }{\partial B}\log L = 0,\) to see if they admit an explicit solution. We have that;

$$\frac{\partial }{{\partial {\text{a}}}}logL = - \left( {\alpha - 1} \right)\frac{b}{a}\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\frac{{x_{i} }}{a}} \right)^{b} }}{{\left( {\frac{{x_{i} }}{a}} \right)^{b} - A}} + \left( { \beta - 1} \right)\frac{b}{a}\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\frac{{x_{i} }}{a}} \right)^{b} }}{{B - \left( {\frac{{x_{i} }}{a}} \right)^{b} }} - \frac{nb}{a} = 0,$$
(28)
$$\frac{\partial }{\partial b}logL = \frac{n}{b} + \mathop \sum \limits_{i = 1}^{n} \log \left( {x_{i} } \right) + \left( {\alpha - 1} \right)\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\frac{{x_{i} }}{a}} \right)^{b} \log \left( {\frac{{x_{i} }}{a}} \right)}}{{\left( {\frac{{x_{i} }}{a}} \right)^{b} - A}} - \left( { \beta - 1} \right)\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\frac{{x_{i} }}{a}} \right)^{b} \log \left( {\frac{{x_{i} }}{a}} \right)}}{{B - \left( {\frac{{x_{i} }}{a}} \right)^{b} }} - nlog\left( a \right) = 0,$$
(29)
$$\frac{\partial }{\partial \alpha }logL = \mathop \sum \limits_{i = 1}^{n} \log \left[ {\left( {\frac{{x_{i} }}{a}} \right)^{b} - A} \right] - nlog\left( {B - A} \right) - n\left[ {\psi \left( \alpha \right) - \psi \left( {\alpha + \beta } \right)} \right] = 0,$$
(30)

where \(\psi\) is the digamma function, Abramowitz and Stegun [6, p. 258],

$$\frac{\partial }{\partial \beta }logL = \mathop \sum \limits_{i = 1}^{n} \log \left[ {B - \left( {\frac{{x_{i} }}{a}} \right)^{b} } \right] - nlog\left( {B - A} \right) - n\left[ {\psi \left( \beta \right) - \psi \left( {\alpha + \beta } \right)} \right] = 0,$$
(31)

and, since \(aA^{{\frac{1}{b}}} < x < aB^{{\frac{1}{b}}} ,\) then the MLE of \(aA^{{\frac{1}{b}}}\) and \(aB^{{\frac{1}{b}}}\) are; respectively, \(x_{1:n}\) and \(x_{n:n}\),; that is \(\widehat{aA}^{{\frac{1}{b}}} = x_{1:n}\) and \(\widehat{aB}^{{\frac{1}{b}}} = x_{n:n}\), and hence;

$$\hat{A} = \left( {\frac{{x_{1:n} }}{{\hat{a}}}} \right)^{{\hat{b}}} ,$$
(32)

and

$$\hat{B} = \left( {\frac{{x_{n:n} }}{{\hat{a}}}} \right)^{{\hat{b}}}$$
(33)

Since Eqs. (28)–(33) are not easy to be solved explicitly, numerical technique, as Newton Rapson method or any other well-known optimization algorithm, see Shi et al. [22], may be employed to do so, or to use a well-known software package, such as maxLik, Henningsen and Toomet [23], or GAMLSS, Stasinopoulos and Rigby [24], to find the MLE of the parameters of the SPBD.

5 A Simulation Study

In order to examine the performance of the MLE method given in Sect. 4, we perform a simulation study to do so. The bias and the mean squares errors (MSE) of the estimates are the principle measures of the performance.

The statistical software R and the Absoft Pro Fortran compiler are employed for computing. The maxLik package of the statistical software R is used mainly for computing the MLEs, see Henningsen and Toomet [23] for details of this package, while the Absoft Pro Fortran is used for other needed computations.

The six miscellaneous SPBD models given in Table 1, that have different pdf’s shapes and variable ranges, will be used to simulated data sets for each model, and for each data set, the bias and the MSE are computed for the MLE of the model parameters for different simulated sample sizes. The sample sizes that will be taken are 25, 50, 100, 300, 500, and 1000. In each situation, the parameters of, \(\theta\) say, the first model of the six SPBD models given in Table 1, are estimated from 5000 random variates generated from the given SPBD model, and the sample mean, bias, variance, and the MSE for the parameters are computed as; \(Mean\left( {\hat{\theta }} \right) = \frac{1}{5000}\mathop \sum \nolimits_{i = 1}^{5000} \hat{\theta }_{i} = \bar{\bar{\theta }}\,{\text{say}}\), Bias \(\left( {\hat{\theta }} \right) = \bar{\bar{\theta }} - \theta\), Var \(\left( {\bar{\bar{\theta }}} \right) = \frac{1}{5000}\mathop \sum \nolimits_{i = 1}^{5000} \left( {\hat{\theta }_{i} - \bar{\bar{\theta }}} \right)^{2}\), and hence M\(SE\left( {\bar{\bar{\theta }}} \right) = {\text{Var}}\left( {\bar{\bar{\theta }}} \right) + \left[ {{\text{Bias}}\left( {\hat{\theta }} \right)} \right]^{2}\). This procedure is repeated for each sample size, then repeated for each SPBD model.

Table 3 shows the bias of the estimated parameters of the different simulated SPBD data sets for each sample size, while Table 4 presents the MSE of the estimated parameters of the different simulated SPBD data sets for each sample size. Both Tables 3 and 4 show, for each of the SPBD model parameters, that the bias and MSE decreases as the sample size increases. Figure 3 shows the behaviour of the MSE plots of the estimated parameters for six the SPBD simulated data sets, which shows graphically, for of the SPBD model parameters, that the MSE decreases as the sample size increases. Hence, from the result, as the MLS plots decreases as the sample size increases, we may conclude that the MLE method seems to have high efficiency as the sample size become large.

Table 3 The bias of the estimated parameters of the simulated SPBD data sets for each sample size n
Full size table
Table 4 The MSE of the estimated parameters of the simulated SPBD data sets for each sample size n
Full size table
Fig. 3
figure 3

Behaviour of the MSE plots of the estimated parameters for the SPBD simulated data sets

Full size image

Table 5 shows the actual values and the MLE parameter values (as the average values for the 5000 replications) of the different simulated SPBD data sets, and Fig. 4 shows visually their corresponding pdf’s plots.

Table 5 Actual and MLE parameters values of the simulated SPBD data sets
Full size table
Fig. 4
figure 4

Plots of the actual and simulated SPBD pdf’s

Full size image

In conclusion, the simulation indicates that the MLE method is appropriate and can be used to estimate the parameters of the SPPBD models.

6 Application of Fitting SPBD Model to Real-Life Data

We consider two real-life data sets in order to show the usefulness of the proposed estimation procedure to estimate and fit the SPBD model to these real-life data sets. The data sets are;

Data Set 1

Represents the waiting period of Muslim worshipers from the time of entering the mosque till the actual time of starting Alfajir pray (the early morning and first pray of the day) in Al-Mani Jamieh Mosque (Masjid no. 942), where Friday prayers are held and it accommodates more than two thousand worshipers, in Al-Waab town in Doha-Qatar. The data consists of 4539 observations recorded in this masjid for the period from 30th October 2017 till 15th January 2020. We will abbreviate this data set by main street mosque data.

Data Set 2

Represents the waiting period of Muslim worshipers from the time of entering the mosque till the actual time of starting Alfajir pray in Saeed bin Fahad Al-Dosari Mosque (Masjid no. 1031), where Friday prayers are not held and it accommodates no more than two hundred fifty worshipers, in Al-Waab town in Doha-Qatar. The data consists of 3360 observations recorded in this mosque for the period from 25th January 2015 to 20th October 2017. We will abbreviate this data set by within streets mosque data.

Table 6 presents some statistics of the observed mosque data sets.

Table 6 Some statistics of the observed mosque data sets
Full size table

Using both mosque data sets, the MLE method was employed to estimate the parameters of the SPBD model for each, and Table 7 shows the actual and the predicted frequencies, model parameters estimates, the Chi squares goodness of fit test for the SPB, the gamma, the exponential, the four parameters beta, and the generalized beta of the first kind distributions, as well as, the likelihood ratio test (LRT) for the nested models of the SPB distribution, namely; the four parameters beta, and the generalized beta of the first kind distributions. Figure 5, illustrating the histograms and the fitted pdfs for both main and within street mosque data sets. Now, for the main street data set case, since the p values of Chi squares goodness of fit test for the gamma, the exponential, the four parameters beta, and the generalized beta of the first kind distributions, is smaller than 0.05, and that the p value of the SPBD model equals to 0.9488, the SPBD performs better than all these distributions. Although, for the within street mosque data set, the Chi squares goodness of fit test p value of the generalized beta of the first kind distribution equals to 0.23087 inducting that this distribution can fit this data, the SPBD model perform better in this case since its p value equals to 0.96088, and since the p values of Chi squares goodness of fit test for the gamma, the exponential, and the four parameters beta, is smaller than 0.05, the SPBD performs better than all these distributions also. Next, the p values of the likelihood ratio test (LRT) for the nested models of the SPB distribution, namely; the four parameters beta, and the generalized beta of the first kind distributions, are less than 0.05, indicating statistically, that SPBD preforms better, in both main and within street data sets. These finding indicates that the SPBD outperforms the gamma, exponential, the four parameters beta, and the generalized beta of the first kind distributions and provides the best fit for both main and within mosque data sets.

Table 7 Observed and predicted frequencies, model parameters estimates and goodness of fit for mosque data sets
Full size table
Fig. 5
figure 5

Histograms and the fitted pdfs for the Mosque data sets

Full size image

7 Summary

A new six parameters beta distribution is introduced, which has a more flexible shape and a wide bounded domain than the than the two (standard) and the four parameters beta distributions, and its properties consisting of, and some of its different various shapes are given to show its flexibility. Its boundaries, limits, mode, quantities, reliability and hazard functions, Renyi entropy, Lorenz and Bonferroni curves are studied. This distribution is closed under scaling and exponentiation, and has reflection symmetry property, and has some well-known distributions as special cases, such as, the two and four parameters beta, generalized modification of the Kumaraswamy, generalized beta of the first kind, the power function, Kumaraswamy power function, Minimax, exponentiated Pareto, and the generalized uniform distributions. Its order statistics, moment generating function, with its moments consisting of the mean, variance, moments about the origin, harmonic, incomplete, probability weighted moments, and mean deviations are derived. The maximum likelihood estimation method is used for estimating its parameters and applied to estimate the parameters of six different simulated data sets of this distribution having different pdf shapes, in order to check the performance of the estimation method through the estimated parameters mean squares errors computed from different simulated sample sizes, which are shown to be decreasing as the sample size increases, indicating that the MLE method is appropriate and can be used to estimate the parameters of the SPPBD models. Finally, two real life data sets, represent the waiting period of Muslim worshipers from the time of entering the mosque till the actual time of starting Alfajir pray in two different mosques, are used in order to show the usefulness and the flexibility of this distribution in application to real-life data sets. The MLE method was employed using these data set to estimate the parameters of the SPBD, the gamma, the exponential, the four parameters beta, and the generalized beta of the first kind distributions, and the Chi squares goodness of fit test for these distributions, as well as, the LRT for the nested models of the SPB distribution, namely; the four parameters beta, and the generalized beta of the first kind distributions, were employed, and all the results through the p values of these tests, statistically, outperforms SPBDs over the other stated distributions.