Introduction

A random variable Y having beta distribution has cumulative distribution function (cdf) and probability density function (pdf) given by

$$\begin{aligned} H(y;a,b)=\frac{1}{B(a,b)}\int _0^y z^{a-1}(1-z)^{b-1}\textrm{d}z, \quad y\in (0,1) \end{aligned}$$
(1)

and

$$\begin{aligned} h(y;a,b)=\frac{1}{B(a,b)}y^{a-1}(1-y)^{b-1}, \quad y\in (0,1), \end{aligned}$$

respectively, where \(a>0\) and \(b>0\) are shape parameters and \(B(a,b)=\int _0^1 z^{a-1}(1-z)^{b-1}\textrm{d}z\) denotes the beta function.

Taking the transformation \(X=-\log Y\), the cdf and pdf of X are given by

$$\begin{aligned} F(x;a,b)=1-\frac{1}{B(a,b)}\int _0^{\textrm{e}^{-x}} z^{a-1}(1-z)^{b-1}\textrm{d}z, \quad x\in (0,\infty ) \end{aligned}$$

and

$$\begin{aligned} f(x;a,b)=\frac{1}{B(a,b)}\textrm{e}^{-ax}(1-\textrm{e}^{-x})^{b-1}, \quad x\in (0,\infty ), \end{aligned}$$
(2)

respectively. Here, we refer to a as a scale parameter and b as a shape parameter. The random variable X with pdf (2) is said to have kagebushin-beta (KB) distribution and is denoted as \(X\sim \text {KB}(a,b)\).

The beta function admits the following relation

$$\begin{aligned} B(a,b)=\frac{\Gamma (a)\Gamma (b)}{\Gamma (a+b)}\quad \text {and}\quad a\Gamma (a)=\Gamma (a+1), \end{aligned}$$

where \(\Gamma (p)=\int _0^\infty z^{p-1}\textrm{e}^{-z}\textrm{d}z\) denotes the gamma function. Under these results, for \(b=1\), the Equation (2) becomes

$$\begin{aligned} f(x;a,1)=a\textrm{e}^{-ax}, \quad x\in (0,\infty ), \end{aligned}$$

that corresponds to the pdf of the exponential distribution. Thus, the KB distribution has the exponential distribution as special case.

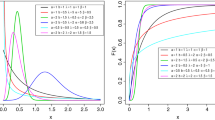
Figure 1 displays plots of the density function of X, for some values of the parameters.

Fig. 1
figure 1

Some pdfs of the KB distribution

Full size image

This paper is organized as follows. In Sect. Properties, mathematical properties and entropy measures are described. In Sect. Estimation, the maximum likelihood method and Monte Carlo simulations are presented. In Sect. Applications, applications to real data are considered. Section Conclusions concludes the paper.

Properties

The first derivative of the log-density (2) is

$$\begin{aligned} \eta (x)=\frac{\textrm{d}}{\textrm{d}x}\log f(x;a,b)=-a+\frac{(b-1)\textrm{e}^{-x}}{1-\textrm{e}^{-x}}. \end{aligned}$$

The mode is obtained by solution of \(\eta (x)=0\). So, the mode of X is

$$\begin{aligned} \text {mode}(X)={\left\{ \begin{array}{ll} 0,&{} b\le 1, \\ -\log \left( \frac{a}{a+b-1}\right) ,&{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

By inverting \(F(x;a,b)=u\), the quantile function of X is

$$\begin{aligned} F^{-1}(u;a,b)=-\log Q_1(1-u;a,b), \quad u\in (0,1), \end{aligned}$$

where \(Q_1(\cdot ;a,b)\) is the inverse function of the Equation (1). Using the quantile function, the random variable

$$\begin{aligned} X=-\log Q_1(1-V;a,b)\quad \text {or}\quad X=-\log Q_1(V;a,b) \end{aligned}$$
(3)

has density function (2), where V is a uniform random variable over the interval (0, 1).

The rth moment of X is obtained as

$$\begin{aligned} \mu ^r=\mathbb {E}[X^r]=\frac{1}{B(a,b)}\int _0^\infty x^r\textrm{e}^{-ax}(1-\textrm{e}^{-x})^{b-1}\textrm{d}x. \end{aligned}$$

Consider the following convergent expansion in power series

$$\begin{aligned} (1-\textrm{e}^{-x})^{b-1}=\sum _{k=0}^\infty (-1)^k\left( {\begin{array}{c}b-1\\ k\end{array}}\right) \textrm{e}^{-kx}. \end{aligned}$$

Using the expansion above, the rth moment of X can be written as

$$\begin{aligned} \mu ^r=\frac{1}{B(a,b)}\sum _{k=0}^\infty (-1)^k\left( {\begin{array}{c}b-1\\ k\end{array}}\right) \int _0^\infty x^r\textrm{e}^{-(a+k)x}\textrm{d}x. \end{aligned}$$

Taking \(w=(a+k)x\), we have

$$\begin{aligned} I=&\int _0^\infty x^r\textrm{e}^{-(a+k)x}\textrm{d}x\\ =&\frac{1}{(a+k)^{r+1}}\int _0^\infty w^r\textrm{e}^{-w}dw\\ =&\frac{\Gamma (r+1)}{(a+k)^{r+1}}. \end{aligned}$$

So, the rth moment of X is given by

$$\begin{aligned} \mu ^r=\frac{1}{B(a,b)}\sum _{k=0}^\infty (-1)^k\left( {\begin{array}{c}b-1\\ k\end{array}}\right) \frac{\Gamma (r+1)}{(a+k)^{r+1}}. \end{aligned}$$

For \(s>0\), the rth incomplete moment of X is obtained as

$$\begin{aligned} m_r(s)=&\frac{1}{B(a,b)}\int _0^s x^r\textrm{e}^{-ax}(1-\textrm{e}^{-x})^{b-1}\textrm{d}x\\=&\frac{1}{B(a,b)}\sum _{k=0}^\infty (-1)^k\left( {\begin{array}{c}b-1\\ k\end{array}}\right) \int _0^s x^r\textrm{e}^{-(a+k)x}\textrm{d}x. \end{aligned}$$

Taking \(t=(a+k)x\), we have

$$\begin{aligned} J=&\int _0^s x^r\textrm{e}^{-(a+k)x}\textrm{d}x\\ =&\frac{1}{(a+k)^{r+1}}\int _0^{(a+k)s} t^r\textrm{e}^{-t}dt\\ =&\frac{\gamma (r+1,(a+k)s)}{(a+k)^{r+1}}, \end{aligned}$$

where \(\gamma (p,x)=\int _0^x z^{p-1}\textrm{e}^{-z}\textrm{d}z\) denotes the lower incomplete gamma function.

Then, the rth incomplete moment of X is given by

$$\begin{aligned} m_r(s)=&\frac{1}{B(a,b)}\sum _{k=0}^\infty (-1)^k\left( {\begin{array}{c}b-1\\ k\end{array}}\right) \frac{\gamma (r+1,(a+k)s)}{(a+k)^{r+1}}. \end{aligned}$$
(4)

An entropy is a measure of variation or uncertainty of a random variable. Two popular entropy measures are the Rényi and Shannon entropies. For \(\rho >0\) and \(\rho \ne 1\), the Rényi entropy of a random variable having pdf \(f(\cdot )\) with support in (a, b) is given by

$$\begin{aligned} \mathcal {I}_R(\rho )=\frac{1}{1-\rho }\log \left( \int _a^b f(x)^\rho \textrm{d}x\right) . \end{aligned}$$

For KB distribution, the Rényi entropy is

$$\begin{aligned} \mathcal {I}_R(\rho )=\frac{1}{1-\rho }\log \left( \frac{1}{B(a,b)^\rho }\int _0^\infty \textrm{e}^{-a\rho x}(1-\textrm{e}^{-x})^{(b-1)\rho } \textrm{d}x\right) . \end{aligned}$$

Setting \(v=\textrm{e}^{-x}\), we have

$$L = \int_{0}^{\infty } {{\text{e}}^{{ - a\rho x}} } (1 - {\text{e}}^{{ - x}} )^{{(b - 1)\rho }} {\text{d}}x = \int_{0}^{1} {v^{{a\rho - 1}} } (1 - v)^{{(b - 1)\rho }} dv = \;B(a\rho ,(b - 1)\rho + 1).{\text{ }}$$

Thus, the Rényi entropy of X becomes

$$\begin{aligned} \mathcal {I}_R(\rho )=\frac{1}{1-\rho }\log \left( \frac{B(a\rho ,(b-1)\rho +1)}{B(a,b)^\rho }\right) . \end{aligned}$$

The Shannon entropy is given by \(\mathcal {I}_s=\mathbb {E}[-\log f(X)]\). So, for KB distribution, the Shannon entropy is

$$\begin{aligned} \mathcal {I}_{S}=\log B(a,b)+a\mathbb {E}[X]-(b-1)\mathbb {E}[\log (1-\textrm{e}^{-X})]. \end{aligned}$$

From the maximum likelihood method, we can show that \(\mathbb {E}[X]=\psi (a+b)-\psi (a)\) and \(\mathbb {E}[\log (1-\textrm{e}^{-X})]=\psi (b)-\psi (a+b)\), where \(\psi (p)=d\log \Gamma (p)/dp\) is the digamma function.

Thus, the Shannon entropy is of X is

$$\begin{aligned} \mathcal {I}_{S}=\log B(a,b)+a\psi (a+b)-a\psi (a)-(b-1)[\psi (b)-\psi (a+b)]. \end{aligned}$$

Thus, we see that for KB distribution, the Rényi and Shannon entropies can be easily computed.

The mean deviations of X about the mean and about the median are given as

$$\varphi _{1} (\mu ^{1} ) = \int_{0}^{1} | x - \mu ^{1} |f(x;a,b){\text{d}}x = \;2\mu ^{1} F(\mu ^{1} ,a,b) - 2m_{1} (\mu ^{1} ){\text{ }}$$

and

$$\begin{aligned} \varphi _2(\omega )=\;&\int _0^1|x-\omega |f(x;a,b)\textrm{d}x,\\ =\;&\mu ^1 - 2m_1(\omega ), \end{aligned}$$

respectively, where \(\mu ^1=\mathbb {E}[X]\) and \(\omega =F^{-1}(0.5; a,b)\) and \(m_1(\cdot )\) is defined in (4).

Estimation

Let the random variables \(X_i,\cdots ,X_n\sim \text {KB}(a,b)\) with observed values \(x_i,\cdots ,x_n\). From Equation (2), the log-likelihood for \((a,b)^\top\) is given by

$$\begin{aligned} \mathcal {L}(a,b)=-n\log B(a,b)-a\sum _{i=1}^nx_i+(b-1)\sum _{i=1}^n\log (1-\textrm{e}^{-x_i}). \end{aligned}$$

The components of the score vector \(U(a,b)=(U_a,U_b)^\top\) of \(\mathcal {L}(a,b)\) are given by

$$\begin{aligned} U_a&=n\psi (a+b)-n\psi (a)-\sum _{i=1}^nx_i,\\ U_b&=n\psi (a+b)-n\psi (b)+\sum _{i=1}^n\log (1-\textrm{e}^{-x_i}). \end{aligned}$$

The maximum likelihood estimates (MLEs) of a and b, say \({\hat{a}}\) and \({\hat{b}}\), are the simultaneous solutions of \(U_a=U_b=0\), which has no closed forms. Thus, this problem can be solved via iteractive numerical methods, such that Newton--Raphson algorithmic. Statistical packages such as R [1] and Ox [2] can be used for this purpose.

The Fisher expected information matrix is

$$\begin{aligned} \mathcal {K}(a,b)=-\left[ \begin{array}{cc} U_{aa} &{} U_{ab}\\ U_{ba} &{} U_{bb} \end{array}\right] , \end{aligned}$$

in which

$$\begin{aligned} U_{aa}&=n\psi ^\prime (a+b)-n\psi ^\prime (a),\\ U_{ab}&= U_{ba}=n\psi ^\prime (a+b),\\ U_{bb}&= n\psi ^\prime (a+b)-n\psi ^\prime (b), \end{aligned}$$

where \(\psi ^\prime (p)=d^2\log \Gamma (p)/dp^2\) is the trigamma function.

Under general regularity conditions, we have the result

$$\begin{aligned} (({\hat{a}},{\hat{b}})-(a,b))\quad {\mathop {\sim }\limits ^{a}}\quad \mathcal {N}_2(0,\mathcal {K}(a,b)^{-1}), \end{aligned}$$

where \(\mathcal {K}(a,b)^{-1}\) is the inverse matrix of \(\mathcal {K}(a,b)\) and \({\mathop {\sim }\limits ^{a}}\) denotes asymptotic distribution. This multivariate normal approximation for \(({\hat{a}},{\hat{b}})\) can be used for construing approximate confidence intervals for the model parameters. The LR statistics can be used for testing hypotheses on these parameters.

Simulation study

To show the accuracy of MLEs for the two parameters of the KB model, Monte Carlo simulations with 15, 000 replications were performed. Two scenarios are considered and the sample sizes chosen are \(n=\{25, 50, 75,100,200,400\}\). The random numbers are generated using Equation (3). The true parameters are: \(a=1.9\) and \(b=1.5\) in scenario 1 and \(a=4.5\) and \(b=2.5\) in scenario 2. The simulations were carried out using the matrix programming language Ox [2].

Tables 1 and 2 list the average estimates (AEs), biases and mean squared errors (MSEs), for scenarios 1 and 2, respectively. As expected, the MLEs converge to the true parameters and the biases and MSEs decrease when the sample size n increases.

Table 1 Monte Carlo simulation results for scenario 1
Full size table
Table 2 Monte Carlo simulation results for scenario 2
Full size table

Applications

In this section, we compare the results of fitting of the KB distribution with three others well-known distributions, for two datasets.

The data are:

  • (Dataset 1) The data refer to remission times (in months) of 128 bladder cancer patients. These data were also analyzed by [3].

  • (Dataset 2) The data consist of the waiting time between 64 consecutive eruptions of the Kiama Blowhole [4].

We compare the KB model (2) with the Weibull, gamma and exponentiated exponential [5] distributions. The pdfs of the Weibull (W), gamma (G) and exponentiated exponential (EE) distributions are

$$\begin{aligned} f_{\textsc {w}}(x;\lambda ,\beta )=\beta \lambda ^\beta x^{\beta -1}\,\textrm{e}^{-(\lambda x)^\beta }, \quad x>0, \\ f_{\textsc {g}}(x;\lambda ,\beta )=\frac{\lambda ^\beta }{\Gamma (\beta )} x^{\beta -1}\,\textrm{e}^{-\lambda x}, \quad x>0 \end{aligned}$$

and

$$\begin{aligned} f_{\textsc {ee}}(x;\lambda ,\beta )=\beta \lambda \textrm{e}^{-\lambda x}(1-\textrm{e}^{-\lambda x})^{\beta -1}, \quad x>0, \end{aligned}$$

respectively, where \(\lambda >0\) is scale parameter and \(\beta >0\) is shape parameter. Note that for \(\beta =1\), all these pdfs become the density function of the exponential distribution.

The goodness-of-fit measures adopted are: Cramér-von Mises (\(W^*\)), Anderson Darling (\(A^*\)), Akaike information criterion (AIC), consistent Akaike information criterion (CAIC), Bayesian information criterion (BIC) and Hannan-Quinn information criterion (HQIC) for model comparisons. The lower the value of these statistics, more evidence we have for a good fit. The graphical analysis is also important to identify the best fitted model. All the computations were done using the Ox language [2].

Tables 3 and 5 list the MLEs with standard errors in parentheses (SEs) for datasets 1 and 2, respectively. Note that, in both applications, all MLEs of all models are significant, since their standard errors are low, when compared to the respective MLE.

The information criteria for datasets 1 and 2 are presented in Tables 4 and 6 , respectively. In both datasets, all information criteria point to the KB distribution as the best model, followed later by the EE distribution.

Table 3 MLEs and SEs for dataset 1
Full size table
Table 4 Information criteria for dataset 1
Full size table
Table 5 MLEs and SEs for dataset 2
Full size table
Table 6 Information criteria for dataset 2
Full size table

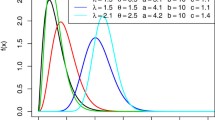
Figures 2 and 3 show the estimated pdfs and cdfs for datasets 1 and 2, respectively, considering the two best fitted models.

Fig. 2
figure 2

Estimated a pdfs and b cdfs for data 1

Full size image
Fig. 3
figure 3

Estimated a pdfs and b cdfs for data 2

Full size image

Conclusions

A new lifetime distribution has been defined. This distribution is obtained from a transformation of a random variable with beta distribution and is called here the kagebushin-beta distribution. Some mathematical properties such as mode, quantile function, ordinary and incomplete moments, mean deviations over the mean and median and the entropies of Rényi and Shannon are demonstrated.

The method used to estimate the parameters was maximum likelihood. Fisher’s expected information matrix has closed form. Monte Carlo simulations showed that the maximum likelihood estimators of the new model are valid, being in accordance with the asymptotic theory.

The usefulness of the kagebushin-beta model is shown with applications to real data. The results of these applications showed that the kagebushin-beta model is better than the Weibull, gamma and exponentiated exponential distributions.