Abstract
We classify normal stable surfaces with \(K_X^2 = 1\), \(p_g = 2\) and \(q=0\) with a unique singular point which is a non-canonical T-singularity, thus exhibiting two divisors in the main component and a new irreducible component of the moduli space of stable surfaces \({{\overline{{{\mathfrak {M}}}}}}_{1,3}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The investigation of (minimal) surfaces of general type with low invariants and their moduli spaces started with the work of Castelnuovo and Enriques (cf. [11]) at the beginning of the 20th century and has remained an active topic ever since. It is fair to say, that Fabrizio Catanese, to whom the present special issue is dedicated, was one the most influential contributors to this topic over the last decades both through his work, e.g., [2, 3, 5,6,7,8,9], and by passing on his enthusiasm to his students and collaborators. Nowadays Gieseker’s moduli space of canonical models \({{\mathfrak {M}}}_{K^2, \chi }\) [13] is known to admit a modular compactification \({{\overline{{{\mathfrak {M}}}}}}_{K^2, \chi }\), the KSBA moduli space of stable surfaces, see Sect. 2.1.
In this article, we continue the investigation of (the moduli space of) stable I-surfacesFootnote 1 begun in [12]. These are stable surfaces with \(K_X^2 = 1\), \(p_g = 2\), and \(q=0\). The Gieseker moduli space \({{\mathfrak {M}}}_{1,3}\subset {{\overline{{{\mathfrak {M}}}}}}_{1,3}\) is an irreducible and rational variety of dimension 28 parametrising double covers of the quadric cone \({\mathcal {Q}}_2\subset {{\mathbb {P}}}^3\) branched over a quintic section and the vertex, a fact that was attributed to Kodaira in [15, §3] and extended to the moduli space \({{\overline{{{\mathfrak {M}}}}}}_{1,3}^{(Gor)}\) of Gorenstein stable surface in [12].
Another important class of singularities on stable surfaces are T-singularities, which are exactly the quotient singularities that can occur in stable surfaces in the closure of the main component (see Sect. 2.2). Here we study what we call T-singular I-surfaces, that is, stable I-surfaces with a unique singular point which is a non-canonical T-singularity. Our main result is:
Theorem 1.1
Let X be an I-surface with unique singular point a non-canonical T-singularity. Then only the following cases can occur:
If all deformations are unobstructed, then the dimension of the \({{\mathbb {Q}}}\)-Gorenstein deformation space of the T-singularity gives the codimension of the corresponding stratum in the moduli space. This is especially interesting for Wahl singularities, which are expected to give rise to divisors. This expectation is only partially met (see Proposition 3.4) in our cases. For T-singular I-surfaces we obtain the following
Corollary 1.2
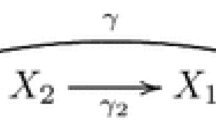
The T-singular I-surfaces of type \(\frac{1}{4}(1,1)\) and \(\frac{1}{18}(1,5)\) form divisors in the main component of \({{\overline{{{\mathfrak {M}}}}}}_{1,3}\), that is, the closure of the Gieseker moduli space. The T-singular surfaces of type \(\frac{1}{25}(1,14)\) form an open subset of another irreducible component of \({{\overline{{{\mathfrak {M}}}}}}_{1,3}\) of dimension 28.
Schematically one might depict the situation as follows, where we include a conjectural connection between the two components:

Notation and conventions We work over the complex numbers. \(\sim \) denotes linear equivalence. For n a positive integer, a \((-n)\)-curve C on a smooth surface Y is a smooth rational curve with \(C^2=-n\). For a Hirzebruch surface \({\mathbb {F}}_n\), we denote by \(\sigma _{\infty }\) the infinity section and by \({\varGamma }\) the class of a ruling, so that a section \(\sigma _0\) disjoint from \(\sigma _{\infty }\) is linearly equivalent to \(n{\varGamma } +\sigma _{\infty }\); we denote by \({{\mathcal {Q}}}_n\) the cone in \({\mathbb {P}}^{n+1}\) over the rational normal curve of degree n in \({\mathbb {P}}^n\), which is the image of \({{\mathbb {F}}}_n\) via the map given by \(|\sigma _0|\).
2 Preliminaries
2.1 Normal stable surfaces
Stable surfaces were first defined to give a geometric compactification of the moduli space of surfaces of general type (see [19,20,21] and references therein). In the construction of the moduli space, one of the main insights was that one cannot allow all flat families of stable surfaces, but only so-called \({{\mathbb {Q}}}\)-Gorenstein deformations, that is, flat families \(\pi :{{\mathcal {X}}}\rightarrow B\) of stable surfaces with fixed invariants such that for all m the reflexive powers \(\omega _{{{\mathcal {X}}}}^{[m]}\) are flat over B and commute with base change.
Here we will consider normal stable surfaces only. Recall that a normal surface X is called stable if it has log-canonical singularities, and \(K_X\) is \({\mathbb {Q}}\)-Cartier and ample. The smallest \(m>0\) such that \(mK_X\) is Cartier is called the (Cartier) index of X.
For a normal stable surface X, we let \(f:\widetilde{Y}\rightarrow X\) be the minimal desingularization and \(\eta :\widetilde{Y}\rightarrow Y\) be the morphism to a minimal model:

Remark 2.1
If X has only rational singularities (for instance cyclic quotient singularities), the Leray spectral sequence gives \(q(Y)=q(\widetilde{Y})=q(X)\) and \(p_g(Y)=p_g(\widetilde{Y})=p_g(X)\). The normal stable surfaces considered in this paper have rational singularities and \(p_g(X)=2\), so the Kodaira dimension of \(\widetilde{Y}\) is \(\ge 1\) and the minimal model Y is unique.
Let X be a normal stable surface with log-terminal singularities. It is possible to generalize the plurigenus formula for smooth minimal surfaces as follows. Let \(\widetilde{Y} \rightarrow X\) be the minimal desingularization and write
where \(-a_i\) is the log discrepancy of the exceptional curve \(E_i\). Then by Prop. 5.2 and Thm. 5.3 in [4], one has:
where \(\{D\}\), as customary, denotes the fractional part of a \({\mathbb {Q}}\)-divisor D.
2.2 T-singularities and T-singular surfaces
A T-singularity is either a rational double point or a quotient 2-dimensional singularity of type \(\frac{1}{dn^2}(1, dna-1)\), where \(n>1\) and \(d,a >0\) are integers with a and n are coprime. These are precisely the quotient singularities that admit a \({\mathbb {Q}}\)-Gorenstein smoothing, that is, that can occur on smoothable stable surfaces (cf. [21, § 3]).
The exceptional divisor of the minimal resolution of a T-singularity \(\frac{1}{dn^2}(1, dna-1)\) is a so-called T-string, a string of rational curves \(A_1, A_2, \ldots , A_r\) with self-intersections \(-b_1,-b_2, \ldots , -b_r\) given by the Hirzebruch-Jung continued fraction expansion \([b_1,b_2,\ldots , b_r]\) of \(\frac{dn^2}{dna-1}\) (see, e.g., [10, Chapter 10]). Following popular convention, we will refer to the expansion \([b_1,b_2,\ldots , b_r]\) corresponding to a T-singularity as a T-string.
The index 2 T-singularity with \(d=1\) has T-string [4]. Those of index 2 and \(d>1\) have T-string \([3,2,\ldots , 2, 3]\), where 2 occurs \(d-2\) times. It is immediate to check that all the log discrepancies are equal to \(-\frac{1}{2}\). More generally, if \([b_1,\ldots , b_r]\) is the T-string of a T-singularity \(\frac{1}{dn^2}(1, dna-1)\) for some \(n>2\), then \(b_1=2\) (or \(b_r=2\)) and \([b_2,\ldots , b_r-1]\) (respectively, \([b_1-1,\ldots , b_{r-1}]\)) is also the T-string of a T-singularity of type \(\frac{1}{dn'^2}(1, dn'a-1)\) for some \(n'< n\). In particular, we obtain all possible T-strings of T-singularities of fixed d by beginning with the corresponding T-string of index 2 listed above and iterating as described [21, § 3]. The T-singularities of index 3 are those obtained from those of index 2 by a single iteration step.
A T-singular surface of type \(\frac{1}{dn^2}(1, dna-1)\) is a normal surface with a singular point of type \(\frac{1}{dn^2}(1, dna-1)\) and smooth elsewhere. The index of X is equal to n. Using the notation of Sect. 2.1 we have ( [22, Prop. 20]):
If, in addition, Y is not a rational surface, then by [23, Prop. 2.3]:
Remark 2.5
Let \(\widetilde{Y}\) be a smooth surface containing a T-string. Then by [18, Prop. 4.10] there is a map \(f:\widetilde{Y}\rightarrow X\) that contracts the T-string to a T-singularity; the surface X is projective and \({\mathbb {Q}}\)-factorial, so it is a T-singular surface. If the class of \(f^*K_X\) is nef and big and the only curves with zero intersection with it are the components of the T-string, then X is also stable.
2.3 I-surfaces
An I-surface X is a stable surface with \(K_X^2=1\), \(p_g(X)=2\) and \(q(X)=0\). In [12] it was shown that the classical description of smooth surfaces of general type with \(K_X^2=1\) and \(\chi (X)=3\) extends to the Gorenstein case, i.e.:
-
a Gorenstein I-surface X is canonically embedded as a hypersurface of degree 10 in (the smooth locus of) \({{\mathbb {P}}}(1,1,2,5)\);
-
the moduli space \({{\overline{{{\mathfrak {M}}}}}}_{1,3}^{(Gor)}\) of Gorenstein stable surfaces with \(K^2=1\) and \(\chi =3\) is irreducible and rational of dimension 28.
-
for a Gorenstein I-surface X, the bicanonical map is a degree 2 morphism \(\varphi _2:X\rightarrow {{\mathcal {Q}}}_2 \subset {{\mathbb {P}}}^3\), where \({{\mathcal {Q}}}_2\) is the quadric cone, branched on the vertex o and on a quintic section D of \({{\mathcal {Q}}}_2\) not containing o.
-
conversely, if D is a quintic section of \({{\mathcal {Q}}}_2\) not containing o and \(({{\mathcal {Q}}}_2, \frac{1}{2} D)\) is a log-canonical pair, then the double cover of \({{\mathcal {Q}}}_2\) branched on D and o is a stable Gorenstein I-surface.
2.4 Extending automorphisms of stable surfaces
Let X be a stable surface and let \(g:{\mathcal {X}}\rightarrow B \) be a 1-parameter \({{\mathbb {Q}}}\)-Gorenstein smoothing of X; denote by \(0\in B\) the point such that \(g^{-1}(0)=X\), write \(B^*:=B{\setminus }\{0\}\) and \({\mathcal {X}}^*:={\mathcal {X}}_{| B^*}\).
Let \({{\,\mathrm{Aut}\,}}({\mathcal {X}}/B)\) be the relative automorphism scheme. The following result is certainly well known to experts; we thank V. Alexeev for explaining it to us. Note as a starting point, that the automorphim group of a stable surface is finite by [17, Thm. 11.12], or more generally by [14].
Proposition 2.6
Let \(\sigma \) be a section of \({{\,\mathrm{Aut}\,}}({\mathcal {X}}^*/B^*)\). Then, up to a finite base change, \(\sigma \) extends to a section of \({{\,\mathrm{Aut}\,}}({\mathcal {X}}/B)\).
Proof
The claim follows from the fact that the family \({\mathcal {X}} \) is the canonical model of any extension of \({\mathcal {X}} ^*\), and the canonical model is unique. Indeed, choose an extension \({\mathcal {X}}' \) of \({\mathcal {X}} ^*\) such that \(\sigma \) induces a morphism \({\mathcal {X}} '\rightarrow {\mathcal {X}} \); up to a base change we may assume that both \({{\mathcal {X}}}\) and \({{\mathcal {X}}}'\) admit a semi-stable resolution. Now taking canonical models of both \({\mathcal {X}} '\) and \({\mathcal {X}} \) one gets a regular map \({{\bar{\sigma }}}:{\mathcal {X}} \rightarrow {\mathcal {X}} \) that restricts to \(\sigma \) on \({\mathcal {X}} ^*\). Since \(\sigma ^m\) is the identity for some m, we have that \({{\bar{\sigma }}}^m\) is also the identity, and therefore \({{\bar{\sigma }}}\) is an automorphism. \(\square \)
As a result, we obtain the following necessary condition for smoothability of I-surfaces:
Corollary 2.7
Let X be a stable I-surface. If X has a \({{\mathbb {Q}}}\)-Gorenstein smoothing then it admits an involution.
Proof
Let \({\mathcal {X}}\rightarrow B\) be a 1-parameter \({\mathbb {Q}}\)-Gorenstein smoothing of X. By [12, Prop. 3.6] (see Sect. 2.3) the bicanonical map of a Gorenstein I-surface is of degree 2, hence the corresponding involution defines a section of \({{\,\mathrm{Aut}\,}}({\mathcal {X}}^*/B^*)\), that, possibly up to a base change, extends to a section \(\sigma \) of \({{\,\mathrm{Aut}\,}}({\mathcal {X}}/B)\) by Proposition 2.6.
The map \({{\,\mathrm{Aut}\,}}({\mathcal {X}}/B)\rightarrow B\) is quasi-finite and étale (cf. [1, Thm. 3.29]), so the restriction of \(\sigma \) to the central fibre X has indeed order 2. \(\square \)
3 The examples
3.1 The case of index \(n=2\)
We start by describing a construction of stable T-singular I-surfaces of index 2.
Example 3.1
Let \({\mathcal {Q}}_2\subset {\mathbb {P}}^3\) be the quadric cone and let \(\varepsilon :{\mathbb {F}}_2\rightarrow {\mathcal {Q}}_2\) be the minimal resolution; as usual, we denote by \(\sigma _{\infty }\) the infinity section of \({\mathbb {F}}_2\), by \({\varGamma }\) the class of a ruling and write \(\sigma _0=\sigma _{\infty }+2{\varGamma }\). Let \(D\subset {\mathbb {F}}_2\) be an effective divisor linearly equivalent to \(4\sigma _0+2{\varGamma }\) and assume that D does not contain \(\sigma _{\infty }\) and is smooth away from \(\sigma _{\infty }\), so that D is either smooth or has a double point p on \(\sigma _{\infty }\).
We let \(\pi :Y\rightarrow {\mathbb {F}}_2\) be the double cover branched on D. The surface Y is smooth when D is, and has a singular point q of type \(A_k\) lying over \(p\in \sigma _{\infty }\) otherwise. The linear system \(\pi ^*|{\varGamma }|\) is a pencil of elliptic curves and coincides with the canonical system of Y. We denote by \( \widetilde{Y}\rightarrow Y\) the minimal desingularization; since the singularities of Y are canonical, \(\widetilde{Y}\) is minimal elliptic with \(p_g(\widetilde{Y})=2\) and again the canonical system coincides with the elliptic pencil. There are the following possibilities for the preimage C of \(\sigma _{\infty }\) in \(\widetilde{Y}\):
-
(1)
if D meets \(\sigma _{\infty }\) at two distinct points, then \(\widetilde{Y}=Y\) and C is a \((-4)\)-curve;
-
(2)
if D is smooth but meets \(\sigma _{\infty }\) at only one point, then \(\widetilde{Y}=Y\) and C is a string of type [3, 3];
-
(3)
if D has a double point \(p\in \sigma _{\infty }\) then the point \(q\in Y\) lying over p is an \(A_k\) point for some \(k>0\). The preimage of \(\sigma _{\infty }\) in Y splits as \(C_1+C_2\), with \(C_1\) and \(C_2\) smooth rational curves meeting at q, and C is a string of type \([3,2,\dots ,2, 3]\) with 2 occurring k times.
Let \(\nu :\widetilde{Y}\rightarrow X\) be the first step in the Stein factorization of the map \(\widetilde{Y}\rightarrow Y \rightarrow {\mathcal {Q}}_2\): \(\nu \) contracts C to a point r lying over the vertex of \({\mathcal {Q}}_2\) and is an isomorphism elsewhere. So r is a singularity of type \(\frac{1}{4d}(1, 2d-1)\) (see Sect. 2.2): in case (1) above one has \(d=1\), in case (2) one has \(d=2\), and in case (3) one has \(d=k+2>2\). So we have \(C^2=-4\), \(K_{\widetilde{Y}}C=2\) and \(\nu ^*K_X=K_{\widetilde{Y}}+\frac{1}{2} C\) (see Sect. 2.2) and therefore \(K_X^2=(K_{\widetilde{Y}}+\frac{1}{2} C)^2=1\). Finally, it is easy to check that \(\nu ^*K_X\) is nef and that the only irreducible curves A with \(\nu ^*K_XA=0\) are the components of C, and therefore \(K_X\) is ample. Finally, \(p_g(X)=p_g(\widetilde{Y})=2\) by Remark 2.1, since T-singularities are rational. Summing up, X is a T-singular I-surface of type \(\frac{1}{4d}(2d-1)\), where \(d=1\) in case (1), \(d=2\) in case (2), and \(d=k+2>2\) in case (3).
Remark 3.2
Let X be an I-surface as in Example 3.1. Then the induced map \(\varepsilon :X\rightarrow {\mathcal {Q}}_2\) is a finite double cover, flat away from the vertex of \({\mathcal {Q}}_2\), with branch locus \({\bar{D}}= \varepsilon (D)\) cut out on \({\mathcal {Q}}_2\) by a quintic hypersurface passing through the vertex of \({\mathcal {Q}}_2\). By the Hurwitz formula we have \(2K_X=\varepsilon ^*H\), where H is the class of a hyperplane section of \({\mathcal {Q}}_2\subset {\mathbb {P}}^3\). Since the canonical system \(|2K_X|\) is 3-dimensional by (2.2), it coincides with \(\varepsilon ^*|H|\). So the map \(\varepsilon :X\rightarrow {\mathcal {Q}}_2\) is the bicanonical map of X. In particular, the branch divisor D is determined by X up to automorphisms of \({\mathcal {Q}}_2\).
In fact, our conditions on D guarantee that \(({\mathcal {Q}}_2, \frac{1}{2} {\bar{D}})\) is a log-terminal pair and thus X is an I-surface by [12, Prop. 4.1]. Deforming \({\bar{D}}\) to a general quintic section of \({\mathcal {Q}}_2\) gives a smoothing of X as a hypersurface of degree 10 inside \({{\mathbb {P}}}(1,1,2,5)\).
We record this fact for later reference.
Corollary 3.3
The I-surfaces constructed in Example 3.1 are smoothable.
To construct surfaces as in Example 3.1 one needs to find a branch divisor D with the required singularity at a point \(p\in \sigma _{\infty }\) and smooth everywhere else. This is a non trivial question, as shown by the following partial answer to it.
Proposition 3.4
Consider T-singular I-surfaces of type \(\frac{1}{4d} (1,2d-1)\) as constructed in Example 3.1. Then
-
(i)
we have \(d\le 32\);
-
(ii)
for \(d=1, 2, 3\) the T-singular I-surfaces of type \(\frac{1}{4d} (1,2d-1)\) obtained as in Example 3.1 give an irreducible subvariety of codimension d inside the main component of the moduli space of stable I-surfaces. In particular, for \(d=1\) one has a divisor.
-
(iii)
There are irreducible families of T-singular I-surfaces of type \(\frac{1}{4d}(1, 2d-1)\) depending on \(\mu \) moduli for the following values of \((d,\mu )\):
$$\begin{aligned} (9,19),\quad (21,7),\quad (25,4). \end{aligned}$$
Proof
We use freely the notation of Example 3.1. (i) Let X be as in Example 3.1 with a singularity of type \(\frac{1}{4d} (1,2d-1)\), with \(d>2\). Then the branch locus \(D\subset {\mathbb {F}}_2\) of the corresponding double cover has exactly a double point \(p\in \sigma _{\infty }\) of type \(A_{d-2}\) and is smooth elsewhere.
Assume first that D is irreducible and let \(\widetilde{D}\rightarrow D\) be the normalization. Since \(D\sim 4\sigma _0+2{\varGamma }\), we have \(p_a(D)=15\) and \(p_a(\widetilde{D})=p_a(D)-\lfloor \frac{d-1}{2}\rfloor \), and therefore \(d\le 32\).
Assume now that \(D=D_1+D_2\) is reducible. If \(D_1\) does not intersect \(\sigma _\infty \), then \(D_1\) and \(D_2\) have to intersect away from \(\sigma _\infty \), contradicting our assumption that D is smooth away from the section at infinity. Thus \(D_1\) and \(D_2\) are smooth divisors not containing \(\sigma _{\infty }\) meeting only at the point \(p\in \sigma _{\infty }\). Write \(m=D_1D_2\): the singular point p is of type \(A_{2m-1}\), so we have \(d=2m+1\). Up to exchanging \(D_1\) and \(D_2\), there are exactly the following possibilities:
-
(R1)
\(D_1\sim {\varGamma }\), \(D_2\sim 4\sigma _0+{\varGamma }\), \(m=4\), \(d=9\);
-
(R2)
\(D_1\sim \sigma _0+ {\varGamma }\), \(D_2\sim 3\sigma _0+{\varGamma }\), \(m=10\), \(d=21\);
-
(R3)
\(D_1\sim 2\sigma _0+ {\varGamma }\), \(D_2\sim 2\sigma _0+{\varGamma }\), \(m=12\), \(d=25\).
(ii) The surface X is determined by the choice of \(D\in |4\sigma _0+2{\varGamma }|\) up to the action of the automorphism group of \({\mathbb {F}}_2\) (equivalently, of \({\mathcal {Q}}_2\)), which has dimension 7. The case \(d=1\) corresponds to a general choice of D, so the number of moduli is \(\dim |4\sigma _0+2{\varGamma }|-7=27\). The case \(d=2\) correspond to D smooth but tangent to \(\sigma _{\infty }\) at a point and the case \(d=3\) corresponds to D with an ordinary double point on \(\sigma _{\infty }\). In both cases simple arguments based on Bertini’s theorem show that D can be chosen in an irreducible and locally closed subset of codimension \(d-1\) of \( |4\sigma _0+2{\varGamma }|\).
(iii) The three families correspond to the cases (R1), (R2) and (R3) above.
We discuss case (R3) first. Let \(D_1\in |2\sigma _0+{\varGamma }|\) a smooth curve such that the point \(p:=D\cap \sigma _{\infty }\) is a Weierstrass point of \(D_1\). By Lemma 3.7 there is a 3-dimensional family of such curves, up to the action of the automorphisms of \({\mathbb {F}}_2\).
Consider the following exact sequence:
Passing to cohomology, we have a surjection \(H^0 ({\mathcal {O}}_{{\mathbb {F}}_2}(D_1))\twoheadrightarrow H^0({\mathcal {O}}_{D_1}(12p))\); so there is a curve \(D'_1\in |2\sigma _0+{\varGamma }|\) that meets \(D_1\) only at p. If we take a general element \(D_2\) of the pencil spanned by \(D_1\) and \(D'_1\) we obtain an example of case (R3). The curve \(D_1\) depends on three moduli up to automorphisms of \({\mathbb {F}}_2\) and for each choice of \(D_1\) we have a 1-dimensional family of possible \(D_2\), so case (R3) gives an irreducible subvariety of dimension 4 of the main component of the moduli space of I-surfaces.
Consider now case (R2). Because \(h^1({{\mathbb {F}}}_2,2\sigma _0)=0\), we have a short exact sequence:
So the curves in \(|3\sigma _0+{\varGamma }|\) that cut out the divisor 10p on \(D_1\) are a linear subsystem |M| of dimension \(9=h^0(2\sigma _0)\); p is the only base point of |M| and for general \(R\in |2\sigma _0|\) the curve \(D_1+R\) is smooth at p. So by Bertini’s Theorem, we can pick \(D_2\) in a non empty open subset of |M|, and we in total have \(h^0(\sigma _0+{\varGamma })-1+9 =14\) parameters for the construction. Taking into account the action of the automorphism group of \({\mathbb {F}}_2\), which is 7-dimensional, we see that we have 7 moduli.
Case (R1) can be analysed in the same way: one gets \(25+1=26\) parameters for the construction and therefore 19 moduli. \(\square \)
Remark 3.5
As explained in the introduction of [23], the log Bomolov-Miyaoka-Yau inequality gives \(d\le 34\) for a stable I-surface with a T-singularity of type \(\frac{1}{4d}(1,2d-1)\), a weaker bound than Proposition 3.4 (i).
Remark 3.6
Proposition 3.4 shows that the expectation that T-singular surfaces of type \(\frac{1}{4d}(1,2d-1)\) give a codimension d subset in the moduli space (see Sect. 2.2) is true for \(d=1,2, 3\) but not for all possible d. In fact, for \(d=25\) one has a family depending on 4 moduli while the expected number is \(28-25=3\).
Lemma 3.7
Let C be a smooth genus 2 curve and let \(p\in C\) be a Weierstrass point. Then there is an embedding \(j:C\rightarrow {\mathbb {F}}_2\) such that \(j(C)\sim 2\sigma _0+{\varGamma }\) and j(C) intersects \(\sigma _{\infty }\) at j(p).
Proof
The canonical double cover \(C\rightarrow {\mathbb {P}}^1\) gives a natural embedding of C in the total space V of the line bundle \({\mathcal {O}}_{{\mathbb {P}}^1}(-3)\). In turn, there is an open immersion \(V\hookrightarrow {\mathbb {F}}_3\) that identifies V with the complement of the infinity section \(\sigma _{\infty }\). Composing these two inclusions one gets an inclusion of C in \({\mathbb {F}}_3\) as a bisection disjoint from \(\sigma _{\infty }\). Blowing up \({\mathbb {F}}_3\) at the Weierstrass point p and contracting the strict transform of the ruling of \({\mathbb {F}}_3\) containing p, one obtains the desired inclusion \(j:C\rightarrow {\mathbb {F}}_2\). \(\square \)
3.2 The case of index \(n=3\)
Here we construct T-singular I-surfaces of type \(\frac{1}{18}(1,5)\). We start by proving an auxiliary result on elliptic surfaces.
Lemma 3.8
Let Y be a minimal elliptic surface with \(p_g(Y)=2\) and \(q(Y)=0\). If Y contains a \((-3)\)-curve B then:
-
(i)
Y is the minimal resolution of a double cover \(\pi :{\bar{Y}}\rightarrow {\mathbb {F}}_6\) branched on a divisor \(D\in |\sigma _{\infty }+3\sigma _0|\) with at most negligible singularities and \(\sigma _{\infty } \) pulls back to 2B on Y;
-
(ii)
Y has no multiple fibers; the reducible fibers of the elliptic fibration \(Y\rightarrow {\mathbb {P}}^1\) are the preimages of the rulings of \({\mathbb {F}}_6\) containing a singular point of D.
Conversely, the minimal resolution Y of a double cover \({\bar{Y}}\rightarrow {\mathbb {F}}_6\) as in (i) is a minimal elliptic surface with \(p_g(Y)=2\), \(q(Y)=0\) and the pull-back of \(\sigma _{\infty }\) to Y is equal to 2B for a \((-3)\)-curve B.
Proof
(i)+(ii) Denote by F a general fiber of the elliptic fibration \(Y\rightarrow {\mathbb {P}}^1\). By the canonical bundle formula for elliptic surfaces we have \(|K_Y|=|aF| +\sum (m_i-1)F_i\), where \(m_1F_1, \dots m_kF_k\) are the multiple fibers. Since \(p_g(Y)=2\) we have \(a=1\); since \(K_YB=1\), we conclude that B is a section of the elliptic fibration and that there are no multiple fibers. Set \(L:=2B+7F\); one has \(LB=1\) and \(L^2=16\), \(K_YL=2\). We write \(L=K_Y+(6F+2B)\); since \(6F+2B\) is nef and big, Kawamata-Viehweg vanishing applies and \(h^0(L)=\chi (L) =10\). A similar argument shows that \(H^1(7F+B)=0\) and therefore the restriction map \(H^0(L)\rightarrow H^0({\mathcal {O}}_B(1))\) is surjective and the linear system |L| is base point free. Let \(\varphi :Y\rightarrow {\mathbb {P}}^9\) be the morphism defined by L and let \({\varSigma }\) be the image of \(\varphi \). The morphism \(\varphi \) maps a general F 2-to-1 onto a line and it maps B to a line r that meets the images of the elliptic fibers of Y at distinct points. So the degree m of \(\varphi \) is equal to 2 and \(\deg {\varSigma }=L^2/2=8\). By the classification of surfaces of minimal degree in \({\mathbb {P}}^N\) the surface is either a cone over the rational normal curve of degree 8 or a smooth linear scroll over \({\mathbb {P}}^1\). Since \({\varSigma }\) contains the line r that meets each ruling at a distinct point, we conclude that \({\varSigma }\cong {\mathbb {F}}_6\) and the line r corresponds to the infinity section \(\sigma _{\infty }\) of \({\mathbb {F}}_6\). In addition, it is not hard to see that B is contained in the ramification locus of \(\varphi \).
Let \(Y\rightarrow {\bar{Y}}\overset{\pi }{\rightarrow } {\mathbb {F}}_6\) be the Stein factorization of f: the map \(Y\rightarrow {\bar{Y}}\) contracts precisely the \((-2)\)-curves of Y that do not meet B, so \({\bar{Y}}\) has canonical singularities. The map \(\pi \) is a flat double cover; we write \(D:=\sigma _{\infty }+D_1\). Since the preimage of a general ruling \({\varGamma }\) of \({\mathbb {F}}_6\) is an elliptic curve and D is divisible by 2 in \({{\,\mathrm{Pic}\,}}({\mathbb {F}}_6)\), we may write \(D_1=3\sigma _{\infty }+2a{\varGamma }\). The usual formulae for double covers give
Since \(p_g({\bar{Y}})=p_g(Y)=2\), we obtain \(a=9\) and \(D_1\in |3\sigma _0|\). The singularities of Y occur above the singularities of D, which are therefore negligible because Y has canonical singularities.
Conversely, given a cover as in (i), \({\bar{Y}}\) has canonical singularities and is smooth above \(\sigma _{\infty }\). If we write \(\pi ^*\sigma _{\infty }=2B\) we get \(-12=2\sigma _{\infty }^2=4B^2\), namely \(B^2=-3\) and B is a \((-3)\)-curve. As noted above, the ruling of \({\mathbb {F}}_6\) pulls back to a pencil |F| of elliptic curves and the curve B is a section of |F|, therefore |F| has no multiple fibers. Denote by \({\bar{Y}}\rightarrow Y\) the minimal desingularization. Then the same computations as before give \(p_g(Y)=p_g({\bar{Y}})=2\). Since \(\sigma _{\infty }\) and \(D_1\) are disjoint, the restriction of D to a ruling of \({\varGamma }\) cannot be divisible by 2. So the strict transform in Y of a ruling of \({\mathbb {F}}_6\) is always irreducible and the components of a reducible fiber that do not meet B are precisely the exceptional curves of \({\bar{Y}}\rightarrow Y\). \(\square \)
Example 3.9
Let Y be an elliptic surface with \(p_g(Y)=2\), \(q(Y)=0\) such that:
-
Y has a \((-3)\)-section B
-
Y has an \(I_2\) fiber \(F_2\), and all the remaining fibers are irreducible.
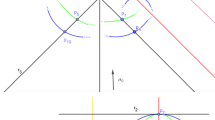
By Lemma 3.8, the surface Y is the minimal resolution of a surface \({\bar{Y}}\) which is a double cover \(\pi :{\bar{Y}}\rightarrow {\mathbb {F}}_6\) branched on a divisor \(D\in |\sigma _{\infty }+3\sigma _0|\) with an ordinary double point \(p_2\) and no other singularity. The \(I_2\) fiber arises as the pull-back of the ruling of \({\mathbb {F}}_6\) through \(p_2\) and B is the preimage of \(\sigma _{\infty }\).
Consider an irreducible singular fiber \(F_1\), of type either \(I_1\) or II, and let \(q\in F_1\) be the singular point. Let \(\widetilde{Y}\rightarrow Y\) be the blow-up at the singular point q, denote by A the strict transform of \(F_1\) and by C (the strict transform of) the component of \(F_2\) that meets B (see Fig. 1). Then A, B, C is a string of type [4, 3, 2] that can be blown down to obtain a surface X with a singularity of type \(\frac{1}{18}(1,5)\), \(K^2_X=1\), \(p_g(X)=2\) and \(q(X)=0\) (see Remarks 2.1 and 2.5). The pull-back of \(K_X\) to \(\widetilde{Y}\) is equal to \(K_{\widetilde{Y}}+\frac{2}{3}A+\frac{2}{3}B+\frac{1}{3}C\). It is not hard to check that it is a nef divisor and that A, B and C are the only curves that have zero intersection with it. So \(K_X\) is ample and X is a stable T-singular surface of type \(\frac{1}{18}(1,5)\).
Remark 3.10
The construction of Example 3.9 depends on 27 moduli. Indeed, the pair (Y, B) determines X up to a finite number of possibilities, so it is enough to count parameters for the pairs (Y, B) with an \(I_2\) fiber. These are determined by the branch locus D of \(\pi :{\bar{Y}}\rightarrow {\mathbb {F}}_6\), that has a double point. The linear system \(|3\sigma _0|\) has dimension 39, and the curves with a double point give a codimension 1 subvariety. Since the automorphism group of \({\mathbb {F}}_6\) has dimension 11, we are left with \(38-11=27\) parameters.
In order to show that the surfaces constructed in Example 3.9 are smoothable, we give an alternative description by computing their canonical ring:
Proposition 3.11
Let X be as in Example 3.9. Then there exist sections \(x_1, x_2\in H^0(X, K_X)\), \(y\in H^0(X, 2K_X)\), \(u\in H^0(X,3 K_X)\) and \(z\in H^0(X, 5K_X)\) such that the canonical ring of X is
for a weighted homogeneous polynomial \(f_{10}\) of degree 10.
In particular, X is embedded into \({{\mathbb {P}}}(1,1,2,3,5)\) as a complete intersection of degree (3, 10).
Proof
Recall that \(p_g(X)= 2\); in addition, one can check that the correction term \(\frac{1}{2}\{m{\varDelta }\}\left( \{m{\varDelta }\}-\{{\varDelta }\}\right) \) vanishes for all values of \(m\ge 2\), so that (2.2) gives:
We want to compute the canonical ring using the identification \(H^0(X, mK_X) =H^0(\widetilde{Y}, \lfloor \pi ^* mK_X\rfloor )\). We want to relate these to linear systems on \({{\mathbb {F}}}_6\) as in the diagram, where we already added some information on the 3-canonical map explained below:

For later reference we compute the relevant divisors on \(\widetilde{Y}\). As above we denote by \({\varGamma }\) a ruling on \({{\mathbb {F}}}_6\) and by \(C'\) the \(-2\)-curve such that \(C+C'\) is a fiber of the elliptic fibration of \(\widetilde{Y}\). The configuration is depicted in Fig. 1.
Note that by construction the branch divisor D of \(\vartheta \) is equal to \(\sigma _{\infty }+D_1\), with \(D_1\in |3\sigma _0| \subset |4\sigma _\infty + 18 {\varGamma }|\), so that
which is the decomposition into the invariant and anti-invariant part. We are ready to compute the relevant pluricanonical systems on Y, but for the ring structure we also need the multiplication maps. Considering these on \(\widetilde{Y}\) we need to account for correction terms, for example,

We now compute the pullback of the canonical ring to \(\widetilde{Y}\). Let us denote the section of a line bundle associated to a curve by the corresponding lower case letter. Then \(H^0(X, K_X) = H^0(\widetilde{Y}, \vartheta ^* {\varGamma }+E) = e\cdot H^0(\widetilde{Y}, \vartheta ^*{\varGamma })\), where the second equality is most easily confirmed by dimension reasons. Thus the canonical pencil is spanned by
Taking the correction into account, the image of the multiplication map is spanned by \(\langle x_1^2 = (cc')^2 ae^2 b, x_1x_2 = cc' (ae^2)^2b, x_2^2 = (ae^2)^3b\rangle \), which together with
forms a basis of \(H^0(\widetilde{Y} , \lfloor 2f^*K_X\rfloor )= H^0(\widetilde{Y}, \vartheta ^* 3{\varGamma } + B) = b\cdot \vartheta ^* H^0({{\mathbb {F}}}_6, 3{\varGamma })\). Looking at the next multiplication map

we find the claimed relation \(x_1^3 = x_2y\). Because of this relation, the image of the multiplication map is of dimension 5 and we need a further generator \(u\in H^0(X, 3K_X)\), not contained in the image.
Remark 3.14
It is now instructive to look at the 3-canonical map, as alluded to in Diagram 3.13. On \(\widetilde{Y}\) we have
Note that \(\vartheta \) maps E and \(C'\) to points \(p_1, p_2\in {{\mathbb {F}}}_6\) such that \(D_1\) is tangent to a ruling in \(p_1\) and \(D_1\) has a node at \(p_2\), necessarily on a different ruling, see Fig. 1. Thus the 3-canonical system is precisely \(\vartheta ^*H^0({{\mathbb {F}}}_6, {{\mathcal {I}}}_{\{p_1, p_2\}} (\sigma _0))\). Since \(|\sigma _0|\) maps \({{\mathbb {F}}}_6\) to the cone \({{\mathcal {Q}}}_6\) over the rational normal curve of degree 6 in \({{\mathbb {P}}}^7\), the image of the 3-canonical map of X is the projection of \({{\mathcal {Q}}}_6 \) from a line through two general points of \({{\mathcal {Q}}}_6\), which is the cone \({{\mathcal {Q}}}_4\subset {{\mathbb {P}}}^5\) over the rational normal curve of degree 4.
In this description, u is the preimage of any hyperplane section of \({{\mathcal {Q}}}_6\) containing \(p_1,p_2\) and not containing the vertex.
We have thus found the subring S generated by elements of degree at most 3 in the canonical ring:
To ease computations later, recall that the Hilbert series of a weighted polynomial ring \({{\mathbb {C}}}[w_1, \dots , w_r]\) with weights \(d_1, \dots , d_r\) is given by \(\prod _{i=1}^r \left( 1- t^{d_i}\right) ^{-1}\) and by the additivity of Hilbert series we get the Hilbert functions for complete intersections. In particular,
because by (3.12) the Hilbert function of R coincides with the Hilbert function of the canonical ring of a smooth I-surface, which in turn is a complete intersection of degree 10 in \({\mathbb {P}}(1,1,2,5)\) (cf. Sect. 2.3).
Note that the surface X carries an involution \(\iota \), which acts on the canonical ring and that birationally \(\iota \) is the covering involution from the double cover of \(\pi :{\bar{Y}} \rightarrow {{\mathbb {F}}}_6\). Thus the whole subring S is invariant under the involution.
A dimension computation gives \(S_4 = R_4\), so we now want to analyse the 5-canonical system, which is of dimension 13, while \(S_5\) is of dimension 12. Since all sections in \(S_2\) are divisible by b, we see that
and in fact equality holds as both sides are of dimension 12. We claim that this is indeed the \(\iota \)-invariant part of the linear system \(|\lfloor f^*5K_X\rfloor |\), in which it is clearly contained.
For this it is enough to find an anti-invariant section of \(\lfloor f^*5K_X\rfloor \). So consider the singular double cover \(\pi :{\bar{Y}} \rightarrow {{\mathbb {F}}}_6\) branched over \(D_1 + \sigma _\infty \) occuring in the Stein factorisation of \(\vartheta \) and write \(\pi ^*(D_1+\sigma _\infty ) = 2R_1 + 2 B\). If \(\rho \) is the anti-invariant section defining the divisor \((R_1+ B)\) we have
as a decomposition into \(\iota \)-eigenspaces. By construction the pull back \(\eta ^*\rho \) to \(\widetilde{Y}\) vanishes along B, E, and \(C'\), thus it defines a section in
We denote this anti-invariant section by z. By the restriction sequence, z restricts to a non-zero constant section on B.
We claim that \(R_{10} = S_{10} \oplus z\cdot S_5\). Computing the dimensions, e.g., using the Hilbert functions, we see that the dimensions match on both sides. The intersection of the two subspaces is zero, since by our choice of z, one is invariant and one is anti-invariant under the action of the involution.
So since \(z^2\) is an invariant section there is a relation of the form \(z^2- f_{10}(x_1, x_2, y, u)\) in \(R_{10}\). We conclude that we have an injection
which has to be an isomorphism because both rings have the same Hilbert function. In total, the canonical ring of X has the claimed format. \(\square \)
Corollary 3.15
A surface X as in Example 3.9 is smoothable.
Proof
Write the canonical ring of X as in Proposition 3.11. Now consider the family \({{\mathcal {X}}}\subset {{\mathbb {P}}}(1,1,2,3,5)\times {{\mathbb {A}}}^1_t\rightarrow {{\mathbb {A}}}^1 = {{\mathcal {B}}}\) cut out by the equations.
where g is a general homogenous polynomial of degree 10.
Note that the general fibre is a smooth I-surface, as if \(t\ne 0\) we can eliminate the variable u to get a hypersurface of degree 10 in \({{\mathbb {P}}}(1,1,2,5)\). When we set \(t=0\) we find the equations of our surface \(X = {{\mathcal {X}}}_0\).
Clearly the family is flat over the curve \({{\mathcal {B}}}\), because every fibre is a surface, i.e., every component of \({{\mathcal {X}}}\) dominates \({{\mathcal {B}}}\). It is also a \({{\mathbb {Q}}}\)-Gorenstein smoothing because Kollár’s condition
is met; this is equivalent to \({{\mathcal {O}}}_{{\mathcal {X}}}(m)\) being flat over \({{\mathcal {B}}}\) by [19]. \(\square \)
3.3 The case of index \(n=5\)
An example of a T-singular I-surface of type \(\frac{1}{25}(1,14)\) can be found in [23] right after the proof of Thm. 3.2. For the reader’s convenience we recall here its description, visualized in Figs. 2 and 3.
Example 3.16
Let Y be an elliptic surface with \(p_g(Y)=2\), \(q(Y)=0\) such that:
-
Y has a \((-3)\)-section A
-
all the elliptic fibers are irreducible.
By Lemma 3.8, the surface Y is a double cover \(\pi :Y\rightarrow {\mathbb {F}}_6\) branched on a smooth divisor \(D\in |\sigma _{\infty }+3\sigma _0|\).
Let \(F_1\) be a singular fiber and let q be its singular point: blow up \(F_1\) at q and then at a point \(q_1\) infinitely near to q and lying on the strict transform of \(F_1\) to get a surface \(\widetilde{Y}\). The strict transform of \(F_1\) is a \((-5)\) curve B, the strict transform of A (that we still denote by A) is a \((-3)\)-curve, the strict transform of the curve of the first blow up is a \((-2)\)-curve, which we call C, so that A, B, C is a string of type [3, 5, 2] (note that this is true both for \(F_1\) nodal and for \(F_1\) cuspidal). Then the string A, B, C can be blown down to obtain a T-singular surface X of type \(\frac{1}{25}(1,14)\) with \(K^2_X=1\), \(p_g(X)=2\), \(q(X)=0\). The pull-back of \(K_X\) to \(\widetilde{Y}\) is equal to \(K_{\widetilde{Y}}+\frac{3}{5}A+\frac{4}{5}B+\frac{2}{5}C\). It is not hard to check that it is a nef divisor and that A, B and C are the only curves that have zero intersection with it. So \(K_X\) is ample and X is a T-singular surface of type \(\frac{1}{25}(1,14)\).
Remark 3.17
Counting parameters as in Remark 3.10, we obtain 28 moduli for the construction in Example 3.9. Since the closure of the locus of smooth I-surfaces is irreducible of dimension 28, we conclude that the general surface obtained via this construction is not smoothable. This confirms the infinitesimal computations of [23], where it is shown that the obstruction space for \({\mathbb {Q}}\)-Gorenstein deformations is non-zero for these surfaces.
The above remark can be made more precise as follows:
Proposition 3.18
Let X be a T-singular surface obtained as in Example 3.16 taking as \(F_1\) an irreducible fiber of type \(I_1\). Then X is not \({{\mathbb {Q}}}\)-Gorenstein smoothable and such surfaces give a dense open subset of an irreducible component of \({{\overline{{{\mathfrak {M}}}}}}_{1,3}\) of dimension 28.
Proof
Assume by contradiction that X admits a \({{\mathbb {Q}}}\)-Gorenstein smoothing. Then by Corollary 2.7, X has an involution that lifts to an involution \(\tau \) of \(\widetilde{Y}\) preserving the exceptional curves A, B and C. In addition, \(\tau \) maps to itself the exceptional curve E of the second blow up of Y, since E is the only irreducible \((-1)\)-curve of \(\widetilde{Y}\). So \(\tau \) maps B to itself and fixes the three distinct points \(B\cap A\), \(B\cap C\) and \(B \cap E\). Since B is a smooth rational curve, \(\tau \) restricts to the identity on B and therefore the induced involution \({{\bar{\tau }}}\) of Y fixes the singular fiber \(F_1\) pointwise. This is impossible since the divisorial part of the fixed locus of an involution on a smooth surface is a smooth curve.
To show that these surfaces give an open subset of an irreducible component of the moduli space it is enough to show that every small \({{\mathbb {Q}}}\)-Gorenstein deformation of such a surface is equisingular, that is, also contains a T-singularity of the same type. Assume for contradiction that we have a non locally trivial \({{\mathbb {Q}}}\)-Gorenstein deformation of such an X. Then, since every non-trivial \({{\mathbb {Q}}}\)-Gorenstein deformation of the singularity \(\frac{1}{25}(1,14)\) has canonical singularities [16, Prop. 2.3], X would deform to a canonical surface and hence admit a \({{\mathbb {Q}}}\)-Gorenstein smoothing—a contradiction. \(\square \)
Remark 3.19
Clearly, the construction from Example 3.16 using a nodal fibre degenerates to the one constructed with a cuspidal fibre. Preliminary computations suggest that the latter surfaces might be smoothable.
4 The classification: proof of Theorem 1.1 and Corollary 1.2
Throughout this section X is a T-singular I-surface with a singularity of type \(\frac{1}{dn^2}(1,dna-1)\); we use freely the notation of Sect. 2.1.
Lemma 4.1
The surface Y is properly elliptic with \(p_g(Y)=2\), \(q(Y)=0\) and there are the following cases to consider:
\(r-d\) | n | \(K_{\widetilde{Y}}^2\) | T-singularity | T-string |
|---|---|---|---|---|
0 | 2 | 0 | \( \frac{1}{4d}(1,2d-1)\) | [4] or [3, 3] or \([3, 2\dots , 3]\) |
1 | 3 | \(-1\) | \( \frac{1}{18}(1,5)\) | [4, 3, 2] |
2 | 5 | \(-2\) | \(\frac{1}{25}(1, 14)\) | [2, 5, 3] |
Proof
Since T-singularities are rational, \(p_g(Y)=p_g(\widetilde{Y})=p_g(X)=2\) and \(q(Y)=q(\widetilde{Y})=q(X)=0\) (Remark 2.1) and \(K^2_{\widetilde{Y}} =d-r\) by (2.3). In addition we have \(K^2_Y<K^2_X =1\) by (2.4), hence \(K^2_Y=0\) and Y is properly elliptic.
By [23, Theorem 1.1] we have \(r-d\le 2\) and if \(r-d=2\), then by [23, Theorem 3.2], the singularity must be of type \(\frac{1}{25}(1,14)\), giving the third row of the table.
If \(r-d=1\), then \(n=3\), \(K_{\widetilde{Y}}^2=-1\) and the T-string is either [5, 2] (the \(\frac{1}{9}(1,2)\) singularity) or \([4,2,\ldots , 2, 3,2]\), where there are \(d-2\) curves of self-intersection \((-2)\) between the \((-3)\)-curve and \((-4)\)-curve (the \(\frac{1}{9d} (1,3d-1)\) singularities). We show that the former cannot occur, and the latter is possible only if \(d=2\), i.e. the chain is [4, 3, 2] and the singularity is \(\frac{1}{18} (1,5)\).
Notice that because \(K_{\widetilde{Y}}^2=-1\) and Y is a minimal elliptic surface, the surface \(\widetilde{Y}\) contains exactly one \((-1)\)-curve E that we contract to obtain Y. By ampleness of X, the curve E must intersect the T-string at least twice, and by nefness of \(K_Y\) the curve E cannot intersect a \((-2)\)-curve.
Let us suppose that the T-string is [5, 2]. Denote by A the \((-5)\)-curve, and by abuse of notation its image in Y. Then as we have just argued, we have \(EA\ge 2\). On the other hand, \(EA\le 3\), because otherwise we would have \(AK_Y<0\). If \(AE=3\), then the curve A in Y has a triple point. On the other hand, we have by adjunction that \(AK_Y=0\), so A must also be contained in a fiber of the elliptic fibration, a contradiction. If instead \(AE=2\), then A has a double point and by adjunction \(AK_Y=1\). This means A is a section of the fibration with a double point, which is impossible.
Now suppose that the T-string is \([4,2,\ldots , 2, 3,2]\). Then E cannot intersect the T-string more than three times, since otherwise one of the curves in the T-string would become \(K_Y\)-negative. Denote by A and B the curves in the T-string of self-intersections \((-4)\) and \((-3)\), respectively, and by abuse of notation, their images in Y. Notice that \(EA\le 2\) and \(EB\le 1\) because otherwise A or B becomes \(K_Y\)-negative.
Then we have three possibilities:
-
1.
\(EA=EB=1\), or
-
2.
\(EA=2\), \(EB=1\), or
-
3.
\(EA=2\), \(EB=0\).
In case (1), upon contracting E, we see that A becomes a \((-3)\)-curve on Y, so by adjunction we have \(K_Y A=1\). On the other hand, the \((-2)\)-curves in the T-chain and the curve B become parts of a fiber on Y, so A also intersects an \(I_k\) fiber twice for some \(k\ge 1\). This forces A to be a multisection. But the canonical bundle formula together with \(p_g=2\) implies that this is impossible.
In cases (2) and (3), contracting E gives us \(A^2=0\), so that A is a fiber of type \(I_1\) or II. In case (2), B is a \((-2)\)-curve passing through the singularity of A, which is impossible. In case (3) if \(r\ge 4\) the curve A intersects a \((-2)\) curve, which is not possible.
Finally, for \(r-d=0\) one has \(n=2\) and we have listed all the possibilities. \(\square \)
Remark 4.2
Note that we have shown in the course of the proof that in the case \(n=3\) the minimal elliptic surface Y contains a \((-3)\)-curve.
Lemma 4.3
If X has index \(n=2\), then:
-
(i)
the surface \(\widetilde{Y}=Y\) is minimal;
-
(ii)
the canonical system \(|K_Y|\) is equal to the pencil |F|, where F is an elliptic fibre.
Proof
(i) This was part of Lemma 4.1.
(ii) Since \(p_g(Y)=2\), the canonical bundle formula for elliptic surfaces gives \(|K_Y|=|F| +\sum (m_i-1)F_i\), where \(m_1F_1, \dots m_kF_k\) are the multiple fibers. The exceptional divisor of the desingularization map \(Y\rightarrow X\) contains a \((-n)\)-curve B for \(n=3\) or 4. So we have
But if there is at least one multiple fibre \(F_0\) of multiplicity \(m_0\) then \(B(F +\sum (m_i-1)F_i)\ge B( m_0 F_0 + (m_0-1) F_0) \ge 3BF_0\ge 3\)—a contradiction. We conclude that there are no multiple fibers and \(|K_Y|=|F|\). \(\square \)
Proposition 4.4
If X has index \(n=2\), then it is obtained as in Example 3.1.
Proof
Denote by \({\varDelta }\) the exceptional divisor of \(Y\rightarrow X\); recall that \({\varDelta }\) is a string of type [4], [3, 3], or \([3,2\dots ,3]\) (with 2 occurring k times), according to whether \(d=1,2\) or \(d=k+2>2\). Since \((K_Y+\frac{1}{2} {\varDelta }) {\varDelta } =0\) and \(K_Y=F\) (cf. Lemma 4.3), we have \(F{\varDelta }=2\).
Set \(L:=3F+{\varDelta }\); one has \(L^2=8\), \(LK_Y=2\) and so \(\chi (L)=6\). We can write \(L=K_Y+(2F+{\varDelta })\), and \(2F+{\varDelta }\) is nef and big since it is the pull-back of \(2K_X\), so by Kawamata-Viehweg vanishing \(h^0(L)=\chi (L)=6\). Restricting to \({\varDelta }\) and taking cohomology we see that the image of the map \(H^0(3F+{\varDelta })\rightarrow H^0({\mathcal {O}}_{{\varDelta }}(2))\) has dimension 2. We are going to use this fact to show that |L| has no fixed components. Note that any fixed component of L must be a component of \({\varDelta }\), since |3F| is free. If \({\varDelta }\) is irreducible, then it is not a fixed component since the map \(H^0(L)\rightarrow H^0(L|_{{\varDelta }})\) is non-zero. If \({\varDelta }\) is reducible, denote by \(A_1\) and \(A_2\) the \((-3)\)-curves of \({\varDelta }\) and suppose that \(A_1\) is in the base locus of |L|: then all the \((-2)\)-curves of \({\varDelta }\) are also in the base locus of |L|, since \(L{\varGamma }=0\) for a \((-2)\)-curve \({\varGamma }\) of \({\varDelta }\), and |L| has a base point on \(A_2\), so \(|L|_{{\varDelta }}\) has dimension \(\le 0\), a contradiction. Assume now that \(d>2\) and a \((-2)\)-curve of \({\varDelta }\) is a fixed component of |L|: then, as above, all the \((-2)\)-curves of \({\varDelta }\) are fixed components of |L| and \(h^0(3F+A_1+A_2)=h^0(L)=6\). Set \(M=3F+A_1+A_2\): we have \(\chi (M)=5\), so \(h^1(M)=1\). On the other hand, \(M=K_Y+2F+A_1+A_2\) and we can write \(2F+A_1+A_2=(2F+\frac{2}{3} A_1+\frac{2}{3} A_2)+\frac{1}{3}A_1+\frac{1}{3} A_2\). Since \(2F+\frac{2}{3} A_1+\frac{2}{3} A_2\) is nef and big, we have \(h^1(M)=0\) by Kawamata-Viehweg’s vanishing, a contradiction. We conclude that |L| has no fixed component.
Now one can argue precisely as in the proof of Lemma 3.8 and prove the following:
-
|L| is base point free and defines a 2-to-1 map \(\varphi :Y\rightarrow {\mathbb {P}}^5\), so the image \({\varSigma }\) of \(\varphi \) is either a smooth rational scroll of degree 4 or a cone over the rational normal curve of degree 4;
-
\(\varphi \) maps the elliptic fibers 2-to-1 to rulings of \({\varSigma }\) and maps \({\varDelta }\) to a line meeting all the rulings, so \({\varSigma }\) is isomorphic to \({\mathbb {F}}_2\);
-
the curves contracted by \(\varphi \) are exactly the \((-2)\)-curves contained in \({\varDelta }\) (if any).
So X is obtained as in Example 3.1. \(\square \)
Proof of Theorem 1.1
We have restricted the number of possible singularities in Lemma 4.1. The fact that the cases of index \(n=2\) are constructed as in Example 3.1 is proved in Proposition 4.4 which gives the bound \(d\le 32\) from Proposition 3.4.
It remains to show that if X has a singularity of type \(\frac{1}{18}(1,5)\), then X is constructed as in Example 3.9, and if X has a singularity of type \(\frac{1}{25}(1,14)\), then X is constructed as in Example 3.16. As explained in Lemma 4.1 the corresponding T-strings in \(\widetilde{Y}\) contain a \((-3)\)-curve and we claim that this maps indeed to a \((-3)\)-curve B in Y. In the former case, this follows from Remark 4.2, while in the latter case this is [23, Theorem 3.2 (A1)]. We know explicitly the possible such pairs (Y, B) by Lemma 3.8 and thus the T-singularities arise as in the Examples 3.9 and 3.16 . \(\square \)
Proof of Corollary 1.2
Recall that the main component of the moduli space of I-surfaces is irreducible of dimension 28. We have shown in Remark 3.2 that every T-singular surface of index 2 is smoothable and in Proposition 3.4 that those of type \(\frac{1}{4}(1,1)\) depend on 27 parameters, hence give a divisor in the main component. For type \(\frac{1}{18}(1,5)\) we argue similarly using Corollary 3.15 and Remark 3.10. The case of type \(\frac{1}{25}(1,14)\) was treated in Proposition 3.18. \(\square \)
Notes
The name was coined by Green, Griffiths, Laza, and Robles in their investigation of Hodge-theoretic stratifications of the moduli space.
References
Alexeev, V.: Moduli spaces \(M_{g,n}(W)\) for surfaces. In: Higher-Dimensional Complex Varieties (Trento, 1994). de Gruyter, Berlin, pp. 1–22 (1996)
Bauer, I.C., Catanese, F., Grunewaldk, F.: The classification of surfaces with \(p_g=q=0\) isogenous to a product of curves. Pure Appl. Math. Q. 4(2, Special Issue: In honor of Fedor Bogomolov. Part 1), 547–586 (2008)
Bauer, I., Catanese, F., Pignatelli, R.: Surfaces of general type with geometric genus zero: a survey. In: Complex and Differential Geometry, Springer Proc. Math., vol. 8, pp. 1–48. Springer, Heidelberg (2011)
Blache, R.: Riemann–Roch theorem for normal surfaces and applications. Abh. Math. Sem. Univ. Hamburg 65, 307–340 (1995)
Catanese, F.: Surfaces with \(K^{2}=p_{g}=1\) and their period mapping. In: Algebraic Geometry (Proc. Summer Meeting, Univ. Copenhagen, Copenhagen, 1978), Lecture Notes in Math., vol. 732, pp. 1–29. Springer, Berlin (1979)
Catanese, F.: Moduli of algebraic surfaces. In: Theory of Moduli (Montecatini Terme, 1985), Lecture Notes in Math., vol. 1337, pp. 1–83. Springer, Berlin (1988)
Catanese, F.: A superficial working guide to deformations and moduli. In: Handbook of Moduli. Vol. I, Adv. Lect. Math. (ALM), vol. 24, pp. 161–215. Int. Press, Somerville (2013)
Catanese, F., Franciosi, M., Hulek, K., Reid, M.: Embeddings of curves and surfaces. Nagoya Math. J. 154, 185–220 (1999)
Catanese, F., Keum, J.: The Bicanonical Map of Fake Projective Planes with an Automorphism. Int. Math. Res. Not. IMRN 21, 7747–7768 (2020)
Cox, D.A., Little, J.B., Schenck, H.K.: Toric Varieties, Graduate Texts in Mathematics, vol. 124. Springer, New York (2012)
Enriques, F.: Le Superficie Algebriche. Nicola Zanichelli, Bologna (1949)
Franciosi, M., Pardini, R., Rollenske, S.: Gorenstein stable surfaces with \(K^2_X=1\) and \(p_g>0\). Math. Nachr. 290(5–6), 794–814 (2017)
Gieseker, D.: Global moduli for surfaces of general type. Invent. Math. 43(3), 233–282 (1977)
Hacon, C.D., McKernan, J., Chenyang, X.: On the birational automorphisms of varieties of general type. Ann. Math. (2) 177(3), 1077–1111 (2013)
Horikawa, E.: Algebraic surfaces of general type with small \(c^{2}_{1}\). II. Invent. Math. 37(2), 121–155 (1976)
Hacking, P., Prokhorov, Y.: Smoothable del Pezzo surfaces with quotient singularities. Compos. Math. 146(1), 169–192 (2010)
Iitaka, S.: Algebraic Geometry, Graduate Texts in Mathematics, vol. 76, p. 24. Springer, New York-Berlin (1982). An introduction to birational geometry of algebraic varieties, North-Holland Mathematical Library
Kollár, J., Mori, S.: Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, vol. 134. Cambridge University Press, Cambridge (1998) With the collaboration of C. H. Clemens and A. Corti, Translated from the 1998 Japanese original
Kollár, J.: Moduli of varieties of general type. In: Handbook of Moduli. Vol. II, Adv. Lect. Math. (ALM), vol. 25, pp. 131–157. Int. Press, Somerville (2013)
Kovács, S.J.: Moduli of stable log-varieties—an update. In: Algebraic Geometry: Salt Lake City 2015, Proc. Sympos. Pure Math., vol. 97, pp. 403–417. Amer. Math. Soc., Providence (2018)
Kollár, J., Shepherd-Barron, N.: Threefolds and deformations of surface singularities. Invent. Math. 91(2), 299–338 (1988)
Lee, Y.: Numerical bounds for degenerations of surfaces of general type. Int. J. Math. 10(1), 79–92 (1999)
Rana, J., Urzúa, G.: Optimal bounds for \(T\)-singularities in stable surfaces. Adv. Math. 345, 814–844 (2019)
Acknowledgements
M.F., R.P. and S.R. would like to thank Fabrizio Catanese, who shaped their view on mathematics in general and algebraic surfaces in particular. We are indebted to Valery Alexeev for explaining Proposition 2.6 to us. We thank the anonymous referee for some improvements of the presentation and interesting remarks. The first and second author are partially supported by the project PRIN 2017SSNZAW\(\_\)004 “Moduli Theory and Birational Classification” of Italian MIUR. The first and second author are members of GNSAGA of INDAM.
Funding
Open access funding provided by Universitá di Pisa within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is dedicated to Fabrizio Catanese, who showed the beauty of algebraic surfaces to us and many others.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Franciosi, M., Pardini, R., Rana, J. et al. I-surfaces with one T-singularity. Boll Unione Mat Ital 15, 173–190 (2022). https://doi.org/10.1007/s40574-021-00280-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40574-021-00280-x