A note on a family of surfaces with $p_g=q=2$ and $K^2=7$

Abstract

We study a family of surfaces of general type with $p_g=q=2$ and $K^2=7$, originally constructed by C. Rito in [35]. We provide an alternative construction of these surfaces, that allows us to describe their Albanese map and the corresponding locus $\mathcal {M}$ in the moduli space of surfaces of general type. In particular we prove that $\mathcal {M}$ is an open subset, and it has three connected components, all of which are 2-dimensional, irreducible and generically smooth

1 Introduction

In the last two decades, several authors worked intensively on the classification of irregular algebraic surfaces (i.e., surfaces S with $q(S) > 0$) and produced a considerable amount of results, see for example the survey papers [1, 23, 26] for a detailed bibliography on the subject.

In particular, irregular surfaces of general type with $\chi (\mathcal {O}_S) = 1$, that is, $p_g(S) = q(S) \ge 1$ were investigated. By Debarre inequality [Deb81, Théorème 6.1] we have $p_g \le 4$. Surfaces with $p_g = q = 4$ and $p_g = q = 3$ are completely classified, see [3, 11, 20, 33]. On the other hand, for the the case $p_g = q = 2$, which presents a very rich and subtle geometry, we have so far only a partial understanding of the situation; we refer the reader to [12,13,14,15, 25, 27,28,29,30,31,32, 34, 38] for an account on this topic and recent results.

As the title suggest, in this paper we consider a family of minimal surfaces of general type with $p_g = q = 2$ and $K^2 = 7$. The existence of these surfaces was originally established by Rito in [35]; the present work provides an alternative construction of them, that allows us to describe their Albanese map and their moduli space.

Our results can be summarized as follows.

Theorem 1.1

The Gieseker moduli space $\mathcal {M}^{\mathrm {can}}_{2, \, 2, \,7}$ of the canonical models of the surfaces of general type with $p_g=q=2$ and $K^2=7$ contains three pairwise disjoint open subsets, all irreducible, generically smooth of dimension 2, such that for each surface S in them, the Albanese map is a generically finite double cover onto a (1, 2)-polarized non simple abelian surface A.

It is worth to notice here, that there is only another known family of surfaces of general type with $p_g = q = 2$ and $K^2 = 7$ found by Cancian and Frapporti in [6] and described in details in [32] whose elements have a different Albanese map. Namely, the Albanese map is a generically finite triple cover of a principally polarized abelian surface. Hence, being the degree of the Albanese map a topological invariant (see Proposition 5.1), these families provide a substantially new piece in the fine classification of minimal surfaces of general type with $p_g=q=2$ in the spirit of [7,8,9].

The paper is organized as follows.

In Sect. 2 we explain our construction in details, pointing out the similarities and the differences with [35], and computing the invariants of the resulting surfaces (Proposition 2.2). We study their Albanese map, giving a precise description of its image, which is an abelian surface isogenous to a product of two curves of genus 1, and of its branch curve.

In Sect. 3 we use our description to study the modular image of Rito’s family, showing that it has three connected components, all irreducible of dimension 2.

The last two sections contain results of deformation theory headed to compute $h^1(S, \, T_S)=2$ (Proposition 5.7) from which it follows that each component is open and generically smooth in the moduli space.

Section 4 is devoted to a general result, Theorem 4.2, about the deformations of the blow-up at a point, that was crucial for the proof and that we find of independent interest. The situation is the following: consider a point p in a smooth surface B, a curve D in B smooth at p and a vector $v \in T_pB$. A standard exact sequence associates to v a first-order deformation $\mathcal {B}$ of the blow-up of B in p. Then Theorem 4.2 says that $\mathcal {B}$ contains a first-order deformation of the strict transform of D if and only if the class of v in the normal vector space $T_pB/T_pD$ extends to a global section of the normal bundle of D in B.

Finally Sect. 5 is devoted to the study of the first-order deformations of the surfaces in $\mathcal {M}$. To show $h^1(S, \, T_S)=2$, we show in fact that the map $H^1(S, \, T_S) \rightarrow H^1(A, \, T_A)$ is injective, and its image is given by the first-order deformations of A that are still isogenous to a product.

Notation and conventions. We work over the field $\mathbb {C}$ of complex numbers. By surface we mean a projective, non-singular surface S, and for such a surface $K_S$ denotes the canonical class, $p_g(S)=h^0(S, \, K_S)$ is the geometric genus, $q(S)=h^1(S, \, K_S)$ is the irregularity and $\chi (\mathcal {O}_S)=1-q(S)+p_g(S)$ is the Euler–Poincaré characteristic.

2 The construction

In this section we give an alternative, but equivalent, construction to the surface S of general type with $p_g=q=2$ and $K^2=7$ constructed by Rito in [35].

Fig. 1

$\sigma _0 :Bl_{p_0}(\mathbb {P}^2) \longrightarrow \mathbb {P}^2$

Let us fix the following points on $\mathbb {P}^2$ :

$$\begin{aligned} p_0=(1:0:0), \, p_1=(0:1:0), \, p_2=(0:0:1), \, p_3=(1:1:1), \, p_4=(1:a:b). \end{aligned}$$

Moreover, let us denote by $r_i$ with $i=1,\ldots ,4$ the four lines joining $p_0$ with each $p_i$ respectively, i.e.,

$$\begin{aligned} r_1=(x_2), \, r_2=(x_1), \, r_3=(x_1-x_2), \, r_4=(bx_1-ax_2), \end{aligned}$$

and the two conics:

$$\begin{aligned} C_1=(x_0^2-x_1x_2), \quad C_2=(abx_0^2-x_1x_2). \end{aligned}$$

Note that both conics are tangent to $r_1$ and $r_2$ respectively in $p_1$ and $p_2$. Finally, $p_3 \in C_1$ and $p_4 \in C_2$.

Fix a square root c of ab and consider the following points on the curves we have just defined

$$\begin{aligned}&p_5=&(1:-1:-1),&p_6=&(1:-a:-b), \\ p_7 =&( c:a:b),&p_8=&(1:c:c),&p_9=&(-c:a:b),&p_{10} =&(-1:c:c). \end{aligned}$$

Finally, let $\ell =(x_0)$ be the line through $p_1$ and $p_2$ and $t=(2x_0-x_1-x_2)$ be the tangent line to $C_1$ through $p_3$, see Fig. 1 to have a visual representation of the situation.

Up to now, we followed Rito in [35], changing the notation only for the curve t (R in Rito’s notation). Now, we proceed a bit differently. Let us apply the following birational transformations of $\mathbb {P}^2$:

• 1. We blow up the point $p_0$ and we get $\sigma _0 :Bl_{p_0}(\mathbb {P}^2) \longrightarrow \mathbb {P}^2$ with exceptional divisor $E_0$ (see Fig. 1 again).

  Considering the pencil of lines through $p_0$ on $Bl_{p_0}(\mathbb {P}^2)$ we have a rational pencil of curves with self-intersection 0, which include the strict transforms of the four lines $r_i$, $i=1, \ldots ,4$. We notice that on $Bl_{p_0}(\mathbb {P}^2)$ we can lift the natural involution on $\mathbb {P}^2$

  $$\begin{aligned} j :(x_0 : \, x_1: \, x_2) \mapsto (-x_0 : \, x_1: \, x_2) \end{aligned}$$

  obtaining an involution whose fixed divisor is $E_0 + \sigma _0^*(\ell )$.

• 2. The quotient by this involution $Bl_{p_0}(\mathbb {P}^2)/ j$ is the Segre–Hirzebruch surface $\mathbb {F}_2$.

  The images of the four lines $r_i$ are fibres of the fibration on $\mathbb {F}_2$. Moreover, the only negative section of this fibration coincide with the image of $E_0$.

• 3. We blow up on $\mathbb {F}_2$ the images of the points $p_1$ and $p_2$, introducing two exceptional divisors $E_1$ and $E_2$.

  We recall that the images of the lines $r_1$ and $r_2$ and of the conics $C_1$ and $C_2$ pass all through these points. Performing this operation the images of $r_1$ and $r_2$ became $(-1)$-curves (see Fig. 2).

• 4. We contract the images of the curves $r_1$ and $r_2$. The resulting surface is exactly $\mathbb {P}^1 \times \mathbb {P}^1$.

Fig. 2

The blow up on $\mathbb {F}_2$ of the images of the points $p_1$ and $p_2$

Summarizing we have obtained a rational map of degree 2

$$\begin{aligned} \sigma :\mathbb {P}^2 \dashrightarrow \mathbb {P}^1 \times \mathbb {P}^1. \end{aligned}$$

Fig. 3

Contracting $r_1$ and $r_2$ we find $\mathbb {P}^1 \times \mathbb {P}^1$

We denote with the same letters the strict transform on $\mathbb {P}^1 \times \mathbb {P}^1$ of all the curves considered on $\mathbb {P}^2$, since no confusion arises (see Fig. 3). The bidouble cover of $\mathbb {P}^1 \times \mathbb {P}^1$ with ramification divisors

$$\begin{aligned} D_1 = 0, \, D_2=E_1+E_2+r_3+r_4, \, D_3=C_1+C_2+E_0+l, \end{aligned}$$

is the product $T_1 \times T_2$ of two double covers $\phi _j :T_j \rightarrow \mathbb {P}^1$ branched at 4 points, two curves of genus 1 (see Fig. 3).

The fibre product of the bidouble cover $T_1 \times T_2 \rightarrow \mathbb {P}^1 \times \mathbb {P}^1$ with $\sigma$ gives the bidouble cover of $\mathbb {P}^2$ studied in [35][Section 3, Step 1], where it is shown that it is birational to an abelian surface that we denote by A (it was $V'$ in [35]). We can summarize this construction with the following diagram.

Note that the map $\iota :A \rightarrow T_1 \times T_2$ is an isogeny of degree 2.

We see from Fig. 3 that the strict transform of the curve $C_1$ is tangent to the curve t on $\mathbb {P}^1 \times \mathbb {P}^1$ at a point p. Locally near p the bi-double cover $T_1 \times T_2 \rightarrow \mathbb {P}^1 \times \mathbb {P}^1$ is given by the equations $u=x^2, \, v=y^2$, $C_1$ has equation $u=0$ and t has equation $u=v^2$. The reduced transform of $C_1$ on A (that we still denote by $C_1$) has equation $x=0$ and the reduced transform of t (that we still denote by t) has equation $x^2=y^4$, therefore it has a tacnode (singularity of type (2, 2)). So the divisor $t+ C_1$ is reduced and has a singularity of type (3, 3) (compare [35][Section 3, Step 2]).

Remark 2.1

We see that we recover the construction due to Rito [35] of an abelian surface with a (1, 2)-polarization, Please notice that in [35] the abelian surface A was labelled by $V'$ and the curves $C_1$ and t by $\hat{C}_1$ and $\hat{R}$.

In [35] it is shown that the divisor $t+ C_1$ is even, i.e. there is a divisor L such that

$$\begin{aligned} t+ C_1\equiv 2L, \end{aligned}$$

and that

$$\begin{aligned} ( t+ C_1)^2=16. \end{aligned}$$

We give an alternative proof of the 2-divisibility of $t+ C_1$ in $\mathrm{Pic}(A)$ in the forthcoming Proposition 3.6. where we also describe all divisor classes L such that $t+ C_1\equiv 2L$. In particular Proposition 3.6 shows that L is a polarization of type (1, 2) which is a pull-back of a (product) principal polarization via the isogeny $A \rightarrow T_1 \times T_2$.

This is exactly the situation described by the first author and F. Polizzi in [27, Remark 2.2]. There the authors suggest how to construct a surface with $p_g=q=2$ and $K^2_S=7$ as a generically finite double cover of A branched along a divisor as $t+C_1$. We follow the suggestion closely and we summarize the situation with the following special case of [35, Proposition 1]

Proposition 2.2

Let A be an Abelian surface. Assume that A contains a reduced curve whose class is 2-divisible in $\mathrm{Pic}(A)$, whose self intersection is 16, with a unique singular point of type (3, 3)-point and no other singularity. Then there exists a double cover $S \rightarrow A$ branched along this curve. Moreover, the numerical invariants of S are $p_g(S)=q(S)=2$ and $K_S^2=7$.

In our case the branch divisor is $C_1+t$.

Let us now construct S step by step starting from A.

• 1. First, we resolve the singularity in p. To do that, we need to blow up A twice, first in p and then in a point infinitely close to p. Let us denote these two blow ups by

  $$\begin{aligned} B' {\mathop {\longrightarrow }\limits ^{\sigma _4}} B {\mathop {\longrightarrow }\limits ^{\sigma _3}} A. \end{aligned}$$

  On $B'$, let us denote by F the exceptional divisor relative to $\sigma _4$, by $E'$ the strict transform of the exceptional divisor E relative to $\sigma _3$, by $C_1$ the strict transform of $C_1$ and, finally, by R the strict transform of t (see Fig. 4).

  In addition, one gathers the following information: $E'\cong \mathbb {P}^1$ and $(E')^2=-2$, $F\cong \mathbb {P}^1$ and $F^2=-1$, $g(C_1)=1$ and $C_1^2=-2$.

• 2. Second, we consider a double cover of $\beta :S'\longrightarrow B'$ ramified over $R+C_1+E'$ (this is even since $t+C_1$ is even on A). The surface $S'$ is a surface of general type, not minimal. Indeed, it contains a $-1$-curve, which is $\hat{E}=\beta ^{-1}(E')$. The ramification divisor is denoted $\hat{R}+\hat{C_1}+\hat{E}$. Notice that $\hat{C_1}$ has genus 1 and $\hat{C_1}^2=-1$.

• 3. Finally, to get S we contract the $-1$-curve $\hat{E}$.

Fig. 4

The birational map $\sigma _3 \circ \sigma _4 :B' \rightarrow A$

We can summarize the construction of S with the following diagram.

We note that since $\alpha$ is the Albanese morphism of S, we obtained in particular that the Albanese variety of these surfaces is isogenous to a product of elliptic curves:

Proposition 2.3

The Albanese variety A of the surface S is isogenous to a product via an isogeny $\iota :A \rightarrow T_1 \times T_2$ of degree 2.

3 Rito’s family has three components of moduli dimension 2

The surfaces S are constructed by a configuration of plane curves determined by two parameters (as noticed already in [35, Section 3, Step 4]), that we denoted by a, b, and a choice of a linear system |L| such that |2L| contains the divisor $|C_1+t|$. So there are $2^4$ possible choice for L, since we can always add to L a $2-$torsion line bundle. In this section we prove that the family has three connected components, all irreducible of moduli dimension 2.

Definition 3.1

Denote by $\mathcal {M}$ the locus of the surfaces S above in the Gieseker moduli space of the surfaces of general type.

The isogeny $\iota$ induces two fibrations $f_i:A \longrightarrow T_i$ with fibres $\Lambda _i$, $i=1,2$ (the fibres are connected by the forthcoming Lemma 3.4).

Remark 3.2

We label the the ramification points of $\phi _1 :T_1 \rightarrow \mathbb {P}^1$ as $a_1,a_2,a_3,a_4$ using Fig. 3 as follows.

$\phi _1(a_1)$ be the projection of the line labeled $E_1$

$\phi _1(a_2)$ be the projection of the line labeled $E_2$

$\phi _1(a_3)$ be the projection of the line labeled $r_3$

$\phi _1(a_4)$ be the projection of the line labeled $r_4$

Similarly, we label the the ramification points of $\phi _2 :T_2 \rightarrow \mathbb {P}^1$ as $b_1,b_2,b_3,b_4$ so that

$\phi _2(b_1)$ be the projection of the line labeled $C_1$

$\phi _2(b_2)$ be the projection of the line labeled $C_2$

$\phi _2(b_3)$ be the projection of the line labeled l

$\phi _2(b_4)$ be the projection of the line labeled $E_0$

Both fibrations have been considered in [35, Section 3, Step 3]. The fibration $f_1$ is the pull back of the pencil of the lines through the point $p_0$ and $a_j$ corresponds to the line $r_j$. So, the branching points of $\phi _1$ correspond to the lines $r_1$, $r_2$, $r_3$ and $r_4$, that, in the natural coordinates, give the 4 points (1 : 0), (0 : 1), (1 : 1) and (a : b), with cross-ratio $\frac{a}{b}$.

The fibration $f_2$ is given by the pencil of conics tangent to the lines $r_i$ in the points $p_i$, $i=1,2$: $b_1$ corresponding to the conic $C_1$, $b_2$ corresponding to $C_2$, $b_3$ corresponding to 2l, $b_4$ corresponding to $r_1+r_2$. Writing this pencil as $\langle x_0^2,x_1x_2 \rangle$ we get a parametrization of $\mathbb {P}^1$ such that the branching points of $\phi _2$ have coordinates (1 : 1), (1 : ab), (1 : 0) and (0 : 1), with cross-ratio ab.

We deduce the following

Proposition 3.3

Every connected component of $\mathcal {M}$ has dimension 2.

Proof

The base of the family of the surfaces S has a finite proper map on an open subset of $\mathbb {C}^2$ given by the parameters (a, b). So, if $\mathcal {C}$ is any irreducible component of it, $\dim \mathcal {C}=2$.

The relative Albanese morphism maps $\mathcal {C}$ to the moduli space of the Abelian surfaces with a polarization of type (1, 2). By Proposition 2.3 the image of ${{\mathcal {C}}}$ is contained in the $2-$dimensional subvariety $\mathcal {I}$ of those isogenous to a product of curves. Since these curves are double covers of $\mathbb {P}^1$ branched at 4 points with cross-ratio respectively $\frac{a}{b}$ and ab the general pair of curves of genus 1 appears in the image of $\mathcal {C}$: the map $\mathcal {C}\rightarrow \mathcal {I}$ is generically finite and therefore dominant.

Since isomorphic manifolds have isomorphic Albanese varieties, $\mathcal {C}\rightarrow \mathcal {I}$ factors through the moduli space of the surfaces of general type, and then the moduli dimension of $\mathcal {C}$ is 2. $\square$

We can now determine the isogeny. Recall that an étale double cover of a variety is determined up to isomorphism by a $2-$torsion line bundle on it, the anti-invariant part of the direct image of the structure sheaf of the cover. Moreover for $\{i, j,h,k\} = \{1,2,3,4\}$, $\mathcal {O}_{T_1}(a_i-a_j) \cong \mathcal {O}_{T_1}(a_k-a_l)$ and $\mathcal {O}_{T_2}(b_i-b_j)\cong \mathcal {O}_{T_2}(b_k-b_l)$ are the $2-$torsion line bundles on the curves $T_1$, $T_2$.

Lemma 3.4

The anti-invariant part of $\iota _*\mathcal {O}_A$ is isomorphic to $\mathcal {O}_{T_1}(a_4-a_3) \boxtimes \mathcal {O}_{T_2}(b_2-b_1)$.

Proof

By Remark 3.2 we can write every 2-torsion line bundle on $T_1 \times T_2$ as $\mathcal {O}_{T_1}(a_i-a_j) \boxtimes \mathcal {O}_{T_2}(b_k-b_l)$. We compute separately each factor by restricting to a fibre of type $\Lambda _1$ resp. $\Lambda _2$. In fact, restricting the isogeny to a fibre of type $\Lambda _1$ (respectively $\Lambda _2$) we obtain an étale double cover of $T_2$ (respectively $T_1$) given by the restriction of the above bundle $\mathcal {O}_{T_2}(b_k-b_l)$ (respectively $\mathcal {O}_{T_1}(a_i-a_j)$).

We did the computation by using the fibres over $a_3$ and $b_1$.

First consider the curve $\hat{r}_3:=f_1^{-1}(a_3) \subset A$, we need to show that the anti-invariant part of $(\iota _{|\hat{r}_3})_* \mathcal {O}_{\hat{r}_3}$ is $\mathcal {O}_{T_2}(b_2-b_1)$.

It is invariant by the $(\mathbb {Z}/2\mathbb {Z})^2$ action on A given by the bidouble cover $\pi$, and in fact $\hat{r}_3$ lies in the locus of the fixed points of one of the three involutions. Thus $\pi$ induces a nontrivial involution on it, whose quotient is the double cover $\hat{r}_3 \rightarrow r_3$ branched on $p_3+ p_5+p_8+p_{10}$ (see Fig. 1). Note that this implies that $\hat{r}_3$ is connected so $k \ne l$.

The involution j acts on $r_3$ permuting those points as $p_3 \leftrightarrow p_5$, $p_8 \leftrightarrow p_{10}$ lifting to an involution on $\hat{r}_3$ without fixed points. Taking the quotient we get a commutative diagram

Let us call $q_j$ the ramification point in A of $\pi _{|\hat{r}_3}$ mapping to $p_j$. Then $\iota (q_3)=\iota (q_5)=b_1$, $\iota (q_8)=\iota (q_{10})=b_2$. So $\iota ^*\mathcal {O}_{T_2}(b_2-b_1)=\mathcal {O}_{\hat{r}_3}(q_8+q_{10}-q_3-q_5)\cong \mathcal {O}_{\hat{r}_3}$: this implies the claim.

The analogous computation for the elliptic curve $C_1=f_2^{-1} (b_1)$ leads to consider the 4 points on the corresponding conic cut by the lines $r_3$ and $r_4$, permuted by j as $p_3 \leftrightarrow p_5$, $p_7 \leftrightarrow p_9$. A fully analogous computation leads to $\iota ^*\mathcal {O}_{T_1}(a_4-a_3)\cong \mathcal {O}_{C_1}$ completing the proof. $\square$

Recalling that the kernel of $\iota ^* :\mathrm{Pic}(T_1 \times T_2) \rightarrow \mathrm{Pic}A$ is a subgroup of order 2 generated by the antiinvariant part of $\iota _* {\mathcal {O}}_A$, we deduce

$$\begin{aligned}&f_1^*\bar{a} \otimes f_2^*\bar{b} \equiv f_1^*\bar{a}' \otimes f_2^*\bar{b}' \Leftrightarrow \text { either } (\bar{a},\bar{b})\nonumber \\&\quad =(\bar{a}',\bar{b}') \text { or } \bar{a}+a_4 \equiv \bar{a}'+a_3 \text { and } \bar{b}+b_2 \equiv \bar{b}'+b_1 \end{aligned}$$

(1)

that can be written equivalently as

$$\begin{aligned}&f_1^*\bar{a} \otimes f_2^*\bar{b} \equiv f_1^*\bar{a}' \otimes f_2^*\bar{b}' \Leftrightarrow \text { either } (\bar{a},\bar{b})\nonumber \\&\quad =(\bar{a}',\bar{b}') \text { or } \bar{a}+a_4 \equiv \bar{a}'+a_3 \text { and } \bar{b}+b_3 \equiv \bar{b}'+b_4 \end{aligned}$$

(2)

Proposition 3.5

We have

$$\begin{aligned} C_1+t \in |f_1^*(a_4+a_3) +f_2^*(b_3+b_1)| \end{aligned}$$

Proof

We compute

$$\begin{aligned} t=\pi ^*t\equiv \pi ^* l =f_1^*a_1+f_1^*a_2+f_2^*b_3 \end{aligned}$$

and the result follows since $C_1=f_2^*b_1$, $a_1+a_2 \equiv a_3+a_4$. $\square$

It follows that we have the following description of the 16 possible linear systems L.

Proposition 3.6

|L| varies among the linear systems $|f_1^*\bar{a} \otimes f_2^*\bar{b}|$ where $\bar{a}$ and $\bar{b}$ solve one of the following

• (1) either $2\bar{a} \equiv 2a_3$ and $2\bar{b} \equiv b_4+b_1$

• (2) or $2\bar{a} \equiv a_4+a_3$ and $2\bar{b} \equiv b_3+b_1$

Notice that each of the two systems of equations has 16 distinct solutions $(\bar{a},\bar{b})$, divided in pairs by the equivalence relation (1); so it gives 8 distinct linear systems. We get then 16 different possible choices of |L| as expected.

Proof

If $(\bar{a},\bar{b})$ solves the system 2), then $2(f_1^*\bar{a} + f_2^*\bar{b}) \equiv f_1^*(a_4+a_3) +f_2^*(b_3+b_1)\equiv C_1+t$ by Proposition 3.5. If $(\bar{a},\bar{b})$ solves the system 1), then $2(f_1^*\bar{a} + f_2^*\bar{b}) \equiv f_1^*(2a_3) +f_2^*(b_4+b_1)\equiv f_1^*(a_4+a_3) +f_2^*(b_3+b_1)$ again by (2).

So all these linear systems are possible choices. Since they are 16, they are all possible choices. $\square$

We observe that $a_3 \in T_1$ and $b_1 \in T_2$ are the images of the essential singularity of the branching curve of the Albanese map of S.

Inspecting the linear equivalences in Proposition 3.6 we observe that in all cases ${\mathcal {O}}_{T_2}(\bar{b}-b_1)$ is a $4-$ torsion line bundle. On the contrary ${\mathcal {O}}_{T_1}(\bar{a}-a_3)$ is a torsion line bundle whose torsion order may change: it is 4 in case (2) whereas in case (1) there are two possibilities: it may be 2 or 1. Recalling that we have two pairs $(\bar{a},\bar{b})$ for each choice of |L| (and then for each S) we deduce the following natural decomposition of $\mathcal {M}$.

Definition 3.7

We say that a surface $S\in \mathcal {M}$ is of type j if the minimal (among the two possible choices of $\bar{a}$) torsion order of ${\mathcal {O}}_{T_1}(\bar{a}-a_3)$ is j.

By Proposition 3.6 the values that j assumes are 1, 2, 4.

Setting $\mathcal {M}_j$ for the subset of $\mathcal {M}$ of the surfaces of type j we observe that each $\mathcal {M}_j$ is open and therefore we have decomposed

$$\begin{aligned} \mathcal {M} = \mathcal {M}_1 \cup \mathcal {M}_2 \cup \mathcal {M}_4 \end{aligned}$$

as union of disjoint not empty open subsets.

Now we prove that each $\mathcal {M}_j$ is irreducible.

Definition 3.8

We denote (as usual) by $\mathcal {M}_{1,3}$ the moduli space of the curves of genus 1 with three ordered marked points. We are not assuming the points to be distinct.

We denote an element of $\mathcal {M}_{1,3}$ as (C, x, y, z) where C is a curve of genus 1 and $x,y,z \in C$.

We denote by $\mathcal {N}_j$, $j \in \{1,2,4\}$ the subvariety of $\mathcal {M}_{1,3} \times \mathcal {M}_{1,3}$ of the form

$$\begin{aligned} \left( \left( T_1, a_3,a_4,\bar{a} \right) , \left( T_2, b_1,b_2,\bar{b} \right) \right) \end{aligned}$$

such that

• 1. $\mathcal {O}_{T_1}(a_4-a_3)$ and $\mathcal {O}_{T_2}(b_2-b_1)$ are torsion line bundles of torsion order 2.

• 2. $\mathcal {O}_{T_2}(\bar{b}-b_1)$ is a torsion line bundle of torsion order 4 such that $\mathcal {O}_{T_2}(\bar{b}-b_1)^{\otimes 2} \not \cong \mathcal {O}_{T_2}(b_2-b_1)$.

• 3.       if $j=1$: $\bar{a}=a_3$

        if $j=2$: $\bar{a}\ne a_4$ and $\mathcal {O}_{T_1}(\bar{a}-a_3)$ is a torsion line bundle of torsion order 2

        if $j=4$: $\mathcal {O}_{T_1}(\bar{a}-a_3)^{\otimes 2} \cong \mathcal {O}_{T_1}(a_4-a_3)$

Note the correspondence among conditions 1, 2, 3 and almost all solutions of the equations Proposition 3.6. The only solutions that do not have a counterpart here are those with $\bar{a}=a_4$. This is the reason for the map in the next statement to have a different degree for $j=1$.

Proposition 3.9

For each $j=1,2,4$ there is a proper finite surjective morphism

$$\begin{aligned} \mathfrak {m}_j :\mathcal {N}_j \rightarrow \mathcal {M}_j. \end{aligned}$$

Moreover $\mathfrak {m}_j$ is birational if $j=1$ whereas $\deg \mathfrak {m}_j=2$ if $j=2$ or 4.

Proof

We construct the map $\mathfrak {m}_j$.

For every $\left( \left( T_1, a_3,a_4,\bar{a} \right) , \left( T_2, b_1,b_2,\bar{b} \right) \right) \in \mathcal {N}_j$ we consider the isogeny $\iota :A \rightarrow T_1 \times T_2$ given by the 2-torsion bundle $\mathcal {O}_{T_1}(a_4-a_3) \boxtimes \mathcal {O}_{T_2}(b_2-b_1)$.

Now we construct a bidouble cover $\pi :A \dashrightarrow \mathbb {P}^2$ as in Rito’s construction.

We consider each $T_j$ with the group structure such that $a_3$ and $b_1$ are the respective neutral elements. This fixes an action of the Klein group $K\cong (\mathbb {Z}/2\mathbb {Z})^2$ as group automorphisms of $T_1 \times T_2$ by $(z_1,z_2)\mapsto (\pm z_1,\pm z_2)$.

Then we choose a point $p \in \iota ^{-1}(a_3,b_1)$ and consider A with the group structure such that p is the neutral element, so that $\iota$ is a group homomorphism. Considering the analogous action of the Klein group on A we get a commutative diagram

where the vertical maps are quotients by K.

The bidouble cover $T_1 \times T_2 \rightarrow \mathbb {P}^1 \times \mathbb {P}^1$ is ramified at the union of 8 elliptic curves, mapping to the four $2-$torsion points on each factor, including $a_3,a_4$ on $T_1$ and $b_1,b_2$ on $T_2$. We note that the 2-torsion bundle $\mathcal {O}_{T_1}(a_4-a_3) \boxtimes \mathcal {O}_{T_2}(b_2-b_1)$, when restricted to them, is not trivial. This implies that their preimage on A, ramification locus of the 8 : 1 morphism $A \rightarrow \mathbb {P}^1 \times \mathbb {P}^1$ is again union of 8 elliptic curves naturally labeled as $a_1,\ldots ,a_4,b_1,\ldots ,b_4$.

A direct computation shows that the Klein group of A acts on each of them, action that is faithful exactly on the curves labeled $a_1,a_2,b_3,b_4$. So the branch locus of the double cover $D \rightarrow \mathbb {P}^1 \times \mathbb {P}^1$ is the image of them, union of 4 rational curves, two on each ruling. Therefore D is a Del Pezzo surface of degree 4 with 4 nodes. Solving the 4 nodes we obtain a weak Del Pezzo surface with a configuration of 8 rational curves whose incidence graph is an octagon with alternating self intersections $-1$ and $-2$: the strict transforms of the ramification lines have self intersection $-1$ whereas the exceptional curves have self intersection $-2$.

Now we consider, among the $-1$ curves in the octagon, the one ‘labeled’ $b_3$: contract first the other three $-1$ curves and then the two exceptional curves now of self intersection $-1$: the resulting surface is $\mathbb {P}^2$ and the remaining three sides of the octagon map to three lines, let’s call them l (the one coming from the $-1$-curve “’$b_3$”), $r_1$ and $r_2$. The preimages of the lines of $\mathbb {P}^1 \times \mathbb {P}^1$ labeled $a_3,a_4,b_1,b_2$ are respectively two lines $r_3$ and $r_4$ and two conics $C_1$, $C_2$ forming the configuration of curves in Fig. 1.

Notice that the two points in $\iota ^{-1}(a_3,b_1)$ map bijectively to the intersection points of $r_3$ and $C_1$. We draw the tangent t to $C_1$ in the image of p. Pulling-back t and adding the elliptic curve dominating $C_1$ we obtain a divisor in A as in Proposition 2.2. We have recovered Rito’s construction.

Then Proposition 3.5 applies and we have 16 double covers $S\rightarrow A$ branched on this divisor, determined by the 32 solutions of the equations in Proposition 3.6. Since the pair $(\bar{a},\bar{b})$ is a solution by assumption, we can define as image of our element in $\mathcal {N}_j$ the surface S of the corresponding double cover. Then S belongs to $\mathcal {M}_j$ by construction.

It is important to recall here that we have done an arbitrary choice in this construction, when we chose $p \in \iota ^{-1}(a_3,b_1)$. We notice now that the isomorphism class of the surface S does not depend on this choice, since the two corresponding double covers of A are conjugated by the involution of A given by the isogeny. So we have a well defined morphism $\mathcal {N}_j \rightarrow \mathcal {M}_j$.

Finally since there are two pairs of possible $(\bar{a},\bar{b})$ for each |L| the maps $\mathfrak {m}_j$ are proper of degree 2 for $j \ge 2$. For $j=1$ the degree is 1 because we are not considering the solutions with $\bar{a}=a_4$. The surjectivity is obvious. $\square$

Now, we shall deal with the problem of irreducibility of $\mathcal {N}_j$ for $j=1,2$ and 4, to do that we need to introduce some notation.

Let us recall some well known fact about modular curves, see e.g. [17, Section 1.5]. The principal congruence subgroup of level N is

$$\begin{aligned} \Gamma (N):=\Bigg \{ \begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \in \text{ SL}_2(\mathbb {Z})| \begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \equiv \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix} \text{ mod } N \Bigg \}. \end{aligned}$$

A subgroup $\Gamma$ of $\text{ SL}_2(\mathbb {Z})$ is a congruence subgroup of level N if $\Gamma (N) \subset \Gamma$ for some $N \in \mathbb {Z}^+$. Some important congruence subgroups are

$$\begin{aligned} \Gamma _1(N):=\Bigg \{ \begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \in \text{ SL}_2(\mathbb {Z})| \begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix} \equiv \begin{pmatrix} 1 &{} * \\ 0 &{} 1 \end{pmatrix} \text{ mod } N \Bigg \}. \end{aligned}$$

The modular curve $\mathcal {Y}(\Gamma )$ for $\Gamma$ is defined as

$$\begin{aligned} \mathcal {Y} (\Gamma ) = \Gamma \setminus \mathcal {H} = \{\Gamma \cdot z | z \in \mathcal {H}\}. \end{aligned}$$

The special cases of modular curves for $\Gamma _1(N)$ is denoted by $\mathcal {Y}_1[N] = \Gamma _1(N)\setminus \mathcal {H}$, where $\mathcal {H}$ is the Poincaré half-space.

Theorem 3.10

Points of $\mathcal {Y}_1[N]$ correspond to pairs (E, P), where E is an elliptic curve and $P \in E$ is a point of exact order N. Two such pairs (E, P) and $(E_0 , P_0)$ are identified when there is an isomorphism of E onto $E_0$ taking P to $P_0$.

We are interested in the case when $N=4$ and in the special modular curve $\mathcal {Y}_1[4]$ which parametrizes elliptic curves with 4-torsion points.

Now, let $\mathcal {Y}_1[2, \, 4]$ be the space parametrizing an elliptic curves with a 2-line bundle point $\mathcal {Q}$ and a 4-torsion line bundle $\mathcal {T}$ such that $\mathcal {T}^2 \ne \mathcal {Q}$, than we have the following proposition.

Proposition 3.11

$\mathcal {Y}_{1}[2, \,4]$ is irreducible and generically smooth of dimension 1.

Proof

We proceed as explained in the Appendix A of [27]. Let $E=\mathbb {C}/\Lambda$ be an elliptic curve (and $\widehat{E}$ its dual abelian variety), E[n] the subgroup of order n torsion points on E and $\widehat{E}[n] \subset \widehat{E}$ the subgroup of n torsion line bundles. Moreover let $G=\text{ SL}_2(\mathbb {Z})$ be the modular group. Then G is the orbifold fundamental group of $\mathcal {H}/G$ and there is an induced monodromy action of G on both E[n] and $\widehat{E}[n]$, see [19].

By the Appell–Humbert theorem, the elements of $\widehat{E}[2]$ can be canonically identified with the 4 characters $\Lambda \rightarrow \mathbb {C}^*$ with values in $\{\pm 1\}$ (see [4, Chapter 2]) which are

$$\begin{aligned} \chi _0:=(1,\,1), \quad \chi _1:=(1, \, -1), \quad \chi _2:=(-1, \, 1), \quad \chi _3:=(-1, \, -1). \end{aligned}$$

Let $\{\omega _1, \omega _2\}$ be a suitable basis of $\Lambda$ by [4, proof of Proposition 8.1.3], the monodromy action of

$$\begin{aligned} M = \begin{pmatrix} \alpha &{} \beta \\ \gamma &{}\delta \end{pmatrix}\in G \end{aligned}$$

induced over a character $\chi$ is as follows:

$$\begin{aligned} \begin{aligned} (M \cdot \chi )(\omega _1)&= \chi (\omega _1)^{\alpha } \chi (\omega _2)^{\beta } \\ (M \cdot \chi )(\omega _2)&= \chi (\omega _1)^{\gamma } \chi (\omega _2)^{\delta }. \end{aligned} \end{aligned}$$

(3)

Therefore we have

$$\begin{aligned}&M \cdot \chi _1= ((-1)^{\beta }, \, (-1)^{\delta }),\quad M \cdot \chi _2=((-1)^{\alpha }, \, (-1)^{\gamma }), \quad \nonumber \\&M \cdot \chi _3=((-1)^{\alpha +\beta }, \, (-1)^{\gamma +\delta }), \end{aligned}$$

(4)

Whereas the 16 elements of $\widehat{E}[4]$ correspond to the 16 characters $\Lambda \rightarrow \mathbb {C}^*$ with values in $\{\pm i\}$:

$$\begin{aligned} \begin{array}{cccc} \psi _1 :=(1, \, 1), &{} \psi _2:=(1, \, -1), &{} \psi _3:=( -1,\, 1), &{} \psi _4 :=(-1, \, -1),\\ \psi _5 :=(1, \, i), &{} \psi _6:=(-1, \, i), &{} \psi _7 :=(1, -i), &{} \psi _8:=(-1, \, -i), \\ \psi _9 :=(i, \, 1), &{} \psi _{10}:=(i, \, -1), &{} \psi _{11}:=(-i, \, 1), &{} \psi _{12} :=(-i, \, -1), \\ \psi _{13} :=(i,\, i),&{} \psi _{14}:=(-i, \, i), &{} \psi _{15}:=(i, \, -i), &{} \psi _{16} :=(-i, \, -i). \\ \end{array} \end{aligned}$$

By using Eq. (3) one can compute the induced action of M over a character $\psi$.

Thus, to prove the first part of the proposition it is sufficient to check that the monodromy action of G is transitive on the set

$$\begin{aligned} \{(\mathcal {Q}, \, \mathcal {T}) \, \in \big (\widehat{E}[2] \setminus \mathcal {O}_E\big ) \times \big (\widehat{E}[4]\setminus \widehat{E}[2]\big ) | \, \mathcal {T}^2 \ne \mathcal {Q}\}. \end{aligned}$$

This is a straightforward computation which can be carried out as the one in the proof of [27, Proposition A1] and it is left to the reader.

Therefore we can consider the set of triples

$$\begin{aligned} (z, \, \chi , \psi ), \quad z \in \mathcal {H}, \, \, \chi \in \{\chi _1, \chi _2, \chi _3\} \subset \widehat{E_z}[2], \, \, \psi \in \{ \psi _5, \ldots , \psi _{16} \} \subset \widehat{E_z}[4], \end{aligned}$$

where $E_z$ is the elliptic curve corresponding to the lattice $\mathbb {Z}\oplus \mathbb {Z}z$.

The group G acts on the set of triple $(z, \chi , \, \psi )$, with the natural action of the modular group on $\mathcal {H}$ and by the induced monodromy action on the second two ones. The corresponding quotient $\mathcal {Y}_{1}[2,4]$ is a quasi-projective variety. Moreover

$$\begin{aligned} \pi :\mathcal {Y}_{1}[2,4] \longrightarrow \mathcal {H}/G \end{aligned}$$

given by the forgetful map, is an $\acute{\text {e}}$tale cover on a smooth Zariski open set $\mathcal {Y}_{1}^0 \subset \mathcal {H}/G$; then it is generically smooth. Finally, by construction $\mathcal {Y}_{1}[2,4]$ is a normal variety, because it only has quotient singularities. Then, since it is connected, it must be also irreducible. $\square$

Finally, let $\mathcal {Y}_1[2, \, 2]$ the space parametrizing an elliptic curves with a 2-line bundle $\mathcal {Q}$ and a second 2-torsion line bundle $\mathcal {T}$ such that $\mathcal {T}\ne \mathcal {Q}$, than we have the following proposition.

Proposition 3.12

$\mathcal {Y}_{1}[2, \, 2]$ is irreducible and generically smooth of dimension 1.

Proof

The proof is analogous to the one for Proposition 3.11. One has to be careful, again, in checking that the monodromy action of G is transitive on the set

$$\begin{aligned} \{(\mathcal {Q}, \, \mathcal {T}) \, \in \big (\widehat{E}[2] \setminus \mathcal {O}_E\big ) \times \big (\widehat{E}[2]\setminus \mathcal {O}_E \big ) | \, \mathcal {T}\ne \mathcal {Q}\}. \end{aligned}$$

But, again, this follows from the actions (4), from which one sees right away that the image of $\mathcal {T}$ is always different form the image of $\mathcal {Q}$. $\square$

Proposition 3.13

The subvariety $\mathcal {N}_j \subset \mathcal {M}_{1,3} \times \mathcal {M}_{1,3}$ is irreducible, generically smooth of dimension 2 for each $j=1,2$ and 4.

Proof

First of all, we mean by an elliptic curve marked with a point that we have fixed a group structure on the curve of genus 1 for which that point is the neutral element. We always choose for $T_1$ the point $a_3$ and for $T_2$ the point $b_1$ as neutral elements.

After this global consideration, we prove the claim case by case as j varies.

Case j=4:

By Definition 3.8 the variety $\mathcal {N}_4$ depends on the following data:

• one elliptic curve $T_1$ marked with a point $a_3$ and a $4-$torsion line bundle $\mathcal {T}_1=\mathcal {O}_{T_1}(\bar{a}-a_3)$ which is not $2-$torsion – its square determines the last point on $T_1$ ($a_4$);

• one elliptic curve $T_2$ marked with a point $b_1$, a $4-$torsion line bundle $\mathcal {T}_2:=\mathcal {O}_{T_2}(\bar{b}-b_1)$ and a $2-$torsion line bundle $\mathcal {O}_{T_2}(b_2-b_1) \not \cong \mathcal {T}^2_2$.

In other words there is a dominant morphism

$$\begin{aligned} \mathcal {Y}_1[4] \times \mathcal {Y}_1[2, \, 4] \rightarrow \mathcal {N}_4. \end{aligned}$$

We observe that $\mathcal {Y}_1[4]$ is a generically smooth quasi-projective variety, connected, and irreducible of dimension 1, [17, Chapter 2]. By Proposition 3.11$\mathcal {Y}_1[2, \, 4]$ is irreducible and generically smooth of dimension 1. This concludes the proof since $\dim \mathcal {N}_4=2$ by Proposition 3.3 and Proposition 3.9.

Case j=2:

By Definition 3.8 the variety $\mathcal {N}_2$ depends on the following data:

• one elliptic curve $T_1$ marked with a point $a_3$ and two $2-$torsion line bundles $\mathcal {T}_1=\mathcal {O}_{T_1}(a_4-a_3)$ and $\mathcal {Q}=\mathcal {O}_{T_1}(\bar{a}-a_3)$ such that $\mathcal {T}_1 \not \cong \mathcal {Q}$;

• one elliptic curve $T_2$ marked with a point $b_1$, a $4-$torsion line bundle $\mathcal {T}_2:=\mathcal {O}_{T_2}(\bar{b}-b_1)$ and a $2-$torsion line bundle $\mathcal {O}_{T_2}(b_1-b_2) \not \cong \mathcal {T}^2_2$.

In other words there is a dominant morphism

$$\begin{aligned} \mathcal {Y}_1[2, \, 2] \times \mathcal {Y}_1[2, \, 4] \rightarrow \mathcal {N}_2. \end{aligned}$$

By Proposition 3.12, we have that $\mathcal {Y}_1[2, \, 2]$ is irreducible and generically smooth of dimension 1. This concludes the proof since $\dim \mathcal {N}_2=2$ by Proposition 3.3 and Proposition 3.9.

Case j=1:

Finally, we have by Definition 3.8 that the variety $\mathcal {N}_1$ depends on the following data:

• one elliptic curve $T_1$ marked with a point $a_3$ and one $2-$torsion line bundles $\mathcal {T}_1=\mathcal {O}_{T_1}(a_4-a_3)$;

• one elliptic curve $T_2$ marked with a point $b_1$, a $4-$torsion line bundle $\mathcal {T}_2:=\mathcal {O}_{T_2}(\bar{b}-b_1)$ and a $2-$torsion line bundle $\mathcal {O}_{T_2}(b_1-b_2) \not \cong \mathcal {T}^2_2$.

In other words there is a dominant morphism

$$\begin{aligned} \mathcal {Y}_1[2] \times \mathcal {Y}_1[2, \, 4] \rightarrow \mathcal {N}_1. \end{aligned}$$

We observe that $\mathcal {Y}_1[2]$ is a generically smooth quasi-projective variety, connected, and irreducible of dimension 1, [17, Chapter 2]. Ad we conclude as the previous cases. $\square$

Corollary 3.14

The components $\mathcal {M}_1$, $\mathcal {M}_2$ and $\mathcal {M}_4$ of $\mathcal {M}$ are irreducible of dimension 2.

Proof

By Proposition 3.9 we have that $\mathfrak {m}_j :\mathcal {N}_j \rightarrow \mathcal {M}_j$ is a proper finte surjective morphism for each $j=1,2$ and 4. Moreover, by Proposition 3.14 we have that each $\mathcal {N}_j$ is irreducible of dimension 2 for each $j=1,2$ and 4. $\square$

4 Some remarks on the deformations of a blown up surface

In this section we shall present some classicall results on deformation of a pairs. The main result is Theorem 4.2, possibly known to the experts, although we could not find it in the literature. This section will be employed systematically in the Moduli Space Sect. 5. In particular the Corollary 4.5 of the Theorem 4.2 is a fundamental step in the proof of the Proposition 5.8, see Remark 5.6.

Let us first recall some basic definition.

Let B an algebraic nonsingular variety over an algebraically closed field k. A first-order deformation of B is a commutative diagram

where $\pi$ is a flat morphism, $\text {Spec}(k[\epsilon ]) =\text {Spec}(k[t]/t^2)$ and such that the induced morphism

$$\begin{aligned} B \rightarrow \text {Spec}(k) \times _{\text {Spec}(k[\epsilon ])}\mathcal {B} \end{aligned}$$

is an isomorphism. There is a natural notion of isomorphism between first-order deformations, see [37, Section 1.2]. The set of first-order deformations, up to isomorphisms, is usually denoted by $T^1(B)$ and it has a natural structure of complex vector space (see [36]). If B has a semiuniversal deformation $\tilde{B} \rightarrow \text {Def}(B)$ then every first-order deformation is induced by a unique map $\text {Spec}(k[\epsilon ]) \rightarrow \text {Def}(B)$ and then there exists an isomorphisms of vector spaces

$$\begin{aligned} T_0\text {Def}_{B} \cong T^1(B) \cong H^1(B, T_B), \end{aligned}$$

for the last isomorphism see e.g. [37, Proposition 1.2.9].

Now, we look at deformations of subvarieties in a given variety. Given a closed embedding D in B, a first-order deformation of D in B (fixed) is a cartesian diagram

where $\pi$ is flat and it is induced by the projection from $B \times \text {Spec}(k[\epsilon ])$. Again we can give a cohomological interpretation to these deformations, indeed there is a natural identification between the first-order deformations of D in B and $H^0(D, \mathcal {N}_{D/B})$, where $\mathcal {N}_{D/B}$ is the normal sheaf of D in B, see e.g. [37, Proposition 3.2.1].

Before introducing the last two situations we are interested in, let us recall the following definition.

Definition 4.1

Let $D_1, \ldots ,D_k$ be divisors in a smooth variety X and let $x_1, \ldots ,x_k$ be local equations for them. Define $\Omega ^1_S(\log D_1, \ldots ,\log D_k)$ to be the subsheaf (as $\mathcal {O}_X$-module) of $\Omega ^1_X(D_1+ \ldots +D_k)$ generated by $\Omega ^1_X$ and by $\frac{dxj}{x_j}$ for $j=1, \ldots k$.

The next situation we want to look at is the case of deformation of a pair (B, D) where $j:D \hookrightarrow B$ is a closed embedding. The deformation theory of morphisms is more subtle if we want to allow both the domain and the target to deform nontrivially. A first-order deformation of the pair (D, B) is a commutative diagram

where $\pi _D$ and $\pi _B$ come from first deformations of D and B respectively and J is a closed embedding. There is a natural notion of isomorphism between first-order deformations of pairs see e.g. [37, Section 3.4]. We denote by $\text {Def}'_j$ the set of isomorphism classes of first-order deformations of the pair (B, D), which are locally trivial. Also in this case we have a cohomological interpretation, by [37, Proposition 3.4.17], $\text {Def}'_j$ has a formal semiuniversal deformation and its tangent space is isomorphic to $H^1( T_{B}( - \log D))$, where $T_{B}( - \log D)$ is the sheaf of germs of tangent vectors to B which are tangent to D.

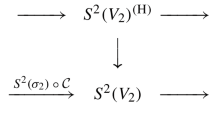
Finally, let us consider the following situation. Let B be a compact complex smooth surface, $p \in B$ and $\sigma :B' \rightarrow B$ the blow up of B in p with exceptional divisor E. Let D be an effective divisor on B which has multiplicity c in p. Moreover, let us denote by $D'=\sigma ^*(D)-cE$ the strict transform of D in $B'$ and assume that $D'$ is a smooth normal crossing divisor, meaning that each component is smooth, no three components share a point and the intersections between them are transversal. We want to describe the relation between the deformations of the pair $(B', \, D')$ with those of D in B.

We know that the first-order locally trivial deformations of the pair $(B', \, D')$ are parameterized by the vector space $H^1(T_{B'}( - \log D'))$. The natural map

$$\begin{aligned} \vartheta :H^1( T_{B'}( - \log D')) \rightarrow H^1(T_{B'}) \end{aligned}$$

corresponds to the forgetful map, which forgets the deformation of $D'$. By [21, Exercise 10.5] we have an exact sequence

$$\begin{aligned} 0 \rightarrow \sigma _*T_{B'} \rightarrow T_B \rightarrow T_pB \rightarrow 0 \end{aligned}$$

where $T_pB \cong \mathbb {C}^2$ is the tangent space of B in p seen as a skyscreaper sheaf concentrated in p. Then we consider the long exact sequence in cohomology and in particular the connecting homomorphism

$$\begin{aligned} \psi :T_pB \rightarrow H^1(\sigma _* T_{B'}) \cong H^1(T_{B'}). \end{aligned}$$

The next result give us a better understanding of the intersection between the images of the maps $\vartheta$ and $\psi$ in $H^1(T_{B'})$.

Theorem 4.2

Keeping the same notation as before, assume that D is smooth at p, so $c=1$, and choose an element $v \in T_pB$.

Then $\psi (v)$ is contained in $Im(\vartheta )$ if and only if the class of v in the normal vector space $T_pB/T_pD$ extends to a global section of the normal bundle $v_D \in H^0(D,{{\mathcal {N}}}_{D|B})$.

In particular v is tangent to D if and only if $v_D$ vanishes in p.

The idea of the proof is the following.

The image of $\vartheta$ corresponds to first-order deformations of $B'$ that contain a first-order deformation of $D'$. The image of $\psi$ corresponds, by the Kodaira–Spencer correspondence, to the first-order deformations of $B'$ obtained by moving the point p in B, thus allowing to project a first-order deformation of the pair $(B', \, D')$ to a first-order deformation of D in B (fixed), which are elements of $H^0(D,{{\mathcal {N}}}_{D|B})$. In the following we compute the value of $v_D$ at p, and see how it determines when the corresponding first-order deformation of D in B (fixed) lift to a first-order deformation of the pair $(B', \,D')$.

Proof

We start constructing a family of first-order deformations of $B'$.

Let U be an affine chart of B centered in p with local coordinates x, y such that $D=\{x=0\}$. We consider a section $s_{a,b}$ of the trivial family $B \times \text {Spec}(\mathbb {C}[\epsilon ]) \rightarrow \text {Spec}(\mathbb {C}[\epsilon ])$ whose image is contained in $U \times \text {Spec}(\mathbb {C}[\epsilon ])$

obtained by mapping $(x,y,\epsilon )$ to $(a\epsilon , b\epsilon , \epsilon )$, so that the image is locally the complete intersection

$$\begin{aligned} x-a\epsilon =y-b\epsilon =0. \end{aligned}$$

Blowing up this section we obtain the following families over $\text {Spec}(\mathbb {C}[\epsilon ])$

where $\Phi _{a,b}$ is a first-order deformation of $B'$. The Kodaira–Spencer correspondence associates to $\Phi _{a,b}$ a class in $\kappa \left( \Phi _{a,b} \right) \in H^1(B',T_{B'})$, its Kodaira–Spencer class. This can be explicitly computed: following e.g. the proof of [37, Proposition 1.2.9, p. 29] we find

$$\begin{aligned} \kappa \left( \Phi _{a,b} \right) =\psi \left( a\frac{\partial }{\partial x} + b\frac{\partial }{\partial y}\right) . \end{aligned}$$

The blown up chart $U'_{a,b}$ is the subscheme of $U \times \mathbb {P}^1 \times B \times \text {Spec}(\mathbb {C}[\epsilon ])$ defined by

$$\begin{aligned} Y(x-a\epsilon )=X(y-b\epsilon ), \end{aligned}$$

where (X, Y) are homogeneous coordinates on the factor $\mathbb {P}^1$. It is the union of two affine charts, given respectively by imposing $X \ne 0$ and $Y\ne 0$.

Let us work locally and restrict to the affine chart of $U'_{a,b}$ given by $Y\ne 0$, and let us introduce the new coordinate $z=\frac{X}{Y}$. Then, we can eliminate x by

$$\begin{aligned} x=zy+(a-bz)\epsilon \end{aligned}$$

and the exceptional divisor $\mathcal {E}$ of the blow-up is $\{y-b\epsilon =0\}$ in the coordinates y, z.

Since $D=\{x=0\}$, the strict transform of D on $B'$ is, in the coordinates y, z, the divisor $D'=\{z=0\}$. Now, $\kappa \left( \Phi _{a,b}\right)$ is in the image of $\vartheta$ if and only if $D'$ can be extended to a divisor $\mathcal {D}'_{a,b}$ in $\mathcal {B}'_{a,b}$. The image of $\mathcal {D}'_{a,b}$ in $B \times \text {Spec}(\mathbb {C}[\epsilon ])$ is

$$\begin{aligned} \mathcal {D}_{a,b}=\{x+\delta (x,y) \epsilon =0\}, \end{aligned}$$

an first-order deformation of D in B over $\text {Spec}\left( {{\mathbb {C}}}[\epsilon ]\right)$ so that $\delta (x,y)$ is the affine trace of a global section of the normal bundle ${{\mathcal {N}}}_{D|B}$, an element $\delta \in H^0(D,{{\mathcal {N}}}_{D|B})$ ([37, Proposition 3.2.1]), locally given by the class of a vector field $\delta (x,y)\frac{\partial }{\partial x}$.

The pullback of $\mathcal {D}_{a,b}$ on $\mathcal {B}'_{a,b}$ contains the exceptional divisor $\mathcal {E}$, thus

$$\begin{aligned} y-b \epsilon \text { divides } zy+(a-bz-\delta (zy,y) )\epsilon =z(y-b\epsilon ) + (a-\delta (zy,y) )\epsilon , \end{aligned}$$

that implies $\delta (0,0)=a$. Conversely, if $\delta (0,0)=a$ the pull-back of $\mathcal {D}_{a,b}$ contains $\mathcal {E}$ and then its strict transform gives an extension ${{\mathcal {D}}}'_{a,b}$ of $D'$ in $\mathcal {B}'_{a,b}$.

Since the class of $v= a\frac{\partial }{\partial x} + b\frac{\partial }{\partial y}$ in $T_pB/T_pD$ equals the class of $a\frac{\partial }{\partial x}$, then $\psi \left( v \right)$ is in the image of $\theta$ if and only if there is some $\delta \in H^0(B,{{\mathcal {N}}}_{D|B})$ whose value at p is the class of v. $\square$

The situation is even simpler if D is a rigid divisor.

Corollary 4.3

Let D be a divisor which is smooth at p and $H^0(D,\mathcal {O}_D(D))=0$. Let $v \in T_pB$ such that $\psi (v) \in Im (\vartheta )$. Then v is tangent to D.

Keeping the same notation as above, the application we have in mind for the next can be summarized in

Proposition 4.4

Let $B' \rightarrow B$ the blow up of B in p and $D'$ the strict transform of D a divisor passing through p. Let us further suppose that $D \ge D_1 + D_2$ with $D_1$ and $D_2$ smooth and transversal in p. Moreover, let us assume that $H^0(D_i,\mathcal {O}_{D_i}(D_i))=0$ for $i=1,2$. Then

$$\begin{aligned} \vartheta ( H^1(B', \, T_{B'}( - \log D'))) \cap \psi (T_pB) = \{ 0 \} . \end{aligned}$$

(5)

Proof

We have that $\vartheta$ factors through the analogous map for $D_j$, $j=1,2$:

$$\begin{aligned} H^1(T_{B'}(-\log (D'))) \rightarrow H^1(T_{B'}(-\log (D_j))) \rightarrow H^1(B',T_{B'}) \qquad \text { for } j=1,2. \end{aligned}$$

Hence, the image of $\vartheta$ is contained in the image of both $H^1(T_{B'}(-\log (D_j)))$ for $j=1,2$. Than we apply the Corollary 4.3 and we obtain a vector v which is tangent to both $D_1$ and $D_2$. Finally, observe that if a vector is tangent to two transversal curves must vanish. $\square$

Corollary 4.5

Let D be as in Proposition 4.4 and suppose moreover $H^0(D', \mathcal {O}_{D'}(D'))=0$. Then the composition

$$\begin{aligned} H^1(B', T_{B'}(-\log D')) \rightarrow H^1(B,T_{B}) \end{aligned}$$

is injective.

Proof

The proof follows directly from the Proposition 4.4 and the following diagram with exact row and column.

$\square$

We conclude the section with the following general result.

Lemma 4.6

Let A be an abelian surface isogenous to a product of elliptic curves $T_1 \times T_2$. Let $H \subset H^1(T_A)$ be the linear subspace corresponding to the projective deformations of A and let $H_j \subset H^1(T_A)$ be the linear subspaces corresponding to the deformations preserving the fibration $A \longrightarrow T_j$ for $j=1,2$. Then H, $H_1$ and $H_2$ are three different hyperplanes such that the intersection of any two of them is contained in the third.

Proof

The isogeny maps $H^1(T_A)$ isomorphically to $H^1(T_{T_1\times T_2})$ by a map preserving H, $H_1$ and $H_2$. Therefore we may assume without loss of generality $A=T_1 \times T_2$.

For a product of curves the period matrix assumes the form

$$\begin{aligned} \Lambda \,=\,\Omega \,\mathbb {Z}^4,\quad \Omega \,:\,\mathbb {Z}^4\,\longrightarrow \,\mathbb {C}^2,\qquad x\,\longmapsto \, \Omega \,x= \left( \begin{array}{cc|cc} 1 &{} 0 &{} \alpha &{} 0 \\ 0 &{} 1 &{} 0 &{} \delta \end{array} \right) \end{aligned}$$

It is well known that one can identify the deformation space $H^1(T_A)$ of a polarized abelian surface $A = V/\Lambda$ with the space of the square matrices (see [22, Chapter 1]). For $\begin{pmatrix} a&{}b\\ c&{}d\\ \end{pmatrix}$ we obtain the deformation given by

$$\begin{aligned} \left( \begin{array}{c|c} \Delta _1&\tau \end{array} \right) = \left( \begin{array}{cc|cc} 1 &{} 0 &{} \alpha +a\epsilon &{} b\epsilon \\ 0 &{} 1 &{} c\epsilon &{} \delta +d\epsilon \end{array} \right) . \end{aligned}$$

The Riemann–Conditions for an abelian surface with a principal polarization yields the existence of an integral basis $\{\lambda _i\}_{i}$ for $\Lambda$ and a complex basis $\{e_i\}$ for V such that the period matrix can be normalized so that the matrix $\tau$ is symmetric with positive definite imaginary part (see [18] p.306). The symmetry condition yields $b=c$, whereas the positive definiteness, being an open condition, does not give any condition on $\begin{pmatrix} a&{}b\\ c&{}d\\ \end{pmatrix}$. So

$$\begin{aligned} H=\{b=c\}. \end{aligned}$$

The subspaces $H_j$ are respectively

$$\begin{aligned} b&=0&c&=0 \end{aligned}$$

and this concludes the lemma. $\square$

5 The moduli space

The following result can be found in [13, Section 5].

Proposition 5.1

Let S be a minimal surface of general type with $q(S) \ge 2$ and Albanese map $\alpha :S \rightarrow A$, and assume that $\alpha (S)$ is a surface. Then this is a topological property. If in addition $q(S)=2$, then the degree of $\alpha$ is a topological invariant.

Proof

By [10] the Albanese map $\alpha$ induces a homomorphism of cohomology algebras

$$\begin{aligned} \alpha ^*:H^*(\text {Alb}(S), \, \mathbb {Z}) \longrightarrow H^*(S, \, \mathbb {Z}) \end{aligned}$$

and $H^*(\text {Alb}(S), \mathbb {Z})$ is isomorphic to the full exterior algebra

$$\begin{aligned} \bigwedge ^* H^1(\text {Alb}(S), \, \mathbb {Z}))\cong \bigwedge ^* H^1(S, \, \mathbb {Z}). \end{aligned}$$

In particular, if $q=2$ the degree of the Albanese map equals the index of the image of $\bigwedge ^4 H^1(S, \, \mathbb {Z})$ inside $H^4(S, \, \mathbb {Z})$ and it is therefore a topological invariant. $\square$

Consider a surface S in ${{\mathcal {M}}}$. By Proposition 5.1 it follows that one may study the deformations of S by relating them to those of the flat double cover $\beta :S' \rightarrow B'$. By [37, p. 162] we have an exact sequence

$$\begin{aligned} 0 \longrightarrow T_{S'} \longrightarrow \beta ^{*}T_{B'} \longrightarrow \mathcal {N}_{\beta } \longrightarrow 0, \end{aligned}$$

(6)

where $\mathcal {N}_{\beta }$ is a coherent sheaf supported on the ramification divisor $\hat{R}+\hat{C_1}+\hat{E}$ called the normal sheaf of $\beta$ (cfr. Fig. 4).

Lemma 5.2

Keeping the notation above it holds

$$\begin{aligned} H^i(S',\mathcal {N}_{\beta })= H^i(\mathcal {O}_{\hat{R}}(2\hat{R})) \oplus H^i(\mathcal {O}_{\hat{C_1}}(2\hat{C_1})) \oplus H^i(\mathcal {O}_{\hat{E}}(2\hat{E})), \, i=0,1. \end{aligned}$$

(7)

Moreover we have:

$$\begin{aligned} h^0\big (\mathcal {O}_{\hat{R}}(2\hat{R})\big )= & {} 0, \quad h^0\big (\mathcal {O}_{\hat{C_1}}(2\hat{C_1})\big )=0, \quad h^0\big (\mathcal {O}_{\hat{E}}(2\hat{E})\big )=0,\\ h^1\big (\mathcal {O}_{\hat{R}}(2\hat{R})\big )= & {} 2,\quad h^1\big (\mathcal {O}_{\hat{C_1}}(2\hat{C_1})\big )=2, \quad h^1\big (\mathcal {O}_{\hat{E}}(2\hat{E})\big )=1. \end{aligned}$$

Proof

The ramification divisor of the double cover $\beta :S' \longrightarrow B$ is the disjoint union of the divisors $\hat{E}$, $\hat{R}$ and $\hat{C_1}$, this is enough for (7).

Since $\hat{C}$ is an elliptic curve with $\hat{C}^2=-1$, we have that $2\hat{C}$ is not effective on $\hat{C}$ and by Riemann–Roch we conclude that $h^1\big (\mathcal {O}_{\hat{C_1}}(2\hat{C_1})\big )=2$.

The computations for $\hat{E} \cong \mathbb {P}^1$ are straightforward.

Finally we work on $\hat{R}$. Recall that $g(\hat{R})=3$ and $\hat{R}^2=0$. Thus, by Riemann–Roch we have $\chi \big (\mathcal {O}_{\hat{R}}(2\hat{R})\big )=-2$. Therefore, it is sufficient to prove that $h^0\big (\mathcal {O}_{\hat{R}}(2\hat{R})\big )=0$.

We notice that $\beta ^*R=2\hat{R}$, and $\beta |_{\hat{R}}:\hat{R} \rightarrow R$ is an isomorphism. Then, $H^0(\mathcal {O}_{\hat{R}}(2\hat{R}))=H^0(\mathcal {O}_R(R))=H^0(\mathcal {N}_{R|B})$. Recall that by adjunction the normal bundle of a curve in an abelian surface equals its canonical bundle, so $\mathcal {N}_{t|A}=\omega _t$. The map $\nu =(\sigma _4 \circ \sigma _3)|_R:R \longrightarrow t$ is the normalization of t. Let $q_1, q_2 \in R$ such that $\nu (q_i)=p$ with $i=1,2$ and recall that p is the tacnode of t. We have

$$\begin{aligned} \omega _R = \nu ^*\omega _t \otimes \mathcal {O}_R(-2q_1-2q_2), \quad \mathcal {\mathcal {N}}_{R|B} = \nu ^*\mathcal {N}_{t|A}\otimes \mathcal {O}_R(-4q_1-4q_2), \end{aligned}$$

this yields

$$\begin{aligned} \mathcal {N}_{R|B} = \omega _R \otimes \mathcal {O}_R(-2q_1-2q_2). \end{aligned}$$

(8)

By construction R is a smooth irreducible curve of genus 3 with a $(\mathbb {Z}/2\mathbb {Z})^2$-action, by [5, Lemma 2.15] R is not hyperelliptic and all 3 involutions are bielliptic, hence all the three double quotients are elliptic curves. Thus, choosing a bases of $H^0(R, K_R)$ coming from the 1-forms of each elliptic curve, we obtain an embedding of R as a plane quartic curve geometrical invariant under the action

$$\begin{aligned} (x_0 : x_1 : x_2) \mapsto (\pm x_0, \pm x_1, \pm x_2). \end{aligned}$$

The quartic equation defining it it is biquadratic equation, in fact we notice that the stabilizer of the coordinate point $(1: \, 0: \, 0)$, is not cyclic hence it cannot be contained in R. Therefore, the monomial $x_0^4$ has non trivial coefficient and so the equation is invariant (biquadratic).

Since the divisor $q_1 + q_2$ is invariant, then $q_1$ and $q_2$ have a stabilizer of order 2 and lie on a coordinate line $x_j$. Assume $j=0$ for simplicity,

By (8)

$$\begin{aligned} H^0(\mathcal {O}_{\hat{R}}(2\hat{R})) \ne 0 \Leftrightarrow (x_0) \text { is a bitangent} \end{aligned}$$

Let $q'_1:=(0:k_1:k_2)$ be the image of $q_1$ (observe that $k_1 \ne 0$ and $k_2 \ne 0$ otherwise the stabilizer of $q_1$ would be not-cyclic), so the ideal $(x_0, k_1x_2- k_2x_1)$ is the defining ideal of the point $q'_1$. Assume by contradiction $x_0$ to be a bitangent in $q'_1$. Then the quartic equation defining R is contained in the ideal $(x_0, (k_1x_2- k_2x_1)^2 )$. Being biquadratic yields that R is contained in the ideal $(x^2_0, (k_1x^2_2- k_2x^2_1)^2 )$. This implies that R is singular in $q_1$ but this is absurd. $\square$

Recall that $S'$ is a surfaces of general type, hence $h^0(T_{S'})=0$ and using the bit of information of the previous lemma, the sequence (6) induces the following long sequence in cohomology.

$$\begin{aligned} 0 \longrightarrow H^1(T_{S'}) \longrightarrow H^1(\beta ^{*}T_{B'}) \longrightarrow H^1(\mathcal {N}_{\beta }) \longrightarrow H^2(T_{S'}) \longrightarrow H^2(\beta ^{*}T_B) \longrightarrow 0. \end{aligned}$$

Proposition 5.3

Keeping the notation as above, then the sheaf $\beta ^*T_{B'}$ satisfies

$$\begin{aligned} \begin{aligned} h^0(S',\beta ^*T_{B'})=&h^0(B', T_{B'} \otimes \mathcal {L}_{B'}^{-1}), \\ h^1(S',\beta ^*T_{B'})=&6+h^1(B', T_{B'} \otimes \mathcal {L}_{B'}^{-1}), \\ h^2(S', \,\beta ^*T_{B'})=&2+h^2(B', T_{B'} \otimes \mathcal {L}_{B'}^{-1}). \end{aligned} \end{aligned}$$

Proof

Since $\beta :S' \rightarrow B'$ is a finite map, by using projection formula and the Leray spectral sequence we deduce

$$\begin{aligned} h^i(S', \, \mathcal {O}_{S'})=h^i(B', \, \mathcal {O}_{B'})+h^i(B', \, \mathcal {L}_{B'}^{-1}), \quad i=0,\,1,\,2. \end{aligned}$$

Recall that $p_g(S')=q(S')=2$ and $B'$ is an abelian surface blown up twice, then we have

$$\begin{aligned} h^0(B', \, \mathcal {L}_{B'}^{-1})=0, \quad h^1(B,\, \mathcal {L}_{B'}^{-1})=0, \quad h^2(B', \, \mathcal {L}_{B'}^{-1})=1, \end{aligned}$$

(9)

By the same argument above we have

$$\begin{aligned} h^i(S', \, \beta ^*T_{B'})=h^i(B', \, \beta _* \beta ^* T_{B'})=h^i(B', \, T_{B'})+h^i(B', \, T_{B'} \otimes \mathcal {L}_{B'}^{-1}), \quad i=0,\,1,\,2. \end{aligned}$$

We look first at $\sigma _3$. There is a short exact sequence

$$\begin{aligned} 0 \longrightarrow T_{B} \rightarrow \sigma _3^*T_A \rightarrow \mathcal {O}_E(-E) \rightarrow 0, \end{aligned}$$

(10)

see [37, p. 73] for the general setting of a blow up. Then a direct computation shows

$$\begin{aligned} h^0(B, \, T_{B})=0, \quad h^1(B, \, T_{B})=4, \quad h^2(B, \, T_{B})=2. \end{aligned}$$

The analogous computation for $\sigma _4$, for the exact sequence

$$\begin{aligned} 0 \longrightarrow T_{B'} \rightarrow \sigma _4^*T_{B} \rightarrow \mathcal {O}_F(-F) \rightarrow 0. \end{aligned}$$

(11)

yields

$$\begin{aligned} h^0(B', \, T_{B'})=0, \quad h^1(B', \, T_{B'})=6, \quad h^2(B', \, T_{B'})=2. \end{aligned}$$

Therefore the claim follows.

$\square$

Let us consider the exact sequence

$$\begin{aligned} 0 \longrightarrow T_{B'} \rightarrow (\sigma _4 \circ \sigma _3)^*T_{A} \rightarrow \mathcal {N}_{\sigma _4 \circ \sigma _3} \rightarrow 0, \end{aligned}$$

(12)

where the last sheaf is supported on E and F. We tensor (12) by $\mathcal {L}^{-1}_{B'}$ and we obtain the sequence

$$\begin{aligned} 0 \longrightarrow T_{B'} \otimes \mathcal {L}^{-1}_{B'} \rightarrow (\mathcal {L}^{-1}_{B'})^{\oplus 2} \rightarrow \mathcal {N}_{\sigma _4 \circ \sigma _3} \otimes \mathcal {L}^{-1}_{B'} \rightarrow 0. \end{aligned}$$

Considering the induced long exact sequence in cohomology, by (9) we get

$$\begin{aligned} h^0\big (T_{B'} \otimes \mathcal {L}^{-1}_{B'} \big )= & {} 0 \end{aligned}$$

(13)

$$\begin{aligned} h^1\big (T_{B'} \otimes \mathcal {L}^{-1}_{B'} \big )= & {} h^0\big (\mathcal {N}_{\sigma _4 \circ \sigma _3} \otimes \mathcal {L}^{-1}_{B'}\big ) \end{aligned}$$

(14)

and

$$\begin{aligned} h^2\big (T_{B'} \otimes \mathcal {L}^{-1}_{B'} \big ) = h^1\big (\mathcal {N}_{\sigma _4 \circ \sigma _3} \otimes \mathcal {L}^{-1}_{B'}\big ) +2 \end{aligned}$$

(15)

Lemma 5.4

It holds

$$\begin{aligned} h^0\big (\mathcal {N}_{\sigma _4 \circ \sigma _3} \otimes \mathcal {L}^{-1}_{B'}\big ) =2. \end{aligned}$$

Proof

Recall that we set $E'=\sigma ^*_4E$. Let us consider the exact sequence (10), it lifts on $B'$ as

$$\begin{aligned} 0 \rightarrow \sigma _4^*T_B \rightarrow \mathcal {O}_{B'}^{\oplus 2} \rightarrow \sigma _4^*\mathcal {O}_{E}(-E)\rightarrow 0. \end{aligned}$$

We put this last exact sequence together with (11) as respectively the middle horizontal sequence and the first vertical sequence in a diagram. Chasing the diagram we obtain the following

(16)

which is a diagram with exact rows and columns. Let us look at the last horizontal sequence. Recall that $F \cong \mathbb {P}^1 \cong E'$, thus $\mathcal {O}_{F}(-F) \cong \mathcal {O}_{\mathbb {P}^1}(1)$ and $\mathcal {O}_{E'}(-E') \cong \mathcal {O}_{\mathbb {P}^1}(1)$. Moreover, the sheaf $\sigma _4^*(\mathcal {O}_{E}(-E))$ is locally free and it is supported on $F \cup E'$. Its restriction to the irreducible components are

$$\begin{aligned} \sigma _4^*(\mathcal {O}_{E}(-E))|_{E'}&\cong \mathcal {O}_{\mathbb {P}^1}(1),&\sigma _4^*(\mathcal {O}_{E}(-E))|_F&\cong \mathcal {O}_{\mathbb {P}^1}. \end{aligned}$$

We tensor the last horizontal sequence in (16) by $\mathcal {L}_B^{-1} \cong \mathcal {O}_{B'}(R+E'+C_1)$ and we get

$$\begin{aligned} 0 \rightarrow \mathcal {O}_{\mathbb {P}^1}(-1) \rightarrow \mathcal {N}_{\sigma _4 \circ \sigma _3} \otimes \mathcal {L}_{B'}^{-1} \rightarrow \sigma _4^*(\mathcal {O}_{E}(-E)) \otimes \mathcal {L}_{B'}^{-1} \rightarrow 0. \end{aligned}$$

The long exact sequence in cohomology yields

$$\begin{aligned} H^i(\mathcal {N}_{\sigma _4 \circ \sigma _3} \otimes \mathcal {L}_{B'}^{-1}) \cong H^i(\sigma _4^*(\mathcal {O}_{E}(-E)) \otimes \mathcal {L}_{B'}^{-1}), \qquad \text {for all} \, i. \end{aligned}$$

By the intersection computation

$$\begin{aligned} (R+E'+C_1)E'=-2 \text { and } (R+E'+C_1)F=4 \end{aligned}$$

the sheaf $\sigma _4^*(\mathcal {O}_{E}(-E)) \otimes \mathcal {L}_{B'}^{-1}$ is a locally free sheaf on $E' \cup F$ which has degree $-1$ on F and degree 2 on $E'$. Hence its global sections vanish on F. Fixing an isomorphism $E' \cong \mathbb {P}^1$, we obtain an isomorphism between $H^0(\sigma _4^*(\mathcal {O}_{E}(-E)) \otimes \mathcal {L}_{B'}^{-1})$ and the subspace of $H^0(\mathcal {O}_{\mathbb {P}^1}(2))$ given by the sections which vanish on the point $E' \cup F$.

Thus

$$\begin{aligned} H^0\big (\mathcal {N}_{\sigma _4 \circ \sigma _3} \otimes \mathcal {L}^{-1}_{B'}\big ) \cong H^0(\mathcal {O}_{\mathbb {P}^1}(1)) \cong \mathbb {C}^2. \end{aligned}$$

$\square$

Remark 5.5

Let $q\in S$ be the point blown-up by $S' \rightarrow S$. The short exact sequence obtained pushing forward (6) produces a cohomology exact sequence

$$\begin{aligned} 0 \rightarrow T_q S \rightarrow H^1(S',T_{S'}) \rightarrow H^1(S,T_S) \rightarrow 0. \end{aligned}$$

Recall that if $\beta :S' \longrightarrow B'$ is a finite double cover, then $H^1(S',T_{S'})= H^1(B',\beta _* T_{S'})$ splits as invariant and anti-invariant part. Since q is an isolated fixed point of the involution induced by the Albanese map, it acts as the multiplication by $-1$ on $T_qS$ and then the image of $T_qS$ is contained in $H^1 (S',T_{S'})^-$. By (e.g. Pardini [24, Lemma 4.2]) we have

$$\begin{aligned} (\beta _*T_{S'})^+&\cong T_{B'}(-\log (R+E'+C_1))&(\beta _*T_{S'})^-&\cong T_{B'} \otimes \mathcal {L}^{-1}_{B'} \end{aligned}$$

By the Lemmas 5.4 and (14) then $h^1 (\beta _*T_{S'})^- =2$, and so $T_qS$ maps isomorphically onto $H^1 (S',T_{S'})^-$.

In particular the map

$$\begin{aligned} H^1(B',T_{B'}(-\log (R+E'+C_1))) \rightarrow H^1(S, T_S), \end{aligned}$$

is an isomorphism. Geometrically, this means that we have a bijection between the first-order deformations of S and the first-order deformations of the pair $(B', R+E'+C_1)$.

Remark 5.6

Corollary 4.5 applies to the blow-up $\sigma _4 :B' \rightarrow B$ with $D'=R+E'+C_1$ since all required rigidites have been proved in Lemma 5.2.

So the natural map

$$\begin{aligned} H^1\big (T_{B'}(-\log (R+E'+C_1)) \big ) \hookrightarrow H^1\big (T_{B} \big ) \end{aligned}$$

is injective. Since the map $H^1\big (T_{B} \big ) \rightarrow H^1\big (T_{A} \big )$ is an isomorphism,

$$\begin{aligned} H^1\big (T_{B'}(-\log (R+E'+C_1)) \big ) \hookrightarrow H^1\big (T_{A} \big ). \end{aligned}$$

is injective as well.

Hence we have a commutative diagram

The left vertical map is an isomorphism by Remark 5.5. The composition of the top horizontal arrow and the right vertical arrow is the map in Remark 5.6, so injective, and therefore the lower horizontal map is injective.

Proposition 5.7

It holds

$$\begin{aligned} h^1(T_S)=2. \end{aligned}$$

Proof

The image of the map $H^1(T_S) \rightarrow H^1(T_A)$ is contained in the hyperplane H of Lemma 4.6, since the Albanese variety of every surface of general type is an abelian variety.

We proved that $H^1(T_{B'}(-\log ((R+E'+C_1))) \cong H^1(T_S)$ and the induced map $\varphi :H^1(T_{B'}(-\log (R+E'+C_1))) \rightarrow H^1(T_A)$ is injective. So it is enough to prove $\dim Im(\varphi )=2$

The function $\varphi$ factorizes as in the following commutative diagram.

where $C_1$ is the elliptic curve in Fig. 4. We recall that A is isogenous to the product of two elliptic curves $T_1 \times T_2$ and $C_1$ is a fibre of the induced elliptic fibration $f_2$ on $T_2$.

So the image of $\epsilon$ is contained in $H_2$. Then $Im(\varphi ) \subset H \cap H_2$ has, by Lemma 4.6, dimension at most 2. On the other hand it is at least 2 by Proposition 3.3, and therefore it equals 2. $\square$

Proposition 5.8

The following holds: for all $j \in \{1,2,4\}$ $\mathcal {M}_j$ is a generically smooth irreducible component of the moduli space of the surfaces of general type of dimension 2.

Proof

We have shown that $\mathcal {M}_j$ is irreducible of dimension 2 in Proposition 3.14. Then by Proposition 5.7$\text {Def}(S)$ is smooth of dimension 2 at each point. It follows that $\mathcal {M}_j$ is an irreducible component, and that this component is generically smooth. $\square$