Abstract
Recently, the discrete element method is increasingly being used for describing the behaviour of isotropic linear elastic materials. However, the common bond models employed to describe the interaction between particles restrict the range of Poisson’s ratio that can be represented. In this paper, to overcome the restriction, a modified bond model that includes the coupling of shear strain energy of neighbouring bonds is proposed. The coupling is described by a multi-bond term that enables the model to distinguish between shear deformations and rigid-body rotations. The positive definiteness of the strain energy function of the modified bond model is verified. To validate the model, uniaxial tension, pure shear and pure bending tests are performed. Comparison of the particle displacements with continuum mechanics solution demonstrates the ability of the model to describe the behaviour of isotropic linear elastic material for values of Poisson’s ratio in the range \(0 \le \nu < 0.5\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The discrete element method (DEM) was initially developed by Cundall [5] for modelling the motion of granular media. However, beginning with the twenty-first century, several works [1, 9, 10, 13, 15, 19, 21, 24] that employ DEM not only to model the linear elastic behaviour of materials, but also for their subsequent crack initiation and propagation have been carried out. Recently, DEM has also been employed to model chemical–thermal–mechanical coupled problem for concrete by Flack [7]. In this regard, as pointed out in the work by Celigueta [4], DEM is to be understood as a discretisation scheme for the continuum, where the immediate neighbouring particles exchange forces through a bond model. The particles remain bonded to each other as long as a critical bond extension is reached, after which a bond cannot transfer forces and is therefore considered broken. In this way, DEM allows for an inherent description of evolution of spontaneous discontinuity without the need for remeshing.
Although the DEM provides a good qualitative description of the crack initiation and subsequent propagation as shown in the works [13, 15, 19, 24], the range of Poisson’s ratio of materials that can be represented are usually restricted to \(0 \le \nu \le 0.25\). This restriction has also been discussed in the following works [4, 7, 10, 14, 15]. Apart from the restricted range of Poisson’s ratio, the response of materials observed within this range are also stiffer in comparison with the solution obtained by continuum mechanics. This behaviour is especially pronounced in bending dominated problems. Such restrictions have also been observed in other bond-based methods such as the Lattice methods as discussed in the work of Ostoja-Starzewski [17]. In order to overcome this restriction and with the argument that an accurate description of material behaviour in the elastic region is a prerequisite for a subsequent qualitative and quantitative description of fracture, two different approaches have been proposed within the framework of DEM [4, 14, 18]. Both of these approaches conclude that a simple bond model, such as a Born model [2], that is commonly employed in DEM and other bond-based methods to describe the interaction of force between particles cannot accurately capture the elastic behaviour of continuum.
Celigueta [4] proposed a nonlocal contact law for the DEM, where apart from the overlap of two interacting particles in contact also the influence of forces in the surrounding of this contact is included. By means of this term a better description of continuum elasticity was obtained in comparison to the classical bond model of DEM. However, in order to calculate this term, information regarding the contact area between two particles in contact and their surrounding is required. Additionally, the nonlocal stress tensor of each particle and its neighbours is required which results in a computationally expensive method. An alternate approach that also includes the deformation of particles, called the deformable discrete element method (DDEM) was proposed in [14, 18]. Unlike the classical approaches in DEM and also that proposed by Celigueta [4], where the particles are considered to be rigid, this new formulation also incorporates the elastic deformation of particles and its subsequent implication on the change of contact overlap to widen the range of Poisson’s ratio that can be represented. Although this approach allows for the representation of a broader range of Poisson’s ratio than the commonly employed bond models in DEM, the exact limit of this approach regarding macroscopic Poisson’s ratio is not explicitly stated.
In contrast to the approaches mentioned, in this work an approach is proposed that shows that Poisson’s ratio in the range \(0 \le \nu < 0.5\) and a sufficiently accurate description of the elastic behaviour of continuum, also under bending, is possible by employing simple bond models as well. In this work, a modification of the Born model is proposed by introducing a multi-bond strain energy term that is capable of distinguishing between shear deformation and rigid-body rotation for the case of two-dimensional elasticity. Two new multi-bonds called L-bond and X-bond employing the proposed coupling of shear strain energy are introduced. Based on the positive definiteness of the strain energy function, we also interpret that the restriction of the Born model up to a certain Poisson’s ratio results from incapability to distinguish between shear deformation and rigid-body rotation. With the modified model it is shown that the strain energy function remains positive definite for values of Poisson’s ratio in the range \(0 \le \nu < 0.5\). To validate the modified model, the results of a thin plate under uniaxial tension, pure shear and pure bending are compared with the respective plane stress continuum mechanics solution.
2 Unit-cells with Born model
An arbitrary rectangular domain discretised with rigid circular particles of radius r is shown in Fig. 1a. Each particle is bonded with its immediate neighbours (separated by length \(l = 2r\)) and also with its second neighbours (separated by length \(l = 2 \sqrt{2} r\)). Similar to the works [10, 16], the fundamental building block called as a unit-cell is extracted from the discretised domain and is shown in Fig. 1b. This square unit-cell is the combination of two unit-cells: one which contains only the bonds with the immediate neighbours and another that contains only the bonds between second neighbours. They are called first-neighbour and second-neighbour unit-cells as shown in Fig. 1c, d, respectively. Although the fundamental idea behind the modification proposed in this paper is general, as a first approach we restrict ourselves to regular configuration such as a square, or an equilateral triangle or a hexagon where the length of bonds are equal. In particular, the square configuration is used here due to its simplicity. The extension of this modification to configurations with unequal bond lengths (as in the case of a random discretisation) is to be carried out as future work. The Born model which is applied here employs springs in normal direction and tangential direction with stiffness parameters \(k_{n}\) and \(k_{s}\) as shown in Fig. 2a. A generic bond oriented at angle \(\theta \) to the global coordinate system along with its local and global displacement components is shown in Fig. 2b.
Regarding Fig. 2a, the strain energy stored in the bond \(\varPi _{b}\) is given in terms of quantities with respect to the bond coordinate system as
where \(\epsilon _{nn} = \frac{u_{B}^{n} - u_{A}^{n}}{l}\) and \(\epsilon _{sn} = \frac{v_{B}^{s} - v_{A}^{s}}{l}\) are the local longitudinal and shear strain, respectively, and l is the length of the undeformed bond.
After substituting the local strain quantities in terms of the components of the global strain tensor by the transformation relations provided by Griffiths [10] the strain energy in a bond is obtained as
where \(c = \cos \theta \) and \(s = \sin \theta \). By substituting the orientation \(\theta \) of the individual constituent bonds in Eq. (3), the strain energy in the first and second neighbour unit-cells are obtained as
where \(k_{n_{1}}^{b}\), \(k_{s_{1}}^{b}\) are the normal and shear stiffness of first neighbour bonds and similarly \(k_{n_{2}}^{b}\), \(k_{s_{2}}^{b}\) are the stiffness parameters of second neighbour bonds. For a unique calibration of stiffness parameters to model linear elastic isotropic material behaviour for all values of \(\nu \), Ockelmann [15, 16] shows that three independent stiffness parameters are required to satisfy the three unique tensor components of the planar elasticity matrix as explained later in Sect. 4.1. Therefore, in order to reduce the number of unknown stiffness parameters to three, we suppose that the shear stiffness parameters of the first and second neighbour bond must be the same, that is, \(k_{s_{2}}^{b} = k_{s_{1}}^{b}\). This assumption is purely made from the point of view of having a deterministic calibration of the stiffness parameters similar to the works [15, 16]. A study on the other possibilities to reduce the number of independent stiffness parameters to three and their possible effects is regarded as an opportunity for further investigation in this direction and not pursued here. However, in “Appendix A” we show by means of the eigenvalues of the unit-cell that the fundamental characteristics of the system as discussed in Sect. 4.3 must hold true for other reduction possibilities as well.
Every bond in the first neighbour unit-cell contributes only 1/2 to the strain energy of the unit-cell due to periodicity (every first neighbour bond is shared by two unit-cells). However the bonds in the second neighbour unit-cell belong completely to a single unit-cell. The strain energy density of the square unit-cell is given by
where t is the thickness of the domain.
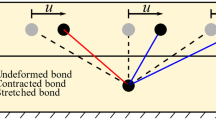
As described before, the Born model cannot distinguish between rigid-body rotation and shear [3, 11, 12, 23]. In Fig. 3a an exploded view of each constituent bond of the unit-cell with first neighbour bonds is shown along with its local and global shear strains. The bonds are assembled back together in Fig. 3b and one observes that although the final geometry describes pure rotation, the strain energy is not zero. Thus strain energy is stored in the unit-cell due to shear of individual bonds although all angles subtended between neighbour bonds are \(90^{\circ }\). This can also be observed in Eq. (4) where the contribution of shear strain energy \(\varPi _{uc_{1}}^\mathrm{shear}\) remains non-zero for any combination of \(\epsilon _{xy}\) and \(\epsilon _{yx}\) except for the trivial case where \(\epsilon _{xy} = \epsilon _{yx} = 0\). This interpretation holds also for the unit-cell with the second neighbour bonds as shown in Fig. 3c, d.
3 Modified bond model
To overcome the limitations explained in Sect. 2, a modified model is proposed where the shear strains of two neighbour bonds (multi-bond) are coupled. With this coupling, strain energy is stored only in the case of shear and not in the case of rotation. Here again, the unit-cell made up of only the first neighbour bonds is looked at first and the unit-cell made up of the second neighbour bonds afterwards.
3.1 L-bond
For a generic L-bond ABC made up of two first neighbour bonds AB and BC as shown in Fig. 4a, the strain energy due to normal strain remains unchanged as before. However the shear strains are combined in such a way that strain energy is stored only for shear deformation and not for rigid-body rotation. The strain energy stored in a generic L-bond with length \(l_{AB} = l_{BC} = l\) is given by
where \(k_{n_{1}}^{m}\) and \(k_{s_{1}}^{m}\) are the normal stiffness and shear stiffness parameters employing the modified model respectively.
The first neighbour unit-cell is now made up of four L-bonds as shown in Fig. 4b. As explained in Sect. 2, a first neighbour bond has a contribution factor of 1/2. Every bond in the unit-cell is obtained by the combination of two L-bonds. For example, the Bond AB is obtained from DAB and ABC. Therefore, in an L-bond the normal stiffness \(k_{n_{1}}^{m}\) and the shear stiffness \(k_{s_{1}}^{m}\) have a contribution factor of 1/4. With the transformation relations provided by Griffiths [10], the local strain components are written in terms of the global strain components and the strain energy of a generic L-bond now yields
where \(c_{AB} = \cos \theta _{AB}\), \(s_{AB} = \sin \theta _{AB}\), \(c_{BC} = \cos \theta _{BC}\) and \(s_{BC} = \sin \theta _{BC}\). Employing the modified bond model, the strain energy stored in the first neighbour unit-cell is obtained from the sum of strain energy stored in individual L-bonds
The strain energy stored in the first neighbour unit-cell employing the modified bond model can be evaluated with respect to the global coordinate system to
Comparing the formulation to that of the first neighbour unit-cell employing the Born model, see Eq. (4), an extra term is added due to the coupling of the shear strain energies of the neighbours. With this term, the modified model is able to distinguish between shear (change in the angle subtended) and rigid-body rotation (no change in the angle subtended), which can be interpreted as a modification to the Born model.
3.2 X-bond
Similar to L-bonds, the unit-cell made up of the second neighbour bonds is to be modified such that strain energy is stored only in the case of shear deformations and not for pure rotation. This is achieved with the X-bonds. Again the shear strains of two neighbouring bonds are coupled and the normal strains of the bonds remain unchanged. The modified strain energy of the unit-cell made up of one X-bond is
where \(k_{n_{2}}^{m}\) and \(k_{s_{2}}^{m}\) are the normal and shear stiffness parameters employing the modified model respectively. Similar to the assumption made in Sect. 2 in order to reduce the number of independent stiffness parameters to three, the shear stiffness parameters of the first and second neighbour bonds are assumed to be same, that is, \(k_{s_{2}}^{m} = k_{s_{1}}^{m}\). In the “Appendix A” it is shown that the modified bond model presented in this work is also valid for other possibilities to reduce the number of stiffness parameters to three. The strain energy stored in the second neighbour unit-cell with respect to the global coordinate system is
Upon expansion of Eq. (12) and comparison with the strain energy of the second neighbour unit-cell, see Eq. (5), one observes that similar to the first neighbour unit-cell with L-bonds, the coupling of shear strain energies results in an extra multi-bond term to distinguish between shear and rotation.
3.3 Unit-cell with the modified model
The strain energy stored in a square unit-cell is obtained by summing up the strain energy of an unit-cell made with L-bonds, Eq. (10), and of an unit-cell with X-bonds, Eq. (12)
The strain energy density \(e_{uc}^\mathrm{mod}\) is obtained similar to that of the unit-cell with the Born model given in Eq. (6).
4 Comparison of the modified model and the Born model
In this section, the stiffness parameters of a square unit-cell employing the modified model and the Born model are calibrated to the macroscopic elastic material parameters. The calibrated parameters are verified if they satisfy the condition of isotropy. The strain energy function of the unit-cell employing these bond models is verified for its positive definiteness.
4.1 Calibration of stiffness parameters
In order to model the behaviour of an isotropic elastic material, the stiffness parameters of the unit-cell employing the modified model must be calibrated with respect to the macroscopic elastic material parameters. In the literature there exist broadly two approaches:
-
1.
A numerical calibration where the stiffness parameters are iteratively calibrated by solving an inverse problem to match the slope of the stress-strain curve of a material in the linear region under uniaxial loading. For more details refer [7, 22].
-
2.
An analytical calibration based on the equivalence of strain energy density of the unit-cell \(e_{uc}\) with that of an equivalent elastic continuum \(e_{co} = \frac{1}{2} \varvec{\sigma } :\varvec{\epsilon }\). In particular, the components of the elastic tensor \(\mathbb {C}_{uc}\) are derived from the strain energy density of the unit-cell and are compared to the continuum description.
In this work, the analytical calibration approach is used due to its independence of the fineness of discretisation. The components of the tensor of elasticity of the unit-cell are obtained by differentiating the strain energy density twice with respect to the corresponding strain components. The individual components are summarised in the tensor of elasticity
where \(\hat{C}_{1} = (k_{n_{1}}^{m} + 2 k_{s_{1}}^{m} + k_{n_{2}}^{m})/t\), \(\hat{C}_{2} = (k_{n_{2}}^{m} - 2 k_{s_{1}}^{m})/t\) and \(\hat{C}_{3} = (k_{n_{2}}^{m} + k_{s_{1}}^{m})/t\) are defined for the modified model and \(\hat{C}_{1} = (k_{n_{1}}^{b} + k_{s_{1}}^{b} + k_{n_{2}}^{b})/t\), \(\hat{C}_{2} = (k_{n_{2}}^{b} - k_{s_{1}}^{b})/t\) and \(\hat{C}_{3} = (k_{n_{2}}^{b} + \frac{1}{2}\, k_{s_{1}}^{b})/t\) for the Born model. The elasticity tensor of the unit-cell has three components similar to that of a planar continuum. By comparing the three components \(\hat{C}_{1}\), \(\hat{C}_{2}\) and \(\hat{C}_{3}\) with those of the planar continuum elasticity tensor, the stiffness parameters are calibrated to the macroscopic Young’s modulus E and the Poisson’s ratio \(\nu \). The calibrated stiffness parameters for the case of plane stress and plane strain are summarised in Table 1.
As expected for a Born model there exists a restriction on the Poisson’s ratio at \(\nu = 1/4\) for plane strain and \(\nu = 1/3\) for plane stress. For higher values negative shear stiffness is obtained. This holds true for the modified model as well. The normal stiffness parameters of the unit-cell employing the Born model and the modified model are identical since only the shear strain energy components were coupled in the modified bond model. The stiffness parameters and the elasticity constants of the unit-cell are plotted as a function of the Poisson’s ratio \(\nu \) for both bond models in Fig. 5 for the case of plane stress. The stiffness parameters are normalised with respect to the Young’s modulus E and the thickness of the specimen t to obtain a qualitative behaviour.
From the Fig. 5b we observe that the components of the elasticity tensor of the unit-cell agree exactly with the equivalent continuum components in the range \(0 \le \nu \le 0.5\). In order to ensure the equality of the elasticity constants, the stiffness parameters of the unit-cell must take on the values as shown in Fig. 5a. Therefore, we interpret the negative value of shear stiffnesses (\(k_{s_{1}}^{b}\), \(k_{s_{1}}^{m}\)) for \(\nu > 1/3\) as a necessity to ensure this equality. Although a negative stiffness parameter of an individual spring seems unintuitive, in the case of a response of the unit-cell the elasticity tensor components are crucial.
4.2 Check for isotropy
Apart from calibrating the stiffness parameters to the macroscopic isotropic elastic material parameters it must also be checked whether and in which case they satisfy the condition for macroscopic isotropy. A material is considered to exhibit isotropy if the anisotropy factor \(\varLambda = 1\). The anisotropic factor for the chosen unit-cell is calculated with the components of the elasticity tensor for both bond models as
This shows that for isotropic elasticity (\(\varLambda = 1\)) the unit-cell has only two independent stiffness parameters and a condition that ensures isotropy for all values of E and \(\nu \). By substituting the stiffness parameters from Table 1 in the condition for isotropy it can be shown that this condition holds for both plane stress and plane strain.
4.3 Positive definiteness of strain energy
The square unit-cell shown in Fig. 1b is made up of four particles with two degrees of freedom per particle. The vector of displacements for one unit-cell is \(\mathbf {u} = [u_{A}, v_{A}, u_{B}, v_{B}, u_{C}, v_{C}, u_{D}, v_{D}]^{T}\). With the displacement vector \(\mathbf {u}\) and the stiffness matrix \(\mathbf {K}_{uc}^\mathrm{mod}\) given in “Appendix C”, the strain energy of the unit-cell in Eq. (13) can alternatively be written as
Equation (17) shows that the strain energy of the unit-cell is a quadratic function of displacements. In order to be thermodynamically stable, it must be positive definite. The necessary and sufficient condition for the positive definiteness of Eq. (17) is that all eigenvalues of the eigenvalue problem \(\mathbf {K}_{uc}^\mathrm{mod} \mathbf {u} = \varvec{\lambda } \mathbf {u}\) are real and positive [8]. The relating stiffness matrices are given in Appendices B and C respectively. The resulting eigenvalues and corresponding eigenforms are summarised in Table 2. After substituting the stiffness parameters of the unit cell from Table 1, the non-zero eigenvalues are plotted as a function of Poisson’s ratio \(\nu \) for both plane stress and plane strain in Fig. 6. The stiffness parameters are normalised with respect to Young’s modulus E and the thickness t to obtain a qualitative behaviour.
From Fig. 6 the following observations are made for both plane stress and plane strain:
-
1.
Regarding the Born model, the eigenvalue \(\lambda _{3}\) of the rigid-body rotation eigenform is non-zero everywhere expect at \(\nu = 1/3\) and \(\nu = 1/4\) for plane stress and plane strain respectively. This implies that the Born model deforms under rigid-body rotation and therefore it is proven that this model cannot distinguish between rigid-body rotation and shear deformations. Also, the eigenvalue becomes negative for \(\nu > 1/3\) and \(\nu > 1/4\) for plane stress and plane strain respectively. This implies that the strain energy function derived from the Born model is not positive definite after this lower limit of the Poisson’s ratio. Therefore we expect the response to be unstable for values of Poisson’s ratio above this limit. However, regarding the modified bond model, the eigenvalue of the rigid-body rotation eigenform remains zero for all values of \(\nu \) and all eigenvalues remain positive. Hence, the strain energy derived from the modified bond model is positive definite and therefore is stable for all values of \(\nu \) although the shear stiffness \(k_{s_{1}}^{m}\) of the unit-cell takes on a negative value after a critical value of \(\nu \) as shown in Fig. 5b. This implies that a negative stiffness does not necessarily lead to unstable results, rather it is due to negative eigenvalues. Similarly, in the work of Esin [6] it was concluded that materials and structures with negative stiffness elements can exist when the negative element energy is compensated by the energy of the rest of the system or an encompassing system that provides stabilisation.
-
2.
The eigenvalues (\(\lambda _{4}\), \(\lambda _{5}\)) related to bending eigenforms result as expected for an isotropic material.
-
3.
Similarly, the eigenvalues of shear (\(\lambda _{6}\), \(\lambda _{7}\)) eigenforms result as expected.
-
4.
As expected, the volumetric form \(\lambda _{8}\) has the highest eigenvalue.
Remark
At \(\nu = 1/3\) and \(\nu = 1/4\) for plane stress and plane strain, the shear stiffness becomes zero and the model reduces to one where it has only normal springs. At this value, the Born model is rotationally invariant and hence we have \(\lambda _{3} = 0\) at this particular value of \(\nu \).
5 Quasi-incompressible behaviour
In this section we verify whether the calibrated stiffness parameters of the unit-cell employing the modified model satisfy the condition of incompressibility as \(\nu \rightarrow 0.5\). A material is said to be incompressible if it resists volume change. The volume change of the unit-cell can be described similar to continuum mechanics with the volumetric strain \(\epsilon _{vol} = \epsilon _{xx} + \epsilon _{yy} + \epsilon _{zz}\), where \(\epsilon _{xx}\), \(\epsilon _{yy}\) and \(\epsilon _{zz}\) are components of the infinitesimal strain tensor. For the case of plane stress, \(\epsilon _{zz} = -\frac{\nu }{1 - \nu }(\epsilon _{xx} + \epsilon _{yy})\) and for plane strain \(\epsilon _{zz} = 0\). Based on the planar elasticity tensor \(\mathbb {C}_{uc}^\mathrm{mod}\) given in Sect. 4.1, the inverse stress-strain relations for the unit-cell is given by
where the components of the elasticity tensor of the unit-cell employing the modified bond model as derived in Sect. 4.1 are \(\hat{C}_{1} = (k_{n_{1}}^{m} + 2 k_{s_{1}}^{m} + k_{n_{2}}^{m})/t\), \(\hat{C}_{2} = (k_{n_{2}}^{m} - 2 k_{s_{1}}^{m})/t\) and \(\hat{C}_{3} = (k_{n_{2}}^{m} + k_{s_{1}}^{m})/t\). The volumetric strain \(\epsilon _{vol}^{uc}\) of the unit-cell employing the bond model for plane stress is now given by substituting the strain components from Eq. (18) as
By substituting the calibrated stiffness parameters of the modified bond model for plane stress given in Table 1 in Eq. (19), the volumetric strain is now given by
Normalising Eq. (20) with respect to \((\sigma _{xx} + \sigma _{yy})/E\), the variation of the volumetric strain as a function of \(\nu \) for the unit-cell employing the modified bond model is given in Fig. 7a. Similarly, the volumetric strain for the unit-cell employing modified bond model for the case of plane strain is \(\epsilon _{vol}^{uc} = ((\sigma _{xx} + \sigma _{yy})/E) \cdot (1 + \nu )(1 - 2\nu )\) and the variation of normalised volumetric strain with respect to \(\nu \) is given in Fig. 7b. From Fig. 7 we observe that the volumetric strain reduces to zero as \(\nu \rightarrow 0.5\) for both plane stress and plane strain. This behaviour is similar to what one would expect from an equivalent continuum mechanics isotropic elastic material. Therefore we conclude that the range of \(\nu \) that can be represented by a unit-cell employing modified bond model is similar to that of an isotropic elastic material.
6 Validation examples
In order to validate the capability of the modified model and compare it to the Born model, four different examples are chosen for which closed-form continuum solutions exist. With the help of these examples and based on the positive definiteness of the strain energy function, the stability of the bond model will also be investigated. The discrete element method results are obtained by solving the linear system of equations \(\mathbf {K} \, \mathbf {u} = \mathbf {f}\) for the unknown particle displacements \(\mathbf {u}\). The system stiffness matrix \(\mathbf {K}\) is obtained by assembling the individual unit-cell stiffness matrices derived in the Appendices B and C. External surface forces are reformulated as line loads by integrating over the thickness and are linearly interpolated between the particles along the edges of the unit-cell. The line load is then integrated along the edge of the unit-cell to obtain particle forces. An example of this procedure is given in “Appendix D”. The particle forces are then added to the corresponding position in the global force vector \(\mathbf {f}\). Point loads can be directly incorporated in the global force vector \(\mathbf {f}\).
Remark regarding the situation at the boundary: Every bond along the edges of the unit-cell were said to contribute only one half to the strain energy of the unit-cell due to periodicity in Sect. 2. As a consequence, when the system of equations are assembled, the strain energy of the bonds that are on the boundaries of the specimen continue to contribute only one half.
6.1 Uniaxial
A thin square plate of length \(l = {0.2}\,\mathrm{{[m]}}\) and thickness \(t = {0.01}\,\mathrm{{[m]}}\) is modelled with the chosen square unit-cell under plane stress conditions with \(E = {2e11}{[\mathrm{N}/\mathrm{m}^2]}\). All particles along the bottom edge and along the left edge of the plate are constrained along \(y-\) and \(x-\) direction, respectively. A stress \(\sigma _{xx}\) is applied on the right edge to model a uniaxial state of deformation as shown in Fig. 8. The analytical solution for the displacement fields is \(u = (\sigma _{xx}/E) x\) and \(v = -((\nu \, \sigma _{xx})/E)y\). The resulting displacements along \(u(x=l, y)\) and \(v(x, y=l)\) for three different values of Poisson’s ratio \(\nu \) are summarised in the Table 3 for both the bond models.
We observe that both unit-cells employing the Born model and the modified bond model produce the exact results for all values of the Poisson’s ratio independent of the discretisation, because the analytical solution is a linear function of the position and both bond models use linear springs. Although both models employ negative shear stiffness for \(\nu > 1/3\), they still produce the expected result. In Sect. 4.3, based on the eigenvalues of the stiffness matrix \(\mathbf {K}_{uc}\) of an unconstrained unit-cell employing the Born model it was observed that the strain energy was not positive definite (due to the rigid-body rotation eigenform) for \(\nu > 1/3\) in the case of plane stress. Therefore we may expect unstable results. However due to the constraints used in the example, all rigid-body eigenforms vanish and only positive eigenvalues exists for all values of \(\nu \). This is shown in Fig. 9, where the normalised eigenvalues of the constrained unit-cell employing the Born model and the modified model are plotted as a function of \(\nu \).
6.2 Pure shear
As a second test, a thin square plate with edge length \(l = {0.2}\,{\mathrm{[m]}}\) and thickness \(t = {0.01}\,\mathrm{{[m]}}\) as shown in Fig. 10 is modelled under plane stress condition with \(E = {2\hbox {e}11}\,{[\mathrm{N}/\mathrm{m}^{2}]}\) applying pure shear stress \(\sigma _{xy} = \sigma _{yx} = \tau _{0} = {1\hbox {e}8}\,[\mathrm{N}/\mathrm{m}^{2}]\).The plate is constrained in both directions along the bottom edge to prevent rigid-body motion similar to that used by Ockelmann [16]. The analytical solution for the displacement fields is obtained as \(u = (\tau _{0}/G) y\) and \(v = 0\), where \(G = E/2(1 + \nu )\) is the shear modulus. Here again, the test is conducted for three different values of \(\nu \) and also for four different discretisations similar to that of the uniaxial test. The u and v displacements of the domain discretised with \(8 \times 8\) unit-cells employing the Born model under pure shear are summarised in Fig. 11a–c. In Fig. 11d, the results of \(8 \times 8\) unit-cells employing the modified model under pure shear for \(\nu = 0.49\) are given. In Fig. 11 the bonds connecting the particles are not visualised for clarity.
We observe that the results for the unit-cell employing the modified model agrees exactly with the analytical solution, because similar to the case of uniaxial tension, the analytical displacement field is a linear function of the position of particles. With the modified bond model, the exact solution was also observed for all the discretisations. However, for the unit-cell employing the Born model the response of the plate is stiffer in comparison with the analytical solution in the range \(0 < \nu \le 1/3\) and unstable for \(\nu > 1/3\). In order to understand the reason for this behaviour, the plate is discretised with one unit-cell employing the Born model and the modified model respectively. The normalised eigenvalues of the constrained stiffness matrix are plotted as function of \(\nu \) as shown in Fig. 12. For the stiffness matrix of an unit-cell employing the Born model, we observe from Fig. 12 that the eigenvalue \(\lambda _{5}^{b}\) decreases with increasing values of \(\nu \) and also becomes negative for \(\nu > 0.4\). The eigenform corresponding to this eigenvalue is plotted as given as a quiver plot in Fig. 13. However, as the plate is further discretised, the eigenvalues of the unit-cells that are not located at the bottom edge of the plate take on the form as previously shown in Fig. 6a for the case of an unconstrained unit-cell stiffness matrix employing the Born model. This unconstrained stiffness matrix also includes the contribution of rigid-body rotation and is unstable for values of \(\nu > 1/3\) for the case of plane stress. Therefore, the upper limit on the Poisson’s ratio for the plate constrained as shown in Fig. 10 is \(\nu = 1/3\) employing the Born model. However, for the unit-cell employing the modified model, due to the coupling of shear strain energy of neighbouring bonds, the eigenvalues remains positive for all values of \(\nu \) as shown in Fig. 12 for the constrained stiffness-matrix and in Fig. 6b for the unconstrained stiffness matrix respectively.
6.3 Pure bending
Next, a thin rectangular plate of length \(l = a = {0.5}\,\mathrm{{[m]}}\), height \(h = 2b = {0.125}\,\mathrm{{[m]}}\) and thickness \(t = {0.01}\,\mathrm{{[m]}}\) under pure bending is considered. The plate is constrained at two points in the \(y-\)direction and at one location in the middle along \(x-\)direction as shown in Fig. 14. The applied bending moment \(M = {2604.17}\) [N m] at the sides is modelled as a linearly varying load \(\sigma _{0}\) with opposite magnitude at both corners. Following Timoshenko [20], the analytical displacement fields are derived to be \(u_{e} = (M y/EI)(-x + \frac{l_{x}}{2})\) and \(v_{e} = (M/2EI)(\nu y^{2} + x^{2} - x l_{x})\), where \(I = th^{3}/12\) under plane stress conditions using the Airy’s stress function assuming no body forces. For the derivation of the analytical solution, symmetry boundary conditions about the \(y-\)axis at \(x = l/2\) were applied and additionally the point at position (\(x = 0, y = 0\)) was constrained along y-axis.
The test was performed with four different discretisations: \(8 \times 2\), \(16 \times 4\), \(32 \times 8\) and \(64 \times 16\). Also, the effect of \(\nu \) on the accuracy has been checked by performing the test for three different values of \(\nu \). The deformed configuration employing the Born model and the modified model for \(\nu = 0.49\) is given in Fig. 15.
The displacement u at the left edge of the plate and the displacement v of the axis of the plate employing the Born model and the modified model are compared with the analytical solution for the finest discretisation and for different Poisson’s ratio and are summarised in Fig. 16. From the results we observe that regarding the Born model for \(\nu = 0\) and \(\nu = 0.3\), the displacements u and v are much smaller in comparison with that of the analytical solution. In the case of pure bending, elements which are located faraway from the boundary undergo rigid body rotations as well. Since the Born model cannot distinguish between rigid-body rotations and shear deformations, strain energy is also stored for the rigid body rotation. As the rigid-body rotation eigenvalue takes on a maximum value at \(\nu = 0\) and approaches zero at \(\nu = 1/3\) for the chosen unit-cell employing the Born model, the response of the plate is much stiffer for \(\nu = 0\) than for \(\nu = 1/3\). And for \(\nu > 1/3\) the results are unstable since the eigenvalue takes a negative value and hence the strain energy function is no longer positive definite. We also observe from Fig. 17 regarding the unit-cell employing the Born model, that the v displacement do not converge to the analytical solution. This is due to the non-zero eigenvalue of the rigid-body rotation eigenform. For the unit-cell employing the modified bond model, the coupling of the shear strain energy of the neighbouring bonds allows the model to distinguish between rigid-body rotations and shear deformations. Therefore, satisfactory results are obtained employing this modified bond model and also convergence to the analytical solution upon refinement is observed.
7 Conclusion
Modelling of continuum isotropic elasticity with the Discrete Element Method is traditionally limited to a certain value of Poisson’s ratio due to the bond model used. The modified bond model presented in this paper for planar continuum overcomes this limitation by introducing a multi-bond term that couples the shear strain energy of neighbour bonds. This term enables the modified bond model to distinguish between rigid-body rotation and shear deformation. Two bonds, namely the L-bond and X-bond that employ this proposed coupling were introduced. The positive definiteness of the strain energy function of the unit-cell employing the modified bond model was ensured for values of Poisson’s ratio in the range \(0 \le \nu < 0.5\). The results obtained under uniaxial tension, pure shear and pure bending were validated with the continuum mechanics solution. Moreover, the agreement of the numerical results with the continuum mechanics solution demonstrates the ability of the modified bond model to describe the behaviour of an isotropic elastic material. The concept of shear strain energy coupling of neighbour bonds provides an approach that is based on simple bond models to overcome the limitation of Poisson’s ratio within DEM. The generalisation of this modified bond model for random discretisation and for three-dimensions are under progress. The implementation of this modified bond model within the framework of the DEM for subsequent fracture analysis is also to be carried out.
Availability of data and materials
Available from the corresponding author upon reasonable request.
References
André D, Iordanoff I, luc Charles J, Néauport J (2012) Discrete element method to simulate continuous material by using the cohesive beam model. Comput Methods Appl Mech Eng 213–216:113–125
Born M, Huang K (1954) Dynamical theory of crystal lattices. Oxford classic texts in the physical sciences. Clarendon Press, Oxford
Buxton GA, Care CM, Cleaver DJ (2001) A lattice spring model of heterogeneous materials with plasticity. Model Simul Mater Sci Eng 9(6):485–497
Celigueta MA, Latorre S, Arrufat F, Oñate E (2017) Accurate modelling of the elastic behavior of a continuum with the discrete element method. Comput Mech 60(6):997–1010
Cundall PA, Strack ODL (1979) A discrete numerical model for granular assemblies. Géotechnique 29(1):47–65
Esin M, Pasternak E, Dyskin AV (2016) Stability of 2d discrete mass-spring systems with negative stiffness springs. Phys Status Solidi (b) 253(7):1395–1409
Flack C (2020) Mehrfeldmodellierung von beton mit diskreten element methoden. Ph.D. thesis, TU Braunschweig
Fung Y (1965) Foundations of solid mechanics. Prentice-Hall, Englewood Cliffs
Gao W, Tan Y, Zang M (2014) A cubic arranged spherical discrete element model. Int J Comput Methods 11(05):1350102
Griffiths DV, Mustoe GGW (2001) Modelling of elastic continua using a grillage of structural elements based on discrete element concepts. Int J Numer Methods Eng 50(7):1759–1775
Hassold GN, Srolovitz DJ (1989) Brittle fracture in materials with random defects. Phys Rev B 39:9273–9281
Keating PN (1966) Effect of invariance requirements on the elastic strain energy of crystals with application to the diamond structure. Phys Rev 145:637–645
Le Danh B, Koval G, Chazallon C (2013) Discrete element approach in brittle fracture mechanics. Eng Comput 30(2):263–276
Madan N (2019) New formulation of the discrete element method with deformable particles. Ph.D. thesis, Institute of Fundamental Technological Research, Polish Academy of Sciences, Warsaw
Ockelmann F (2018) Modellierung und numerische analyse von beton und faserverstärktem ultrahochleistungsbeton mit der diskrete elemente methode. Ph.D. thesis, TU Braunschweig
Ockelmann F, Dinkler D (2017) A discrete element model for the investigation of the geometrically nonlinear behaviour of solids. Comput Part Mech 5(3):335–344
Ostoja-Starzewski M (2002) Lattice models in micromechanics. Appl Mech Rev 55(1):35–60
Rojek J, Zubelewicz A, Madan N, Nosewicz S (2018) The discrete element method with deformable particles. Int J Numer Methods Eng 114(8):828–860
Tavarez FA, Plesha ME (2007) Discrete element method for modelling solid and particulate materials. Int J Numer Methods Eng 70(4):379–404
Timoshenko S, Goodier J (1969) Theory of elasticity. Engineering mechanics series. McGraw-Hill, New York
Wang Y, Mora P (2008) Macroscopic elastic properties of regular lattices. J Mech Phys Solids 56(12):3459–3474
Zhao C, Hobbs BE, Ord A, Hornby P, Peng S, Liu L (2007) Particle simulation of spontaneous crack generation problems in large-scale quasi-static systems. Int J Numer Methods Eng 69(11):2302–2329
Zhao GF, Fang J, Zhao J (2011) A 3d distinct lattice spring model for elasticity and dynamic failure. Int J Numer Anal Methods Geomech 35(8):859–885
Zhao GF, Yin Q, Russell AR, Li Y, Wu W, Li Q (2019) On the linear elastic responses of the 2d bonded discrete element model. Int J Numer Anal Methods Geomech 43(1):166–182
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Code availability
Available from the corresponding author upon reasonable request.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Another possibility to reduce the number of stiffness parameters
In Sects. 2 and 3 it was supposed that the shear stiffness parameters of the first and second neighbour bonds were equal, that is, \(k_{s_{2}} = k_{s_{1}}\), to reduce the number of independent stiffness parameters to three. Now we show that the fundamental characteristics of the unit-cell employing the Born model and the modified bond model remain true also when we suppose that the normal stiffness of the first and second neighbour unit-cell are equal, that is, \(k_{n_{2}} = k_{n_{1}}\) instead of \(k_{s_{2}} = k_{s_{1}}\), based on the positive definiteness of the strain energy. As a consequence, the three independent stiffness parameters of the unit-cell are now \(k_{n_{1}}, k_{s_{1}} \text {and} \, k_{s_{2}}\). Following the procedure introduced in Sect. 4.1, the calibrated stiffness parameters of the unit-cell employing the Born model and the modified bond model for the case of plane stress and plane strain are summarised in Table 4.
Similar to Sect. 4.3, the eigenvalues of this alternate unit-cell stiffness matrix are calculated. The positive definiteness of the strain energy is verified by plotting the eigenvalues of stiffness matrix as a function of \(\nu \) in Fig. 18 for plane stress. All observations made in Sect. 4.3 hold true also for this alternate unit-cell. Therefore, based on Fig. 18b we conclude that the modified bond model introduced in this work also works for other combinations of stiffness parameters and overcomes the limitation of the Born model.
Stiffness matrix of the unit-cell with Born model
In the work of Griffiths [10], the stiffness matrix of a unit-cell was obtained by assembling the stiffness matrix of individual constituent bonds in a procedure that is similar to that of the Finite Element Method (FEM). Here an alternative approach of deriving the stiffness matrix from the strain energy of the unit-cell is taken. The strain energy stored in a generic bond in terms of the local displacement components was given in Eq. (1). The local displacements of particles in a generic bond oriented at an angle \(\theta \) to the global coordinate system can be written in terms of the global displacement with the transformation matrix \(\mathbf {Q}\) as \(\mathbf {u}_{lo} = \mathbf {Q} \, \mathbf {u}_{gl}\),
With this transformation, the strain energy in a bond in terms of the global particle displacements is given by
The strain energy of the unit-cell in terms of displacements are obtained by summing up the strain energy of individual constituent bonds given in equation (22) by taking in to account their orientation as
While summing up, the stiffness factor of individual bonds have to be considered as well. The stiffness factor for bonds with first neighbours is 1/2, since they are shared by two unit-cells (periodicity). However, the stiffness factor for bonds with second neighbours is 1 as they belong exclusively to each unit-cell. By using the appropriate stiffness factors and by substituting the orientation of individual bonds, the stiffness matrix of the unit-cell is obtained by differentiating Eq. (23) twice with respect to the appropriate global displacement as
Stiffness matrix of the unit-cell with the modified bond model
For a generic L-bond as shown in Fig. 4a, the strain energy stored in terms of the local displacements of the particles can be written as
With the transformation matrix \(\mathbf {Q}\) and Eq. (22), the strain energy is now given in terms of the global particle displacements as
where \(c_{AB} = \cos \theta _{AB}\), \(s_{AB} = \sin \theta _{AB}\), \(c_{BC} = \cos \theta _{BC}\) and \(s_{BC} = \sin \theta _{BC}\). The strain energy stored in the unit-cell made up of L-bonds \(\varPi _{uc_{1}}^\mathrm{mod}\) is obtained by summing up the strain energy of individual constituent L-bond as shown in Fig. 4b and in Eq. (10). Similarly the strain energy stored in the unit-cell made up of X-bond is given in terms of the local displacements as
Similar to L-bond, the local displacements are expressed in terms of the global displacements with the transformation matrix \(\mathbf {Q}\). After this, the strain energy stored in the unit-cell with the modified bond model is given by
By differentiating the strain energy twice with respect to the appropriate global displacements, the stiffness matrix is given by
Incorporation of surface forces
Consider a thin plate under plane stress condition discretised with one unit-cell loaded by a surface force \(\sigma {yy}\) as shown in Fig. 19. The surface force is reduced to a line load \(F_{L}\) by integrating the surface load along the thickness t by
The line load \(F_L\) is then linearly interpolated between the particles along the edge of the unit-cell using a linear approach and is then integrated along the length of the unit-cell to obtain the vector of particle forces as
For the case of constantly distributed line load, that is, \(F_{L_{C}} = F_{L_{C}} = F_{L}\), the particle forces reduces to
Similarly, when the plate is discretised with more unit-cells, the particle forces as calculated above are incorporated into their corresponding position in the global force vector \(\mathbf {f}\) during assembly.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Venkateswaran, R.G., Kowalsky, U. & Dinkler, D. A modified bond model for describing isotropic linear elastic material behaviour with the discrete element method. Comp. Part. Mech. 9, 465–483 (2022). https://doi.org/10.1007/s40571-021-00422-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40571-021-00422-0