1 Introduction

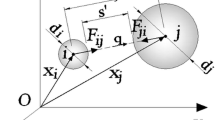
Energetic composites containing metallic fuel and inorganic oxidizer have become a research topic of current interest due to their high energy density, tunable energy release rate and ignition sensitivity, and benign reaction products [1–4]. While simple physical mixing leads in general to a nonhomogeneous distribution of fuel and oxidizer nanostructures [3, 4], optimal performance would require tailored structure and morphology. Toward this end, composite system designs, such as the self-assembled thermitic composites consisting of discrete CuO and Al nano-structures shown in Fig. 1, have been produced [3, 4]. The Al/CuO composite system has been investigated at the continuum level using an equation of state (EoS) for the reaction products, formulated under the assumption of a pressure-dependent reaction rate that is infinite for the pressure greater than some threshold value but zero otherwise, and complete neglect of nano structural features [4]. However, the real combustion behavior of a nano energetic composite is affected by several important factors such as ingredient ratio, mass density, composite morphology, and the often diffusion-limited interactions among discrete nano structures of various sizes and shapes. Clearly, inclusion of such details in a high-fidelity simulation requires the use of a suitable multiscale method.

Fig. 1
figure 1

Transmission electron microscopy images of a CuO nanostructures and b unreacted self-assembled mixture of CuO nanostructures and Al nanoparticles [3]

Full size image

It can be observed from Fig. 1 that, under impact loading, discrete zero-dimensional (particle) and one-dimensional (rod and beam) nano structures of suitable sizes will interact with each other via longitudinal (particle-to-rod or rod-to-rod), transverse (particle-to-beam or beam-to-beam), and/or mixed modes. Available experimental techniques do not enable direct, real-time observation of the nanoscale interactions under impact loading. While recent molecular dynamics (MD) simulations have demonstrated the size effects on the responses of single-crystal Cu nanostructures to transverse [5] and longitudinal [6] impact loading, the complex nature of general impact modes hinders computer simulations of nanoscale impacts with atomic resolution due to the large number of particles required to simulate non-trivial geometries and associated large CPU requirements. Hence, an effective spatial discretization procedure must be developed to model and simulate the multiscale interactions involved in the impact responses of nano energetic composites.

The material point method [7] (MPM, http://en.wikipedia.org/wiki/Material_Point_Method) is useful for simulating multi-phase interactions in processes that involve failure evolution, such as impact, penetration, perforation and blast-fragment interaction. As reviewed by Chen et al. [8], the MPM is an extension to solid mechanics of the hydrodynamics method called FLIP which, in turn, evolved from the Particle-in-Cell Method. The essential idea of the MPM is to take advantage of the strengths of both the Eulerian and Lagrangian methods while avoiding the shortcomings of each. In comparison to other meshless methods [8], the MPM is less complex and has a cost factor of at most twice that associated with the use of corresponding finite elements. In addition, it can be easily interfaced with the finite element method (FEM) codes due to the use of the same weak formulation for both methods. In the original MPM [7], however, there exists a cell-crossing issue due to the use of local mapping functions; and in addition, special care is required to deal with a moving boundary condition. Much effort has been expended, especially over the past decade, to improve the original MPM through the use of nonlocal treatments (which increase the computational expense), as illustrated in the representative references [9–11]. We note three particular advances in the MPM that are relevant for multiscale simulation: A multi-level refinement scheme has been designed for the generalized interpolation material point (GIMP) Method [12]; a hierarchical approach has been proposed and demonstrated in which material points at the fine level in the MPM are coupled directly with the atoms in MD simulations [13]; and a sequential procedure has been recently developed to formulate the EoS, based on MD results, for use in macroscopic MPM simulations [14]. However, each of the hierarchical/sequential or multi-level refinement approaches just mentioned requires a transition region between different spatial scales, which limits their usefulness for the study of physical situations where discrete nano/micro structures (for example, nano/micro rods and beams in energetic composites) interact with each other. Recently, a particle-based multiscale procedure has been proposed wherein cluster dynamics (CD) is linked hierarchically with MD for sub-micron scale domains and concurrently with the MPM for simulations on larger scales [15]. The method was used to explore the longitudinal impact response between two metallic microrods with different nanostructures. However, the CD method used in [15] relies on certain assumptions that limit the range of applicability, and much work remains to generalize the method to more realistic situations.

In the present study we improve on the particle-based multiscale procedure described in [15]. Specifically, we combine a hierarchical bridge from MD to dissipative particle dynamics (DPD) for nanoscale simulations with a concurrent link between DPD and the MPM for microscale simulations. Focusing on the link between DPD and the MPM, we first demonstrate that the dynamics of DPD particles, which interact via pairwise particle–particle forces, can be coarse-grained using a straightforward adaptation of the standard MPM algorithm. Using this capability we then demonstrate how DPD and MPM subdomains can be treated concurrently, and nearly seamlessly, in a single simulation domain. Particular attention is devoted to the development of an effective interfacial scheme for use in the concurrent simulations. To provide the foundation for the proposed procedure, the essential features of the governing equations for MD, DPD, and the MPM are summarized in Sect. 2. The proposed hierarchical and concurrent multiscale solution schemes are described in Sect. 3. Representative examples are used in Sect. 4 to illustrate the proposed procedure. Finally, we summarize the current status and mention future research tasks in Sect. 5.

2 Governing equations at different scales

2.1 Molecular dynamics

Molecular dynamics is a widely used tool for atomic simulations. The dynamics of a conservative system consisting of \(N\) particles is governed by Newton’s equation of motion for each particle \(i\):

$$\begin{aligned} m_i \frac{d^{2}{\varvec{r}}_i}{dt^{2}}=m_i {\varvec{a}}_i =-\frac{\partial }{\partial {\varvec{r}}_i}{\varvec{U}}_{tot} \left( {\varvec{r}}_1, {\varvec{r}}_2, \ldots , {\varvec{r}}_N\right) , \end{aligned}$$
(2.1)

where \(m_i, {\varvec{r}}_i\) and \({\varvec{a}}_i\) are the mass, position, and acceleration vectors of particle \(i\), respectively, and \(U_{tot} \) is the total potential energy that depends only on the particle positions. In this paper, we focus on an atomic solid (Cu) and describe the interatomic potential energy using the Sutton–Chen (SC) potential [16].

2.2 Dissipative particle dynamics

To bridge the temporal and spatial gaps between nano and sub-micron scale simulations, the DPD with conserved energy (DPDE) method [17, 18] has been developed starting from the classical isothermal DPD [19]. In the DPD method atomic-scale details are averaged and associated with effective coarse-grained particles. The extent of coarse graining, that is, the numbers of atoms subsumed by a single DPD particle, varies widely depending on the application. The DPDE governing equations for each coarse-grained particle \(i \)are written as follows [17]:

$$\begin{aligned} m_i \frac{d^{2}{\varvec{r}}_i}{dt^{2}}&= m_i {\varvec{a}}_i ={\varvec{f}}_i^C +{\varvec{f}}_i^D +{\varvec{f}}_i^R, \end{aligned}$$
(2.2)
$$\begin{aligned} {\varvec{f}}_i^C&= \sum _{i\ne j} -\nabla U\left( {\varvec{r}}_{{i}j}\right) {\varvec{e}}_{ij}, \end{aligned}$$
(2.3)
$$\begin{aligned} {\varvec{f}}_i^D&= \sum _{i\ne j} -\gamma _{ij} w^{D}\left( {\varvec{r}}_{ij} \right) {\varvec{v}}_{ij}, \end{aligned}$$
(2.4)
$$\begin{aligned} {\varvec{f}}_i^R&= \sum _{i\ne j} \sigma _{ij} w^{R}(r_{ij})dW_{ij} {\varvec{e}}_i, \end{aligned}$$
(2.5)

where \({\varvec{f}}_i^C, {\varvec{f}}_i^D\) and \({\varvec{f}}_i^R\) represent, respectively, the conservative force, dissipative force, and random force vectors acting on particle \(i\). As before, \(m_i, {\varvec{r}}_i\), and \({\varvec{a}}_i\) are, respectively, the mass, position, and acceleration vectors of particle \(i\), and \(U\) is the inter-particle potential. The quantities \(\gamma _{ij}\) and \(\sigma _{ij}\) are coefficients characterizing the strengths of the non-conservative forces, \(w^{D}\) and \(w^{R}\) are the weight functions of \({\varvec{r}}_{ij} ={\varvec{r}}_i -{\varvec{r}}_j, {\varvec{v}}_{ij} ={\varvec{v}}_i -{\varvec{v}}_j\) is the velocity difference vector between particles \(i\) and \(j\), and \(W_{ij}\) is the independent \(d\)-dimensional Wiener process. The quantity \({\varvec{e}}_i ={{\varvec{r}}_i}/\left| {\varvec{r}}_i\right| \) is the normalized position vector of particle \(i\) and \({\varvec{e}}_{ij}={\varvec{r}}_{ij}/\left| {\varvec{r}}_{ij}\right| \) is the unit vector between particles \(i\) and \(j\). The parameters in the DPD force expression used here were calibrated by using a genetic algorithm to optimize the fit between the Sutton-Chen force field for Cu and an analogous coarse-grained form wherein one mesoparticle corresponds to eight copper atoms and the coarse-grained lattice parameter is twice that for atomic Cu in the MD model [20]. The DPD parameter \(\gamma \) was set to 0.2 amu/ps and the fit was performed based on the 298 K isotherm.

2.3 Material point method

At the continuum scale, the governing differential equations under purely mechanical loading can be derived from the conservation equations for mass and momentum,

$$\begin{aligned} \frac{d\rho }{dt}+\rho \nabla \cdot {\varvec{v}}=0 \end{aligned}$$
(2.6)
$$\begin{aligned} \rho {\varvec{a}}=\nabla \cdot {s}+\rho {\varvec{b}} \end{aligned}$$
(2.7)

supplemented with a suitable constitutive equation to describe the internal interactions among material points and the kinematic relation between strain and displacement. In Eqs. (2.6) and (2.7), \(\rho ({\varvec{x}},t)\) is the mass density, \({\varvec{v}}({\varvec{x}},t)\) the velocity, \({\varvec{a}}({\varvec{x}},t)\) is the acceleration, \({s}({\varvec{x}},t)\) is the Cauchy stress, and \({\varvec{b}}({\varvec{x}},t)\) is the specific body force due to, for example, gravity. The vector \({\varvec{x}}\) is the time-dependent position vector of the material points in the continuum. For given boundary conditions and initial data, the governing differential equations, if they are well-posed, can be solved either analytically or numerically. The key difference among different spatial discretization methods is how the gradient and divergence terms are calculated.

As a particle method, the MPM discretizes a continuum body in the original configuration into a finite set of \(N_{p}\) material points (particles) that are tracked throughout the deformation process. Let \({\varvec{x}}_p^t\) denote the position vector of material point \(p ( p=1,2,\ldots , N_{p})\) at time \(t\). Each material point at time \(t\) has an associated mass \(M_{p}\), density \(\rho _p^t\), velocity \({\varvec{v}}_p^t\), Cauchy stress \({s}_p^t\), strain \({\varvec{e}}_p^t\), and any other internal state variables required by the constitutive description. Thus, these material points provide a Lagrangian description of the continuum body. Because the mass for a given material point is independent of time, Eq. (2.6) is automatically satisfied. At each time step, information from the material points is mapped to a background computational mesh. This mesh spans the computational domain, and the details of its specification are chosen for computational convenience. After information is mapped from the material points to the mesh nodes, the discrete formulation of Eq. (2.7) can be obtained on the mesh nodes, as briefly described in Sect. 3.

The weak form of Eq. (2.7) can be found, based on the standard procedure used in the FEM [7], to be

$$\begin{aligned} \int \limits _\varOmega \rho {\varvec{w}}\cdot {\varvec{a}}d\varOmega&= -\int \limits _\varOmega \rho {s}^{{s}} :\nabla {\varvec{w}}d\varOmega +\int \limits _{S^{c}} \rho {\varvec{c}}^{s}\cdot {\varvec{w}}dS\nonumber \\&+\int \limits _\varOmega \rho {\varvec{w}}\cdot {\varvec{b}}d\varOmega , \end{aligned}$$
(2.8)

where \({\varvec{w}}\) denotes the test function, \({\varvec{S}}^{{s}}\) specific stress, \(\varOmega \) the current configuration of the continuum body, and \(S^{C}\) the part of the boundary subject to a prescribed traction. A boundary layer can be used to enforce the moving traction boundary condition given by the prescribed traction vector \({\varvec{c}}^{s}\). Because the whole continuum body is described with the use of a finite set of material points, the mass density can be written as

$$\begin{aligned} \rho \left( {\varvec{x}},t\right) =\sum _{p=1}^{N_p} M_p \delta \left( {\varvec{x}}-{\varvec{x}}_p^t\right) , \end{aligned}$$
(2.9)

where \(\delta \) is the Dirac delta function with dimension of reciprocal volume. The substitution of Eq. (2.9) into Eq. (2.8) converts the integrals to the sums of quantities evaluated at the material points, namely

$$\begin{aligned}&\sum _{p=1}^{N_p} M_p \left[ {\varvec{w}}\left( {\varvec{x}}_p^{t}, t\right) \cdot {\varvec{a}}\left( {\varvec{x}}_p^{t}, t\right) \right] \nonumber \\&\quad \!=\!\sum _{p=1}^{N_p} M_p \left[ \!-{s}^{{s}}\left( {\varvec{x}}_{p}^{t}, t\right) {:}\left. \nabla {\varvec{w}}\right| _{{x}_{p}^{t}} \!+\!{\varvec{w}}\left( {\varvec{x}}_{p}^{t}, t\right) \cdot {\varvec{c}}^{{s}}\left( {{\varvec{x}}_{p}^{t}, t} \right) h^{-1}\right. \nonumber \\&\qquad \left. +\,{\varvec{w}}\left( {{\varvec{x}}_{p}^{t} ,t} \right) \cdot {\varvec{b}}\left( {{\varvec{x}}_{p}^{t} ,t} \right) \right] , \end{aligned}$$
(2.10)

where \(h\) is the thickness of the boundary layer. As can be seen from Eq. (2.10), the interactions among different material points are only present in the gradient terms, and a suitable set of material points must be chosen to represent the boundary layer. In the MPM, a background computational mesh is required to calculate the gradient terms. To do so, suppose that a computational mesh is constructed of 8-node cubic cells (for three-dimensional problems). These cells are used to define standard nodal basis functions, \(N_{i}({\varvec{x}})\), associated with spatial nodes \({\varvec{x}}_{i}(t), i = 1, 2,\ldots , N_{n}\), where \(N_{n}\) is the total number of mesh nodes. The nodal basis functions are selected from conventional finite element shape functions. The spatial coordinates of any material point in a given cell at time \(t\) can then be represented by

$$\begin{aligned} {\varvec{x}}_{p}^{t} =\sum _{i=1}^{N_n} {\varvec{x}}_{i}^{t} N_i\left( {\varvec{x}}_{p}^{t}\right) , \end{aligned}$$
(2.11)

where \({\varvec{x}}_i^{t}\) are the nodal coordinates. Similarly, the displacement vector of any material point in a cell is defined by the nodal displacements, \({\varvec{u}}_i^t(t)\), as follows:

$$\begin{aligned} {\varvec{u}}_{p}^{t} =\sum _{i=1}^{N_n} {\varvec{u}}_{i}^{t} N_i\left( {\varvec{x}}_{p}^{t}\right) . \end{aligned}$$
(2.12)

Because the same basis functions are used for both spatial coordinates and displacements, kinematic compatibility requires that the basis functions advect with the material, as in the updated Lagrangian framework; that is, the basis functions must be independent of time. It follows that the velocity and acceleration of any material point in a cell can be represented in the same way as that for the displacement in Eq. (2.12). The test function associated with any material point also has the same form,

$$\begin{aligned} {\varvec{w}}_p^t =\sum _{i=1}^{N_n} {\varvec{w}}_i^t N_i\left( {\varvec{x}}_{p}^{t}\right) , \end{aligned}$$
(2.13)

where \({\varvec{w}}_{i}^{t}\) is the nodal test function. While the kinematic vectors, Eqs. (2.11)–(2.13), are continuous across the cell boundary, the gradients of these vectors are not—due to the use of linear shape functions for computational efficiency in the original MPM formulation [7] that is used here.

With the use of the above equations and the standard procedure as employed in the FEM, the discretized governing differential equations can be obtained as

$$\begin{aligned} m_i^t {\varvec{a}}_{i}^{t} =\left( {\varvec{f}}_{i}^{t}\right) ^{int}+\left( {\varvec{f}}_{i}^{t}\right) ^{ext}, \end{aligned}$$
(2.14)

for a lumped mass matrix; where the internal force vector is given by

$$\begin{aligned} \left( {\varvec{f}}_{i}^{t} \right) ^{int}=-\sum _{p=1}^{N_p} M_p {s}_{p}^{{s},{t}} \cdot {\varvec{G}}_{i} \left( {\varvec{x}}_{p}^{t}\right) , \end{aligned}$$
(2.15)

with \({s}_{p}^{{s},{\varvec{t}}} ={s}^{{s}}\left( {{\varvec{x}}_{p}^{t} ,t} \right) \) and \({\varvec{G}}_{i} \left( {\varvec{x}}_{p}^{t}\right) =\left. {\nabla N_i} \right| _{{\varvec{x}}_{p}^{t}} \); and the external force vector takes the form

$$\begin{aligned} \left( {\varvec{f}}_{i}^{t}\right) ^{ext}= {\varvec{c}}_{i}^{t}+{\varvec{b}}_{i}^{t}, \end{aligned}$$
(2.16)

where \({\varvec{c}}_{i}^{t}\) and \({\varvec{b}}_{i}^{t}\) denote, respectively, the specific traction and body force vectors evaluated at the mesh nodes. Note that the internal force, which represents the interactions among material points and can be local or nonlocal depending on the stress-strain relation, is not continuous across the cell boundary due to the use of linear shape functions. However, the prescribed traction and body force vectors are continuous across the cell boundary, provided they are continuous before the spatial discretization is performed.

For large-scale simulations, an explicit time integrator is usually used to solve Eq. (2.14) for the nodal accelerations, with a time step that satisfies the stability condition, that is, the quotient of the smallest cell size to the wave speed. If a MPM cell includes multiple material points, the material properties are homogenized over the cell via the mapping and re-mapping scheme. During each time step, the information on each material point is mapped to the corresponding nodes of the cell in which the material point is located. After the equations of motion are solved on the cell nodes, the new nodal values of velocity are then used to update the positions of the material points via the mapping from the cell nodes to the related material points.

The strain increment for each material point is determined from the gradient of the nodal velocity evaluated at the material point position. The corresponding stress increment can then be found from the constitutive model. Internal state variables can also be assigned to the material points and transported along with them. Once the material points have been completely updated, if desired, the background mesh can be discarded and a new mesh defined for the next time step. Due to the use of the same set of nodal basis functions for both the mapping from material points to cell nodes and the re-mapping from cell nodes to material points at each time step, the interpenetration between material bodies is precluded in the MPM. This enables simulations of impact and penetration problems without the need for a special contact algorithm.

3 Particle-based multiscale simulation procedure

Equations (2.1), (2.2), and (2.14) have similar forms although they are formulated at different scales and with different domains of influence. The right-hand sides of these equations—the force expressions for MD and DPD and constitutive laws for the MPM, which are different for different materials—include the internal interactions among discrete particles (atoms, DPD particles, or material points) as well as the external forces. The difference between the MPM and DPD or MD is that Eq. (2.14) is evaluated at the background mesh nodes rather than at the material points. As a result, the strain and stress fields in the MPM can be easily determined using the gradient of nodal basis functions and the constitutive model, respectively, instead of defining a representative domain (a cutoff radius) to determine the strain and stress as required in DPD and MD.

The proposed multiscale simulation procedure consists of a concurrent link between the DPD and MPM particles to simulate microscale responses and a hierarchical bridge from MD to DPD for nano and sub-micron scale simulations (in which the DPD force expression is parameterized by fitting to MD results). In the concurrent DPD and MPM computational domain, a particle is a DPD mesoparticle if its force expression is defined by Eq. (2.2), which involves a cutoff distance. A particle is a material point if a constitutive model at the continuum level is used to calculate the internal force vector as shown in Eq. (2.15). Within the MPM framework, the DPD cutoff distance should be larger than the cubic cell edge length (for three-dimensional problems). It will be shown in the next section that the DPD details can be effectively averaged through the use of a coarse MPM background grid. A single MPM cell can include both DPD and MPM particles at a given time such that the mapping and re-mapping procedure in the MPM algorithm yields a computational homogenization scheme over the cell domain. The concurrent link between the MPM and DPD enables a nearly seamless integration of constitutive modeling at the continuum level with force-based modeling at the mesoparticle level. The simplicity of the proposed particle-based simulation procedure provides a robust way for zoom-in to near-atomic-scale details and zoom-out to microscale responses. The remainder of Sect. 3 describes the specific solution steps required for a concurrent MPM and DPD simulation.

3.1 Preprocessor

The followings steps are performed prior to the first time step:

  1. 1.

    A continuum body (with single or multiple material phases) is discretized into a finite set of \(N_{p}\) material points determined with respect to the original configuration of the body. Each material point carries its original material properties. The material points are followed throughout the deformation process of the body.

  2. 2.

    An arbitrary background mesh with appropriate spatial resolution is defined and used to find the natural coordinates of any material point and to identify the mesh cell that contains the material point.

  3. 3.

    All state variables at the material points are initialized, control parameters for the computer code are specified, and the system of DPD particles and/or material points is equilibrated to minimize the stress of the initial system.

3.2 Central processing unit

The following detailed steps are performed at each time step increment:

  1. 1.

    For each material point (both DPD and MPM particles), perform the mapping operation from the material point to the cell nodes enclosing the material point.

Map the mass from the material points to the nodes of the cell containing these points,

$$\begin{aligned} m_i^t =\sum _{p=1}^{N_p} M_p N_i \left( {\varvec{x}}_{p}^{t}\right) , \end{aligned}$$
(s1)

where \(m_i^t\) is the mass at node \(i\) at time \(t, M_p\) is the material point mass, \(N_i\) is the shape function associated with node \(i\), and \({\varvec{x}}_{p}^{t}\) is the location of the material point at \(t\). Analogously, for each material point, map the momentum from the material point to the nodes of the cell enclosing the material point,

$$\begin{aligned} (m{\varvec{v}})_i^t =\sum _{p=1}^{N_p} (M{\varvec{v}})_p^t N_i ({\varvec{x}}_{p}^t), \end{aligned}$$
(s2)

where \((m{\varvec{v}})_i^t\) denotes the nodal momentum at node \(i\) at time \(t\), and \((M{\varvec{v}})_p^t\) is the material point momentum at that same time. Find the internal force vector at the cell nodes for the MPM particles associated with that cell,

$$\begin{aligned} \left( {\varvec{f}}_{i}^{t}\right) ^{int}=-\sum _{p=1}^{N_p} {\varvec{G}}_{i} \left( {\varvec{x}}_{p}^{t}\right) \cdot {s}_p^t \frac{M_p}{\rho _p^t}, \end{aligned}$$
(s3a)

where \({\varvec{G}}_i ({\varvec{x}}_p^t)\) is the gradient of the shape function associated with node \(i\) evaluated at \({\varvec{x}}_{p}^{t}\). The quantities \({s}_{p}^{t}\) and \(\rho _p^t\) are, respectively, the particle stress tensor and the particle mass density at time \(t\). For the DPD particles associated with that cell, Eq. (s3a) is replaced with the following expression:

$$\begin{aligned} \left( {\varvec{f}}_{i}^{t}\right) ^{int}=\sum _{p=1}^{N_p} \left( {\varvec{f}}_{pj}^C +{\varvec{f}}_{pj}^D +{\varvec{f}}_{pj}^R \right) N_i ({\varvec{x}}_p^t), \end{aligned}$$
(s3b)

where \({\varvec{f}}_{pj}^C, {\varvec{f}}_{pj}^D\) and \({\varvec{f}}_{pj}^R\) represent, respectively, the conservative force, dissipative force, and random force vectors on particle \(p\) due to particle \(j (j=1,2,\ldots N_p^j\), where \(N_p^j\) is the number of DPD particles within the cutoff radius of particle \(p\)).

  1. 2.

    Apply essential and natural boundary conditions to the cell nodes, and compute the nodal force vector,

    $$\begin{aligned} {\varvec{f}}_{i}^{t} =\left( {\varvec{f}}_{i}^{t}\right) ^{int}+\left( {\varvec{f}}_{i}^{t}\right) ^{ext}, \end{aligned}$$
    (s4)

    where \(\left( {\varvec{f}}_{i}^{t}\right) ^{ext}\) denotes the external nodal force vector as defined in Eq. (2.16).

  2. 3.

    Update the momenta at the cell nodes:

    $$\begin{aligned} (m{\varvec{v}})_i^{t+\Delta t} =(m{\varvec{v}})_i^t +{\varvec{f}}_{i}^t \Delta t. \end{aligned}$$
    (s5)
  3. 4.

    For each material point, perform the mapping operation from the nodes of the cell containing the material point to that point.

Map the nodal accelerations back to the material point:

$$\begin{aligned} {\varvec{a}}_{p}^{t} =\sum _{i=1}^{N_n} \frac{{\varvec{f}}_{i}^{t}}{m_i^t}N_i \left( {\varvec{x}}_{p}^{t}\right) . \end{aligned}$$
(s6)

Map the current nodal velocities back to the material point to get the velocity \({\bar{{\varvec{v}}}}_{p}^{{t}+\Delta {t}}\) of the particle at the current time step:

$$\begin{aligned} {\bar{{\varvec{v}}}}_{p}^{{t}+\Delta {t}} =\sum _{i=1}^{N_n} \frac{\left( {m{\varvec{v}}}\right) _i^{t+\Delta t}}{m_i^t}N_i \left( {{\varvec{x}}_{p}^{t}}\right) . \end{aligned}$$
(s7)

Compute the current material point position:

$$\begin{aligned} {\varvec{x}}_{p}^{{\varvec{t}}+\Delta {\varvec{t}}} ={\varvec{x}}_{p}^{t} +{\bar{{\varvec{v}}}}_{p}^{{t}+\Delta {t}} \Delta t, \end{aligned}$$
(s8)

which represents a backward integration.

Compute the material point displacement:

$$\begin{aligned} {\varvec{u}}_{p}^{{t}+\Delta {t}} ={\varvec{x}}_{p}^{{t}+\Delta {t}} -{\varvec{x}}_{p}^{0}. \end{aligned}$$
(s9)

As can be seen from Eqs. (s7) and (s8), nodal shape functions are used to map the nodal velocity continuously to the interior of the cell so that the positions of the material points are updated by moving them in a single-valued, continuous velocity field. Because the velocity \({\bar{{\varvec{v}}}}_{p}^{{\varvec{t}}+\Delta {\varvec{t}}}\) is used to update the material point position, the potential numerical error accumulated by the mapping operations is eliminated, such that the interpenetration between material bodies is precluded. This unique feature of the MPM enables simulations of impact and penetration problems without the need for a special contact algorithm.

  1. 5.

    Map the updated material point momenta back to the nodes of the cells containing these material points:

    $$\begin{aligned} (m{\varvec{v}})_i^{t+\Delta t} =\sum _{p=1}^{N_p} \left( {M{\varvec{v}}}\right) _p^{t+\Delta t} N_i \left( {{\varvec{x}}_{p}^{t}}\right) . \end{aligned}$$
    (s10)
  2. 6.

    Find the updated nodal velocities:

    $$\begin{aligned} {\varvec{v}}_{i}^{{t}+\Delta {t}} =\frac{(m{\varvec{v}})_i^{t+\Delta t}}{m_i^t}. \end{aligned}$$
    (s11)
  3. 7.

    Apply the essential boundary conditions to the nodes of the cells containing the boundary points. For the essential boundary conditions, this treatment is consistent with the weak form of the governing equations because the test functions \({\varvec{w}}_{i}^{t}\) are assumed to be zero on the essential boundary.

  4. 8.

    If needed for the constitutive model of a MPM particle, find the current gradient of particle velocity,

    $$\begin{aligned} {\varvec{L}}_{p}^{{t}+\Delta {t}} =\sum _{i=1}^{N_n} {\varvec{v}}_{i}^{{t}+\Delta {t}} {\varvec{G}}_{i} \left( {\varvec{x}}_{p}^{t}\right) , \end{aligned}$$
    (s12)

    and the particle strain increment,

    $$\begin{aligned} \Delta {\varvec{e}}_p =\left( sym{\varvec{L}}_{p}^{{t}+\Delta {t}}\right) \Delta t, \end{aligned}$$
    (s13)

    so that the stress increment can be obtained from the constitutive model for the given strain increment to update the stress tensor of the MPM particle:

    $$\begin{aligned} {s}_{p}^{{t}+\Delta {t}} ={s}_{p}^{t} +\Delta {s}. \end{aligned}$$
    (s14)
  5. 9.

    Identify which cell each material point belongs to, and update the natural coordinates of the material point. This is the convective phase for the next time increment.

  6. 10.

    Repeat steps 1–9 until the time has advanced to the desired value.

As can be seen from Eqs. (s6), (s7), and (s11), the simulation process will fail if \(m_i^t \) is close to zero, which happens when material points are close to the cell boundary. Various nonlocal mapping procedures have been developed over the past decade to avoid the cell-crossing error in the original MPM [9–11]. However, incorporating these improvements into the proposed multiscale simulation procedure will incur considerable computational expense and is beyond the scope of the current work. Instead, a simple measure is taken here to circumvent the cell-crossing issue within the original MPM framework: If \(m_i^t\) is less than a small number set by machine precision, the solutions from the equations in which \(m_i^t \) appears in the denominator are not used to update the variables associated with those equations at that time step.

The procedures associated with Eqs. (s1)–(s14) should apply equally to DPD and MPM particles simulated within the MPM framework. Because the method has not been applied previously to DPD particles, it is necessary to determine whether (or under what conditions) the “coarse grained DPD” that results from using the MPM mapping/remapping algorithm will reproduce the results obtained using standard, energy-conserving DPD (i.e. DPDE, Eqs. (2.2)–(2.5)). This intermediate description, which we refer to as the DPD/MPM-grid model, is tested in Sect. 4.1.1 for the case of a Cu nanorod flyer impacting a Cu nanorod target, and in Sect. 4.1.2 for symmetric tensile extension of a Cu nanorod. Specifically, we compare results obtained using DPDE (hereafter, the DPD-only model) [20] to those obtained using the DPD/MPM-grid model for several choices of MPM background grid resolution. These DPD/MPM-grid model calculations are a necessary validation step on the path to the fully concurrent DPD/MPM framework, which we refer to as the DPD/MPM model.

In this paragraph, an interfacial treatment for the DPD/MPM model is proposed to capture the essential physics by smoothing the difference in force calculations for DPD and MPM particles. For simplicity we consider the case where the DPD and MPM particles are of the same size. The internal force due to the DPD and MPM particles in the interfacial region is calculated using the following equation:

$$\begin{aligned} \left( {\varvec{f}}_{i}^{t}\right) ^{int}&= \sum _{p=1}^{N_p^d} \left( {{\varvec{f}}_{pj}^C +{\varvec{f}}_{pj}^D +{\varvec{f}}_{pj}^R}\right) N_i \left( {{\varvec{x}}_p^t}\right) \nonumber \\&-\sum _{p=N_p^d +1}^{N_p^d +N_p^m} {{\varvec{G}}_{i} \left( {{\varvec{x}}_p^{t}}\right) \cdot {s}_p^t \frac{M_p}{\rho _p^t}} , \end{aligned}$$
(3.1)

where \(N_p^d \) and \(N_p^m \) are, respectively, the number of DPD and MPM particles within the interfacial region. For each DPD particle in the interfacial region, \({\varvec{f}}_{pj}^C, {\varvec{f}}_{pj}^D\) and \({\varvec{f}}_{pj}^R \) in the first term of Eq. (3.1) are determined as follows:

$$\begin{aligned} {\varvec{f}}_{pj}^C&= \sum _{k=1,k\ne j}^{N_p^j} {-\nabla U\left( {{\varvec{r}}_{jk}}\right) {\varvec{e}}_{jk}} \end{aligned}$$
(3.2)
$$\begin{aligned} {\varvec{f}}_{pj}^D&= \sum _{k=1,k\ne j}^{N_p^j} {-\gamma _{jk} w^{D}\left( {{\varvec{r}}_{jk}}\right) {\varvec{v}}_{jk}} \end{aligned}$$
(3.3)
$$\begin{aligned} {\varvec{f}}_{pj}^R&= \sum _{k=1,k\ne j}^{N_p^j} {\sigma _{jk} w^{R}(r_{jk})dW_{jk} {\varvec{e}}_j} , \end{aligned}$$
(3.4)

where \(N_p^j\) is the total number of the particles within the cutoff radius of DPD particle \(p\). In combination with Eq. (3.1), Eqs. (s3a) and (s3b) are used to find the internal forces due to the MPM and DPD particles respectively, outside the interfacial region. It can be seen from Eq. (3.1) that each DPD particle inside the interfacial region is subject to interactions with the MPM particles within its cutoff radius. Similarly, because Eq. (3.1) includes the internal force contributions from both DPD and MPM particles located within the interfacial region, each interfacial MPM particle is also connected with its neighbor DPD particles via the mapping and re-mapping process within the MPM framework.

4 Demonstration

4.1 DPD particles coupled with the MPM background grid

4.1.1 Impact and wave propagation

Our first demonstration of the proposed multiscale simulation procedure is the impact of a Cu flyer onto a Cu target. We consider two simulation models, the DPD-only model as shown in Fig. 2a and the DPD/MPM-grid model in which DPD particles are coupled to the MPM background grid as shown in Fig. 2b. The target size is \(216 {\AA } \times 72.3 {\AA } \times 72.3 {\AA } (10a \times 10a \times 30a\), where \(a = 7.23 {\AA }\) is the coarse-grained lattice constant for face-centered-cubic (fcc) Cu crystal). The system is non-periodic in all three directions. The flyer is 15 Å thick and is treated as a rigid body with initial velocity 5 Å/ps. Two reference regions of thickness 6 Å each are centered at 100 Å and 150 Å from the impact surface in order to estimate the longitudinal wave speed. Prior to impact, the initial DPD configuration was equilibrated for 1000 ps at 298 K by using the Berendsen thermostat [21]. The final phase space point from the equilibration was used as the initial condition for the DPD-only model governed by Eqs. 2.2–2.5. That same phase space point was also embedded into the MPM background grid for the coupled DPD/MPM-grid simulations. Common Neighbor Analysis (CNA) [22] with the lattice constant \(a\) was used to identify the local coarse-grained crystal structures. In the results discussed in connection with Fig. 4, fcc coarse-grained particles are shown as green, hexagonal-close-packed (hcp) particles are shown as red, and the remaining atoms (classified as disordered or surface particles) are shown as white.

Fig. 2
figure 2

Schematic of a Cu target impacted by a Cu flyer, simulated using a the DPD-only model and b the DPD/MPM-grid model

Full size image

As shown in Fig. 3, the time histories of displacements of reference regions 1 and 2 in the Cu target, simulated with the DPD/MPM-grid model for three choices of the background mesh resolution, apparently converge to that obtained from the DPD-only model for sufficiently small cell edge length during the MPM mapping and re-mapping operation. Although the displacement values obtained from the simulations with different cell sizes may be different at a given time, the wave speeds estimated by examining the displacement history—in particular the difference in times at which particles in regions 1 and 2 first undergo significant displacements—are almost the same for the two models (\(\sim 3846\,\hbox {m/s}\)), which indicates that DPD/MPM-grid coupling captures the essential features of elastic wave propagation. The estimated wave speed is close to the value (3630 m/s) obtained in an all-atom MD simulation of wave propagation in a Cu nanobar with \(20a \times 20a\) cross section (where in this case \(a\) is the Cu atomic lattice spacing, 3.63 Å) [6]. Thus, the elastic wave speed is not strongly affected by the coarse-graining process.

Fig. 3
figure 3

Time histories of displacements of reference regions 1 and 2 in the Cu target, simulated using the DPD-only model (solid curve) and the coupled DPD/MPM-grid model with different MPM cell edge lengths (dashed, dot-dashed, and dotted curves)

Full size image

By contrast, as can be seen in Fig. 4, the MPM mapping and re-mapping operation leads to coarsening of the detailed features of the deformation, as characterized using CNA, compared to the DPD-only result. The DPD-only result is shown in Fig. 4a and serves as a baseline. Corresponding results for the DPD/MPM-grid model are shown in Fig. 4b, c for grid edge lengths 2 Å and 8 Å, respectively. The DPD/MPM-grid result for the 2 Å grid is similar, though by no means identical, to the DPD-only result. By contrast, for the 8 Å grid there is no sign of local structural evolution. This is not surprising as the mapping/remapping is effectively a coarse-graining procedure and thus increasing loss of structural detail is expected as the spatial resolution is decreased.

Fig. 4
figure 4

Deformed configurations of the Cu target at 10 ps after impact, simulated using a the DPD-only model and the DPD/MPM-grid model for MPM cell edge lengths of b 2 Å and c 8 Å

Full size image

4.1.2 Tensile test

We next consider a Cu rod under dynamic tensile loading using the DPD-only and DPD/MPM-grid models, as illustrated in Fig. 5. The rod has the dimension of \(216 {\AA } \times 72.3 {\AA } \times 72.3 {\AA }\). The two ends, each of thickness 15 Å, are treated as rigid bodies with a constant velocity of 2.169 Å/ps applied in opposite directions. The loading procedure is similar to that adopted in our previous MD simulations [23, 24].

Fig. 5
figure 5

Schematic of a Cu rod subjected to tensile loading at both ends, simulated using a the DPD-only model and b the DPD/MPM-grid model

Full size image

Figure 6 contains plots of the stress–strain relations of the Cu rod under tensile loading. As can be seen there, the elastic responses for the DPD-only model and the coupled DPD/MPM-grid model are generally consistent. The initial slope of the stress–strain curve is quite similar, which implies that, for sufficiently small MPM grid edge length, the elastic modulus is independent of the spatial resolution of the MPM background grid; and, therefore, the elastic wave speed is not affected by the coupling between DPD and the MPM background grid, a conclusion that was reached independently in connection with Fig. 3. Moreover, it can be seen that as the resolution of the grid is increased the peak stress approaches the value predicted by the DPD-only model, which is consistent with the convergence study of displacement histories discussed in connection with Figs. 3 and 4.

Fig. 6
figure 6

Stress–strain relations for the Cu rod under tensile loading at strain rate 0.02/ps, simulated using the DPD-only model (solid curve) and coupled DPD/MPM-grid model for different MPM cell edge lengths (dashed, dot-dashed, and dotted curves)

Full size image

It should be noted that for the DPD force expression used here [20], the values of the peak stress predicted by both the DPD-only model and the DPD/MPM-grid model are higher than that obtained from all-atom MD simulations [23, 24]. This may be due to the fact that only the pressure-density relations from the DPD and all-atom MD systems were used in parameterizing the DPD force expression. Further work is required to improve the DPD forces, for example, by including additional information such as the stacking fault energy and surface energy in the DPD parameterization.

4.2 Concurrent simulation

Having demonstrated the consistency between DPD-only and coupled DPD/MPM-grid models, we now test the concurrent model wherein both DPD and MPM particles exist in a single computational domain (the DPD/MPM model). As an initial validation case, we investigate elastic wave propagation across the interface between DPD and MPM subdomains, as illustrated in Fig. 7. The flyer/target scenario studied is the same as discussed in Sect. 4.1.1 (see Fig. 2) except that here the left and right halves of the sample consist of MPM and DPD particles, respectively. Both particle types are the same size; the MPM particles in Fig. 7 are artificially increased in size for ease of visualization.

Fig. 7
figure 7

Schematic of a Cu target impacted by a Cu flyer, simulated using the concurrent DPD/MPM model. The physical situation is the same as depicted in Fig. 2 (see Sect. 4.1.1) except that in the present case the right half of the target (and the flyer) consists of DPD particles and the left half consists of MPM particles. The MPM particles are displayed with an artificially increased diameter for clarity of visualization

Full size image

Figure 8 shows the displacement profiles for the concurrent DPD/MPM model at different times. Although there is some apparent effect of the coupling at the midpoint of the target at the shortest time shown, the wave propagates essentially smoothly through the interface between MPM and DPD regions. The elastic wave speed (\(\sim 4338\,\hbox {m/s}\)) estimated in this case is in reasonable agreement with those obtained in Sect. 4.1 (percentage difference = 12 %); and in good agreement with the values obtained from all-atom MD simulations of wave propagation in a Cu nanobar with \(40a \times 40a\) cross section and samples with periodic boundary conditions in directions transverse to the propagation direction (\(\sim 4537\,\hbox {m/s}\) in both cases, percentage difference = 4.5 %) [6]. That the agreement is better for the case of large-cross-section nanobars or periodic samples is not surprising because the MPM description is based on a constitutive model that does not include the effects of the free surfaces that significantly affect wave propagation in the smaller nanobars. Additional work would be required to incorporate such free-surface effects into the MPM constitutive description for the kinds of nanoscale structures studied here.

Fig. 8
figure 8

Displacement profiles at various times for the physical situation depicted in Fig. 7, simulated using the concurrent DPD/MPM model. The edge length of the MPM grid used is 4 Å. The interface between the DPD and MPM subdomains is initially located at \(x \approx 9.35\,\hbox {nm}\)

Full size image

5 Concluding remarks

A particle-based multiscale simulation procedure has been described that includes a hierarchical bridge from MD to DPD and a concurrent link between DPD and the MPM. A simple interfacial treatment has been proposed for concurrent DPD/MPM simulations based on the features of the DPD force expression and the MPM constitutive model, and demonstrated by simulating the dynamic and impact responses of discrete nano structures. It was shown that the DPD details can be effectively coarse grained through the use of a coarse MPM background grid (the DPD/MPM-grid model) while the concurrent link between the MPM and DPD enables the near-seamless integration of constitutive modeling at the continuum level with force-based modeling at the mesoparticle level (the DPD/MPM model). Although the elastic responses predicted by the proposed procedure are reasonable, further studies are required to improve the current DPD forces, understand the size effect on the inelastic responses, and simulate the impact responses of discrete nano structures with various shapes and compositions.