Advertisement

Mitigation of power system forced oscillations based on unified power flow controller

  • Ping JIANG
  • Zikai FAN
  • Shuang FENG
  • Xi WU
  • Hui CAI
  • Zhenjian XIE
Open Access
Article
First Online:
Received:
Accepted:

Abstract

Forced oscillations (FOs), or low-frequency oscillations (LFOs) caused by periodic, continuous, small power disturbances, threaten the security and stability of power systems. Flexible AC transmission system (FACTS) devices can effectively mitigate LFOs via stability control. We propose a novel method that mitigates FOs by shifting the resonant frequency. Based on the features of the linearized swing equation of a generator, a resonant frequency shift can be achieved by controlling the synchronous torque coefficient using a unified power flow controller (UPFC). Because of the resonance mechanism, the steady-state response of an FO can be effectively mitigated when the resonant frequency changes from the original one, which was close to the disturbance frequency. The principle is that a change in resonant frequency affects the resonance condition. Simulations are conducted in a single-machine infinite-bus (SMIB) system, and the simulation results verify that the method is straightforward to implement and can significantly mitigate FOs. The controller robustness when the resonant frequency is not accurately estimated is also analyzed in the simulations.

Keywords

Forced oscillations Flexible AC transmission systems Unified power flow controller Stability control 

1 Introduction

The probability of low-frequency oscillations (LFOs) is increasing with the increasing size of power grids, thereby threatening the normal operation of power systems [1, 2, 3]. As a result, the LFOs of large-area power systems have become an important issue [4]. The traditional theory of power system dynamic analysis claims that LFOs are the result of a negative damping mechanism. Under this theory, an LFO is caused by the lack of damping [5, 6, 7]. However, in recent years, an increasing number of LFO incidents have arisen that cannot be explained by the negative damping mechanism. Instead, forced oscillations (FOs) originate from periodic, continuous, small disturbances in the system [8, 9]. In these cases, a resonance mechanism is required to explain the behavior of power systems. An LFO is explained by resonances between the transmission power and the disturbances in the system [10, 11]. Relative to the LFOs of negative damping mechanisms, FOs start faster and have a larger amplitude; they also spread more broadly. As a result, FOs are more harmful to power systems than the LFOs of a negative damping mechanism [12].

Many studies on the localization and identification of FOs have been conducted. In contrast, few studies on the mitigation of FOs have been conducted. The existing methods for mitigating LFOs are typically based on the ideas of removing the disturbance sources and a power oscillation damping controller (PODC). Methods based on the first approach include removing the disturbing generators and loads, reducing the output of generators, splitting the system and modifying the control model of the prime mover [13, 14]. A PODC is also a valid method for reducing the amplitude of power oscillations and suppressing LFOs [15, 16]. Reference [17] proposed a new approach to design the parameters of the power system stabilizer (PSS) to mitigate FOs. Reference [18] provided a method to mitigate FOs using flexible AC transmission system (FACTS) devices with energy storage. This method directly reduces the disturbance sources to prevent the spread of the oscillation energy. However, damping control cannot provide ideal mitigation of FOs because the lack of damping is not the major cause of FOs. The method neglects the continuity of energy injection in the situation of a resonance mechanism; it is also limited by damping conservation theory, i.e., if we adopt a large damping ratio for one mode, then the other modes of the power system become less stable [19]. As a result, a new approach is required to mitigate FOs.

In this research, the proposed method can be realized by FACTS devices, which can mitigate power oscillations via appropriate control strategies. The unified power flow controller (UPFC) is the most comprehensive example of a FACTS device at present [20]. UPFCs have received much research attention. Reference [21] presented an approach of UPFC stability control to damp inter-area power oscillations. We adopt a UPFC because it is a serial-parallel FACTS device that can realize both voltage control and impedance control [22]. Therefore, we can carry out coordinated control between both sides to simultaneously shift the resonant frequency and guarantee large damping.

To overcome the defects of a PODC, we propose a resonant frequency controller (RFC) based on a UPFC to mitigate FOs. An RFC is added to the UPFC to control the resonant frequency. This RFC method is different from a PODC method because the effect of a PODC depends on the variation in the damping coefficient D. The proposed method can reach a mitigation independently. It can also work in conjunction with a PODC to reach a better result. A large compensation of D is required to provide adequate damping. In contrast, with the proposed method, we simply shift the synchronous torque coefficient K from its original value, which is therefore not affected by the limitation of damping conservation theory. With a resonant controller, the resonant frequency is shifted only when a FO occurs. The principle of the method is analyzed in Section 2. Section 3 presents and analyzes the proposed method of this study, providing a comprehensive model of the system. Section 4 provides a detailed design of the supplementary controller. The method effectively mitigates FOs and exhibits higher performance than a PODC. The effect of the proposed method is verified by the simulations described in Section 5. The performance of the UPFC and the robustness of the proposed method are also provided in this section.

2 Principle of the proposed method

2.1 Introduction of the system

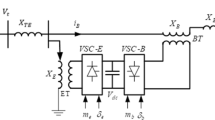
As shown in Fig. 1, a single-machine infinite-bus (SMIB) system with a UPFC installed at the midpoint is analyzed using a third-order generator model to illustrate the impact of the UPFC and the principle of the proposed method [7]. In Fig. 1, E’ is the transient electromotive force and δg is its phase; Xd’ is the transient reactance of the generator and XT is the reactance of the transformer; X is the reactance of the transmission line; VUPFC and XUPFC are the voltage of UPFC shunt side and the reactance of UPFC serial side, respectively; V is the sending terminal voltage.
Fig. 1

SMIB system with a UPFC

Equation (1) is the linearized swing equation of the generator rotor:
$$\frac{{T_{\text{J}} }}{{\omega_{ 0} }}\frac{{{\text{d}}^{2} \Delta \delta }}{{{\text{d}}t^{2} }} + D_{\text{g}} \frac{{{\text{d}}\Delta \delta }}{{{\text{d}}t}} = - \Delta P_{\text{e}} + \Delta P_{\text{m}}$$
(1)
where δ is the power angle of the generator; ω0 is the base frequency; TJ and Dg are the inertial constant and damping coefficient of the generator, respectively; ∆Pe and ∆Pm are the variation in the electromagnetic power and mechanical power output, respectively. The mechanical power is regulated by the governor; a disturbance from the governor is a common cause of FOs [12].
In the generator model, the variation in electromagnetic power ∆Pe is approximately equal to the variation in electromagnetic torque ∆Te [7]. The variation in electromagnetic power is given by (2).
$$\Delta P_{\text{e}} \approx \Delta T_{\text{e}} = K\Delta \delta + D_{\text{e}} \frac{{{\text{d}}\Delta \delta }}{{{\text{d}}t}}$$
(2)
where De is the damping coefficient. The original values of K and De are influenced by the parameters of the generator and its excitation system. These values are also related to the transmission line impedance [23].

A UPFC is installed at the midpoint of the transmission line. It can simultaneously control the local bus voltage and circuit impedance. The UPFC is implemented using two similar solid-state phase voltage source converters (VSCs) that are connected via a common DC link capacitor, as shown in Fig. 1, and each converter is coupled with a transformer [24]. The UPFC in this case is separated into a serial side and a shunt side. Both sides can be used to mitigate FOs; the corresponding models are given in the following sections.

2.2 Resonance mechanism

When a continuous sinusoidal disturbance with frequency Ω and amplitude r arises in the governor, an equation in the form of (3) can be obtained. In (3), D represents the total damping coefficient.
$$\frac{{T_{\text{J}} }}{{\omega_{0} }}\frac{{{\text{d}}^{2} \Delta \delta }}{{{\text{d}}t^{2} }} + D\frac{{{\text{d}}\Delta \delta }}{{{\text{d}}t}} + K\Delta \delta = r\sin \left( {\varOmega t} \right)$$
(3)
The solution of (3) can be separated into two parts, namely, the general solution and the particular solution, which are combined to form the synthesized response of the system:
$$\Delta \delta = B\sin \left( {\varOmega t - \varphi } \right) + B_{1} \left( t \right)\cos \left( {\omega_{\text{d}} t} \right) + B_{2} \left( t \right)\sin \left( {\omega_{\text{d}} t} \right)$$
(4)

The first item of (4) is the steady-state response of FOs. φ is the initial phase of this component. The value of the maximum amplitude B is related to the damping coefficient D, synchronous torque coefficient K and disturbance amplitude r. The detailed expression of B is given in the following section. The frequency of the steady-state response is equal to the disturbance frequency Ω. The second and third items are the transient responses. ωd is the frequency of the transient responses. The amplitudes of transient responses B1(t) and B2(t) decrease to relatively small values several seconds after the starting point.

The transient responses can also be classified as free oscillations which are caused by the initial conditions and accompanied free oscillations which are caused by a disturbance. Based on theoretical analysis, the curves of the synthesized FO are as shown in Fig. 2. Transient responses 1 and 2 represent the free oscillation and the accompanied free oscillation, respectively. The starting process of the synthesized FO is slightly different from the real situation because an ideal phase step is used. As shown in Fig. 2, the main factor influencing the amplitude of the FO is the steady-state response. Thus, minimizing the amplitude of the steady-state response can effectively mitigate the FO.
Fig. 2

Curves of a synthesized FO

2.3 Influence of synchronous torque coefficient

According to the resonance mechanism, the resonant frequency is equal to the frequency of free oscillation without damping. When D=0 and r=0, the linearized swing equation of a SMIB system without damping is given in (5) [7].
$$\frac{{T_{\text{J}} }}{{\omega_{0} }}\frac{{{\text{d}}^{2} \Delta \delta }}{{{\text{d}}t^{2} }} + K\Delta \delta = 0$$
(5)
By solving this equation, the frequency of \(\Delta \delta\) can be derived; this frequency is equal to the resonant frequency. As a result, we have
$$\omega_{\text{n}} = \sqrt {\frac{{\omega_{0} K}}{{T_{\text{J}} }}}$$
(6)

This result shows that the resonant frequency is related to both the synchronous torque coefficient and the inertial constant of the generator.

Analogous to a mechanical system, when the disturbance frequency is close to the resonant frequency, the disturbance performs positive work on the system. The disturbance energy is continuously transformed into the system’s potential energy, thereby causing FOs. In contrast, when the resonant frequency is different from the disturbance frequency, the disturbance performs negative work, and the oscillations are damped. According to this theory, when the synchronous torque coefficient changes, the resonant frequency changes, and FOs are mitigated.

If the damping coefficient and the disturbance amplitude of the system are constant, then the expression of maximum amplitude B in (4) can be shown to be a function of K, as expressed in (7) [12].
$$B\left( K \right) = \frac{1}{{\sqrt {\left( {1 - \varOmega \sqrt {\frac{{T_{\text{J}} }}{{\omega_{0} K}}} } \right)^{2} + \left( {\frac{D}{K}\varOmega } \right)^{2} } }}\frac{r}{K}$$
(7)
Based on the derivation above, when the synchronous torque coefficient changes, the resonance condition is affected, and the steady-state response amplitude is much smaller. The expected result is shown in Fig. 3. According to the curves, the steady-state response is mitigated, and the transient state responses remain. Therefore, the proposed method is ideally suited to mitigating a FO. The method transforms FOs into LFOs of a negative damping mechanism. The problem of FOs cannot be completely solved via a simple damping control. However, by transforming the FO into a LFO of a negative damping mechanism, the oscillation can be effectively mitigated via the damping control method. When the oscillation is mitigated to a small range, the stability of the system can be guaranteed.
Fig. 3

Curves of a mitigated synthesized FO

The variation in active power and the variation in the power angle have the relationship ∆P = K∆δ. When the disturbance frequency is fixed, the relationship between the maximum steady-state response amplitude B and synchronous torque coefficient K can be derived from (7). The relationship curves between K and B are shown in Fig. 4. The four curves represent four different disturbance frequencies.
Fig. 4

Curves of the relationship between synchronous torque coefficient and maximum power amplitude of FO

2.4 Generalization of the principle

To generalize the proposed principle to a multimachine system, the linearized swing equation set should be analyzed. The swing equation set of the multi-machine system is given by (8).
$$\left[ {\begin{array}{*{20}l} {\frac{{T_{{\text{J}1}} }}{{\omega_{0} }}\frac{{\text{d}^{2} \Delta \delta_{1} }}{{\text{d}t^{2} }}} \hfill \\ {\frac{{T_{{\text{J}2}} }}{{\omega_{0} }}\frac{{\text{d}^{2} \Delta \delta_{2} }}{{\text{d}t^{2} }}} \hfill \\ \vdots \hfill \\ {\frac{{T_{{{\text{J}}n}} }}{{\omega_{0} }}\frac{{{\text{d}}^{2} \Delta \delta_{n} }}{{{\text{d}}t^{2} }}} \hfill \\ \end{array} } \right] =\Delta \varvec{P}_{\text{M}} - \left[ {\begin{array}{*{20}l} {D_{1} \frac{{\text{d}\Delta \delta_{1} }}{{\text{d}t}}} \hfill \\ {D_{2} \frac{{\text{d}\Delta \delta_{2} }}{{\text{d}t}}} \hfill \\ \vdots \hfill \\ {D_{n} \frac{{{\text{d}}\Delta \delta_{n} }}{{\text{d}t}}} \hfill \\ \end{array} } \right] - \left[ {\begin{array}{*{20}l} {K_{{\text{s1}}} \Delta \delta_{1} } \hfill \\ {K_{{\text{s2}}} \Delta \delta_{2} } \hfill \\ \vdots \hfill \\ {K_{{{\text{s}}n}} \Delta \delta_{n} } \hfill \\ \end{array} } \right]$$
(8)
where TJ1, TJ2, …, TJn denote the inertial constants of n oscillation modes; D1, D2, …, D n denote the damping coefficients of the oscillation modes; Ks1, Ks2, …, Ksn denote the synchronous torque coefficients of the oscillation modes; ∆δ1, ∆δ2, …, ∆δ n are the variations in the power angles of the oscillation modes; \(\Delta \varvec{P}_{\text{M}}\) is a vector that represents the power of disturbance from the mechanical power of the generators. The process for solving the equation set is complex [25]. Assuming that only one disturbance signal exists in the system, the final expression of the amplitude of the ith-order steady-state response is as follows:
$$B_{i} \left( {K_{i} } \right) = \sqrt {\frac{{\left( {\frac{{r_{\text{a}} }}{{K_{i} }}} \right)^{2} + \left( {\frac{{\varOmega r_{\text{b}} }}{{K_{i} }}} \right)^{2} }}{{\left( {1 - \varOmega \sqrt {\frac{{T_{{{\text{J}}i}} }}{{\omega_{0} K_{i} }}} } \right)^{2} + \left( {\frac{{D_{i} }}{{K_{i} }}\varOmega } \right)^{2} }}}$$
(9)
where ra and rb are constants determined by the amplitude of the disturbance; TJi, K i and D i denote the inertial coefficient, the synchronous torque coefficient and the damping coefficient of the ith-order response, respectively.

Equation (9) shows that the amplitude of the steady-state response of the FO in a multimachine system is related to the synchronous torque coefficient of the relevant mode K i . By controlling K i , the resonant frequency of the ith-order mode can be changed, and the ith-order FO is mitigated, thereby demonstrating that the proposed method can be generalized to a multimachine system.

3 Analysis of UPFC

3.1 Integrated model of the system

This section provides a detailed analysis of the SMIB system with a UPFC shown in Fig. 1 to explain the principle of the proposed controller.

The UPFC can be separated into the shunt side and the serial side. The shunt side of the UPFC achieves voltage control at the midpoint, and the serial side is used to control the impedance of the transmission line. The serial side of the UPFC interacts with the shunt side because the shunt-side voltage VUPFC is influenced by the serial-side impedance XUPFC. Considering this interaction, the integrated model of the system is as shown in Fig. 5, where impedances X1, X2 and XΣ are defined using the impedances shown in Fig. 1 and transformed by (A1) in Appendix A. The expressions for K1-K6 can also be found in Appendix A (see (A2) to (A7)) [7, 26]. Some variables in the expressions for K1-K6 are defined as follows. In Fig. 5, all the input signals are marked with dashed lines. Gsh(s) and Gse(s) are first-order inertia elements that simulate the function of the shunt side and the serial side, respectively. The expressions of these elements are given later. Input signals ∆PRFC and ∆VRFC are obtained from the proposed supplementary RFC. ∆XUPFC and ∆BUPFC are the output signals of the serial side and the shunt side, respectively. The physical meanings of these signals are discussed in the following subsections. In a real system, the effect of this control is realized via the transmission of an equivalent injected power or current from the UPFC to its installation point [26, 27].
Fig. 5

Block diagram of SMIB system with a UPFC

This diagram and the derivations below can be used to find the additional angle for the design of the supplementary controller. Details regarding the supplementary control strategy of the UPFC are discussed in the next section.

3.2 Impact of UPFC shunt side

With the shunt side of the UPFC, midpoint voltage control can be achieved. An equivalent circuit of the UPFC shunt side is shown in Fig. 6.
Fig. 6

Equivalent circuit of UPFC shunt side

The midpoint voltage Vm is set to the shunt side voltage VUPFC. The network equation of Fig. 6 is:
$$\left\{ {\begin{array}{*{20}l} {\dot{E}^{{\prime }} = \dot{V}_{\text{UPFC}} + \text{j}X_{1} \dot{I}_{1} } \hfill \\ {\dot{V}_{\text{UPFC}} = \dot{V} + \text{j}X_{2} \dot{I}_{2} } \hfill \\ {\dot{I}_{1} = \dot{I}_{2} - \dot{I}_{\text{UPFC}} } \hfill \\ {\dot{I}_{\text{UPFC}} = \text{j}\dot{V}_{\text{UPFC}} B_{\text{UPFC}} } \hfill \\ \end{array} } \right.$$
(10)
where BUPFC denotes an equivalent susceptance to control the midpoint voltage.
We use a first-order inertia element Gsh(s) given by (11) to simulate the UPFC midpoint voltage control on the shunt side with a gain of Ksh and time constant Tsh.
$$G_{\text{sh}} (s) = \frac{{K_{\text{sh}} }}{{1 + sT_{\text{sh}} }}$$
(11)
The following can be derived:
$$\left\{ {\begin{array}{*{20}l} {T_{\text{sh}} \frac{{{\text{d}}\Delta B_{\text{UPFC}} }}{{{\text{d}}t}} = - K_{\text{sh}} \left( {\Delta V_{\text{UPFC}} - \Delta V_{\text{RFC}} } \right) - \Delta B_{\text{UPFC}} } \hfill \\ {\Delta T_{\text{e}} \approx \Delta P_{\text{e}} = K_{1} \Delta \delta + K_{2} \Delta B_{\text{UPFC}} } \hfill \\ {\Delta V_{\text{UPFC}} = K_{4} \Delta \delta + K_{5} \Delta B_{\text{UPFC}} } \hfill \\ \end{array} } \right.$$
(12)

In this section, we consider only the function of the shunt side; thus, the serial-side impedance XUPFC is equal to 0 in the expressions for K1-K6.

A supplementary modulated signal given by (13) is used to control the resonant frequency, as shown in Fig. 5. The detailed design of this signal is discussed in the next section.
$$\Delta V_{\text{RFC}} = G_{\text{RFC}} (s)\Delta \delta = (\varGamma + s\varPsi )\Delta \delta$$
(13)
where Γ and Ψ denote the real and imaginary parts of the transform function, respectively. Let s=jΩ, and combine (12) and (13). The expression of variation in the complex electromagnetic torque is:
$$\Delta T_{\text{e}} = K_{1} \Delta \delta - \frac{{K_{2} K_{{\text{sh}}} \left( {K_{4} - G_{{\text{RFC}}} (s)} \right)}}{{1 + K_{5} K_{{\text{sh}}} + \text{j}\varOmega T_{{\text{sh}}} }}\Delta \delta$$
(14)
Based on (2) and (14), the expression of the synchronous torque coefficient is given by (15).
$$K = K_{1} - \frac{{K_{2} K_{\text{sh}} \left[ {(1 + K_{5} K_{\text{sh}} )(K_{4} - \varGamma ) + \varOmega \varPsi T_{\text{sh}} } \right]}}{{1 + K_{5} K_{\text{sh}} + \varOmega^{2} T_{\text{sh}} }}$$
(15)
Define A1 and A2 as:
$$\left\{ {\begin{array}{*{20}l} {A_{1} = \frac{{K_{2} K_{\text{sh}} (1 + K_{5} K_{\text{sh}} )}}{{1 + K_{5} K_{\text{sh}} + \varOmega^{2} T_{\text{sh}} }}} \hfill \\ {A_{2} = \frac{{K_{2} K_{\text{sh}} \varOmega T_{\text{sh}} }}{{1 + K_{5} K_{\text{sh}} + \varOmega^{2} T_{\text{sh}} }}} \hfill \\ \end{array} } \right.$$
(16)
Then the following can be derived:
$$K = K_{0} + A_{1} \varGamma - A_{2} \varPsi$$
(17)
where K0 = K1 − A1K4. If the shunt side operates strictly in a constant midpoint voltage mode, then the UPFC can exert a natural influence only on the synchronous torque coefficient of the mode. The resonant frequency changes after the installation of the UPFC. However, when a disturbance arises at the new frequency, FOs still occur. To solve this problem, the shunt side voltage should be modulated, and control of the synchronous torque coefficient can be achieved according to (17). A clearer derivation follows.
The transmission power of this system is:
$$P_{\text{e}} = \frac{{VV_{\text{m}} }}{{X_{2} }}\sin \left( {\frac{\delta }{2}} \right)$$
(18)
Equation (18) has this linearized form:
$$\Delta P_{\text{e}} = \frac{{\partial P_{\text{e}} }}{\partial V}\Delta V + \frac{{\partial P_{\text{e}} }}{{\partial V_{\text{m}} }}\Delta V_{\text{m}} + \frac{{\partial P_{\text{e}} }}{\partial \delta }\Delta \delta + \frac{{\partial P_{\text{e}} }}{{\partial X_{2} }}\Delta X_{2}$$
(19)
When the sending terminal voltage V and impedance of the transmission line X2 are constant, combining (19) and (1) yields
$$\frac{{T_{\text{J}} }}{{\omega_{0} }}\frac{{{\text{d}}^{2} \Delta \delta }}{{{\text{d}}t^{2} }} + D_{\text{g}} \frac{{{\text{d}}\Delta \delta }}{{{\text{d}}t}} + \frac{{\partial P_{\text{e}} }}{{\partial V_{\text{m}} }}\Delta V_{\text{m}} + \frac{{\partial P_{\text{e}} }}{\partial \delta }\Delta \delta = \Delta P_{\text{m}}$$
(20)
If an ideal modulated output voltage ∆Vm = KM∆δ is realized via an appropriate design of GRFC(s) to take control of the resonant frequency of a certain mode, then (20) can be rewritten as:
$$\frac{{T_{\text{J}} }}{{\omega_{0} }}\frac{{{\text{d}}^{2} \Delta \delta }}{{{\text{d}}t^{2} }} + D\frac{{{\text{d}}\Delta \delta }}{{{\text{d}}t}} + \left( {\left. {\left. {K_{\text{M}} \frac{{\partial P_{\text{e}} }}{{\partial V_{\text{m}} }}} \right|_{0} + \frac{{\partial P_{\text{e}} }}{\partial \delta }} \right|_{0} } \right)\Delta \delta = \Delta P_{\text{m}}$$
(21)
The supplementary controller realizes control of K according to (21). Based on (6), the new resonant frequency can be calculated as:
$$\omega_{\text{n}} = \sqrt {\frac{{\omega_{0} }}{{T_{\text{J}} }}\left( {K_{\text{M}} \frac{{\partial P_{\text{e}} }}{{\partial V_{\text{m}} }} + \frac{{\partial P_{\text{e}} }}{\partial \delta }} \right)}$$
(22)

When the resonant frequency changes, FOs are mitigated according to the theory presented in Section 2.

Regarding a multimachine system, when the supplementary signal is designed to compensate for the synchronous torque of a certain ith-order mode, the FOs of this mode are mitigated, as is apparent in (9).

3.3 Impact of UPFC serial side

An equivalent circuit of the system with a UPFC serial side is shown in Fig. 7. The UPFC serial side can provide impedance control.
Fig. 7

Equivalent circuit of UPFC serial side

A first-order inertia element Gse(s) with a gain of Kse and time constant Tse, as shown in Fig. 5, is used to simulate the UPFC transmission line impedance control on the UPFC serial side. The measured power of the transmission line is chosen as the input signal. The following can be derived:
$$\left\{ {\begin{array}{*{20}l} {T_{\text{se}} \frac{{{\text{d}}\Delta X_{\text{UPFC}} }}{{{\text{d}}t}} = K_{\text{se}} \left( {\Delta P_{\text{e}} - \Delta P_{\text{RFC}} } \right) - \Delta X_{\text{UPFC}} } \hfill \\ {\Delta T_{\text{e}} \approx \Delta P_{\text{e}} = K_{1} \Delta \delta + K_{3} \Delta X_{\text{UPFC}} } \hfill \\ \end{array} } \right.$$
(23)
Using (12) and (23), the diagram in Fig. 5 can be obtained. Using a similar derivation, it is straightforward to find that if the serial-side impedance is modulated by a supplementary signal, for example, ∆X2 = KX∆δ, then the resonant frequency is given by:
$$\omega_{\text{n}} = \sqrt {\frac{{\omega_{0} }}{{T_{\text{J}} }}\left( {K_{\text{X}} \frac{{\partial P_{\text{e}} }}{{\partial X_{2} }} + \frac{{\partial P_{\text{e}} }}{\partial \delta }} \right)}$$
(24)

Moreover, the serial side of the UPFC can compensate for the damping of the system [28] and can work in conjunction with the shunt side to improve the effectiveness of FO mitigation.

4 Design of resonant frequency controller

4.1 Structure of UPFC resonant frequency controller

In Fig. 5, the fluctuations in ∆Pm lead to FOs. The magnification of the disturbances is related to the synchronous torque coefficient K according to (7). As shown in Fig. 5, K is determined by the transfer function of the UPFC. In fact, merely the installation of the UPFC can change the original synchronous torque coefficient. However, without a supplementary controller, FOs still occur when a disturbance exists at a new resonant frequency. In this section, we propose the structure of the UPFC RFC to mitigate such FOs.

Taking the shunt side as an example, the general structure of the RFC is as shown in Fig. 8. In Fig. 8, xi is the input signal and xref is the reference value of it; Vi is the voltage of the installment point and Vref is the reference voltage; B is the equivalent susceptance caused by the controller. The controller contains a resonant controller R(s), a DC block element T ω (s), and a phase compensation unit T(s). The supplementary signal ∆VRFC is added to the corresponding location in Fig. 5. Gsh(s) is the first-order inertia element used to simulate the UPFC shunt side, as shown in Fig. 5. The detailed design of each control unit is discussed in the following subsections.
Fig. 8

Structure of the resonant frequency controller

The chosen input signal ∆x can be the variation in the power angle ∆δ, the variation in the generator speed ∆ω, the opposite of the variation in the transmission power −∆Pe, and so on. To shift the resonant frequency from the disturbance frequency when an FO of a certain mode arises, the resonant controller R(s) must be adopted [29]. Thus, for maximum compensation with synchronous torque coefficient K, a phase compensation unit T(s) is adopted to change the phase of the signal. The expression for the DC block element T ω (s) is shown in (25), which is used to remove the DC components of the signals. In (25), K ω is the gain of the element and T ω is the time constant of it.
$$T_{\omega } \left( s \right) = \frac{{K_{\omega } s}}{{(1 + T_{\omega } s)}}$$
(25)

The RFC design of the serial side is similar to the design of the shunt side. In this study, to enable a contrast, a PODC can be used on the serial side of the UPFC [30].

4.2 Design of resonant controller

The expression of the resonant controller is:
$$R\left( s \right) = \frac{{K_{\text{R}} \omega_{\text{c}} s}}{{s^{2} + \xi \omega_{\text{c}} s + \omega_{\text{c}}^{2} }}$$
(26)
where ωc is the center frequency; KR is the proportional coefficient; ξ is the damping coefficient of the element. The values of KR and ξ determine the gain and bandwidth of the resonant controller, respectively [31]. The damping ratio ξ can be set to a small number under ideal conditions. The center frequency ωc should be set to the original resonant frequency ωn0. In this study, the value of ωn0 is obtained by performing small signal analysis.
The frequency response of R(s) is as shown in Fig. 9. The RFC has maximum gain at the original resonant frequency, thereby guaranteeing that the controller maintains the stability of the system. KR can be set to a small number to make the effect of the resonant controller more ideal, as this approach substantially reduces the gain at frequencies other than the center frequency. In real cases, considering the error in identifying the resonant frequency, the damping coefficient should be set to a larger value to improve the robustness of the controller.
Fig. 9

Frequency response of R(s) when ωc=2π×1.67 and KR=0.16

The main component of FOs is the steady-state response. In (2), the frequency of the steady-state response is found to be equal to the disturbance frequency Ω instead of the resonant frequency ωn. This point is important because if the resonant frequency changes from ωn0 to ωn1, then the frequency of the input signal is still Ω, which can maintain the RFC’s effectiveness. Moreover, if the disturbance frequency is equal to ωn1, then the gain of the resonant controller is close to zero because Ω is equal to ωn1. As the resonant frequency is still ωn0 under this condition, FOs can be avoided. The only problem occurs when oscillation modes of ωn0 and ωn1 exist simultaneously in the system; this situation is a low-probability event. However, the higher harmonics of the oscillation mode ωn0 have been observed to exist in real systems [32]. Therefore, when we design the RFC, we should avoid the situation in which the final ωn is equal to the frequency of any higher harmonics of the oscillation mode ωn0.

4.3 Design of phase compensation unit

The transfer function of the phase compensation unit is:
$$T\left( s \right) = \left( {\frac{{1 + T_{1} s}}{{1 + T_{2} s}}} \right)^{m}$$
(27)
where m is the number of lead-lag components. To compensate for the synchronous torque coefficient K, the input signal should be modulated to keep the signal synchronous with respect to the variation in the power angle, which lags the input signal by 90°. The relationships between those vectors are shown in Fig. 10 for the case in which the input signal is synchronous with respect to −∆Pe (which is opposite to ∆δ). ∆TRFC is the complex torque caused by the RFC. The compensation angle is
$$\theta_{\text{RFC}} = - \theta_{\text{com}} - \theta_{\text{add}}$$
(28)
where θcom is determined by the input signal; θadd is the additional angle caused by the original system with the UPFC. The value of θcom should be set to compensate for the synchronous torque coefficient K. The value of θadd is affected by the excitation system [33]. From (16) and (17), we find that θadd can be influenced by the angle of the first-order inertia element Gsh(s) with an independent shunt side. In fact, θadd is also affected by the influence of the serial side, as shown in Fig. 7. Moreover, the influence of the resonant controller on θadd should be considered in a similar manner.
Fig. 10

Phase diagram to illustrate the proposed method

The center frequency of the phase compensation unit ωTc should be set as close as possible to the original resonant frequency ωn0. This design achieves an appropriate gain for this unit [17]. The design of time constant values should follow:
$$\left\{ {\begin{array}{*{20}l} {\frac{{T_{2} }}{{T_{1} }} = \frac{{1 - \sin \left( {\frac{{\theta_{\text{RFC}} }}{m}} \right)}}{{1 + \sin \left( {\frac{{\theta_{\text{RFC}} }}{m}} \right)}}} \hfill \\ {\omega_{\text{n0}} \approx \frac{1}{{\sqrt {T_{1} T_{2} } }}} \hfill \\ \end{array} } \right.$$
(29)
The final control strategy is illustrated in Fig. 11. Assuming that the system has a mode of negative damping (which can be represented by the complex torque ∆Te0 having a negative imaginary part) via a supplementary damping controller at the UPFC serial side, ∆TPODC is added to ∆Te0. In addition, ∆Te1 is obtained with a imaginary part. The LFO of the negative damping mechanism is mitigated using this method.
Fig. 11

Phase diagram to illustrate the comprehensive control strategy

When a disturbance exists at the original resonant frequency, the RFC operates, and ∆TRFC is added to ∆Te1. ∆Te2 has a larger real part, i.e., the synchronous torque coefficient becomes larger. The change in ∆Te1 can shift the resonant frequency; as a result, FOs are mitigated in this situation.

In a multimachine system in which no infinite bus is considered, the relationship between the response of the rotor angle and the disturbance is no longer a 90° lag. Optimization algorithms such as the genetic algorithm (GA) and particle swarm optimization (PSO) can be used to design the parameters of the phase compensation unit [34, 35].

5 Simulation verification

5.1 Results of PODC method

In this section, we investigate the effectiveness of the proposed method in a SMIB system. A comparison between the traditional method and the new method is conducted to demonstrate the advantages of the proposed method.

A sixth-order SMIB system with an excitation system and governor has been constructed in MATLAB/SIMULINK. The parameters are listed in Appendix B. Before the UPFC is installed, the resonant frequency of the system is 1.44 Hz. The resonant frequency changes to 1.67 Hz after the installation of the UPFC. In this system, the active power delivered is 0.75 p.u. A 0.05 p.u. sinusoidal disturbance at 1.67 Hz is added to the mechanical power output from 0 to 40 s. Typical FO curves for the synthesized FO in Fig. 2 are denoted by PFO in Fig. 12. The maximum amplitude of the power oscillation is approximately 0.6 p.u., which amplifies the disturbance by approximately 12 times, demonstrating the adverse consequences of FOs.
Fig. 12

Simulation results for UPFC using a PODC

First, a conventional PODC on the UPFC serial side is used to mitigate PFO. Two lead-lag components are used in this supplementary controller; thus, m = 2. The shunt-side UPFC works in a constant-voltage mode that does not compensate for the synchronous torque coefficient of this mode. The optimized parameters of the PODC are: T ω  = 10.0, K = 30.0, T1 = 0.31, T2 = 0.05. The simulation results are as shown in Fig. 12, where PFO reflects the oscillation caused by the disturbance in this system and PPODC represents the mitigated power oscillation.

In this situation, the maximum amplitude of the power oscillation is approximately 0.15 p.u., which is approximately 25% of the original oscillation. The result demonstrates that using a PODC is a valid method for damping FOs. Figure 13 shows related curves regarding the performance of the UPFC, including the equivalent injected current of the UPFC Iinj, the reactive power of the UPFC Qc, and the voltage of the converters Vconv.
Fig. 13

Performance of UPFC with PODC method

With a current is injected on the UPFC serial side, the impedance of the system changes when an oscillation arises. In addition, the UPFC current increases the damping of the oscillation mode. The injected current can reflect the influence on the active power of the system from the UPFC. FOs are mitigated when the damping is enhanced. However, the effect is not ideal because there is a limit to the amount of damping compensation that can occur.

Moreover, the disturbance source continuously injects energy into the system, making it challenging to damp FOs with a PODC because we need higher damping compensation. The reactive power in Fig. 13b is caused by the UPFC capacitor. The reactive power and the converter voltage reflect the UPFC working condition. When the controller gain is too high, they may be distorted.

5.2 Results of the proposed method

Graphs of a mitigated FO, similar to the synthesized one in Fig. 3 are shown in Fig. 14, where PFO reflects the oscillation caused by the disturbance and PRFC represents the mitigated power oscillation. We use two different sets of parameters to mitigate oscillations, corresponding to the different directions of K, and they are shown in Table 1.
Fig. 14

Simulation results for UPFC using a RFC

Table 1

Parameters of RFC

Parameter set

K R

ξ

ω n0

T ω

K ω

T 1

T 2

I

0.03

0.01

10.5

10.0

9.0

0.04

0.23

II

0.62

0.01

10.5

10.0

9.0

0.48

0.02

K is decreased when parameter set I is used. The resonant frequency changes to approximately 1.05 Hz, compared to the resonant frequency of 1.67 Hz after the installation of the UPFC. The amplitude of the oscillation is reduced to approximately 13% of the original amplitude, as shown in Fig. 14a. When using parameter set II, K is increased, and the resonant frequency is temporarily shifted to approximately 3.55 Hz. This simulation achieves a better effect, as shown in Fig. 14b, because the variation in the resonant frequency is larger.

Both simulation results demonstrate the effectiveness of the proposed method. It is better to increase K than to decrease K because a wider adjustable range exists within which K can be increased. The increase in K can also provide better static stability. Note that this result is reached without a large compensation for the damping of this mode. As a result, a transient oscillation remains at the starting stage of the oscillation. The principle of this phenomenon is analyzed in Section 2.3. Thus, we can use other methods to compensate for the damping in conjunction with the proposed method and improve the effect of mitigation.

The performance of the UPFC is shown in Fig. 15. The curves corresponding to a decrease in K show that the UPFC provides relatively less current when the proposed method is used, achieving satisfactory mitigation. The amplitudes of reactive power and converter voltage are also smaller. Moreover, based on the curves corresponding to an increase in K, the effect of the proposed method is much better than that of the conventional method when similar current is provided. The function of the UPFC is to shift the synchronous torque coefficient instead of compensating for the damping. Thus, less output of the UPFC is required in the proposed method.
Fig. 15

Performance of UPFC with the proposed method

To solve the problem of the transient response, the UPFC serial side is added to compensate for the damping of this mode. The method is similar to the one described in Section 5.1. The result is shown in Fig. 16, where PFO reflects the oscillation caused by the disturbance and PUPFC represents the mitigated power oscillation. The effect is much better than that shown in Fig. 12 showing the superiority of the UPFC compared to a single PODC. In Fig. 14, we can draw a conclusion that a RFC can mitigate FOs independently, especially their steady-state responses. In this case, these results verify that the proposed method can work in conjunction with a PODC to reach a better result.
Fig. 16

Simulation results for comprehensive method

The curves corresponding to the UPFC with the comprehensive method described in Section 4.3 are shown in Fig. 17. For comparison, the injected current is equivalent on both sides. The results demonstrate a better mitigation effect following the control of resonant frequency when the UPFC output is similar. The reactive power and converter voltage also lie within a reasonable range.
Fig. 17

Performance of UPFC with comprehensive method

5.3 Robustness of the proposed method

In this subsection, simulations are conducted to discuss the robustness of the controller. When designing the resonant controller, the original resonant frequency is required. The parameter is obtained after identifying the oscillation. However, identification errors should be considered in the design of the proposed controller. In common cases, the identification errors are too small to be considered [36]. However, the controller should still be designed to address certain extreme situations.

Three sets of parameters, as shown in Table 2, are used to simulate identification errors. In those cases, the original resonant frequency is not estimated correctly. These errors are much larger than those typically encountered. The serial side of the UPFC operates in the same condition as that shown in Fig. 14.
Table 2

Parameters of RFC used to study robustness

Parameter set

K R

ξ

ω n0

T ω

K ω

T 1

T 2

III

0.62

0.01

12.3

10.0

9.0

0.48

0.02

IV

0.62

0.01

16.2

10.0

9.0

0.48

0.02

V

0.62

0.50

16.2

10.0

9.0

0.48

0.02

The effect of the controller is shown in Fig. 18. The results show that the effect is influenced by identification errors. For parameter sets III and IV, the effect is compromised relative to that of parameter set II, but FOs are still mitigated with both sides of the UPFC. The results of parameter set III show that the controller exhibits strong robustness when the error is not excessive. However, in parameter set IV, the error of the original resonant frequency is significant, which strongly affects the performance of the controller. In this case, the contribution to the mitigation of FOs comes mainly from the PODC on the serial side. To achieve better performance, the damping ratio of resonant controller ξ should be set to a larger value if the identification system is not ideal, as it is in parameter set V. The results of parameter set V show strong robustness of the proposed controller when ξ is appropriately designed.
Fig. 18

Simulation results characterizing robustness of controller

6 Conclusion

We proposed a novel method for mitigating FOs that involves controlling the resonant frequency using a UPFC. Because the new method is based on changing the resonance conditions, this method is a targeted and efficient approach to mitigating FOs. We designed a supplementary controller to control the resonant frequency, which is achieved via compensation of the synchronous torque coefficient. The detailed derivations theoretically show that FOs are significantly mitigated by this method without any negative effect on the normal operation of the power systems. The simulations conducted in an example SMIB system demonstrate the effectiveness of the proposed method. The results show that the proposed method can achieve an outcome superior to that of the traditional PODC. The controller also offers strong robustness even when the resonant frequency is not estimated correctly.

Many noteworthy issues regarding the mitigation of FOs remain to be studied. Firstly, online frequency identification can be adopted to meet the requirement of accuracy of the resonant controller. Secondly, considering that several oscillation modes are typically present in a real system, parallel resonant controllers can be designed to address the situation of multimode oscillations in multimachine systems. Finally, optimization algorithms should be considered to achieve a proper selection of parameters, so that the RFC can compensate for the synchronous torque coefficient of a certain mode in a multimachine system and mitigate corresponding FOs. The design of these parameters is a worthwhile topic for future study.

Notes

Acknowledgements

This work was supported by National Natural Science Foundation of China (No. 51577032) and State Grid Corporation of China (No. 5210K017000C).

References

  1. [1]
    Ma J, Wang T, Wang S et al (2014) Application of dual youla parameterization based adaptive wide-area damping control for power system oscillations. IEEE Trans Power Syst 29(4):1602–1610CrossRefGoogle Scholar
  2. [2]
    Zhang J, Chung CY, Han Y (2015) A novel modal decomposition control and its application to PSS design for damping interarea oscillations in power systems. IEEE Trans Power Syst 27(4):2015–2025CrossRefGoogle Scholar
  3. [3]
    Chung CY, Wang L, Howell F et al (2004) Generation rescheduling methods to improve power transfer capability constrained by small-signal stability. IEEE Trans Power Syst 19(1):524–530CrossRefGoogle Scholar
  4. [4]
    Klein M, Rogers GJ, Kundur P (1991) A fundamental study of inter-area oscillations in power systems. IEEE Trans Power Syst 6(3):914–921CrossRefGoogle Scholar
  5. [5]
    Zhang Y, Mao XM, Chen XL et al (2008) Mechanism and performance of power system damping control. Guangdong Electric Power 21(3):9–12Google Scholar
  6. [6]
    Deng J, Li C, Zhang XP (2015) Coordinated design of multiple robust FACTS damping controllers: a BMI-based sequential approach with multi-model systems. IEEE Trans Power Syst 30(6):1–10CrossRefGoogle Scholar
  7. [7]
    Kundur P (1994) Power system stability and control. McGraw Hill Education, New YorkGoogle Scholar
  8. [8]
    Ma J, Zhang P, Fu HJ et al (2010) Application of phasor measurement unit on locating disturbance source for low-frequency oscillation. IEEE Trans Smart Grid 1(3):340–346CrossRefGoogle Scholar
  9. [9]
    Sarmadi SAN, Venkatasubramanian V (2016) Inter-area resonance in power systems from forced oscillations. IEEE Trans Power Syst 31(1):378–386CrossRefGoogle Scholar
  10. [10]
    Magdy MA, Coowar F (1990) Frequency domain analysis of power system forced oscillations. IEEE Proc C Gener Transm Distrib 137(4):261–268CrossRefGoogle Scholar
  11. [11]
    Vournas CD, Krassas N, Papadias BC (1991) Analysis of forced oscillations in a multimachine power system. In: Proceedings of international conference on control, Edinburgh, UK, 25–28 March 1991, pp 443–448Google Scholar
  12. [12]
    Tang Y (2006) Fundamental theory of forced power oscillation in power system. Power Syst Technol 30(10):29–33Google Scholar
  13. [13]
    Wang X, Li XX, Li FS (2009) Analysis and online diagnosis on plugging fault of servo valve in electro-hydraulic regulating system of steam turbine. Chin J Mech Eng 22(2):233–237CrossRefGoogle Scholar
  14. [14]
    Su C, Hu W, Chen Z et al (2013) Mitigation of power system oscillation caused by wind power fluctuation. IET Renew Power Gener 7(6):639–651CrossRefGoogle Scholar
  15. [15]
    Larsen EV, Sanchez-Gasca JJ, Chow JH (1995) Concepts for design of FACTS controllers to damp power swings. IEEE Trans Power Syst 10(2):948–956CrossRefGoogle Scholar
  16. [16]
    Chaudhuri B, Pal BC, Zolotas AC et al (2003) Mixed-sensitivity approach to H ∞, control of power system oscillations employing multiple facts devices. IEEE Trans Power Syst 18(3):1149–1156CrossRefGoogle Scholar
  17. [17]
    Feng S, Jiang P, Wu X (2016) PSS design method for suppressing low-frequency oscillation of resonance mechanism. Power Syst Prot Control 44(7):1–6Google Scholar
  18. [18]
    Beza M, Bongiorno M (2015) An adaptive power oscillation damping controller by STATCOM with energy storage. IEEE Trans Power Syst 30(1):484–493CrossRefGoogle Scholar
  19. [19]
    Zhao SQ, Chang XR, He RM et al (2004) Borrow damping phenomena and negative damping effect of PSS control. Proc CSEE 24(5):7–11Google Scholar
  20. [20]
    Keri AJF, Mehraban AS, Lombard X et al (1999) Unified power flow controller (UPFC): modeling and analysis. IEEE Trans Power Deliv 14(2):648–654CrossRefGoogle Scholar
  21. [21]
    Gyugyi L, Schauder CD, Williams SL et al (1995) The unified power flow controller: a new approach to power transmission control. IEEE Trans Power Deliv 10(2):1085–1097CrossRefGoogle Scholar
  22. [22]
    Jiang S, Gole AM, Annakkage UD et al (2011) Damping performance analysis of IPFC and UPFC controllers using validated small-signal models. IEEE Trans Power Deliv 26(1):446–454CrossRefGoogle Scholar
  23. [23]
    Zhu X, Sun H, Wen J et al (2014) Improved complex torque coefficient method using CPCM for multi-machine system SSR analysis. IEEE Trans Power Syst 29(5):2060–2068CrossRefGoogle Scholar
  24. [24]
    Song C, Duan SX, Li C (2007) Comparison of UPFC performance between cross coupling and decoupling controls. Electric Power Autom Equip 27(5):45–49Google Scholar
  25. [25]
    Yu YP, Min Y, Chen L (2009) Analysis of forced power oscillation steady-state response properties in multi-machine power systems. Autom Electric Power Syst 33(22):5–9Google Scholar
  26. [26]
    Wang Y, Song X, Yan Z et al (2011) Modeling and simulation studies of unified power flow controller based on power-injected method in PSASP. In: Proceedings of 2nd international conference on artificial intelligence, management science and electronic commerce, Dengleng, China, 8–10 August 2011, pp 4076–4079Google Scholar
  27. [27]
    Meng ZJ, So PL (2000) A current injection UPFC model for enhancing power system dynamic performance. In: Proceedings of IEEE power engineering society winter meeting, Singapore, 23–27 January 2000, pp 1544–1549Google Scholar
  28. [28]
    Tso SK, Liang J, Zeng QY et al (1997) Coordination of TCSC and SVC for stability improvement of power systems. In: Proceedings of 4th international conference on advances in power system control, operation and management, Hong Kong, China, 11–14 November 1997, pp 371–376Google Scholar
  29. [29]
    Nabavi-Niaki A, Iravani MR (1996) Steady-state and dynamic models of unified power flow controller (UPFC) for power system studies. IEEE Trans Power Syst 11(4):1937–1943CrossRefGoogle Scholar
  30. [30]
    Subramanian DP, Devi RPK (2010) Application of TCSC power oscillation damping controller to enhance power system dynamic performance. In: Proceedings of joint international conference on power electronics, drives and energy systems (PEDES) and 2010 power India, New Delhi, India, 20–23 December 2010, 5 ppGoogle Scholar
  31. [31]
    Hasanzadeh A, Onar OC, Mokhtari H et al (2010) A proportional-resonant controller-based wireless control strategy with a reduced number of sensors for parallel-operated UPSS. IEEE Trans Power Deliv 25(1):468–478CrossRefGoogle Scholar
  32. [32]
    Kamarposhti MA, Alinezhad M, Lesani H (2008) Comparison of SVC, STATCOM, TCSC, and UPFC controllers for static voltage stability evaluated by continuation power flow method. In: Proceedings of IEEE Canada electric power conference, Vancouver, Canada, 6–7 October 2008, 8 ppGoogle Scholar
  33. [33]
    Zha W, Yuan Y (2010) Mechanism of active-power-PSS low-frequency oscillation suppression and characteristic of anti-regulation. In: Proceedings of 3rd international conference on measuring technology and mechatronics automation (ICMTMA), Shangshai, China, 6–7 January 2011, pp 538–541Google Scholar
  34. [34]
    Mahdad B, Bouktir T, Srairi K (2009) Strategy based PSO for dynamic control of UPFC to enhance power system security. J Electr Eng Technol 4(3):315–322CrossRefGoogle Scholar
  35. [35]
    Mok TK, Ni Y, Wu FF (2000) Design of fuzzy damping controller of UPFC through genetic algorithm. In: Proceedings of IEEE power engineering society summer meeting, Seattle, USA, 16–20 July 2000, pp 1889–1894Google Scholar
  36. [36]
    Sanchez-Gasca JJ, Chow JH (1999) Performance comparison of three identification methods for the analysis of electromechanical oscillations. IEEE Trans Power Syst 14(3):995–1002CrossRefGoogle Scholar

Copyright information

© The Author(s) 2018

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  1. 1.School of Electrical EngineeringSoutheast UniversityNanjingChina
  2. 2.State Grid Jiangsu Economic Research InstituteNanjingChina

Personalised recommendations