1 Introduction

As energy demand and resource depletion increase, managing power generation becomes more complex. It now requires a fast and robust coordinated control technique. Power systems can withstand strained situations with less difficulty because of the rapid development of intelligent algorithms. The rises in electric power demand and stability requirements in a competitive environment require more sophisticated control systems with high speed and flexibility [1,2,3].

Low-frequency oscillations are considered one of the most common issues regarding power system stability. LFO ranges from 0.1 to 3 Hz typically. Moreover, LFO reduces power transfer capacity and disturbs the power system operation of modern power system networks. The undesired oscillation is due to the coupling of a high gain and an inadequately tuned generator excitation system. Undamped LFOs can cause system instability problems or even a total blackout if not considered carefully. A straightforward and efficient supplementary excitation controller becomes essential to improve power system stability [4].

Researchers apply a power system stabilizer (PSS) with various structures to reduce oscillations in the electrical power system. During the increase in electrical power demand, PSS devices can improve the performance of excitation systems and maintain high-power quality standards. This improvement depends on the efficiency of the design of artificial intelligence tools in designing the PSS controller alone or in coordination with another controller [5].

Typically, PSS provides an appropriate stabilization signal under various operating conditions and disturbances [3]. In [3,4,5,6], the authors emphasize that the primary function of PSSs is to reduce generator rotor oscillations by modulating their excitation with an auxiliary stabilizing signal. A comprehensive analysis of various PSS controllers’ impact on the overall dynamic performance of the power system is presented in [7]. In addition to PSS, flexible AC transmission system (FACTS) devices have received considerable attention from researchers in the last decade as essential auxiliary devices for damping power system oscillations [8].

FACTS relies mainly on rapidly developing power electronics to offer an attractive solution to many stability issues. FACTS devices can effectively improve the power transmission capacity and system stability by employing it as a power oscillation damper (POD) [9, 10]. The static VAR compensator (SVC), a widely used shunt FACTS device, can offer enough damping of the LFOs in modern networks if correctly adopted [10, 11]. The primary purpose of the SVC is to maintain bus voltages within an acceptable range. In general, if correctly coordinated with PSS, SVC can improve the damping of power system oscillations [11]. Uncoordinated controllers of both SVC and PSS can cause system instability. The coordination between SVC and PSS controllers to improve overall power system stability has received considerable attention from researchers [12, 13]. Reference [14] investigates the coordinated PSS and SVC controller for a synchronous generator.

The PSS and SVC controllers have various parameters that must be tuned. The tuning process is a large-scale, nondifferentiable, nonlinear problem. Particle swarm optimization optimized the coordinated lead-lag (LL-PSS) and PID-SVC gains [15]. Due to the rapid advancement of computer technology in recent years, it has become possible to implement power system stabilization controllers with the help of AI optimization tools. Several novel metaheuristic algorithms present the improved, coordinated design between SVC and PSS controllers [4].

Alternatively, various coordinated controller designs for both SVC and PSS to enhance the damping of LFO and improve the power system stability have been suggested in different works. In [16], PSSs and SVC damping controllers are designed using a linearized power system model for small-signal stability enhancement considering a specific operating point. In [17], a coordination controller for the single-machine infinite bus (SMIB) with SVC was designed using input–output linearization and pole assignment techniques.

Several researchers heavily rely on the traditional lead-lag controller when modeling the coordinated structure of SVC with PSS, as in [12, 13, 18,19,20]. In [21], a comparison has been performed between the PID controller and LL controller for SVC to reduce power system oscillations. The results show the superiority of the SVC-based LL-power oscillation damping (LL-POD) compared to the PID-POD.

Recently, control schemes have drastically improved, which resulted in industrial advancements and special attention focused on the FOPID [1]. Unlike the PID controller, which only accepts integer values for the Laplace operator “s,” the FOPID controller accepts fraction values for the “s” operator. Therefore, the FOPID controller system is superior to other controllers. The reliability and robustness of the FOPID controllers have led to widespread implementation [22,23,24].

Several studies are devoted to employing various intelligent techniques to study and analyze coordinated control of SVC devices and PSS. Coordination tuning of PSS and SVC controllers using bacterial swarming optimization (BSO) is observed [25]. The study achieves proper damping of electromechanical oscillations. In [26], the author utilizes the crow search algorithm (CSA) to find the optimal coordinated SVC and PSS dynamic control of SMIB. The antlion optimizer (ALO) developed technique [27].

The PSS and FACTS-PODs controllers are tuned, considering interconnected multimachine power systems. A PSS controller parameter tuning issue in [28] utilizes a new population-based moth flame optimization (MFO) algorithm in a multimachine power system. In [28,29,30], there is a comparison process between the MFO, firefly algorithm (FA), and bacteria foraging (BF) in designing controllers for enhancing power system stability. The comparison results have emphasized the effectiveness of MFO in enhancing overall system stability. The MFO was suggested for optimal tuning of the PSS controller in [31] to damping LFO in electrical power systems.

The MFO applied to design the FOPID coordinated with other controllers to present novel control structures or cascade controllers to employ as automatic generation control (AGC) with different electric power system topologies [2, 32,33,34]. Different optimization tools are applied to design the AGC as ALO [35], MFO [36], gray wolf optimizer (GWO) [37], and grasshopper algorithm [38].

All the control structures are compared in a single-machine infinite bus system (SMIB). Four different severe short circuit tests were applied to test the designed controller. Six different performance indices analyze the test results: maximum overshot, settling time, integral absolute of the error (IAE), integral time absolute of the error (ITAE), integral square of the error (ISE), and integral square time of the error (ISTE).

There is no single best objective function that can suit all situations. However, some standard criteria are four main types [39, 40]: eigenvalue-based objective functions [40,41,42], time-domain objective functions [44], frequency-domain objective functions [45], and multi-objective functions mix the objective functions with weighting factors [46].

The time-domain objective function mainly includes ISE, ITSE, IAE, and ITAE. The ITAE as an objective function has many advantages over the other objective functions in stability studies. ITAE can improve the dynamic performance of a control system by giving more weight to the errors that occur later. ITAE can reduce the steady-state error, which is often more important than the transient response in many applications. ITAE can also result in a more robust and stable control system, especially when there are uncertainties and variations in the system parameters or operating conditions. Furthermore, ITAE can tune PID controllers more effectively than other criteria, such as ISE, because it can balance the trade-off between the proportional, integral, and derivative gains [47,48,49].

This work aims to increase the power system stability by utilizing the MFO to design the coordinated FOPID-PSS and SVC controller as a power oscillation damper (POD). The POD controller is an additional signal to the SVC having a FOPID control structure. The developed method will use the MFO algorithm to obtain optimal parameters for the FOPID controller. The robustness of the MFO algorithm is compared with ALO. On the other hand, the proposed method will be compared with lead-lag PID controllers to ensure the robustness of the developed technique.

The rest of the present paper is constructed as follows: power system modeling is shown in Sect. 2. Then, the controller structure is explained in Sect. Optimization techniques are presented in Sect. 4. Further, in Sect. 5, results and discussions are presented. The conclusion is shown in Sect. 6.

2 Power system modeling

2.1 Modeling of SMIB with SVC

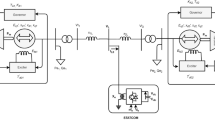
The SMIB system consists of a synchronous generator connected to an infinite bus through a step-up transformer, followed by a transmission line divided into two equal lines connected in series. All data related to the dynamic model of SMIB are listed in [50]. The single-line diagram of the SMIB system is shown in Fig. 1. The SVC comprises a three-phase fixed capacitor thyristor-controlled reactor (FC-TCR) connected in the middle of the transmission line and in parallel with the network [21]. SVC acts as a variable reactance to control specific power system parameters, typically bus voltages. It is widely used for support for reactive power and voltage regulation [50].

Fig. 1
figure 1

Power system model of a SMIB equipped with SVC

Full size image

In Fig. 1, the terms Xl1 and Xl2 refer to the transmission line reactance. Additionally, Vt and Vb refer to the voltages at the generator terminals and the infinite bus, respectively. The SVC controls bus voltage within the desired level [51].

2.2 Linear Model of the SMIB with SVC Facts Device

To optimize the SVC-based power system damping controller, a fourth-order state-space model of the SMIB system with an SVC device and an IEEE Type-ST1A excitation system has been developed, as shown in Fig. 1 [52]. Generally, linearized incremental models around an equilibrium operating point are employed in the design of PSS and SVC. Therefore, the linear Heffron-Phillips model of a SMIB system with SVC can be formulated as in Eqs. (1–4) [26, 52].

Figure 2 shows the Heffron–Phillips SMIB linearized model equipped with SVC [5, 52]. In Fig. 2, K1–K6, Kpβ, Kqβ, Kvβ, and T3 are constants for the Heffron–Phillips SMIB linearized model with SVC. These constants are calculated in [3, 6, 53]. M is the inertia constant, KA is the exciter system circuit constant, D is the coefficient of damping torque, and TA is the exciter time constant. The whole parameters of the SMIB test system are listed in Appendix 1 [3, 6].

$$\dot{\updelta }= {\upomega }_{^\circ } \Delta\upomega $$
(1)
$$ \Delta \dot{\omega } = \frac{{\left[ { - K_{1} \Delta \delta - K_{2} \Delta \mathop E\limits^{\prime }_{q} - K_{P} \Delta \beta svc - D\Delta \omega } \right]}}{2H} $$
(2)
$$ \Delta \mathop {\mathop E\limits^{\prime }_{q} }\limits^{ \cdot } = \frac{{\left[ { - K_{4} \Delta \delta - K_{3} \Delta \mathop E\limits^{\prime }_{q} - K_{q} \Delta \beta svc + \Delta E_{fd} } \right]}}{{T_{{{\text{do}}}}^{\prime } }} $$
(3)
$$ \Delta \mathop {E_{fd} }\limits^{ \cdot } = \frac{{\left[ { - \Delta E_{fd} - K_{A} \left( { K_{5} \Delta \delta + K_{6} \Delta \mathop E\limits^{\prime }_{q} + K_{v} \Delta \beta svc} \right)} \right]}}{{T_{A} }} $$
(4)

where:

$$ \begin{gathered} K_{1} = \frac{{\partial P_{t} }}{\partial \delta }, K_{2} = \frac{{\partial P_{t} }}{{\partial \mathop E\limits^{\prime }_{q} }}, K_{p\beta } = \frac{{\partial P_{t} }}{{\partial \beta_{{{\text{svc}}}} }} \hfill \\ K_{3} = \frac{{\partial E_{q} }}{{\partial \mathop E\limits^{\prime }_{q} }}, K_{4} = \frac{{\partial E_{q} }}{\partial \delta }, K_{q\beta } = \frac{{\partial E_{q} }}{{\partial \beta_{{{\text{svc}}}} }}, \hfill \\ K_{5} = \frac{{\partial V_{t} }}{\partial \delta },K_{6} = \frac{{\partial V_{t} }}{{\partial \mathop E\limits^{\prime }_{q} }},K_{v\beta } = \frac{{\partial V_{t} }}{{\partial \beta_{{{\text{svc}}}} }} \hfill \\ \end{gathered} $$
(5)
Fig. 2
figure 2

Heffron–Phillips SMIB linearized model equipped with SVC

Full size image

3 Controller structure

This section discusses the three types of power system stabilizers used in the investigation. The PSS enhances the stability of the power system network by acting through the excitation system. The excitation system used in this work is based on the IEEE Type-ST1 excitation system with PSS, as shown in Fig. 3. The system is expressed by Eq. (6) [54].

Fig. 3
figure 3

IEEE type-ST1 excitation system with PSS

Full size image
$$\Delta {\mathrm{E}}_{\mathrm{fd}}={\mathrm{K}}_{\mathrm{A}} \left({\mathrm{V}}_{\mathrm{ref}}- {\mathrm{V}}_{\mathrm{t}}+{\mathrm{U}}_{\mathrm{s}}\right)-{\mathrm{E}}_{\mathrm{fd}})/{\mathrm{T}}_{\mathrm{A}}$$
(6)

where Vref and Vt represent the reference and generator terminal voltages, and KA and TA are the excitation system amplifier gain and time constants, respectively. Typically, the stabilizer prevents the power system from oscillating after being subjected to a significant perturbation. The input signal for a PSS structure is typically a deviation from synchronous speed [55].

3.1 Lead lag-PSS.

Figure 4 shows the structure of the LL-PSS, consisting of a washout block, a gain block, and two phase-compensation blocks. The washout block acts as a high-pass filter for input gained from the gain block; it typically lasts from one to twenty seconds. The gain block controls the damping signal received from the PSS input. Two phases at different levels work together to provide the necessary phase-lead feature. The time constants for the first and second compensation phases are T1, T2, T3, and T4, respectively. The transfer function of the PSS is expressed by Eq. (7) [15].

Fig. 4
figure 4

The PSS-LL structure

Full size image
$${\mathrm{G}}_{\mathrm{PSS}}\left(\mathrm{s}\right)={\mathrm{K}}_{\mathrm{S}} [\left(\frac{\mathrm{S }{\mathrm{T}}_{\mathrm{w}}}{1+\mathrm{s }{\mathrm{T}}_{\mathrm{w}}}\right)*\left(\frac{1+\mathrm{s }{\mathrm{T}}_{1}}{1+\mathrm{s }{\mathrm{T}}_{2}}\right)*\left(\frac{1+\mathrm{s }{\mathrm{T}}_{3}}{1+\mathrm{s }{\mathrm{T}}_{4}}\right)]$$
(7)

where Ks, T1, T2, T3, and T4 the controller gains.

3.2 PID-PSS

Since the 1930s, three-mode controllers that work in proportional, integral, and derivative (PID) ways have been used for various industrial applications. The PID controller transfer function is represented by Eq. (8). Kp, Ki, and Kd are the controller gains. The structure of the PID-PSS considered in this work is shown in Fig. 5. [56].

Fig. 5
figure 5

The PID-PSS structure

Full size image
$${\mathrm{G}}_{\mathrm{PSS}}\left(\mathrm{s}\right)={\mathrm{K}}_{\mathrm{p}}+ \frac{{\mathrm{K}}_{\mathrm{i}}}{\mathrm{S}}+{\mathrm{K}}_{\mathrm{d}}\mathrm{ S}$$
(8)

3.3 FOPID-PSS

Podlubny has proposed a modification to the PID control system, commonly known as a fractional-order PID controller, due to the inclusion of the differentiator of order (µ) and integrator of order (λ). Therefore, the FOPID controller has a higher stability range than the PID controller. This PI−λDμ is a highly multilateral control system that allows fine-tuning. The modification led to a more robust control system with distinguishable dynamic characteristics [22]. The differential equation and the transfer function for the PI−λDμ controller are given by Eq. (9) and (10) [1, 22].

$$\mathrm{U}\left(\mathrm{t}\right)= {\mathrm{K}}_{\mathrm{p}}\mathrm{ e}\left(\mathrm{t}\right)+\mathrm{ Ki }{\mathrm{D}}^{-\uplambda }\mathrm{e}\left(\mathrm{t}\right)+{\mathrm{K}}_{\mathrm{d}} {\mathrm{D}}^{\upmu }\mathrm{ e}\left(\mathrm{t}\right)$$
(9)
$${\mathrm{G}}_{\mathrm{PSS}}\left(\mathrm{s}\right)= {\mathrm{K}}_{\mathrm{p}}+\mathrm{ Ki }{\mathrm{S}}^{-\uplambda }+{\mathrm{K}}_{\mathrm{d}} {\mathrm{S}}^{\upmu } ,\uplambda ,\upmu >0$$
(10)

The block diagram of the FOPID controller is shown in Fig. 6, where Ki, Kd, Kp, λ, and µ represent the proportional, differential, integral constants, fractional-order integral, and fractional-order derivative elements, respectively [1].

Fig. 6
figure 6

The FOPID-PSS structure

Full size image

3.4 SVC-POD controller

In order to maintain or regulate specific power system variables, the SVC device is commonly used. SVC is a shunt-connected VAR generator or load. Typically, the bus voltage is the controlled variable; however, oscillation damping can also be achieved by superimposing an additional stabilizing signal and supplementary control on the SVC voltage control loop. The configuration of an SVC, particularly that of an FC-TCR, is illustrated in the schematic diagram of Fig. 7 [14]. The power oscillation damper (POD) controller was added to the SVC to increase the system stability with the PSS. The POD structure is also like the proposed PSS FOPID. A proportional-integral (PI) controller regulates this firing angle, maintaining the bus voltage at the reference (Vref) value [6, 21, 57, 58]. As a function of the SVC switch firing angle (90° \(\le \) α \(\le \) 180°), the inductive susceptance of the thyristor-controlled reactor (\({\upbeta }_{\mathrm{TCR}}\)) can be determined using Eq. (11) and (12). Consequently, Eq. (13) can be used to determine the SVC effective reactance (\({\mathrm{X}}_{\mathrm{SVC}}\)). Hence, the SVC equivalent susceptance (\({\upbeta }_{\mathrm{SVC}})\) can be calculated using Eq. (14) [46,47,48].

Fig. 7
figure 7

The schematic diagram of SVC-FCTCR [6, 21, 57, 58]

Full size image
$${\upbeta }_{\mathrm{TCR}}= \frac{1}{{\mathrm{X}}_{\mathrm{L}}} \frac{(2\uppi -2\mathrm{\alpha }-\mathrm{sin}\left(2\mathrm{\alpha }\right))}{\uppi }$$
(11)
$${\mathrm{X}}_{\mathrm{TCR}}= \frac{1}{{\upbeta }_{\mathrm{TCR}}}= {\mathrm{X}}_{\mathrm{L}} \frac{\uppi }{[2\left(\mathrm{\alpha }-\uppi \right)-\mathrm{sin}\left(2\mathrm{\alpha }\right)]}$$
(12)
$${\mathrm{X}}_{\mathrm{SVC}}= \frac{{\mathrm{X}}_{\mathrm{C}} {\mathrm{X}}_{\mathrm{TCR}}}{{\mathrm{X}}_{\mathrm{TCR}}- {\mathrm{X}}_{\mathrm{C}}}= \frac{\uppi {\mathrm{X}}_{\mathrm{L}} {\mathrm{X}}_{\mathrm{C}}}{{\mathrm{X}}_{\mathrm{C}}\left[2\left(\mathrm{\alpha }-\uppi \right)-\mathrm{sin}\left(2\mathrm{\alpha }\right)\right]+\uppi {\mathrm{X}}_{\mathrm{L}}}$$
(13)
$${\upbeta }_{\mathrm{SVC}}= \frac{1}{{\mathrm{X}}_{\mathrm{SVC}}}= \frac{{\mathrm{X}}_{\mathrm{C}}\left[2\left(\mathrm{\alpha }-\uppi \right)-\mathrm{sin}\left(2\mathrm{\alpha }\right)\right]+\uppi {\mathrm{X}}_{\mathrm{L}}}{\uppi {\mathrm{X}}_{\mathrm{L}} {\mathrm{X}}_{\mathrm{C}}}$$
(14)

where XC denotes thyristor-switched capacitor (TSC) reactance, and XL represents thyristor-controlled reactor (TCR) reactance. The output signal (susceptance provided by SVC (βsvc)) as a function of change in speed is considered in this work. The SVC and its firing control system can be described by Eq. (15) [26].

$${\dot{\upbeta }}_{\mathrm{SVC}}= \frac{[ {\mathrm{K}}_{\mathrm{SVC}} \left(-{\mathrm{V}}_{\mathrm{t}\_\mathrm{SVC}}+ {\mathrm{V}}_{\mathrm{ref}\_\mathrm{SVC}}+ {\mathrm{U}}_{\mathrm{SVC}}\right)-{\upbeta }_{\mathrm{SVC}}]}{{\mathrm{T}}_{\mathrm{SVC}}}$$
(15)

where βsvc is the SVC equivalent susceptance, Vt_svc is the bus voltage magnitude, Vref_svc is the reference voltage for the SVC, and Usvc is the supplemental control input. The gain and time constant of the SVC regulator is Ksvc and Tsvc, respectively. Figure 8 shows the block diagram for the SVC with the supplementary damping controller [62]. This work will use the FOPID controller with the SVC device as a POD unit to enhance power oscillation damping.

Fig. 8
figure 8

Block diagram of the POD-SVC controller

Full size image

3.5 Objective function

Considering power system oscillations, the PSS and SVC controller gains can be adjusted to minimize the overshot and settling time. Consequently, the power system oscillation will be damped, increasing power system dynamic stability. This research aims to simultaneously tune the gains of the PSS and SVC controllers to achieve optimum system stability. Therefore, the performance index ITAE (integral time absolute error) was employed as an objective function, as shown in Eq. (16).

$$\mathrm{J}={\int }_{\mathrm{t}=0}^{\mathrm{t}={\mathrm{t}}_{\mathrm{sim}}}\left|\Delta\upomega \right|\mathrm{t dt}$$
(16)

where tsim is the simulation time, and Δω is the speed deviation. The system response can be improved by minimizing this objective function [13, 63].

3.6 Stability performance index

Four performance indices are considered in different scenarios to evaluate controller performance. These indices are the integral of square error (ISE), the integral of absolute error (IAE), the integral of time absolute error (ITAE), and the integral of square absolute error (ISAE). The four indices are mathematically formulated as in [24].

The optimal set of PSS and SVC-based damping controller gains in this study are obtained using ALO and MFO algorithms. The following section is a brief overview of the ALO and MFO techniques. Table 1 shows the typical ranges of the optimized parameters. The time constant Tw is considered 20.0 s in this study.

Table 1 Controllers optimized gains typical ranges
Full size table

4 Optimization techniques

4.1 Antlion optimizer

The ALO algorithm is inspired by how antlions naturally forage during ant hunting. The ant’s random walk positions are offered in Eq. (17) [29].

$$ M_{{{\text{Ant}}}} = \left[ {\begin{array}{*{20}c} {A_{1,1} } & \cdots & {A_{1,d} } \\ \vdots & \ddots & \vdots \\ {A_{n,1} } & \cdots & {A_{n,d} } \\ \end{array} } \right] $$
(17)

where (n) refers to the number of ants, and (d) refers to the number of variables. The locations of all antlions in the traps across search space were recorded in Eq. (18) [29, 64].

$$ M_{Antlion} = \left[ {\begin{array}{*{20}c} {AL_{1,1} } & \cdots & {AL_{1,d} } \\ \vdots & \ddots & \vdots \\ {AL_{n,1} } & \cdots & {AL_{n,d} } \\ \end{array} } \right] $$
(18)

In their exploration of the search space, the ants use Eq. (19) for random walks [30, 43].

$${\mathrm{X}}_{\mathrm{i}}^{\mathrm{t}}= \frac{\left({\mathrm{X}}_{\mathrm{i}}^{\mathrm{t}}-{\mathrm{a}}_{\mathrm{i}}\right)*({\mathrm{d}}_{\mathrm{i}}-{\mathrm{c}}_{\mathrm{i}}^{\mathrm{t}})}{({\mathrm{d}}_{\mathrm{i}}^{\mathrm{t}}-{\mathrm{a}}_{\mathrm{i}})}+{\mathrm{c}}_{\mathrm{i}}$$
(19)

The mathematical equation determining how ants trap antlions is given in Eqs. 20 and 21) [29, 64, 65].

$${\mathrm{c}}_{\mathrm{i}}^{\mathrm{t}}={\mathrm{Antlion}}_{\mathrm{j}}^{\mathrm{t}}+{\mathrm{c}}^{\mathrm{t}}$$
(20)
$${\mathrm{d}}_{\mathrm{i}}^{\mathrm{t}}={\mathrm{Antlion}}_{\mathrm{j}}^{\mathrm{t}}+{\mathrm{d}}^{\mathrm{t}}$$
(21)

where Antlionjt is the position of the chosen jth antlion at tth iteration, ct is the minimum value for all variables at tth iteration, dt is the maximum value for all variables at tth iteration, Cit is the minimum of ith variable at tth iteration, and dit is the maximum of ith variable at tth Iteration. The antlions will attempt to slide the ants against them once they are inside the trap by shooting the sand outward from the trap’s center.

The ant will finally fit more than the antlion. This process occurs when the antlion catches the ant in the trap deeply. Later, the antlion will adjust its position to suit the position of the hunted ant. Thus, the chances of the following hunt will be improved, the position update can be expressed as in Eq. (22) for the next iteration [29, 51].

$${\mathrm{Ant}}_{\mathrm{j}}^{\mathrm{t}}=({\mathrm{R}}_{\mathrm{A}}^{\mathrm{t}}+{\mathrm{R}}_{\mathrm{E}}^{\mathrm{t}})/2$$
(22)

where REt is the random walk around the elite at the tth iteration, and RAt is the random walk around the chosen antlion at the tth iteration. Figure 9 provides the pseudo-code representation of the ALO algorithm [66].

Fig. 9
figure 9

The ALO algorithm pseudo-code

Full size image

4.2 Moth flame optimization algorithm

The MFO algorithm is another nature-inspired algorithm used to determine the coefficients of suggested controllers. The MFO algorithm is based on the flying characteristics of a moth [67]. Typically, the algorithm consists of three components: the moth (M), their fitness values (OM), and flames (F), which represent the recent best position of each fitness value, whereas flames are the best solutions. Moths are the search agents that explore the solution space. As a result, the flame is considered a flag that the best moths have raised. All moths search around the flame and shift the flame to a new position if a better solution is found [31, 67].

The general organization of the MFO procedure, which incorporates the three-tuple approximation function, can be expressed as in Eq. (23). A random population of moths is generated using the initialization function I, and the values of the corresponding objective function are illustrated in Eqs. (24) and (25), respectively [29, 67].

$$\mathrm{MFO}=(\mathrm{I},\mathrm{P},\mathrm{T})$$
(23)
$$\mathrm{M}\left(\mathrm{i},\mathrm{j}\right)=(\mathrm{ub}\left(\mathrm{i}\right)-\mathrm{lb}\left(\mathrm{i}\right))*\mathrm{rand}\left( \right)+\mathrm{lb}(\mathrm{i})$$
(24)
$$\mathrm{OM}=\mathrm{FitnessFunction}(\mathrm{M})$$
(25)

where ub(i) and lb(i) define the upper and lower bounds, respectively, P is a procedure that searches for neighbor solutions of the moths until the termination condition T is met. T is the procedure that returns whether or not the termination condition has been met. Based on Eq. (26), the moth updates its position regarding the flame [30, 67, 68].

$${\mathrm{M}}_{\mathrm{i}}=\mathrm{S}({\mathrm{M}}_{\mathrm{i}},{\mathrm{F}}_{\mathrm{j}})$$
(26)

Mi denotes the position of the ith moth, and Fj denotes the jth position of the flame. Consequently, the moth’s logarithmic spiral is composed as in Eq. (27) [30, 67, 68].

$$\mathrm{S}\left({\mathrm{M}}_{\mathrm{i}},{\mathrm{F}}_{\mathrm{j}}\right)={\mathrm{D}}_{\mathrm{i}}*{\mathrm{e}}^{\mathrm{bt}}*\mathrm{cos}(2\mathrm{\pi t})+{\mathrm{F}}_{\mathrm{j}}$$
(27)

where (t) is a random number [−1, 1], b is the constant shape of the logarithmic spiral, and Di is the distance between the ith moth and the jth flame, which is to be minimized and can be determined by Eq. (28).

$${\mathrm{D}}_{\mathrm{i}}= \left|{\mathrm{F}}_{\mathrm{j}}{-\mathrm{M}}_{\mathrm{i}}\right|$$
(28)

The mathematical definition of the adaptive mechanism to solve the number of flames during each iteration can be expressed as in Eq. (29) [31, 46, 47].

$$ {\text{flame\_no}}\;{ = }\;{\text{round}}\left( {N - l*\frac{N - 1}{T}} \right) $$
(29)

where N is the maximum number of flames, l is the current iteration, and T is the maximum number of iterations (Table 2). The algorithm pseudo-code representation is shown in Fig. 10 [30, 31, 67,68,69].

Table 2 Hyper parameters of ALO and MFO algorithms
Full size table
Fig. 10
figure 10

The MFO algorithm pseudo-code

Full size image

The values of the initial parameters of the ALO and MFO algorithms are listed in Table 3.

Table 3 The three operating conditions active and reactive power values
Full size table

5 Results and discussions

5.1 System setup

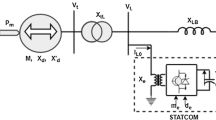
Experimental evaluation of the proposed coordinated controller has been performed using the MATLAB Simulink model. The Simulink model and static VAR compensator (SVC) parameters are shown in Fig. 11, as listed in [59].

Fig. 11
figure 11

Dynamic test Simulink model

Full size image

The MATLAB Simulink model has been modified to fit this study. These modifications can be summarized as follows:

  • Machine No.2 is set as an infinite bus with a large capacity.

  • Replacing the default PSS controller with the modified controller.

  • C hanging the SVC mode from the “VAR control (fixed susceptance)” mode of operation to the “voltage regulation,” and

  • Adding the proposed power oscillation damping controller (FOPID-POD) to vary the SVC equivalent susceptance in response to the deviation of synchronous speed.

The transmission line length is 700 km, and the generator capacity is 1 GVA, where the generator is assumed to be hydro salient with 32 pairs of poles.

5.2 Simulation results

In this section, the results of the numerical investigation will be discussed. The SMIB system and the attached SVC device, as shown in Fig. 11, are simulated using MATLAB Simulink. Conventional LL-PSS, PID-PSS, and FOPID-PSS are considered for comparative purposes to verify the proposed method’s effectiveness. In this study, the performance of the SMIB system with a FOPID-PSS controller is compared to PID-PSS and LL-PSS control.

In addition, the performance of SMIB with and without SVC is also investigated. Three cases with various operating conditions are simulated, as shown in Table 3. Based on the nominal operating condition and other system parameters shown in Appendix A, MATLAB M-file has been used to obtain the complete Heffron–Phillips model parameter. These parameters will be used in the optimization process later.

The gains of the FOPID-PSS, PID-PSS, LL-PSS, and the proposed FOPID controllers for PSS and SVC are optimized using the MFO algorithm. The results obtained using the MFO algorithm were compared to ALO algorithms. The convergence rate of the objective function for the MFO-PSS and ALO-PSS with FOPID control designs is summarized in Fig. 12. It is worth mentioning that Case No.3 shows that the final value of the objective function (J) resulting from MFO-PSS was found to be much better than that achieved by using ALO-PSS. The final solution of the optimized parameters and optimal objective function values for the proposed stabilizers under case No.1 is reported in Table 4.

Fig. 12
figure 12

Comparative convergence curves for proposed stabilizers FOPID-PSS at case No .3

Full size image
Table 4 Optimization result at Case 1
Full size table

As shown in Table 5, all of the suggested stabilizers were tested against different types of disturbances. Different loading conditions have also been taken into consideration. Thus, twelve different scenarios are addressed and simulated concerning faults on the power transmission line. The scenarios considered involve a single-line-to-ground (L-G) fault set to occur 100 km from the generation unit. Moreover, different faults have also been covered, including double-line-to-ground (LL-G) and three-line-to-ground (LLL-G) faults at the generation unit terminal. All scenarios were applied individually at t = 5 s from the simulation starting, lasting for 100 ms.

Table 5 Testing scenarios map
Full size table

The robustness of the proposed coordinated controller was evaluated through a performance analysis, which is achieved by using a group of performance indices. These indices are settling time, overshoot, IAE, ISE, ITAE, and ITSE. Tables 6, 7, and 8 summarize the values of the adopted performance indices for each test scenario of the proposed coordinated design MFO-FOPID-PSS&SVC compared with FOPID-PSS, PID-PSS, and LL-PSS. MFO and ALO algorithms have been used to tune the gains of all controllers to ensure a fair comparison.

Table 6 Performance index values at Case 1
Full size table
Table 7 Performance index values at Case 2
Full size table
Table 8 Performance index values at Case 3
Full size table

The effectiveness of the performance of the proposed FOPID-PSS controller without SVC-POD under insignificant disturbance is verified by applying an L-G fault at 100 km of transmission line away from the generator unit (test scenario No. 9). Figure 13 shows the signal of both Δω and Δδ of the generator in the responses of multiple controllers under investigation (FOPID-PSS, PID-PSS, and LL-PSS). The gains of these controllers were adjusted using MFO and ALO algorithms. As can be seen from the figure, the FOPID-PSS controller has effectively reduced the settling time and damping power system oscillations. Furthermore, the results reported in Fig. 13 show that the MFO algorithm has fewer oscillations than other optimization-based controllers. MFO is much quicker than the ALO algorithm for all PSS control structures. Consequently, it can be concluded that the proposed MFO-FOPID-PSS controller has a superior response over the other stabilizers.

Fig. 13
figure 13

Response of Δω, Δδ, and \({V}_{t}(p.u.)\) to test scenario No. 9

Full size image

Moreover, some of the test scenarios in different case studies will be discussed in detail in the following subsection with the aid of the system response in terms of Δω, Δδ, and \({V}_{t}\) of the generator.

5.2.1 Case study no. 1–test scenario no. 4.

The most severe case, symmetrical fault, has been covered in case study No. 1. Figure 14 shows the corresponding signals (Δω, Δδ, and \({V}_{t}\)) of the simulated case. The depicted signals represent the behavior of each controller in response to the LLL-G fault. As can be seen, the proposed coordinated controller MFO-FOPID-PSS&SVC dramatically improves the power system dynamic stability and has a higher capacity for damping power system oscillations than other controllers. Figure 14a reports that the settling times of these oscillations are about 7.1 s for a coordinated controller, 7.3 s for MFO-FOPID-PSS, and 7.9 s for ALO-FOPID-PSS, which emphasizes that the well-adjusted proposed coordinated controller can provide sufficient damping to the system oscillatory modes.

Fig. 14
figure 14

Response of Δω, Δδ, and \({V}_{t}(p.u.)\) to test scenario No. 4

Full size image

5.2.2 Case study no. 2–test scenario no. 6.

In case No. 2, an L-G fault has been applied at the generation terminals. Figure 15 shows the system response to a minor disturbance. The figure shows that the system response with the proposed coordinated controller MFO-FOPID-PSS&SVC has good damping characteristics to low-frequency oscillations than MFO-FOPID-PSS and ALO-FOPID-PSS stabilizers. Moreover, shown in Fig. 15-a, the developed method has lower overshoots than other methods. The overshoots are 0.2155, 0.2772, and 0.2823 p.u for the coordinated controller MFO-FOPID-PSS&SVC, MFO-FOPID-PSS, and ALO-FOPID-PSS, respectively. Hence, the simulation results emphasized the superiority the superiority of a coordinated controller MFO-FOPID-PSS&SVC.

Fig. 15
figure 15

Response of Δω, Δδ, and \({V}_{t}(p.u.)\) to test scenario No. 6

Full size image

5.2.3 Case study no. 3–test scenario no. 11.

A double-line-to-ground fault at the generation terminals has been covered in this case. Figure 16 illustrates the system’s speed deviation and rotor angle deviation signals under study. The responses illustrated in Fig. 16 represent the responses of all adopted controllers in this study for the LL-G fault. It can be noticed that the proposed coordinated controller MFO-FOPID-PSS&SVC achieves a better dynamic response. From Fig. 16a, the settling time and overshoot are 8.678 s and 0.4249 p.u for ALO-FOPID-PSS, 8.6216 s and 0.4247 p.u for MFO-FOPID-PSS, and 7.3711 s and 0.4026 p.u for coordinated design MFO-FOPID-PSS&SVC. Thus, the robustness and effectiveness of the proposed controller are proved, considering that obtained settling time and overshot of the proposed method are less than other controllers.

Fig. 16
figure 16

Response of Δω, Δδ, and \({V}_{t}(p.u.)\) to test scenario No. 11

Full size image

5.3 Analysis of the results.

Figures 17 and 18 summarize the performance comparison of all adopted controllers in this study. The arithmetic means was adopted and calculated for all cases to summarize the performance of each controller. Figure 17 shows the performance of the MFO algorithm compared with the ALO algorithm, and Fig. 18 shows the coordinated FOPID-PSS&SVC compared with the FOPID-PSS controller.

Fig. 17
figure 17

MFO performance outperformed ALO algorithm for FOPID controller in percentage

Full size image
Fig. 18
figure 18

MFO-FOPID-PSS&SVC performance outperformed MFO-FOPID-PSS in percentage

Full size image

The results show that considering all study cases, the FOPID-PSS-based methodology design significantly performs better than LL-PSS and PID-PSS. Furthermore, the performance indices for FOPID-PSS are the most minor compared with other controllers. These significant reductions in performance indices values ensure the robustness and effectiveness of the developed method. Consequently, the proposed controller offers the system excellent performance in maintaining the system stability and damping the oscillations than other controllers.

6 Conclusion

The purpose of this research was to determine the best settings for a power system stabilizer (PSS) based on a coordinated fractional-order proportional-integral-derivative (FOPID) and a static variable-reluctance (var) compensator (SVC). The moth flame optimization technique was adopted to optimize the parameters of both controllers and achieve a coordinated operation between devices. The objective function is formulated in this study based on the integral time absolute of the error (ITAE), and various performance indices were applied to analyze the performance of the proposed controller. The proposed moth flame-based coordinated FOPID and SVC combination has been compared with lead-lag, proportional-integral-derivative (PID), and antlion-based coordinated FOPID with SVC controllers. The comparison and various simulation scenarios were performed, and results were analyzed and reported. The results analysis has revealed that the proposed coordinated controller PSS&SVC-FOPID-POD improved the power system stability higher than the other controllers. The performance indices, settling time, overshoot, IAE, ITAE, ISE, and ITSE, have improved by 11.61%, 11.45%, 36.58%, 41.07%, 48.32%, and 49.86%, respectively, compared with MFO-FOPID-PSS without SVC.

In a few words, the study shows that using the MFO-based FOPID control scheme for both PSS and SVC guarantees much excellent stability of the system and oscillation damping capability.