Abstract
As power to gas (P2G) technology gradually matures, the coupling between electricity networks and natural gas networks should ideally evolve synergistically. With the intent of characterizing market behaviors of integrated electric power and natural gas networks (IPGNs) with P2G facilities, this paper establishes a steady-state model of P2G and constructs optimal dispatch models of an electricity network and a natural gas network separately. In addition, a concept of slack energy flow (SEF) is proposed as a tool for coordinated optimal dispatch between the two networks. To study how the market pricing mechanism affects coordinated optimal dispatch in an IPGN, a market equilibrium-solving model for an IPGN is constructed according to game theory, with a solution based on the Nikaido-Isoda function. Case studies are conducted on a joint model that combines the modified IEEE 118-node electricity network and the Belgian 20-node gas network. The results show that if the game between an electric power company and a natural gas company reaches market equilibrium, not only can both companies maximize their profits, but also the coordinated operation of the coupling units, i.e., gas turbines and P2G facilities, will contribute more to renewable energy utilization and carbon emission reduction.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, with an increasing share of combined cycle gas turbines (CCGTs) in total electricity generation, natural gas is playing a significant role in low-carbon power generation [1,2,3]. In a traditional energy system, the interaction between a natural gas network and an electricity network can be implemented only via gas turbines. However, with the maturity of P2G technology [4,5,6], it becomes possible to achieve bidirectional energy flow between an electricity network and a natural gas network. Based on P2G technology, surplus electricity generated from renewable energy can be converted into natural gas or hydrogen that can be stored afterwards in the natural gas pipeline network or storage devices. It provides a new solution to renewable energy accommodation [7, 8]. In addition, P2G technology can also convert electricity into natural gas at times of electric transmission congestion, where the gas is transmitted through natural gas pipelines to gas turbines out of the congested area for electricity generation. In this way, transmission congestion can be avoided or alleviated [9]. In the future, P2G technology will play an important role in realizing comprehensive optimization of multiple energy sources, and accordingly, P2G technology and coordinated operation of integrated electric power and natural gas networks (IPGNs) will become research priorities in support of this goal [10, 11].
In [12, 13], hybrid energy flow in an IPGN was explored based on methods developed from traditional power flow calculations. In [14, 15], a planning method for IPGNs was proposed considering the capacity and location of gas turbine units, electricity transmission networks and gas pipelines. IPGN reliability was discussed in [16] based on the Monte Carlo method. As far as optimized operation is concerned, [17, 18] proposed an optimal power flow model for IPGNs and then derived a solution by an interior point method and a multi-agent genetic algorithm, respectively. Uncertainties of intermittent energy resources and loads were taken into account in [19] to establish a probabilistic optimal power flow model for IPGNs based on a multi-linear method.
Though energy conversion between two networks is calculated in the above references, an IPGN is still seen as a single network in terms of control and operation, and such treatment cannot reflect the interaction between two networks which are operated by different companies. In most cases, the electricity network and the natural gas network are supervised and operated by the electric power company and the natural gas company, respectively. Due to related problems, such as operating authorization, information privacy, etc., coordinated operation of IPGNs by exchanging necessary information between power and natural gas companies is facing challenges [20]. Moreover, the electric power company and the natural gas company could also be the energy retailers [21, 22]. That means the market behaviors of the two companies, each aiming to gain more profit, will affect the two networks’ coordinated operation. Specifically, a natural gas company is able to adjust its earnings by changing the gas price for turbines which are connected to the natural gas network, and that will affect the quantity of electricity generated. Conversely, an electric power company can install P2G facilities to consume surplus electricity generated from renewable energy, and it can sell the gas generated to a natural gas company. Therefore, the electric power company is able to regulate the price of the gas generated from P2G facilities in competition with the natural gas company.
Few references have attempted to study such coordinated optimization and market dynamics. Reference [23] presented a two-stage optimization model of an IPGN. In order to ensure reliable supply through the natural gas network, the operation of P2G plants was governed by adjusting gas prices. In [24, 25], the coordinated operation of an IPGN was optimized with the goal of maximizing profits of each company. However, P2G facilities have not yet been included in the analysis IPGNs.
This paper hence focuses on the coordinated optimal dispatch and market equilibrium of IPGNs with embedded P2G facilities, and is organized as follows. In Section 2, the P2G process is modelled. In Section 3, optimal dispatch models for an electricity network and a natural gas network are separately formulated. Moreover, the concept of slack energy flow (SEF) is put forward and used as the interface for energy interactions between two networks. Section 4 describes the analysis of market equilibrium on IPGN. In Section 5, simulation results from a modified test system are provided. Finally, conclusions are drawn in Section 6.
2 Steady-state model of P2G facility
Power to gas (P2G) technology can be classified into power to hydrogen and power to natural gas (methane, CH4) [26]. Methane has 3 times the volumetric energy density of hydrogen and it can be directly injected into the existing natural gas pipelines or storage devices for transmission and storage, without any extra cost, so the prospects for application of power to natural gas is presently stronger than for power to hydrogen [27, 28]. Considering this, this paper studies the application of power to natural gas technology in IPGNs. When P2G is mentioned below it should be taken to mean power to natural gas, unless stated otherwise.
Figure 1 shows the principle processes of a P2G facility, which includes two chemical reaction processes, as shown in (1), namely electrolysis and methanation. Under steady state conditions, the key problems of P2G modelling lie in: ① quantifying the energy transfer between electricity and natural gas, which can be used as a bridge to connect electric power networks and natural gas networks; ② quantifying CO2 absorption, which can be used to analyze the environmental benefit of P2G facilities.
For the first problem, an energy conversion efficiency index can be introduced into the model. In addition, because natural gas is commonly measured by volume, the calorific value of methane, which describes the relationship between energy and volume of methane, should be taken into consideration in the model. For the second problem, from the quantitative relation in (1), synthesizing 1 mol of CH4 absorbs 1 mol of CO2 [5]. Bringing these together, the relationship between the synthesized methane VCH4 (m3), the consumed electricity Ep (kWh), and the CO2 absorption MCO2 (g) is:
In (2), ηP2G is the conversion efficiency of the P2G facility and its value increases as P2G technology becomes more mature. For example, operating demonstration projects have shown an average conversion efficiency of around 60% [5], and there are also technologies that could elevate the efficiency of P2G conversion to 80% [29]. GHV (MJ/m3) is the calorific value of methane. VCH4(M) (L/mol) and MCO2(M) (g/mol) refer to the molar volume of CH4 and the molar mass of CO2 respectively. This model will be used in Sections 3 and 4.
3 Coordinated optimal dispatch of IPGN
The coordinated optimal dispatch model presented below considers a daily time frame. It includes an energy trading scheme within the operational constraints of both electric power and natural gas networks.
3.1 Optimal dispatch model for electricity network
Besides energy cost, the model considers renewable energy penetration in the electricity network. This paper takes wind power as an example and includes a penalty for wind curtailment in the objective function.
3.1.1 Objective function
The objective function for dispatch in the electricity network is given as:
where T is the number of time intervals for scheduling; subscripts i, j and t are the counting variables for conventional generators, wind farms, and time intervals, respectively; ΩG is the set of indices of conventional generators, including gas turbines; Nw denotes the number of wind farms; \(P_{\text{w}}^{*}\) and Pw are the forecast and actual power output of wind farms; ςw is the penalty factor of wind curtailment and its value is set relatively high to make sure that full use is made of wind energy [30]; hG(*) and PG are bidding curves function and power output of a conventional generator.
The bidding among power generation companies is assumed to achieve a Nash equilibrium under complete information, such that all the conventional generators bid according to their marginal costs, which include the costs of fuel and carbon emissions. Then, hG(*) can be calculated by (4), and the effect of the gas price on the dispatch of gas turbines is reflected in the model because the bidding curve is a factor in electricity network dispatching.
where ΩGT (ΩGT⊆ΩG) is the set of indices of gas turbines; a, b and c are cost parameters of non-gas conventional generators; CGT is the unit cost of gas consumed by gas turbines, which can be priced by the natural gas company; g1(*) is the relationship between power output of a gas turbine and natural gas consumption; δG and λ respectively denote total carbon emissions and the carbon emissions exempted from the carbon tax per unit of power generated by a conventional generator; CCO2 denotes the unit cost of carbon emissions.
3.1.2 Equality constraints
The DC power flow method is used to solve this optimal dispatch model. The equality constraint is described by:
where subscript k is the counting variable for P2G facilities; NTR and PTR are the number and the power consumed of P2G facilities; PD is the total load.
3.1.3 Inequality constraints
The model of electricity network is subject to inequality constraints, including limitations of conventional generators’ capacities and ramping rates, wind farms’ power output, power consumption of P2G facilities, spinning reserve capacity considering P2G facilities’ reserve capacity and transmission capacity:
where superscripts max and min indicate upper/lower limits of a variable; \(P_{\text{G}}^{\text{up}}\) and \(P_{\text{G}}^{\text{down}}\) are the maximum upward and downward ramping rates of generators per time interval; \(P_{\text{G}}^{\text{M}}\) and \(P_{\text{G}}^{\text{N}}\) are maximum and minimum available outputs of generators; P r is the power transmitted on line r; ΔD is the reserve capacity for load prediction errors; ΔW is the reserve capacity for wind energy fluctuations and uncertainty; ΔSTR is the reserve capacity which the P2G facilities provide. ΔD, ΔW and ΔSTR are all considered constant in this paper.
3.2 Optimal dispatch model for natural gas network
3.2.1 Objective function
The objective function for dispatch in the natural gas network is given as:
where NGA is the number of conventional gas sources; subscript m is the corresponding counting variable of NGA; \(\omega_{\text{TR}}\) and \(\omega_{\text{GA}}\) are natural gas flows from P2G facilities and conventional gas sources; CTR and CGA are the corresponding unit cost coefficients, in this paper, CTR can be priced by the electricity company because the P2G facilities are regarded as its assets; \(\omega_{\text{G}}^{\text{S}}\) is the SEF corresponding to the gas turbine, defined in Section 3.3; ςs is the corresponding penalty factor. ςs is set relatively high to make sure that \(\omega_{\text{G}}^{\text{S}}\) is close to zero in the optimization results unless the gas demand of the gas turbine exceeds gas network operating constraints.
3.2.2 Equality constraints
The equality constraint of natural gas network is based on nodal flow balance [12], given by:
where A is the node-pipeline incidence matrix; U is the node-compressor incidence matrix; T is the node-compressor loss matrix; ω is the flow rate vector of nodal gas injection; τ is the flow rate vector of gas consumed by compressors; f is the flow rate vector of gas injected by pipelines or compressors, denoted by fa and fb respectively, which satisfy the equation below.
Equation (14) is the natural gas pipeline flow equation, where fa,pq is an element of fa between head end p and tail end q; θ pq indicates the direction of flow in element pq; π is the nodal pressure; and M is the flow coefficient for each pipeline element. Equation (16) is the model of a gas-driven compressor, where fb,n and τ n are the element of fb and τ respectively and the subscript n is the counting variable for compressors. In addition, superscripts suc and disc denote the suction and discharge ends of the compressor; H is the electricity consumed by compressor; B and Z are constants defined by compressor operation; α, β and γ are energy transfer coefficients.
3.2.3 Inequality constraints
Inequality constraints of P2G facilities are given as follows:
If the optimization results in Section 3.1 for the power consumption of P2G facilities is \(P_{{{\text{TR,}}k,t}}^{\text{A}}\) and their corresponding synthetic natural gas output is \(\omega_{{{\text{TR,}}k ,t}}^{\text{A}}\) and g2(*) is the relationship between them, then
The power conversion relationship g2(*) can be obtained from (2).
Constraints on the capacity of conventional gas sources, the pressure ratio of compressors, pipeline or compressor flow rates and nodal pressures in the gas network are described by:
where S is the maximum pressure ratio of a compressor and \({\varvec{\pi}}\) is the vector of nodal pressures.
3.3 Coordinated optimal dispatch of IPGN based on SEF
The concept of SEF is proposed in this paper to serve as the interface for coordinated optimal dispatch. SEF can modify the energy flow in the coupling units of an IPGN based on the dispatch scheme for the two independent networks.
-
1)
SEF corresponding to gas turbine
This concept has been mentioned in Section 3.2 and is expressed in a variable \(\omega_{{{\text{G}},i,t}}^{\text{S}}\). When \(\omega_{{{\text{G}},i,t}}^{\text{S}}\) is not equal to zero, the gas demand of the electricity network exceeds the maximum gas supply due to operational constraints. Therefore, the maximum output of the gas turbine \(P_{{{\text{G,}}i,t}}^{\hbox{max} }\) should be revised:
where \(g_{1}^{ - 1} (*)\) is the inverse function of g1(*) and \(\omega_{{{\text{G,}}i,t}}^{*}\) is described by:
where \(P_{\text{G}}^{\text{A}}\) is the gas turbine’s output obtained by optimal dispatch for the electricity network and \(\omega_{\text{G}}^{\text{A}}\) is the corresponding natural gas flow rate required.
-
2)
SEF corresponding to P2G facility
This concept is expressed in a variable \(\omega_{\text{TR}}^{\text{S}}\) and can be calculated by:
where \(\omega_{\text{TR}}^{\text{B}}\) is the natural gas supply from the P2G facility obtained by optimal dispatch for the natural gas network. When \(\omega_{{{\text{TR,}}k ,t}}^{\text{B}}\) is not equal to zero, the natural gas network is unable to fully accommodate the natural gas provided by P2G facilities. Therefore, \(P_{{{\text{TR,}}k ,t}}^{\hbox{max} }\) should be revised, as shown in (22) where \(g_{2}^{ - 1} (*)\) is the inverse function of g2(*):
The initial value of \(P_{{{\text{TR,}}k ,t}}^{\hbox{max} }\) is equal to the capacity of P2G facilities minus ΔSTR,k,t. After \(P_{{{\text{G,}}i ,t}}^{\hbox{max} }\) and \(P_{{{\text{TR,}}k ,t}}^{\hbox{max} }\) are revised, the optimal dispatch for the electricity network and the natural gas network can be calculated again. This constitutes an iterative process by which \(\omega_{{{\text{G,}}i ,t}}^{\text{A}}\) and \(\omega_{{{\text{TR,}}k ,t}}^{\text{A}}\) are updated repeatedly to obtain the gas flow rates in the coupling units of the IPGN. When the SEFs are equal to zero, the iterations end and the coordinated optimal dispatch of the IPGN is obtained.
Figure 2 shows the complete process of coordinated optimal dispatch of an IPGN. In this paper, the optimal dispatch models of the electricity network and the natural gas network are solved by the primal-dual interior point method [31,32,33]. With the help of SEF, information about gas flow rates in the coupling units is only needed for coordinating the results of the two networks’ optimal dispatch.
4 Market equilibrium analysis on IPGN
Market equilibrium analysis is conducted to determine how the electric power company and the natural gas company can get maximum benefits from selling the gas in the coupling units of the IPGN through optimal pricing strategies. The electric power company sells the gas generated by P2G facilities to the gas company, while the natural gas company, sells gas to the electricity company to be used by gas turbines. Here, game theory is introduced for problem solving, and the Nash equilibrium solution for the IPGN is the market equilibrium state.
4.1 Nash equilibrium and Nikaido-Isoda function
A strategy set for all participants can be defined as x = (x1, x2, …, x L ) and the value space X is Cartesian product of all participant strategy spaces x l (l = 1, 2, …, L, x l ∈ \({\mathbf{R}}^{{\varGamma_{l} }}\)), where Γ l denotes the dimensionality of strategy space x l in real number space R. If the revenue function of each participant is ϕ l (x), then, according to definition of the Nash equilibrium, there exists
where \(\varvec{x}^{\varvec{*}}\) = (\(\varvec{x}_{1}^{\varvec{*}}\), \(\varvec{x}_{2}^{\varvec{*}}\), …, \(\varvec{x}_{L}^{\varvec{*}}\)) is the Nash equilibrium point, and (y l |x*) is a strategy set developed by participant l who changes the strategy into y l while other participant strategies remain unchanged.
The Nikaido-Isoda function can be defined as [34, 35]:
Every series in (24) represents the revenue change of participant l with a strategy varied while those of other participants are invariant. Combining with the Nash equilibrium definition, the following equation can be obtained:
Equation (26) describes the relationship between Nash equilibrium points and the Nikaido-Isoda function. The non-positive part indicates that, when x is a Nash equilibrium point, it is less likely for participants to gain revenue increase by changing their strategies, i.e., max ψ(x*, y) = 0.
In conformity with this characteristic, individual revenue maximization optimization can be carried out for each participant, given an initial strategy set x(K), so as to acquire a new strategy set x(K+1). The Nash equilibrium can be deemed to be achieved when ψ(x(K), y)<ε after multiple iterations, where K is the number of iterations and ε is the convergence precision which can be set as a relatively small positive number. In this way, equilibrium constraints are converted into optimization problems.
4.2 Nash equilibrium solution of IPGN
The game between the electric power company and the natural gas company can be regarded as a non-cooperative game with two players. Defining the strategy spaces of the electric power company and the natural gas company as xele = {CTR,t} and xgas = {CGT,t}, where CTR,t and CGT,t are the decision variables that should meet upper/lower limit constraints over gas price. Then the combined strategy set is x = {xele, xgas}, in which every element is the unit natural gas price of a P2G facility or a gas turbine at a certain time, so that the outcome of the game is a pricing strategy.
Revenue functions ϕele(x) for the electric power company and ϕgas(x) for the natural gas company are defined by:
The gas flow rates in the coupling units of the IPGN, \(\omega_{{{\text{GT,}}i,t}}^{\text{A}}\) and \(\omega_{{{\text{TR}},k,t}}^{\text{A}}\), have become dependent variables and are calculated according to the flow chart in Fig. 2.
According to the method described in Section 4.1, the process for finding the equilibrium state of the IPGN is shown in Fig. 3 where \(\phi_{\Sigma } (\varvec{x}) \) is defined in (28). Note that \(\phi_{\Sigma } (\varvec{x}^{(0)}) \) is equal to zero.
In (28), J is set to a high value (108) to ensure the algorithm’s convergence. Specifically, convergence of such an algorithm depends on whether the Nikaido-Isoda function defined in (26) increases monotonically in the updating direction of the strategy set. If so, boundedness of the Nikaido-Isoda function should be taken into account so that this algorithm to a valid solution, which according to the analysis in Section 4.1 is a Nash equilibrium point.
As P2G is an approach to accommodating renewable energy in our dispatch models, the pricing strategy xele mainly affects the consumption of renewable energy and it has little influence on the optimal scheduling of conventional generators. In other words, there is no influence of xele on \(\omega_{{{\text{GT,}}i,t}}^{\text{A}}\) and \(\omega_{{{\text{GT,}}i,t}}^{\text{A}}\) depends on xgas. Consequently, ϕgas(x) always increases or remains unchanged (arriving at its maximum value) in the iterative process when the strategy set is updated to x(K+1). In comparison, the following two situations exist when the strategy set is updated to x(K+1) as far as ϕele(x) is concerned.
-
1)
In the case that xgas remain unchanged, ϕele(x) should go up or stay the same (arriving at its maximum value). Thus, \(\phi_{\Sigma } (\varvec{x}) \) increases or remains unchanged.
-
2)
In the case that xgas changes, ϕgas(x) increases while ϕele(x) may increase or decrease. However, due to the large coefficient J, any decrease in ϕele(x) is offset by the increase in ϕgas(x). Thus, \(\phi_{\Sigma } (\varvec{x}) \) increases.
To sum up, \(\phi_{\Sigma } (\varvec{x}) \) always increases monotonically and finally converges on its maximum value in the iterative process.
In addition, optimization I in Fig. 3 targets the solution xele that maximizes ϕele(x) under a circumstance that the natural gas company’s strategies remain unchanged during the Kth iteration. Similarly, optimization II targets the solution xgas that maximizes ϕgas(x) with the electric power company’s strategies remaining unchanged during the Kth iteration. The objective functions ϕele(x) and ϕgas(x) can be determined by control variables xele and xgas. However, their solutions involve the procedure given in Fig. 2, and as a consequence, gradient information for the objective functions cannot be acquired. Considering this, the genetic algorithm is used to solve this problem by searching for the best solution from many initial points and obtaining the optimum solution by means of crossover and mutation operators [36, 37].
5 Case studies
The IEEE 118-node system [38] is used for the simulation of an electricity network and it has 54 generators, including 40 coal-fired power generators, 8 gas turbines, and 6 wind farms. Also, 4 P2G facilities are added to it for this study. Detailed parameter settings of the generators and P2G facilities are given in Appendix A.
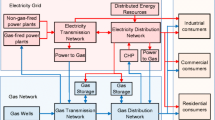
For the natural gas network, a modified Belgian 20-node natural gas network is adopted for simulation studies. The configuration of the gas network and the connection relationship between the electricity network and the gas network are shown in Fig. 4. Appendix B illustrates the detailed parameters of the gas network.
In addition, in this paper, the value of λ is set to 0.798 t/MWh. Both ςw and ςs are set to 105. The data of system loads and wind power forecast setting is shown in Figs. 5 and 6.
5.1 Market equilibrium state of IPGN
In this case, the price of gas provided by conventional gas sources CGA is set to 0.30 $/m3, and the price of gas sold to the gas turbines CGT ranges from 0.30 $/m3 to 0.38 $/m3. In addition, the P2G gas price CTR ranges from 0.28 $/m3 to 0.38 $/m3 and the carbon emission price CCO2 is set to 42 $/t. Based on the method described in Sections 3 and 4, the market equilibrium state of the IPGN is obtained and the results are shown in Figs. 7 and 8. The resulting energy mix of electric power sources and natural gas sources are shown in Appendix C.
According to Figs. 7 and 8, during the 1st~8th hour when electrical loads are low and wind energy is in surplus, P2G facilities are operating to accommodate the surplus wind energy, which is thus converted into methane and provided to the natural gas network. However, the power consumption of P2G facilities does not reach the upper limit (600 MW) which would accommodate more wind energy. This is because P2G facilities’ reserve constraint is considered in the electricity dispatch model to cope with load prediction errors and wind energy fluctuations. Moreover, during this period, the coal-fired power generators are arranged to generate electricity with their minimum output, and the low-cost wind power is provided to the loads. Such power can meet the demand of electrical loads, which is low while wind energy is in surplus in this period, so the gas turbines are shut down. With the rise of electrical loads during the 9th~21st hour, wind power becomes insufficient, and thus the P2G facilities are shut down because synthesis of methane by P2G facilities using electric power generated by coal-fired generators or gas turbines is not efficient. Both gas turbines and coal-fired generators are used to ensure that the electrical loads can be supplied.
From the perspective of market equilibrium, it can be seen in Fig. 7 that the natural gas company is inclined to raise the gas price to obtain more benefits when electrical loads are very high (e.g., in the 11th or 17th hour). Results shown in Tables 1 and 2 will further explain this phenomenon. Taking the 11th hour, for example, the electrical load at this time is 5263 MW. Subtract the 1455 MW generated by wind energy to leave 3808 MW that should be offered by coal-fired generators and gas turbines. Even if the ramping rate and spinning reserve capacity constraints are ignored, the maximum power output of coal-fired generators is 3500 MW (shown in Table 1), which is not sufficient. The gas turbines are needed though their cost is higher. The bidding curves of all the gas turbines are the same in this simulation model, and are shown in Table 2. According to Tables 1 and 2, as CGT keeps rising, the power outputs of gas turbines go down when their marginal cost exceeds that of one of the coal-fired generators. Meanwhile, ϕgas(x) increases first and then decreases. The market equilibrium is thus used to find the balance between the gas price CGT and the power output of gas turbines for maximizing ϕgas(x). Specifically, the optimal solution to maximizing ϕgas(x) in the 11th hour is that CGT equals 0.34 $/m3 and the power output of gas turbines is 1548 MW.
Furthermore, if the electrical loads go down, the gas price should be brought down as well to be more competitive. If the coal-fired generators play strategically, the value of hG(*) shown in Table 1 will change. In this case, as CGT changes from 0.30 $/m3 to 0.38 $/m3, the power output of gas turbines and ϕgas(x) will be different from those given in Table 2. In this way, the market equilibrium state may be changed to maximize ϕgas(x).
Likewise, when gas loads rise (e.g., in the 7th hour) the system uses gas provided by P2G facilities, though the price of P2G-generated gas is 0.34 $/m3, higher than the price of conventional gas sources. This is because gas losses incurred by long-distance gas transmission mean P2G facilities are still more competitive in the market. By contrast, when gas loads are low and the nearby supply from conventional gas sources is sufficient, the price of gas provided by P2G facilities should be lower than marginal price 0.30 $/m3, so that the natural gas company purchases P2G gas and the electric power company acquires some revenue. Such a dynamic market equilibrium state illustrates the supply-demand relationship.
5.2 Benefit comparison between fixed-price mode and market equilibrium mode
Here a comparative analysis is performed between fixed-price mode and market equilibrium mode. The gas prices for three scenario-in fixed-price mode are shown in Table 3. For the purpose of comparison, the market equilibrium of this simulation model without P2G facilities is included as a scenario for benefit analysis of P2G.
The comparison results are shown in Table 4, where BEW and BEC represent the wind power curtailment rate and total carbon emissions, respectively, calculated by (29), and Fig. 9 shows the curve of wind power accommodation.
where δTR is the carbon absorption from P2G facilities of per unit power consumption, which can be deduced from (2).
Comparing the data presented in the last two rows of Table 4, it can be seen that utilizing P2G helps to reduce wind power curtailment rate greatly, from 25.01% to 14.03%, which enhances the rate of renewable energy accommodation. Incidentally, it can reduce the net carbon emissions due to the requirement for CO2 when the P2G facilities are operated to synthesize methane. It can be inferred that the advantages of wind power accommodation and carbon emissions will be greater as the P2G capacity increases.
Data presented in the first four rows of Table 4 show that the pricing strategy under market equilibrium is optimal in terms of the benefits to the electric power company and the natural gas company. If the gas price is high (Scenario 1), power generation by gas turbines and gas purchased from P2G facilities drop correspondingly. As a consequence, not only are the benefits to both companies reduced, but the wind curtailment rate and carbon emissions are increased. In contrast, when the gas price is low (Scenario 2), carbon emissions and wind power accommodation are close to those obtained under market equilibrium. The reason is that the low gas price leads to an increase in power generation by gas turbines, displacing coal-fired power generation and reducing carbon emissions. Simultaneously, the natural gas company tends to purchase natural gas from P2G facilities, encouraging a better accommodation of wind power. Nevertheless, a low price can reduce revenues of both companies, so such a strategy is not adopted in practice.
5.3 Impact of CO2 price on market equilibrium
Pricing for CO2 (denoted by CCO2 in Section 3) is a policy measure used in some jurisdictions to control carbon emission [39]. Different prices on CO2 would affect the cost of power generation, which would in turn influence the price of gas provided to gas turbines under market equilibrium, as shown in Fig. 10.
According to Fig. 10, if CCO2 increases, CGT would show an increasing tendency, too. This is because the gas turbines which generate electricity with low carbon emissions become more competitive in the case of increasing CCO2. Moreover, the natural gas company aiming for higher profits can increase the price of gas supplied to gas turbines as long as the corresponding unit power generation cost is still lower than that of other generators with higher carbon emissions. In contrast, if CCO2 goes down, the price CGT tends to drop in a market equilibrium state.
In addition, CCO2 has a minor influence on the gas price of P2G facilities in the equilibrium state, as the price is mainly constrained by the gas price from other gas sources and the gas load demand.
6 Conclusion
This paper focuses on coordinated optimal dispatch and market equilibrium in an IPGN with P2G facilities embedded. Two proposed models, the coordinated optimal dispatch model for an IPGN based on SEF and the market equilibrium-solving model for an IPGN based on the Nikaido-Isoda function, have been formulated. The models are tested on a joint model made from a modified IEEE 118-node electricity network and the Belgian 20-node gas network. Extensive simulation studies have indicated the following:
-
1)
As one of the important facilities of an IPGN, P2G is able to effectively improve renewable energy accommodation. Meanwhile, it has great potential to promote construction of green and low carbon energy systems due to its carbon-capture ability.
-
2)
The concept of SEF is proposed in this paper, and used as a criterion to decide whether or not to revise the dispatch strategy made by the electricity network and the natural gas network, so that the two networks’ optimal dispatch can be coordinated.
-
3)
The market equilibrium state of an IPGN is affected by the networks’ constraints and loads, as well as by the price for CO2 emissions. For future efficient IPGN systems, energy markets with full information transparency should be strongly supported to aid the game between the electric power company and the natural gas company to achieve market equilibrium. In this case, not only can these two companies acquire more benefits, but more contribution will be made to renewable energy utilization and carbon emission reduction.
Market gaming between the electric power company and the natural gas company is just a part of energy markets in the future. When a number of power generating agents participate in this gaming, some influence can be exerted on gas pricing for gas turbines, and the outcome is difficult to determine. In our future research, a multi-energy, multi-agent game model will be applied to model market dynamics in an IGPN, and the impacts of the uncertainties of renewable energy generation on an IPGN will also be investigated.
References
Bass RJ, Malalasekera W, Willmot P et al (2011) The impact of variable demand upon the performance of a combined cycle gas turbine (CCGT) power plant. Energy 36(4):1956–1965
Tan ZF, Chen KT, LW JW et al (2016) Issues and solutions of China’s generation resource utilization based on sustainable development. J Mod Power Syst Clean Energy 4(2):147–160
Qiu J, Dong Z, Zhao J et al (2015) Expansion co-planning for shale gas integration in a combined energy market. J Mod Power Syst Clean Energy 3(3):1–10
Qadrdan M, Abeysekera M, Chaudry M et al (2015) Role of power-to-gas in an integrated gas and electricity system in Great Britain. Int J Hydrog Energy 40(17):5763–5775
Grond L, Schulze P, Holstein J (2016) Systems analyses power to gas: technology review. http://www.europeanpowertogas.com/fm/download/28. Accessed 4 May 2016
Guandalini G, Campanari S, Romano M (2015) Power-to-gas plants and gas turbines for improved wind energy dispatch ability: energy and economic assessment. Appl Energy 147:117–130
Götz M, Lefebvre J, Mörs F et al (2016) Renewable power-to-gas: a technological and economic review. Renew Energy 85:1371–1390
Jentsch M, Trost T, Sterner M (2014) Optimal use of power-to-gas energy storage systems in an 85% renewable energy scenario. Energy Procedia 46:254–261
Clegg S, Mancarella P (2015) Integrated modeling and assessment of the operational impact of power-to-gas (P2G) on electrical and gas transmission networks. IEEE Trans Sustain Energy 6(4):1234–1244
Xue YS (2015) Energy internet or comprehensive energy network? J Mod Power Syst Clean Energy 3(3):297–301
Krause T, Andersson G, Fröhlich K et al (2016) Multiple-energy carriers: modeling of production, delivery, and consumption. Proc IEEE 99(1):15–27
Martinez-Mares A, Fuerte-Esquivel CR (2012) A unified gas and power flow analysis in natural gas and electricity coupled networks. IEEE Trans Power Syst 27(4):2156–2166
Erdener BC, Pambour KA, Lavin RB et al (2014) An integrated simulation model for analysing electricity and gas systems. Int J Electr Power Energy Syst 61:410–420
Qiu J, Dong ZY, Zhao JH et al (2015) Low carbon oriented expansion planning of integrated gas and power systems. IEEE Trans Power Syst 30(2):1035–1046
Barati F, Seifi H, Sepasian MS et al (2015) Multi-period integrated framework of generation, transmission, and natural gas grid expansion planning for large-scale systems. IEEE Trans Power Syst 30(5):2527–2537
Chaudry M, Wu J, Jenkins N (2013) A sequential Monte Carlo model of the combined GB gas and electricity network. Energy Policy 62(9):473–483
Geidl M, Andersson G (2007) Optimal power flow of multiple energy carriers. IEEE Trans Power Syst 22(1):145–155
Moeini-Aghtaie M, Abbaspour A, Fotuhi-Firuzabad M et al (2014) A decomposed solution to multiple-energy carriers optimal power flow. IEEE Trans Power Syst 29(2):707–716
Chen S, Wei Z, Sun G et al (2017) Multi-linear probabilistic energy flow analysis of integrated electrical and natural-gas systems. IEEE Trans Power Syst 32(3):1970–1979
Rifkin J (2011) The third industrial revolution: how lateral power is transforming energy, the economy, and the world. Palgrave MacMillan, New York
Karthikeyan SP, Raglend IJ, Kothari DP (2013) A review on market power in deregulated electricity market. Int J Electr Power Energy Syst 48:139–147
Lévêque F (2011) France’s new electricity act: a potential windfall profit for electricity suppliers and a potential incompatibility with the EU law. Electr J 24(2):55–62
Clegg S, Mancarella P (2016) Storing renewables in the gas network: modelling of power-to-gas seasonal storage flexibility in low-carbon power systems. IET Gener Transm Distrib 10(3):566–575
Gil M, Dueñas P, Reneses J (2016) Electricity and natural gas interdependency: comparison of two methodologies for coupling large market models within the European regulatory framework. IEEE Trans Power Syst 31(1):361–369
Spiecker S (2013) Modeling market power by natural gas producers and its impact on the power system. IEEE Trans Power Syst 28(4):3737–3746
Bunger U, Landinger H, Pschorr-Schoberer E et al (2016) Power-to-gas (PtG) in transport status quo and perspectives for development. http://www.bmvi.de/SharedDocs/EN/Anlagen/UI-MKS/mks-studie-ptg-transport-status-quo-and-perspectives-for-development.pdf. Accessed 11 June 2014
Maroufmashat A, Elkamel A, Fowler M et al (2015) Modeling and optimization of a network of energy hubs to improve economic and emission considerations. Energy 93:2546–2558
Huang JH, Zhou HS, Wu QH et al (2016) Assessment of an integrated energy system embedded with power-to-gas plant. In: Proceedings of IEEE innovative smart grid technologies-Asia (ISGT-Asia), Melbourne, Australia, 28 November–1 December 2016, pp 196–201
Redissi Y, Er-Rbib H, Bouallou C (2013) Storage and restoring the electricity of renewable energies by coupling with natural gas grid. In: Proceedings of 2013 international renewable and sustainable energy conference (IRSEC), Ouarzazate, Morocco, 7–9 March 2013, pp 430–435
Wang Y, Xia Q, Kang CQ (2011) A novel security stochastic unit commitment for wind-thermal system operation. In: Proceedings of 2011 4th international conference on electric utility deregulation and restructuring and power technologies (DRPT), Weihai, China, 6–9 July 2011, pp 386–393
Jabr RA, Coonick AH, Cory BJ (2002) A prime-dual interior point method for optimal power flow dispatching. IEEE Trans Power Syst 17(3):654–662
An S, Li Q, Gedra TW (2003) Natural gas and electricity optimal power flow. In: 2003 IEEE PES Proceedings of transmission and distribution conference and exposition, Dallas, USA, 7–12 September 2003, pp 138–143
Bishe HM, Kian AR, Esfahani MS (2011) A primal-dual interior point method for solving environmental/economic power dispatch problem. Int Rev Electr Eng 6(3):1463–1473
Molina JP, Zolezzi JM, Contreras J et al (2011) Nash-cournot equilibria in hydrothermal electricity markets. IEEE Trans Power Syst 26(3):1089–1101
Lalitha CS, Dhingra M (2013) Optimization reformulations of the generalized Nash equilibrium problem using regularized indicator Nikaidô-Isoda function. J Glob Optim 57(3):843–861
Golberg DE (1989) Genetic algorithms in search, optimization and machine learning reading. Addisonn-Wisley, Boston
Yanik S, Sürer Ö, Öztayşi B (2016) Designing sustainable energy regions using genetic algorithms and location-allocation approach. Energy 97:161–172
University of Washington. Power systems test case archive. http://www.ee.washington.edu/research/pstca/. Accessed 14 Aug 1999
Eser P, Chokani N, Abhari RS (2016) Impact of carbon taxes on the interconnected central European power system of 2030. In: Proceedings of international conference on the European energy market, Porto, Portugal, 6–9 June 2016, 6 pp
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 51377060) and the Major Consulting Program of Chinese Academy of Engineering (No. 2015-ZD-09-09).
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 16 September 2017
Appendices
Appendix A
Parameters of coal-fired power generators, gas turbines and P2G facilities are shown in Tables A1, A2 and A3, respectively.
Appendix B
Node data of Belgian natural gas system is shown in Table B1. Pipeline data of Belgian natural gas system is shown in Table B2. Compressor data of Belgian natural gas system is shown in Table B3.
Appendix C
Composition of electricity production from various power sources under market equilibrium state is shown in Fig. C1. Composition of natural gas production from various gas sources under market equilibrium state is shown in Fig. C2.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
CHEN, Z., ZHANG, Y., JI, T. et al. Coordinated optimal dispatch and market equilibrium of integrated electric power and natural gas networks with P2G embedded. J. Mod. Power Syst. Clean Energy 6, 495–508 (2018). https://doi.org/10.1007/s40565-017-0359-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0359-z