Skip to main content
SpringerLink
Log in

Active-reactive power scheduling of integrated electricity-gas network with multi-microgrids

  • Research Article
  • Published:
Frontiers in Energy Aims and scope Submit manuscript

Abstract

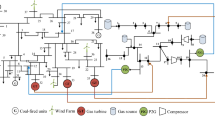
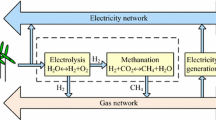
Advances in natural gas-fired technologies have deepened the coupling between electricity and gas networks, promoting the development of the integrated electricity-gas network (IEGN) and strengthening the interaction between the active-reactive power flow in the power distribution network (PDN) and the natural gas flow in the gas distribution network (GDN). This paper proposes a day-ahead active-reactive power scheduling model for the IEGN with multi-microgrids (MMGs) to minimize the total operating cost. Through the tight coupling relationship between the subsystems of the IEGN, the potentialities of the IEGN with MMGs toward multi-energy cooperative interaction is optimized. Important component models are elaborated in the PDN, GDN, and coupled MMGs. Besides, motivated by the non-negligible impact of the reactive power, optimal inverter dispatch (OID) is considered to optimize the active and reactive power capabilities of the inverters of distributed generators. Further, a second-order cone (SOC) relaxation technology is utilized to transform the proposed active-reactive power scheduling model into a convex optimization problem that the commercial solver can directly solve. A test system consisting of an IEEE-33 test system and a 7-node natural gas network is adopted to verify the effectiveness of the proposed scheduling method. The results show that the proposed scheduling method can effectively reduce the power losses of the PDN in the IEGN by 9.86%, increase the flexibility of the joint operation of the subsystems of the IEGN, reduce the total operation costs by $32.20, and effectively enhance the operation economy of the IEGN.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A-R-OPF:

Active-reactive optimal power flow

AC:

Absorption chillers

ACOPF:

Alternating current optimal power flow

CCHP:

Combined cooling, heating, and power

DG:

Distributed generators

DPV:

Distributed photovoltaic

EC:

Electric chillers

GB:

Gas boilers

GDN:

Gas distribution network

GT:

Gas turbines

HSS:

Heat storage systems

IEGN:

Integrated electricity-gas network

MMG:

Multi-microgrids

OID:

Optimal inverter dispatch

PCS:

Power conditioning systems

PDN:

Power distribution network

P2G:

Power to gas

SOC:

Second-order cone

WHB:

Waste heat boilers

i/j :

Index of nodes in the PDN

ij :

Index of branches in the PDN

I/J :

Set of the beginning/ending nodes of the branches in the PDN

m :

Index of the microgrids

M :

Set of the nodes of the PDN where the microgrids are located

t :

Index of time slots

uv :

Index of branches in the GDN

u/v :

Index of nodes in the GDN

U/V :

Set of the beginning/ending nodes of the pipelines in the GDN

\(B_{i,t}^{\rm{c}}/B_{i,t}^{\rm{d}}\) :

Charging/discharging power of the power storage system of node i of the PDN at the tth hour

C uv :

Weymouth equation coefficient

\(C_t^{\rm{P}}/C_t^{\rm{Q}}\) :

Active/reactive power price of the utility grid at the tth hour

\(C_{i,t}^{{\rm{DPV}}}\) :

Operation cost of the distributed photovoltaic of node i in the distribution network, which is assumed to be a constant

COP AC :

Coefficient of performance of the absorption chiller in the mth microgrid

COP EC :

Performance coefficient of the electrical chiller in the mth microgrid

\(cm_m^{{\rm{HSS}}}\) :

Coefficient of the cost function of the heat storage system in the mth microgrid

\(cm_m^{{\rm{EC}}}/cm_m^{{\rm{AC}}}\) :

Coefficient of the cost function of the electrical chiller/absorption chiller in the mth microgrid

\(cm_m^{{\rm{WHB}}}\) :

Coefficient of the cost function of the waste heat boiler in the mth microgrid

\(C_{m,t}^{{\rm{gas}}}\) :

Purchased gas cost of the mth microgrids at the tth hour

\(C_{i,t}^{{\rm{DPV}}}\) :

Operation cost of the distributed photovoltaic of node i in the distribution network

\(C_{i,t}^{{\rm{ESS}}}\) :

Operation cost of the ESS of node i in the distribution network

\(E_{i,t}^{{\rm{ESS}}}\) :

Amount of electricity stored in the energy storage system of node i of the PDN at the tth hour

\(H_{m,t}^{{\rm{GB}}}\) :

Heating power production of the gas boiler of the mth microgrid at the tth hour

\(H_{m,t}^{{\rm{AC}}}\) :

Heating power absorption of the absorption chiller of the mth microgrid at the tth hour

\(H_{m,t}^{\rm{c}}/H_{m,t}^{\rm{d}}\) :

Charging/discharging power of the heat storage system in the mth microgrid at the tth hour

\(H_{m,t}^{\rm{D}}/H_{m,t}^{\rm{D}}\) :

Heating and cooling power loads of the mth microgrid at the tth hour

\(H_{m,min}^{{\rm{AC}}}/H_{m,\max }^{{\rm{AC}}}\) :

Minimum/maximum heating power consumption of the absorption chiller in the mth microgrid

\(H_{m,min}^{{\rm{WHB}}}/H_{m,\max }^{{\rm{WHB}}}\) :

Minimum/maximum heating power absorption of the waste heat boiler in the mth microgrid

\(H_{m,min}^{{\rm{GB}}}/H_{m,\max }^{{\rm{GB}}}\) :

Minimum/maximum heating power generation of the gas boiler in the mth microgrid

\(H_{m,min}^{\rm{c}}/H_{m,\max }^{\rm{c}}\) :

Minimum/maximum heating power charging of the heat power storage in the mth microgrid

\(H_{m,min}^{\rm{d}}/H_{m,\max }^{\rm{d}}\) :

Minimum/maximum heating power discharging of the heat power storage in the mth microgrid

I ij,t :

Current flowing in branch ij in the distribution network at the tth hour

\(kf_i^{{\rm{DPV}}}\) :

Minimum power factor of the distributed photovoltaic inverter of node i in the PDN

K G/K m :

Utility grid/microgrids located nodes correlation matrix

K ESS/K DPV :

ESS/distributed photovoltaic located nodes correlation matrix

l ij,t :

Square of the current flowing in branch ij in the distribution network at the tth hour

L NG :

Heating value of natural gas

\(m_i^{{\rm{ESS}}}\) :

Coefficient of the cost function of the node i of the electricity storage system (ESS) in the PDN

\(M_{m,t}^{{\rm{op}}}\) :

Operation cost of the mth the microgrids at the tth hour

\(M_{m,t}^{{\rm{HSS}}}\) :

Operation cost of the heat storage system in the mth microgrid at the tth hour

\(M_{m,t}^{{\rm{WHB}}}\) :

Operation cost of waste heat boiler in the mth microgrid at the tth hour

\(M_{m,t}^{{\rm{WT}}}\) :

Operation cost of the wind turbine of the mth microgrid at the tth hour, which is assumed to be a constant

\(M_{m,t}^{{\rm{AC}}}/M_{m,t}^{{\rm{EC}}}\) :

Operation cost of the absorption chiller/electrical chiller of the mth microgrid at the tth hour

P ij,t :

Active power flow in branch ij in the distribution network at the tth hour

\(P_{m,t}^{{\rm{EC}}}\) :

Active power consumption of the electrical chiller of the mth microgrid at the tth hour

\(P_{i,t}^{{\rm{DPV,max}}}\) :

Maximum forecasted active power production of the distributed photovoltaic of node i in the PDN at the tth hour

\(P_{m,t}^{\rm{D}}/Q_{m,t}^{\rm{D}}\) :

Active and reactive power loads of the mth microgrid at the tth hour

\(P_t^{\rm{G}}/Q_t^{\rm{G}}\) :

Active/reactive power transported from the utility grid at the tth hour

\(P_{i,t}^{\rm{D}}/Q_{i,t}^{\rm{D}}\) :

Active and reactive power of node i of the PDN at the tth hour

\(P_{m,\max }^{{\rm{PCC}}}/Q_{m,\max }^{{\rm{PCC}}}\) :

Maximum amount of active/reactive power traded at the point of common coupling between the mth microgrid and the PDN

\(P_{m,\min }^{{\rm{GT}}}/P_{m,max}^{{\rm{GT}}}\) :

Minimum/maximum active power production of the gas turbine in the mth microgrid

\(P_{m,\min }^{{\rm{EC}}}/P_{m,max}^{{\rm{EC}}}\) :

Minimum/maximum active power consumption of the electrical chiller in the mth microgrid

\(P_{t,\min }^{\rm{G}}/P_{t,max}^{\rm{G}}\) :

Minimum/maximum active power transported from the utility grid at the tth hour

\(P_{m,\max }^{{\rm{PCC}}}/Q_{m,max}^{{\rm{PCC}}}\) :

Maximum amount of active/reactive power traded at the point of common coupling between the mth microgrid and the PDN

\({P_{m,t}}/{Q_{m,t}}\) :

Transported quantity of the mth microgrid of active/reactive power at the tth hour

\(P_{m,t}^{{\rm{GT}}}/H_{m,t}^{{\rm{GT}}}\) :

Active/heating power production of the gas turbine at the tth hour

\(P_{i,t}^{{\rm{DPV}}}/Q_{i,t}^{{\rm{DPV}}}\) :

Active/reactive power production of the distributed photovoltaic of node i of the PDN at the tth hour

Q ij,t :

Reactive power flowing in branch ij in the distribution network at the tth hour

\(Q_{t,\min }^{\rm{G}}/Q_{t,\max }^{\rm{G}}\) :

Minimum/maximum reactive power transported from the utility grid at the tth hour

r ij,t/x ij,t :

Resistance/reactance of branch ij in the distribution network

\(S_i^{{\rm{DPV}}}\) :

Capacity of the distributed photovoltaic inverter of node i of the PDN

\(S_{m,t}^{{\rm{HSS}}}\) :

Amount of heat stored in the electrical chiller at the tth hour

\(SOC_{i,\min }^{{\rm{ESS}}}/SOC_{i,\max }^{{\rm{ESS}}}\) :

Minimum/maximum state of charge of the ESS in the node i in the PDN

V min,i,t /V max,i,t :

Voltage limitations of node i in the distribution network

V i,t :

Nodal voltage in node i in the distribution network at the tth hour

U i,t :

Square of nodal voltage in node i in the distribution network at the tth hour

U b,t :

Voltage drop in branch b in the distribution network at the tth hour

\(w_{\min }^{{\rm{well}}}/w_{\max }^{{\rm{well}}}\) :

Limitations of the gas supplied quantity from the gas well at the tth hour

w uv,t :

Gas flow from node u to node v in the GDN at the tth hour

\(w_t^{{\rm{well}}}\) :

Gas production by node u in the gas well at the tth hour

\(w_{u,t}^{{\rm{GT}}}/w_{u,t}^{{\rm{GB}}}\) :

Gas consumption by GT/GB at node u in the gas distribution system at the tth hour

ψ min/ψ max :

Limitations of the gas nodal pressure in the GDN at the tth hour

ρ c :

Compression factor of the compressor

ψ u,t :

Gas nodal pressure in node u in the gas distribution network at the tth hour

ψ ct,t/ψ cf,t :

Gas nodal pressure of the inlet and outlet of the compressor in the GDN at the tth hour

\(\eta _m^{{\rm{GT}}}\) :

Efficiency of the gas turbine in the mth microgrid

\(\eta _m^{{\rm{GB}}}\) :

Efficiency of the gas boiler in the mth microgrid

\(\eta _m^{{\rm{WHB}}}\) :

Efficiency of the waste heat boiler in the mth microgrid

\(\eta _i^{{\rm{c,ESS}}}/\eta _i^{{\rm{d,ESS}}}\) :

Charging/discharging efficiency of the ESS of node i in the PDN

\(\eta _m^{{\rm{c,HSS}}}/\eta _m^{{\rm{d,HSS}}}\) :

Charging/discharging efficiency of the heat storage system in the mth microgrid

References

  1. Zhu M, Xu C, Dong S, et al. Integrated multi-energy flow calculation method for electricity-gas-thermal integrated energy systems. Protection and Control of Modern Power Systems, 2021, 6(1): 1–12

    Article  Google Scholar 

  2. Amanpour S, Huck D, Kuprat M, et al. Integrated energy in Germany—a critical look at the development and state of integrated energies in Germany. Frontiers in Energy, 2018, 12(4): 493–500

    Article  Google Scholar 

  3. Nasiri N, Zeynali S, Najafi Ravadanegh S, et al. A tactical scheduling framework for wind farm integrated multi-energy systems to take part in natural gas and wholesale electricity markets as a price setter. IET Generation, Transmission & Distribution, 2022, 16(9): 1849–1864

    Article  Google Scholar 

  4. Abomazid A M, El-Taweel N A, Farag H E Z. Energy management system for minimizing hydrogen production cost using integrated battery energy storage and photovoltaic systems. In: 2021 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, D.C., USA, 2021

  5. Koirala B, Hers S, Morales-España G, et al. Integrated electricity, hydrogen and methane system modeling framework: application to the Dutch Infrastructure Outlook 2050. Applied Energy, 2021, 289: 116713

    Article  Google Scholar 

  6. Wang H, Hou K, Zhao J B, et al. Planning-oriented resilience assessment and enhancement of integrated electricity-gas system considering multi-type natural disasters. Applied Energy, 2022, 315: 118824

    Article  Google Scholar 

  7. Liu H Z, Shen X W, Guo Q L, et al. A data-driven approach towards fast economic dispatch in electricity-gas coupled systems based on artificial neural network. Applied Energy, 2021, 286: 116480

    Article  Google Scholar 

  8. Chen S, Conejo A J, Sioshansi R, et al. Investment equilibria involving gas-fired power units in electricity and gas markets. IEEE Transactions on Power Systems, 2020, 35(4): 2736–2747

    Article  Google Scholar 

  9. Ahmad F, Iqbal A, Ashraf I, et al. Optimal location of electric vehicle charging station and its impact on distribution network: a review. Energy Reports, 2022, 8: 2314–2333

    Article  Google Scholar 

  10. Clegg S, Mancarella P. Integrated electrical and gas network flexibility assessment in low-carbon multi-energy systems. IEEE Transactions on Sustainable Energy, 2016, 7(2): 718–731

    Article  Google Scholar 

  11. Liu M X, Shi Y, Fang F. A new operation strategy for CCHP systems with hybrid chillers. Applied Energy, 2012, 95: 164–173

    Article  Google Scholar 

  12. Ahmadi S E, Sadeghi D, Marzband M, et al. Decentralized bilevel stochastic optimization approach for multi-agent multi-energy networked micro-grids with multi-energy storage technologies. Energy, 2022, 245(15): 123223

    Article  Google Scholar 

  13. Nasiri N, Zeynali S, Ravadanegh S N, et al. A hybrid robust-stochastic approach for strategic scheduling of a multi-energy system as a price-maker player in day-ahead wholesale market. Energy, 2021, 235(15): 121398

    Article  Google Scholar 

  14. Kazemi-Razi S M, Askarian Abyaneh H, Nafisi H, et al. Enhancement of flexibility in multi-energy microgrids considering voltage and congestion improvement: robust thermal comfort against reserve calls. Sustainable Cities and Society, 2021, 74: 103160

    Article  Google Scholar 

  15. Yang L, Xu Y, Zhou J, et al. Distributionally robust frequency constrained scheduling for an integrated electricity-gas system. IEEE Transactions on Smart Grid, 2022, 13(4): 2730–2743

    Article  Google Scholar 

  16. Yang L, Xu Y, Sun H, et al. Two-stage convexification-based optimal electricity-gas flow. IEEE Transactions on Smart Grid, 2020, 11(2): 1465–1475

    Article  Google Scholar 

  17. Baherifard M A, Kazemzadeh R, Yazdankhah A S, et al. Intelligent charging planning for electric vehicle commercial parking lots and its impact on distribution network’s imbalance indices. Sustainable Energy, Grids and Networks, 2022, 30: 100620

    Article  Google Scholar 

  18. Sadeghi D, Amiri N, Marzband M, et al. Optimal sizing of hybrid renewable energy systems by considering power sharing and electric vehicles. International Journal of Energy Research, 2022, 46(6): 8288–8312

    Article  Google Scholar 

  19. Cao Z, Wang J, Zhao Q, et al. Decarbonization scheduling strategy optimization for electricity-gas system considering electric vehicles and refined operation model of power-to-gas. IEEE Access: Practical Innovations, Open Solutions, 2021, 9: 5716–5733

    Article  Google Scholar 

  20. Gao H, Li Z. A benders decomposition based algorithm for steady-state dispatch problem in an integrated electricity-gas system. IEEE Transactions on Power Systems, 2021, 36(4): 3817–3820

    Article  Google Scholar 

  21. Chen S, Wei Z, Sun G, et al. Identifying optimal energy flow solvability in electricity-gas integrated energy systems. IEEE Transactions on Sustainable Energy, 2017, 8(2): 846–854

    Article  Google Scholar 

  22. Zhang Y, Ren Z. Optimal reactive power dispatch considering costs of adjusting the control devices. IEEE Transactions on Power Systems, 2005, 20(3): 1349–1356

    Article  Google Scholar 

  23. El-Samahy I, Bhattacharya K, Canizares C, et al. A procurement market model for reactive power services considering system security. IEEE Transactions on Power Systems, 2008, 23(1): 137–149

    Article  Google Scholar 

  24. Li Z, Yu J, Wu Q H. Approximate linear power flow using logarithmic transform of voltage magnitudes with reactive power and transmission loss consideration. IEEE Transactions on Power Systems, 2018, 33(4): 4593–4603

    Article  Google Scholar 

  25. Yu J, Dai W, Li W, et al. Optimal reactive power flow of interconnected power system based on static equivalent method using border PMU measurements. IEEE Transactions on Power Systems, 2018, 33(1): 421–429

    Article  Google Scholar 

  26. Li W, Liang Z, Ma C, et al. Reactive power optimization in distribution network considering reactive power regulation capability and fuzzy characteristics of distributed generators. In: 2019 4th International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 2019

  27. Miller N W, Zrebiec R S, Hunt G, et al. Design and commissioning of a 5 MVA, 2.5 MWh battery energy storage system. In: Proceedings of 1996 Transmission and Distribution Conference and Exposition, Los Angeles, USA, 1996

  28. Walker L H. 10-MW GTO converter for battery peaking service. IEEE Transactions on Industry Applications, 1990, 26(1): 63–72

    Article  MathSciNet  Google Scholar 

  29. Gabash A, Li P. Active-reactive optimal power flow in distribution networks with embedded generation and battery storage. IEEE Transactions on Power Systems, 2012, 27(4): 2026–2035

    Article  Google Scholar 

  30. Yang K, Gong Y, Zhang P, et al. A reactive power compensation method based on tracing the power flow and loss function of power system. In: 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 2015

  31. Wang Y, Wang T, Zhou K P, et al. Reactive power optimization of wind farm considering reactive power regulation capacity of wind generators. In: 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 2019

  32. Zhang X, Sugishita H, Ni W, et al. Economics and performance forecast of gas turbine combined cycle. Tsinghua Science and Technology, 2005, 10(5): 633–636

    Article  Google Scholar 

  33. Chen H H, Wang D, Zhang R F, et al. Optimal participation of ADN in energy and reserve markets considering TSO-DSO interface and DERs uncertainties. Applied Energy, 2022, 308(15): 118319

    Article  Google Scholar 

  34. Wang C, Hong B, Guo L, et al. A general modeling method for optimal dispatch of combined cooling, heating and power microgrid. Proceedings of the CSEE, 2013, 33(31): 26–33 (in Chinese)

    Google Scholar 

  35. Li G Q, Yan K F, Zhang R F, et al. Resilience-oriented distributed load restoration method for integrated power distribution and natural gas systems. IEEE Transactions on Sustainable Energy, 2022, 13(1): 341–352

    Article  Google Scholar 

  36. Farivar M, Low S H. Branch flow model: relaxations and convexification—parts I. IEEE Transactions on Power Systems, 2013, 28(3): 2554–2564

    Article  Google Scholar 

  37. Chen H H, Fu L B, Bai L Q, et al. Distribution market-clearing and pricing considering coordination of DSOs and iso: an EPEC approach. IEEE Transactions on Smart Grid, 2021, 12(4): 3150–3162

    Article  Google Scholar 

  38. Bai L, Wang J, Wang C, et al. Distribution locational marginal pricing (DLMP) for congestion management and voltage support. IEEE Transactions on Power Systems, 2018, 33(4): 4061–4073

    Article  MathSciNet  Google Scholar 

  39. Chen H H, Li H Y, Lin C, et al. An integrated market solution to enable active distribution network to provide reactive power ancillary service using transmission-distribution coordination. IET Energy Systems Integration, 2022, 4(1): 98–115

    Article  Google Scholar 

  40. Chen Z, Zhang Y, Ji T, et al. Coordinated optimal dispatch and market equilibrium of integrated electric power and natural gas networks with P2G embedded. Journal of Modern Power Systems and Clean Energy, 2018, 6(3): 495–508

    Article  Google Scholar 

  41. Teodor O. Coordination of battery energy storage and power-togas in distribution systems. Protection and Control of Modern Power Systems, 2017, 2(1): 1–8

    Google Scholar 

Download references

Acknowledgments

This work was partially supported by the National Natural Science Foundation of China (Grant Nos. 51877033, 52061635103, 52007026, and 52077028).

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, Northeast Electric Power University, Jilin, 132012, China

    Tao Jiang, Xinru Dong, Rufeng Zhang, Xue Li, Houhe Chen & Guoqing Li

Authors
  1. Tao Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xinru Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rufeng Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xue Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Houhe Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Guoqing Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rufeng Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, T., Dong, X., Zhang, R. et al. Active-reactive power scheduling of integrated electricity-gas network with multi-microgrids. Front. Energy 17, 251–265 (2023). https://doi.org/10.1007/s11708-022-0857-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11708-022-0857-1

Keywords

Search

Navigation