Abstract
This paper proposes a novel hybrid multilevel converter with DC fault-blocking capability, i.e., the neutral-point clamped hybrid multilevel converter (NHMC). By employing two types of unipolar full-bridge submodules along with director switches, which are composed of series-connected insulated-gate bipolar transistors, the NHMC combines the features and advantages of the neutral-point clamped converter and the modular multilevel converter. The basic topology, operating principles, modulation scheme, and energy-balancing scheme of the NHMC are presented. The DC fault-blocking capability of the NHMC is investigated. The number of power electronic devices used by the NHMC is calculated and compared with other multilevel converters, showing that the proposed NHMC can be an economical and feasible option for medium-voltage DC transmission with overhead lines. Simulation results demonstrate the features and operating scheme of the proposed NHMC.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the past few decades, several voltage source converters (VSCs) have been developed for medium- and high-voltage DC transmission [1], such as the two-level converter (TLC), the neural-point clamped converter (NPC) [2], the modular multilevel converter (MMC) [3], and so on. As analyzed in [4] and [5], these converters fall into two distinct groups: the controllable switch converter, which consists of insulated-gate bipolar transistors (IGBTs) in series (such as the TLC and NPC); and the controllable voltage source converter, which consists of submodules (SMs) in series (such as the MMC). As a typical controllable voltage source converter, the MMC offers significant advantages over the controllable switch converter, such as high modularity, low dv/dt, low switching frequency and power loss, and reduced current harmonics [3, 6]. As a result, the MMC has been widely studied and applied in many medium- and high-voltage applications [6,7,8], especially in VSC high-voltage DC (HVDC) transmission.
However, the MMC has inherent drawbacks. One of the main drawbacks is that the MMC employs a large number of IGBTs, thereby increasing the cost and scale of the converter. Another drawback that cannot be ignored is that the MMC that employs half-bridge SMs (HBSM–MMC) lacks DC fault-blocking capability [9, 10]. When a pole-to-pole DC fault occurs, the arm currents and DC fault current of the HBSM–MMC increase at a very fast speed and might damage the freewheeling diodes. Although employing another kind of SM, such as full-bridge SMs (FBSMs) and clamp-double SMs (CDSMs) can solve this problem [11,12,13], the cost and scale of the MMC increases significantly.
To overcome the drawbacks of the MMC, a new type of VSC called a hybrid multilevel converter has been proposed in recent years [14, 15]. The hybrid multilevel converter combines features and advantages of the aforementioned two groups of VSCs and employs IGBTs and SMs in series. The alternate arm converter (AAC) proposed in [14] and the hybrid cascaded multilevel converter (HCMC) proposed in [15] are two typical hybrid multilevel converters that can be regarded as hybrids of the TLC and MMC. By employing IGBTs in series as director switches (DSs) in place of some SMs, the AAC and HCMC employ fewer SMs, and therefore can reduce the number and cost of power electronic devices. By using FBSMs as SMs, the two converters are capable of blocking the DC fault current during a pole-to-pole DC fault [16]. Under normal conditions, the DSs in the AAC operate at the fundamental frequency (i.e., 50/60 Hz), thereby reducing the switching loss of the DSs. However, as analyzed in [14], the AAC needs to operate at the “sweet spot” to maintain the energy balance of stacks; thus, the modulation range is limited [17]. Compared with the AAC, the HCMC reduces the number of power electronic devices [16]. By employing a symmetrical modulation scheme [18, 19], the modulation range of the HCMC can be [0, 4/π], which is wider than that of the AAC. However, in the symmetrical modulation scheme, the DSs in the HCMC switch at a higher frequency [18, 19]; thus, the switching loss is higher than for the AAC. In [5] and [20], asymmetrical modulation methods for the HCMC are investigated to reduce the switching frequency and thereby the switching loss of the DSs. The asymmetrical modulation schemes are suitable for the HCMC for operation with a high modulation index but cannot be applied to the HCMC when the modulation index is lower than 2√3/π [5].
This paper proposes a novel hybrid multilevel converter with DC fault-blocking capability, i.e., the neutral-point clamped hybrid multilevel converter (NHMC). Compared with the HCMC, the proposed NHMC replaces the TLC stage with a three-level NPC stage and replaces the FBSMs with two types of unipolar full-bridge SMs (UFBSMs) [21], thereby reducing the number of IGBTs and the cost of the converter. The special hybrid design offers the proposed NHMC the capability to control the DSs to switch the fundamental frequency while working in a wide modulation range.
The rest of this paper is organized as follows. Section 2 presents the topology and operating modes of the proposed NHMC. Section 3 analyzes the operating principle, modulation scheme, and energy-balancing scheme of the NHMC during normal operation. Section 4 presents the DC fault-blocking scheme of the NHMC and compares between the NHMC and other multilevel converters. Section 5 demonstrates the features and operation scheme of NHMC through PSCAD/EMTDC simulation results. Section 6 concludes the paper.
2 Topology and operation modes
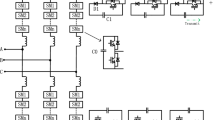
The NHMC is a hybrid topology that combines the features of the three-level NPC and the MMC. Figure 1 depicts the circuit configuration of an NHMC, which consists of three phases and two DC capacitors. Each phase of the NHMC consists of four director switches (DSs), two clamp switches (CSs), one stack, and one inductor. The DS and CS are composed of IGBTs and diodes in series, respectively, as shown in Fig. 2. The DSs can be switched on and off to conduct currents and withstand voltages, respectively. The neutral point of the whole circuit, i.e., point N, as shown in Fig. 1, is clamped by the CSs in each phase.
The stack in each phase is composed of two types of SM. The first type of SM is a UFBSM, which was first proposed in [18] as shown in Fig. 3a. This type of SM can work as an FBSM to provide bipolar voltages when the current that flows through it is negative; therefore, it is referred to as negative UFBSM. The second type of SM in the stack is modified from the negative unipolar UFBSM, as shown in Fig. 3b. It can work as an FBSM to provide bipolar voltages when the current that flows through it is positive; therefore, it is referred to as positive UFBSM. The operating states of the positive and negative UFBSMs are shown in Table 1. Each stack is composed of N s series-connected positive UFBSMs and N s series-connected negative UFBSMs, as shown in Fig. 2.
Table 1 shows that the positive UFBSMs altogether in one stack can generate voltage levels from −N s U c to +N s U c when the AC-side current is positive, and can be bypassed when the AC-side current is negative. On the other hand, the negative UFBSMs altogether in one stack can generate voltage levels from −N s U c to +N s U c when the AC-side current is negative and can be bypassed when the AC-side current is positive. Therefore, all the positive and negative UFBSMs can work together to generate voltage levels from −N s U c to +N s U c regardless of the AC-side current direction, as is the case with N s series-connected FBSMs. Under fault conditions, when all the positive and negative UFBSMs in one stack are blocked, they can generate reverse voltage levels as high as 2N s U c , again as can 2N s series-connected FBSMs.
The NHMC has two operating modes: the normal operating mode and the DC fault-blocking mode. The working states of the DSs and the stacks in phase a in each operating mode are listed in Table 2, and the operating principles of the NHMC in the two modes are explained in detail in the following two sections.
3 Normal operating scheme
The operating principle of the NHMC in the normal mode is similar to the HCMC [15] where the NPC stage is controlled to generate the fundamental component of AC grid voltages, while the stacks are controlled to attenuate the voltage harmonics produced by the NPC. However, owing to the differences between the NPC and the TLC, some obvious differences exist between the operating schemes of the NHMC and the HCMC. As discussed in the following subsection, the DSs in the NHMC switch at the fundamental frequency (50 Hz or 60 Hz) which helps to reduce the switching loss of the DSs.
3.1 Modulation scheme of the DSs
The three phases of NHMC are symmetrical, and phase a can be taken as an example to explain the modulation scheme of the DSs and stacks as shown in Fig. 4.
Table 2 shows the three different operating states of the DSs in phase a in the normal mode. To reduce the switching frequency of the DSs, a fundamental frequency modulation scheme is applied to the DSs to generate the fundamental component of the AC voltage of phase a (u a).
Figure 5 shows how the operating states of the DSs change at θ 1, θ 2, θ 3, and θ 4, and the switching frequency of each DS is the same as the frequency of u a, i.e., the fundamental frequency.
To balance the conducting time of the DSs, the following equations should be satisfied:
The voltage generated by the NPC stage can be expressed as:
where ω = 2π/T, T denotes the period of AC grid voltage, and U dc denotes the DC-link voltage. Therefore, based on (1) and (2), the amplitude of the fundamental voltage generated by the NPC can be calculated as follows:
The AC voltage and current of phase a are given as:
where φ is the power factor angle. The power flowing from the stack into the AC grid can be calculated as:
The power flowing from the NPC into the stack can be calculated as:
To ensure the energy of the stack is balanced, P NtoS should be equal to P StoG . Therefore, based on (3), (5), and (6), θ 1 can be calculated as follows:
Then θ 2, θ 3 and θ 4 can be solved simply by substituting (7) into (1), and the energy balance of each stack is achieved independently of the power factor angle φ. As a result, the switching states of DSs can be determined according to (1), (7) and Fig. 5.
3.2 Modulation scheme of the stacks
As previously analyzed, the stacks are controlled to work as a series-active power filter to attenuate the harmonics generated by the NPC stage. Moreover, similarly to the symmetrical modulation scheme of the HCMC [18, 19], a third-harmonic voltage u 3h (t) is injected to reduce the number of UFBSMs needed in each stack as shown in Fig. 6.
The injected third-harmonic voltage can be expressed as:
Therefore, the stack voltage of phase a can be calculated as:
As analyzed in Section 2, the stack voltage generated by the positive and negative UFBSMs together, i.e. u sa(t), should satisfy the following equation:
At time t = θ 1/ω, (10) can be expressed as:
From (11) the following equation can be derived:
Therefore, the minimum N s needed to satisfy (11) can be calculated as:
where ceil(X) equals the smallest integer which is no less than X.
The following equation can be obtained by substituting (13) into (11):
From (14), U 3h can be solved as:
where m denotes the modulation index of the NHMC and is defined as:
Based on (7), (15), and (16), the absolute value of U 3h becomes quite large when θ 1 is very close to zero, or when m is very close to 4/π (approximately 1.273). This condition indicates that the NHMC cannot operate when m is very close to 4/π. Table 3 lists m, θ 1, and U 3h when m is larger than 1.23, and shows that the absolute value of U 3h does not exceed U dc/4 as long as m is no greater than 1.25. Therefore, the modulation range of the NHMC can be 0 ≤ m ≤ 1.25, which is slightly narrower than for the HCMC (0 ≤ m ≤ 4/π) and is wider than for the MMC (0 ≤ m ≤ \(2 /\sqrt 3\)) [22] and AAC (m = 4/π at the “sweet spot” [14]).
The voltage generated by the stack of phase a, i.e. u sa(t), can be determined by (9). By applying the nearest level modulation (NLM) scheme [23], the voltage level number generated by the stack of phase a, i.e. N sa(t) can be calculated as follows:
Although the voltage level number of the stack is determined, the operating states of the SMs in the stack remain undetermined. Through the SM capacitor voltage balancing scheme described in Section 3.3, the operating states of the SMs in the stack can be obtained, and then the control signals for the IGBTs in the stack can be determined according to Table 1.
3.3 Voltage balancing scheme of SM capacitors
The modulation scheme of the DSs can ensure that the total energy of each stack is balanced. However, the energy balance inside the stack, i.e. the voltage balance of the SM capacitors, is not ensured. In the MMC and the HCMC, sorting strategies [5, 6, 23] are used to balance the SM capacitor voltages and obtain operating states of SMs. In fact, in the MMC and the HCMC, the SMs inside one stack can produce the same voltage levels; thus, their capacitor voltages can be sorted together to determine the operating states of the SMs. In the NHMC, however, each stack is composed of two different types of UFBSM which may produce different voltage levels. As a result, in some situations, the SM capacitor voltages of the NHMC cannot be sorted together to obtain the operating states of the SMs; thus, the existing sorting strategies cannot be simply transplanted to the NHMC. This paper proposes a modified sorting strategy for the NHMC to balance the SM capacitor voltages inside each stack. Taking the stack of phase a as an example, the proposed sorting strategy depends on the direction of the AC-side current i a and the voltage level number N sa as follows.
Situation 1: When i a > 0 and N sa > 0, the capacitor voltages of the positive and negative UFBSMs are sorted together, and then the UFBSMs with the lowest capacitor voltages whose sorted serial numbers are 1, 2, …, N sa are positively inserted for charging, and the other UFBSMs whose sorted serial numbers are N sa + 1, N sa + 2,…, N s are bypassed.
Situation 2: When i a > 0 and N sa < 0, the negative UFBSMs are bypassed, and only the capacitor voltages of the positive UFBSMs are sorted. The positive UFBSMs with the lowest capacitor voltages whose sorted serial numbers are 1, 2,…, N s − N sa are bypassed, and the other positive UFBSMs whose sorted serial numbers are N s − N sa + 1, N s − N sa + 2, …, N s are negatively inserted for discharging.
Situation 3: When i a < 0 and N sa < 0, the capacitor voltages of the positive and negative UFBSMs are sorted together, and the UFBSMs with the lowest capacitor voltages whose sorted serial numbers are 1, 2, 3,…, N sa are negatively inserted for charging, and the other UFBSMs whose sorted serial numbers are N sa + 1, N sa + 2,…, N s are bypassed.
Situation 4: When i a < 0 and N sa > 0, the positive UFBSMs are all bypassed, and only the capacitor voltages of the negative UFBSMs are sorted. The negative UFBSMs with the lowest capacitor voltages whose sorted serial numbers are 1, 2, …, N s − N sa are bypassed, and the other negative UFBSMs whose sorted serial numbers are N s − N sa + 1, N s − N sa + 2, …, N s are positively inserted for discharging.
As explained, the key feature of the modified sorting strategy is to maintain the capacitor voltage balance of the positive UFBSMs and the capacitor voltage balance of the negative UFBSMs separately in situations 2 and 4, and to achieve the capacitor voltage balance of the two types of UFBSMs in situations 1 and 3. The energy balance of the stack is ensured by modulating the DSs, and the SM capacitor voltages can be maintained around the nominated value by using the proposed modified sorting strategy.
3.4 Energy balancing scheme of DC capacitors
Similar to the conventional NPC, the energy balance of the DC capacitors is also an issue that requires attention. As analyzed in [24], in the fundamental period T, the energy difference between the two DC capacitors is mainly determined by the neutral line current i N (t). To maintain the energy balance of the DC capacitors, the following equation should be satisfied according to [24]:
As illustrated in Fig. 3, i N (t) can be calculated as:
while i aN (t) can be expressed as:
The following equation can be proved when θ 1, θ 2, θ 3 and θ 4 satisfy (1):
Therefore i N (t) satisfies (18) because of the symmetry of i aN (t), i bN (t) and i cN (t). Thus, the energy balance of the DC capacitors can be achieved.
4 DC fault blocking scheme and comparison with other multilevel converters
4.1 DC fault mechanism
When the NHMC is applied to DC transmission using overhead lines, the DC fault protection scheme becomes an important concern. Generally, two types of DC-side short-circuit faults exist in the NHMC-based HVDC system, the pole-to-pole short-circuit fault and the pole-to-ground short-circuit fault. The mechanisms of these two types of faults are analyzed as follows.
When a pole-to-pole DC fault occurs, the DC capacitors of the NHMC are discharged rapidly, and thus the DC-link voltage drops to zero, and the DC current increases to a high level at a fast speed. The discharging current of the DC capacitors does not flow through the DSs or stack, and therefore does not cause damage to the IGBTs or diodes. However, if the stacks do not provide reverse voltages against the AC-side currents, then the AC-side currents flow directly into the DC fault site because of the freewheeling effects of the anti-parallel diodes, and the DC fault turns into an AC-side short circuit fault, as shown in Fig. 7. The increasing AC-side short-circuit fault current flows through the stacks and DSs and might damage the power electronic devices.
The mechanism of the pole-to-ground fault is similar to that of the pole-to-pole fault. The positive pole-to-ground fault is taken as an example. After the DC fault occurs, the upper DC capacitor is discharged and the positive-pole DC current increases rapidly to a high level, as shown in Fig. 8. The discharging current of the upper DC capacitor does not flow through the DSs or stacks; thus, it will not cause damage to the IGBTs or diodes. On the other hand, the AC-side currents flow through the stacks and DSs and into the DC fault site. If the stacks do not provide reverse voltages, the AC-side currents increase rapidly and might damage the power electronic devices.
4.2 DC fault blocking scheme
To block the current paths between the AC side and the DC fault site, the NHMC should be switched to the DC fault-blocking mode in which all IGBTs in the DSs and stacks are switched off. According to Table 1, when all the SMs are blocked, the SM capacitors are charged and each stack provides reverse voltage as high as 2N s U c to oppose the current that flows between the two sides of the NHMC, regardless of the current direction.
During a pole-to-pole fault, as shown in Fig. 7, the following condition should be satisfied to ensure that the current can be eliminated and will not reignite:
where U lm is the amplitude of the AC grid line-to-line voltage, and satisfies the following equation:
Based on (22) and (23), the minimum N s needed to block the pole-to-pole DC fault can be calculated as:
On the other hand, as shown in Fig. 8, during a pole-to-ground fault, the number of UFBSMs in each stack should satisfy the following condition to block the AC-side currents:
Based on (23) and (25), the minimum N s needed to block the pole-to-ground DC fault can be derived as:
As N s,p2g is smaller than N s,p2p , the minimum N s needed to block both pole-to-pole and pole-to-ground faults is given by (24). From (13) and (24), the minimum N s needed in the normal and DC fault-blocking modes can be derived as follows:
4.3 Comparison with other multilevel converters
Several multilevel converter topologies have been proposed in previous studies for medium- or high-voltage DC transmission, such as the HBSM-MMC, FBSM-MMC, CDSM-MMC, hybrid FBSM-MMC, hybrid CDSM-MMC, hybrid UFBSM-MMC, AAC, HCMC, and so on, as described in Section 1. The number of power electronic devices employed in these converter topologies is compared to the proposed NHMC in Table 4. The table shows that among the multilevel converters with DC fault-blocking capability, the proposed NHMC uses the smallest number of IGBTs. Compared with the AAC, the proposed NHMC can work over a wide modulation range. Compared with the HCMC, the DSs of the NHMC switch at the fundamental frequency; thus, the switching loss can be reduced.
Attention should be paid to the hybrid multilevel converters, such as the AAC, HCMC, and the proposed NHMC, in which DC filters are essential to attenuate DC current harmonics. As the cost and volume of the additional DC filters increase rapidly with the DC-link voltage, the hybrid multilevel converters might not be economical when the DC-link voltage increases to a high level. Therefore, the proposed NHMC is likely to be more suitable for medium-voltage DC transmission with overhead lines.
5 Simulation
To verify the operating scheme and features of the NHMC, a detailed simulation model of the NHMC which has the same configuration as shown in Fig. 1 has been set up in PSCAD/EMTDC. The parameters of the simulation model are listed in Table 5. The following cases are simulated.
5.1 Verification of normal operating principle
In case 1, the NHMC works in the normal operating mode, and the rated AC-side line-to-line RMS voltage is set as 22 kV, i.e., the modulation index is 0.9. Before t = 0.3 s, the reference values of the active and reactive power are −16 MW and 8 Mvar, respectively. At t = 0.3 s, the reference value of active power steps to 16 MW. At t = 0.4 s, the reference value of the reactive power steps to −8 Mvar. Waveforms of the active and reactive power, AC-side currents, DC-link voltage, DC current, DC capacitor voltages, and SM capacitor voltages of phase a are shown in Fig. 9.
As illustrated in Fig. 9a, b, the NHMC is able to transmit active and reactive power following the reference value accurately with very low AC current harmonics. As shown in Fig. 9c–e, the DC voltage and current of the NHMC have six-pulse ripple which is effectively attenuated by DC capacitors and inductors. The DC capacitor voltages are also balanced and maintained around 20 kV. The SM capacitor voltages are well balanced and maintained around 1.7 kV, as shown in Fig. 9f. The simulation results shown in Fig. 9 verify the normal operating scheme of the NHMC.
5.2 Verification of high modulation index operation
In case 2, the rated AC-side line-to-line RMS voltage of the NHMC is 30.6 kV, i.e., the modulation index is 1.25. The reference values of the active and reactive power are set as −16 MW and +8 Mvar, respectively. Waveforms of the active and reactive power, the AC-side currents, the DC-link voltage, the DC current, the DC capacitor voltages, the SM capacitor voltages of phase a, the AC-side voltages, and the injected third-harmonic voltage are shown in Fig. 10. It is evident that the NHMC can be controlled well to follow the active and reactive power references, and the AC-side currents have little harmonics. The magnitude of the injected third-harmonic voltage is approximately 10 kV, which is not extremely large compared to the AC grid voltage. Simulation results in Fig. 10 verify that the NHMC can operate at a high modulation index.
5.3 Verification of DC fault blocking capability
In cases 3 and 4, the rated AC-side line-to-line RMS voltage of the NHMC is 22 kV, i.e., the modulation index is 0.9. Before t = 0.35 s, the NHMC is working in the normal operating mode to transmit an active power of −16 MW and generate a reactive power of +8 Mvar. In case 3, a pole-to-pole DC fault occurs at the DC port at t = 0.35 s, and the NHMC is switched to the DC fault-blocking mode when the absolute value of the DC fault current exceeds the activating threshold of 1 kA. Waveforms of the active and reactive power, AC-side currents, DC-link voltage, DC-side current, DC capacitor voltages, SM capacitor voltages of phase a, and currents flowing through DSs are presented in Fig. 11. The currents flowing through the first, second, third, and fourth DS of phase a are denoted as i a1, i a2, i a3, and i a4, respectively.
Figure 11 shows that, after the DC fault occurs at t = 0.35 s, the DC filters behave in a manner similar to an RLC circuit, and the DC capacitors are discharged rapidly, thereby resulting in a rapidly increasing DC fault current. However, after being switched to the DC fault-blocking mode, the NHMC is able to block the current path between the AC and DC fault sites, and the AC and DC currents decay to zero and do not reignite. The current flowing through each DS is cleared quickly after the NHMC is blocked, and therefore does not damage the power electronic devices.
In case 4, a pole-to-ground DC fault occurs at the DC port at t = 0.35 s, and the NHMC is switched to the DC fault-blocking mode when the absolute value of the DC current exceeds 1 kA. Waveforms of the active and reactive power, AC-side currents, DC voltage, DC current, DC capacitor voltages, SM capacitor voltages of phase a, and currents flowing through DSs are reported in Fig. 12a–h, with currents denoted as in Fig. 11. Figure 12 shows that the NHMC is capable of blocking the pole-to-ground fault as well. The simulation results in Figs. 11 and 12 demonstrate the DC fault-blocking capability of the NHMC.
5.4 Comparison with the HCMC
In case 5, a simulation model of the HCMC proposed in [15] is presented for comparison with the NHMC proposed in this paper. In the HCMC model, each stack is composed of 12 FBSMs, and each DS consists of 12 IGBTs. The rated AC-side line-to-line RMS voltage is set as 22 kV, i.e., the modulation index is 0.9. The other parameters of the HCMC model are the same as those in Table 5. Before t = 0.35 s, the reference values of the active and reactive power are −16 MW and +8 Mvar, respectively. At t = 0.35 s, a pole-to-pole DC fault occurs at the DC port, and the HCMC is switched to the DC fault-blocking mode when the absolute value of the DC fault current exceeds 1 kA. Waveforms of the active and reactive power, AC-side currents, DC-link voltage, DC-side current, currents flowing through the DSs of phase a, and SM capacitor voltages of phase a are shown in Fig. 13.
As illustrated in Figs. 11 and 13, the performance of the NHMC is similar to that of the HCMC during a pole-to-pole fault, and both converters are able to block the DC fault current. However, as shown in Table 4, the proposed NHMC uses fewer IGBTs. Comparing between Figs. 11g and 13e also indicates that the switching frequency of the DSs in the NHMC is lower than that of the DSs in the HCMC; therefore, the switching power loss can be reduced.
6 Conclusion
This paper proposes a new hybrid multilevel converter for medium-voltage DC transmission, i.e., the NHMC. The basic topology, operating principle, modulation scheme, energy balancing scheme, and DC fault-blocking capability of the NHMC were studied and presented. Compared to the existing multilevel converters for medium-voltage DC transmission, the main merits of the proposed NHMC are its capability to operate the DSs at fundamental frequency while working in a wide modulation range and its capability of blocking DC fault currents with a relatively small number of IGBTs. Simulation results, including a comparison with an existing multilevel converter, demonstrate the features and merits of the proposed NHMC and show that it can be an economical and feasible option for medium-voltage DC transmission with overhead lines.
References
Flourentzou N, Agelidis VG, Demetriades GD (2009) VSC-based HVDC power transmission systems: an overview. IEEE Trans Power Electron 24(3):592–602
Nabae A, Takahashi I, Akagi H (1981) A new neutral-point-clamped PWM inverter. IEEE Trans Ind Appl 17(5):518–523
Lesnicar A, Marquardt R (2003) An innovative modular multilevel converter topology suitable for a wide power range. In: Proceedings of the 2003 IEEE power tech conference, vol 3, Bologna, Italy, 23–26 June 2003, 6 pp
Davidson CC, Trainer DR (2010) Innovative concepts for hybrid multi-level converters for HVDC power transmission. In: Proceedings of the 9th IET international conference on AC and DC power transmission (ACDC 2010), London, UK, 19–21 October 2010, pp 1–5
Xue Y, Xu Z, Tu Q (2012) Modulation and control for a new hybrid cascaded multilevel converter with dc blocking capability. IEEE Trans Power Deliv 27(4):2227–2237
Saeedifard M, Iravani R (2010) Dynamic performance of a modular multilevel back-to-back HVDC system. IEEE Trans Power Deliv 25(4):2903–2912
Tang G, He Z, Pang H (2014) R&D and application of voltage sourced converter based high voltage direct current engineering technology in China. J Mod Power Syst Clean Energy 2(1):1–15. doi:10.1007/s40565-014-0045-3
Yuan Y, Li P, Kong X et al (2016) Harmonic influence analysis of unified power flow controller based on modular multilevel converter. J Mod Power Syst Clean Energy 4(1):10–18. doi:10.1007/s40565-015-0175-2
Li B, He J, Tian J et al (2017) DC fault analysis for modular multilevel converter-based system. J Mod Power Syst Clean Energy 5(2):275–282. doi:10.1007/s40565-015-0174-3
Li X, Song Q, Liu W et al (2013) Protection of nonpermanent faults on DC overhead lines in MMC-Based HVDC systems. IEEE Trans Power Deliv 28(1):483–490
Jung J, Cui S, Lee J et al (2017) A new topology of multilevel VSC converter for a hybrid HVDC transmission system. IEEE Trans Power Electron 32(6):4199–4209
Marquardt R (2010) Modular multilevel converter: an universal concept for HVDC-networks and extended dc-bus-applications. In: Proceedings of the 2010 international power electronic conference (IPEC 2010), Sapporo, Japan, 21–24 June 2010, pp 502–507
Cui S, Kim S, Jung J et al (2016) A comprehensive DC short-circuit fault ride through strategy of hybrid modular multilevel converters (MMCs) for overhead line transmission. IEEE Trans Power Electron 31(11):7780–7796
Merlin MMC, Green TC, Mitcheson PD et al (2014) The alternate arm converter: a new hybrid multilevel converter with DC-fault blocking capability. IEEE Trans Power Deliv 29(1):310–317
Adam GP, Ahmed KH, Finney SJ et al (2012) New breed of network fault-tolerant voltage-source-converter HVDC transmission system. IEEE Trans Power Syst 28(1):335–346
Adam GP, Finney SJ, Williams BW (2013) Hybrid converter with ac side cascaded H-bridge cells against H-bridge alternative arm modular multilevel converter: steady-state and dynamic performance. IET Gener Transm Distrib 7:318–328
Wickramasinghe HR, Konstantinou RG, Pou J et al (2016) Asymmetric overlap and hysteresis current control of zero-current switched alternate arm converter. In: Proceedings of the IECON 2016-42nd annual conference of the IEEE industrial electronics society, Florence, Italy, 23–26 October 2016, pp 2526–2531
Adam GP, Abdelsalam I, Finney SJ et al (2013) Comparison of two advanced modulation strategies for a hybrid cascaded converter. In: Proceedings of the 2013 IEEE energy conversion congress and exposition (ECCE) Asia Downunder, Melbourne, Australia, 3–6 June 2013, pp 1334–1340
Zhang Y, Adam G, Finney S et al (2013) Improved pulse-width modulation and capacitor voltage-balancing strategy for a scalable hybrid cascaded multilevel converter. IET Power Electron 6(4):783–797
Xiang W, Lin W, Yao L et al (2016) Parameter design and operating zone of hybrid cascaded multilevel converter under asymmetrical square-wave modulation method of the director switch. IET Gener Transm Distrib 10(9):2155–2164
Qin J, Saeedifard M, Rockhill A et al (2015) Hybrid design of modular multilevel converters for HVDC systems based on various submodule circuits. IEEE Trans Power Deliv 30(1):385–394
Rohner S, Bernet S, Hiller M et al (2010) Modulation, losses, and semiconductor requirements of modular multilevel converters. IEEE Trans Ind Electron 57(8):2633–2642
Guan M, Xu Z, Chen H (2011) Control and modulation strategies for modular multilevel converter based HVDC system. In: Proceedings of the IECON 2011-37th annual conference of the IEEE industrial electronics society, Melbourne, VIC, Australia, 7–10 November 2011, pp 849–854
Zhu R, Wu X, Jiang X et al (2010) An improved neutral-point-potential balance control strategy for three-level PWM rectifier. In: Proceedings of the 2010 Asia Pacific conference on postgraduate research in microelectronics and electronics (PrimeAsia 2010), Shanghai, China, 22–24 September 2010, pp 1–4
Acknowledgements
This work was supported by Key Science and Technology Project of China Southern Power Grid (Research on Key Technologies and Demonstration Application of Flexible Coordinated Control of Electromagnetic Loop Network in Metropolitan Power Grid with High Load Density, No. GZHKJ00000101).
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 16 May 2017
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
YU, X., WEI, Y., JIANG, Q. et al. Neutral-point-clamped hybrid multilevel converter with DC fault blocking capability for medium-voltage DC transmission. J. Mod. Power Syst. Clean Energy 5, 524–536 (2017). https://doi.org/10.1007/s40565-017-0297-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0297-9