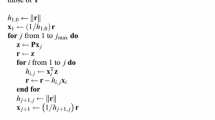1 Introduction

In this paper, we study the effectiveness of obtaining reduced order system of ordinary differential equations (ODEs) for delay differential equations (DDEs) with variable delays using a Galerkin projection scheme. Three different variations in the time-delay viz. a periodic variation, a random variation and a state-dependent delay have been considered. The procedure for each kind of variation has been demonstrated for the practical example of a relevant model for chatter during turning.

The study of time-periodic delays gained popularity in the 1970s when several researchers [1–4] started focussing on the suppression of tool-chatter using continuous modulation of the spindle speed. The governing mathematical model for machining with periodic spindle speed modulation is a DDE with a variable delay as opposed to a DDE with constant delay for machining with a constant spindle speed. This complicates the stability analysis of machining with spindle speed modulation. Sexton et al. [4] assumed a periodic solution for the problem and used harmonic balance to obtain the stability boundary. Jayaram et al. [5] improved on the results of Sexton et al. [4] by assuming a quasi-periodic solution for the model which is expanded in terms of Bessel functions and obtained the stability boundary using the method of harmonic balance. Sri Namachchivaya and co-workers [6–8] incorporated nonlinearity in the mathematical model for cutting with variable spindle speed and performed a detailed nonlinear analysis for small amplitudes of the modulation. Insperger et al. [9, 10], Long and Balachnadran [11], Bediaga et al. [12], and Seguy et al. [13] obtained stability charts for machining with periodic modulation of the spindle speed using semi-discretization (introduced by Insperger and Stépán [14]). Recently, Zhang and Ni [15] obtained analytical estimates for the stability boundary of turning with spindle speed variation using an internal energy based analysis. In this work, we perform the stability analysis of cutting with periodic spindle speed modulation using an approach similar to the Galerkin projection technique introduced by Wahi and Chatterjee [16] and Wahi [17] which can handle variable delays. The Galerkin projection for periodic delays results in system of ODEs with periodic coefficients whose stability is accessed using the Floquet theory [18, 19].

In contrast to the case of periodic delays, very limited studies have been reported on the application of random delays to real-world systems even though several studies have appeared on developing the mathematical theory of systems with random delays [20–23]. Most literature on the application of random delays have focused on the effect of random delays introduced in large scale communication networks on the stability and subsequent control of these networks [24–28]. Sinha and Lyschevski [29] considered microelectromechanical motion devices and used a random delay based fuzzy controller for the control of energy processes in these devices. Mattia and Giudice [30] studied the role of random synaptic delays in determining the average dynamics of a network of neurons. Wen et al. [31] obtained conditions for synchronization of chaotic systems in the presence of random delays in the feedback loop. Random delays became relevant to mechanical engineering when Yilmaz et al. [32] considered the possibility of suppression of chatter using a random modulation of the spindle speed. They analyzed the stability of the linear system with the random delay using a procedure developed by Grigoriu [33]. In this paper, we will consider the mechanical system analyzed by Yilmaz et al. [32] and obtain stability results using a system of ODEs obtained using a Galerkin projection technique. The stability of the system of these stochastic ODEs has been ascertained using Lyapunov exponents [34].

The study of delayed systems with state-dependent delays is in its nascent stage and the rigorous mathematical theory for the stability and bifurcation analysis of these systems is still under development. However, there has been a splurge of studies on the application of state-dependent delays for modeling machining processes and we present a brief account of some important studies in this direction. Insperger et al. [35] recently noted that an accurate modeling of the regenerative effect involves a state-dependent delay (wherein the delay is determined by a combination of the workpiece rotation and tool vibration). In [36], Insperger et al. have shown using a numerical continuation technique that there is a transition from subcritical to supercritical bifurcation as the feed-rate is increased. Wahi [37] investigated the Hopf bifurcation in the state-dependent delay model proposed by Insperger et al. [35] analytically using the method of multiple scales and confirmed the change of criticality of the Hopf bifurcation. In this paper, we present some results on the stability and bifurcation behavior of the same model as obtained through a system of ODEs obtained via. a Galerkin projection scheme. Some more results for the same can be obtained in [38, 39].

The rest of the paper is organized as follows. In Sect. 2, the Galerkin projection technique based on embedding the variable delay in a fixed interval is presented followed by its application to the study of stability of turning with periodic and random modulation of the spindle speed in Sects. 3 and 4 respectively. An alternate approach based on dynamic scaling of the variable delay to a fixed delay is presented in Sect. 5 followed by its application to the stability and bifurcation study of a two degree of freedom state-dependent delay model for turning in Sect. 6. Finally some conclusions are drawn in Sect. 7.

2 Galerkin projections for DDEs with variable delays using embedding

The Galerkin projection technique presented in [16, 17] assumed fixed delays. In what follows, we present some modifications required for the method to be applied to the case of variable delay and also summarize the Galerkin projection technique for completeness. This method for handling variable delays has been reported in [40].

Consider a DDE with finitely many delays which are bounded and vary in time (for simplicity we will present the variation with time \(t\) only even though the method is equally applicable to cases where the delay depends on other variables)

$$\begin{aligned} \dot{x}(t)&= \hat{f}\left( t, x(t), x(t-\tau _1(t)),x(t-\tau _2(t)), \ldots , x(t-\tau _n(t))\right) .\nonumber \\ \end{aligned}$$
(1)

All the delays are assumed to be bounded functions of time. Hence, we can choose

$$\begin{aligned} \tau _{i,\text{ max }}=\sup _{t>0} \tau _i(t),\quad i=1,2,\ldots ,n. \end{aligned}$$

Now define the maximum delay as

$$\begin{aligned} \tau _{\text{ max }} = \max \left( \tau _{1,\text{ max }}, \tau _{2,\text{ max }}, \ldots , \tau _{n,\text{ max }}\right) \end{aligned}$$

and scale time as \(\displaystyle \bar{t} = \frac{t}{\tau _{\text{ max }}}\). This modifies Eq. (1) to

$$\begin{aligned} x^{\prime }(\bar{t})&= f\left( \bar{t}, \tau _{\text{ max }}, x(\bar{t}), x(\bar{t}-\bar{\tau }_1(\bar{t})), x(\bar{t}\right. \nonumber \\&\left. -\bar{\tau }_2(\bar{t})), \ldots , x(\bar{t}-\bar{\tau }_n(\bar{t}))\right) , \end{aligned}$$
(2)

where \(\prime \) represents differentiation w.r.t. the scaled time \(\bar{t}\) and \(\displaystyle \bar{\tau }_i(\bar{t}) = \frac{\tau _i(t)}{\tau _{\text{ max }}}, i=1,2,\ldots ,n\). Note that \(\bar{\tau }_i(\bar{t}) \le 1\).

Now we are in a position to proceed with the Galerkin projection as presented in [16, 17]. At any given instant of time \(\bar{t}\), we introduce a local time variable \(s\) which lies in the interval \([0,1]\) and define a bivariate function \(F(\bar{t}, s)\) as

$$\begin{aligned} F(\bar{t}, s)\,=\,x_s(\bar{t})\,=\,x(\bar{t} - s),\quad s \in [0,1]. \end{aligned}$$
(3)

which gives us

$$\begin{aligned} \frac{\partial F}{\partial \bar{t}} + \frac{\partial F}{\partial s}\, =\, 0 \end{aligned}$$
(4)

in the interior of the \(s\)-interval. We note at this point that the domain of interest for the local time variable \(s\) changes with \(t\), but we have embedded it in the fixed interval \(s\in [0,1]\) over which we proceed with our approximation for the bivariate function \(F(\bar{t}, s)\). This embedding scheme is represented pictorially in Fig. 1. We next approximate this bivariate function \(F(\bar{t}, s)\) as

$$\begin{aligned} F(\bar{t}, s)\,\approx \,a_0(\bar{t})\,+\,a_1(\bar{t})\,s\,+\,\sum _{k=1}^{N-2}\,a_{k+1}(\bar{t})\, \sin (k \pi s), \end{aligned}$$
(5)

where \(N\) is a finite number chosen by us. From Eqs. (3) and (5), we have

$$\begin{aligned} x(\bar{t}- \bar{\tau }_i(\bar{t}))&= F(\bar{t}, \bar{\tau }_i(\bar{t}))\,\approx \,a_0(\bar{t})\,+\,a_1(\bar{t})\,\bar{\tau }_i(\bar{t})\nonumber \\&+\sum _{k=1}^{N-2}\,a_{k+1}(\bar{t})\, \sin (k \pi \bar{\tau }_i(\bar{t})) \end{aligned}$$
(6)

for \(i=1,2,\ldots , n\). Note from Eq. (6) that time-varying delayed terms translate into time-varying coefficients in our approximation. In addition, we have \(x(\bar{t})\,\equiv \,F(\bar{t},0)\,=\,a_0(t),\) which on differentiation with respect to \(\bar{t}\) gives

$$\begin{aligned} a_0^{\prime }(\bar{t})\!=\! x^{\prime }(\bar{t}) \!=\! f\left( \bar{t}, \tau _{max}, a_0(\bar{t}), a_1(\bar{t}), a_2(\bar{t}), \ldots , a_{N\!-\!1}(\bar{t})\right) , \end{aligned}$$
(7)

where the function \(f\) is obtained by substituting Eqs. (3), (5) and (6) in \(\hat{f}\) of Eq. (2). As shown in Fig. 1, Eq. (7) defines the boundary condition for Eq. (4) on the semi-infinite edge with \(s=0\) and \(\bar{t}>0\), as it governs the evolution of the function \(F(\bar{t},s)\) on this boundary.

Fig. 1
figure 1

A schematic representation of the embedding of the variable \(s\)-domain in a fixed domain \([0,1]\)

Full size image

Substituting Eq. (5) in Eq. (4), we define

$$\begin{aligned} r(\bar{t},s)&= a_0^{\prime }(\bar{t}) + a_1^{\prime }(\bar{t}) \, s + \sum _{k=1}^{N-2} a_{k+1}^{\prime }(\bar{t}) \sin (k \pi s) + a_1(\bar{t})\nonumber \\&+ \sum _{k=1}^{N-2} a_{k+1}(\bar{t}) k \pi \cos (k \pi s), \end{aligned}$$
(8)

where \(r(t,s)\) is called the residual. The residual is made orthogonal to the shape functions (this is the Galerkin projection) to obtain the following \(N-1\) equations:

$$\begin{aligned}&\int _0^1 \left\{ a_0^{\prime }(\bar{t}) + a_1^{\prime }(\bar{t}) \, s + \sum _{k=1}^{N-2} a_{k+1}^{\prime }(\bar{t}) \sin (k \pi s) + a_1(\bar{t})\right. \nonumber \\&\quad \left. + \sum _{k=1}^{N-2} a_{k+1}(\bar{t}) k \pi \cos (k \pi s) \right\} \, \cdot \, s \, ds = 0 \end{aligned}$$
(9)

and

$$\begin{aligned}&\int _0^1 \left\{ a_0^{\prime }(\bar{t}) + a_1^{\prime }(\bar{t}) \, s + \sum _{k=1}^{N-2} a_{k+1}^{\prime }(\bar{t}) \sin (k \pi s) + a_1(\bar{t}) \right. \nonumber \\&\quad \left. + \sum _{k=1}^{N-2} a_{k+1}(\bar{t})\, k \pi \cos (k \pi s) \right\} \, \cdot \, \sin (m \pi s) \, ds = 0, \end{aligned}$$
(10)

for \(m = 1, 2, \ldots , N-2\).

Equations (7), (9) and (10) constitute \(N\) ODEs governing the evolution of the variables \(a_i(\bar{t})\) and can be written in the form

$$\begin{aligned} \mathbf{A} \mathbf{a}^{\prime }(\bar{t})+ \mathbf{B} \mathbf{a}(\bar{t})= \mathbf{b}(\mathbf{{a}}(\bar{t}),\bar{t}), \end{aligned}$$
(11)

where \(\mathbf{A}\) and \(\mathbf{B}\) are \(N+1 \times N+1\) matrices, \(\mathbf{a}\) is a vector containing the \(a_{i}\)s, and \(\mathbf{b}(\mathbf{{a}}(\bar{t}), \bar{t})\) is a vector with a single nonzero element representing time varying and/or nonlinear terms from the DDE (Eq. (2)). Almost all elements of both \(\mathbf{A}\) and \(\mathbf{B}\) can be evaluated once and for all, independent of the specific DDE (the last \(N-1\) rows as determined by Eqs. (9) and (10) and have constant coefficients which are independent of the given DDE).

In the case of either Eq. (1) being a linear DDE with only time-varying coefficients as the time-dependence (or time-periodic delays) or for stability analysis of Eq. (1), Eq. (11) can be written as a linear time-dependent set of ODEs as

$$\begin{aligned} \mathbf{A} \mathbf{a}^{\prime }(\bar{t})+ \mathbf{B}(\bar{t}) \mathbf{a}(\bar{t})= \mathbf{0}, \end{aligned}$$
(12)

where only the first row of \(\mathbf{B}(\bar{t})\) contains time-varying terms. In the special case of the delays being periodic functions of time, i.e., \(\tau _i(t)=\tau _i(t+T)\) for some \(T\), the time dependent terms in \(\mathbf{B}(\bar{t})\) will also be periodic with a period \(\displaystyle \frac{T}{\tau _{\text{ max }}}\) and the Floquet theory [18, 19] can be used to study the stability of Eq. (12).

We would like to emphasize that the above description of the Galerkin projection method can also be applied for state-dependent delays and also for random bounded delays. The only requirement is that the delays should be bounded above by some maximum delay \(\tau _{\text{ max }}\). For random delays, Eq. (6) would include random coefficients resulting in a set of stochastic ODEs whose stability properties can be ascertained using tools from stochastic ODEs. The precise bound on the delay in the case of state-dependent delays are difficult to obtain apriori since it depends on the solution itself. However, depending on the particular application a conservative upper bound for the delay can be obtained which can be used for the scaling. The only difficulty with the treatment of state-dependent delays using this method is that the dependence of the delay on the state might be implicit or explicit and depending on the particular case, we might end up with a nonlinear algebraic equation for the definition of the delay. This results in a set of differential algebraic equations (DAEs) whose stability and bifurcation analysis is not as easy as the study of ODEs. An alternative procedure to handle variable delays based on dynamic scaling of the time variable in the delayed interval which circumvents the above-mentioned difficulty for state-dependent delays will be presented in Sect. 5.

First we present the application of this approach to the case of time-periodic and random delays in the next two sections. In the next section, we present some stability results obtained for a single degree of freedom (SDOF) model for tool vibration in turning with periodically modulated spindle speed.

3 A SDOF model of turning with varying spindle speed as an illustrative example for periodic delays

A schematic of the turning process in 3-D, and a 2-D projection of the same on the \({x}-{y}\) plane, are shown in Fig. 2. The tool travels along the negative \({x}\)-axis with a constant nominal feed rate of \(C_0\) (length units/revolution). The chip width \(w\) is the depth of cut in this cutting process, and is along the negative \({z}\)-axis. The tool and tool-holder assembly is approximated by a single degree of freedom spring-mass-damper system in the \({x}\) direction with coefficients \(k\), \(m\) and \(c\), respectively. Let the instantaneous chip thickness be denoted by \(C(t)\). The equation of motion for the tool about the steady-state deflection is usually given as [41–43]

$$\begin{aligned} m\, \ddot{x}(t) + c\, \dot{x}(t) + k\, {x}(t) = F_{x}(C(t))-F_{x}(C_0). \end{aligned}$$
(13)
Fig. 2
figure 2

A simple single degree of freedom model for tool vibrations

Full size image

Alternately, we can write

$$\begin{aligned} \ddot{x}(t) + 2\, \zeta \, \omega _n\, \dot{x}(t) + \omega _n^2\, {x}(t) =\frac{F_{x}(C(t))}{m}-\frac{F_{x}(C_0)}{m}, \end{aligned}$$
(14)

where \(\displaystyle \omega _n = \sqrt{\frac{k}{m}}\) is the natural angular frequency of the tool and \(\displaystyle \zeta = \frac{c}{2 \sqrt{m\,k}}\) is the damping ratio. Using the power law model of Taylor [44]

$$\begin{aligned} F_{x}(C(t)) = K\, w\, C(t)^{3/4}, \end{aligned}$$

where \(w\) is the chip width and \(K\) incorporates the dependence on other cutting parameters like cutting velocity, nominal feed, tool geometry etc., all assumed constant for our analysis, we get

$$\begin{aligned} \ddot{x}(t) + 2\, \zeta \, \omega _n\, \dot{x}(t) + \omega _n^2\, {x}(t) = \frac{K\, w}{m} C(t)^{3/4}-\frac{K\, w}{m} C_0^{3/4}, \end{aligned}$$
(15)

Equation (15) provides the basic model for the tool-workpiece dynamics. The instantaneous chip thickness due to tool vibrations is defined by

$$\begin{aligned} C(t)=C_0+x(t-\tau (t))-x(t), \end{aligned}$$

where \(\tau (t)\), the time delay is the time taken for the workpiece to complete one revolution. Note that the time taken for one revolution is no longer a constant since the spindle speed is varying. Using the above definition of the instantaneous chip thickness and linearizing about the nominal chip thickness, we have the linearized model for tool vibration as

$$\begin{aligned} \ddot{x}(t) + 2\, \zeta \, \omega _n\, \dot{x}(t) + \omega _n^2\, {x}(t) = P \left( x(t-\tau (t))-x(t)\right) , \end{aligned}$$
(16)

where \(\displaystyle P =\frac{3\,K\, w}{4\,m\,C_0^{1/4}}\).

If the modulation of the spindle speed is represented as

$$\begin{aligned} \Omega (t) = \Omega _0 + \Omega _1 \cos (\omega _m t), \end{aligned}$$
(17)

where \(\Omega _0\) is the mean value of the spindle speed, \(\Omega _1\) is the amplitude of the modulation and \(\omega _m\) is the angular frequency of the modulation, it has been shown in [10] that for small \(\Omega _1\), the time taken to complete one revolution \(\tau (t)\) can be approximated fairly accurately by the function

$$\begin{aligned} \tau (t) \approx \tau _0 - \tau _1 \cos (\omega _m\,t), \end{aligned}$$
(18)

where \(\displaystyle \tau _0 =\frac{2\pi }{\Omega _0}\) and \(\displaystyle \frac{\tau _1}{\tau _0} = \frac{\Omega _1}{\Omega _0}\). Accordingly the time period of modulation which is also the time-period of the delay \(\tau (t)\) is given as \(\displaystyle T=\frac{2\pi }{\omega _m}\).

Substituting Eq. (18) for \(\tau (t)\) in Eq. (16) and introducing the dimensionless time \(\tilde{t} = \omega _n t\), we get the dimensionless linearized equation of motion as

$$\begin{aligned} \ddot{x}(\tilde{t}) + 2\, \zeta \, \dot{x}(\tilde{t}) + {x}(\tilde{t}) \!=\! \tilde{P} \left( x(\tilde{t}-\tilde{\tau }_0 + \tilde{\tau }_1 \cos (\tilde{\omega }_m \tilde{t}))\!-\!x(\tilde{t})\right) , \end{aligned}$$
(19)

where \(\displaystyle \tilde{P} = \frac{P}{\omega _n^2} = \frac{3\,K\, w}{4\,m\,C_0^{1/4}\omega _n^2}\) is the dimensionless chip width, \(\tilde{\tau }_0 = \omega _n \tau _0\) is the dimensionless mean delay, \(\tilde{\tau }_1 = \omega _n \tau _1\) is the dimensionless delay amplitude and \(\displaystyle \tilde{\omega }_m = \frac{\omega _m}{\omega _n}\) is the dimensionless modulation frequency. Next we introduce the modulation amplitude ratio (as in [10])

$$\begin{aligned} R_a = \frac{\tilde{\tau }_1}{\tilde{\tau }_0}= \frac{\tau _1}{\tau _0} \end{aligned}$$
(20)

and the ratio of the modulation time period and the mean time delay as

$$\begin{aligned} R_m = \frac{\tilde{T}}{\tilde{\tau }_0}= \frac{2\pi }{\tilde{\omega }_m\, \tilde{\tau }_0} = \frac{2\pi }{\omega _m\,\tau _0} \end{aligned}$$
(21)

With the introduction of the above two ratios in Eq. (19) and dropping the tildes with abuse of notation (for notational convenience), we obtain

$$\begin{aligned}&\ddot{x}(t) + 2\, \zeta \, \dot{x}(t) + {x}(t)\nonumber \\&\quad = P \left( x \left( t-\tau _0\left( 1 - R_a \cos \left( \frac{2 \pi t}{R_m \tau _0}\right) \right) \right) -x(t)\right) . \end{aligned}$$
(22)

We now need to set Eq. (22) in the framework of the procedure presented in Sect. 2. Accordingly we scale time as \(\displaystyle \bar{t} = \frac{t}{\tau _0(1+R_a)}\) which modifies Eq. (22) to

$$\begin{aligned}&{x}^{\prime \prime }(\bar{t}) + 2\, \zeta \,\tau _0 \left( 1+R_a\right) {x}^{\prime }(\bar{t}) + \tau _0^2 \left( 1+R_a\right) ^2 {x}(\bar{t})\nonumber \\&\quad = \tau _0^2 \left( 1+R_a\right) ^2 P \left( x\left( \bar{t}- \frac{1}{1+R_a}\left( 1\right. \right. \right. \nonumber \\&\qquad \left. \left. \left. - R_a \cos \left( \frac{2 \pi (1+R_a) \bar{t}}{R_m}\right) \right) \right) -x(t)\right) . \end{aligned}$$
(23)

Now substituting the approximation for \(x(\bar{t}) = F(\bar{t}, 0) \approx a_0(\bar{t})\) and

$$\begin{aligned}&\displaystyle x\left( \bar{t}- \frac{1}{1+R_a}\left( 1 - R_a \cos \left( \frac{2 \pi (1+R_a) \bar{t}}{R_m}\right) \right) \right) \nonumber \\&\quad = F \left( \bar{t}, \frac{1}{1+R_a}\left( 1 - R_a \cos \left( \frac{2 \pi (1+R_a) \bar{t}}{R_m}\right) \right) \right) \end{aligned}$$

in Eq. (23) yields

$$\begin{aligned}&{a_0}^{\prime \prime }(\bar{t}) + 2\, \zeta \,\tau _0 \left( 1+R_a\right) {a_0}^{\prime }(\bar{t}) + \tau _0^2 \left( 1+R_a\right) ^2 {a_0}(\bar{t})\nonumber \\&\quad = P \left( \frac{a_1(\bar{t})}{1+R_a}\left( 1 - R_a \cos \left( \frac{2 \pi (1+R_a) \bar{t}}{R_m}\right) \right) \right. \nonumber \\&\qquad \left. +\,\sum _{k=1}^{N-2}\,a_{k+1}(\bar{t})\, \sin \left( \frac{k \pi }{1+R_a}\left( 1\right. \right. \right. \nonumber \\&\qquad \,\left. \left. \left. - R_a \cos \left( \frac{2 \pi (1+R_a) \bar{t}}{R_m}\right) \right) \right) \right) \tau _0^2 \left( 1+R_a\right) ^2, \end{aligned}$$
(24)

where again \(N\) is a finite number representing the order of our approximation. Equation (24) along with Eqs. (9) and (10) constitute our finite-dimensional linear model for turning with periodic spindle speed modulation.

For illustration, we consider the stability charts for the parameter values \(\zeta =0.03\), \(R_a=0.25\) and \(R_m = 0.4\) which was considered by Jayaram et al. [5] and Insperger and Stépan [10]. The stability chart (the parameters \(P\) and \(\Omega _0\) corresponding to the absolute value of the largest Floquet multiplier equal to 1) for these parameter values for different values of \(N\) is shown in Fig. 3 along with the results from direct numerical simulations. The results from direct numerical simulations have been included in this figure because there was a disagreement between the stability charts for these parameters obtained using semi-discretization [14] by Insperger and Stépán [10] and those obtained using Harmonic balance combined with Bessel functions by Jayaram et al. [5]. Our stability chart matches the one presented in Insperger and Stépán [10] wherein there are slanting stability lobes for these parameter values. Details of the procedure followed to obtain the stability charts using direct numerical simulation can be found in [40]. The match of the stability boundaries from the ODE approximation with the boundary obtained from direct numerical simulation improves with an increase in \(N\). For the range of \(\Omega _0\) considered in Fig. 3, we note that the smallest number \(N\) required to properly represent the solution in the maximum delayed interval is around 20. Accordingly we have started from \(N=20\). It can be seen that the qualitative nature of the stability diagram has been captured well with \(N=20\) but the quantitative match is not very good. \(N=30\) improves the match but leads to an overestimate of the stable regions for higher \(P\) values. The quantitative match is very good for \(N=40\) and \(N=50\) as can be seen clearly from a zoomed view of the boxed region shown in the right figure of Fig. 3.

Fig. 3
figure 3

Left Stability chart for turning with periodic spindle speed modulation for the parameters \(\zeta =0.03\), \(R_a=0.25\) and \(R_m = 0.4\). The stability chart is shown for \(\Omega _0\) in rpm which translates to \(\tilde{\Omega }_0\) using the natural frequency of the tool as \(f_n=100\) Hz. The approximation parameter \(N\) has been chosen to be \(20, 30, 40\) and \(50\). Right A zoomed view of the boxed region in left clearly demonstrating the variation of the stability boundary with varying \(N\)

Full size image

Continuing further, we present some more stability results which are different from the ones reported in Insperger and Stépán [10] wherein the modulation amplitude ratio \(R_a\) was fixed to \(0.1\) and the modulation period ratios \(R_m\) varied over a range of values from \(2\) to \(20\). In physical cases, it might be more realistic to assume that the modulation time period \(T\) is a constant for the system which induces the modulation of the spindle speed. A series of stability charts with modulation amplitude ratio \(R_a\) varying from \(0.01\) to \(0.2\) for a fixed modulation time period \(T=1\) is shown in Fig. 4.

Fig. 4
figure 4

Stability charts for turning with periodic spindle speed modulation for the parameters \(\zeta =0.03\), \(T=1\), \(\omega _n=200\,\pi \) and a \(R_a=0.01\), b \(R_a=0.05\), c \(R_a=0.1\), d \(R_a=0.2\). The approximation parameter \(N\) is \(22\) in each case resulting in a \(23 \times 23\) transition matrix

Full size image

For \(R_a=0.01\), it can be seen in Fig. 4a that the stability charts for turning with periodic spindle speed modulation and conventional turning are almost coincident. This is expected since the periodic variation in the spindle speed is very small. From Fig. 4, it can be seen that the stable region increases as the modulation amplitude ratio \(R_a\) is increased. However, it can be seen from Fig. 4d that for larger modulation amplitude ratio \(R_a\), regions in the parameter space which were stable for conventional cutting become unstable in the presence of periodic modulation of the spindle speed. Hence, it can be concluded that periodic modulation of the spindle speed leads to an increase in the chatter-free region but caution has to be taken in choosing the right parameters for the modulation depending on the nominal operating range. At this point, we would like to note that the value of the modulation time period of \(1\) may not be physically realizable due to the requirement of very high acceleration and deceleration from the modulation system. However, the trends obtained for increasing \(R_a\) remain the same for different values of \(T\) as shown in [40].

In the next section, we consider the effect of a random variation of the spindle speed about a nominal value on the stability boundary as considered by Yilmaz et al. [32].

4 A SDOF model for turning with the spindle speed having a random variation

We will only be interested in the linearized model for machine tool vibration as presented earlier

$$\begin{aligned} \ddot{x}(t) + 2\, \zeta \, \dot{x}(t) + {x}(t) = P \left( x(t-\tau (\xi ,t))-x(t)\right) , \end{aligned}$$
(25)

where \(\tau (\xi ,t)\), the time taken for the workpiece to complete one revolution is random in nature similar to one of the case considered in [32]. For this study, we consider the delay to be uniformly distributed in the interval \(\displaystyle \left[ \tau _0 \left( 1 - R_a\right) , \tau _0 \left( 1 + R_a\right) \right] \), i.e.,

$$\begin{aligned} \tau (\xi ,t)&\approx \tau _0 \left[ 1 + R_a \left( 1 - 2\,\xi (t,h)\right) \right] ,\nonumber \\&\,\qquad \text{ with }\,\,\, \xi (t,h) \in [0,1], \end{aligned}$$
(26)

where \(\displaystyle \tau _0 = \frac{2\,\pi }{\Omega _0}\) represents the nominal time taken for one revolution in the non-dimensional time and \(r_a\) represents the amplitude modulation ratio as in the previous section. Note that the delay variation is as considered in [32] but written in a slightly different form to better suit the presentation in this paper. The variable \(\xi (t,h)\) can take any value in the interval specified above with equal probability at any instant of time \(t\). However, once \(\xi (t,h)\) assumes a value, it remains constant for a holding time of \(h\). For simplicity we have chosen \(h\!=\!1\). We note that Yilmaz et al. [32] restricted themselves to finitely many possibilities for the time-delay in accordance with the time-step used in their time-discretization to convert the DDE into discrete maps. However, since our approximation does not involve any discretization of time, we have not put any restriction on the admissible values for the time-delay. However, to ensure solvability of the equation, we restrict the number of instances of changes in values of the time-delay. If the delay changes at every instant of time, \(\ddot{x}(t)\) from Eq. (25) will not be continuous anywhere and hence, is not integrable in the Riemmanian sense which is the basis for most numerical schemes for solving differential equations. Accordingly, the numerical solution for \(x(t)\) and \(\dot{x}(t)\) is meaningless. From the practical view point as well, the delay value cannot be changed at every time instant and any change becomes effective only after a certain response time which is denoted by the holding time in our system. A typical realization of the delay evolution for \(\tau _0=2\pi \) and \(R_a=0.1\) for the time interval \([0, 30]\) and \([70, 100]\) is shown in Fig. 5.

Fig. 5
figure 5

A typical realization of the random time delay at two different time windows

Full size image

We again scale time in Eq. (22) as \(\displaystyle \bar{t} = \frac{t}{\tau _0(1+R_a)}\) (and drop the bar for notational convenience) to get

$$\begin{aligned}&{x}^{\prime \prime }(t) + 2\, \zeta \,\tau _0 \left( 1+R_a\right) {x}^{\prime }(t) + \tau _0^2 \left( 1+R_a\right) ^2 {x}(t)\nonumber \\&\quad =\tau _0^2 \left( 1+R_a\right) ^2 P \left( x(t- \tau (\xi , t))-x(t)\right) , \end{aligned}$$
(27)

where the delay in the rescaled time is

$$\begin{aligned} \tau (\xi , t) = \tau _0 \left[ 1 + R_a \left( 1 - 2\,\xi (t,h)\right) \right] . \end{aligned}$$
(28)

From Eqs. (3) and (5), we have

$$\begin{aligned} x(t- \tau (\xi ,t))&= F(t, \tau (\xi ,t))\,\approx \,a_0( t)\,+\,a_1(t)\,\tau (\xi ,t)\nonumber \\&+\sum _{k=1}^{N-2}\,a_{k+1}(t)\, \sin (k \pi \tau (\xi ,t)) \end{aligned}$$
(29)

for \(i=1,2,\ldots , n\) where we substitute for \(\tau \) from Eq. (28). Again the random delay translates into random coefficients in our approximation. In addition, we have \(x(t)\,\equiv \,F(t,0)\,=\,a_0(t)\). Substituting for \(x(t)=a_0(t)\) and \(x(t- \tau (\xi ,t))\) from Eq. (29) into Eq. (27) yields

$$\begin{aligned}&\ddot{a_0}(t) + 2\, \zeta \,\tau _0 \left( 1+R_a\right) \, {\dot{a}}_{0}(t) + \tau _0^2 \left( 1+R_a\right) ^2\, \left[ {a_0}(t)\right. \nonumber \\&\quad \left. - P \left( \,a_1(t)\,\tau (\xi ,t)\,+\,\sum _{k=1}^{N-2}\,a_{k+1}(t)\, \sin (k \pi \tau (\xi ,t))\right) \right] \,=0.\nonumber \\ \end{aligned}$$
(30)

Equations (30), (9) and (10) constitute \(N\) ODEs governing the evolution of the variables \(a_i(t)\) and can be written in the form

$$\begin{aligned} \mathbf{A} {\dot{\mathbf{a}}}+ \mathbf{B}(\tau (\xi ,t)) \mathbf{a}= \mathbf{0}, \end{aligned}$$
(31)

where \(\mathbf{A}\) and \(\mathbf{B}\) are \(N+1 \times N+1\) matrices, \(\mathbf{a}=[\dot{a}_0, a_{0}, a_1, a_2, \ldots , a_N]^T\), and \(\mathbf{0}\) represents the \(N+1\) dimensional zero vector. The last \(N-1\) rows of both \(\mathbf{A}\) and \(\mathbf{B}\) are determined by Eqs. (9) and (10) and can be evaluated once and for all, independent of the specific DDE. The first row of the matrix \(\mathbf{B}\) is the only row that depends on the specific DDE and hence, involves random coefficients.

Before proceeding further, a note regarding the smoothness of the solutions for Eq. (25) and that obtained from the reduced set of equations (Eqs. (30), (9) and (10)) is due. We first observe from Eq. (25) that \(\ddot{x}(t)\) will have discontinuities since \(\tau \) and consequently \(x(t-\tau )\) varies discontinuously after each time-increment of \(h\). However, \(x(t)\) and its first derivative \(\dot{x}(t)\) are continuous and can be reliably obtained for any realization of \(\tau (\xi ,t)\). This implies that there is a meaningful solution \(x(t)\) to the differential equation represented by Eq. (25). However, the issue of discontinuities in derivatives raises concerns about the validity of the Galerkin projection. At this point, we note that discontinuities in the DDE does not affect our Galerkin projection technique since the projection is applied on the PDE governing the evolution of the bivariate function \(F(t,s)\) in the domain as shown in Fig. 1. The DDE only provides the boundary condition for this PDE and discontinuities in the boundary conditions do not put restrictions on the projection. We further note that the bivariate function \(F(t,s)\) represents the solution to the DDE only and hence will have the same level of smoothness as the solution to the original DDE, i.e., a discontinuous second derivative. Our approximation for \(F(t,s)\) has functions which are infinitely smooth and hence, we only get an approximation to the solution. The solutions obtained from our approximation as well as from direct numerical integration of Eq. (25) for the same realization of \(\tau (t)\) showed a very good correspondence with each other giving us confidence in our reduced system of equations.

Next, we study the stability of the reduced system of stochastic ODEs using Lyapunov exponents [34]. The Lyapunov exponent has also been evaluated from a direct integration of the delayed equation using a fixed-step size DDE solver reported in [16] with appropriate modifications to handle a random bounded variation in the delay. To avoid numerical errors due to largeness or smallness of \(x(t)\), the entire history of the solution is scaled after a specific time interval (typically \(1/5\) times the nominal delay) to make the maximum value of \(x(t)\) to be \(1\). The slope of a linear fit between time \(t\) and a cumulative sum of the logarithm of the scaling factor gives us an estimate for the largest Lyapunov exponent. A positive slope implies unstable equilibrium with an average growth of the perturbation while negative slope implies average decay of the perturbation and hence, stable equilibria. A similar procedure has been repeated with the system of stochastic ODEs. The results obtained for both the approaches are very similar but here we present the results for the approximate set of ODEs only. For the set of ODEs, the solution at each time step is known analytically in closed form and hence the computation is much faster. The numerical integration is performed till a non-dimensional time of 5000 starting with a random initial condition. The solution for the first 200 time units are discarded as transients and for the remaining time, we fit a linear curve to the consecutive extrema of the solution whose slope gives us the average rate of growth or decay (the average Lyapunov exponent). Care has been taken to renormalize the magnitude of the solution after every 4 time units to avoid numerical inaccuracies because of the solutions becoming very small or very large. For each combination of \(\tau _0\) and \(P\) for a given \(R_a\), this calculation is repeated for 20 different realizations of the random time-delay and an average Lyapunov exponent over these realizations is taken to represent the Lyapunov exponent at that combination of the parameter values. The contour of zero Lyapunov exponents in the relevant parameter plane represents the stability boundary of our system.

The stability boundaries in the \(P-\tau _0\) plane so obtained for \(\zeta =0.02\) have been presented in Fig. 6 for \(R_a=0.01\) and \(R_a=0.1\). Similar to the case of periodic delays we notice from Fig. 6 that the stability charts for turning with random spindle speed modulation and conventional turning are almost coincident for \(R_a=0.01\) which is attributable to the fact that variation in the spindle speed is very small. However, for \(R_a=0.1\), there is a significant enlargement of the stable regions in Fig. 6 implying that a random change of the spindle speed caused by various factors during actual turning operation by around \(10\%\) has a stabilizing effect on the process. A detailed investigation of the overall effect has been left for future work.

Fig. 6
figure 6

Stability charts for turning with random spindle speed modulation for \(\zeta =0.02\), \(\omega _n=200\,\pi \) and left \(R_a=0.01\), right \(R_a=0.1\). The approximation parameter \(N\) is \(50\) in each case resulting in a \(51 \times 51\) transition matrix

Full size image

We next present an alternative approach to handle variable delays which requires no apriori bound on the time-delay but requires the first time-derivative of the delay to exist. It is especially suited for system of state-dependent delays especially when the delay is implicitly defined.

5 An alternate approach for DDEs with variable delays involving dynamic rescaling

In this section, we will consider a DDE with a variable delay of the form

$$\begin{aligned}&\dot{y}(t) = f\left( t, \tau , y(t), y(t-\tau )\right) ,\quad \text{ for }\,\, t>0, \text{ and } x_s(0)\nonumber \\&\qquad \;\; \equiv x(-s) = X(s), s \in (0,\tau (0)], \end{aligned}$$
(32)

where \(X(s)\) is a given “initial function”. The dependence of the delay \(\tau \) on the time \(t\) is defined by

$$\begin{aligned} g\left( \tau , t, y(t), y(t-\tau )\right) =0. \end{aligned}$$
(33)

The above general form for the determination of the delay encompasses most cases of variable delays including the periodic as well as state-dependent delays. Note from Eqs. (32) and (33) that the calculation of the evolution of \(y(t)\) will require tracking the solution over an immediately preceding interval of time \([t,t-\tau ]\). Accordingly, we define a local variable \(s \in [0,1]\) (as in [16, 17]) but to account for the variability in the time delay we scale the \(s\)-domain by \(\tau \) to get an instantaneous time interval \([0, \tau ]\). In this scaled time interval, we define a bivariate function \(F(t, s)\) which coincides with the function \(y(t)\) as

$$\begin{aligned} F(t, s)\,=\,y(t - s\, \tau )\,, \quad s \in [0,1]. \end{aligned}$$
(34)

In the interior of the \(s\)-domain, Eq. (34) leads us to the equation

$$\begin{aligned} \tau \frac{\partial F}{\partial t} + \left( 1 - s \frac{d \tau }{d t}\right) \frac{\partial F}{\partial s}\, =\, 0. \end{aligned}$$
(35)

Note from Eq. (35) that for this alternate approach to be valid, we require the delay \(\tau \) to be at least once differentiable w. r. t. \(t\) which in turn requires the function \(g\) in Eq. (33) as well as the solution \(y(t)\) to be sufficiently smooth as well. Following [16, 17], we approximate this bivariate function \(F(t, s)\) as

$$\begin{aligned} F(t, s)\,\approx \,a_0(t)\,+\,a_1(t)\,s\,+\,\sum _{k=1}^{N-2}\,a_{k+1}(t)\, \sin (k\pi s). \end{aligned}$$
(36)

From Eqs. (34) and (36), we have \(y(t) = F(t,0) \approx a_0(t)\,\) and \(y(t-\tau ) = F(t,1) \approx a_0(t) + a_1(t)\) which on substitution in Eqs. (32) and (33) gives us the evolution equations for \(a_0(t)\) and \(\tau \). The evolution equations for the remaining \(a_i\)’s is obtained by substituting Eq. (36) in Eq. (35) and making the residue orthogonal to the relevant shape functions. This gives

$$\begin{aligned}&\int _0^1 \left\{ \tau \left( \dot{a}_0(t) + \dot{a}_1(t) \, s + \sum _{k=1}^{N-2} \dot{a}_{k+1}(t) \sin (k \pi s) \right) + \left( 1 - s \frac{d \tau }{d t}\right) \right. \nonumber \\&\quad \left. \left( a_1(t) + \sum _{k=1}^{N-2} a_{k+1}(t) k \pi \cos (k \pi s)\right) \right\} \, \cdot \, s \, ds = 0,\end{aligned}$$
(37)
$$\begin{aligned}&\int _0^1 \left\{ \tau \left( \dot{a}_0(t) + \dot{a}_1(t) \, s + \sum _{k=1}^{N-2} \dot{a}_{k+1}(t) \sin (k \pi s) \right) + \left( 1 - s \frac{d \tau }{d t}\right) \right. \nonumber \\&\quad \left. \left( a_1(t) + \sum _{k=1}^{N-2} a_{k+1}(t) k \pi \cos (k \pi s)\right) \right\} \, \cdot \, \sin (m \pi s) \, ds = 0, \end{aligned}$$
(38)

for \(m = 1, 2, \ldots , N-2\). The system of equations, Eqs. (32), (33), (37) and (38) defines our finite-dimensional system. We further note that Eq. (33) is an algebraic equation while Eqs. (32), (37) and (38) are ODEs resulting in a system of differential-algebraic systems (DAEs). However, due to this scaling the value of the solution at the delayed instant has a very simple representation and for most cases like the example considered in this paper for the state-dependent delay, we can solve Eq. (33) for the delay \(\tau \) in terms of the \(a_i\)’s resulting in a system of ODEs only. We note that this alternate procedure has already been reported in [38, 39]. The dynamic rescaling scheme presented in this section is represented pictorially in Fig. 7.

Fig. 7
figure 7

A schematic representation of the dynamic rescaling to convert the variable \(s\)-domain to a fixed domain \([0,1]\)

Full size image

We note further that this approach can also be used for cases of periodic as well as random delays. However, the resulting system of equations will have time-periodic coefficients or random coefficients in Eqs. (37) and (38) which amounts to almost the entire system of equations as opposed to the approach presented in Sect. 2 where these terms were restricted only to Eq. (7). As a result of this, the computations required to obtain the stability matrix becomes more involved and hence, this approach is not desirable for time-periodic delays. Moreover, for the case of random delays, the differentiability requirement of the time-delay \(\tau \) need not be valid, e.g., the delay could be considered to be white noise in which case it is not differentiable. Therefore, the approach in this section is best suited for the case of a state-dependent delay. In the next section, we present the application of this alternative approach to the state-dependent delayed model for regenerative turning proposed by [35] and studied numerically in [36].

6 A state-dependent delay model for turning

The non-dimensionalized 2-DOF model for regenerative turning process with a state-dependent delay (see [35, 36]), considering vibrations along the \(x\) and \(y\) axis of Fig. 2, is:

$$\begin{aligned}&\ddot{x}(t) \!+\! 2\, \zeta \, \dot{x}(t) \!+\! x(t) \!=\! \frac{1}{k_r}\, K_1\, \rho ^{q-1}\left( \frac{\tau }{\tau _0} \!+\! y(t\!-\!\tau ) \!-\! y(t)\right) ^q\!\!\!,\nonumber \\ \end{aligned}$$
(39)
$$\begin{aligned}&\ddot{y}(t) \!+\! 2\, \zeta \, \dot{y}(t) \!+\! y(t) \!=\! K_1 \rho ^{q-1}\left( \frac{\tau }{\tau _0} \!+\! y(t\!-\!\tau ) \!-\! y(t)\right) ^q\!,\nonumber \\ \end{aligned}$$
(40)

where \(\displaystyle k_r=F_y/F_x\) is the cutting force ratio, \(K_1\) is the dimensionless depth of cut, \(\rho \) is the dimensionless feed rate, \(\tau _0\) is the time-period of one revolution which is inversely proportional to the scaled spindle speed \(\Omega /\omega _n\) (\(\omega _n\) being the natural frequency of the tool-workpiece assembly) and \(q\) is the cutting force exponent (a measure of the nonlinearity in the cutting force). In the above, we have used the equivalent stiffness and the damping coefficient in the \(x\) and the \(y\) direction to be identical. The time-delay \(\tau \) in Eqs. (39) and (40) is determined implicitly by the equation

$$\begin{aligned} \frac{\tau }{\tau _0} = 1 + \rho \left( x(t) -x(t-\tau )\right) . \end{aligned}$$
(41)

We first note that a substitution of \(x(t)=y(t)/k_r\) in Eq. (39) reduces it identically to Eq. (40). Hence, this 2-DOF system can effectively be studied as a SDOF system in the \(y\)-coordinate alone, i.e., Eq. (40), with the equation determining the delay modified to

$$\begin{aligned} \frac{\tau }{\tau _0} = 1 + \frac{\rho }{k_r} \left( y(t) - y(t-\tau )\right) . \end{aligned}$$
(42)

Substituting the approximation for \(y(t)\) and \(y(t-\tau )\) as described in Sect. 5 in Eq. (42), we get

$$\begin{aligned} \frac{\tau }{\tau _0} = 1 - \frac{\rho }{k_r} a_1(t). \end{aligned}$$
(43)

We next substitute Eq. (43) for \(\tau \) and the approximations for \(y(t)\) and \(y(t-\tau )\) in Eq. (40) to get

$$\begin{aligned} \ddot{a}_0(t) \!+\! 2\, \zeta \, \dot{a}_0(t) \!+\! a_0(t) \!=\! K_1 \rho ^{q-1}\left( 1 \!+\! \frac{k_r-\rho }{k_r}a_1(t) \right) ^q\!\!,\nonumber \\ \end{aligned}$$
(44)

A final substitution of Eq. (43) in Eqs. (37) and (38) completes out finite-dimensional system of ODEs. The system of ODEs, Eqs. (44), (37) and (38) can now be used to generate the relevant stability diagram and the bifurcation diagrams for the state-dependent delay turning model as presented in [35, 36]. Complete results wherein we have continued the branch of limit cycles arising due to the Hopf bifurcation till the point of loss of contact (furthering the bifurcation diagrams in [36]) and more results have been reported in [39]. Here we present only a few of these results.

Figure 8 compares the stability chart and the frequencies at the Hopf points obtained using the ODE approximation with \(N=20\) and the analytical results obtained in [35] and [37] for \(k_r=0.3\), \(\zeta =0.02\), \(\rho =0.1\) and \(q=3/4\). It can be seen that the match is very good. Detailed procedure for obtaining the stability chart has been reported in [39]. In summary, the system of equations, Eqs. (44), (37) and (38) are first solved for the steady-state solution, and a subsequent linearization about this steady state gives us the matrix whose eigenvalues determine the stability properties of the system. The characteristic equation for this matrix is obtained and conditions on the system parameters corresponding to a purely imaginary eigenvalues are obtained to obtain the stability chart. We note here that we had to resort to numerical root finding using Newton-Raphson in conjunction with a continuation scheme to obtain the stability boundary.

Fig. 8
figure 8

Stability chart and frequencies at the Hopf bifurcation point for \(k_r=0.3\), \(\zeta =0.02\), \(\rho =0.1\) and \(q=3/4\) from the ODE approximation with \(N=20\). Also shown are the results obtained analytically in [35] and [37]. The match is quite good

Full size image

Having established the accuracy of the ODE approximation through the linear stability analysis above, we use the system of ODEs, Eqs. (44), (37) and (38) for nonlinear bifurcation analysis. The bifurcation diagram for \(k_r=0.3\), \(\zeta =0.02\), \(\displaystyle \frac{\Omega }{\omega _n}=1.2566\) and \(q=3/4\) is shown in Fig. 9 which matches very well with a similar figure presented in [36] for the same system parameters. These bifurcation diagrams have been generated using a code developed for this purpose by the author in the platform MATLAB based on obtaining limit cycles as roots of an appropriately defined map and continuation as reported in [17, 45]. It can be seen from the figure that the nature of the bifurcation changes from subcritical to supercritical with an increase in \(\rho \), consistent with the numerical observation in [36] and the analytical observation in [37].

Fig. 9
figure 9

Bifurcation diagram for \(k_r=0.3\), \(\zeta =0.02\), \(\displaystyle \frac{\Omega }{\omega _n}=1.2566\) and \(q=3/4\) and different values of \(\rho \)

Full size image

7 Conclusions

Galerkin projection has been used to obtain finite dimensional ODE approximations of DDEs with variable delays. Two different strategies for handling variable delays in the Galerkin projection scheme has been presented. Effectiveness of these strategies in studying the stability and bifurcation behavior of systems with three different kinds of variable delays viz. the periodic delay, random delay and state-dependent delay has been demonstrated. It has been shown that embedding of the variable delay with a known upper bound in a fixed delayed domain is best for periodic and random delays. The stability boundaries obtained using the finite-dimensional ODE approximations matches very well with those obtained from full numerical simulations. For the case of a state-dependent delay, the strategy of dynamic scaling of the delayed time to convert the variable delayed interval into a fixed interval works quite well. The results obtained from the approximation for the example of a state-dependent delay model of turning are in close agreement with the previous results reported for this problem in the literature. The bifurcation diagrams obtained for the state-dependent delayed example also show a good correspondence with existing results. In summary, Galerkin projection as presented in this paper is a useful tool to obtain finite-dimensional ODE approximations for systems with variable delays which can be used to extract stability and bifurcation behavior of these delayed systems.