The flow dynamics in a short annulus with rotating end-walls

Abstract

The paper reports on the 3D direct numerical simulation (DNS) results of the flow in a short annulus of aspect ratios 3.8–4.8 and radius ratios 0.45, 0.5 with end-walls attached to a rotating inner cylinder. The research is focused on the bifurcation processes occurring in the local unsteady area, existing at very low Reynolds numbers (Re = 90–164) - this unsteady area is associated with the presence of the codimension-2 point occurring in this range of parameters. The study has revealed many interesting phenomena, e.g. the period-doubling, the homoclinic collision and the second modulated wave. New bifurcation lines have been determined. The DNS results are analyzed in the light of experimental data published so far. At higher Reynolds numbers the next unsteady area occurs, dynamical features of which have been studied in detail for Re up to 1000. The computations have also been performed for the configurations with cylinders rotating in the co- and counter-rotating systems with rotational rate Ω_out/Ω_in =  ± 0.1 and ± 0.2, to determine the impact of these new boundary conditions on the bifurcation processes.

1 Introduction

The flows in the Taylor-Couette configurations (the area between two concentric rotating cylinders and two rotating discs) are well-known examples of the wall-bounded shear flows accommodating wide range of the flow states under both laminar and turbulent regimes. The large variety of observed phenomena results from a very high sensitivity of the flow dynamics to the boundary conditions and to the geometrical and physical parameters: aspect ratio Γ=H/(R₂-R₁), radius ratio η=R₁/R₂ and Reynolds number Re = R₁ (R₂-R₁) Ω₁/ν, where R₁ and R₂ are the radiuses of the inner and outer cylinders, H denotes the inter disc spacing, ν is the kinematic viscosity and Ω₁ is the angular rotation of the inner cylinder. The main goals of the extensive worldwide research have always been to explain the mechanisms responsible for laminar-turbulent transition and to explore the fully turbulent flow. There are two main types of transitions to the turbulent flow: The first one, called subcritical, occurs when there is a direct transition from laminar flow to turbulent flow (this transition is related to very rapid phenomena). The second type, called supercritical, begins with a gentle increase of disturbances. Then, a series of consecutive bifurcations occur, ultimately leading to the turbulent flow. Both types of transition can occur in the Taylor-Couette flow. In the classic approach, the flows in the infinitely long configurations have been studied numerically (this is synonymous with the assumption of the axial periodicity of the flow). With this assumption, the numerical cost of the DNS studies is lower. But the influence of the end-walls on the flow dynamics is significant (particularly in the short Taylor-Couette configurations) and is taken into account in most present numerical studies. Different end-wall boundary conditions have been considered, e.g. the end-walls attached to the outer steady cylinder or to the inner rotating cylinder, the asymmetric end-walls, the co- and counter-rotating end-walls or the co- and counter-rotating cylinders.

The tremendous interest in the Taylor-Couette studies all over the world comes also from the fact that the obtained results can be directly used for interpretation of the phenomena occurring in the astrophysics (accretion discs), the geophysics and the fluid flow machines, among others.

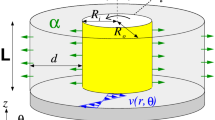
The present paper concerns the instability processes occurring in the Taylor-Couette flow cases of aspect ratio Γ = H/(R₂-R₁) = 3.8–4.8 and radius ratios η = R₁/R₂ = 0.45, 0.5 with end-walls attached to the inner rotating cylinder. The computations are performed using highly precise 3D direct numerical simulation method (DNS) based on the Chebyshev and Fourier series – the code is well-tested and can be used with confidence. In the first part of the research, the DNS computations are carried out for the stationary outer cylinder. Attention is mainly focused on the codimension-2 bifurcation, which results from the interaction between a Hopf bifurcation and a steady state fold bifurcation [1,2,3,4,5,6,7,8,9]. The co-dimension-2 point occurrence is associated with the local unsteady area – the bifurcation phenomena occurring in this area are the main object of interest here. The results are analyzed in the light of the diagram established experimentally in [1]. Then, the investigations are continued up to Re = 1000 to show the basic features of the next unsteady area and to study the influence of the local unsteady area, related to codimension-2 point, on the bifurcation processes occurring at higher Re. In the second part, the computations are performed for the configurations with rotating inner and outer cylinders  (Γ  = 3.8–4.05, η = 0.5, the end-walls attached to the inner cylinder). In these flow cases, the cylinders rotate in co- and counter-rotating systems with rotational speed rates α = Ω₂/Ω₁ =  ± 0.1 and ± 0.2 (Ω₁ and Ω₂ denote the angular velocities of the inner cylinder and the outer cylinders, respectively). The positive value of α means the co-rotating system and the negative value the counter-rotating system.

The presence of the codimension-2 point is associated with many bifurcation phenomena such as the fold-Hopf bifurcation, the saddle-node bifurcation and the period-doubling cascade, among others, [1,2,3,4,5,6,7,8,9]. These phenomena were studied experimentally [7] and numerically (DNS) [8] in the cavity with the asymmetric end-wall boundary conditions (the outer cylinder was attached to one end-wall and the rotating inner cylinder was attached to the second end-wall). The authors have shown that the flow dynamics is governed by the pair of codimension-2 points, i.e. the cusp point (where two saddle-node bifurcation lines intersect) and the double Hopf bifurcation point (where two Hopf bifurcation lines intersect). The DNS study [8] has revealed that the Hopf bifurcations result in two rotating waves of the wave numbers 1 and 2. The study of the flow dynamics in the fold region (where the Hopf bifurcation neutral line and the saddle-node line intersect tangentially) has revealed the period-doubling bifurcation and the homoclinic / heteroclinic collision, [8]. The influence of η on the bifurcation phenomena was also explored, [9]. The investigations of the Taylor-Couette flows with symmetric end-walls attached to the stationary outer cylinder (Re = 0–1000, Γ = 2.8–3.5, η = 0.5) have shown that in such configurations the flow dynamics is organized by several codimension-2 bifurcations. As a consequence, a very large number of bifurcation phenomena have appeared [10,11,12]. This issue has been researched a lot using the DNS method. The research on the short Taylor-Couette configurations with end-walls attached to the rotating inner cylinder was carried out in [1] using the experimental method (Laser-Doppler-Velocimetry, LDV) and numerical method (the 2D model, [13]). However, according to the best of author’s knowledge, this problem hasn’t been explored using the DNS method. The results presented in the paper are the author’s attempt to fill in this gap in existing studies. The experimental data contained in [1] are used to verify the present DNS computations.

The first studies on the Taylor-Couette flow with the co- and counter-rotating cylinders were carried out in [14] (Reynolds number of the outer cylinder was kept constant, while Reynolds number of the inner cylinder was gradually increased). For two decades we have observed increased interest in the experimental and numerical (DNS) investigations of the Taylor-Couette flows in the configurations with co- and counter-rotating cylinders at high Reynolds numbers, [15,16,17], which is mostly connected with accretion discs phenomenon. These cited articles determine the direction of the author’s further research. However, in the present paper the investigations are limited to the flow cases with the low rotational rates α = Ω₂/Ω₁ =  ± 0.1 and ± 0.2. In the investigations, the rotation ratio α has been kept constant for all Re.

The outline of the paper is as follows: The considered problem is defined and the 3D DNS algorithm based on the spectral collocation method is described shortly in Sect. 2. In Sect. 3 the results, obtained for the outer cylinder at rest, are analyzed. The bifurcation phenomena occurring near the codimension-2 point are presented and compared with the experimental results of [1] in Sects. 3.1–3.4. The results obtained for higher Re (up to Re = 1000) are discussed in Sect. 3.5. The data obtained for the configurations with cylinders rotating in the co- and counter-rotating systems are presented in Sect. 4. The results are summarized in Sect. 5.

2 The numerical method

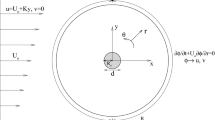
In the paper, the 3D incompressible flow in the Taylor-Couette configuration is investigated using the DNS method, which is based on a pseudo-spectral collocation Chebyshev-Fourier approximation. The code has been developed among others in [18,19,20,21,22,23]. The inner cylinder of radius R₁, rotating with uniform angular velocity Ω₁[rad^.s⁻¹], is attached to both end-walls. The outer cylinder of radius R₂ is at rest (Sect. 3) or rotates in the co-rotating / counter-rotating systems (Sect. 4). The flow is described by the Navier–Stokes and continuity equations written in a cylindrical coordinate system (R, φ, Z) with respect to a rotating frame of reference. In the algorithm, the velocity components are normalized by Ω₁R₂ (the dimensionless components of the velocity vector in radial, azimuthal and axial directions are denoted by: u, v, w). The dimensionless axial and radial coordinates are z = Z/(H/2), z $\in$[− 1, 1], r = (2R-(R₂ + R₁))/(R₂-R₁), r $\in$[− 1, 1], and time is normalized by Ω₁⁻¹. The main governing parameters are: aspect ratio Γ  = H/(R₂-R₁), radius ratio η = R₁/R₂, and Reynolds number Re = R₁(R₂-R₁) Ω₁/ν.

The Navier–Stokes equation is approximated in time by using the second-order semi-implicit scheme (which combines an implicit treatment of the diffusive terms and the explicit Adams–Bashforth scheme for the non-linear terms). The boundary conditions for velocity components are as follows: u = w = 0 for all rigid walls. For the flow cases with stationary outer cylinder, the azimuthal velocity component is equal to zero, v = 0, on the rotating walls and v = − [(1 + η)/(1-η) + r]/[(1 + η)/(1-η) + 1] on the stationary cylinder. At the junctions between the rotating discs (Ω₁) and the outer cylinder, the azimuthal velocity is regularized by the exponential function. For the flow cases with co- and counter-rotating cylinders, on the outer cylinder we have a difference between the angular velocities − (Ω₁- Ω₂). The regularization function also must be changed accordingly. In the algorithm the predictor / corrector method is used. The spatial approximation of the flow variable ${\Psi }$ = [u^p, v^p, w^p, p^p,Φ]^T is given by a series:

$$\begin{gathered} \Psi \left( {r_{i} ,\;z_{j} ,\;\varphi_{l} } \right) = \mathop \sum \limits_{{k = - \frac{K}{2}}}^{{\frac{K}{2} - 1}} \mathop \sum \limits_{m = 0}^{M} \mathop \sum \limits_{n = 0}^{N} \hat{\Psi } \cdot T_{n} \left( {r_{i} } \right) \cdot T_{m} \left( {z_{j} } \right) \hfill \\ - 1 \le r,\;z \le 1,\quad 0 \le \varphi \le 2\pi \hfill \\ r_{i} = \cos (\pi i/N)\quad i \in \left[ {0, \ldots N} \right] \hfill \\ z_{j} = \cos (\pi j/M)\quad j \in \left[ {0, \ldots M} \right] \hfill \\ \varphi_{l} = 2\pi l/K\quad l \in \left[ {0, \ldots K - 1} \right] \hfill \\ \end{gathered}$$

(1)

where: u^p, v^p, w^p are the predictors of velocity components, p^p is the pressure predictor, Φ is the correction function defined below in the text, T_n(r_i) and T_m(z_j) are the Chebyshev polynomials of degrees n and m. The numbers of the collocation points in the radial, axial and azimuthal directions are denoted by N, M and K, respectively. The non-homogeneous distributions of the collocation points in the radial r_i = cos(iπ /N) and axial z_j = cos (πj/M) directions (the Gauss–Lobatto points) guarantee the high accuracy of the computations. The calculation procedure begins with solving the Poisson equation with the Neumann boundary condition to obtain the pressure predictor p^p, then the Helmholtz equation with appropriate boundary conditions is solved to obtain the velocity components u^p, v^p, w^p. The predicted velocity field is corrected by the pressure gradient at time section t⁽ⁱ⁺¹⁾. The correction of the velocity field is performed using a new variable $\Phi = 2\delta t\left( {p^{i + 1} - p^{p} } \right)/3$, which is computed from the following equation:

$${\Delta }\Phi = {\text{div}}\left( {{\text{V}}^{{\text{p}}} } \right){\Gamma }/\left[ {\left( {{\upeta } + 1} \right)/\left( {1 - {\upeta }} \right) + 1} \right]$$

(2a)

with the boundary condition:

$$\nabla \left( \Phi \right) \cdot {\text{n}} = 0,$$

(2b)

where n is the normal vector and δt is the increment of time. Generally, the solutions of the Navier–Stokes equation are obtained by solving the Helmholtz equation written in the following form:

$$\Gamma^{2} \frac{{\partial^{2} \Psi }}{{\partial r^{2} }} + \frac{{\Gamma^{2} }}{{\left[ {\frac{1 + \eta }{{1 - \eta }} + r} \right]}}\frac{\partial \Psi }{{\partial r}} + \frac{{\Gamma^{2} }}{{\left[ {\left( {1 + \eta } \right)/\left( {1 - \eta } \right) + r} \right]^{2} }}\frac{{\partial^{2} \Psi }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} \Psi }}{{\partial z^{2} }} - q\Psi = S$$

(3a)

where

$$q = \frac{{\Gamma^{2} }}{{[\frac{1 + \eta }{{1 - \eta }} + r]^{2} }} + \frac{{3 {\text{Re}} \Gamma^{2} }}{{4\delta t\left[ {\frac{1 + \eta }{{1 - \eta }} - 1} \right]}},{\text{for}}\;u^{p} , v^{p} ,$$

(3b)

$$q = \frac{{3 {\text{Re}} \Gamma^{2} }}{{4\delta t\left[ {\frac{1 + \eta }{{1 - \eta }} - 1} \right]}},\;{\text{for}}\;w^{p} ,$$

(3c)

$${\text{q}} = 0, {\text{for }} {\text{p}}^{{\text{p}}} , \Phi .$$

(3d)

Equation (3a) contains the results obtained during the predictor stage u^p, v^p, w^p, p^p or during the previous iteration. S and ${\Psi }$ are described as follows:

$$S = \mathop \sum \limits_{{k = - \frac{K}{2}}}^{{\frac{K}{2} - 1}} \hat{S}_{k} \left( {r, z} \right) \cdot e^{{ik\varphi_{{}} }} ,$$

$$\Psi = \mathop \sum \limits_{{k = - \frac{K}{2}}}^{{\frac{K}{2} - 1}} \hat{\Psi }_{k} \left( {r, z} \right) \cdot e^{{ik\varphi_{{}} }} .$$

(3e)

Finally, the discretization in the radial and axial directions is carried out using Eq. (1), which leads to the following system of equations:

$$A\Psi + \Psi B = S ,$$

(4a)

$${\Psi } = {\hat{\Psi }}_{{{\text{i}},{\text{j}},{\text{k}}}} = {\hat{\Psi }}_{{\text{k}}} \left( {{\text{r}}_{{\text{i}}} ,\;{\text{z}}_{{\text{j}}} } \right),\;\;{\text{S}} = {\hat{\text{S}}}_{{{\text{i}},{\text{j}},{\text{k}}}} = {\hat{\text{S}}}_{{\text{k}}} \left( {{\text{r}}_{{\text{i}}} ,\;{\text{z}}_{{\text{j}}} } \right) ,$$

(4b)

$$A = \Gamma^{2} (Dr)_{i,j}^{\left( 2 \right)} + \Gamma^{2} (Dr)_{i,j}^{\left( 1 \right)} /\left[ {\left( {\frac{\eta + 1}{{\eta - 1}}} \right) + r_{i} } \right] - \{ q_{i} + \Gamma^{2} k^{2} /[\left( {\frac{\eta + 1}{{\eta - 1}}} \right) + r_{i} ]^{2} \} \delta_{i,j} ,$$

(4c)

$${\text{B}} = ({\text{Dz}})_{{{\text{i}},{\text{j}}}}^{\left( 2 \right)} ,$$

(4d)

where $({\text{Dr}})_{{{\text{i}},{\text{j}}}}^{\left( 2 \right)} ,\;\;({\text{Dr}})_{{{\text{i}},{\text{j}}}}^{\left( 1 \right)} ,\;\;({\text{Dz}})_{{{\text{i}},{\text{j}}}}^{\left( 2 \right)}$ are differentiating matrices, [18]. The computations are carried out using the following numbers of collocation points: N = 100, M = 200, K = 50. The time increment is equal to δt = 0.005 (approximately 4∙10⁵–10⁶ time iterations are needed for one flow case) and the divergence error is in the range of 10^–7-^.10^–6. To visualize the flow structure, the λ₂ criterion is used as described in [24]. The time series are computed in the middle point of the cavity: r = 0, z = 0, φ = 0. More information about the DNS algorithm can be found in [9, 19].

In order to compare the present results obtained using the DNS method with those published in the literature, all variables are re-normalized in the following way: the gap between cylinders R₂-R₁ is used as the length scale, the diffusive time (R₂-R₁)²/ν is used as the time scale, and the velocity components are normalized by ν/(R₂-R₁).

3 The results obtained in the configurations with discs attached to the rotating inner cylinder and with the stationary outer cylinder

3.1 The flow structure

The first unsteady area occurs approximately between Re = 90–164. Figure 1a presents the example flow structure in the (φ, z) plane obtained for Re = 123.75, Γ = 4.05, η = 0.45, r = 0.0. In Fig. 1a we observe a vortex in the central part of the cavity between two strong Ekman vortices on the discs – this flow structure is typical of the unsteady area associated with the presence of codimenion-2 point. The Ekman vortices grow with increasing Re and finally squeeze out the central vortex, then the flow becomes steady again and 2-cell. The next unsteady area appears for higher Reynolds numbers, for example, it is about Re = 415 for Γ = 3.975 and η = 0.5. This critical Re depends on geometrical parameters Γ and η. The flow structure obtained for Re = 400.95, Γ = 4.05, η = 0.45 (Fig. 1b) shows the existence of 7 vortices originating in the rotating end-wall boundary layers. At Re = 1039.5 (Fig. 1c) the flow is dominated by the irregularly distributed small vortices.

Fig. 1

The flow structure in the (φ, z) plane obtained for: a Re = 123.75, b Re = 400.95, c Re = 1039.5. Γ = 4.05,  η= 0.45. For visualization the iso-surfaces of instantaneous λ₂ are used, with − 0.6 > .λ₂ > − 1. The colors are visible in the online version

3.2 The bifurcation lines

In order to explore the unstable area connected with the codimension-2 point discussed in [1], detailed DNS computations have been performed for Reynolds numbers from the range Re = 90–164 and for low aspect ratios. The obtained bifurcation lines are presented in Fig. 2a (η = 0.5, Γ = 3.75–4.35) and Fig. 2b (η = 0.45, Γ = 3.85–4.85). In Fig. 2a and Fig. 2b the AB line stands for the symmetry-breaking bifurcation line. The primary flow, symmetric about the mid-plane (z = 0) of the annulus, with the 4-cell structure, exists only at Re lower than these at the AB line (the notations used in [1] are preserved, see Fig. 2 [1]). The CB line is the neutral line of the Hopf bifurcation (the Hopf bifurcation breaks the flow axisymmetry). The frequency of this fundamental Hopf wave equals f = 0.123–0.126 (f is the frequency normalized by Ω₁). The value of f depends slightly on the geometrical parameters Γ, η and Reynolds number. The AB and CB lines intersect tangentially in the codimension-2 point (B), which gives rise to the complicated flow dynamics. At slightly higher Reynolds numbers than these at the CB line, the Hopf bifurcation undergoes secondary bifurcation and produces a modulated rotating wave (MRW). The area of MRW occurrence is marked by the DEF line (Fig. 2a and Fig. 2b). It was shown in [1] that in the most part of the DEF area the MRW time series are irregular, which confirms present observations (this irregular IMRW area is marked by the DHG line, Fig. 2a and Fig. 2b). The most interesting phenomenon presented in [1] is a narrow “grey window” inside the DHG area in which the irregular modulated wave becomes regular again. This phenomenon has also been observed in the present research (see the black ribbon in Fig. 2a), although the shape of the ribbon obtained numerically slightly differs from the shape presented in [1]. The uniform oscillations occur for Re greater than those on the EG line. Between the KL and MN lines (marked by empty circles) the second modulated wave SMRW has been found, which is characterized by a large regularity. Then, between the bifurcation lines MN and IJ again the wave with uniform oscillations occurs. The uniform oscillations finally fade away on the IJ line, which ends the Hopf bifurcation area.

Fig. 2

The bifurcation lines obtained for: a η = 0.5, b η = 0.45. The colors are visible in the online version

In Fig. 2a and Fig. 2b the line marked by the green squares separates the area of the stable flow (4-cell) from the area of the unstable flow (2-cell). This line is obtained by the successive increase of Γ with fixed Re (the one-dimensional path analysis, [8]). The transition from the unstable to stable flow is rapid (it resembles the homoclinic collision observed in the Taylor-Couette configuration with asymmetric end-wall boundary conditions, [8, 9]). However, for Re = 112–114 (η  = 0.5) and for Γ slightly lower than those on the line with green squares, the wave with oscillations of f = 0.123–0.126 slowly disappears (the 2D low frequency wave begins to dominate). With a further increase of Γ only the regular low-frequency wave exists – the period of this wave (denoted by T_LFW) increases with increasing Γ until the flow becomes steady. For the flow case of η = 0.45 this phenomenon occurs for Re = 102–130 (the solid green line shows Γ at which the wave packets with oscillations of  f = 0.123–0.126 disappear, Fig. 2b). The example time series (Γ = 4.355, Re = 117.56, η = 0.45) is presented in Fig. 3a, in which we can see the randomly distributed packets with oscillations of the frequency f = 0.123–0.126 but the remaining part is filled with a regular 2D wave of low frequency. For Γ slightly higher than 4.355 (Re = 117.56) the packets with frequency f = 0.123–0.126 disappear on the green solid line. The frequency of this 2D wave (marked by f_a) takes values from the range f_a = 0.01–0.00001. For higher Re (e.g. Re = 146.02 and Γ = 4.71, Fig. 3b) the time series still consist of the wave packets with oscillations of f = 0.123–0.126 and the remaining part is filled with the 2D wave, but the 2D wave is not as regular and dominating as for Re = 117.56. Figure 3b additionally shows the distribution of the correlation function Rτ(τ) (the red line, τ is the replacement parameter) - the observed tendency of the R(τ) distribution is consistent with one presented in [1].

Fig. 3

a The time series obtained for Γ = 4.355, Re = 117.56, b the time series and the correlation function R(τ) obtained for Γ = 4.71, Re = 146.02, c the PSD analysis performed for Re = 146.02 and for different Γ. η = 0.45. The colors are visible in the online version

The present DNS results have reconstructed all bifurcation lines obtained in [1], i.e. the AB, CB, DEF, DHF lines. The agreement is very good, e.g. Reynolds number and aspect ratio at point E obtained by the DNS method and experimentally in [1] are Re = 99.5 and Γ= 3.78 (η = 0.5).

The results presented in Fig. 2a and Fig. 2b show that all bifurcation lines obtained for η = 0.5 are also observed for η = 0.45, except the narrow “window” in the interior of the DHF line, which is not observed in the flow case of η = 0.45. It is worth noting that the bifurcation lines obtained for η = 0.45 are shifted towards higher Γ (e.g. for η = 0.45 point E is located at Γ = 3.9, whereas for η = 0.5 it is located at Γ = 3.78). The influence of radius ratio η on the bifurcation lines is clearly visible from the comparison of Fig. 2a and Fig. 2b and it is consistent with observations made for the flow cases with asymmetric end-wall boundary conditions, [9].

Figure 3c shows the power spectrum density (PSD) as a function of frequency: ${\text{PSD}}\left( f \right) = \left( \frac{1}{N} \right) \left| {\mathop \sum \limits_{n = 0}^{N} u_{n} \left( {t = n\Delta t} \right)e^{ - i2\pi fn\Delta t} \Delta t} \right|^{2} .$ The results are obtained for η = 0.45, Re = 146.02 and for Γ = 4.71, 4.69, 4.67, 4.65, 4,63, 4.61, 4.59 (in the PSD computation, the radial velocity component u is normalized by Ω₁R₂). For all considered flow cases in Fig. 3c the highest peak is at the frequency of about f = 0.126. The flow cases of Γ = 4.63, 4.61 and 4.59 fall in the area between the FG and KL lines (Fig. 2b), where the uniform distributions of u occur (for these flow cases the PSD goes up to 670). The flow cases of Γ = 4.71, 4.69, 4,67, 4.65 fall on the area between the FG line and the line with green squares, where the time series are strongly irregular (for these flow cases the PSD goes up to 50). The PSD peaks of much lower values are associated with the frequency of approximately f = 0.0025.

In order to further investigate the basic features of the considered unsteady area the changes of the squared amplitudes (2A)² of the radial velocity component u as a function of Re have been analyzed, see Fig. 4. From Fig. 4 (Γ = 4.025 and Γ = 3.9, η = 0.5) we can see that (2A)² increases linearly with Re in accordance with the Taylor-Couette Hopf bifurcation theory. However, each crossing through the bifurcation line is associated with a jump of  the  amplitude value. The second conclusion is that the largest amplitudes occur near the MN line (Fig. 2a and Fig. 2b) at which the second modulated wave (SMRW) disappears. For slightly larger Re than these at the MN line a rapid reduction of (2A)² occurs. The IJ line bounds the Hopf bifurcation area. The distributions of (2A)² as a function of Re obtained for η = 0.45 are very similar to those presented in Fig. 4 (η = 0.5) but the area of the second modulated wave (between KL and MN lines) is narrower.

Fig. 4

The profiles of the squared amplitudes (2A)² = f(Re) as a function of Re obtained for: a) Γ = 4.025, b) Γ = 3.9. From left to right we observe: the uniform disturbances (UND), the modulated rotating wave (MRW), the irregularly modulated wave (IMRW), the uniform disturbances (UND), the second modulated rotating wave (SMRW), the uniform disturbances (UND). η = 0.5

3.3 The modulated wave

In [1] the authors have shown that the modulated wave in the DHG area, is mostly irregular, which fully agrees with the present DNS results. For Reynolds numbers and Γ very close to those at the DHG line (Fig. 2a and Fig. 2b) the weak period-doubling phenomenon is observed. In the flow cases with Γ slightly higher than those at the DHG line the period-doubling phenomenon fades out and the irregular modulation is observed. In the time series presented in Fig. 3a (Re = 117.56, Γ = 4.355, η = 0.45) we observe the wave packets with oscillations of the frequency f = 0.123–0.126, separated by the wave of the low frequency f_a, but additionally, the grouping process of the wave packets takes place - the wave packets of frequency f = 0.123–0.126 are connected to form one large group. For the flow case of Re = 146.02, Γ = 4.71, η = 0.45 (Fig. 3b) the packets with the wave of frequency f = 0.123–0.126 have a similar shape, but the distances between them are different. In [8] it was shown that the one-dimensional path analysis is a very effective way to determine the line with green squares  along which the transition to steady flow occurs. However, due to the strong irregularity of the modulated wave time series (Fig. 3a) it is very difficult to track the modulated wave period T_MRW as a function of Γ. The main difficulty comes from the grouping of the wave packets - averaging is needed (averaging was also used in [8]). The example one-dimensional path is presented in Fig. 5 (η = 0.45, Re = 117.56). We can see that at the beginning the increase of (T_MRW)_AVG with increasing Γ is small, but for the critical aspect ratio Γ, (T_MRW)_AVG takes a large value and finally the wave disappears. For the flow cases of Re = 117.56, η = 0.45 the critical value of aspect ratio equals Γ_cr = 4.36 (the point Re = 117.56, Γ_cr = 4.36 can be found on the green solid line in Fig. 2b). With further increase of Γ the period of the low frequency wave T_LFW increases gradually, leading to transition to the steady 4-cell flow at Γ_cr = 4.43 (the point Re = 117.56, Γ_cr = 4.43 can be found on the line with green squares,  Fig. 2b).

Fig. 5

The averaged period of the irregular modulated wave (T_MRW)_AVG a and the period of the low frequency wave T_LFW b as a function of Γ, Re = 117.56, η = 0.45

The rotating discs produce a strong symmetric forcing on the flow. Actually, in the considered range of Reynolds number (Re = 90–164) the flow three-dimensionality is limited to the packets with oscillations of frequency f = 0.123–0.126. The ranges of time in which these packets are observed coincide with areas in which modal energy k₁ = (u₁.u₁^* + v₁.v₁^* + w₁.w₁^*)/2 (m = 1) reaches a large value (the asterisk means complex conjugate). Figure 6a shows an example time series of the fluid kinetic energy k = (u² + v² + w²)/2 (the black line), the modal energy k₀ (m = 0, the grey line) and k₁ (m = 1, the red line) obtained in the middle point of the cavity for Re = 106.25, Γ = 4.04, η = 0.5. The time series of k₁ shows that in the most part of the presented time series the m = 1 modal energy has a zero value. Only in the narrow ranges of time, where k₁ is of high value, the flow is 3D. In the ranges of time dominated by the wave of frequency f_a the flow is 2D. To illustrate the three-dimensionality of the flow, in Fig. 6b the time series of the radial velocity component u obtained in 100 azimuthal sections are presented, Γ = 4.04, Re = 106.25, η = 0.5.

Fig. 6

a The time series of the fluid kinetic energy k and modal energy k₀, k₁ obtained in the middle point of the cavity, b time series of the radial velocity component u obtained in 100 azimuthal sections. Re = 106.25, Γ = 4.04, η = 0.5. The colors are visible in the online version

3.4 The second modulated wave – area between the KL-MN lines

The time series of the second modulated wave occurring between the KL and MN lines are very regular - an example time series of the radial velocity component u together with correlation function R(τ) τ are presented in Fig. 7a (Γ = 3.95, Re = 133.75, η = 0.5). The fundamental Hopf wave is of frequency f = 0.123–0.126 (the exact value depends on Γ and Re). The period of the second modulated wave T_SMRW depends very strongly on Re and on Γ, see Fig. 7b. The study has shown that T_SMRW reaches very large values close to the bifurcation lines KL and MN (at the KL and MN lines, smooth transitions from the uniform oscillation to the regularly modulated wave, and from the regularly modulated wave to the uniform flow take place). The minimum value of T_SMRW is observed in the middle of the area between the KL and MN lines. The distribution of R(τ) (Fig. 7a) shows the same trend as it is observed in Fig. 3b (Γ = 4.71, Re = 146.02, η = 0.45). Figure 7c shows the example time series of fluid kinetic energy k and modal energy k₀, k₁, k₂ obtained in the middle point of the cavity for Re = 133.75, Γ = 3.95, η = 0.5 (the logarithmic scale is used). The time series of k₁ shows that in the whole T_SMRW modal energy k₁ has a positive value. It means that in the whole T_SMRW period the flow is 3D. The flow three-dimensionality in the area between the KL and MN lines is also visible in Fig. 8 where the time series of the radial velocity component u obtained in 100 azimuthal sections for η = 0.45, Γ = 4.235, Re = 136.12 are presented.

Fig. 7

a The time series of the radial velocity component u and the correlation function R(τ), b the T_SMRW period as a function of Re and Γ, c the time series of kinetic energy k and modal energy k₀, k₁, k₂ (the logarithmic scale). Re = 133.75, Γ = 3.95, η = 0.5. The colors are visible in the online version

Fig. 8

The time series of the radial velocity component u obtained in 100 azimuthal sections for η = 0.45, Γ = 4.235, Re = 136.12. The colors are visible in the online version

3.5 The instability processes at higher Re

For Reynolds numbers greater than those on the IJ line (Fig. 2a and Fig. 2b) the flow is 2D, 2-cell and steady. Only above the next critical Re (approximately between 380–420, the exact value of critical Re depends on η, Γ) a new unstable area appears. The bifurcation processes observed in these two unstable areas are basically distinct from each other - the flow structures, the amplitudes of oscillations and their frequencies are different. This chapter briefly presents the basic information about the bifurcation phenomena occurring for Reynolds numbers slightly larger than the critical value Re > Re_cr = 380 (η = 0.45, Γ = 4.05). The initial increase of disturbances is very mild and is accompanied by a series of consecutive bifurcations, which is typical of the supercritical laminar-turbulent transition. In the area of Re = 380–430 we observe regular oscillations of high frequency f = 0.78. The squared amplitudes of these oscillations increase linearly with Re but the amplitudes are very small. The observed flow structures are regular (see Fig. 1b) – we can see 7 regular vortices coming out of the rotating disc boundary layers. Above Re = 430 a new wave appears with the frequency equal to 0.195. With the appearance of this wave (mildly modulated) the jump in (2A)² is observed. Another wave appears between Re = 472.7–475.2, which is associated with a rapid increase of the amplitudes. The new wave is regularly modulated with the basic frequency 0.195. Above Re = 535 the time series become irregular and also the meridian flow loses its symmetry with respect to the z = 0 line - see Fig. 9, where the meridian flows obtained for different Re are presented (η = 0.45, Γ = 4.05). In Fig. 9 the green colour depicts the area between Re = 90–164, the blue colour depicts the regular structure above Re = 380, and the red colour depicts the area of the irregular disturbances. Figure 10b shows PSD obtained for two flow cases of Re = 498, η = 0.45, Γ = 4.05 (the red line) and Re = 547, η = 0.45, Γ = 4.05 (the black line). The PSD analysis has been performed using the time series presented in Fig. 10a. From Fig. 10b we can see two peaks: the first one, with the highest value of PSD, falls at the frequency of 0.195, and the second one, which falls at the frequency of 0.06.

Fig. 9

The flow in the meridian plane obtained for Re: a 116.3, b 131.2, c 396.2, d 425.7, e 524.7, f 549.5, g 846.4, h 1106.3. Γ = 4.05, η = 0.45. The iso-surfaces of intantaneous λ₂ are used for visualization, with − 0.6 >  λ₂ > − 1. The colors are visible in the online version

Fig. 10

a The time series obtained for Re = 498 (at the top) and Re = 547 (at the bottom). b PSD as a function of frequency obtained for two flow cases: Re = 498 (the red line) and Re = 547 (the black line). Γ = 4.05, η = 0.45. The colors are visible in the online version

4 The results obtained in the configurations with co- and counter-rotating cylinders

In this section the DNS results obtained for the Taylor-Couette configurations with the modified boundary condition on the outer cylinder are presented – the outer cylinder rotates with angular velocity Ω₂ =  α Ω₁, α =  ± 0.1, ± 0.2. The other boundary conditions are not changed. The study has been performed to determine the changes in bifurcation processes triggered by the introduction of the new boundary condition, in comparison to processes described in the previous section (α = 0). The flow cases with the following geometrical parameters are considered: Γ = 3.8–4.025, η = 0.5, α =  ± 0.2 and Γ = 4.025, η = 0.5, α =  ± 0.1. For the co-rotating flow case with α = + 0.1 (Γ  = 4.025, η = 0.5) the local unsteady area has been found in the following range of Reynolds numbers: Re = 107–122. For these parameters the 3D wave of the wave number 1 (located in the central part of the configuration) exists as in the flow case with the stationary outer cylinder (α= 0). But for α = + 0.1 this wave is very weak. When the outer cylinder rotates faster, with α = + 0.2, this unstable area does not exist anymore - the unsteady area begins only at Re = 320 (Γ = 3.975), see Fig. 12. The example flow structures obtained for Re = 330 (η = 0.5, Γ = 3.975, α = + 0.2, r = 0) are presented in the (φ, z) plane (Fig. 11a). In Fig. 11a we can see 4 structures symmetrically distributed with respect to the z = 0 line (in the flow case of α = + 0.1, 5 structures have been observed). The wave oscillations are regular with the frequency of 0.332. For slightly higher Re a series of consecutive bifurcations occurs. For instance, at Re = 432.5 we observe the small decrease of the wave amplitudes, which is followed by another bifurcation at Re = 510–527.5, which in turn is connected with the increase of (2A)² and the decrease of frequency to 0.049. For Reynolds numbers slightly larger than 600 the time series become irregular. The complexity of the bifurcation processes is shown in Fig. 12 where the squared amplitudes (2A)² as a function of Re are presented for the co-rotating cylinders (marked with the colored circles) and the counter-rotating cylinders (marked with the colored squares).

Fig. 11

a The flow structure in the (φ, z) plane, Re = 330, α =+ 0.2, r = 0, Γ = 3.975, b) the flow structure in the (φ, z) plane, Re = 335, α = − 0.2, r = 0, Γ = 3.975. The iso-surfaces of instantaneous λ₂ are used for visualization, with  − 0.6 >  λ₂ > − 1. The colors are visible in the online version

Fig. 12

The squared amplitudes of the radial velocity component (2A)² as a function of Re, Γ and α. The colored circles depict the co-rotating cylinders (α = + 0.2), the colored squares depict the counter-rotating cylinders (α = − 0.2). η = 0.5. The colors are visible in the online version

For the counter-rotating flow cases no local unstable area at very low Re has been found. For the α=-0.2, η=0.5 flow cases the unstable areas begin at about Re = 180–200 (the exact value depends on Γ), Fig. 12. The flow structures in the (φ, z) plane (r = 0) obtained for Re = 335, Γ = 3.975 are presented in Fig. 11b, where we can see three regular vortices located asymmetrically with respect to the z = 0 line. For Re = 335, Γ = 3.975 the time series is uniform with frequency f = 0.46 (the weak period-doubling phenomenon is observed). After reaching the next critical Reynolds number (between 420–470), the rapid increase of the amplitudes occurs. From Fig. 12, it can be seen that for the largest values of Γ (Γ = 4.025, 3.975), a rapid jump of the amplitudes occurs at the smallest Re values. After this jump the time series become irregular. More computations are needed to explain this issue. The author has performed additional computations in the short Taylor-Couette configurations with α = −0.3, −0.4, −0.5 and with α from + 0.05 up to + 0.3 (η = 0.5), and for much higher Re than in the present paper. The results are discussed in the light of the DNS data published in [16, 25, 26]. However, the analysis of these results is beyond the scope of this paper.

5 Conclusions

In the paper, the precise 3D DNS code based on the Chebyshev – Fourier approximation has been used to study the flows in the short Taylor-Couette configurations with end-walls attached to the inner cylinder rotating with angular velocity Ω₁. The attention is focused on the bifurcation processes.

In the Taylor-Couette configurations of Γ = 3.8–4.8, η = 0.5 and 0.45, with rotating inner cylinder and stationary outer one, the local unsteady area associated with codimension-2 point has been found at low Reynolds numbers Re = 90–164. This area has been carefully examined – all bifurcation lines found experimentally (LDV) in [1] have been reconstructed. At the same time, new bifurcation lines and bifurcation phenomena associated with them have been revealed (the period-doubling, the homoclinic collision and the second modulated wave). As a result of the research, the author states as follows: The appearance of the Hopf bifurcation (the CB line, Fig. 2a, Fig. 2b) breaks the flow axisymmetry and leads to the appearance of the rotating 3D wave of the wave number 1. The PSD study shows that the frequency of this fundamental oscillation equals f = 0.123–0.126. For higher Re than those at the IJ line (which closes the area dominated by the Hopf instability) the flow is axisymmetric, steady and 2-cell. The study has shown that the local unsteady area is shifted towards higher Γ values along with decreasing values of η.

The computations performed for Reynolds numbers up to about Re = 1000 have revealed that the next unstable area begins at approximately Re = 380 -420. For Reynolds numbers slightly higher than the critical one, 7 three-dimensional regular structures (in the form of the arms originating from the end-wall boundary layers) have been observed. The frequency of the regular oscillations is 0.78. With further increase of Re, a series of the successive Hopf bifurcations occurs. For Reynolds number Re = 1000, the time series is irregular and the observed structures are randomly distributed (see Fig. 1c).

The research carried out for the flow examples with co- and counter-rotating cylinders (α =Ω₂/Ω₁, α  =  ± 0.1, ± 0.2, Γ = 3.8–4.025, η = 05) has shown a huge variety of bifurcation phenomena. For the co-rotating flow case with α = + 0.1 (Γ = 4.025, η = 05), a small local unstable area with the wave of wave number 1 has been found in the central part of the cavity at low Re = 90–164. But for α = + 0.2 the unstable area begins only at about Re = 320 (Γ = 3.975). For this flow case, slightly above critical Reynolds number, 4 three-dimensional structures originating from the end-wall boundary layers appear (the frequency of the uniform oscillations is f = 0.332). The observed vortices are located symmetrically with respect to the z = 0 line. For the counter-rotating cylinders the unstable area begins at Reynolds numbers from the range 180–200 (depending on Γ and η). Above critical Reynolds number, three regular vortices, located asymmetrically with respect to the z = 0 line, have been found (f = 0.46). For the higher Re a series of the consecutive bifurcations occurs.

The study has shown that it is of great interest to continue the DNS computations (in the short configurations with cylinders rotating in the co- and counter-rotating systems) for higher rotational ratios α and for higher Re than considered in the present paper. Under such boundary conditions, the influence of aspect ratio Γ on the laminar-turbulent transition requires special attention, which is particularly important in the Kepler flow cases.