Influence of Reynolds number and rotational number on the features of a transitional flow in short Taylor-Couette cavity

Abstract

The paper reports on the DNS results of the flow in co- and counter-rotating coaxial cylinders of aspect ratios Γ = H/(R₂ − R₁) between 3.8 and 4.05, and radius ratio η = R₁/R₂ = 0.5, with the end-walls rotating with the angular velocity of the inner cylinder Ω₁. The computations are performed for a wide range of rotational number R_Ω = (1 − η)(Re₁ + Re₂)/(ηRe₂ − Re₁), from − 1.069 to 0.0, which includes both the linearly unstable flows and the Rayleigh stable flows. The considered Reynolds numbers of the inner cylinder Re₁ = Ω₁R₁(R₂ − R₁)/ν are up to 3000 (Re₂ = Ω₂R₂(R₂ − R₁)/ν). The obtained flow structures appearing at various stages of the laminar-turbulent transition and the radial profiles of statistical parameters are discussed in the light of the data published by other authors. The critical bifurcation lines are determined as functions of the inner and outer cylinder Reynolds numbers. Many interesting phenomena have been found.

1 Introduction

The Taylor-Couette flow (TCF)—the flow between two coaxial rotating cylinders—is one of the paradigmatic systems in the physics of fluids. Many ideas in the field of flow instability and in the field of fully turbulent flow have been investigated in this simple configuration, perfectly suitable for both numerical and experimental investigations. Traditionally, TCF has been characterized by four control parameters: Reynolds numbers of the inner and outer cylinders Re₁ = Ω₁R₁(R₂-R₁)/ν, Re₂ = Ω₂R₂(R₂-R₁)/ν, radius ratio η = R₁/R₂, and aspect ratio Γ = H/(R₂-R₁), where Ω₁, Ω₂ are angular velocities of the inner and outer cylinders, R₁, R₂ are radiuses of the inner and outer cylinders, H denotes the distance between the end-walls and ν is kinematic viscosity. The radius difference (R₂-R₁) is used as the length scale and Ω₁R₁ is used as the velocity scale. However, alternative parameters have been introduced to improve the understanding of observed bifurcation processes. Instead of Reynolds numbers Re₁ and Re₂, authors often use shear Reynolds number Re = 2|ηRe₂ − Re₁|/(1 + η) and rotational number R_Ω = (1-η)(Re₁ + Re₂)/(ηRe₂ − Re₁)—for example, the flow is cyclonic for R_Ω > 0 and anti-cyclonic for R_Ω < 0. The TCF dynamics strongly depends on all these parameters, as well as on the end-wall boundary conditions, which results in a large variety of observed bifurcation processes. In all this wealth of phenomena, two main paths leading to turbulence can be distinguished: supercritical, where the sequence of bifurcations eventually leading to turbulence occurs, and subcritical, where the catastrophic route to turbulence takes place.

One of the articles which set the directions of the TCF studies for many years is the paper by Andereck, Liu, Swinney [1], where the authors investigated experimentally the transitional TCF in tall configurations (Γ = 20–48, η = 0.883), with the co- and counter-rotating cylinders, and with the end-walls rotating with the angular velocity of the outer cylinder (in experimental investigations it means that the outer cylinder is attached to the end-walls). The authors gradually increased Re₁ with fixed Re₂, and analyzed the consecutive bifurcations in the (Re₂, Re₁) plane. They found that the laminar flow, known as the circular Couette flow (in which fluid elements follow the circular paths) is linearly unstable above the neutral line (see Fig. 1. [1]). With the increase of Re_1, the circular Couette flow is replaced by the Taylor-Couette (TC) vortices. With further increase of Re₁, the Taylor-Couette vortices become unstable themselves, which begins the transition to more complex states. Below the neutral line, the circular Couette flows are linearly stable, however they can be unstable with respect to the finite-amplitude disturbances. In the linearly stable cyclonic area the subcritical transition can occur. The linearly stable flows in the anti-cyclonic area are called the quasi-Keplerian flows (these flows are characterized by the radially increasing angular momentum and the radially decreasing angular velocity).

Fig. 1

a The critical lines obtained for the Taylor-Couette configurations with η = 0.5 in the (Re₂, Re₁) plane. The red symbols depict the neutral line obtained experimentally in [2], the blue line is the neutral line obtained in [3] using the approximate formula, the black dashed lines are the lines of different α along which the present computations have been performed (the green solid line depicts α = − 0.5, the black solid line α = 0.0), the black symbols depict the appearance of the 3D structures for particular α- present computations, the yellow segments indicate the critical Reynolds numbers of the appearance and disappearance of the small unstable area at very low Re₁ (the results of codimension-2 point), present computations. b The critical lines in the (R_Ω, Re) plane, the numerical data obtained in [4] for η = 0.2, 0.8 and 0.935, predictions obtained in [3] for η = 0.2 and 0.8, the present prediction obtained for η = 0.5 based on [3]. The colors are visible in the online version

The research of Andereck et al. [1] was continued by many authors [5,6,7,8], which led to new scenarios of the laminar-turbulent transition. More recently, in [9] the authors reviewed the main features of both supercritical and subcritical ways to turbulence in TCF.

The inviscid linear stability theory shows that the flow between rotating cylinders is Rayleigh stable if α = Ω₂/Ω₁ > (R₁/R₂)² or if Re₁(Re₂ − ηRe₁)² > 0. The flow is unstable with respect to infinitesimal disturbances if − 1 < R_Ω < 1/η − 1. Esser, Grossmann [3] have derived the approximate formula for the boundary of the linearly stable area in the (R_Ω, Re) plane for all radius ratios η (see also [10]). Based on this formula, the neutral stability line has been computed in the present paper for η = 0.5 and shown in Fig. 1b, together with the results obtained numerically for η = 0.2, 0.8 and 0.935 by Snyder [4]. We can see that with the increasing value of η the neutral curve becomes symmetrical about R_Ω = − 0.5 (α = 0.0). For η very close to 1.0, the stability curve diverges at R_Ω = 0.0 and − 1.0. For the currently considered configuration of η = 0.5, the neutral line diverges at R_Ω = 1.0 and − 1.0 (the red solid line in Fig. 1b).

The scientists’ attention has always been focused on the Rayleigh stable flows, with Re_Ω < − 1, due to their potential application to the astrophysical flows (the accretion discs). In the Rayleigh stable flow cases, the q parameter (η^q = α) is used to better characterize the studied phenomena. The flow cases limited to these with 0 < q < 2 are related to the accretion discs. The accretion phenomenon requires the orbiting gas to be transported radially towards the centre of mass, which in turn requires the equivalent outward transport of the angular momentum. If we assume that the orbiting gas is laminar, the molecular viscosity is too weak for the accretion phenomenon to occur. In the common opinion of scientists, the flow of the orbiting gas must be turbulent, [11,12,13,14,15,16,17,18,19]. The question of the source of turbulence in such configurations is still open—several mechanisms are considered, for example the turbulence via the magneto-rotational instability, [17, 20, 21].

One of the problems discussed widely in publications is the influence of the end-wall boundary conditions on the bifurcation processes. With the assumption of infinitely long cavity, the Taylor-Couette vortices appear from a pitchfork bifurcation and their wavelength in the axial direction is well defined, [22,23,24]. The pitchfork bifurcation is destroyed due to the presence of end-walls. In the numerical investigations the periodic boundary conditions in axial direction are often used, or the end-walls are attached to the inner cylinder or to the outer cylinder. If the numerical studies take into account the confinement effect in the axial direction, and additionally, if the configuration is short, then the effect of such boundary conditions can be large due to the energy dissipation and the Ekman pumping, [25,26,27]. The optimized rotating discs have been used to minimize the influence of the Ekman vortices in both experimental and numerical studies (including the discs divided in some rings, rotating with optimized rotational speed, see for example [28, 29]).

The aim of the research presented here is to show, the changes in the laminar-turbulent transition occurring in the short TC configurations (with the end-walls rotating with the rotation of inner cylinder), caused by changes of the governing parameters α and Re₁. In the TC cavities with the end-walls attached to the inner cylinder, the flow is directed towards higher radiuses along discs, and recirculates towards the inner cylinder. The size of so-called Ekman vortices and their impact on the TC flow dynamics depend on α. To illustrate the basic trends in the bifurcation phenomena occurring in the short TC configurations with the end-walls attached to the inner cylinder, computations have been performed for the cavities of Γ = 3.85–4.05, η = 0.5, with α = Ω₂/Ω₁ between − 0.5 and 0.275, and with Re₁ up to 3000 (the computations cover the linearly unstable flows and one quasi Keplerian flow case). The simulations are performed along the Re₁ = Re₂η/α lines, for 14 different values of α. The author has focused on the time series, bifurcation processes and changes of the meridian flows. The statistical quantities have also been examined. For all considered flow cases the large impact of the end-walls on the flow dynamics has been observed. For α with values close to zero a small unsteady area connected with the existence of the codimension-2 point has been found. To the best of the author’s knowledge, this is the only research done for such configurations and for the governing parameters mentioned above. The obtained results are discussed in the light of [1, 8, 16, 19, 25, 30].

The outline of the paper is as follows: the considered problem is defined and the 3D DNS algorithm based on the spectral collocation method is described shortly in Sect. 2. In Sect. 3 the obtained results are presented, i.e., in Sect. 3.1 the critical lines in the (Re₂, Re₁) and (R_Ω, Re) planes are presented and analyzed, the counter-rotating and the co-rotating TCF cases are discussed in Sects. 3.2 and 3.3, respectively. In Sect. 3.4 the changes in meridian flows observed with subsequent increase of α are analyzed. The results are summarized in Sect. 4.

2 Numerical methods

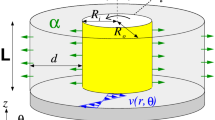
The flow is governed by the incompressible Navier–Stokes equations written in the cylindrical coordinates R, φ, Z. In the research the inner and outer cylinders rotate with the angular velocities Ω₁[rad s⁻¹] and Ω₂[rad s⁻¹], respectively. The end-walls are rotating with angular velocity of Ω₁. The dimensionless axial and radial coordinates are denoted by z = Z/(H/2), z $\in$[− 1, 1], r = [2R − (R₂ + R₁)]/(R₂-R₁), r $\in$[− 1, 1]. In the algorithm the velocity components in the radial (U), azimuthal (V) and axial (W) directions are normalized by Ω₁R₂ (the dimensionless components are denoted by u, v, w). Time is normalized by Ω₁⁻¹. The computations are performed along the Re₁ = Re₂η/α lines, for 14 values of α = Ω₂/Ω₁ (from − 0.5 to 0.275) and for Re₁ up to 3000.

The DNS code is based on a pseudo-spectral Chebyshev-Fourie approximation, [31,32,33,34]. In temporal approximation a projection scheme is used (based on backward differentiation in time). The governing equations are approximated in time by using the second-order semi-implicit scheme i.e., an implicit scheme for the diffusive terms is used and an explicit Adams–Bashforth scheme is used for the non-linear convective terms. The spatial approximation of the flow variables $\Psi = [u^{p} ,\;v^{p} ,\;w^{p} ,p^{p} ,\;\phi ]^{T}$ i.e., the predictors of velocity components, predictor of pressure and correction function ϕ (described below) is given in the following form:

$$\begin{gathered} \Psi (r_{i} ,\;z_{j} ,\;\varphi_{l} ,\;t) = \sum\limits_{k = - K/2}^{K/2 - 1} {\sum\limits_{m = 0}^{M} {\sum\limits_{n = 0}^{N} {\tilde{\Psi }(t) \cdot T_{n} (r_{i} )} } } \cdot T_{m} (z_{j} )e^{{ik\varphi_{l} }} , \hfill \\ \;r \in [ - 1,\;1],\;z \in [ - 1,\;1],\;\varphi \in [0,\;2\pi ], \hfill \\\end{gathered}$$

(1a)

$$r_{i} = \cos (\pi i/N)\quad i \in [0,...N],\quad z_{j} = \cos (\pi j/M)\quad j \in [0,...M],\quad \varphi_{l} = 2\pi l/K\quad l \in [0,..,K - 1],$$

(1b)

where r_i and z_j are the Gauss–Lobatto collocation points, T_n(r_i) and T_m(z_j) are the Chebyshev polynomials of degrees n and m, respectively. The numbers of collocation points in the radial, axial and azimuthal directions are depicted by N, M and K, respectively. The numerical procedure begins with solving the Poisson equation (with the Neumann boundary condition) to obtain the pressure predictor, then the Helmholtz equation with the appropriate boundary conditions is solved to obtain the velocity predictor. The predicted velocity components are corrected by taking into account the pressure gradient at time section (i + 1). The finally obtained velocity components satisfy the incompressibility constraint:

$$3\Gamma \cdot (V^{i + 1} - V^{p} )/\{ [(\eta + 1)/(\eta - 1) + 1]2\delta t\} = - (\nabla p^{i + 1} - \nabla p^{p} ),$$

(2a)

$$\nabla \cdot V^{i + 1} = 0,$$

(2b)

with the boundary conditions $V^{i + 1} \cdot n = V^{p} \cdot n.$ In above equations δt denotes the increment of time and n is the normal vector. The correction of the velocity components is performed by using new parameter ϕ = 2δt(pⁱ⁺¹ − p^p)/3 computed from the Poisson equations

$$\Delta \phi = div(V^{p} )\Gamma /[(\eta + 1)/(1 - \eta ) + 1],$$

(3)

with the boundary condition $\nabla (\phi ) \cdot n = 0.$ The predictor of velocity components (u^p, v^p, w^p), predictor of pressure p^p and function ϕ are computed from the Helmholtz equation written in the following form:

$$\Gamma^{2} \frac{{\partial^{2} \Psi }}{{\partial r^{2} }} + \frac{{\Gamma^{2} }}{[(1 + \eta )/(1 - \eta ) + r]}\frac{\partial \Psi }{{\partial r}} + \frac{{\Gamma^{2} }}{{[(1 + \eta )/(1 - \eta ) + r]^{2} }}\frac{{\partial^{2} \Psi }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} \Psi }}{{\partial z^{2} }} - q\Psi = S,$$

(4)

where term S contains the flow variables obtained in the predictor stage or during the previous iteration, q is a function of r (for v^p and u^p) or takes the constant value for (w^p, p^p, ϕ). Then, Eq. (4) is expanded into Fourier series, and finally, the discretization in the radial and axial directions is carried out which leads to the following equations:

$$A\Psi + \Psi B = S$$

(5)

where

$$\Psi = \hat{\Psi }_{i,j,\,k} = \hat{\Psi }_{k} (r_{i} ,\;z_{j} ),$$

(6a)

$$\;S = \hat{S}_{i,j,\,k} = \hat{S}_{k} (r_{i} ,\;z_{j} ),$$

(6b)

$$A = \Gamma^{2} (Dr)_{i,j}^{(2)} + \Gamma^{2} (Dr)_{i,j}^{(1)} /[(\eta + 1)/(\eta - 1) + r_{i} ] - \{ q_{i} + k^{2} \Gamma^{2} /[(\eta + 1)/(\eta - 1) + r_{i} ]^{2} \} \delta_{i,j} ,$$

(6c)

$$B = (Dz)_{i,j}^{(2)} .$$

(6d)

In above equations $(Dr)_{i,j}^{(2)} ,\;\;(Dr)_{i,j}^{(1)} ,\;\;(Dz)_{i,j}^{(2)}$ are differentiating matrices. The system of Eqs. (5) is solved using the diagonalization technique. The numerical computations are performed for the following meshes N = 100, M = 200, K = 50, 100, 150. The numerical error has been tested for α from − 0.5 up to 0.2, and for Re₁ = 1500–2500. In the considered ranges of Re₁ and α the divergence error is from 10^–7 to 10^–6. For the α = − 0.5, Re₁ = 2000 flow case, and for the mesh (100, 150) the following values have been obtained at z = 0: (ΔR⁺)₁ = 0.035, (ΔR⁺)₂ = 0.14, (ΔZ⁺)₁ = 0.022, (ΔZ⁺)₂ = 0.357 where:

$$\Delta R_{1}^{ + } = \Delta R \cdot u_{\sigma } /\nu ,\;\Delta R_{2}^{ + } = \Delta R \cdot u_{\sigma } /\nu ,\;u_{\sigma } = \{ \nu^{2} [(\partial W/\partial R)_{w}^{2} + (\partial V/\partial R)_{w}^{2} ]\}^{0.25} ,$$

(7a)

$$\Delta Z_{2}^{ + } = \Delta Z \cdot u_{\sigma } /\nu ,\;\Delta Z_{1}^{ + } = \Delta Z \cdot u_{\sigma } /\nu ,\;u_{\sigma } = \{ \nu^{2} [(\partial V/\partial Z)_{w}^{2} + (\partial U/\partial Z)_{w}^{2} ]\}^{0.25} ,$$

(7b)

$$\Delta R = (H/2\Gamma ) \cdot \Delta r,\;\Delta Z\, = (H/2) \cdot \Delta z.$$

(7c)

For the α = 0.2 (z = 0.0) flow case the results are as follows: (ΔR⁺)₁ = 0.008, (ΔR⁺)₂ = 0.0079; for α = 0.2 (r = 0.0): (ΔZ⁺)₁ = 0.082, (ΔZ⁺)₂ = 0.261. The computations are performed for the time increment from the range δt = 0.001–0.005.

In order to compare the present results with those published in literature, velocity components are normalized again by the inner wall rotation velocity Ω₁R₁. More information about the DNS algorithm can be found in [34,35,36,37].

3 Results

3.1 The critical lines in the (Re₂, Re₁) and (R_Ω, Re) planes

In [1] the authors determined experimentally the neutral line of the linear instability area (η = 0.883), and the lines of the successive bifurcations appearances in the (Re₂, Re₁) plane. The shape of the neutral line depends on η. Figure 1a presents the η = 0.5 neutral line in the (Re₂, Re₁) plane, obtained experimentally in [2] (the red symbols), and obtained with the approximate formula [3] (the blue solid line). In Fig. 1a all lines along which the computations have been performed (Re₁ = Re₂η/α) are marked by the dashed black lines or by the colored lines. The critical Rayleigh line Re₁ = Re₂η/α_cr is marked by the double black line. The studies have been conducted for Reynolds numbers up to Re₁ = 3000, but in Fig. 1a the range of Re₁ is reduced to (− 400, 400) to emphasize the critical lines occurring at lower Reynolds numbers. From Fig. 1b we can see that in the (R_Ω, Re) plane the unstable anti-cyclonic flow area for η = 0.5 occurs between R_Ω = − 1 and R_Ω = 0. For R_Ω < − 1 the anti-cyclonic flow is stable. The flow cases under investigation are listed in Table 1 with the obtained critical Reynolds numbers crRe₁, crRe₂ of the occurrence of the 3D flow structure.

Table 1 The basic flow parameters of the studied flow cases (α, R_Ω) and respective critical Reynolds numbers of the appearance of the 3D flow structures (the black points in Fig.1a)

3.2 The counter-rotating flow cases

3.2.1 The flow case of α = − 0.5

In this subsection we analyze the present results obtained from the investigations of the counter-rotating flow case of α = − 0.5 (α = − 0.5 means that the computations are performed along the line separating the cyclonic flow from the anti-cyclonic flow). The detailed DNS study for α = − 0.5 has been carried out by Dong [8] for the same radius ratio η = 0.5, but with the assumption of infinitely long configuration (the computations for the same configuration have been performed also in [38]). His research has resulted in many interesting discoveries, which are analyzed here in the light of the present data obtained for the short configuration of Γ = 4.05.

In the present investigations, for the α = − 0.5 flow case, the instability process starts at about Re₁ = 185 with a regular time series of very low frequency of f = 0.05 (Fig. 2a), which is connected with the appearance of 2D flow structures (the frequency f is normalized by the rotation of the end-walls). The meridian flow shows the existence of two counter-rotating TC vortices, between two Ekman vortices (the Ekman vortices transport fluid of high velocity along the end-walls from the area near the inner cylinder towards the higher radiuses). However, unlike in the classic TCF (α = 0.0), for α = − 0.5 the TC vortices do not fill the entire area between the cylinders—they are located near the inner cylinder and in the central part of the cavity. The outflow boundaries of the TC vortices contain the high speed fluid which is transported towards higher radiuses. This transport takes place along two stripes located at both sides of the z = 0 line in the (φ, z) plane. At the beginning of the instability process, the TC vortices are spaced regularly in the axial direction and the high speed fluid stripes are parallel (for larger Re₁ this regularity is slightly disturbed, see Fig. 3a). The distance between stripes coincides with this obtained in [8].

Fig.2

The time series, a Re₁ = 205, b Re₁ = 237.5, c Re₁ = 2500. α = − 0.5, Γ = 4.05

Fig. 3

The flow structure obtained in the (φ, z) plane near the inner cylinder (r = − 0.8) for Re₁ = 500 (a) and for Re₁ = 2500 (b). The perspective view of 3D flow, Re₁ = 3000 (c). α = − 0.5, Γ = 4.05. The colors are visible in the online version

The first irregular time series appears at Reynolds number Re₁ = 232. In the time series shown in Fig. 2b (Re₁ = 237.5) we observe fluctuations with two different frequencies of f = 0.05 and f = 0.14. Only in the time intervals where the fluctuations with higher frequency (f = 0.14) occur, the flow is 3D (in the time intervals where the regular oscillations of f = 0.05 occur, the flow is 2D). These 3D structures are irregular and stretched in the circumferential direction along the stripes of high speed fluid, see Fig. 3a. With further increases of Re₁ (to 2500 for example), the time series becomes chaotic and the small-scale perturbations stretched in the azimuthal direction dominate (the level of the flow turbulence gradually increases). A characteristic feature of the flow at higher Re₁ is the formation of groups of the small-scale disturbances: in the (φ, z) plane (Fig. 3b) we can see the areas in which the small-scale disturbances do not occur, and the areas in which they are densely packed. This phenomenon is consistent with the description given in [8]. At Re₁ = 3000 the small-scale disturbances occur in the whole cavity, but their concentration is the largest near the cylinders (the perspective view of the 3D flow obtained for Re₁ = 3000 is presented in Fig. 3c).

In the original Andereck, Liu, Swinney [1] diagram (in the Re_2, Re₁ plane) the line Re₁ = Re₂η/α (α = − 0.5) runs mainly through the area described by the authors as “unexplored”, but close to “featureless turbulence”. The present study has shown that above Re₁ = 237.5 there are no rapid bifurcations, only a gradual increase of the small-scale vortices concentration is observed, which ultimately leads to turbulent flow. This agrees with the results presented in [1, 8].

Figure 4a shows the radial profiles of the azimuthal velocity < v > _{t, A(R)} (averaged over the time, axial and azimuthal directions) obtained for α from − 0.5 up to 0.0 (the averaged values are denoted as follows: <…> _{t, A(R)}, [39]). In Fig. 4a the present profiles obtained for α = − 0.5 (marked by the blue lines, Re₁ = 1500, 2000, 2500) are compared with the profile obtained for Re₁ = 4000 in [8] (the blue line with symbols, α = − 0.5). The <v> _{t, A(R)} profiles show the existence of the high velocity gradient areas in the vicinity of the cylinders and the distinct core area in the middle of cavity. The increase of Re₁ causes an increase of the velocity gradients near the cylinders, decrease of the thickness of the boundary layers on both cylinders, and the enlargement of the central core. This is in agreement with the results published in [8].

Fig. 4

a The averaged azimuthal velocity component <v>_{t, A(R)} profiles obtained for different α and for different Re₁, the profile with blue symbols is reconstructed from Fig. 15a in [8] (α = − 0.5, Re₁ = 4000, η = 0.5). b The dimensionless parameter (R* − R₁)/(R₂ − R₁) as a function of Re₁; the red symbols indicate the present results obtained for α = − 0.5, the black dots show the reconstructed results from Fig. 15b in [8] (α = − 0.5, η = 0.5). c The radial profiles of the normalized turbulent kinetic energy production <P⁺> (averaged in time, and in the axial and azimuthal directions) obtained for α = − 0.5 and α = 0.0, Re₁ = 1500, 2000 and 2500 (the area adjacent to the inner cylinder is considered). The colors are visible in the online version

In the TC flows between infinitely long cylinders (as in [8]) the transverse current of azimuthal motion J^Ω (see Eq. 8, [39]) is conserved, which means that this parameter must be a constant across the cavity gap. However, this rule does not apply to the TC flow cases with no-slip axial boundary condition. In [8] the author used the second term of Eq. (8), i.e. –ν∂ < (V/R) > _{t, A(R)}/∂R, to determine the thickness of boundary layers at the cylinders. The present investigations are conducted in a very short cylindrical configurations (Γ up to 4.05, closed by the end-walls), in which the condition of constant J^Ω value across the cavity gap is not conserved—the thickness of boundary layers at the cylinders can only be estimated based on Eq. (8), but these approximate values agree with those published by [8]).

$$J^{\Omega } = R^{3} [U \cdot /RV - \nu \partial \left( {V/R} \right)/\partial R]$$

(8)

In the present profiles (α = − 0.5, Fig. 4a) the azimuthal velocity values in the core are almost constant and close to zero, whereas the profiles presented in [8] show a slight slope in this area. But, such a small slope occurs for the flow example of α = 0.0 (the yellow lines, Fig. 4a). The occurrence of profiles with a non-zero slope implies the production of the turbulent kinetic energy in the central core. Figure 4c shows the averaged turbulent kinetic energy production <P⁺>_{t, A(R)} as a function of r obtained for α = − 0.5 and α = 0.0, and for different Re₁. The production, defined in Eq. (9a), is normalized by (R₂-R₁)/u_σ³ (see [40]), where the total friction velocity u_σ is computed based on the parameters at the inner cylinder (r = − 1). Figure 4c presents the results only near the inner cylinder areas, r ∈ [− 1, 0]). The results show that < P⁺ > _{t, A(R)} is close to zero in the central core (r = 0.0) for α = − 0.5, while for α = 0.0 the production value < P⁺ > _{t, A(R)} (r = 0) is equal to about 15% of its peak value.

$$P^{ + } = - R \cdot \overline{{U^{\prime } V^{\prime } }} \cdot \frac{\partial (V/R)}{{\partial R}} \cdot \frac{{R_{2} - R_{1} }}{{u_{\sigma }^{3} }},$$

(9a)

$$u_{\sigma } = \{ \nu^{2} [(\partial W/\partial R)_{w}^{2} + (\partial V/\partial R)_{w}^{2} ]\}^{0.25} .$$

(9b)

In the counter-rotating flow cases there is a cylindrical surface of the radius marked by R* in [8], with the zero averaged azimuthal velocity < v(R*) > _{t, A(R)} = 0.0. Figure 4b shows the dimensionless radius of this surface (R* − R₁)/(R₂ − R₁) as a function of Re₁, obtained here and in [8]. We can see that the (R* − R₁)/(R₂ − R₁) parameter increases with the increase of Re₁, but only up to a certain limit value, then remains at a constant level. The (R* − R₁)/(R₂ − R₁) values obtained in the present investigations for particular Re₁ are about 0.2 higher than those presented in [8], which can be attributed to the end-walls effect. The velocity profiles < v > _{t, A(R)} obtained for α = − 0.5, − 0.4, − 0.2, − 0.1 and 0.0 (Fig. 4a) show that (R* − R₁)/(R₂ − R₁) also increases with the increase of α until α = 0.0, for which it has the value of 1.0. Such an analysis has been carried out (among others) in [41], where the authors have found that the TC vortices occur mostly in the areas of the radius smaller than R*, which is in agreement with the present observations.

The radial profiles of the square root of the averaged Reynolds stress tensor component (<(v’v’)>_{t, A(R)})^0.5 and <v′u′>_{t, A(R)} obtained for different α (from − 0.5 up to 0.0), and Re₁ = 1500–2500 are presented in Fig. 5a, b, respectively. The (<(v′v′)>_{t, A(R)})^0.5 distributions show the two-peak profiles for all α—such profiles are typical for the bounded shear flows. At lower Re₁ (not presented in Fig. 5a) the velocity gradients at the cylinders are small, and the (<(v′v′)>_{t, A(R)})^0.5 values are relatively large in the core (it is the result of the large-scale vortices presence in this area). For higher Re₁ = 1500, 2000, 2500, 3000, the flow is dominated by the small-scale disturbances occurring mostly near both cylinders. The peak values of (<(v′v′)>_{t, A(R)})^0.5 in the profiles obtained for higher Re₁ and their locations are similar to those published in [8], where the profiles of r.m.s. azimuthal velocity fluctuations are presented. However, the present (<(v′v′)>_{t, A(R)})^0.5 values in the central part of the cavity are lower than those obtained by Dong [8] for the infinitely long cavity. Figure 5b shows that maximum values of the Reynolds stress tensor component <u′v′>_{t, A(R)} occur near the inner cylinder—there is an agreement with the results in [8] as to the maximum values and their locations. The present peak values show a slight increase with increasing Reynolds number, but this increase gradually disappears for higher Re₁. The existing tail of zero or even negative values of <u′v′>_{t, A(R)} near the outer cylinder is longer in comparison with the results of [8]. The tail shrinks slightly with the increase of Re₁, but still the present <u′v′>_{t, A(R)} values in the central part of the cavity are smaller. The differences between the current results obtained for the short configuration and those obtained in [8] can be attributed to the end-walls effect.

Fig. 5

The averaged radial profiles of (< (v′v′)>_{t, A(R)})^0.5 (a) and <u′v′>_{t, A(R)} (b), obtained for Re₁ = 1500, 2000 and 2500, and for different α. The colors are visible in the online version

3.2.2 The flow cases of α = (− 0.4) − (− 0.3)

The flow structures obtained for α = − 0.5 are substantially different from those observed for α from − 0.4 up to 0.0. In the α = − 0.4, − 0.3 flow cases, two TC vortices exist between the Ekman vortices (as in the α = − 0.5 flow case), and again these large-scale vortices do not fill the entire space between cylinders (see Fig. 4a), however, in many aspects these flow cases differ from α = − 0.5. For α = − 0.4 and − 0.3, the 3D structures appear at about Re₁ = 190 with the smooth increase of regular oscillations of the frequency about f = 0.44–0.5. The appearance of these waves is accompanied by three regular structures observed in the azimuthal direction, asymmetrically located with respect to the z = 0.0 line (see Fig. 6a, α = − 0.4, Re₁ = 235). The structures are located in the vicinity of two narrow stripes along which the high speed fluid is transported by the TC vortices from the inner cylinder area to higher radiuses. Figure 6b shows the flow structure in the meridian section (we can see two TC vortices between the Ekman vortices, regularly distributed in the axial direction). In the flow case of α = − 0.5, the 3D structures are also formed in the vicinity of the stripes of high speed fluid, but they are irregular and stretched in the azimuthal direction.

Fig. 6

The flow structures: a in the (φ, z) plane, r = 0.0, Re₁ = 235, b in the meridian section, Re₁ = 235, c in the (φ, z) plane, r = 0.0, Re₁ = 2500, d in the meridian section, Re₁ = 2500, e the axial profiles of the turbulence kinetic energy normalized by squared total friction velocity at the disc (denoted by k), obtained in the middle section of the cavity (r = 0) for different Re₁ (the top part of the cavity is presented). α = − 0.4. The colors are visible in the online version

The flow structures obtained for α = − 0.4 and − 0.3 are similar to those obtained experimentally in [1] (η = 0.883, Re₁ = 350, Re₂ = − 100), where the authors have found 6–7 waves around the annulus. In [42] the authors have found numerically 5 waves in the cavity of η = 0.75, Γ = 6, with the end-walls attached to the outer cylinder (Re₁ = 750, Re₂ = − 250). They proposed the following formula to measure the wave speed in the TC configurations with independently rotating cylinders: γ = [f(1 + η)/2k − α]/(η − α), where k is the number of vortices in the azimuthal direction (see Fig. 1 in [42]). Figure 7 includes the data reconstructed from [42] (this includes the results obtained in [43,44,45]), and the present results: γ = 0.56 (α = − 0.4, k = 3, f = 0.44, Γ = 3.95, the red dot) and γ = 0.45 (α = − 0.2, k = 3, Γ = 4.025, f = 0.46, γ = 0.45, the blue dot). We can see that the value obtained for α = − 0.2 (γ = 0.45) agrees well with the result obtained in [44]. Generally, the results presented in Fig. 7 show large variation.

Fig. 7

The wave speed parameter γ as a function of aspect ratio Γ. The present results are marked by the red and blue symbols. The remaining results are reconstructed from Fig. 2 in [42]. The colors are visible in the online version

With further increase of Re₁, the period doubling phenomenon appears and the amplitudes of oscillations become irregular and finally chaotic (at about Re₁ = 500). In Fig. 6c, we can see the turbulent flow structure obtained for α = − 0.4 in the (φ, z) plane (Re₁ = 2500, r = 0.0), and Fig. 6d presents the corresponding flow in the meridian section. The meridian flow shows two dominant Ekman vortices, which occupy a large part of the cavity, and some smaller structures near the z = 0.0 line. In order to better characterize the distribution of the turbulence in the meridian section, in Fig. 6e the axial profiles of the turbulence kinetic energy (normalized by the squared total friction velocity at the disc) obtained for different Re₁ are presened. We can see that the smallest values occur in the vicinity of the rotating end-wall.

3.2.3 The flow cases of α = (− 0.2) − (− 0.15)

For α = − 0.2 and − 0.15, the 3D structures appear at about Re₁ = 190 and 212, respectively, together with the regular oscillations of frequency 0.46 and 0.44. However, the influence of the rotating outer cylinder becomes weaker in comparison with the α = − 0.5 flow case, which results in the appearance of only one counter-rotating vortex between the Ekman vortices. In contrast to the flow examples of α = − 0.5, − 0.4 and − 0.3, for α = − 0.2 and − 0.15 the TC vortex fills almost the entire area between the cylinders—the (R* − R₁)/(R₂ − R₁) parameter is close to 1.0. The example 3D flow structures in the (φ, z) plane obtained for α = − 0.2, Re₁ = 210 are presented in Fig. 8. For higher Re₁, the strong modulation occurs and the regularity of the structures gradually fades away. The time series become chaotic at about Re₁ = 500 and the small-scale vortices begin to dominate in the vicinity of the cylinders.

Fig. 8

The flow structure in the (φ, z) plane obtained for Re₁ = 210, α = − 0.2. The colors are visible in the online version

3.2.4 The flow cases of α = (− 0.1) − (− 0.05)

With the further increase of α (up to − 0.1 and − 0.05) rapid changes are observed. For α = − 0.1, at the beginning of the instability process one counter-rotating TC vortex occurs. The first instability wave of very low frequency f = 0.006 appears at Re₁ = 257.5 and at Re₁ = 267 the transition to a new wave, with an extremely irregular time series, takes place. At Re₁ = 267 the 3D structure emerges (of the wave number 1, see Fig. 9a) in the central part of cavity (this structure resembles this occurring for α = 0.0 at very low Re₁, which is connected with the codimension-2 point, [37]). With Re₁ above 267, the TC vortex fades gradually to disappear at Re₁ = 320. Above Re₁ = 320 the time series become regular, with the oscillations of frequency 0.55, and simultaneously two 3D vortices appear, asymmetrically located with respect to the z = 0.0 line, Fig. 9b.

Fig. 9

The flow structure in the (φ, z) plane obtained for a–b Re₁ = 300, Re₁ = 325, α = − 0.1, c–d Re₁ = 170 and 590, α = − 0.05. r = 0.0. The colors are visible in the online version

For α = − 0.05, the local unsteady area with one 3D vortex in the central part of cavity occurs in the range of Re₁ = 167–201 (see Fig. 9c). For Re₁ higher than 201, the flow is steady and 2D, up to the new unsteady area occurring at about Re₁ = 410, where regular oscillations of frequency f = 0.22 is observed. However, the period doubling phenomenon very quickly leads to the new wave of f = 0.52. Both waves are associated with the 3D structures presented in Fig. 9d.

3.2.5 The flow case of α = 0.0

A special role in the analysis is played by the classic TCF with the stationary outer cylinder. In the flow case of α = 0.0, the steady meridian flow consists of one TC vortex between two Ekman vortices. The first unsteady area, with the regular oscillations of f = 0.126, appears at about Re₁ = 100 and is associated with the presence of one 3D vortex (Fig. 10a) located in the central part of cavity, see [37]. This is the same structure which has been observed for α = − 0.1 and − 0.05, but its range of occurrence for α = 0.0 is larger: Re₁ = 100–167 (the exact value depends on Γ). This 3D vortex is squeezed out due to the gradual enlargement of the Ekman vortices with increasing Re₁. For Re₁ higher than 167, the flow is steady, 2D and only the Ekman vortices exist. The next unsteady area begins at Re₁ = 428 with the appearance of regular oscillations of f = 0.86, which is connected with the occurrence of 8 structures symmetrically distributed with respect to the z = 0.0 line (Fig. 10b). With further increase of Re₁, many consecutive bifurcations are observed (the example time series are presented in Fig. 11a–c), which finally lead to turbulent flow.

Fig. 10

The flow structure in the (φ, z) plane obtained for Re₁ = 117 (a), Re₁ = 435 (b), α = 0.0. The colors are visible in the online version

Fig. 11

The time series obtained for: a Re₁ = 497.5, b Re₁ = 535, c Re₁ = 590. α = 0.0, Γ = 3.95

From Fig. 5a we can see that the formation of the turbulent (<(v′v′) > _{t, A(R)})^0.5 profile for α = 0.0 requires much higher Re₁ than for negative α, but shear Reynolds number is far smaller for α = 0.0 than for α = − 0.5: Re = 3333 for α = 0.0, Re₁ = 2500, and Re = 5000 for α = − 0.5, Re₁ = 2500. For Re₁ between 1500 and 25,000, and for α between − 0.5 and − 0.2, a clear maximum of (<(v′v′)>_{t, A(R)})^0.5 occurs in the vicinity of the inner cylinder, and a second lower maximum occurs in the vicinity of the outer cylinder. The profiles obtained for α = 0.0 are different: although two peaks of (<(v′v′)>_{t, A(R)})^0.5 near the inner and outer cylinders are visible, their values are much smaller (generally the profiles are flatter). The <v′u′>_{t, A(R)} profiles are also different from these obtained for negative α: from Fig. 5b we can see the almost linear decrease of <v′u′>_{t, A(R)} with the radius in the central part of cavity (α = 0.0), while for other α the values are close to zero or are even negative in this area.

3.3 The co-rotating flow cases

3.3.1 The flow cases of α = 0.05–0.15

The α = 0.05, 0.1, 0.15 and 0.2 flow cases are located in the linear instability area (Fig. 1a), but only the bifurcation processes occurring for α = 0.05 and 0.1 resemble those observed for α = 0.0. At the beginning of the instability process for α = 0.05 and 0.1 one TC vortex exists between the Ekman vortices. The small unsteady area with regular oscillations connected with the existence of one-arm structure (as in the flow case of α = 0.0, − 0,05, − 0.1) has been observed in the range of Re₁ = 108.75–132.5 for α = 0.05 (f = 0.12) and in Re₁ = 108–120 for α = 0.1 (f = 0.11). For Re₁ higher than in the mentioned ranges, the flows are steady, 2D and only the Ekman vortices occur. The example one-arm structure, obtained for α = 0.1 and Re₁ = 117 in the (φ, z) plane, is presented in Fig. 12a. A new unstable area (with regular oscillations) begins at Re₁ = 355 for α = 0.05 (f = 0.745, 7 symmetric vortices are observed), and at Re₁ = 317.5 for α = 0.1 (f = 0.5, 5 symmetric vortices are observed, Fig. 12b). With further increase of Re₁, a series of bifurcations similar to these found for α = 0.0 occurs, which finally lead to the chaotic time series and turbulence.

Fig. 12

The flow structure in the (φ, z) plane obtained for Re = 117 (a) and Re₁ = 370 (b), α = 0.1. The colors are visible in the online version

In the flow cases of higher α (starting from α = 0.15) only the Ekman vortices have been observed in the meridian flows (these observations are consistent with the results presented in [25], η = 0.5, Γ = 8, 10 and 12). For α = 0.15 the flow is stable up to Re₁ = 287.5 (there is no local unstable area at low Re₁ for this flow case). Above Re₁ = 287.5 the time series are uniform with regular oscillations of frequency f = 0.46. In the (φ, z) plane 5 symmetric vortices occur, which are regular up to about Re₁ = 520.

3.3.2 The flow case of α = 0.2

For α = 0.2, the Re₁ = Re₂η/α line (q = 2.232, R_Ω = − 0.875) is located close to the Rayleigh criterion line (α_cr = 0.25, q = 2, R_Ω = − 1), which causes the analyzed bifurcation phenomena to be extremely diverse. Again, in the meridian flow only the Ekman vortices occur. The instability process begins with the appearance of the regular oscillations of frequency f = 0.34 at Re₁ = 315, which is connected with four vortices in the (φ, z) plane, located symmetrically with respect to the z = 0.0 line. For slightly higher Re₁ these structures become asymmetric, but still are regular up to Re₁ = 525. At Re₁ = 525 the transition to the new wave with the oscillations of frequency 0.05 appears, then with the further increase of Re₁ some consecutive bifurcations occur. Generally, for higher Re₁ two global flow structures are observed. The first one is presented in Fig. 13a, b (Γ = 3.85, Re₁ = 1000) and the second one, obtained for Re₁ = 3000, is presented in Fig. 13c, d. These flow structures are very similar to those obtained in [30] for the quasi-Keplerian flow case of R_Ω = − 1.04686, Γ = 11.47, η = 0.7245 (the end-walls attached to the outer cylinder, Fig. 2a, b, [30]). For α = 0.2 computations have been performed for Γ from the range of [3.85–4.025], but no significant effect on the bifurcation processes in this narrow range of Γ has been found. However, such a symmetrical structure (with respect to the z = 0 line) as in Fig. 13a, b has been found only for Γ = 3.85.

Fig. 13

The flow structures in the (φ, z) plane (r = 0.0) and the perspective view of 3D flow a–b Re₁ = 1000, c–d Re₁ = 3000. α = 0.2, Γ = 3.85. The colors are visible in the online version

3.3.3 The flow cases of α = 0.25–0.275- the quasi-Keplerian flows

The experimental investigations of the quasi-Keplerian flows performed in the short cavity (Γ = 2.1), with the end-walls divided into two independently rotating rings [11, 12], have shown that the bulk flow is laminar up to Reynolds number 10⁶. The optimal rotational speed was chosen for every ring to minimize the influence of the Ekman circulations. However, the DNS results obtained in [30] for the configuration used in [12] have shown that the flow is turbulent at Re about 10³. Then, in [16] the authors performed new experimental investigations which showed that if the end-wall boundary conditions are optimal, the quasi-Keplerian flow remains stable up to Re about 10⁶. The authors pointed out that the different boundary conditions on the discs caused discrepancies. In [19], the authors presented the new DNS computations obtained for Reynolds numbers up to 5^.10⁵ and stated that “the occurrence of turbulence at low Re appears to be a robust feature of quasi-Keplerian Taylor–Couette flows.” However, they showed that with increase of Reynolds number up to 5^.10⁵ the gradual relaminarization of the flow in the middle part of cavity occurs and that the turbulence finally is confined only in the thin boundary layers near the end-walls. The authors showed that this process depends strongly on the end-wall boundary conditions. In [19] the authors studied the flow cases with the end-walls rotating independently from cylinders (named WR), and the flow cases with end-walls divided into three rings with optimized rotational speeds (named HTX). In the WR flow case the Ekman vortices (covering the entire cavity) destabilize the flow. The vortices typical for the linear unsteady regime are observed in the equatorial region (the turbulence does not reach the end-walls). In the HTX flow case, the Ekman vortices are only confined to the vicinity of the end-walls. Only in the HTX flow case the relaminarization process occurs.

In the present paper, the computations have been performed for one quasi-Keplerian flow case (α = 0.275) to check the influence of the end-walls attached to the inner cylinder on the flow dynamics in the linearly stable area. With such end-wall boundary conditions, the Ekman circulations generate the strong inflow in the central part of the cavity (along the z = 0.0 line, Fig. 14c)—the observed supercritical Hopf bifurcations begin in this area. In considered Reynolds numbers the 3D structures obtained in the quasi-Keplerian area are triggered only by the Ekman vortices. The instability processes observed for α = 0.275 are connected with the appearance of four asymmetric (with respect to the z = 0.0 line) vortices in the middle area of the (φ, z) plane. The flow structures obtained for α = 0.275, Re₁ = 435 are presented in Fig. 14a—these structures are similar to those obtained numerically in [19] for the short cavity named WR (Γ = 2.2, η = 0.3478, q = 1.8). However, in [19] the authors obtained two asymmetric structures in the equatorial area, whereas in the present configurations four structures have been found. For higher Reynolds numbers the small-scale disturbances are observed in the middle part of cavity—see Fig. 14b, where the result obtained for Re₁ = 2000 is shown. In Fig. 14c the strong Ekman circulation (Re₁ = 2000) in the meridian flow section is presented – we can see that the smaller vortices are concentrated only in the middle region. Studies have shown that, despite different boundary conditions at the end-walls, the observed here structures resemble those obtained in [30] and partly those obtained in the WR cavity ([19]). However, the results obtained in [19] for the HTX case differ significantly from the present results and those obtained in [30].

Fig. 14

The flow structures in the (φ, z) plane obtained for Re₁ = 435 (a), Re₁ = 2000 (b). The flow circulation in the meridian section obtained for Re₁ = 2000 (c). Γ = 4.025, α = 0.275. The colors are visible in the online version

Selected results obtained for α = 0.275 (R_Ω = − 1.069, Γ = 4.025) are presented below, together with the results of α = 0.25 (R_Ω = − 1, Γ = 4.025). For α = 0.25 and α = 0.275 the first oscillations (regular) appear at Re₁ = 412 (f = 0.318) and Re₁ = 427.5 (f = 0.306), respectively. In Fig. 15 these neutral points are analyzed in the (Γ, Re) plane and are compared with those published in [30] (R_Ω = − 1.1, η = 0.5, Γ = 5 and 10, the end-walls attached to the outer cylinder). The critical Reynolds numbers of the appearance of 3D structures in the quasi-Keplerian area were also determined (numerically and experimentally) in [25], where the authors studied flows in the TC configurations of Γ = 6, 8, 10 and 12 with the stationary end-walls (η = 0.5). They have shown that the onset of 3D structures strongly depends on the aspect ratio Γ (the study covers a significant range of α, up to about 0.6, see Fig. 5b [25]). However, this dependence on Γ is relatively small in the vicinity of the Rayleigh line—the present critical Re₁ obtained for α = 0.275 is in agreement with critical Reynolds numbers obtained in [25] near the Rayleigh line.

Fig. 15

Critical Reynolds numbers Re of the quasi-Keplerian flows in the (Γ, Re) plane obtained for the short cavity with the end-walls attached to the inner cylinder (the red symbol, α = 0.25, R_Ω = − 1; the blue symbol, α = 0.275, R_Ω = − 1.069). The results denoted by the black symbols are obtained in the cavity with the end-walls attached to the outer cylinder, R_Ω = − 1.1, [30]. η = 0.5. The colors are visible in the online version

Figure 16a, b show the radial statistical profiles of (<(v′v′)>_{t, A(R)})^0.5 and <u′v′>_{t, A(R)} obtained for α = 0.0 (the yellow lines), 0.1 (the green lines), 0.15 (the blue line), 0.2 (the red lines), 0.25 (the navy blue lines) and 0.275 (the black lines), and for Re₁ = 1500, 2000 and 2500. The (<(v′v′)>_{t, A(R)})^0.5 profiles show that with increasing α the profiles become flatter, which suggests that the disturbances are concentrated in the central part of cavity. The values obtained for α = 0.2, 0.25 and 0.275 are very small so they are additionally presented in the inserts of Fig. 16a, b. In the <u′v′>_{t, A(R)} profiles obtained for α = 0.0, 0.1 and 0.15 there is a gentle peak near the inner cylinder, while for α = 0.2, 0.25 and 0.275 the <u′v′>_{t, A(R)} values are close to zero or even are negative in this area.

Fig. 16

The averaged radial profiles of (<(v′v′)>_{t, A(R)})^0.5 (a) and <u′v′>_{t, A(R)} (b) obtained for different α and different Re₁. The colors are visible in the online version

3.4 The influence of α on the meridian flow structures

To summarize the flow structures obtained during the investigations performed here for α from the range of [− 0.5, 0.275], in Fig. 17 the structures occurring in the meridian section at the initial stage of the laminar-turbulent transition process are presented schematically in the (Re₂, Re₁) plane. Figure 17 shows that for the strongly counter-rotating flow examples (α = − 0.5, − 0.4, − 0.3) two TC vortices between two relatively small Ekman vortices occur. The TC vortices do not fill the entire area between the cylinders—they are located near the inner cylinder and in the middle part of cavity. As α increases, the Ekman vortices grow in the axial direction, squeezing the TC vortices. As a result of this process, only one TC vortex occurs between two Ekman vortices for α = − 0.2 and − 0.15. For α from the range of [− 0.1, 0.1] this one TC vortex still exists (and fills the entire gap between the cylinders), but only at very low Re₁ and in a very narrow range of Re₁. This narrow range of Re₁ is related to the occurrence of a small, local unstable area triggered by the codimensio-2 point. The local unstable area disappears for slightly higher Reynolds numbers and only the Ekman vortices remain. In Fig. 17 two meridian flows connected with α from the range of [− 0.1, 0.1] are shown: first one (on left) is obtained for Re₁ from the local unstable area, the second one (on right) is obtained for Re₁ at which only the Ekman vortices exist. Starting from α = 0.15, the TC vortices do not appear any longer—the Ekman vortices fill the entire space between the discs and cylinders. A similar analysis of the meridian flows obtained for the co-rotating configurations (η = 0.5) is presented in Fig. 3a ([25]), where the multi-cell states obtained for Γ = 8 are presented.

Fig. 17

The critical lines obtained for the Taylor-Couette configurations in the (Re₂, Re₁) plane are presented (see also Fig. 1a), together with the schematic pictures of the meridian flows obtained for different α. Only the first stage of the laminar-turbulent transition is analyzed. The colors are visible in the online version

The radial averaged azimuthal velocity profiles <v>_{t, A(R)} obtained for α = − 0.5 (Re = 5000, Re₁ = 2500) and α = 0.0 (Re = 3333, Re₁ = 2500), which are presented in Fig. 4a, are compared in this section additionally with the experimental data published in [46]. The reconstructed data from [46], obtained in the long configuration of Γ = 22 (η = 0.917, Re = 14,000, closed by the end-walls attached to the outer cylinder) for α = − 0.5 and α = 0.0 are presented in Fig. 18. Following [46], all profiles are normalized by S_d = 2R₁(Ω₂-Ω₁)/(1 + η). We can see agreement between the present results and those obtained in [46], despite the different end-wall boundary conditions, different geometrical parameters Γ, η, and also different Re. The comparison shows that the core of the profiles is clearly visible for α = − 0.5 and α = 0.0. It is noteworthy that in [46] the authors obtained non-zero slope profile for α = − 0.5, similarly to the solutions obtained using DNS in [8] (the computations have been performed for infinitely long cavity). Problem has been discussed in Sect. 3.2.1. The present computations performed for different α show that in the short configurations (Γ about 4.0), with the discs rotating together with the inner cylinder, the slope of the azimuthal velocity profile in the core gradually increases with α.

Fig. 18

The comparison of the present averaged azimuthal velocity profiles obtained for α = − 0.5 (Re₁ = 2500, Re = 5000) and α = 0.0 (Re₁ = 2500, Re = 3333) in configurations of η = 0.5 with the end-walls attached to the inner cylinder, with the experimental results obtained in [46] (α = − 0.5 and 0.0, Re = 14,000, η = 0.917, Γ = 22, the end-walls attached to the outer cylinder). The colors are visible in the online version

4 Conclusions

In the paper, the bifurcation mechanisms occurring in the Taylor-Couette flows between cylinders rotating independently, with the rotational rate α = Ω₂/Ω₁ from − 0.5 to 0.275 (Γ = 3.85–4.05, η = 0.5, the end-walls attached to the inner cylinder), have been investigated numerically using the DNS method. In the research Re₁ has been gradually increased (up to 3000) along the Re₁ = Re₂η/α lines. The computations have been performed in the linearly unstable area (13 flow cases) and in the quasi-Keplerian area (one flow case). As it is known, the sensitivity of the transitional phenomena to the changes of the governing parameters (α, Re₁, Γ), and to the end-wall boundary conditions is large (particularly in the quasi-Keplerian area), which also is confirmed by the present results. The large variety of the laminar-turbulent scenarios has been observed and new interesting phenomena have been found. The conducted investigations lead to the following conclusions:

• For all investigated flow cases, the critical Reynolds numbers Re₁ of the appearance of the 3D structures have been determined and displayed in the (Re₂, Re₁) plane (Fig. 1a). These 3D structures are connected with the instability waves of regular oscillations of the frequency approximately from 0.4 to 0.8 (the value depends on α). The only exception is the flow case of α = − 0.5, for which the time series connected with the appearance of the 3D structures is chaotic.

• The characteristic feature of the considered flow cases is the occurrence of a local unsteady area at a very low Re₁ for α from − 0.1 to 0.1, in which the only TC vortex, observed between two Ekman vortices, gradually disappears with increasing Re₁ (this unsteady area is connected with the codimension-2 point). For the flow cases of α from − 0.1 to 0.1 the next unstable area, leading finally to turbulence, occurs for much higher Re₁ (see Fig. 1a).

• The number of the TC vortices occurring between two Ekman vortices varies with α: for α from − 0.5 to − 0.3 two TC vortices occur, for α = − 0.2 and − 0.15 only one vortex is observed. For α from − 0.1 to 0.1 one TC vortex exists, but it disappears due to the influence of the small unsteady area occurring at low Re₁. Starting from α = 0.15 only the Ekman vortices are observed in the meridian sections.

• The DNS computations obtained for α from − 0.5 to 0.275 (the anti-cyclonic flows cases) show that the transport of the angular momentum is due to the large scale structures.

• For α = − 0.5 the existing 3D instability structures (of the azimuthal wave number 1) are irregular. In all other flow cases the instability structures are regular with the azimuthal wave numbers from 2 to 8 (value depends on α). The structures are mostly asymmetric with the respect to z = 0.0 line, but for α from − 0.1 up to 0.1 they are symmetric.

• With increasing Re₁ the consecutive bifurcations are observed, which lead to the chaotic time series and finally to turbulence. The number of observed bifurcations depends on α—the largest number has been observed for α close to 0.0. In order to obtain better characteristics of the processes taking place for higher Re₁, the radial profiles of the averaged parameters <(v)>_t,A(R), (<(v′v′)>_{t, A(R)})^0.5, <u′v′>_t,A(R), <P⁺>_t,A(R) have been determined, which enabled quantitative comparison of the present results with those published in literature. The comparison has shown agreement with the results obtained for α = − 0.5 and α = 0.0 in [8, 25, 46], despite different boundary conditions applied at the discs. The flow cases with larger positive values of α turned out to be the most sensitive to the boundary conditions at the discs, but also for these flow cases a qualitative agreement with the flow structures presented in [25, 30] has been observed. The results have also shown that in the considered range or Re₁, the Ekman circulations are the only source of instability in the considered quasi Keplerian flow case of α = 0.275, Γ = 4.025 (the end-walls attached to the inner cylinder).