Vibration of an axially loaded heterogeneous fixed–fixed beam with an intermediate roller support

Abstract

The present paper investigates how an axial load can change the natural frequencies of heterogeneous fixed–fixed beams with an intermediate roller support. The problem is treated as a three-point boundary value problem (eigenvalue problem) that is paired with homogeneous boundary conditions. The Green functions are determined for the unloaded and pre-loaded beams as well—in the later case, both for compression and tension. With these, the eigenvalue problems can be transformed into eigenvalue problems governed by a homogeneous Fredholm integral equations. It is then replaced by an algebraic eigenvalue problem, that is solved numerically with an effective solution algorithm which is based on the boundary element method.

1 Introduction

When it comes to the mechanical behavior of straight beams, due to their numerous practical applications, there is a variety of selections within the available literature. Regarding the research progress on the free vibrations of beams in recent years, it is mentioned that the vibrations of buckled beams are investigated in [2]. The model introduced is nonlinear through the mid-plane stretching. With the Galerkin method, the partial differential equations are reduced to one ordinary differential equation. The variational iteration method and the parameterized method are used to study the transverse vibrations. Both techniques yield the same results. An exact solution is provided for the mode-shape equation of self-weight loaded columns and cables in [3]. The mode shapes are given by a family of complex Hankel–Airy functions. Axially functionally graded beams are considered in [13], resting on Pasternak foundation. The equation of motion is found using the Hamilton principle and parametric studies are made to reveal the effect of the geometry, material and foundation. The dynamic behavior of cracked Timoshenko beams on Winkler foundation is reported through the transverse vibrations in [14]. The cracked beam is modeled by two segments connected by an extensional and a rotational spring. The natural frequencies are obtained in terms of the elastic foundation stiffness, crack position and initial crack-length.

As for the vibrations under external load, it is known how an axial load changes the natural frequencies of a uniform single-span beam from [5]. Accordingly, Galef’s formula is only applicable to a few end-conditions as the supports have a significant impact on the eigenfrequencies. The vibratory behavior of clamped-free beams with an intermediate axial force is the subject in [9], using the classical Hamilton principle. As per the findings, the frequencies increase as the force edges closer to the clamped end. Two beams, elastically connected with a Winkler layer are in the spotlight in [20]. The effect of an axial load is incorporated into the model to find the frequencies of vibrations. Actually, two non-homogeneous partial differential equations are solved. Moreover, the continuous transfer matrix method is applied to find the frequencies of vibrating axially loaded multi-step beams carrying an arbitrary number of concentrated elements [24]. Furthermore, it is found that rigidly attached lumped masses have no effect on the buckling loads. Article [16] is about large vibrations of beams on variable Winkler foundation. A cubic nonlinear term is kept in the dynamic equilibrium equation and the second-order homotopy perturbation method is used to solve it. Article [18] presents the forced vibrations of a Timoshenko beam with a concentrated mass at the center. The coupled displacement field method is used. The related equation of motion is found from the conservation of energy principle and is solved with the Newmark method. The focus is on both thermally and mechanically loaded two-layered beams in [15]. The model is based on the nonlinear extended Timoshenko-theory. The governing nonlinear partial differential equations are reduced to ordinary differential equations which are solved and the findings are compared with experiments.

Since the present article uses the Green function to tackle some beam problems, a brief historical overview is also provided. The Green theorem and Green function were first introduced in [8] to solve an electrostatic problem. After that, the Green function for two-point boundary value problems given by ordinary differential equations was published in [4]. Sources [6, 7] define the Green function for ordinary linear differential equations. Furthermore, the Green function was generalized for a class of ordinary differential equation systems in [17]. When it is about degenerated ordinary differential equation systems, the definition is provided in [21]. For some second-order ordinary differential equations, a technique is given in [25] for the construction of the Green functions for three-point boundary value problems. Furthermore, constructing the Green function is shown [19] for a special class of third-order three-point boundary value problems.

Based on the literature review, this paper aims to tackle multiple issues. The article presents the related Green function for the free vibrations of beams and gives the numerical solution of the problem. The issue is transformed to a Fredholm integral equation, whose kernel is proportional to the Green function, and solution is given using the boundary element technique. Furthermore, the construction of the Green function is also made when there is an axial compressive or tensile preload on the beam. With this, it becomes possible to find how this preload affects the vibration frequencies.

2 Differential equations

2.1 Governing equations

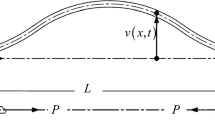
Figure 1 shows a uniform beam of length L. The axial force N ($N>0$) is compressive in the figure. The transverse coordinates are $\hat{y},\hat{z}$ while the longitudinal is $\hat{x}$. The coordinate plane $\hat{x}\hat{z}$ is a symmetry plane for the beam. The beam has three supports: a clamped one at $\hat{x}=0$, a roller at $\hat{x}=\hat{b}$ and at $\hat{x}=L$ a slider without rotations at. The beam is called FrsF beam—fixed–fixed beam with an intermediate roller support. The cross-sectional area is A. It is assumed that the beam has cross-sectional heterogeneity, i.e., the modulus of elasticity E fulfills the relation $E(\hat{y},\hat{z})=E(-\hat{y},\hat{z})$. It is also assumed that the E-weighted first moment $Q_{\hat{y}}$ of the cross section is zero in this coordinate system [1]:

$$\begin{aligned} Q_{\hat{y}}=\int _{A}\hat{y}E(\hat{y},\hat{z})\,\mathrm {d}A=0. \end{aligned}$$

This is the reason why the coordinate axis $\hat{x}$ is referred to as E-weighted centerline (or centerline for short)—if the modulus of elasticity is constant the E-weighted centerline is obviously the centerline of the beam.

Fig. 1

An FrsF beam subjected to a compressive axial force

Equilibrium problems of Euler–Bernoulli beams subjected to an axial force are governed by the ordinary differential equation:

$$\begin{aligned} \frac{ {d}^{4}\hat{\mathrm{w}}}{ {d}\hat{\mathrm{x}}{}^{4}}\pm {\hat{\mathcal{N}}} \frac{ {d}^{2}\hat{\mathrm{w}}}{ {d}\hat{\mathrm{x}}{}^{2}}=\frac{\hat{f}_{z} }{I_{ey}},\qquad {\hat{\mathcal{N}}}=\frac{N}{I_{ey}} \end{aligned}$$

(1)

where the sign of ${\hat{\mathcal{N}}}$ is (positive)[negative] if the axial force ${\hat{\mathcal{N}}}$ is (compressive)[tensile], $\hat{w}(\hat{x})$ is the vertical displacement component of the material points on the centerline, $\hat{f} _{z}(\hat{x})$ is the intensity of the vertical distributed load acting on the centerline, positive if it points up, while the E-weighted moment of inertia $I_{ey}$ is defined by equation [1]:

$$\begin{aligned} I_{ey}=\int _{A}E(\hat{y},\hat{z})\hat{z}^{2}\,\mathrm {d}A. \end{aligned}$$

(2)

If E is constant the beam is homogeneous and

$$\begin{aligned} I_{ey}=IE,\qquad I=\int _{A}\hat{z}^{2}\,\mathrm {d}A \end{aligned}$$

(3)

where I is the moment of inertia. It is worthy of mentioning that the effect of the material composition on $I_{ey}$ is demonstrated through examples in [10].

In what follows, we shall use dimensionless quantities defined by the following relations

$$\begin{aligned}&x=\hat{x}/L,\qquad \xi =\hat{\xi }/L,\qquad w=\hat{w}/L, \end{aligned}$$

(4a)

$$\begin{aligned}&y=\frac{\mathrm {d}\hat{w}}{\mathrm {d}\hat{x}}=\frac{\mathrm {d}w}{\mathrm {d} x},\qquad b=\hat{b}/{\ell },\qquad \ell =\left. \frac{\hat{x}}{L}\right| _{\hat{x}=L}=1, \end{aligned}$$

(4b)

where $\hat{\xi }$ is also a coordinate measured on the axis $\hat{x}$ and it is introduced here for our later considerations. Applying dimensionless quantities to equation (1) we have

$$\frac{{{\text{d}}^{4} w}}{{{\text{d}}x^{4} }} \pm {\mathcal{N}}\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} = f_{z} ,\qquad {\mathcal{N}} = L^{2} {\hat{\mathcal{N}}} = \frac{{L^{2} N}}{{I_{{ey}} }}\qquad f_{z} = \frac{{L^{3} \hat{f}_{z} }}{{I_{{ey}} }}$$

(5)

where $\mathcal {N}$ and $f_{z}$ are axial and vertical distributed loads with no dimension.

The following mechanical issues will be considered:

• (a) Static equilibrium problems ($\mathcal {N}=0$) for which the dimensionless displacement w should fulfill the simple ordinary differential equation (ODE)

  $$\frac{{d^{4} w }}{{dx^{4} }} = f_{z}.$$

  (6a)

• (b) The problem of free vibrations for which the dimensionless amplitude w should fulfill the following homogeneous ODE

  $$\frac{{d^{4} w }}{{dx^{4} }} = \lambda w ,\;\lambda = \frac{{\rho_{a} A\omega ^{2} L^{4} }}{{I_{{ey}} }}$$

  (6b)

  where $\lambda$ is the eigenvalue sought,

  $$\rho _{a} = \frac{1}{A}\int_{A} \rho {\mkern 1mu} {\text{d}}A{\text{ }}$$

  (6c)

  is the average surface density over the cross section, $\omega$ is the natural circular frequency of the vibrations.

• (c) The stability problem of the beam for which the dimensionless displacement w should fulfill the homogeneous ODE

  $$\begin{aligned} \frac{\mathrm {d}^{4}w}{\mathrm {d}x^{4}}+\mathcal {N}\frac{\mathrm {d}^{2} w}{\mathrm {d}x{}^{2}}=0, \end{aligned}$$

  (6d)

  where the buckling load (the critical load) ${\mathcal {N}}$ is the quantity to be determined.

• (d) The equilibrium problem of the axially loaded beam for which the dimensionless displacement w should fulfill the inhomogeneous ODE

  $$\begin{aligned} \frac{\mathrm {d}^{4}w}{\mathrm {d}x^{4}}\pm \mathcal {N}\frac{\mathrm {d}^{2} w}{\mathrm {d}x{}^{2}}=f_{z}, \end{aligned}$$

  (6e)

  where the sign is [positive](negative) if the axial force is [compressive](tensile).

• (e) The vibration problem of the axially pre-loaded beam for which the dimensionless amplitude w should fulfill the homogeneous ODE

  $$\begin{aligned} \frac{\mathrm {d}^{4}w}{\mathrm {d}x^{4}}\pm {\mathcal {N}}\frac{\mathrm {d}^{2} w}{\mathrm {d}x{}^{2}}=\lambda w,\qquad \lambda =\frac{\rho _{a}A\omega ^{2} L^{4}}{I_{ey}}. \end{aligned}$$

  (6f)

For FrsF beams ODEs (6a), (6b)$_1$, (6d), (6e) and (6f)$_1$ are associated with the following boundary and continuity conditions:

$$\begin{aligned} w(0)=0,\qquad w^{(1)}(0)=0;\qquad w(\ell )=0,\qquad w^{(1)}(\ell )=0; \end{aligned}$$

(7)

and

$$\begin{aligned}&w(b-0)=0,\qquad \qquad w(b+0)=0; \end{aligned}$$

(8a)

$$\begin{aligned}&w^{(1)}(b-0)=w^{(1)}(b+0);\end{aligned}$$

(8b)

$$\begin{aligned}&w^{(2)}(b-0)=w^{(2)}(b+0). \end{aligned}$$

(8c)

With the Green function $G(x,\xi )$ that belongs to the three-point boundary value problem determined by differential equation (6a) and boundary and continuity conditions (7), (8a, 8b and 8c), the solution to the boundary value problem mentioned is given by the integral

$$\begin{aligned} w(x)=\int _{\xi =0}^{\ell =1} G(x,\xi )\,f(\xi )\,\mathrm {d}\xi . \end{aligned}$$

(9)

Substituting $\lambda w(\xi )$ for $f(\xi )$ in (9) yields the homogeneous Fredholm integral equation

$$\begin{aligned} w(x)=\lambda \int _{\xi =0}^{\ell =1} G(x,\xi )\,w(\xi )\,\mathrm {d}\xi . \end{aligned}$$

(10)

In this way, the three-point eigenvalue problem determined by differential equation (6b) and the boundary and continuity conditions (7), (8a, 8b and 8c) is reduced to an eigenvalue problem governed by the homogeneous Fredholm integral equation (10).

Let us define $\mathcal {K}(x,\xi )$ and y(x) by the equations

$$\begin{aligned} \mathcal {K}(x,\xi )=\frac{\partial ^{2} G(x,\xi )}{\partial x\,\partial \xi },\qquad y=\frac{\mathrm {d} w}{\mathrm {d}x}. \end{aligned}$$

(11)

Utilizing equation (11), the three-point eigenvalue problem (6d), (7) and (8a, 8b and 8c) with $\mathcal {N}$ as the eigenvalue can be reduced to an eigenvalue problem governed by the homogeneous Fredholm integral equation [12]:

$$\begin{aligned} y(x)=\mathcal {N}\int _{\xi =0}^{\ell =1} \mathcal {K}(x,\xi ) \,y(\xi )\,\mathrm {d}\xi . \end{aligned}$$

(12)

3 Solutions for the free vibrations and stability

3.1 Free vibrations

The Green function $G(x,\xi )$ that belongs to the three-point boundary value problem determined by differential equation (6a) and the boundary and continuity conditions (7), (8a, 8b and 8c) is given by the following equations [12]:

$$\begin{aligned} G(x,\xi )=\left\{ \begin{array}{ll} G_{1I}(x,\xi ) &{} \text {if}\;\;x,\xi \in [0,b],\\ G_{2I}(x,\xi ) &{} \text {if}\;\;x\in [b,\ell ]\text { and }\xi \in [0,b],\\ G_{1II}(x,\xi ) &{} \text {if}\;\;x\in [0,b]\text { and }\xi \in [b,\ell ],\\ G_{2II}(x,\xi ) &{} \text {if}\;\;x,\xi \in [b,\ell ], \end{array} \right. \end{aligned}$$

(13)

where

$$\begin{aligned} G_{{1I}} (x,\xi ) = & \left( { - \frac{1}{{12}}\xi ^{3} \pm \frac{1}{{12}}\xi ^{3} } \right) + \left( {\frac{{3\xi ^{2} }}{{12}} \pm \left( { - \frac{{3\xi ^{2} }}{{12}}} \right)} \right)x \\ + & \left( {\frac{{3\xi }}{{12\ell b^{2} }}\left( { - \xi b^{2} + \ell b^{2} + \xi ^{2} b - 3b\ell \xi + \ell \xi ^{2} } \right) \pm \frac{{3\xi }}{{12}}} \right)x^{2} \\ + & \left( { - \frac{1}{{12\ell b^{3} }}\left( {3b\xi ^{3} - 3b^{2} \xi ^{2} - 3\ell \xi ^{2} b + \ell \xi ^{3} + \ell b^{3} } \right) \pm \frac{{ - 1}}{{12}}} \right)x^{3} {\mkern 1mu} , \\ \end{aligned}$$

(14a)

$$\begin{aligned} G_{2I}(x,\xi )&=\frac{1}{4\ell b\left( \ell -b\right) }\xi ^{2}\left( \ell -x\right) ^{2}\left( x-b\right) \left( \xi -b\right) \,, \end{aligned}$$

(14b)

$$\begin{aligned} G_{1II}(x,\xi )&=\frac{1}{4\ell b\left( \ell -b\right) }x^{2}\left( \ell -\xi \right) ^{2}\left( \xi -b\right) \left( x-b\right) \end{aligned}$$

(14c)

and

$$\begin{aligned} G_{{2II}} (x,\xi ) = & - \frac{1}{{{\mathcal{D}}_{1} }}\left( { - 3\ell b^{3} \xi ^{2} + b^{3} \ell ^{3} + b^{3} \xi ^{3} - 3\ell ^{3} b^{2} \xi + 6b^{2} \xi ^{2} \ell ^{2} - 3\ell ^{2} b\xi ^{3} + \ell ^{3} \xi ^{3} } \right) \pm \frac{{\xi ^{3} }}{{12}} \\ + & \left( {\frac{3}{{{\mathcal{D}}_{1} }}( - b^{3} \xi ^{2} + \ell ^{3} b^{2} + 2b^{2} \xi ^{3} - 3\ell b\xi ^{3} - 3b\xi \ell ^{3} + 3\xi ^{2} \ell ^{2} b + \xi ^{2} \ell ^{3} ) \pm \frac{{ - 3\xi ^{2} }}{{12}}} \right)x \\ + & \left( { - \frac{3}{{{\mathcal{D}}_{1} \ell }}\left( {b^{3} \xi \ell - b^{3} \xi ^{2} - \ell ^{2} b^{3} + 2\ell ^{3} b^{2} + b^{2} \xi ^{3} - 3b\xi \ell ^{3} + 4\xi ^{2} \ell ^{3} - \xi \ell ^{4} - 2\ell ^{2} \xi ^{3} } \right) \pm \frac{{3\xi }}{{12}}} \right)x^{2} \\ + & \left( {\frac{1}{{{\mathcal{D}}_{1} \ell }}\left( {3b\xi ^{3} - 3b^{2} \xi ^{2} - 9b\xi \ell ^{2} - 4\ell \xi ^{3} + 6\xi ^{2} \ell ^{2} - \ell b^{3} + 6b^{2} \xi \ell - \ell ^{4} + 3b\ell ^{3} } \right) \pm \frac{{ - 1}}{{12}}} \right)x^{3} , \\ \end{aligned}$$

(14d)

where

$$\begin{aligned} \mathcal {D}_{1}=12\left( \ell -b\right) ^{3}. \end{aligned}$$

(15)

Table 1 Solutions for the eigenvalues $\lambda$

Remark 1

In (14a) and (14d), the sign is [positive](negative) if [$x<\xi$]($x>\xi$). It can be checked by performing paper and pencil calculations that the Green function given by (13) and (14) satisfies symmetry condition $G(x,\xi )=G(\xi ,x)$.

Making use of the algorithm detailed in Subsection 7.2 of [22], a Fortran 90 program was developed for solving the eigenvalue problem (11), i.e., for computing the eigenvalues $\lambda$ (the natural circular frequencies $\omega$) of the freely vibrating FrsF beam (the axial force is now zero) shown in Fig. 1. Table 1 presents the values of $\lambda _{i}/4.73004^{2}$ $(i=1,2,3)$ for twenty one uniformly increasing b in the interval [0.0, 0.5].

Remark 2

If $b=0$ the beam behaves as a fixed–fixed beam for which the exact $\lambda _{i}$ values are as follows—see Table 7.5 on page 227 in [23] for a comparison:

$$\begin{aligned} \dfrac{\sqrt{\lambda _{1}}}{4.73004^{2}} =1.0000,\;\, \dfrac{\sqrt{\lambda _{2}}}{4.73004^{2}} =2.7565,\;\, \dfrac{\sqrt{\lambda _{3}} }{4.73004^{2}}\approx 5.4039,\;\, \dfrac{\sqrt{\lambda _{4}}}{4.73004^{2} }\approx 8.9330. \end{aligned}$$

Polynomials (16), (17) and (18) are fitted onto the discrete values of $\sqrt{\lambda _{k}}/4.73004^{2}$ $(k=1,2,3)$ presented in Table 1:

$$\begin{aligned} \sqrt {\lambda _{1} } /4.73004^{2} = & - 2.546852{\mkern 1mu} b^{5} + 8.962026b^{4} + 1.594603b^{3} \\ + & 2.409135b^{2} + 1.495{\mkern 1mu} 175b + 1.000020,b \in [0.0,0.3] \\ \end{aligned}$$

(16a)

$$\begin{aligned} \sqrt {\lambda _{1} } /4.73004^{2} = & 37433.982b^{6} - 91260.563b^{5} + 91046.168b^{4} \\ - & 47671.931b^{3} + 13844.741b^{2} - 2113.637b + 133.978,\qquad b \in [0.3,0.5] \\ \end{aligned}$$

(16b)

$$\begin{aligned} \sqrt {\lambda _{2} } /4.73004^{2} = & - 3031.958b^{6} + 2384.141b^{5} - 702.263b^{4} + 107.824b^{3} \\ + & 1.225103b^{2} + 4.268510b + 2.75650,\qquad b \in [0.0,0.325] \\ \end{aligned}$$

(17a)

$$\begin{aligned} \sqrt {\lambda _{3} } /4.73004^{2} = & 192059.101b^{6} - 515667.619b^{5} + 570538.129b^{4} - 332139.461b^{3} \\ + & 107050.688b^{2} - 18080.164b + 1253.909,\qquad b \in [0.325,0.5] \\ \end{aligned}$$

(17b)

$$\begin{aligned} \sqrt {\lambda _{3} } /4.73004^{2} = & - 73980.811b^{6} + 54375.702b^{5} - 15074.686b^{4} \\ + & 1945.740b^{3} - 93.797780b^{2} + 10.303203b + 5.4020.\qquad b \in [0.0,0.25] \\ \end{aligned}$$

(18a)

$$\begin{aligned} \sqrt {\lambda _{3} } /4.73004^{2} = & - 242856.192b^{6} + 175220.310b^{5} + 96631.871b^{4} - 138606.718b^{3} \\ + & 54415.1559b^{2} - 9238.59747b + 593.798{\mkern 1mu} 021,\qquad b \in [0.25,0.375] \\ \end{aligned}$$

(18b)

$$\begin{aligned} \sqrt {\lambda _{3} } /4.73004^{2} = & 1310146.492b^{6} - 3480566.618b^{5} + 3833310.308b^{4} - 2241935.5998b^{3} \\ + & 734955.949b^{2} - 128134.222b + 9293.7718.\qquad b \in [0.375,0.5] \\ \end{aligned}$$

(18c)

Fig. 2

Function $\sqrt{\lambda _{1}}/4.73004^{2}$ against b

Fig. 3

Function $\sqrt{\lambda _{2}}/4.73004^{2}$ against b

Fig. 4

Function $\sqrt{\lambda _{3}}/4.73004^{2}$ against b

Remark 3

In Figs. 2, 3 and 4, the discrete point pairs are denoted by diamonds. The continuous lines are drawn by using polynomials (16), (17) and (18) which fit onto the discrete point pairs three- to four-digit accuracy. The results obtained for the first eigenvalue will be utilized when we clarify the issue of how the axial force acting on FrsF beams affects the eigenfrequencies of the vibrations.

3.2 The stability problem of FrsF beams

Table 2 Critical dimensionless loads for FrsF beams

The stability problem of FrsF beams is reduced to an eigenvalue problem governed by the homogeneous Fredholm integral equation (12). The numerical solution to this eigenvalue problem is presented in paper [12]. The smallest dimensionless critical load $\mathcal {N}_{1}$ is given by the polynomial

$$\begin{aligned} \sqrt {{\mathcal{N}}_{1} (b)} /\pi = & - 34.584{\mkern 1mu} 863{\mkern 1mu} 786{\mkern 1mu} 2b^{5} + 23.{\mkern 1mu} 541{\mkern 1mu} 707{\mkern 1mu} 674{\mkern 1mu} 9b^{4} - 5.{\mkern 1mu} 871{\mkern 1mu} 904{\mkern 1mu} 397{\mkern 1mu} 86b^{3} \\ + & 1.877{\mkern 1mu} 289{\mkern 1mu} 692{\mkern 1mu} 9b^{2} + 1.{\mkern 1mu} 468{\mkern 1mu} 021{\mkern 1mu} 408{\mkern 1mu} 69b + 2.{\mkern 1mu} 000{\mkern 1mu} 266{\mkern 1mu} 921{\mkern 1mu} 3. \\ \end{aligned}$$

(19)

Remark 4

Table 2 contains the computed results. Note that the third column contains the approximations computed using polynomial (19). The numbers in columns two and three are the same with the accuracy of four to five digits.

4 The Green function for axially loaded FrsF beams

4.1 Equilibrium problems

Let us assume that we know the Green functions $\mathcal {G}_{c} (x,\xi )$ (Green function if the axial force is compression) and $\mathcal {G}_{t} (x,\xi )$ (Green function if the axial force is tensile) for the three-point boundary value problems determined by differential equation (6e) and boundary and continuity conditions boundary and continuity conditions (7), (8a, 8b and 8c). Then the dimensionless displacement field is given by

$$\begin{aligned} w(x)=\int _{\xi =0}^{\ell =1} \mathcal {G}(x,\xi )\,f(\xi )\,\mathrm {d}\xi ,\qquad \mathcal {G}(x,\xi )= {\left\{ \begin{array}{ll} \mathcal {G}_{c} (x,\xi ) &{} \text {(compression)},\\ \mathcal {G}_{t} (x,\xi ) &{} \text {(tension)}. \end{array}\right. } \end{aligned}$$

(20)

4.2 Vibrations of axially pre-loaded beams

If the axially loaded FrsF beam vibrates, the eigenvalue problem determined by differential equation (6f)$_{1}$ and boundary and continuity conditions (7), (8a, 8b and 8c) can be reduced to an eigenvalue problem governed by the homogeneous Fredholm integral equation

$$\begin{aligned} w(x)=\lambda \int _{\xi =0}^{\ell =1} \mathcal {G}(x,\xi )\,w(\xi )\,\mathrm {d} \xi ,\qquad \mathcal {G}(x,\xi )= {\left\{ \begin{array}{ll} \mathcal {G}_{c} (x,\xi ) &{} \text {(compression)},\\ \mathcal {G}_{t} (x,\xi ) &{} \text {(tension)} \end{array}\right. } \end{aligned}$$

(21)

for which $\lambda$ is given by (6f)$_{2}$. The Green functions $\mathcal {G}_{c} (x,\xi )$ and $\mathcal {G}_{t} (x,\xi )$ are needed for solving numerically the eigenvalue problem defined by the homogeneous Fredholm integral equation (21).

4.3 The Green function for compressive load

It can be checked easily that the linearly independent particular solutions of the homogeneous differential equation

$$\begin{aligned}&\sum _{i=0}^{4}p_{i}(x) w^{(i)}= w^{(4)}\!+\mathcal {N}w^{(2)}=0, \quad w^{(j)}=\frac{\mathrm {d}^{j}w}{\mathrm {d}x^{j}},\;\;(j=1,\ldots ,4); \quad w^{(0)}=w\nonumber \\&\quad p_{4}=1,\;\, p_{2}=\mathcal {N}, \;\,p_{3}=p_{1}=p_{0}=0 \end{aligned}$$

(22)

are given by

$$\begin{aligned} w_{1}=1,\quad w_{2}=x,\quad w_{3}=\cos px,\quad w_{4}=\sin px,\quad p=\sqrt{\mathcal {N}}. \end{aligned}$$

(23)

In accordance with (13), the Green function $\mathcal {G}_{c}(x,\xi )$ has the following form

$$\begin{aligned} \mathcal {G}_{c}(x,\xi )=\left\{ \begin{array}{ll} \mathcal {G}_{1Ic}(x,\xi ) &{} \text {if}\;\;x,\xi \in [0,b],\\ \mathcal {G}_{2Ic}(x,\xi ) &{} \text {if}\;\;x\in [b,\ell ]\text { and }\xi \in [0,b],\\ \mathcal {G}_{1IIc}(x,\xi ) &{} \text {if}\;\;x\in [0,b]\text { and }\xi \in [b,\ell ],\\ \mathcal {G}_{2IIc}(x,\xi ) &{} \text {if}\;\;x,\xi \in [b,\ell ], \end{array} \right. \end{aligned}$$

(24)

where

$$\begin{aligned}&\mathcal {G}_{1Ic}(x,\xi )=\left\{ \begin{array}{ll} \sum _{k=1}^{4}\left( a_{kI}(\xi )+b_{kI}(\xi )\right) w_{k}(x) &{} \text {if}\;\;x\le \xi ,\\ \sum _{k=1}^{4}\left( a_{kI}(\xi )-b_{kI}(\xi )\right) w_{k}(x) &{} \text {if}\;\;x\ge \xi , \end{array} \right. \quad \xi ,x\in [0,b], \end{aligned}$$

(25a)

$$\begin{aligned}&\mathcal {G}_{2Ic}(x,\xi )x=\sum _{k=1}^{4}c_{kI}(\xi )w_{k}(x),\quad \xi \in [0,b],\;\;x\in [b,\ell ], \end{aligned}$$

(25b)

$$\begin{aligned}&\mathcal {G}_{1IIc}(x,\xi )x=\sum _{\ell =1}^{4}c_{kII}(\xi )w_{k}(x),\quad \xi \in [b,\ell ],\;\;x\in [0,b], \end{aligned}$$

(25c)

$$\begin{aligned}&\mathcal {G}_{2IIc}(x,\xi )=\left\{ \begin{array}{ll} \sum _{k=1}^{4}\left( a_{kII}(\xi )+b_{kII}(\xi )\right) w_{k}(x) &{} \text {if}\;\;x\le \xi ,\\ \sum _{k=1}^{4}\left( a_{kII}(\xi )-b_{kII}(\xi )\right) w_{k}(x) &{} \text {if}\;\;x\ge \xi , \end{array} \right. \quad \xi ,x\in [b,\ell ], \end{aligned}$$

(25d)

The coefficients $a_{kI}(\xi )$, $b_{kI}(\xi )$, $c_{kI}(\xi )$ and $a_{kII} (\xi )$, $b_{kII}(\xi )$, $c_{kII}(\xi )$ are the unknown quantities in the above representation of the Green function.

Remark 5

As regards the definition of the Green function we refer to book [22]. We do not repeat it here. Instead, we present those properties of the Green function only which are sufficient for deriving the corresponding equation systems.

4.3.1 Equation systems for the unknowns $a_{kI}(\xi )$, $b_{kI}(\xi )$, $c_{kI} (\xi )$

Let $\xi$ be fixed in [0, b]. The function $G_{1Ic}(x,\xi )$ and its derivatives

$$\begin{aligned} G_{1Ic}^{(n)}(x,\xi )=\frac{\partial ^{n}G_{1Ic}(x,\xi )}{\partial x^{n} },\qquad n=1,2 \end{aligned}$$

(26)

should be continuous for $x=\xi$:

$$\mathop {\lim }\limits_{{\varepsilon \to 0}} \left[ {G_{{1I}}^{{(n)}} (\xi + \varepsilon ,\xi ) - G_{{1Ic}}^{{(n)}} (\xi - \varepsilon ,\xi )} \right] = \left[ {G_{{1Ic}}^{{(n)}} (\xi + 0,\xi ) - G_{{1Ic}}^{{(n)}} (\xi - 0,\xi )} \right] = 0\quad n = 0,1,2$$

(27a)

The derivative $G_{1Ic}^{(3)}(x,\xi )$ should, however, have a jump if $x=\xi$:

$$\begin{gathered} \mathop {\lim }\limits_{{\varepsilon \to 0}} \left[ {G_{{1Ic}}^{{(3)}} (\xi + \varepsilon ,\xi ) - G_{{1Ic}}^{{(3)}} (\xi - \varepsilon ,\xi )} \right] \hfill \\ = \left[ {G_{{1Ic}}^{{(3)}} (\xi + 0,\xi ) - G_{{1Ic}}^{{(3)}} (\xi - 0,\xi )} \right] = - \frac{1}{{2 }}. \hfill \\ \end{gathered}$$

(27b)

In contrast to this, $G_{2Ic}(x,\xi )$ and its derivatives

$$\begin{aligned} G_{2Ic}^{(n)}(x,\xi )=\frac{\partial ^{n}G_{2Ic}(x,\xi )}{\partial x^{n} },\qquad n=1,\ldots ,4 \end{aligned}$$

(28)

are all continuous functions for any x in $[b,\ell =1]$.

Remark 6

Assume that $\xi \in [b,\ell =1]$. Then the continuity and discontinuity conditions (27a and 27b) are also to be satisfied for any $x\in [b,\ell ]$ by $G_{2IIc}(x,\xi )$. As regards $G_{1IIc}(x,\xi )$ and its derivatives with respect to x they should also be continuous functions for any $x\in [0,b]$.

Continuity and discontinuity conditions (27a and 27b) yield an equation system for the functions $b_{\ell I}$:

$$\begin{aligned} \left[ \begin{array}{cccc} 1 &{} \xi &{} \cos p\xi &{} \sin p\xi \\ 0 &{} 1 &{} -p\sin p\xi &{} p\cos p\xi \\ 0 &{} 0 &{} -p^{2}\cos p\xi &{} -p^{2}\sin p\xi \\ 0 &{} 0 &{} p^{3}\sin p\xi &{} -p^{3}\cos p\xi \end{array} \right] \left[ \begin{array}{c} b_{1I}\\ b_{2I}\\ b_{3I}\\ b_{4I} \end{array} \right] =\left[ \begin{array}{c} 0\\ 0\\ 0\\ -\frac{1}{2} \end{array} \right] \end{aligned}$$

from where we get

$$\begin{aligned} \left[ \begin{array}{c} b_{1I}\\ b_{2I}\\ b_{3I}\\ b_{4I} \end{array} \right] =\frac{1}{2p^{3}}\left[ \begin{array}{c} p\xi \\ -p\\ -\sin p\xi \\ \cos p\xi \end{array} \right] . \end{aligned}$$

(29)

It is obvious that the functions $b_{1I},\ldots ,b_{4I}$ are independent of the boundary conditions.

Let us assume that $\alpha$ is an arbitrary but finite nonzero constant. The product $\mathcal {G}_{c}(x,\xi )\alpha$ as a function of the variable x ($x\ne \xi$, $\xi \in [0,\ell =1]$ ) should fulfill the homogeneous differential equation (22).

It follows from (25a) that this condition is fulfilled.

The product $\mathcal {G}_{c}(x,\xi )\alpha$ as a function of x should also satisfy the boundary conditions (7) and the continuity conditions (8a, 8b and 8c). Thus we get: (a) Boundary conditions if $x=0$:

$$\begin{aligned} a_{{1I}} w_{1} (0) + & a_{{2I}} w_{2} (0) + a_{{3I}} w_{3} (0) + a_{{4I}} w_{4} (0) \\ = & - b_{{1I}} w_{1} (0) - b_{{2I}} w_{2} (0) - b_{{3I}} w_{3} (0) - b_{{4I}} w_{4} (0), \\ \end{aligned}$$

(30a)

$$\begin{gathered} a_{{1I}} w_{1}^{{(1)}} (0) + a_{{2I}} w_{{2I}}^{{(1)}} (0) + a_{{3I}} w_{3}^{{(1)}} (0) + a_{{4I}} w_{4}^{{(1)}} (0) \hfill \\ = - b_{{1I}} w_{1}^{{(1)}} (0) - b_{{2I}} w_{2}^{{(1)}} (0) - b_{{3I}} w_{3}^{{(1)}} (0) - b_{{4I}} w_{4}^{{(1)}} (0). \hfill \\ \end{gathered}$$

(30b)

(b) Continuity conditions if $x=b$:

$$\begin{gathered} a_{{1I}} w_{1} (b) + a_{{2I}} w_{2} (b) + a_{{3I}} w_{3} (b) + a_{{4I}} w_{4} (b) \hfill \\ = b_{{1I}} w_{1} (b) + b_{{2I}} w_{2} (b) + b_{{3I}} w_{3} (b) + b_{{4I}} w_{4} (b), \hfill \\ \end{gathered}$$

(30c)

$$\begin{aligned}&c_{1I}w_{1}(b)+c_{2I}w_{2}(b)+c_{3I}w_{3}(b)+c_{4I}w_{4}(b)=0, \end{aligned}$$

(30d)

$$\begin{gathered} a_{{1I}} w_{1}^{{(1)}} (b) + a_{{2I}} w_{{2I}}^{{(1)}} (b) + a_{{3I}} w_{3}^{{(1)}} (b) + a_{{4I}} w_{4}^{{(1)}} (b) \hfill \\ - c_{{1I}} w_{1}^{{(1)}} (b) - c_{{2I}} w_{2}^{{(1)}} (b) - c_{{3I}} w_{3}^{{(1)}} (b) - c_{{4I}} w_{4}^{{(1)}} (b) \hfill \\ = b_{{1I}} w_{1}^{{(1)}} (b) + b_{{2I}} w_{2}^{{(1)}} (b) + b_{{3I}} w_{3}^{{(1)}} (b) + b_{{4I}} w_{4}^{{(1)}} (b), \hfill \\ \end{gathered}$$

(30e)

$$\begin{gathered} a_{{1I}} w_{1}^{{(2)}} (b) + a_{{2I}} w_{{2I}}^{{(2)}} (b) + a_{{3I}} w_{3}^{{(2)}} (b) + a_{{4I}} w_{4}^{{(2)}} (b) \hfill \\ - c_{{1I}} w_{1}^{{(2)}} (b) - c_{{2I}} w_{2}^{{(2)}} (b) - c_{{3I}} w_{3}^{{(2)}} (b) - c_{{4I}} w_{4}^{{(2)}} (b) \hfill \\ = b_{{1I}} w_{1}^{{(2)}} (b) + b_{{2I}} w_{2}^{{(2)}} (b) + b_{{3I}} w_{3}^{{(2)}} (b) + b_{{4I}} w_{4}^{{(2)}} (b). \hfill \\ \end{gathered}$$

(30f)

(c) Boundary conditions if $x=\ell$:

$$\begin{aligned}&c_{1I}w_{1}(\ell )+c_{2I}w_{2}(\ell )+c_{3I}w_{3}(\ell )+c_{4I}w_{4} (\ell )=0, \end{aligned}$$

(30g)

$$\begin{aligned}&c_{1I}w_{1}^{(1)}(\ell )+c_{2I}w_{2}^{(1)}(\ell )+c_{3I}w_{3}^{(1)}(\ell )+c_{4I}w_{4}^{(1)}(\ell )=0\,. \end{aligned}$$

(30h)

Substituting $w_{1},\ldots ,w_{4}$ from (23) and $b_{1I},\ldots ,b_{4I}$ from (29) into (30a–30h) yields the following linear equation system:

$$\begin{aligned}&\left[ \begin{array}{cccccccc} 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} p &{} 0 &{} 0 &{} 0 &{} 0\\ 1 &{} b &{} \cos pb &{} \sin pb &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} b &{} \cos pb &{} \sin pb\\ 0 &{} 1 &{} -p\sin pb &{} p\cos pb &{} 0 &{} -1 &{} p\sin pb &{} -p\cos pb\\ 0 &{} 0 &{} -\cos pb &{} -\sin pb &{} 0 &{} 0 &{} \cos pb &{} \sin pb\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} \ell &{} \cos p\ell &{} \sin p\ell \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} -p\sin p\ell &{} p\cos p\ell \end{array} \right] \left[ \begin{array}{c} a_{1I}\\ a_{2I}\\ a_{3I}\\ a_{4I}\\ c_{1I}\\ c_{2I}\\ c_{3I}\\ c_{4i} \end{array} \right] \nonumber \\&\quad =\frac{1}{2p^{3}}\left[ \begin{array}{c} -p\xi +\sin p\xi \\ p-p\cos p\xi \\ p\xi -pb-\sin p\xi \cos pb+\cos p\xi \sin pb\\ 0\\ -p+p\sin p\xi \sin pb+p\cos p\xi \cos pb\\ \sin p\xi \cos pb-\cos p\xi \sin pb\\ 0\\ 0 \end{array} \right] . \end{aligned}$$

(31)

4.3.2 Equation systems for the unknowns $a_{kII}(\xi )$, $b_{kII}(\xi )$, $c_{kII} (\xi )$

Utilizing Remark 6 and the fact that the parameters $b_{1I},\ldots ,b_{4I}$ are independent of the boundary conditions we may conclude that

$$\begin{aligned} b_{kII}(\xi )=b_{kI}(\xi ),\qquad (k=1,\ldots ,4). \end{aligned}$$

(32)

If we recall that $\mathcal {G}_{c}(x,\xi )$ should also fulfill boundary conditions (7) and continuity conditions (8a, 8b and 8c) for $x\in [0,\ell ]$ and $\xi \in [b,\ell ]$ we obtain: (a) Boundary conditions if $x=0$:

$$\begin{aligned}&c_{1II}w_{1}(0)+c_{2II}w_{2}(0)+c_{3II}w_{3}(0)+c_{4II}w_{4}(0)=0, \end{aligned}$$

(33a)

$$\begin{aligned}&c_{1II}w_{1}^{(1)}(0)+c_{2II}w_{2}^{(1)}(0)+c_{3II}w_{3}^{(1)}(0)+c_{4II} w_{4}^{(1)}(0)=0. \end{aligned}$$

(33b)

(b) Continuity conditions if $x=b$:

$$\begin{aligned}&c_{1II}w_{1}(b)+c_{2II}w_{2}(b)+c_{3II}w_{3}(b)+c_{4II}w_{4}(b)=0, \end{aligned}$$

(33c)

$$\begin{aligned} a_{{1II}} w_{1} (b) + & a_{{2II}} w_{2} (b) + a_{{3II}} w_{3} (b) + a_{{4II}} w_{4} (b) \\ = & - b_{{1II}} w_{1} (b) - b_{{2II}} w_{2} (b) - b_{{3II}} w_{3} (b) - b_{{4II}} w_{4} (b), \\ \end{aligned}$$

(33d)

$$\begin{aligned} a_{{1II}} w_{1}^{{(1)}} (b) + & a_{{2II}} w_{{2I}}^{{(1)}} (b) + a_{{3II}} w_{3}^{{(1)}} (b) + a_{{4II}} w_{4}^{{(1)}} (b) \\ - & c_{{1II}} w_{1}^{{(1)}} (b) - c_{{2II}} w_{2}^{{(1)}} (b) - c_{{3II}} w_{3}^{{(1)}} (b) - c_{{4II}} w_{4}^{{(1)}} (b) \\ = & - b_{{1II}} w_{1}^{{(1)}} (b) - b_{{2II}} w_{2}^{{(1)}} (b) - b_{{3II}} w_{3}^{{(1)}} (b) - b_{{4II}} w_{4}^{{(1)}} (b) \\ \end{aligned}$$

(33e)

$$\begin{aligned} a_{{1II}} w_{1}^{{(2)}} (b) + & a_{{2II}} w_{{2I}}^{{(2)}} (b) + a_{{3II}} w_{3}^{{(2)}} (b) + a_{{4II}} w_{4}^{{(2)}} (b) \\ - & c_{{1II}} w_{1}^{{(2)}} (b) - c_{{2II}} w_{2}^{{(2)}} (b) - c_{{3II}} w_{3}^{{(2)}} (b) - c_{{4II}} w_{4}^{{(2)}} (b)) \\ = & - b_{{1II}} w_{1}^{{(2)}} (b) - b_{{2II}} w_{2}^{{(2)}} (b) - b_{{3II}} w_{3}^{{(2)}} (b) - b_{{4II}} w_{4}^{{(2)}} (b) \\ \end{aligned}$$

(33f)

(c) Boundary conditions if $x=\ell$:

$$\begin{aligned} a_{{1II}} w_{1} (\ell ) + & a_{{2II}} w_{2} (\ell ) + a_{{3II}} w_{3} (\ell ) + a_{{4II}} w_{4} (\ell ) \\ - & b_{{1II}} w_{1} (\ell ) - b_{{2II}} w_{2} (\ell ) - b_{{3II}} w_{3} (\ell ) - b_{{4II}} w_{4} (\ell ) = 0 \\ \end{aligned}$$

(33g)

$$\begin{aligned} a_{{1II}} w_{1}^{{(1)}} (\ell ) + & a_{{2II}} w_{2}^{{(1)}} (\ell ) + a_{{3II}} w_{3}^{{(1)}} (\ell ) + a_{{4II}} w_{4}^{{(1)}} (\ell ) \\ - & b_{{1II}} w_{1}^{{(1)}} (\ell ) - b_{{2II}} w_{2}^{{(1)}} (\ell ) - b_{{3II}} w_{3}^{{(1)}} (\ell ) - b_{{4II}} w_{4}^{{(1)}} (\ell ) = 0. \\ \end{aligned}$$

(33h)

Substituting $w_{1},\ldots ,w_{4}$ from (23) and $b_{kII}=b_{kI}$ ($k=1,\ldots ,4$) from (29) into (33a–33h) results in the following linear equation system:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & p \\ 0 & 0 & 0 & 0 & 1 & b & {\cos pb} & {\sin pb} \\ 1 & b & {\cos pb} & {\sin pb} & 0 & 0 & 0 & 0 \\ 0 & 1 & { - p\sin pb} & {p\cos pb} & 0 & { - 1} & {p\sin pb} & { - p\cos pb} \\ 0 & 0 & { - \cos pb} & { - \sin pb} & 0 & 0 & {\cos pb} & {\sin pb} \\ 1 & \ell & {\cos p\ell } & {\sin p\ell } & 0 & 0 & 0 & 0 \\ 0 & 1 & { - p\sin p\ell } & {p\cos p\ell } & 0 & 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {a_{{1II}} } \\ {a_{{2II}} } \\ {a_{{3II}} } \\ {a_{{4I}} } \\ {c_{{1II}} } \\ {c_{{2II}} } \\ {c_{{3II}} } \\ {c_{{4II}} } \\ \end{array} } \right] \hfill \\ = \frac{1}{{2p^{3} }}\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ { - p\xi + pb + \sin p\left( {\xi - b} \right)} \\ {p - p\cos p\left( {\xi - b} \right)} \\ { - \sin p\left( {\xi - b} \right)} \\ {p\xi - p\ell - \sin p\left( {\xi - \ell } \right)} \\ { - p + p\cos p\left( {\xi - \ell } \right)} \\ \end{array} } \right] \hfill \\ \end{gathered}$$

(34)

Remark 7

Equation systems (31) and (34) can be solved in an analytical (closed) form. The formulae resulted are, however, very long. In addition to this, the numerical algorithm we shall use requires the value of the Green function at discrete point pairs of x and $\xi$. For this reason, we shall not present the analytical solutions in this paper.

Fig. 5

The Green function for a compressive axial force

For demonstrational purposes assume that $b=0.5$ and $\xi =0.75.$ Assume further that the load is compressive. Figure 5 depicts the Green function for $p=0.4p_{crit}$ and $p=0.8p_{crit}$. Note that the Green function is the dimensionless vertical displacement due to a dimensionless vertical unit force applied to the beam at $\xi =0.75$. Hence the bending moment that belongs to the compressive force $\mathcal {N}$ has the same sign as the bending moment caused by the dimensionless unit force. Its magnitude obviously increases with $\mathcal {N}$. The same is valid for the magnitude of the Green function. Figure 5 clearly shows that the bending moment increases with p. This phenomenon is basically the same as that reported for pinned–pinned beams with intermediate roller support (PrsP beams) in paper [11].

Remark 8

Since the corresponding three-point eigenvalue problem is self-adjoint, it follows that the Green function should be symmetric in the independent variables $x,\xi$. Our computational results prove the fulfillment of the symmetry condition $\mathcal {G}_{c}(x,\xi )=\mathcal {G}_{c}(\xi ,x)$.

4.4 The Green function for tensile load

It can be checked easily that the linearly independent particular solutions of the homogeneous differential equation

$$\begin{aligned} \begin{aligned} \sum _{i=0}^{4}p_{i}(x) w^{(i)}= w^{(4)}\!-\mathcal {N}w^{(2)}=0, \quad w^{(j)}=\frac{\mathrm {d}^{j}w}{\mathrm {d}x^{j}},\;\;(j=1,\ldots ,4); \quad w^{(0)}=w\\ p_{4}=1,\;\, p_{2}=\mathcal {N}, \;\,p_{3}=p_{1}=p_{0}=0 \end{aligned} \end{aligned}$$

(35)

are given by

$$\begin{aligned} w_{1}=1,\quad w_{2}=x,\quad w_{3}=\cosh px,\quad w_{4}=\sinh px,\quad p=\sqrt{\mathcal {N}}. \end{aligned}$$

(36)

In accordance with (13) and (24), the Green function $\mathcal {G}_{t}(x,\xi )$ has the following form

$$\begin{aligned} \mathcal {G}_{t}(x,\xi )=\left\{ \begin{array}{ll} \mathcal {G}_{1It}(x,\xi ) &{} \text {if}\;\;x,\xi \in [0,b],\\ \mathcal {G}_{2It}(x,\xi ) &{} \text {if}\;\;x\in [b,\ell ]\text { and }\xi \in [0,b],\\ \mathcal {G}_{1IIt}(x,\xi ) &{} \text {if}\;\;x\in [0,b]\text { and }\xi \in [b,\ell ],\\ \mathcal {G}_{2IIt}(x,\xi ) &{} \text {if}\;\;x,\xi \in [b,\ell ], \end{array} \right. \end{aligned}$$

(37)

where

$$\begin{aligned}&\mathcal {G}_{1It}(x,\xi )=\left\{ \begin{array}{ll} \sum _{k=1}^{4}\left( a_{kI}(\xi )+b_{kI}(\xi )\right) w_{k}(x) &{} \text {if}\;\;x\le \xi ,\\ \sum _{k=1}^{4}\left( a_{kI}(\xi )-b_{kI}(\xi )\right) w_{k}(x) &{} \text {if}\;\;x\ge \xi , \end{array} \right. \quad \xi ,x\in [0,b], \end{aligned}$$

(38a)

$$\begin{aligned}&\mathcal {G}_{2It}(x,\xi )x=\sum _{k=1}^{4}c_{kI}(\xi )w_{k}(x),\quad \xi \in [0,b],\;\;x\in [b,\ell ], \end{aligned}$$

(38b)

$$\begin{aligned}&\mathcal {G}_{1IIt}(x,\xi )x=\sum _{\ell =1}^{4}c_{kII}(\xi )w_{k}(x),\quad \xi \in [b,\ell ],\;\;x\in [0,b], \end{aligned}$$

(38c)

$$\begin{aligned}&\mathcal {G}_{2IIt}(x,\xi )=\left\{ \begin{array}{ll} \sum _{k=1}^{4}\left( a_{kII}(\xi )+b_{kII}(\xi )\right) w_{k}(x) &{} \text {if}\;\;x\le \xi ,\\ \sum _{k=1}^{4}\left( a_{kII}(\xi )-b_{kII}(\xi )\right) w_{k}(x) &{} \text {if}\;\;x\ge \xi , \end{array} \right. \quad \xi ,x\in [b,\ell ], \end{aligned}$$

(38d)

The coefficients $a_{kI}(\xi )$, $b_{kI}(\xi )$, $c_{kI}(\xi )$ and $a_{kII} (\xi )$, $b_{kII}(\xi )$, $c_{kII}(\xi )$ are again the unknown quantities in the above representation of the Green function. Here we have applied the same notations as earlier since this fact might not cause misunderstanding.

4.4.1 Equations for $a_{kI}(\xi )$, $b_{kI}(\xi )$, $c_{kI} (\xi )$

The continuity and discontinuity conditions detailed in Subsection 4.3.1—see equations (27a and 27b) and (28) for details—are valid for $\mathcal {G}_{t}$ as well. Making use of these continuity and discontinuity conditions and utilizing solutions (36), we get

$$\begin{aligned} \left[ \begin{array}{cccc} 1 &{} \xi &{} \cosh p\xi &{} \sinh p\xi \\ 0 &{} 1 &{} p\sinh p\xi &{} p\cosh p\xi \\ 0 &{} 0 &{} p^{2}\cosh p\xi &{} p^{2}\sinh p\xi \\ 0 &{} 0 &{} p^{3}\sinh p\xi &{} p^{3}\cosh p\xi \end{array} \right] \left[ \begin{array}{c} b_{1}\\ b_{2}\\ b_{3}\\ b_{4} \end{array} \right] =\left[ \begin{array}{c} 0\\ 0\\ 0\\ -\frac{1}{2} \end{array} \right] \end{aligned}$$

from where

$$\begin{aligned} \left[ \begin{array}{c} b_{1I}\\ b_{2I}\\ b_{3I}\\ b_{4I} \end{array} \right] =\frac{1}{2p^{3}}\left[ \begin{array}{c} -p\xi \\ p\\ \sinh p\xi \\ -\cosh p\xi \end{array} \right] . \end{aligned}$$

(39)

By repeating the line of thought leading to (31)—the details are omitted—the following equation system is obtained for $a_{kI}(\xi )$ and $c_{kI} (\xi )$:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & p & 0 & 0 & 0 & 0 \\ 1 & b & {\cosh pb} & {\sinh pb} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & b & {\cosh pb} & {pb} \\ 0 & 1 & {p\sinh pb} & {p\cosh pb} & 0 & { - 1} & { - p\sinh pb} & { - p\cosh pb} \\ 0 & 0 & {\cosh pb} & {a\sinh pb} & 0 & 0 & { - \cosh pb} & { - \sinh pb} \\ 0 & 0 & 0 & 0 & 1 & \ell & {\cosh p\ell } & {\sinh p\ell } \\ 0 & 0 & 0 & 0 & 0 & 1 & {p\sinh p\ell } & {p\cosh p\ell } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {a_{{1I}} } \\ {a_{{2I}} } \\ {a_{{3I}} } \\ {a_{{4I}} } \\ {c_{{1I}} } \\ {c_{{2I}} } \\ {c_{{3I}} } \\ {c_{{4I}} } \\ \end{array} } \right] \hfill \\ = \frac{1}{{2p^{3} }}\left[ {\begin{array}{*{20}c} {p\xi - \sinh p\xi } \\ { - p + p\cosh p\xi } \\ { - p\xi + pb + \sinh p\left( {\xi - b} \right)} \\ 0 \\ {p - p\cosh p\left( {\xi - b} \right)} \\ {\sinh p\left( {\xi - b} \right)} \\ 0 \\ 0 \\ \end{array} } \right]. \hfill \\ \end{gathered}$$

(40)

4.4.2 Equations for $a_{kII}(\xi )$, $b_{kII}(\xi )$, $c_{kII} (\xi )$

The coefficients $b_{kI}(\xi )$ in (38a) are the same as those in (38d), i.e., $b_{kII}(\xi )=b_{kI}(\xi )$, $(k=1,\ldots ,4)$. The reasoning for this statement is the same as that of equation (32). As regards the coefficients $a_{kII}(\xi )$ and $c_{kII}(\xi )$ repeating the steps that led to equation (34)—the details are again omitted—we arrive at the following equation system:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & p \\ 0 & 0 & 0 & 0 & 1 & b & {\cosh pb} & {\sinh pb} \\ 1 & b & {\cosh pb} & {\sinh pb} & 0 & 0 & 0 & 0 \\ 0 & 1 & {p\sinh pb} & {p\cosh pb} & 0 & { - 1} & { - p\sinh pb} & { - p\cosh pb} \\ 0 & 0 & {\cosh pb} & {\sinh pb} & 0 & 0 & { - \cosh pb} & { - \sinh pb} \\ 1 & \ell & {\cosh p\ell } & {\sinh p\ell } & 0 & 0 & 0 & 0 \\ 0 & 1 & {p\sinh p\ell } & {p\cosh p\ell } & 0 & 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {a_{{1II}} } \\ {a_{{2II}} } \\ {a_{{3II}} } \\ {a_{{4II}} } \\ {c_{{1II}} } \\ {c_{{2II}} } \\ {c_{{3II}} } \\ {c_{{4II}} } \\ \end{array} } \right] \hfill \\ = \frac{1}{{2p^{3} }}\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ {p\xi - pb - \sinh p(\xi - b)} \\ { - p + p\cosh p(\xi - b)} \\ { - \sinh p\left( {\xi - b} \right)} \\ { - p\xi + p\ell + \sinh p(\xi - \ell )} \\ {p - p\cosh p(\xi - \ell )} \\ \end{array} } \right]. \hfill \\ \end{gathered}$$

(41)

Remark 9

Equation systems (40 and 41) can also be solved in an analytical (closed) form. In the same manner as equations (31) and (34). The formulae resulted this way are, however, very long. Since the numerical algorithm we shall use requires the value of the Green function at the discrete point pairs of x and $\xi$ the analytical solutions are not presented in this paper.

Fig. 6

The Green function for a tensile axial force

Assume again that $b=0.5$ and $\xi =0.75$ but the axial load is tensile. Figure 6 shows the Green function for $p=0.4p_{crit}$ and $p=0.8p_{crit}$. This time there is, however, a sign difference between the bending moments caused by the dimensionless vertical unit force and the tensile force. Hence the magnitude of the Green function decreases as the axial force, i.e., p increases. Figure 6 clearly represents this phenomenon which is basically the same as that reported for PrsP beams in paper [11].

5 Computational results for vibrating axially loaded beams

5.1 Integral equation of the problem

It is worthy to mention the inertia forces caused by the longitudinal motion are neglected in our model. We have applied the Euler–Bernoulli beam theory, therefore, the moments of the inertia forces obtained from the rotation of cross section are also regarded as negligible quantities. These assumptions are the same as those applied in paper [11]. Under these assumptions the dimensionless amplitude w of the vibration problem of axially loaded FrsF beams is governed by the homogeneous Fredholm integral equation (21) for which the kernels $\mathcal {G}_{c}(x,\xi )$ (compression) and $\mathcal {G}_{t}(x,\xi )$ (tension) are presented in Subsections 4.3 and 4.4. It is obvious that the eigenvalue problem determined by integral equation (21) is equivalent to the eigenvalue problem determined by differential equation (6f)$_{1}$ and boundary and continuity conditions (7), (8a, 8b and 8c).

Making use of the boundary element algorithm presented in [22]—see Subsection 7.2—the eigenvalue problem (21) can be reduced to an algebraic eigenvalue problem which can be solved numerically. A Fortran 90 code has been developed and applied to find numerical solutions for the eigenvalue $\lambda$. The interval $[0,\ell =1]$ was divided into 12 elements and a quadratic isoparametric approximation was used over the elements in the code we developed. In order to make a difference the lowest dimensionless eigenvalue and circular frequency for the unloaded FrsF beams will be denoted by $\check{\lambda }_{1}$ and $\check{\omega }_{1}$ in the present Section. See Table 1 and equations (16), (6b)$_{2}$ for details.

5.2 Numerical results if b tends to zero

Table 3 and Fig. 7 represent the computational results if $b\longrightarrow 0$. The quotient $\sqrt{\mathcal {N}_{\text {crit}}}/\pi$ is computed using equation (19). The value of $\check{\lambda }_{1}$ is given by equation (16) or can be taken from Table 1. This is also valid for Tables 4, 5, 6, 7 and 8 which have the same structure as Table 3. The numerical results for the quotient $\omega _{1}^{2}/\check{\omega }_{1}^{2}=\lambda _{1}/\check{\lambda }_{1}$ are presented for $\mathcal {N}/\mathcal {N}_{\mathrm {crit} }=0.00,0.10,\ldots ,0.90$—see columns 2, 3 and 5 in Tables 3, 4, 5, 6, 7 and 8.

The numerical results for $\omega _{1}^{2}/\check{\omega }_{1}^{2}=\lambda _{1}/\check{\lambda }_{1}$ are denoted by diamonds in Figs. 7, 8, 9, 10, 11 and 12. The difference between two subsequent values of $\omega _{1}^{2}/\check{\omega }_{1}^{2}$ is also included in Tables 3, 4, 5, 6, 7 and 8—see columns 4 and 6. If the function $\omega _{1}^{2}/\check{\omega }_{1} ^{2}(\mathcal {N}/\mathcal {N}_{\mathrm {crit}})$ is [nonlinear](linear) the difference [varies](is constant).

It should be mentioned that the values of $\omega _{1}^{2}/\check{\omega } _{1}^{2}=\lambda _{1}/\check{\lambda }_{1}$ were computed for $\mathcal {N} /\mathcal {N}_{\mathrm {crit}}= 0.000001,0.05,0.1,0,15,\ldots ,0.95$. The quadratic polynomials (42),...,(47) are fitted onto these computational results. Their graphs are drawn using continuous lines in Figs. 7, 8, 9, 10, 11 and 12. As it is said above, Tables 3, 4, 5, 6, 7 and 8 contain the values of $\omega _{1}^{2}/\check{\omega }_{1}^{2}=\lambda _{1}/\check{\lambda }_{1}$ for $\mathcal {N}/\mathcal {N}_{\mathrm {crit}}=0.00,0.10,\ldots ,0.90$ only.

The beam behaves as if it were a fixed–fixed beam if $b\longrightarrow 0$. Hence the results obtained should be the same as those valid for fixed–fixed beams. A comparison of the present results to those published in [23]—see Section 8.17.2—proves that there is a very good agreement.

Table 3 Results if $b\longrightarrow 0$

Fig. 7

The quotient $\omega _1^{2}/\check{\omega }{}_1^{2}$ against $\mathcal {N}/\mathcal {N}_{\mathrm {crit}}$ for $b\rightarrow 0$

The quadratic polynomials fitted onto the computational results both for compression and tension are given by the following equations:

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=0.9999-0.9656\,\frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}-3.4067\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}\right) ^{2}, \end{aligned}$$

(42a)

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=1.0002+0.9698\frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}-1.8552\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}\right) ^{2}. \end{aligned}$$

(42b)

5.3 Numerical results if $b=0.1$

Table 4 and Fig. 8 represent the results obtained.

Table 4 Results if $b=0.1$

Fig. 8

The quotient $\omega _1^{2}/\check{\omega }{}_1^{2}$ against $\mathcal {N}/\mathcal {N}_{\mathrm {crit}}$ for $b=0.1$

Two quadratic polynomials are fitted onto the computational results:

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=0.9997-0.969668\,\frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}-2.970310\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}\right) ^{2}, \end{aligned}$$

(43a)

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=1.0001+0.971\,319\frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}-1.618626\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}\right) ^{2}. \end{aligned}$$

(43b)

5.4 Numerical results if $b=0.2$

The computational results are shown in Table 5 and Fig. 9.

Table 5 Results if $b=0.2$

Fig. 9

The quotient $\omega _1^{2}/\check{\omega }{}_1^{2}$ against $\mathcal {N}/\mathcal {N}_{\mathrm {crit}}$ for $b=0.2$

The quadratic polynomials fitted onto the computational results are given by:

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=0.9998-0.975666\,\frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}-2.369757\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}\right) ^{2}, \end{aligned}$$

(44a)

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=1.00017+0.977\,018\,\frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}-1.308672\,\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N}_{\text {crit}}}\right) ^{2}. \end{aligned}$$

(44b)

5.5 Numerical results if $b=0.3$

The computational results are shown in Table 6 and Fig. 10.

Table 6 Results if $b=0.3$

Fig. 10

The quotient $\omega _1^{2}/\check{\omega }{}_1^{2}$ against $\mathcal {N}/\mathcal {N}_{\mathrm {crit}}$ for $b=0.3$

Two quadratic polynomials are fitted onto the computational results:

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=1.0003-0.9770253\,\frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}-2.3019979\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N}_{\text {crit}}}\right) ^{2}, \end{aligned}$$

(45a)

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=1.00062+0.978493\,\frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}-1.2758350\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N}_{\text {crit}}}\right) ^{2}. \end{aligned}$$

(45b)

5.6 Numerical results if $b=0.4$

The computational results are shown in Table 7 and Fig. 11.

Table 7 Results if $b=0.4$

Fig. 11

The quotient $\omega _1^{2}/\check{\omega }{}_1^{2}$ against $\mathcal {N}/\mathcal {N}_{\mathrm {crit}}$ for $b=0.4$

The quadratic polynomials fitted onto the computational results are presented below:

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=1.\,0015-0.9615166\,\frac{\mathcal {N} }{\mathcal {N}_{\text {crit}}}-3.876\,9054\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N}_{\text {crit}}}\right) ^{2}, \end{aligned}$$

(46a)

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=1.0021+0.9653536\,\frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}-1.7576144\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N}_{\text {crit}}}\right) ^{2}. \end{aligned}$$

(46b)

5.7 Numerical results if $b=0.5$

The computational results are shown in Table 8 and Fig. 12.

Table 8 Results if $b=0.5$

Fig. 12

The quotient $\omega _1^{2}/\check{\omega }{}_1^{2}$ against $\mathcal {N}/\mathcal {N}_{\mathrm {crit}}$ for $b=0.5$

The quadratic polynomials fitted onto the computational results are given below:

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=1.0007-0.9754370\,\frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}-2.4501686\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N}_{\text {crit}}}\right) ^{2}, \end{aligned}$$

(47a)

$$\begin{aligned}&\frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=1.00101+0.9770195\frac{\mathcal {N}}{\mathcal {N} _{\text {crit}}}-1.2982543\times 10^{-2}\left( \frac{\mathcal {N}}{\mathcal {N}_{\text {crit}}}\right) ^{2}. \end{aligned}$$

(47b)

5.8 Example

Consider an FrsF beam with cross section shown in Fig. 13. It is assumed that $a=100\,\mathrm {mm}$, $a_1=a_2=a/3$, $E_{1}=E_{aluminum} =0.71\times 10^{5}\,\mathrm {N/mm}^{2}$ while $E_{2}=E_{steel}=2.0\times 10^{5}\,\mathrm {N/mm}^{2}$. The length L of the beam is $4000\,\mathrm {mm}$, the location of the middle support is given by the parameter $b=0.3$. The surface densities have the following values: $\rho _{1}=\rho _{\text {aluminum} }=2.71\times 10^{-6}\;\mathrm {kg/}\mathrm {mm}^{3}$, $\rho _{2}=\rho _{\text {steel} }=7.850\times 10^{-6}\;\;\mathrm {kg/}\mathrm {mm}^{3}$.

Fig. 13

The cross section of an FrsF beam

Under these conditions

$$\begin{aligned} I_{{ey}} = & \frac{{a^{4} }}{{12}}\left( {\frac{{2E_{1} + E_{2} }}{3}} \right) = \frac{{100^{4} }}{{12}}\left( {\frac{{2 \times 0.71 + 2.0}}{3}} \right)10^{5} \\ = & 9.5 \times 10^{{11}} {\text{Nmm}}^{2} = 9.5 \times 10^{{14}} {\text{kgmm}}^{3} /s^{2} \\ \end{aligned}$$

(48)

and

$$\begin{aligned} \rho _{a} = \frac{1}{A}\int_{A} \rho {\mkern 1mu} {\text{d}}A = & \frac{{\left( {2\rho _{1} + \rho _{2} } \right)A_{1} }}{A} = \frac{{\left( {2 \times 2710 + 7850} \right) \times 100 \times \frac{{100}}{3}}}{{10^{9} \times 100^{2} }} \\ = & 4.423333 \times 10^{{ - 6}} \;{\text{kg/mm}}^{3} {\mkern 1mu} \\ \end{aligned}$$

(49)

According to Table 2, the dimensionless critical load for $b=0.3$ is given by the equation $\sqrt{\mathcal {N}_{crit}}/\pi =2.55756$ from where we get

$$\begin{aligned} \mathcal {N}_{crit}=64.558. \end{aligned}$$

(50)

With $\mathcal {N}_{crit}$ equation (5)$_{2}$ yields

$$\begin{aligned} N_{crit}=\frac{I_{ey}\mathcal {N}_{crit}}{L^{2}}=\frac{9.5\times 10^{11} \times 64.558}{4000^{2}}=3.8331\times 10^{6}\text { N}. \end{aligned}$$

(51)

As regards the first eigenvalue $\check{\lambda }_{1}$ of the axially unloaded beam, it follows from Table 1 that

$$\begin{aligned} \sqrt{\check{\lambda }_{1}|_{b=0.3}}=1.7749\times 4.73004^{2}=39.71033. \end{aligned}$$

(52)

With $\sqrt{\check{\lambda }_{1}|_{b=0.3}}$ equation (6b)$_{2}$ yields

$$\begin{aligned} \check{\omega }_{1}=\frac{\sqrt{\lambda _{1}|_{b=0.3}}}{L^{2}}\sqrt{\frac{I_{ey}}{\rho _{a}A}} \end{aligned}$$

from where substituting (48), (49) and (52) we obtain

$$\begin{aligned} \check{\omega }_{1}=\frac{39.710\,33}{4000^{2}}\times \sqrt{\frac{9.5\times 10^{14}}{4.423333\times 10^{-6}\times 100^{2}}}=363.723\frac{\text {rad}}{s }. \end{aligned}$$

(53)

If the axial load is compression and it is the half of the critical load then using equation (45a) for the first circular frequency of the axially loaded beam we get

$$\begin{aligned} \omega _{1} = & \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } _{1} \sqrt {1.0003 - 0.9770253{\mkern 1mu} \frac{{\mathcal{N}}}{{{\mathcal{N}}_{{{\text{crit}}}} }} - 2.3019979 \times 10^{{ - 2}} \left( {\frac{{\mathcal{N}}}{{{\mathcal{N}}_{{{\text{crit}}}} }}} \right)^{2} } \\ = & 363.723 \times \sqrt {1.0003 - 0.9770253 \times {\mkern 1mu} 0.5 - 2.3019979 \times 10^{{ - 2}} \times 0.25} \\ = & 258.737\frac{{{\text{rad}}}}{{\sec }} \\ \end{aligned}$$

(54)

The above results are validated by the commercial finite element program Ansys. 480 uniform hexahedral elements (SOLID185) were used to generate the geometry mesh. Table 9 shows a comparison.

Table 9 Comparison of the results

When calculating the relative error our solution was the denominator.

Note that there is a very good agreement between our and the finite element solutions.

6 Concluding remarks

The main objective of the present paper is to clarify what effect the axial load (compressive or tensile) has on the eigenfrequencies of FrsF beams with cross-sectional heterogeneity. From mathematical point of view, this mechanical problem is equivalent to a three-point boundary value problem (eigenvalue problem) associated with homogeneous boundary conditions.

The solution to this problem assumes that the first eigenfrequencies and critical loads concerning the axially unloaded FrsF beam are all known. In order to find these eigenfrequencies, we determined the Green function for the corresponding eigenvalue problem and then we reduced this eigenvalue problem to an eigenvalue problem governed by a homogeneous Fredholm integral equation—see equation (10). The computational results for this problem are presented in Sect. 5. Note that polynomial approximations have also been included.

As regards the first critical load we have utilized the results presented in paper [12].

As regards our main objective the eigenvalue problem that provides the eigenfrequencies for the axially loaded FrsF beam is transformed into an eigenvalue problem governed by a homogeneous Fredholm integral equation with the Green function as its kernel. The elements of the corresponding Green functions are provided by equation systems (31), (40), (34) and (41). This eigenvalue problem is reduced to an algebraic eigenvalue problem in the same way as the eigenvalue problem of the free vibrations. We solved it numerically by using an effective solution algorithm based on the boundary element method. We have derived polynomial approximations for the sought function $\omega _{1}^{2}/\check{\omega }_{1} ^{2}(\mathcal {N}/\mathcal {N}_{\mathrm {crit}}).$

It is a well known fact that for an axially loaded simply supported beam the following equation holds

$$\begin{aligned} \frac{\omega _{1}^{2}}{\check{\omega }_{1}^{2}}=\frac{\lambda _{1}}{\check{\lambda }_{1}}=1.0000\pm \frac{\mathcal {N}}{\mathcal {N}_{\text {crit}}}, \end{aligned}$$

(55)

where the sign is (negative)[positive] for (compression)[tension]. A comparison of this equation to (42a), (43a), (44a), (45a), (46a) and (47a) shows that the linearity is lost, however, a relatively acceptable first approximation can be obtained for $\omega _{1}$ if we use (55) in the case of a compressive axial force.

It is worthy of mentioning that the solution procedure presented in this paper can also be applied to other support arrangements including for example fixed–pinned beams with an intermediate roller support—this work is in progress—or for those cases when the intermediate support is a spring.