Estimates for low Steklov eigenvalues of surfaces with several boundary components

R\'esum\'e

In this article, we give computable lower bounds for the first non-zero Steklov eigenvalue $\sigma _1$ of a compact connected 2-dimensional Riemannian manifold M with several cylindrical boundary components. These estimates show how the geometry of M away from the boundary affects this eigenvalue. They involve geometric quantities specific to manifolds with boundary such as the extrinsic diameter of the boundary. In a second part, we give lower and upper estimates for the low Steklov eigenvalues of a hyperbolic surface with a geodesic boundary in terms of the length of some families of geodesics. This result is similar to a well known result of Schoen, Wolpert and Yau for Laplace eigenvalues on a closed hyperbolic surface.

Résumé

Dans cet article, nous donnons des bornes inférieures calculables pour la première valeur propre non nulle $\sigma _1$ de Steklov d’une variété riemannienne compacte et connexe M de dimension 2 avec un bord formé de plusieurs composantes connexes. Ces estimations montrent comment la géométrie de M loin du bord affecte cette valeur propre. Elles font intervenir des quantités géométriques spécifiques aux variétés à bord comme le diamètre extrinsèque du bord. Dans une deuxième partie, nous donnons des bornes inférieures et supérieures pour les valeurs propres basses d’une surface hyperbolique à bord géodésique, qui dépendent de la longueur de certaines familles de géodésiques. Ce résultat est similaire à un résultat bien connu de Schoen, Wolpert et Yau pour les valeurs propres du laplacien d’une surface hyperbolique fermée.

1 Introduction

We study lower bounds for low Steklov eigenvalues of a compact connected 2-dimensional Riemannian manifold with several boundary components. Few lower bounds are known for the first non-zero Steklov eigenvalue $\sigma _1$. For a Riemannian manifold with connected boundary, there are generalizations (see e.g. [12, 13, 21]) of a result of Payne [18] of 1970 saying that $\sigma _1$ of a convex domain in the plane is bounded from below by the minimum curvature of its boundary. In a general setting, Escobar [12] has given a lower bound depending on an isoperimetric constant and the first non-zero eigenvalue of a Robin problem (see also [15] for lower bounds depending on eigenvalues of auxiliary problems). In [16], Jammes gives lower bounds in terms of isoperimetric constants. This result has been generalized by Hassannezhad and Miclo [15] for higher eigenvalues. These lower bounds however are not easily computable. In [9], Colbois, Girouard and Hassannezhad show that under some assumptions on the geometry of the boundary and near the boundary, Steklov eigenvalues are well approximated by the Laplace eigenvalues of the boundary. But when a connected Riemannian manifold has $b\ge 2$ boundary components, such estimates do not give lower bounds for the b first eigenvalues of the Steklov problem.

For obtaining lower bounds, conditions on the intrinsic geometry of the boundary as well as conditions on the geometry near the boundary are expected. But even if the boundary and the geometry of M near the boundary are fixed, $\sigma _1$ is not bounded below if the boundary has multiple connected components, as shows the case of a right cylinder whose first eigenvalue tends to zero as its height goes to infinity.

In this article, we give explicit estimates for the b first Steklov eigenvalues of some families of compact connected 2-dimensional Riemannian manifolds with $b\ge 2$ boundary components having each one a neighborhood which is a right or a hyperbolic cylinder. This strong assumption on the geometry near the boundary allows us to focus on how the geometry of the manifold away from the boundary affects these eigenvalues. The first result is an explicit lower bound for $\sigma _1$ of a 2-dimensional Riemannian manifold with a cylindrical boundary. It does not require any assumption on the Gaussian curvature and involves the following quantity.

Definition 1

Let (M, g) be a compact connected 2-dimensional Riemannian manifold with $b\ge 2$ boundary components. We consider the family of curves (not necessarily connected) not intersecting $\partial M$ and dividing M into two connected components, each containing at least one connected component of $\partial M$. We let C(M) denote this family of curves and define

$$\begin{aligned} {{\,\textrm{l}\,}}(M):=\inf \{l(c): c\in C(M)\} \end{aligned}$$

where l(c) is the length of the curve c.

We can now state the result.

Theorem 1

Let (M, g) be a compact connected 2-dimensional Riemannian manifold with a boundary having $b\ge 2$ components of length a. Assume that the boundary $\partial M=\Sigma _1\cup \dots \cup \Sigma _b$ has a neighborhood $V(\partial M)$ which is isometric to the union of disjoint right cylinders $\cup _{i=1}^{b}\Sigma _i\times [0,1)$. We have

$$\begin{aligned} \sigma _1(M)\ge \frac{\min \{{{\,\textrm{l}\,}}(M),1\}^2}{2(b-1)a|M|}. \end{aligned}$$

Examples 2 and 3 in Sect. 3 show that the exponent of the geometric quantities involved in the lower bound are optimal. Another natural question to ask for evaluating a lower bound is how close to $\sigma _1$ it is. We construct a family of surfaces which shows that the presence of the area of the manifold in the denominator makes the lower bound given in Theorem 1 sometimes inaccurate since it can go to zero while $\sigma _1$ is constant.

For surfaces whose Gaussian curvature is bounded below, we succeeded in removing the depency of the area from the lower bound. This estimate involves the extrinsic diameter of the boundary and the injectivity radius of a certain subset of M.

Definition 2

Let (M, g) be a compact connected Riemannian manifold with boundary $\partial M$.

• (1) The extrinsic diameter of the boundary is

  $$\begin{aligned} {{\,\textrm{diam}\,}}_M(\partial M)=\max \{d(x,y)| x, y\in \partial M\}, \end{aligned}$$

  where d(x, y) denotes the distance on M induced by g.

For simplification, we will omit the term "extrinsic" and call it the diameter of the boundary. Assume now that the boundary $\partial M=\Sigma _1\cup \dots \cup \Sigma _b$ has a neighborhood $V(\partial M)$ which is isometric to the union of disjoint right cylinders $\cup _{i=1}^{b}\Sigma _i\times [0,1)$.

• (2) Let $\Gamma$ be the subset of M

  $$\begin{aligned} \Gamma= & {} \{x\in M, \exists p,q \in \partial M \text { and a length minimising geodesic }\gamma \\{} & {} \text { between p and q such that } x\in \gamma \}. \end{aligned}$$

  We denote ${{\,\textrm{inj}\,}}_{\partial M}(M)$ the injectivity radius of $\Gamma {\setminus } V(\partial M)\subset M$, that is

  $$\begin{aligned} {{\,\textrm{inj}\,}}_{\partial M}(M)={{\,\textrm{inj}\,}}(\Gamma \setminus V(\partial M))=\min \{{{\,\textrm{inj}\,}}_M(x): x\in \Gamma \setminus V(\partial M)\}. \end{aligned}$$

  We note that ${{\,\textrm{inj}\,}}_{\partial M}(M)\le 1$.

Theorem 2

Let (M, g) be a compact connected 2-dimensional Riemannian manifold with a boundary having $b\ge 2$ boundary components of length a. Assume that the boundary $\partial M=\Sigma _1\cup \dots \cup \Sigma _b$ has a neighborhood $V(\partial M)$ which is isometric to the union of disjoint right cylinders $\cup _{i=1}^{b}\Sigma _i\times [0,1)$. Assume that the Gaussian curvature of M satisfies $K(p)\ge \kappa$ for all $p\in M$, where $\kappa$ is a negative constant, and assume that $a\le {{\,\textrm{diam}\,}}_M(\partial M)$. Then we have an explicit positive constant $C(\kappa ,b)$ such that

$$\begin{aligned} \sigma _1(M)\ge C(\kappa ,b)\frac{{{\,\textrm{inj}\,}}_{\partial M}(M)}{a{{\,\textrm{diam}\,}}_{M}(\partial M)}. \end{aligned}$$

As for Theorem 1, we show that the exponent of the geometric quantities involved in Theorem 2 cannot be improved (see Remark 6). With the stronger assumption that the injectivity radius is bounded from below at each point of M outside the cylindrical neighborhood of the boundary, Theorem 2 can also be obtained from the combination of the lower bound given in [19] for $\sigma _1$ of the Steklov problem on graphs and the discretization process described in [10].

We note that results for surfaces with cylindrical boundary are significant since they can be used for deducing results for any manifolds with boundary by using quasi-isometries as it has been done in [6] (see Theorem 1.1). Since surfaces that are conformal inside and isometric on the boundary are Steklov isospectral, the results also give lower bounds for surfaces that are conformal inside and isometric on the boundary to one with cylindrical boundary.

In a second part, we give an upper and lower estimate for the b first Steklov eigenvalues of compact hyperbolic surfaces with b geodesic boundary components. It shows that these eigenvalues are equivalent to the length of some separating curves of the manifold. The result is similar to a result of Schoen, Wolpert and Yau [20] for Laplace eigenvalues. However, the family of curves that are relevant is different.

Definition 3

Let M be a compact hyperbolic surface with $b\ge 2$ geodesic boundary components. For $1\le n\le b-1$, we consider the family of curves which consist of a union of disjoint simple closed geodesics, not intersecting $\partial M$, and dividing M into $n+1$ connected components, each containing at least one connected component of $\partial M$. We denote $C_n(M)$ the family of such curves. If $C_n(M)\not =\emptyset$, we define

$$\begin{aligned} {{\,\textrm{l}\,}}_n(M):=\min \{l(c): c\in C_n(M)\} \end{aligned}$$

where l(c) is the length of the curve c.

We have the following result.

Theorem 3

Let M be a hyperbolic surface of genus g with $b\ge 2$ geodesic boundary components, each of them having length $a\le 2{{\,\textrm{arcsinh}\,}}(1)$. Assume that $g\not =0$ or $b>3$. There exists a constant $C_1$ depending only on g and b and a universal constant $C_2$ such that for $1\le n<\lceil \frac{b}{2}\rceil$ we have

$$\begin{aligned} C_1{{\,\textrm{l}\,}}_n^2\le \sigma _n\le C_2 \frac{{{\,\textrm{l}\,}}_n}{a}. \end{aligned}$$

The inequality is also true for $\lceil \frac{b}{2}\rceil \le n <b$ if $C_n(M)\not =\emptyset$ and there exists $c\in C_n(M)$ such that each simple closed geodesic of c is of length $l\le L_{g+b}$, where $L_{g+b}=4(3(g+b)-3)\log (\frac{8\pi (g+b-1)}{3(g+b)-3})$.

If a becomes small, we see that the upper bound becomes big, but we are also able to show that for $0\le n<b$, $\sigma _n$ is bounded above by $\frac{1}{\arctan (\frac{1}{\sinh {\frac{a}{2}}})}\le \frac{2}{\pi }$.

Remark 1

It is possible to obtain results similar to Theorems  1, 2 and  3 without the assumption that all the boundary components have the same length. In this case, we have to replace a by the maximum length of the boundary components in Theorems 1 and 2. In Theorem 3, we have to replace a in the upper bound by the minimum length of the boundary components and make the assumption that the maximum length of the boundary components is $\le 2 {{\,\textrm{arcsinh}\,}}(1)$. The results are obtained by slightly modifying the proofs given in Sect. 3.

An important tool for obtaining our results is estimating isoperimetric constants in an improved statement of a lower bound given by Jammes for the first non-zero Steklov eigenvalue. The strategy of estimating isoperimetric constants has been used in the past for obtaining lower bounds for the first non-zero Laplace eigenvalue on closed surfaces (see e.g. [2] and [20]). We also use comparisons with mixed problems.

The article is structured as follows. In Sect. 2 we introduce mixed problems and Cheeger-type estimates for Steklov eigenvalues. The main results are proved in Sect. 3, which is divided in two parts. In the first part, we prove a generalization of Theorem 1 and then use it to prove Theorem 2. In the second part, we recall some useful properties of hyperbolic surfaces and prove Theorem 3.

2 Cheeger-type estimates and mixed problems

2.1 Steklov eigenvalues

Let (M, g) be a compact connected Riemannian manifold with Lipschitz boundary $\partial M$. The Steklov problem on M is the eigenvalue problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \triangle u=0\\ \frac{\partial u}{\partial \nu }=\sigma u \end{array}\right. } \end{aligned}$$

where $\sigma$ is the spectral parameter. The Stekov eigenvalues form a sequence $0=\sigma _0<\sigma _1\le \sigma _2\le \dots \nearrow$. They can be characterized variationally as follows:

$$\begin{aligned} \sigma _k(M)=\min _{E\in V_k}\max _{0\not =u\in E} R(u), \end{aligned}$$

where $V_k$ is the set of all $k+1$ dimensional subspaces of the Sobolev space $H^1(M)$, and R(u) is the Rayleigh quotient associated to the Steklov problem,

$$\begin{aligned} R(u)=\frac{\int _{M} |\nabla u|^2dv_g}{\int _{\partial M} u^2 dS_g}. \end{aligned}$$

There is a connection between Steklov eigenvalues of a Riemannian manifold (M, g) with boundary $\partial M$, and eigenvalues of mixed problems on a Lipschitz open subset $A\subset M$ containing $\partial M$. Given a Lipschitz open subset $A\subset M$ such that $\partial M\subset A$, we denote $\partial A$ the topological boundary of A as a subset of M. The mixed Steklov-Neumann problem on A is

$$\begin{aligned} {\left\{ \begin{array}{ll} \triangle u=0 &{}\text { in }A,\\ \frac{\partial u}{\partial \nu }=\sigma u &{}\text { on }A\cap \partial M,\\ \frac{\partial u}{\partial \nu }=0 &{}\text { on }\partial A, \end{array}\right. } \end{aligned}$$

and the mixed Steklov-Dirichlet problem on A is

$$\begin{aligned} {\left\{ \begin{array}{ll} \triangle u=0 &{}\text { in }A,\\ \frac{\partial u}{\partial \nu }=\sigma u &{}\text { on }A\cap \partial M,\\ u=0 &{}\text { on }\partial A.\\ \end{array}\right. } \end{aligned}$$

The eigenvalues of the mixed Steklov-Neumann problem form a discrete sequence $0=\sigma _0^N(A)\le \sigma _1^N(A)\le \sigma _2^N(A)\le \dots \nearrow$ and the eigenvalues of the mixed Steklov-Dirichlet problem form a discrete sequence $0<\sigma _0^D(A)\le \sigma _1^D(A)\le \sigma _2^D(A)\le \dots \nearrow$.

The eigenvalues satisfy

$$\begin{aligned} \sigma _k^N(A)\le \sigma _k(M)\le \sigma _k^D(A). \end{aligned}$$

(1)

The proof of this inequality follows from a comparison between the Rayleigh quotients of these problems, see [7] for more details.

2.2 Cheeger-type estimates

In 1969, J. Cheeger [5] gave a lower bound in term of an isoperimetric constant for the first non-zero Laplace eigenvalue of a compact Riemannian manifold. A similar estimate for the first non-zero Steklov eigenvalue was shown by P. Jammes in 2015 [16]. We give an improvement of this result that we use to obtain the explicit lower bounds presented in this article.

Definition 4

We define the following geometric constants:

• (1)
  $$\begin{aligned} h_1(M):=\inf _{|D|\le \frac{|M|}{2}}\frac{|\partial D|}{|D|}, \end{aligned}$$
• (2)
  $$\begin{aligned} h_2(M):=\inf _{|D|\le \frac{|M|}{2}}\frac{|\partial D|}{|D\cap \partial M|}, \end{aligned}$$

  where in both cases, D is taken among the domains of M satisfying $D\cap \partial M \not =\emptyset$, and such that $M\setminus D$ is also connected and intersects $\partial M$.

Remark 2

The set $\partial D$ is the topological boundary of the open subset D of the manifold with boundary M; this set does not contain $D\cap \partial M$.

Remark 3

Jammes defines two constants in a similar way but the domain D is only required to satisfy $|D|\le \frac{|M|}{2}$.

Proposition 1

Let (M, g) be a compact Riemannian manifold with boundary $\partial M$. We have

$$\begin{aligned} \sigma _1(M)\ge \frac{ h_1(M)\cdot h_2(M)}{4}. \end{aligned}$$

This is the result of Jammes but with slightly modified constants. It is obtained by modifying the conclusion of Jammes’s proof. Example 1 below shows that in dimension 2 this inequality is stronger than the one given by Jammes where D is only required to satisfy $|D|\le \frac{|M|}{2}$ in the isoperimetric constants. Another situation where the constants $h_1$ and $h_2$ will not go to zero while the constants of Jammes do is Example 4.5 of [8].

Fig. 1

A cylinder on which we have glued a surface of revolution

Example 1

Let C be a 2-dimensional right cylinder in $\mathbb {R}^3$ whose base contains a line segment. We consider the surfaces obtained by gluing a surface of revolution containing a thin collapsing cylinder on the middle of the flat part of C, as shown in Fig. 1. These surfaces are all Steklov isospectral to C (see [7], Appendix A, and [1] for more details). However, Jammes’s constants tend to zero as the thin passage collapses. In contrast, the constants $h_1$ and $h_2$ that we use remain bounded (see Lemma 2).

Proof of Proposition 1

Let u be an eigenfunction associated to the first non-zero Steklov eigenvalue on M. We define

$$\begin{aligned} D(t):=\{x\in M, u(x)>t\}. \end{aligned}$$

Without loss of generality, we can assume $|D(t)|\le \frac{|M|}{2}$ for all $t\ge 0$. From the proof of Jammes’s result, which is similar to the classical proof of Cheeger, we have

$$\begin{aligned} \sigma _1(M)\ge \frac{1}{4}\min _{t\ge 0}\frac{|\partial D(t)|}{|D(t)|}\cdot \min _{t\ge 0}\frac{|\partial D(t)|}{|D(t)\cap \partial M|}. \end{aligned}$$

Since u is harmonic and not constant, it follows from the maximum principle that each connected component of $M{\setminus } \{u^{-1}(t)\}$ intersects $\partial M$. Therefore, the inequalities $\min _{t\ge 0}\frac{|\partial D(t)|}{|D(t)|}\ge \inf _{|D|\le \frac{|M|}{2}}\frac{|\partial D|}{|D|}$ and $\min _{t\ge 0}\frac{|\partial D(t)|}{|D(t)\cap \partial M|}\ge \inf _{|D|\le \frac{|M|}{2}}\frac{|\partial D|}{|D\cap \partial M|}$ are true if the infima are taken among all sets D such that each connected component of D and of $M\setminus D$ intersects $\partial M$. Finally, as observed by S.-T. Yau in [22], we can assume that both D and $M\setminus D$ are connected. $\square$

Remark 4

It has been showed (see e.g. [3], Theorem 1.14) that the lower bound of Cheeger for the first non-zero Laplace eigenvalue is sharp. It would be interesting to know if the lower bound of Jammes is sharp too.

Remark 5

Given a domain A in M such that $A\cap \partial M\not =\emptyset$, we define the constants $h_1(A)$ and $h_2(A)$ in the same way as for M, by replacing M by A and $\partial M$ by $\partial M\cap A$ in the conditions that D has to satisfy. The same proof as for Proposition 1 shows that $\sigma _1^N(A)\ge \frac{ h_1(A)\cdot h_2(A)}{4}$.

In the construction described in Example 1, if we glue two surfaces of revolution of equal volume on C instead of one and let grow the volume of these surfaces of revolution, we see that $h_1$ tends to zero by choosing a domain that contains one of the two surfaces of revolution. This shows that in this case, the estimate of Proposition 2 is not equivalent to the first non-zero Steklov eigenvalue, which is constant since the surfaces obtained are isospectral to C.

The following proposition shows a way of improving Proposition 1.

Proposition 2

Let (M, g) be a compact Riemannian manifold with boundary $\partial M$. For any domain A in M such that $\partial M\subset A$, we have

$$\begin{aligned} \sigma _1(M)\ge \frac{ h_1(A)\cdot h_2(A)}{4}. \end{aligned}$$

Proof

The proof follows from the comparison (1) between Steklov and mixed Steklov-Neumann eigenvalues and Remark 5. $\square$

This estimate is interesting if we can find domains such that $h_1$ and $h_2$ are bounded below. Finally, having in mind Question 4.6 of [8], we remark that by taking the supremum over the domains A, a new constant is defined. It is more acurate than the product $h_1(M)\cdot h_2(M)$ but difficult to calculate.

3 Explicit estimates for Steklov eigenvalues

3.1 Lower bounds for $\sigma _1$ of surfaces with several cylindrical boundary components

We recall the following estimate for Steklov eigenvalues of surfaces with cylindrical boundary components, which follows directly from the comparison (1) with eigenvalues of mixed Steklov-Neumann and Steklov-Dirichlet problems on the union of the cylindrical boundary nieghborhoods, and the explicit calculation of these.

Lemma 1

Let (M, g) be a compact 2-dimensional Riemannian manifold with $b\ge 1$ boundary components having length a. Assume that the boundary $\partial M=\Sigma _1\cup \dots \cup \Sigma _b$ has a neighborhood $V(\partial M)$ which is isometric to the union of disjoint right cylinders $\cup _{i=1}^{b}\Sigma _i\times [0,L)$. The Steklov eigenvalues $\sigma _k$ of M satisfy

$$\begin{aligned} 0\le \sigma _k\le \frac{1}{L} \end{aligned}$$

if $k<b$, and

$$\begin{aligned} \frac{2\pi j}{a}\tanh \left( \frac{2\pi j}{a}L\right) \le \sigma _k\le \frac{2\pi j}{a}\coth \left( \frac{2\pi j}{a}L\right) \end{aligned}$$

if $(2j-1)b\le k< (2j+1)b$, where $j\in \mathbb {N}^*$.

We see that if $b=1$, $\sigma _1$ is bounded below by $\frac{2\pi }{a}\tanh (\frac{2\pi }{a}L)$, but if $b>1$ this lemma does not give a lower bound for $\sigma _1$. Therefore, our results concern only the case $b\ge 2$ which is interesting.

Theorem 1 is in fact a particular case of a more general result (Theorem 4 below) that involves domains of M containing the cylindrical neighborhood of $\partial M=\Sigma _1\cup \dots \cup \Sigma _b$, which is in this result assumed to be isometric to the union of disjoint right cylinders $\cup _{i=1}^{b}\Sigma _i\times [0,L)$. We note that given such a domain A, we can define ${{\,\textrm{l}\,}}(A)$ in the same way as we have defined ${{\,\textrm{l}\,}}(M)$ in Definition 1 by considering curves that divide A into two connected components without intersecting $\partial M$. The reason for proving this result instead of Theorem 1 is that it is needed in the proof of Theorem 2.

Theorem 4

Let (M, g) be a compact connected 2-dimensional Riemannian manifold with a boundary having $b\ge 2$ components of length a. Assume that the boundary $\partial M=\Sigma _1\cup \dots \cup \Sigma _b$ has a neighborhood $V(\partial M)$ which is isometric to the union of disjoint right cylinders $\cup _{i=1}^{b}\Sigma _i\times [0,L)$. For any domain A in M such that $V(\partial M)\subset A$ (possibly $A=M$), we have

$$\begin{aligned} \sigma _1(M)\ge \frac{\min \{{{\,\textrm{l}\,}}(A),L\}^2}{2(b-1)a|A|}. \end{aligned}$$

The proof of Theorem 4 involves estimating the constants $h_1$ and $h_2$ of compact connected 2-dimensional manifolds with cylindrical boundary.

Lemma 2

Let (M, g) be a compact connected 2-dimensional Riemannian manifold with $b\ge 2$ boundary components having length a. Assume that the boundary $\partial M=\Sigma _1\cup \dots \cup \Sigma _b$ has a neighborhood $V(\partial M)$ which is isometric to the union of disjoint right cylinders $\cup _{i=1}^{b}\Sigma _i\times [0,L)$. Let A be a domain in M such that $V(\partial M)\subset A$ (me may have $A=M$). We have the following estimates of $h_1$ and $h_2$:

$$\begin{aligned} h_1(A)\ge \frac{2\min \{{{\,\textrm{l}\,}}(A),L\}}{|A|}, \\ h_2(A)\ge \frac{\min \{{{\,\textrm{l}\,}}(A),L\}}{(b-1)a}. \end{aligned}$$

Proof

We recall that

$$\begin{aligned} h_1(A)=\inf \frac{|\partial D|}{|D|} \end{aligned}$$

where the infimum is taken among all domains satisfying $|D|\le \frac{|A|}{2}$, $D\cap \partial M\not =\emptyset$ and such that $A\setminus D$ is also connected and intersects $\partial M$. Given such a domain D the following situations can happen.

• (1) $\partial D$ intersects a boundary component $\Sigma _i$ and is contained in the cylindrical neighborhood of $\Sigma _i$. If $|\partial D|\ge L$, the fact that $aL<|A|$ gives $\frac{|\partial D|}{|D|}\ge \frac{|\partial D|}{aL}\ge \frac{L}{aL}=\frac{1}{a}>\frac{L}{|A|}$. If $|\partial D|<L$, we know from the isoperimetric inequality that the domain D minimising $\frac{|\partial D|}{|D|}$ is the half-disk with radius $r=\frac{|\partial D|}{\pi }$ and area $\frac{|\partial D|^2}{2\pi }$. This gives $\frac{|\partial D|}{|D|}\ge |\partial D|\cdot \frac{2\pi }{|\partial D|^2}=\frac{2\pi }{|\partial D|}>\frac{2\pi }{L}>\frac{2\pi a}{|A|}\ge \frac{2\pi l(A)}{|A|}>\frac{2{{\,\textrm{l}\,}}(A)}{|A|}$.

• (2) $\partial D$ intersect a boundary component $\Sigma _i$ but D is not contained in the cylindrical neighbourhood of $\Sigma _i$. The length of the curve $\partial D$ between its extremity in $\Sigma _i$ and the point where it leaves the cylindrical neighborhood is greater or equal to L. Hence, we have $\frac{|\partial D|}{|D|}\ge \frac{2L}{|A|}$.

• (3) $\partial D$ contains a curve of C(A). Since ${{\,\textrm{l}\,}}(A)$ is the minimal length of such a curve, $|\partial D|\ge {{\,\textrm{l}\,}}(A)$. Moreover, D satisfies $|D|\le \frac{|A|}{2}$. Hence we have $\frac{|\partial D|}{|D|}\ge \frac{2{{\,\textrm{l}\,}}(A)}{|A|}$.

In each case, we have either $\frac{|\partial D|}{|A|}\ge \frac{2{{\,\textrm{l}\,}}(A)}{|A|}$ or $\frac{|\partial D|}{|A|}\ge \frac{2\,L}{|A|}$. Since we have considered all possible cases, we conclude that $h_1\ge \frac{2\min \{{{\,\textrm{l}\,}}(A),L\}}{|A|}$.

We now estimate $h_2(A)$. We recall that

$$\begin{aligned} h_2(A):=\inf \frac{|\partial D|}{|D\cap \partial M|} \end{aligned}$$

where the infimum is taken among all domains satisfying $|D|\le \frac{|A|}{2}$, $D\cap \partial M\not =\emptyset$ and such that $A\setminus D$ is also connected and intersects $\partial M$. Given such a domain D the following situations can happen.

• (1) $\partial D$ intersects a boundary component $\Sigma _i$ and D is contained in the cylindrical neighborhood of $\Sigma _i$. Since the the complement of D in M is connected, $\partial D$ is homotopic to $D\cap \Sigma _i$. Since $D\cap \Sigma _i$ is a geodesic arc and the cylindrical neighborhood has zero curvature, $|\partial D|\ge |D\cap \Sigma _i|= |D\cap \partial M|$ and finally $\frac{|\partial D|}{|D\cap \partial M|}\ge 1$.

• (2) $\partial D$ intersects a boundary component $\Sigma _i$ but D is not contained in the cylindrical neighborhood of $\Sigma _i$. The length of the curve $\partial D$ between its extremity in $\Sigma _i$ and the point where it leaves the cylindrical neighborhood is greater or equal to L. Hence, we have $\frac{|\partial D|}{|D\cap \partial M|}\ge \frac{2\,L}{ba}\ge \frac{L}{(b-1)a}$.

• (3) $\partial D$ contains a curve of C(A). Since ${{\,\textrm{l}\,}}(A)$ is the minimal length of such a curve, $|\partial D|\ge {{\,\textrm{l}\,}}(A)$. Moreover, D cannot contain all the connected components of $\partial M$, which implies $|D\cap \partial M|\le (b-1)a$. Hence, we have $\frac{|\partial D|}{|D\cap \partial M|}\ge \frac{{{\,\textrm{l}\,}}(A)}{(b-1)a}$.

We have considered all possible cases. To conclude, we observe that ${{\,\textrm{l}\,}}(A)\le a$ since the curves $\Sigma _i\times \{L\}$ belong to C(A). Hence, we have $1\ge \frac{{{\,\textrm{l}\,}}(A)}{a}\ge \frac{{{\,\textrm{l}\,}}(A)}{(b-1)a}$. Since $\frac{|\partial D|}{|D\cap \partial M|}\ge \frac{{{\,\textrm{l}\,}}(A)}{(b-1)a}$ or $\frac{|\partial D|}{|D\cap \partial M|}\ge \frac{L}{(b-1)a}$ for all possible D, we have $h_2(A)\ge \frac{\min \{{{\,\textrm{l}\,}}(A),L\}}{(b-1)a}$. $\square$

We note that in higher dimensions, similar estimates cannot be obtained because in the second situation, the volume of $\partial D$ cannot be bounded below by L.

Proof of Theorem 4

Theorem 4 follows from Lemma 2 and Proposition 2. $\square$

The exponent of the geometric quantities involved in the estimate given in Theorem 1 cannot be improved. This is obtained by showing that $\sigma _1$ and the lower bound are equivalent, in the sense that $\sigma _1$ goes to zero if and only if the lower bound goes to zero, for families of surfaces for which all geometric quantities involved in the lower bound except one are fixed. We recall that the Steklov eigenvalues of right cylinders can be computed.

Proposition 3

The Steklov eigenvalues of the right cylinder $S_R^1\times [-T,T]$, where $S_R^1$ denotes the circle of radius R, are

$$\begin{aligned} 0, \frac{1}{T}, \frac{k}{R}\tanh \left( \frac{k}{R}T\right) <\frac{k}{R}\coth \left( \frac{k}{R}T\right) , \quad k\in \mathbb {N}^*. \end{aligned}$$

We note that if $\frac{T}{R}\ge \rho$, where $\rho \approx 1,19968$ is the positive root of $1=x\tanh (x)$, the first non-zero eigenvalue is $\frac{1}{T}$.

Example 2

Consider the sequence $\{M_n\}_{n\ge 1}$ where $M_n$ are right cylinders that have height $4\pi n$ and whose bases are unit circles. Since $2\pi n\ge \rho \text { } \forall n \ge 1$, $\sigma _1(M_n)=\frac{1}{2\pi n}$. Hence, we have $\frac{4\pi }{|M_n|}=\frac{1}{2\pi n}=\sigma _1(M_n)\ge \frac{{{\,\textrm{l}\,}}(M_n)^2}{2(b-1)a|M_n|}= \frac{\pi }{|M_n|}$.

Fig. 2

A surface with two cylindrical boundary neighborhoods connected by a thin cylinder

Example 3

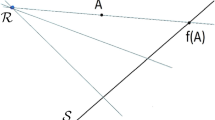
Consider a surface $M_{\epsilon }$ with two boundary components of length 1, having a cylindrical neighborhood of length L and connected by a thin cylinder $C_{\epsilon }$ of circumference $\epsilon <1$ and of length $\frac{1}{\epsilon }$ (see Fig. 2). Consider the function taking the value $-1$ on one side of $C_{\epsilon }$, 1 on the other side, and extended continuously to a linear function on $C_{\epsilon }$, that is, on $C_{\epsilon }=S^1_{\frac{\epsilon }{2\pi }} \times [-\frac{1}{2\epsilon },\frac{1}{2\epsilon }]$, we have $f(s,t)=2\epsilon t$. Its Dirichlet energy is zero except on $C_{\epsilon }$ where it is

$$\begin{aligned} \int _{C_{\epsilon }}|\nabla f|^2 dv_g=\int _0^{\epsilon }\int _{\frac{-1}{2\epsilon }}^{\frac{1}{2\epsilon }}4\epsilon ^2dtds=\int _0^{\epsilon } 4 \epsilon ds=4\epsilon ^2. \end{aligned}$$

Since the restriction of f to the boundary is orthogonal to a constant function and $\int _{\partial M}f^2 dS_g=\int _{\partial M}1 dS_g=2$, we obtain

$$\begin{aligned} \sigma _1(M)=\min \left\{ R(u): u\in H^1(M), \int _{\partial M}u=0\right\} \le R(f)=\frac{4\epsilon ^2}{2}=2\epsilon ^2. \end{aligned}$$

We note that if L is small enough, the volume of $M_{\epsilon }$ satisfies $|M_{\epsilon }|\le 2$. Hence, we have $2{{\,\textrm{l}\,}}(M_{\epsilon })^2=2\epsilon ^2\ge \sigma _1(M_{\epsilon })\ge \frac{{{\,\textrm{l}\,}}(M_{\epsilon })^2}{2(b-1)a|M_{\epsilon }|}\ge \frac{ {{\,\textrm{l}\,}}(M_{\epsilon })^2}{4}$.

Since we have shown that the exponent of $\min \{{{\,\textrm{l}\,}}(M),1\}$ and |M| cannot be improved, we can deduce that the exponent of a must be $-1$ from the fact that the degree of homogeneity of the lower bound has to be consistent with the degree of homogeneity of $\sigma _1$. We conclude that, up to a constant, we cannot have a better lower bound for $\sigma _1$ depending on these geometric quantities (however, we may have different geometric quantities).

A lower bound is optimal if we can show that it goes to zero if and only if $\sigma _1$ goes to zero. Using the same strategy as in Example 1, it is easy to construct a family of surfaces such that $\sigma _1$ is constant but the volume goes to infinity and therefore the lower bound given in Theorem 1 tends to zero. This example shows that the volume of the manifold seems not to be an optimal quantity for estimating $\sigma _1$. Theorem 2 is an improvement of Theorem 1 for surfaces whose Gaussian curvature is bounded below, which does not involve the volume of the manifold.

Proof of Theorem 2

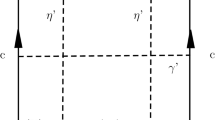
For $2\le i\le b$, we let $\gamma _i$ be a geodesic minimising the distance between $\Sigma _1$ and $\Sigma _i$. Around each $\gamma _i$, we consider the tube

$$\begin{aligned} T_i= & {} \{x\in M, \text { there exists a geodesic }\xi \text { of length } \\ {}{} & {} l(\xi )<{{\,\textrm{inj}\,}}_{\partial M}(M) \text { from } x \text { meeting } \gamma _i \text { orthogonally}\}. \end{aligned}$$

Since $\gamma _i$ meets $\partial M$ orthogonally, $T_i=\{x\in M, d(x,\gamma _i) < {{\,\textrm{inj}\,}}_{\partial M}(M) \}$. We define ${A=\cup _{i=1}^{b}(\Sigma _i\times [0,{{\,\textrm{inj}\,}}_{\partial M}(M)))\cup (\cup _{i=2}^{b}T_i)}$ (see Fig. 3). We approximate the volume of A by using a Bishop-Günther inequality for tubes (Theorem 8.16, point ii, in [14]). In the particular case of a tube T of radius r around a geodesic $\gamma$ in a surface whose Gaussian curvature is bounded from below by $\kappa <0$, this comparison result says that

$$\begin{aligned} |T|\le \frac{2l(\gamma )\sinh (\sqrt{-\kappa }r)}{\sqrt{-\kappa }}. \end{aligned}$$

Fig. 3

The domain $A=\cup _{i=1}^{b}(\Sigma _i\times [0,{{\,\textrm{inj}\,}}_{\partial M}(M)))\cup (\cup _{i=2}^{b}T_i)$

By applying this inequality to estimate the volume of the tubes $T_i$, we obtain

$$\begin{aligned} |A|&=|\cup _{i=1}^{b}(\Sigma _i\times [0,{{\,\textrm{inj}\,}}_{\partial M}(M)))\cup (\cup _{i=2}^{b}T_i)|\\&\le ab{{\,\textrm{inj}\,}}_{\partial M}(M)+\sum _{i=2}^{b}|(T_i)|\\&\le ab{{\,\textrm{inj}\,}}_{\partial M}(M)+\sum _{i=2}^{b}\frac{2l(\gamma _i)\sinh (\sqrt{-\kappa }{{\,\textrm{inj}\,}}_{\partial M}(M))}{\sqrt{-\kappa }}\\&\le ab{{\,\textrm{inj}\,}}_{\partial M}(M)+\frac{2(b-1){{\,\textrm{diam}\,}}_M(\partial M)\sinh (\sqrt{-\kappa }{{\,\textrm{inj}\,}}_{\partial M}(M))}{\sqrt{-\kappa }}. \end{aligned}$$

The set A can be approximated by smooth domains in the following way (for more details, see [11], Section 8.2). We define $V_n:=\{x\in A: d(x,\partial A)>\frac{1}{n}\}$ and consider $\phi _n$ a bump function for $\overline{V_{n}}$ supported in $V_{n+1}$ (on bump functions, see [17], Proposition 2.25). By Sard’s Theorem, there exists $t_n\in (0,1)$ such that $E_n:=\{x\in M:\phi _n(x)>t_n\}$ is a smooth domain. Since $E_1\subset E_2\subset \dots$ and $\cup _{n\in \mathbb {N}^*}E_n=A$, $|E_n|\rightarrow |A|$ as n tends to infinity. Let $n_0$ be such that $\frac{1}{n_0}<\frac{{{\,\textrm{inj}\,}}_{\partial M}(M)}{8}$. By taking $\tilde{A}=E_{n_0}$, we have that $\tilde{A}$ contains a cylindrical neighborhood of length $\frac{{{\,\textrm{inj}\,}}_{\partial M}(M)}{2}$ of $\partial M$, $|A|\ge |\tilde{A}|$ and ${{\,\textrm{l}\,}}(\tilde{A})\ge \frac{{{\,\textrm{inj}\,}}_{\partial M}(M)}{2}$. This last statement follows from the fact that a curve c which divides $\tilde{A}$ into two connected components, each containing at least one connected component of $\partial M$, must intersect a geodesic $\gamma _i$ at a point x and cannot be contained in the ball $B_{\frac{{{\,\textrm{inj}\,}}_{\partial M}(M)}{2}}(x)\subset \tilde{A}$.

Hence, by Theorem 4, we have

$$\begin{aligned} \sigma _1(M)\ge \frac{\min \{{{\,\textrm{l}\,}}(\tilde{A}),\frac{{{\,\textrm{inj}\,}}_{\partial M}(M)}{2}\}^2}{2(b-1)a|\tilde{A}|}\ge \frac{{{\,\textrm{inj}\,}}_{\partial M}(M)^2}{8(b-1)a|A|}. \end{aligned}$$

By combining the above inequality with the approximation of the volume of A, we obtain

$$\begin{aligned} \sigma _1(M)\ge \frac{{{\,\textrm{inj}\,}}_{\partial M}(M)^2}{8(b-1)a(ab{{\,\textrm{inj}\,}}_{\partial M}(M)+\frac{2(b-1){{\,\textrm{diam}\,}}_M(\partial M)\sinh (\sqrt{-\kappa }{{\,\textrm{inj}\,}}_{\partial M}(M))}{\sqrt{-\kappa }})}. \end{aligned}$$

Since by definition we have ${{\,\textrm{inj}\,}}_{\partial M}(M)\le 1$, we obtain using the Taylor-Lagrange formula that

$$\begin{aligned} \frac{\sinh (\sqrt{-\kappa }{{\,\textrm{inj}\,}}_{\partial M}(M))}{\sqrt{-\kappa }}\le \cosh (\sqrt{-\kappa }){{\,\textrm{inj}\,}}_{\partial M}(M). \end{aligned}$$

Hence, we have

$$\begin{aligned} \sigma _1(M)\ge \frac{{{\,\textrm{inj}\,}}_{\partial M}(M)}{8(b-1)a(ab+2(b-1){{\,\textrm{diam}\,}}_M(\partial M)\cosh (\sqrt{-\kappa }))} \end{aligned}$$

We note that this inequality is interesting in itself because it shows clearly how the different geometric quantities affect the lower bound. If we assume that $a\le {{\,\textrm{diam}\,}}_M(\partial M)$, we obtain

$$\begin{aligned} \sigma _1(M)&\ge \frac{{{\,\textrm{inj}\,}}_{\partial M}(M)}{8(b-1)a({{\,\textrm{diam}\,}}_M(\partial M)b+2(b-1){{\,\textrm{diam}\,}}_M(\partial M)\cosh (\sqrt{-\kappa }))}\\&\ge \frac{{{\,\textrm{inj}\,}}_{\partial M}(M)}{16b^2\cosh (\sqrt{-\kappa })a{{\,\textrm{diam}\,}}_M(\partial M)}\\&=C(\kappa ,b)\frac{{{\,\textrm{inj}\,}}_{\partial M}(M)}{a {{\,\textrm{diam}\,}}_M(\partial M)}, \end{aligned}$$

where $C(\kappa ,b)=\frac{1}{16b^2\cosh (\sqrt{-\kappa })}$. $\square$

Remark 6

The exponent of the geometric quantities involved in Theorem 2 cannot be improved. To show this, we proceed in the same way as for Theorem 1. We first observe that the exponent of the diameter of the boundary cannot be improved because the family of right cylinders of fixed base and growing height $\{M_n\}_{n\ge 1}$ of Example 2 satisfy $\sigma _1(M_n)=\frac{1}{2\pi n}=\frac{2}{{{\,\textrm{diam}\,}}_M(\partial M_n)}$ and, except the diameter of the boundary, the quantities involved in the lower bound are fixed. We consider now the family of right cylinders $\{M_a\}_{a\ge 1}$ of height 2 and growing base of length a. The only quantities involved in the lower bound that are changing are the diameter of the boundary and the length of the boundary. We have $\sigma _1(M_a)\le \frac{4\pi }{a^2}$, which shows that the exponent of a is also optimal because we have already showed that the exponent of the diameter of the boundary cannot be improved. For obtaining that the exponent of the injectivity radius if optimal, we note that in Example 3 we can construct the surfaces $M_{\epsilon }$ so that their Gaussian curvature is bounded from below. This can be done by joining the inner cylinder and the two cylindrical neighborhoods of the boundary by a cylinder of constant Gaussian curvature equal to $-1$ and smoothing the joints. Here, the only quantities involved in the lower bound that are changing are the injectivity radius and the diameter of the boundary. From Example 3, we have $\sigma _1(M_{\epsilon })\le 2\epsilon ^2\le 8{{\,\textrm{inj}\,}}_{\partial M_{\epsilon }}(M_{\epsilon })^2$. On the other hand, by construction, ${{\,\textrm{diam}\,}}_M(\partial M_\epsilon )$ is of the same order as $\frac{1}{{{\,\textrm{inj}\,}}_{\partial M_{\epsilon }}(M_{\epsilon })}$ as $\epsilon$ goes to zero. This implies that there exists a constant c such that $\sigma _1(M_{\epsilon })\ge c {{\,\textrm{inj}\,}}_{\partial M_{\epsilon }}(M_{\epsilon })^2$. Hence the exponent of the injectivity radius is optimal because we have already showed that the exponent of the diameter of the boundary cannot be improved.

We remark that if a goes to zero, ${{\,\textrm{l}\,}}(M)$ and ${{\,\textrm{inj}\,}}_{\partial M}(M)$ also go to zero. Therefore, Theorems 1 and 2 do not say that $\sigma _1$ goes to infinity as a goes to zero, which is not true, as shown by the following example. We consider the sequence of right cylinders $\{S^1_{\frac{1}{n}}\times [-1,1]\}_{n\ge 1}$. Proposition 3 shows that if $n\ge 2$, $\sigma _1=1$. By taking the sequence $\{S^1_{\frac{1}{n}}\times [-n,n]\}_{n\ge 1}$, we even have that $\sigma _1$ tends to zero as the length of the boundary tends to zero. This is in contrast to the case of surfaces with one cylindrical boundary component where Lemma 1 shows that $\sigma _1$ goes to infinity as the length of the boundary goes to zero.

3.2 Geometric bounds on the low Steklov eigenvalues of a compact hyperbolic surface with geodesic boundary

A compact hyperbolic surface of signature (g, b) is a compact 2-dimensional Riemannian manifold of constant Gaussian curvature equal to $-1$ with genus g and a geodesic boundary having b connected components. An important property of hyperbolic surfaces is that they are isometric to a warped product around simple closed geodesics.

Proposition 4

Let M be a closed hyperbolic surface of genus $g\ge 2$ and let $\gamma _1,\dots ,\gamma _m$ be pairwise disjoint simple closed geodesics on M. Then $m\le 3g-3$ and there exist simple closed geodesics $\gamma _{m+1},\dots ,\gamma _{3g-3}$ which, together with $\gamma _1,\dots ,\gamma _m$, decompose M into surfaces of signature (0, 3). Moreover, the collars

$$\begin{aligned} K(\gamma _i)=\{p\in M, dist(p,\gamma _i)\le w(\gamma _i)\} \end{aligned}$$

where

$$\begin{aligned} w(\gamma _i)={{\,\textrm{arcsinh}\,}}\left( \frac{1}{\sinh (\frac{1}{2}l(\gamma _i))}\right) \end{aligned}$$

are pairwise disjoint and each collar $K(\gamma _i)$ is isometric to the cylinder $S^1\times [-w(\gamma _i),w(\gamma _i)]$ with the metric $g(s,t)=\frac{l^2(\gamma _i)\cosh ^2(t)}{(2\pi )^2}g_{S^1}(s)+dt^2$ where $g_{S^1}$ is the canonical metric on $S^1$.

For a proof of this result, we refer to [4], Theorem 4.1.1. A direct consequence is that a hyperbolic surface with geodesic boundary has a boundary neighborhood which is isometric to a union of disjoint warped products. This implies the following approximation of the Steklov eigenvalues.

Lemma 3

Let M be a hyperbolic surface with $b\ge 2$ geodesic boundary components of length a. Then, the Steklov eigenvalues $\sigma _k$ of M satisfy

$$\begin{aligned} 0\le \sigma _k\le \frac{1}{\arctan (\frac{1}{\sinh {\frac{a}{2}}})} \end{aligned}$$

if $k<b$, and

$$\begin{aligned} \frac{2\pi j}{a}\tanh \left( \frac{2\pi j}{a}\arctan \left( \frac{1}{\sinh (\frac{a}{2})}\right) \right) \le \sigma _k\le \frac{2\pi j}{a}\coth \left( \frac{2\pi j}{a}\arctan \left( \frac{1}{\sinh (\frac{a}{2})}\right) \right) \end{aligned}$$

if $(2j-1)b\le k< (2j+1)b$, where $j\in \mathbb {N}^*$.

Proof

Let $\Sigma _1,...,\Sigma _b$ be the b boundary components, where $l(\Sigma _1)=...=l(\Sigma _b)=a$. By gluing a hyperbolic surface of signature (1, 1) to each boundary component, we obtain a closed hyperbolic surface of genus $g\ge 2$. Theorem  4 says that the collars $K(\Sigma _i)=\{p\in M, dist(p,\Sigma _i)\le w(\Sigma _i)\}$, where $w(\Sigma _i)={{\,\textrm{arcsinh}\,}}(\frac{1}{\sinh (\frac{a}{2})})$, are disjoint and isometric to cylinders $S^1\times [0,w(\gamma _i)]$ with the metric $g(s,t)=\frac{a^2\cosh ^2(t)}{(2\pi )^2}g_{S^1}(s)+dt^2$. Let $A=\cup _i K(\Sigma _i)$ be the union of these collars. We consider the mixed Steklov-Neumann and Steklov-Dirichlet problems on A. From Eq. 1, we have

$$\begin{aligned} \sigma _i^N(A)\le \sigma _i(M)\le \sigma _i^D(A). \end{aligned}$$

Since the $K(\Sigma _i)$ are warped products, the eigenvalues of these mixed problems can be explicitly calculated. The result is obtained by replacing $\sigma _i^N(A)$ and $\sigma _i^D(A)$ by the their exact value in the previous equation. $\square$

A classical result due to L. Bers says that every closed hyperbolic surface of genus $g\ge 2$ admits a decomposition into surfaces of signature (0, 3) such that the length of the separating geodesics is controlled by a constant depending on the genus. We give a statement of this result due to P. Buser (see [4], Theorem 5.2.3) which is convenient to deduce an analog result for surfaces with geodesic boundary of controlled length.

Proposition 5

Let M be a closed hyperbolic surface of genus $g\ge 2$ and let $\gamma _1,...,\gamma _m$ be the set of all distinct simple closed geodesics of length $l\le 2{{\,\textrm{arcsinh}\,}}(1)$. This system is extendable to a partition $\gamma _1,\dots ,\gamma _{3g-3}$ satisfying

$$\begin{aligned} l(\gamma _k)\le 4k\log (\frac{8\pi (g-1)}{k}), \quad k=1,...,3g-3. \end{aligned}$$

Corollary 1

There exists a constant $L_{g+b}$, depending only on g and b, such that every hyperbolic surface M of genus g with $b\ge 2$ geodesic boundary components of length $l\le 2{{\,\textrm{arcsinh}\,}}(1)$ can be decomposed into surfaces of signature (0, 3) by simple closed geodesics $\gamma _1,...,\gamma _{3g-3+b}$ satisfying

$$\begin{aligned} l(\gamma _i)\le L_{g+b}, \quad i=1,...,3g-3+b. \end{aligned}$$

Proof

Let $\gamma _1,...,\gamma _b$ be the geodesic boundary components of M. By gluing a hyperbolic surface of signature (1, 1) to each boundary component, we obtain a closed hyperbolic surface $M'$ of genus $g+b\ge 2$ and $\gamma _1,\dots ,\gamma _b$ are closed geodesics of $M'$ of length $l\le 2{{\,\textrm{arcsinh}\,}}(1)$. We add to this set all distinct simple closed geodesics on $M'$ of length $l\le 2{{\,\textrm{arcsinh}\,}}(1)$. From Bers’Theorem, the resulting set $\gamma _1,\dots ,\gamma _m$ can be extended to a partition $\gamma _1,...,\gamma _{3(g+b)-3}$ of simple closed geodesics satisfying $l(\gamma _k)\le 4k\log (\frac{8\pi (g+b-1)}{k}) \text { for }k=1,...,3(g+b)-3$. In particular, there exists a constant $L_{g+b}=4(3(g+b)-3)\log (\frac{8\pi (g+b-1)}{3(g+b)-3})$ such that $l(\gamma _k)\le L_{g+b}$ for $k=1,...,3(g+b)-3$. Among this family of geodesics, we have the b geodesics $\gamma _1,...,\gamma _b$ of the boundary of M and we also have b simple closed geodesics that divide the surfaces of signature (1, 1) glued at each boundary to make them surfaces of signature (0, 3). The $3g-3+b$ remaining geodesics decompose M into surfaces of signature (0, 3) and their length is bounded by $L_{g+b}$. $\square$

We are now able to give the proof of Theorem 3. The strategy is the same as the strategy used in [20] for obtaining a result for Laplace eigenvalues.

Proof of Theorem 3

Step 1: ${{\,\textrm{l}\,}}_n\le \beta _1$ where $\beta _1$ is a constant depending only on g and b. From Corollary 1 there exists a family of simple closed geodesics of length $l\le L_{g+b}$, dividing M into $3g-3+b$ surfaces of signature (0, 3). Since we assume that M is connected, each of this surfaces of signature (0, 3) contains at most two components of $\partial M$. Hence, by choosing a subset of these geodesics, we can obtain for $1\le n<\lceil \frac{b}{2}\rceil$ a division of M into $n+1$ connected components, each one containing at least one component of $\partial M$. Let $\gamma$ denote the curve consisting of the union of these geodesics. Because $\gamma$ consists of at most $3g-3+b$ geodesics of length $l\le L_{g+b}$, there exists a constant $\beta _1$, depending only on g and b and such that $l(\gamma )\le \beta _1$. Let $c\in C_n(M)$ be a curve satisfying $l(c)={{\,\textrm{l}\,}}_n$. Since $\gamma \in C_n(M)$, we have ${{\,\textrm{l}\,}}_n \le l(\gamma ) \le \beta _1$. For $\lceil \frac{b}{2}\rceil \le n<b$, the assumption says that there exists $c\in C_n(M)$ such that each simple closed geodesic of c is of length $l\le L_{g+b}$. Since c consists of at most $3g-3+b$ geodesics, we have ${{\,\textrm{l}\,}}_n \le l(c) \le \beta _1$.

Step 2: $\sigma _n\le C_2 \frac{{{\,\textrm{l}\,}}_n}{a}$. If ${{\,\textrm{l}\,}}_n>1$, we obtain from the combination of Lemma 3 and the hypothesis that $a\le 2{{\,\textrm{arcsinh}\,}}(1)$ that $\sigma _n\le \frac{1}{\arctan (\frac{1}{\sinh {\frac{a}{2}}})}<\frac{8{{\,\textrm{arcsinh}\,}}(1){{\,\textrm{l}\,}}_n}{\pi a}$. Now assume that ${{\,\textrm{l}\,}}_n\le 1$. Let $c\in C_n(M)$ be the curve from step 1 satisfying $l(c)={{\,\textrm{l}\,}}_n$. This curve decompose M into $n+1$ connected components $M_1,\dots ,M_{n+1}$, each one containing at least one boundary component. We suppose $c=\gamma _1\cup \dots \cup \gamma _p$ where the $\gamma _i$ are simple closed geodesics on M. From Proposition 4, we know that there exist disjoint collars $K(\gamma _1),\dots ,K(\gamma _p)$ about the geodesics $\gamma _1,\dots , \gamma _p$. If $K_j\cap M_i\not =\emptyset$, $K_j\cap \overline{M_i}$ is isometric to $S^1\times [0,w(\gamma _j)]$ with the metric $g(s,t)=\frac{l^2(\gamma _i)\cosh ^2(t)}{(2\pi )^2}g_{S^1}(s)+dt^2$, and $K_j\cap \partial M_i$ corresponds to $S^1\times \{0\}$. The upper bound is obtained by using test functions. We define

$$\begin{aligned} \phi _i(x)= {\left\{ \begin{array}{ll}1 &{} \text {if } x \in M_i\setminus \cup _{j=1}^{p}K_j;\\ \phi _{i,j}(x)&{} \text {if } x\in M_i\cap K_j \text { for a }j=1,\dots ,p;\\ 0 &{}\text { otherwise;} \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \phi _{i,j}:S^1\times [0,w(\gamma _j)]&\rightarrow \mathbb {R}\\ (s,t)&\mapsto \frac{\arctan (\sinh (t))}{\arctan (\frac{1}{\sinh (\frac{l(\gamma _i)}{2})})}. \end{aligned}$$

The Dirichlet energy of this function on the half-collar $M_i\cap K_j$ is

$$\begin{aligned} \int _{S^1\times [0,w(\gamma _i)]}|\nabla \phi _{i,j} |^{2}dv=\frac{l(\gamma _j)}{\arctan (\frac{1}{\sinh (\frac{l(\gamma _j)}{2})})}. \end{aligned}$$

Let E be the set of indices j such that $M_i\cap K_j\not = \emptyset$. The total Dirichlet energy of $\phi _i$ satisfies

$$\begin{aligned} \int _{M_i}|\nabla \phi _i |^{2}dv&=\sum _{j\in E}\frac{l(\gamma _j)}{\arctan (\frac{1}{\sinh (\frac{l(\gamma _j)}{2})})}\\&\le \frac{\sum _{j\in E}l(\gamma _j)}{\arctan (\frac{1}{\sinh (\frac{\sum _{j=1}^{r}{l(\gamma _j)}}{2})})}\\&\le \frac{{{\,\textrm{l}\,}}_n}{\arctan (\frac{1}{\sinh (\frac{{{\,\textrm{l}\,}}_n}{2})})}. \end{aligned}$$

We also have

$$\begin{aligned} \int _{\partial M_i} \phi _i^2 dS=m\times a\ge a, \end{aligned}$$

where m is the number of boundary components included in $M_i$. Hence the Rayleigh quotient of $\phi _i$ satisfy

$$\begin{aligned} R(\phi _i)\le \frac{{{\,\textrm{l}\,}}_n}{a \arctan (\frac{1}{\sinh (\frac{{{\,\textrm{l}\,}}_n}{2})})}. \end{aligned}$$

Since ${{\,\textrm{l}\,}}_n\le 1$, we have $\frac{1}{\arctan (\frac{1}{\sinh (\frac{{{\,\textrm{l}\,}}_n}{2})})}<\frac{1}{\arctan (\frac{1}{\sinh (\frac{1}{2})})}=:\beta _2$ and

$$\begin{aligned} R(\phi _i)\le \beta _2\frac{{{\,\textrm{l}\,}}_n}{a}. \end{aligned}$$

Let V be the linear span of $\phi _1,\dots ,\phi _{n+1}$ in $H^1(M)$. Since the functions $\phi _i$ have disjoint support, V is an $(n+1)$-dimensional vector space and we have

$$\begin{aligned} \max \{R(u), u\in V\}=\max \{R(\phi _1),...,R(\phi _{n+1})\}. \end{aligned}$$

Since $R(\phi _i)\le \beta _2\frac{{{\,\textrm{l}\,}}_n}{a}$ for $i=1,...,n+1$, we have $\max \{R(\phi _1),...,R(\phi _{n+1})\} \le \beta _2\frac{{{\,\textrm{l}\,}}_n}{a}$. Using the variational characterization $\sigma _n(M)=\min _{V\in V_k}\max _{0\not = u\in V} R(u)$, where $V_k$ is the set of all $(k+1)$-dimensional linear subspace of $H^1(M)$, we obtain

$$\begin{aligned} \sigma _n(M)\le \beta _2\frac{{{\,\textrm{l}\,}}_n}{a}. \end{aligned}$$

Because we have obtained the desired result both when ${{\,\textrm{l}\,}}_n >1$ and when ${{\,\textrm{l}\,}}_n\le 1$, we have

$$\begin{aligned} \sigma _n(M)\le C_2\frac{{{\,\textrm{l}\,}}_n}{a}, \end{aligned}$$

where $C_2=\max \{\frac{8{{\,\textrm{arcsinh}\,}}(1)}{\pi },\beta _2\}$ is a universal constant.

Step 3: $C_1{{\,\textrm{l}\,}}_n^2\le \sigma _n$. Since $l(c)={{\,\textrm{l}\,}}_n$, one of the p components $\gamma _i$ of c must satisfy $l(\gamma _i)\ge \frac{{{\,\textrm{l}\,}}_n}{p}$; we call it $\gamma _{\max }$. The geodesic $\gamma _{\max }$ is contained in the boundary of two sets $M_j$ and $M_k$. We let $\Omega _1=M_j\cup M_k\cup (\partial M_j\cap \partial M_k)$ and $\Omega _2,\dots ,\Omega _n$ be the remaining $M_i$. Let $A=\cup _{i=1}^{n}\Omega _i$. On each $\Omega _i$, we consider the mixed Steklov-Neumann problem with Steklov condition on $\Omega _i\cap \partial M$ and Neumann condition on $\partial \Omega _i$. Since the $\Omega _i$ are disjoint, we have

$$\begin{aligned} \sigma _{n}^N(A)=\min \{\sigma _1^N(\Omega _1),...,\sigma _1^N(\Omega _{n})\} \end{aligned}$$

and since A contains all boundary components of M, we have

$$\begin{aligned} \sigma _k(M)\ge \sigma _k^N(A). \end{aligned}$$

Therefore, the proof will be finished if we can show that $\sigma _1^N(\Omega _i)\ge \alpha _1 {{\,\textrm{l}\,}}_n^2$ for $i=1,\dots ,n$. If $\Omega _i$ contains only one boundary component $\Sigma _i$, we consider the mixed Steklov-Neumann problem on the half-collar $K(\Sigma _i)$. By comparing the Rayleigh quotients, we see that $\sigma _1^N(\Omega _i)\ge \sigma _1^N(K(\Sigma _i))$. We have already mentioned that a calculation shows that $\sigma _1^N(K(\Sigma _i))=\frac{2\pi }{a}\tanh (\frac{2\pi }{a}\arctan (\frac{1}{\sinh (\frac{a}{2})}))$. Since $a\le 2{{\,\textrm{arcsinh}\,}}(1)$, by letting $\beta _3=\frac{\pi }{{{\,\textrm{arcsinh}\,}}(1)}\tanh (\frac{\pi }{{{\,\textrm{arcsinh}\,}}(1)\arctan (1)})$, we obtain $\sigma _1^N(K)\ge \beta _3$.

If $\Omega _i$ contains several boundary components, we obtain the result by estimating the constants $h_1(\Omega _i)$ et $h_2(\Omega _i)$ and using Proposition 1 and Remark 5.

Estimation of $h_1(\Omega _i)$ We recall that

$$\begin{aligned} h_1(\Omega _i):=\inf \frac{|\partial D|}{|D|} \end{aligned}$$

where the infimum if taken among all domains D of $\Omega _i$ satisfying $|D|\le \frac{|\Omega _i|}{2}$, $D\cap \partial M \not =\emptyset$, and such that $M\setminus D$ is also connected and intersects $\partial M$. Given such a domain D, we have the following possibilities that are illustrated in Fig. 4.

Fig. 4

A schematic representation of possible configurations of D in $\Omega _i$ corresponding to each of the five cases

• (1) $\partial D$ intersects a component $\Sigma _i$ of $\partial M$ and D is contained in the collar neighborhood $K(\Sigma _i)$. From the isoperimetric inequality for simply connected domains in the hyperbolic plane we know that $|D|\le |\partial D|$. So we have $\frac{|\partial D|}{|D|}\ge \frac{|\partial D|}{ |\partial D|}=1$.

• (2) $\partial D$ intersects a boundary component $\Sigma _i$ but D is not contained in $K(\Sigma _i)$. Since $w(\Sigma _i)\ge {{\,\textrm{arcsinh}\,}}(1)$, we have $|\partial D|\ge w(\Sigma _i)\ge {{\,\textrm{arcsinh}\,}}(1)$. Therefore $\frac{|\partial D|}{|D|}\ge \frac{{{\,\textrm{arcsinh}\,}}(1)}{|M|}=\frac{{{\,\textrm{arcsinh}\,}}(1)}{2\pi (2\,g-2+b)}=:\beta _4$. We see that $\beta _4$ only depends on g and b.

• (3) $\partial D$ intersects a boundary geodesic $\gamma _i$ of $\partial \Omega _i$. Since both D and $\Omega _i\setminus D$ have to intersect $\partial M$, $\partial D$ cannot be contained in $K(\gamma _i)$. Since $l(\gamma _i)\le L_{g+b}$, $|\partial D|\ge w(\gamma _i)\ge \beta _5$ where $\beta _5$ is a constant depending only on g and b. Thus $\frac{|\partial D|}{|D|}\ge \frac{\beta _5}{|M|}=\frac{\beta _5}{2\pi (2\,g-2+b)}=:\beta _6$.

• (4) $\partial D$ does not intersect $\partial M$ and a component $\Gamma$ of $\partial D$ is freely homotopic to a boundary component $\Sigma _i$. In this case $\Gamma \cup \Sigma _i$ bounds an annulus and since the Gaussian curvature is negative and $\Sigma _i$ is a geodesic, $|\Gamma |\ge l(\Sigma _i)$. If $|\Gamma |\ge 1$, we have $\frac{|\partial D|}{|D|}\ge \frac{1}{|M|}=\frac{1}{2\pi (2\,g-2+b)}$. If $|\Gamma |<1$, we deduce that $\frac{|\partial D|}{|D|}\ge \frac{1}{10}$ from the isoperimetric inequality given in Theorem 3 of [22] and the fact that $|\Gamma |\ge l(\Sigma _i)$. Thus we have $\frac{|\partial D|}{|D|}\ge \min \{\frac{1}{2\pi (2\,g-2+b)},\frac{1}{10}\}=\frac{1}{2\pi (2\,g-2+b)}\ge \beta _4$.

• (5) $\partial D$ does not intersect $\partial M$ and none of its components is freely homotopic to a boundary component. We note that each component of $\partial D$ is freely homotopic to a simple closed geodesic of $\Omega _i$. Let $\Gamma$ be the union of these geodesics. We have $|\partial D|\ge |\Gamma |$. $\Gamma$ divides $\Omega _i$ into two connected components, each of them containing at least one connected component of $\partial M$. We recall that the geodesics $\gamma _1,...,\gamma _p$ divide M into $n+1$ regions and that a subset of these geodesics divides M into n regions $\Omega _1,...,\Omega _n$. Let $\tilde{\gamma }$ be the union of the geodesics that do not belong to this subset. We have $\gamma _{max}\in \tilde{\gamma }$. If $|\Gamma |$ were smaller than $l(\tilde{\gamma })$ there would be a family of geodesics of M, dividing M into $n+1$ regions and their total length would be smaller than ${{\,\textrm{l}\,}}_n$, which is a contradiction. Hence we have $|\Gamma |\ge l(\tilde{\gamma })\ge l(\gamma _{\max })\ge \frac{{{\,\textrm{l}\,}}_n}{p}$ and since $3g-3+b$ is the maximal number of these geodesics, $|\Gamma |\ge \frac{{{\,\textrm{l}\,}}_n}{3g-3+b}$. Therefore, $\frac{|\partial D|}{|D|}\ge \frac{|\Gamma |}{|M|}\ge \frac{{{\,\textrm{l}\,}}_n}{(3\,g-3+b)2\pi (2\,g-2+b)}=\frac{{{\,\textrm{l}\,}}_n}{\beta _7}$ where $\beta _7$ is a constant depending only on g and b.

Since we have considered all possibilities for $\partial D$, we have

$$\begin{aligned} h_1(\Omega _i)\ge \min \left\{ 1,\beta _4,\beta _6, \frac{{{\,\textrm{l}\,}}_n}{\beta _7}\right\} . \end{aligned}$$

Since ${{\,\textrm{l}\,}}_n\le \beta _1$, $h_1(\Omega _i)\ge \beta _8 {{\,\textrm{l}\,}}_n$ where $\beta _8=\min \{\beta _1^{-1},\beta _4\beta _1^{-1},\beta _6\beta _1^{-1},\frac{1}{\beta _7}\}$ is a constant depending only on g and b.

Estimation of $h_2(\Omega _i)$ We recall

$$\begin{aligned} h_2(\Omega _i):=\inf \frac{|\partial D|}{|D\cap \partial M|} \end{aligned}$$

where the infimum if taken among all domains D of $\Omega _i$ satisfying $|D|\le \frac{|\Omega _i|}{2}$, $D\cap \partial M \not =\emptyset$, and such that $M\setminus D$ is also connected and intersects $\partial M$. Given such a domain D, we have the following possibilities that are illustrated in Fig. 4.

• (1) $\partial D$ intersects a component $\Sigma _i$ of $\partial M$ and D is contained in the collar neighborhood $K(\Sigma _i)$. Since the Gaussian curvature is negative and $\Sigma _i$ is a geodesic, $|\partial D|\ge l(D\cap \Sigma _i)$. Thus, we have $\frac{|\partial D|}{|D\cap \partial M|}\ge \frac{|D\cap \Sigma _i|}{ |D\cap \Sigma _i|}=1$.

• (2) $\partial D$ intersects a boundary component $\Sigma _i$ but D is not contained in $K(\Sigma _i)$. Since $l(\Sigma _i)\le 2{{\,\textrm{arcsinh}\,}}(1)$, we have $|\partial D|\ge w(\Sigma _i)\ge {{\,\textrm{arcsinh}\,}}(1)$, which implies$\frac{|\partial D|}{|D\cap \partial M|}\ge \frac{{{\,\textrm{arcsinh}\,}}(1)}{ba}\ge \frac{1}{2b}$.

• (2) $\partial D$ intersects a boundary geodesic $\gamma _i$ of $\partial \Omega _i$. Since both D and $\Omega _i\setminus D$ have to intersect $\partial M$, $\partial D$ cannot be contained in $K(\gamma _i)$. Since $l(\gamma _i)\le L_{g+b}$, $|\partial D|\ge w(\gamma _i)\ge \beta _5$ where $\beta _5$ is a constant depending only on g and b. Thus $\frac{|\partial D|}{|D\cap \partial M|}\ge \frac{\beta _5}{ba}=\frac{\beta _5}{2{{\,\textrm{arcsinh}\,}}(1)b}=:\beta _9$.

• (3) $\partial D$ does not intersect $\partial M$ and a component $\Gamma$ of $\partial D$ is freely homotopic to a boundary component $\Sigma _i$. Since the Gaussian curvature is negative and $\Sigma _i$ is a geodesic, $|\partial D|\ge l(\Sigma _i)$. Therefore, we have $\frac{|\partial D|}{|D\cap \partial M|}\ge \frac{|\Sigma _i|}{ |\Sigma _i|}=1$.

• (4) $\partial D$ does not intersect $\partial M$ and none of its components is freely homotopic to a boundary component. We note that each component of $\partial D$ is freely homotopic to a simple closed geodesic of $\Omega _i$. Let $\Gamma$ be the union of these geodesics. We have $|\partial D|\ge |\Gamma |$. $\Gamma$ divides $\Omega _i$ into two connected components, each of them containing at least one connected component of $\partial M$. We recall that the geodesics $\gamma _1,...,\gamma _p$ divide M into $n+1$ regions and that a subset of these geodesics divides M into n regions $\Omega _1,...,\Omega _n$. Let $\tilde{\gamma }$ be the union of the geodesics that do not belong to this subset. We have $\gamma _{max}\in \tilde{\gamma }$. If $|\Gamma |$ were smaller than $l(\tilde{\gamma })$ there would be a family of geodesics of M, dividing M into $n+1$ regions and their total length would be smaller than ${{\,\textrm{l}\,}}_n$, which is a contradiction. Hence we have $|\Gamma |\ge l(\tilde{\gamma })\ge l(\gamma _{\max })\ge \frac{{{\,\textrm{l}\,}}_n}{p}$ and since $3g-3+b$ is the maximal number of these geodesics, $|\Gamma |\ge \frac{{{\,\textrm{l}\,}}_n}{3g-3+b}$. Therefore, $\frac{|\partial D|}{|D\cap \partial M|}\ge \frac{|\Gamma |}{ab}\ge \frac{{{\,\textrm{l}\,}}_n}{(3\,g-3+b)(2{{\,\textrm{arcsinh}\,}}(1)b)}=\beta _{10} {{\,\textrm{l}\,}}_n$ and $\beta _{10}$ is a constant depending only on g and b.

Since we have considered all possibilities for $\partial D$, we have

$$\begin{aligned} h_2(\Omega _i)\ge \min \left\{ 1,\frac{1}{2b},\beta _9,\beta _{10} {{\,\textrm{l}\,}}_n\right\} . \end{aligned}$$

Since ${{\,\textrm{l}\,}}_n\le \beta _1$, $h_2(\Omega _i)\ge \beta _{11} {{\,\textrm{l}\,}}_n$, where $\beta _{11}:=\min \{\beta _1^{-1},\frac{1}{2b}\beta _1^{-1},\beta _9\beta _1^{-1},\beta _{10}\}$ is a constant depending only on g and b.

If $\Omega _i$ has several boundary components, we have shown that $\sigma _1^N(\Omega _i)\ge \frac{h_1(\Omega _i) h_2(\Omega _i)}{4}\ge \frac{\beta _8\beta _{11} {{\,\textrm{l}\,}}_n^2}{4}=\beta _{12} {{\,\textrm{l}\,}}_n^2$ where $\beta _{12}$ is a constant depending only on g and b.

We conclude that $\sigma _1^N(\Omega _i)\ge \min \{\beta _3, \beta _{12} {{\,\textrm{l}\,}}_n^2\}$. Since ${{\,\textrm{l}\,}}_n\le \beta _1$, $\sigma _1^N(\Omega _i)\ge \beta _{13} {{\,\textrm{l}\,}}_n^2$ where $\beta _{13}=\min \{\beta _3\beta _1^{-2},\beta _{12}\}$. Since it is true for all $\Omega _i$, we obtain

$$\begin{aligned} \sigma _{n}(M)\ge \min \{\sigma _1^N(\Omega _1),...,\sigma _1^N(\Omega _n)\}\ge \beta _{13} {{\,\textrm{l}\,}}_n^2, \end{aligned}$$

where $\beta _{13}$ is a constant depending only on g and b. $\square$

Remark 7

We have seen that the presence of the area of M in the denominator of the lower bound of Theorem 1 can make this estimate inaaccurate. In Theorem 3 the weight of the area of M is hidden in the constant since it depends only on the signature of the hyperbolic surface.