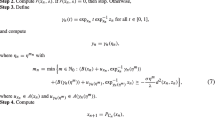Self-adaptive Technique with Double Inertial Steps for Inclusion Problem on Hadamard Manifolds

Abstract

In this article, we investigate monotone and Lipschitz continuous variational inclusion problem in the settings of Hadamard manifolds. We propose a forward–backward method with a self-adaptive technique for solving variational inclusion problem. To increase the rate of convergence of our proposed method, we incorporate our iterative method with double inertial steps and establish a convergence result of our iterative method under some mild conditions. Finally, in order to illustrate the computational effectiveness of our method, some numerical examples are also discussed. The result present in this article is new in this space and extends many related results in the literature.

1 Introduction

Let $\mathcal {K}$ be a nonempty, closed geodesic convex subset of a Hadamard manifold $\mathbb {P},~ T_{x}\mathbb {P}$ be the tangent space of $\mathbb {P}$ at $x \in \mathbb {P}$ and $T\mathbb {P}$ be the tangent bundle of $\mathbb {P}$. The variational inclusion problem (VIP) is to find $\overline{x} \in \mathbb {P}$ such that

$$\begin{aligned} \textbf{0} \in \Phi \overline{x} + \Psi \overline{x}, \end{aligned}$$

(1)

where $\Phi : \mathcal {K} \rightarrow T \mathbb {P}$ is a single-valued vector field, $\Psi : \mathcal {K} \rightarrow 2^{T\mathbb {P}}$ is a multi-valued vector field and 0 denotes the zero section of $T\mathbb {P}$. We denote the solution set of (1) by $\Omega$. The variational inclusion problem has received much attention due to its various applications in signal processing, image recovery and statistical regression, (see [3, 13, 44, 47, 49]). It is known that several optimization problem such as convex optimization problem can be translated into finding a zero of a maximal monotone operator defined on a Hilbert space $\mathbb {M}$. The problem of finding a zero of the sum of two (maximal) monotone operators is of fundamental importance in convex optimization and variational analysis (see [1, 19, 26, 33, 43, 52]). For solving VIP (1), the forward–backward splitting method (FBM) (see [13, 28, 29, 48]) is usually employed and is defined in the following manner: $q_1 \in \mathbb {M}$ and

$$\begin{aligned} q_{k+1}=(I+ r \Psi )^{-1}(q_k-r\Phi q_k),~k \geqslant 1, \end{aligned}$$

(2)

where $r > 0, ~\Psi : \mathbb {M} \rightarrow 2^{\mathbb {M}}$ is a set-valued operator and $\Phi : \mathbb {M} \rightarrow \mathbb {M}$ is an operator. In this case, each step of iterates involves only with $\Phi$ as the forward step and $\Psi$ as the backward step, but not the sum of operators. The FBM defined in (2) above requires one of the operators to be inverse strongly monotone. This assumption imposed on one of the operators is very difficult to meet the practical problems. In order to dispense with the condition, many authors have introduced several iterative methods. For instance, Tseng [48] introduced the following forward–backward–forward method which is a two-step iterative scheme as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} w_k=(I + r_k \Psi )^{-1}(I-r_k \Phi )q_k,\\ q_{k+1}=w_k-r_k (\Phi w_k-\Phi q_k), \end{array}\right. } \end{aligned}$$

(3)

where the step size $\{r_k\}$ can be updated by Armijo linesearch methods. When the mapping $\Phi$ is Lipschitz continuous and the mapping $\Psi$ is maximal monotone, (3) converges weakly to a solution of VIP in the settings of real Hilbert spaces.

In 2019, Shehu [41] extended Tseng’s splitting method to the settings of real Banach spaces. He proposed the following iterative method for approximating solution of VIP in a 2-uniformly convex Banach space $\mathbb {E}$ which is also uniformly smooth as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} q_1 \in \mathbb {E},\\ w_k=J_{r_k}^{\Psi } J^{-1}(Jq_k-r_k \Phi q_k),\\ q_{k+1}=Jw_k-r_k(\Phi w_k-\Phi q_k),~\forall ~k \geqslant 1, \end{array}\right. } \end{aligned}$$

(4)

where $\Phi : \mathbb {E} \rightarrow \mathbb {E}$ is monotone and L-Lipschitz continuous, $J_{r_k}^{\Psi }=(J+ r_k \Psi )^{-1}J$ is the resolvent of $\Psi$ and J is the duality mapping from $\mathbb {E}$ to $\mathbb {E}^{*}$ ($\mathbb {E}^*$ is the dual of $\mathbb {E}$). He obtained a weak convergence result.

In 1964, Polyak [38] introduced the inertial extrapolation method which is a useful tool for speeding up the rate of convergence of iterative methods. The idea of inertial extrapolation method was inspired by an implicit discretization of a second-order in-time dissipative dynamical system, so-called heavy ball with friction. The heavy ball friction is a simplified version of the differential system describing the motion of a heavy ball that rolls over the graph f and that keep rolling under its own inertia until friction stop it at a critical point of f. This nonlinear oscillation with damping, which is called the "heavy ball with friction" system, has been considered by several authors from the optimization point of view, establishing different convergence results and identifying circumstances under which the rate of convergence is better than the one of the first-order-steepest descent method (see [4, 6, 38]). Alvarez and Attouch [5] introduced and constructed the heavy-ball method with the proximal point algorithm to solve a problem of maximal monotone operator. They defined their method as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} q_0, q_1 \in \mathbb {M},\\ w_k=q_k + \theta _{k}(q_k-q_{k-1}),\\ q_{k+1}=(I+ r_k \Psi )^{-1}w_k,~\forall ~k \geqslant 1, \end{array}\right. } \end{aligned}$$

(5)

where $\{\theta _{k}\} \subset [0,1)$ and $\{r_k\}$ is nondecreasing with $\sum \limits _{k=1}^{\infty }\theta _k\Vert q_k-q_{k-1}\Vert < \infty .$ They established that the sequence generated by (5) converges weakly to a zero of the monotone operator $\Psi$. In 2003, Moudafi and Oliny [32] introduced the following inertial proximal point method for finding the zero of the sum of two monotone operators:

$$\begin{aligned} {\left\{ \begin{array}{ll} w_k=q_k + \theta _{k}(q_{k}-q_{k-1}),\\ q_{k+1}=(I+ r_k \Psi )^{-1}(w_k-r_k\Phi q_k),~k \geqslant 1. \end{array}\right. } \end{aligned}$$

(6)

They obtained a weak convergence theorem provided that $r_k < \frac{2}{L}$ with L being the Lipschitz constant of $\Phi$ and $\sum \limits _{k=1}^{\infty }\theta _{k}\Vert q_{k}-q_{k-1}\Vert < \infty$ holds. Polyak [37] explored the potential of enhancing the convergence speed of numerical iteration methods for solving optimization problems by incorporating multistep inertial extrapolation steps. However, it is important to note that [37, 39] do not provide an established convergence analysis or rate of convergence for these multi-step inertial methods. Thus, the use of two or more inertial terms could guarantee necessary acceleration (see [30]). For growing interests in this direction (see [1, 2, 24, 51]).

Recently, Dong et al. [16] introduced the double inertial Mann algorithm and proved the convergence of the proposed algorithm under some suitable conditions: the algorithm is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} z_k=q_k + \lambda _k (q_k-q_{k-1}),\\ y_k=q_k + \theta _{k}(q_{k}-q_{k-1}),\\ q_{k+1}=(1-\phi _k) z_k + \phi T(y_k), \end{array}\right. } \end{aligned}$$

(7)

where T is a nonexpansive mapping, $\lambda , \theta \in [0,1]$ and $\phi \in (0,1).$

Very recently, Suantai et al. [45] also considered a double inertial forward–backward algorithm in the settings of real Hilbert spaces.

Extension of concepts and techniques from linear spaces to Riemannian manifolds has some important advantages (see [17, 22, 40]). For instance, some optimization problems with nonconvex objective functions become convex from the Riemannian geometry point of view, and some constrained optimization problems can be regarded as unconstrained ones with an appropriate Riemannian metric. In addition, the study of convex minimization problems and inclusion problems in nonlinear spaces have proved to be very useful in computing medians and means of trees, which are very important in computational phylogenetics, diffusion tensor imaging, consensus algorithms and modeling of airway systems in human lungs and blood vessels (see [9,10,11]). Thus, nonlinear spaces are more suitable frameworks for the study of optimization problems from linear to Riemannian manifolds.

Very recently, Khammahawong et al. [20] proposed the following forward–backward splitting method for solving variational inclusion problem (1) in the settings of a Hadamard manifold:

$$\begin{aligned} {\left\{ \begin{array}{ll} \textbf{0} \in \Gamma _{q_k, p_k}\Phi (p_k) + \Psi (q_k)-\frac{1}{\tau _k}\exp _{q_k}^{-1}p_k,\\ p_{k+1}=\exp _{q_k}(\tau _k(\Gamma _{q_k, p_k}\Phi (p_k)-\Psi (q_k))), \end{array}\right. } \end{aligned}$$

(8)

where

$$\begin{aligned} \tau _{k+1}= {\left\{ \begin{array}{ll} \min \left\{ \dfrac{\mu d(p_k,q_{k})}{\Vert \Gamma _{q_k,p_k}\Phi (p_k)-\Phi (q_{k})\Vert } ~~,~{\tau _k} \right\} ,\quad \text {if}~~ \Gamma _{q_k,p_k}\Phi (p_k)-\Phi (q_{k}) \ne 0, \\ \tau _k, \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \text {otherwise}, \end{array}\right. } \end{aligned}$$

(9)

and $\mu > 0.$ They proved that the sequence by their proposed method converges to an element in $\Omega$.

Furthermore, it will be crucial to expand the idea of the double inertial method to the Hadamard manifold because of the significance of our space of interest and the importance of the inertial method in dynamical systems.

Motivated by the aforementioned results in linear and nonlinear spaces, we proposed a forward–backward method together with a double step inertial method for solving variational inclusion problem in the settings of a Hadamard manifold. We prove that the sequence generated by our method converges to a solution of VIP (1) without the prior knowledge of the Lipschitz constant via a self-adaptive technique. In order to fasten the rate of convergence of our proposed method, we introduce a double inertial steps. Lastly, we compare our results with some related results in the literature to show the performance of our method. To the best of our knowledge, no result on double inertial steps have been discussed in the settings of nonlinear spaces. Our result extends and generalizes many related results in the literature.

2 Preliminaries

Let $\mathbb {P}$ be an m-dimensional manifold, let $x \in \mathbb {P}$ and let $T_x \mathbb {P}$ be the tangent space of $\mathbb {P}$ at $x \in \mathbb {P}$. We denote by $T\mathbb {P}=\bigcup _{x \in \mathbb {P}}T_x \mathbb {P}$ the tangent bundle of $\mathbb {P}$. An inner product $\mathcal {R}\langle \cdot , \cdot \rangle$ is called a Riemannian metric on $\mathbb {P}$ if $\langle \cdot ,\cdot \rangle _x:T_x \mathbb {P} \times T_x \mathbb {P} \rightarrow \mathbb {R}$ is an inner product for all $x \in \mathbb {P}.$ The corresponding norm induced by the inner product $\mathcal {R}_x \langle \cdot ,\cdot \rangle$ on $T_x \mathbb {P}$ is denoted by $\Vert \cdot \Vert _x.$ We will drop the subscript x and adopt $\Vert \cdot \Vert$ for the corresponding norm induced by the inner product. A differentiable manifold $\mathbb {P}$ endowed with a Riemannian metric $\mathcal {R}\langle \cdot ,\cdot \rangle$ is called a Riemannian manifold. In what follows, we denote the Riemannian metric $\mathcal {R} \langle \cdot ,\cdot \rangle$ by $\langle \cdot ,\cdot \rangle$ when no confusion arises. Given a piecewise smooth curve $\gamma :[a,b] \rightarrow \mathbb {P}$ joining x to y (that is, $\gamma (a)=x$ and $\gamma (b)=y$), we define the length $l(\gamma )$ of $\gamma$ by $l(\gamma ):= \int _{a}^{b}\Vert \gamma ^{\prime }(t)\Vert \textrm{d}t$. The Riemannian distance d(x, y) is the minimal length over the set of all such curves joining x to y. The metric topology induced by d coincides with the original topology on $\mathbb {P}$. We denote by $\nabla$ the Levi-Civita connection associated with the Riemannian metric [40].

Let $\gamma$ be a smooth curve in $\mathbb {P}$. A vector field X along $\gamma$ is said to be parallel if $\nabla _{\gamma ^{\prime }}X=\textbf{0}$, where $\textbf{0}$ is the zero tangent vector. If $\gamma ^{\prime }$ itself is parallel along $\gamma$, then we say that $\gamma$ is a geodesic and $\Vert \gamma ^{\prime }\Vert$ is a constant. If $\Vert \gamma ^{\prime }\Vert =1$, then the geodesic $\gamma$ is said to be normalized. A geodesic joining x to y in $\mathbb {P}$ is called a minimizing geodesic if its length equals d(x, y). A Riemannian manifold $\mathbb {P}$ equipped with a Riemannian distance d is a metric space $(\mathbb {P},d)$. A Riemannian manifold $\mathbb {P}$ is said to be complete if for all $x \in \mathbb {P}$, all geodesics emanating from x are defined for all $t \in \mathbb {R}$. The Hopf–Rinow theorem [40] posits that if $\mathbb {P}$ is complete, then any pair of points in $\mathbb {P}$ can be joined by a minimizing geodesic. Moreover, if $(\mathbb {P},d)$ is a complete metric space, then every bounded and closed subset of $\mathbb {P}$ is compact. If $\mathbb {P}$ is a complete Riemannian manifold, then the exponential map $\exp _{x}: T_x \mathbb {P} \rightarrow \mathbb {P}$ at $x \in \mathbb {P}$ is defined by

$$\begin{aligned} \exp _{x}v:= \gamma _{v}(1,x), \; ~~\forall ~ v \in T_x \mathbb {P}, \end{aligned}$$

where $\gamma _v(\cdot ,x)$ is the geodesic starting from x with velocity v (that is, $\gamma _v(0,x)=x$ and $\gamma _{v}^{\prime }(0,x)=v$). Then, for any t,  we have $\exp _{x}tv=\gamma _v(t,x)$ and $\exp _{x}{} \textbf{0}=\gamma _v(0,x)=x.$ Note that the mapping $\exp _x$ is differentiable on $T_x \mathbb {P}$ for every $x \in \mathbb {P}.$ The exponential map $\exp _{x}$ has an inverse $\exp _{x}^{-1}: \mathbb {P} \rightarrow T_x \mathbb {P}.$ For any $x,y \in \mathbb {P},$ we have $d(x,y)=\Vert \exp _{y}^{-1}x\Vert =\Vert \exp _{x}^{-1}y\Vert$ (see [40] for more details). The parallel transport $\Gamma _{\gamma ,\gamma (b),\gamma (a)}: T_{\gamma (a)}\mathbb {P} \rightarrow T_{\gamma (b)}\mathbb {P}$ on the tangent bundle $T\mathbb {P}$ along $\gamma :[a,b] \rightarrow \mathbb {R}$ with respect to $\nabla$ is defined by

$$\begin{aligned} \Gamma _{\gamma ,\gamma (b),\gamma (a)}v=F(\gamma (b)),~~\forall ~a,b \in \mathbb {R} ~~\text{ and }~ v \in T_{\gamma (a)}\mathbb {P}, \end{aligned}$$

where F is the unique vector field such that $\nabla _{\gamma ^{\prime }(t)}v=\textbf{0}$ for all $t\in [a,b]$ and $F(\gamma (a))=v.$ If $\gamma$ is a minimizing geodesic joining x to y,  then we write $\Gamma _{y,x}$ instead of $\Gamma _{\gamma ,y,x}.$ Note that for every $a,b,r,s \in \mathbb {R},$ we have

$$\begin{aligned} \Gamma _{\gamma (s),\gamma (r)} \circ \Gamma _{\gamma (r),\gamma (a)}=\Gamma _{\gamma (s),\gamma (a)}~~\text{ and }~~\Gamma _{\gamma (b),\gamma (a)}^{-1}=\Gamma _{\gamma (a),\gamma (b)}. \end{aligned}$$

Also, $\Gamma _{\gamma (b),\gamma (a)}$ is an isometry from $T_{\gamma (a)}\mathbb {P}$ to $T_{\gamma (b)}\mathbb {P},$ that is, the parallel transport preserves the inner product

$$\begin{aligned} \langle \Gamma _{\gamma (b),\gamma (a)}(u),\Gamma _{\gamma (b),\gamma (a)}(v) \rangle _{\gamma (b)} =\langle u,v \rangle _{\gamma (a)}, ~~\forall ~u,v \in T_{\gamma (a)}\mathbb {P}. \end{aligned}$$

(10)

Below is an example of a Hadamard manifold.

Space 1: Let $\mathbb {R}_{++}^{m}$ be the product space $\mathbb {R}_{++}^m:= \{(x_1,x_2, \cdots , x_m): x_i \in \mathbb {R}_{++},~i=1,2, \cdots , m\}$. Let $\mathbb {P} = (\mathbb {R}^m_{++}, \langle \cdot ,\cdot \rangle )$ be the m-dimensional Hadamard manifold with the Riemannian metric $\langle p,q \rangle =p^\textrm{T} q$ and the distance $d(x,y)=|\ln \frac{x}{y}|=|\ln \sum \limits _{i=1}^{m}\frac{x_i}{y_i}|,$ where $x,y \in \mathbb {P}$ with $x=\{x_i\}_{i=1}^{m}$ and $y=\{y_i\}_{i=1}^{m}$.

A subset $\mathcal {K} \subset \mathbb {P}$ is said to be convex if for any two points $x,y \in \mathcal {K},$ the geodesic $\gamma$ joining x to y is contained in $\mathcal {K}.$ That is, if $\gamma :[a,b] \rightarrow \mathbb {P}$ is a geodesic such that $x=\gamma (a)$ and $y=\gamma (b),$ then $\gamma ((1-t)a+tb) \in \mathcal {K}$ for all $t \in [0,1].$ A complete simply connected Riemannian manifold of non-positive sectional curvature is called a Hadamard manifold. We denote by $\mathbb {P}$ a finite dimensional Hadamard manifold. Henceforth, unless otherwise stated, we represent by $\mathcal {K}$ a nonempty, closed and convex subset of $\mathbb {P}.$

Next, let $\mathcal {H(K)}$ denote the set of all single-valued vector fields $U:\mathcal {K} \rightarrow T\mathbb {P}$ such that $U(p) \in T_{p}\mathbb {P}$, for each $p \in \mathcal {K}.$ Let $\mathcal {X(K)}$ denote to the set of all multivalued vector fields $V: \mathcal {K} \rightarrow 2^{T\mathbb {P}}$ such that $V(p)\subseteq T_{p}\mathbb {P}$ for each $p \in \mathcal {K},$ and the denote $\textrm{Dom}(V)$ the domain of V defined by $\textrm{Dom}(V)=\{p \in \mathcal {K}: V(p)\ne \varnothing \}.$

We state some results and definitions which are needed in the next section.

Definition 1

[50] A vector field $U \in \mathcal {H(K)}$ is said to be

• (i) monotone, if

  $$\begin{aligned} \langle U(p), \exp _{p}^{-1}q\rangle \leqslant \langle U(q), -\exp _{q}^{-1}p\rangle ,~\forall ~p,q \in \mathcal {K}, \end{aligned}$$

• (ii) L-Lipschitz continuous if there exists $L> 0$ such that

  $$\begin{aligned} \Vert \Gamma _{p,q}U(q)-U(p)\Vert \leqslant Ld(p,q),~\forall ~p, q \in \mathcal {K}. \end{aligned}$$

Definition 2

[14] A vector field $V \in \mathcal {X(K)}$ is said to be

• (i) monotone, if for all $p, q \in \textrm{Dom}(V)$,

  $$\begin{aligned} \langle u, \exp _{p}^{-1}q\rangle \leqslant \langle v, -\exp _{q}^{-1}p\rangle ,~\forall ~u \in V(p)~ \text {and}~\forall ~ v \in V(q), \end{aligned}$$

• (ii) maximal monotone if it is monotone and $\forall ~p \in \mathcal {K}$ and $u \in T_{p}\mathcal {K},$ the condition

  $$\begin{aligned} \langle u, \exp _{p}^{-1}q\rangle \leqslant \langle v, -\exp _{q}^{-1}p\rangle ,~\forall ~q \in \textrm{Dom}(V)~\text {and}~ \forall ~v \in V(q)~\text {implies that}~u \in V(p). \end{aligned}$$

Definition 3

[17] Let $\mathcal {K}$ be a nonempty, closed and subset of $\mathbb {P}$ and $\{x_n\}$ be a sequence in $\mathbb {P}$. Then, $\{x_n\}$ is said to be Fejèr convergent with respect to $\mathcal {K}$ if for all $p \in \mathcal {K}$ and $n \in \mathbb {N},$

$$\begin{aligned} d(x_{n+1}, p) \leqslant d(x_n, p). \end{aligned}$$

Definition 4

[25] Let $V \in \mathcal {X(K)}$ be a vector field and $x_0 \in \mathcal {K}.$ Then, V is said to be upper Kuratowski semicontinuous at $x_0$ if for any sequences $\{x_n\} \subseteq \mathcal {K}$ and $\{v_n\} \subset T\mathbb {P}$ with each $v_n \in V(x_n),$ the relations $\lim \limits _{n\rightarrow \infty } {v_n}=v_0$ imply that $v_0 \in V(x_0)$. Moreover, V is said to be upper Kuratowski semicontinuous on $\mathcal {K}$ if it is upper Kuratowski semicontinuous for each $x \in \mathcal {K}.$

Lemma 1

[17] Let $\mathcal {K}$ be a nonempty, closed and closed subset of $\mathbb {P}$ and $\{x_n\} \subset \mathbb {P}$ be a sequence such that $\{x_n\}$ be a Fejér convergent with respect to $\mathcal {K}.$ Then, the following hold:

• (i) For every $p \in \mathcal {K},~ d(x_n, p)$ converges.

• (ii)  $\{x_n\}$ is bounded.

• (iii) Assume that every cluster point of $\{x_n\}$ belongs to $\mathcal {K}$, then $\{x_n\}$ converges to a point in $\mathcal {K}$.

Proposition 1

[40]. Let $x \in \mathbb {P}$. The exponential mapping $\exp _{x}: T_x \mathbb {P} \rightarrow \mathbb {P}$ is a diffeomorphism. For any two points $x,y \in \mathbb {P},$ there exists a unique normalized geodesic joining x to y,  which is given by

$$\begin{aligned} \gamma (t)=\exp _{x}t\exp _{x}^{-1}y, \; ~~\forall ~ t \in [0,1]. \end{aligned}$$

A geodesic triangle $\Delta (p,q,r)$ of a Riemannian manifold $\mathbb {P}$ is a set containing three points p,  q,  r and three minimizing geodesics joining these points.

Proposition 2

[40]. Let $\Delta (p,q,r)$ be a geodesic triangle in $\mathbb {P}$. Then

$$\begin{aligned} d^2(p,q)+d^2(q,r)-2\langle \exp _{q}^{-1}p,\exp _{q}^{-1}r \rangle \leqslant d^2(r,q) \end{aligned}$$

(11)

and

$$\begin{aligned} d^2(p,q) \leqslant \langle \exp _{p}^{-1}r,\exp _{p}^{-1}q \rangle + \langle \exp _{q}^{-1}r,\exp _{q}^{-1}p \rangle . \end{aligned}$$

(12)

Moreover, if $\theta$ is the angle at p,  then we have

$$\begin{aligned} \langle \exp _{p}^{-1}q,\exp _{p}^{-1}r\rangle =d(q,p)d(p,r)\cos \theta . \end{aligned}$$

(13)

Also,

$$\begin{aligned} \Vert \exp _{p}^{-1}q\Vert ^2=\langle \exp _{p}^{-1}q,\exp _{p}^{-1}q \rangle =d^2(p,q). \end{aligned}$$

(14)

Remark 1

[25] If $x, y \in \mathbb {P}$ and $v \in T_{y}\mathbb {P},$ then

$$\begin{aligned} \langle v, -\exp _{y}^{-1}x\rangle =\langle v, \Gamma _{y,x}\exp _{x}^{-1}y\rangle =\langle \Gamma _{x,y}v, \exp _{x}^{-1}y\rangle . \end{aligned}$$

(15)

Lemma 2

[21] Let $\mathbb {P}$ be a Hadamard manifold and let $u,v, w \in \mathbb {P}.$ Then,

$$\begin{aligned} \Vert \exp _{u}^{-1}w-\Gamma _{u,v}\exp _{v}^{-1}w\Vert \leqslant d(u,v). \end{aligned}$$

Lemma 3

[25] Let $x_0 \in \mathbb {P}$ and $\{x_n\} \subset \mathbb {P}$ with $x_n \rightarrow x_0.$ Then, the following assertions hold:

• (i) For any $y \in \mathbb {P},$ we have $\exp _{x_n}^{-1}y \rightarrow \exp _{x_0}^{-1}x_n$ and $\exp _{y}^{-1}x_n \rightarrow \exp _{y}^{-1}x_0.$

• (ii) If $v_n \in T_{x_n}\mathbb {P}$ and $v_n \rightarrow v_0,$ then $v_0 \in T_{x_0}\mathbb {P}.$

• (iii) Given $u_n,v_n \in T_{x_n}\mathbb {P}$ and $u_0, v_0 \in T_{x_0}\mathbb {P}$, if $u_n \rightarrow u_0,$ then $\langle u_n, v_n\rangle \rightarrow \langle u_0, v_0\rangle .$

• (iv) For any $u \in T_{x_0}\mathbb {P},$ the function $F: \mathbb {P} \rightarrow T\mathbb {P},$ defined by $F(x)=\Gamma _{x, x_0}u$ for each $x \in \mathbb {P}$ is continuous on $\mathbb {P}$.

The next lemma presents the relationship between triangles in $\mathbb {R}^2$ and geodesic triangles in Riemannian manifolds (see [12]).

Lemma 4

[12]. Let $\Delta (x_1,x_2,x_3)$ be a geodesic triangle in $\mathbb {P}.$ Then, there exists a triangle $\Delta (\bar{x}_1,\bar{x}_2,\bar{x}_3)$ corresponding to $\Delta (x_1,x_2,x_3)$ such that $d(x_i,x_{i+1})=\Vert \bar{x}_{i}-\bar{x}_{i+1}\Vert$ with the indices taken modulo 3. This triangle is unique up to isometries of $\mathbb {R}^2.$

The triangle $\Delta (\bar{x}_1,\bar{x}_2,\bar{x}_3)$ in Lemma 4 is said to be the comparison triangle for $\Delta (x_1,x_2,x_3) \subset \mathbb {P}.$ The points $\bar{x}_1,$ $\bar{x}_2$ and $\bar{x}_3$ are called comparison points to the points $x_1,x_2$ and $x_3$ in $\mathbb {P}.$

A function $h: \mathbb {P} \rightarrow \mathbb {R}$ is said to be geodesic if for any geodesic $\gamma \in \mathbb {P},$ the composition $h \circ \gamma : [u,v] \rightarrow \mathbb {R}$ is convex, that is,

$$\begin{aligned} h \circ \gamma (\lambda u+(1-\lambda )v) \leqslant \lambda h \circ \gamma (u)+(1-\lambda )h\circ \gamma (v),~~u,v \in \mathbb {R}, ~\lambda \in [0,1]. \end{aligned}$$

Lemma 5

[25] Let $\Delta (p,q,r)$ be a geodesic triangle in a Hadamard manifold $\mathbb {P}$ and $\Delta (p^{\prime }, q^{\prime }, r^{\prime })$ be its comparison triangle.

• (i) Let $\alpha , \beta , \gamma$ (resp. $\alpha ^{\prime }, \beta ^{\prime }, \gamma ^{\prime })$ be the angles of $\Delta (p,q,r)$ (resp. $\Delta (p^{\prime }, q^{\prime }, r^{\prime }))$ at the vertices p,q,r (resp. $p^{\prime }, q^{\prime }, r^{\prime })$. Then, the following inequalities hold:

  $$\begin{aligned} \alpha ^{\prime } \geqslant \alpha , ~\beta ^{\prime } \geqslant \beta ,~\gamma ^{\prime }\geqslant \gamma . \end{aligned}$$

• (ii) Let z be a point in the geodesic joining p to q and $z^{\prime }$ its comparison point in the interval $[p^{\prime }, q^{\prime }].$ Suppose that $d(z,p)=\Vert z^{\prime }-p^{\prime }\Vert$ and $d(z^{\prime },q^{\prime })=\Vert z^{\prime }-q^{\prime }\Vert$. Then, the following inequality holds:

  $$\begin{aligned} d(z,r)\leqslant \Vert z^{\prime }-r^{\prime }\Vert . \end{aligned}$$

Lemma 6

[25] Let $x_0 \in \mathbb {P}$ and $\{x_n\} \subset \mathbb {P}$ be such that $x_n \rightarrow x_0.$ Then, for any $y \in \mathbb {P},$ we have $\exp _{x_n}^{-1}y \rightarrow \exp _{x_0}^{-1}y$ and $\exp _{y}^{-1}x_n \rightarrow \exp _{y}^{-1}x_0.$

The following propositions (see [17]) are very useful in our convergence analysis:

Proposition 3

Let $\mathbb {P}$ be a Hadamard manifold and $d: \mathbb {P} \times \mathbb {P}: \rightarrow \mathbb {R}$ be the distance function. Then the function d is convex with respect to the product Riemannian metric. In other words, given any pair of geodesics $\gamma _1: [0,1] \rightarrow \mathbb {P}$ and $\gamma _2: [0,1] \rightarrow \mathbb {P},$ then for all $t \in [0,1],$ we have

$$\begin{aligned} d(\gamma _1(t),\gamma _2(t)) \leqslant (1-t)d(\gamma _1(0),\gamma _2(0))+td(\gamma _1(1),\gamma _2(1)). \end{aligned}$$

In particular, for each $y \in \mathbb {P},$ the function $d(\cdot ,y): \mathbb {P} \rightarrow \mathbb {R}$ is a convex function.

Proposition 4

Let $\mathbb {P}$ be a Hadamard manifold and $x \in \mathbb {P}$. The map $\Phi _x=d^2(x,y)$ satisfying the following:

• (1) $\Phi _x$ is convex. Indeed, for any geodesic $\gamma : [0,1] \rightarrow \mathbb {P}$, the following inequality holds for all $t \in [0,1]:$

  $$\begin{aligned} d^2(x, \gamma (t)) \leqslant (1-t)d^2(x, \gamma (0)) + td^2(x, \gamma (1))-t(1-t)d^2(\gamma (0), \gamma (1)). \end{aligned}$$

• (2) $\Phi _x$ is smooth. Moreover, $\partial \Phi _x(y)=-2\exp _{y}^{-1}x.$

Lemma 7

[18] Let $\{v_n\}$ and $\{\delta _n\}$ be nonnegative sequences which satisfy

$$\begin{aligned} v_{n+1}=(1+\delta _n)v_n + \delta _n v_{n-1},~n \geqslant 1. \end{aligned}$$

Then,

$$\begin{aligned} v_{n+1}\leqslant M \cdot \prod \limits _{j=1}^{n}(1+ 2 \delta _j),~\text {where}~M=\max \{v_1, v_2\}. \end{aligned}$$

Moreover, if $\sum \limits _{n=1}^{\infty }\delta _n < + \infty ,$ then $\{v_n\}$ is bounded.

Lemma 8

[34] Let $\{a_n\}, \{\varphi _n\}$ and $\{\beta _n\}$ be nonnegative sequences which satisfy

$$\begin{aligned} a_{n+1}=(1+ \beta _n)a_n + \varphi _n,~n \geqslant 1. \end{aligned}$$

If $\sum \limits _{n=1}^{\infty }\beta _n< + \infty$ and $\sum \limits _{n=1}^{\infty }\varphi _n < + \infty ,$ then $\lim \limits _{n \rightarrow \infty }a_n$ exists.

3 Main Result

In this section, we present an iterative method for solving variational inclusion problem in the settings of Hadamard manifolds. We state the following assumptions:

Assumption 1

 

• (L1) $\Phi \in \mathcal {H(K)}$ is monotone and L-Lipschitz continuous, and $\Psi \in \mathcal {X(K)}$ is maximal monotone.

• (L2) The solution set $\Omega := (\Phi +\Psi )^{-1}(\textbf{0})$ is nonempty.

• (L3) $\{\lambda _k\}$ is a nonnegative real numbers sequence such that $\sum \limits _{k=1}^{\infty }\lambda _k< \infty .$

We start by establishing a technical lemma useful to our analysis.

Lemma 9

[2, 27] Let $\{q_k\}$ be a sequence generated by Algorithm 19 and the sequence $\{\rho _{k}\}$ is generated by (19). Then we have that $\lim \limits _{k \rightarrow \infty }\rho _{k}=\rho$ and $\rho \in \bigg [\min \big \{\frac{\mu }{L},~ \rho _{0}\big \}, \rho _{0}+ \lambda \bigg ],$ where $\lambda =\sum \limits _{k=0}^{\infty }\lambda _k.$

Remark 10

It is obvious that the stepsize in Algorithm 19 is allowed to increase from iteration to iteration and so (19) reduces the dependence on the initial stepsize $\rho _{0}$. Also, since $\{\lambda _k\}$ is summable, we obtain $\lim \limits _{k \rightarrow \infty }\lambda _k=0.$ Thus the stepsize $\lambda _{k}$ may be non-increasing when k is large. If $\lambda _k \equiv 0,$ the step size in (19) reduces to the one in [20].

Theorem 1

Suppose that Assumptions (L1)-(L3) holds and let $\{q_k\}$ be a sequence generated by Algorithm 19. If $\sum \nolimits _{k=1}^{\infty }\alpha _k < +\infty$ and $\sum \nolimits _{k=1}^{\infty }\theta _k < + \infty ,$ then

• (i) $d(q_{k+1}, p) \leqslant M \cdot \prod \limits _{j=1}^{k}(1+ 2(\alpha _j + \theta _j(1+\alpha _j))),$ where $M:=\max \{d(q_1, p), d(q_2, p)\}.$

• (ii) The sequence $\{q_k\}$ converges to an element in $\Omega .$

Proof

Let $p \in \Omega ,$ then $-\Phi (q) \in \Psi (p)$. Using (16) of Algorithm 19, we get $\frac{1}{\rho _k}\exp _{t_k}^{-1}z_k-\Gamma _{t_k,z_k}\Phi (z_k) \in \Psi (t_k).$ By applying the monotonicity of $\Psi$, we deduce that

$$\begin{aligned} \big \langle \frac{1}{\rho _k}\exp _{t_k}^{-1}z_k-\Gamma _{t_k,z_k}\Phi (z_k), \exp _{t_k}^{-1}p\big \rangle&\leqslant \langle -\Phi (p),-\exp _{p}^{-1}t_k \rangle \nonumber \\&=\langle \Phi (p), \exp _{p}^{-1}t_k \rangle . \end{aligned}$$

(20)

Since $\Phi$ is a monotone vector field, then

$$\begin{aligned} \langle \Phi (p), \exp _{p}^{-1}t_k \rangle \leqslant \langle -\Phi (t_k), \exp _{t_k}^{-1}p\rangle . \end{aligned}$$

(21)

By combining (20) and (21), we have

$$\begin{aligned} \big \langle \frac{1}{\rho _k}\exp _{t_k}^{-1}z_k-\Gamma _{t_k,z_k}\Phi (z_k), \exp _{t_k}^{-1}p\big \rangle \leqslant \langle -\Phi (t_k), \exp _{t_k}^{-1}p\rangle , \end{aligned}$$

thus

$$\begin{aligned} \langle \exp _{t_k}^{-1}z_k, \exp _{t_k}^{-1}p\rangle \leqslant \rho _k \langle \Gamma _{t_k, z_k}\Phi (z_k)-\Phi (t_k), \exp _{t_k}^{-1}p\rangle . \end{aligned}$$

(22)

Now, for $k \in \mathbb {N}.$ Let $\Delta (z_k, t_k, p) \subseteq \mathbb {P}$ be a geodesic triangle with vertices $z_k, t_k$ and p and let $\Delta (z_k^{\prime }, t_k^{\prime }, p^{\prime })\subset \mathbb {R}^2$ be the corresponding comparison triangle, thus we have from Lemma 5 (ii) that $d(z_k, p)=\Vert z_k^{\prime }-p^{\prime }\Vert ,~ d(t_k, p)=\Vert t_k^{\prime }-p^{\prime }\Vert$ and $d(t_k^{\prime }, z_k^{\prime })=\Vert t_k^{\prime }-z_k^{\prime }\Vert$. Also, let $\Delta (q_{k+1}, t_k, p) \subseteq \mathbb {P}$ be a geodesic triangle with vertices $q_{k+1},~ t_k$ and p, then $\Delta (q_{k+1}^{\prime }, t_k^{\prime }, p^{\prime }) \subseteq \mathbb {R}^2$ is the corresponding comparison triangle. Hence, we have $d(q_{k+1}, p)=\Vert q_{k+1}^{\prime }-p^{\prime }\Vert , ~d(t_k, p)=\Vert t_k^{\prime }-p^{\prime }\Vert$ and $d(q_{k+1}, t_k)=\Vert q_{k+1}^{\prime }-t_k^{\prime }\Vert .$

Now,

$$\begin{aligned} d^2(q_{k+1},p)&\leqslant \Vert q_{k+1}^{\prime }-p^{\prime }\Vert ^2\nonumber \\&=\Vert q_{k+1}^{\prime }-t_k^{\prime }+ t_k^{\prime }-p^{\prime }\Vert ^2\nonumber \\&=\Vert t_k^{\prime }-p^{\prime }\Vert ^2 +\Vert q_{k+1}^{\prime }-t_k^{\prime }\Vert ^2 + 2\langle q_{k+1}^{\prime }-t_k^{\prime }, t_k^{\prime }-p^{\prime }\rangle \nonumber \\&=\Vert (t_k^{\prime }-z_k^{\prime })+(z_k^{\prime }-p^{\prime })\Vert ^2+\Vert q_{k+1}^{\prime }-t_k^{\prime }\Vert ^2 + 2\langle q_{k+1}^{\prime }-t_k^{\prime }, t_k^{\prime }-p^{\prime }\rangle \nonumber \\&=\Vert t_k^{\prime }-z_k^{\prime }\Vert ^2 + \Vert z_k^{\prime }-p^{\prime }\Vert ^2 +\Vert q_{k+1}^{\prime }-t_k^{\prime }\Vert ^2 + 2 \langle t_{k}^{\prime }-z_k^{\prime }, z_k^{\prime }-p^{\prime }\rangle \nonumber \\&\quad + 2\langle t_k^{\prime }-p^{\prime },t_k^{\prime }-p^{\prime } \rangle -2\Vert t_k^{\prime }-p^{\prime }\Vert ^2 +2\langle q_{k+1}^{\prime }-t_k^{\prime }, t_k^{\prime }-p^{\prime }\rangle \nonumber \\&\quad + 2\langle t_k^{\prime }-z_k^{\prime }, t_k^{\prime }-z_k^{\prime }\rangle \nonumber \\&\quad -2\langle t_k^{\prime }-z_k^{\prime }, t_k^{\prime }-z_k^{\prime }\rangle \nonumber \\&=d^2(z_k, p) - d^2(t_k,z_k) + \Vert q_{k+1}^{\prime }-t_k^{\prime }\Vert ^2 + 2\langle t_k^{\prime }-z_k^{\prime }, t_k^{\prime }-p^{\prime }\rangle \nonumber \\&\quad + 2 \langle q_{k+1}^{\prime }-t_k^{\prime }, t_k^{\prime }-p^{\prime }\rangle \nonumber \\&\quad + 2\langle t_k^{\prime }-p^{\prime }, t_k^{\prime }-p^{\prime }\rangle -2d^2(t_k,p) \nonumber \\&=d^2(z_k,p) -d^2(t_k, z_k) + \Vert q_{k+1}^{\prime }-t_k^{\prime }\Vert ^2 + 2 \langle t_k^{\prime }-z_k^{\prime }, t_k^{\prime }-p^{\prime }\rangle \nonumber \\&\quad + 2\langle q_{k+1}^{\prime }-p^{\prime }, t_k^{\prime }-p^{\prime }\rangle -2d^2(t_k, p). \end{aligned}$$

(23)

Let r and $r^{\prime }$ be the angles of the vertices $t_k$ and $t_k^{\prime }$, respectively. By Lemma 5 (i), we get $r^{\prime } \geqslant r$. Therefore, we obtain from Lemma 4 and (13) that

$$\begin{aligned} \langle t_k^{\prime }-z_k^{\prime }, t_k^{\prime }-p^{\prime }\rangle&=\Vert t_k^{\prime }-z_k^{\prime }\Vert \cdot \Vert t_k^{\prime }-p^{\prime }\Vert \textrm{cos} r^{\prime }\nonumber \\&=d(t_k,z_k)d(p,t_k)\textrm{cos} r^{\prime }\nonumber \\&\leqslant d(t_k, z_k)d(p, t_k)\textrm{cos} r\nonumber \\&=\langle \exp _{t_k}^{-1}z_k, \exp _{t_k}^{-1}p\rangle . \end{aligned}$$

(24)

Following the same argument as in (24), we have

$$\begin{aligned} \langle q_{k+1}^{\prime }-p^{\prime }, t_k^{\prime }-p^{\prime }\rangle&=\langle \exp _{p}^{-1}q_{k+1}, \exp _{p}^{-1}t_k\rangle . \end{aligned}$$

(25)

Hence, we deduce from (18) that

$$\begin{aligned} \Vert q_{k+1}^{\prime }-t_k^{\prime }\Vert ^2 \leqslant \rho _k^{2}\Vert \Gamma _{t_k, z_k}\Phi (z_k)-\Phi (t_k)\Vert ^2. \end{aligned}$$

(26)

On substituting (24), (25) and (26) into (23), we obtain

$$\begin{aligned} d^2(q_{k+1},p)&\leqslant d^2(z_k,p) - d^2(t_k,z_k) + \rho _{k}^2\Vert \Gamma _{t_k,z_k}\Phi (z_k)-\Phi (t_k)\Vert ^2 \nonumber \\&\quad + 2\langle \exp _{t_k}^{-1}z_k, \exp _{t_k}^{-1}p\rangle -2d^2(t_k, p)\nonumber \\&\quad + 2\langle \exp _{p}^{-1}q_{k+1}, \exp _{p}^{-1}t_k\rangle . \end{aligned}$$

(27)

Using Remark 1, Lemma 2 and (27), we get

$$\begin{aligned} d^2(q_{k+1}, p)&\leqslant d^2(z_k, p)-d^2(t_k,z_k) + \rho _{k}^2\Vert \Gamma _{t_k,z_k}\Phi (z_k)-\Phi (t_k)\Vert ^2-2 d^2(t_k,p)\nonumber \\&\quad + 2 \langle \exp _{p}^{-1}q_{k+1}-\Gamma _{p,t_k} \exp _{t_k}^{-1}q_{k+1}+\Gamma _{p,t_k}\exp _{t_k}^{-1}q_{k+1}, \exp _{p}^{-1}t_k\rangle \nonumber \\&\quad + 2\langle \exp _{t_k}^{-1}z_k, \exp _{t_k}^{-1}p\rangle \nonumber \\&= d^2(z_k,p)-d^2(t_k, z_k)+ \rho _{k}^2\Vert \Gamma _{t_k,z_k}\Phi (z_k)-\Phi (t_k)\Vert ^2-2 d^2(t_k,p)\nonumber \\&\quad + 2 \langle \exp _{t_k}^{-1}z_k, \exp _{t_k}^{-1}p\rangle + 2 \langle \exp _{p}^{-1}q_{k+1}-\Gamma _{p,t_k}\exp _{t_k}^{-1}q_{k+1}, \exp _{p}^{-1}t_k\rangle \nonumber \\&\quad + 2 \langle \Gamma _{p,t_k} \exp _{t_k}^{-1}q_{k+1}, \exp _{p}^{-1}t_k\rangle \nonumber \\&\leqslant d^2(z_k,p)-d^2(t_k,z_k) + \rho _{k}^2\Vert \Gamma _{t_k,z_k}\Phi (z_k)-\Phi (t_k)\Vert ^2-2 d^2(t_k,p)\nonumber \\&\quad + 2 \Vert \exp _{p}^{-1}q_{k+1}-\Gamma _{p,t_k} \exp _{t_k}^{-1}q_{k+1}\Vert \Vert \exp _{p}^{-1}t_k\Vert + 2 \langle \exp _{t_k}^{-1}z_k, \exp _{t_k}^{-1}p\rangle \nonumber \\&\quad -2 \langle \exp _{t_k}^{-1}q_{k+1}, \exp _{t_k}^{-1}p\rangle , \end{aligned}$$

(28)

which also implies that

$$\begin{aligned} d^2(q_{k+1}, p)&\leqslant d^2(z_{k}, p)-d^2(t_k,z_k)+ \rho _{k}^2\Vert \Gamma _{t_k,z_k}\Phi (z_k)-\Phi (t_k)\Vert ^2-2 d^2(t_k,p)\nonumber \\&\quad + 2d^2(p,t_k) + 2 \langle \exp _{t_k}^{-1}z_k, \exp _{t_k}^{-1}p\rangle -2 \langle \exp _{t_k}^{-1}q_{k+1}, \exp _{t_k}^{-1}p\rangle \nonumber \\&=d^2(z_k,p) -d^2(t_k,z_k) + \rho _{k}^2\Vert \Gamma _{t_k,z_k}\Phi (z_k)-\Phi (t_k)\Vert ^2+ 2 \langle \exp _{t_k}^{-1}z_k, \exp _{t_k}^{-1}p\rangle \nonumber \\&\quad -2 \langle \exp _{t_k}^{-1}q_{k+1}, \exp _{t_k}^{-1}p\rangle . \end{aligned}$$

(29)

It follows from the definition of $q_{k+1}$ that $\exp _{t_k}^{-1}q_{k+1}=\rho _k(\Gamma _{t_k,z_k}\Phi (z_k)-\Phi (t_k)).$ Using the last inequality, we obtain that

$$\begin{aligned} d^2(q_{k+1},p)&\leqslant d^2(z_k,p)-d^2(t_k,z_k) +\rho _{k}^2\Vert \Gamma _{t_k,z_k}\Phi (z_k)-\Phi (t_k)\Vert ^2 + 2 \langle \exp _{t_k}^{-1}z_k, \exp _{t_k}^{-1}p\rangle \nonumber \\&\quad -2 \rho _{k} \langle \Gamma _{t_k,z_k} \Phi (z_k)-\Phi (t_k), \exp _{t_k}^{-1}p\rangle \nonumber \\&=d^2(z_k,p)-d^2(t_k,z_k) + \rho _{k}^2\Vert \Gamma _{t_k,z_k}\Phi (z_k)-\Phi (t_k)\Vert ^2 + 2 \langle \exp _{t_k}^{-1}z_k, \exp _{t_k}^{-1}p\rangle \nonumber \\&\quad + 2 \rho _k \langle \Phi (t_k)-\Gamma _{t_k,z_k}\Phi (z_k), \exp _{t_k}^{-1}p\rangle . \end{aligned}$$

(30)

By substituting (19) and (22) in (30), we get

$$\begin{aligned} d^2(q_{k+1},p)&\leqslant d^2(z_k,p)-d^2(t_k,z_k) + \mu ^2 \frac{\rho _k^2}{\rho _{k+1}^2}d^2(t_k,z_k)\nonumber \\&\quad + 2\rho _k\langle \Phi (t_k)-\Gamma _{t_k,z_k}\Phi (z_k), \exp _{t_k}^{-1}p\rangle -2 \rho _k \langle \Phi (t_k) -\Gamma _{t_k,z_k}\Phi (z_k), \exp _{t_k}^{-1}p\rangle \nonumber \\&=d^2(z_k,p)-\big (1-\mu ^2\frac{\rho _k^2}{\rho _{k+1}^{2}}\big )d^2(t_k,z_k). \end{aligned}$$

(31)

By utilizing the geodesic triangles $\bigtriangleup (w_k, q_k, p) \subset \mathbb {P}$ and $\bigtriangleup (q_k, q_{k-1}, p) \subset \mathbb {P}$ with their respective comparison triangles $\bigtriangleup (w_k^{\prime }, q_{k}^{\prime }, p^{\prime }) \subseteq \mathbb {R}^2$. Then, by Lemma 5 (ii), we have $d(w_k, q_k)= \Vert w_k^{\prime }-q_k^{\prime }\Vert ,~ d(w_k, p)=\Vert w_k^{\prime }-p^{\prime }\Vert$ and $d(q_{k}, q_{k-1})=\Vert q_{k}^{\prime }-q_{k-1}^{\prime }\Vert$. Similarly, using the geodesic triangles $\bigtriangleup (z_k, w_k, p) \subset \mathbb {P}$ and $\bigtriangleup (q_k, q_{k-1}, p) \subset \mathbb {P}$ with their respective comparison triangle $\bigtriangleup (z_{k}^{\prime }, w_{k}^{\prime }, p^{\prime }) \subseteq \mathbb {R}^2$. Then, by Lemma 5 (ii), we have $d(z_k, w_k)=\Vert z_k^{\prime }-w_{k}^{\prime }\Vert ,~ d(z_k, q_k)=\Vert z_{k}^{\prime }-q_{k}^{\prime }\Vert$ and $d(z_k, p)=\Vert z_{k}^{\prime }-p^{\prime }\Vert$. From step 1 of Algorithm 19, we have that $w_k^{\prime }=q_k^{\prime } + \alpha _k(q_{k}^{\prime }-q_{k-1}^{\prime })$ and $z_{k}^{\prime }=w_{k}^{\prime } + \theta _k(w_{k}^{\prime }-q_{k-1}^{\prime })$, thus

$$\begin{aligned} d(w_k, p)&=\Vert w_k^{\prime }-p^{\prime }\Vert \nonumber \\&=\Vert q_{k}^{\prime } + \alpha _k(q_{k}^{\prime }-q_{k-1}^{\prime })-p^{\prime }\Vert \nonumber \\&\leqslant \Vert q_{k}^{\prime }-p^{\prime }\Vert + \alpha _k\Vert q_{k}^{\prime }-q_{k-1}^{\prime }\Vert \nonumber \\&=d(q_k, p) + \alpha _kd(q_{k}, q_{k-1}). \end{aligned}$$

(32)

Similarly, it is easy to see that

$$\begin{aligned} d(w_k, q_{k-1})&=\Vert w_{k}^{\prime }-q_{k-1}^{\prime }\Vert \nonumber \\&=\Vert q_{k}^{\prime }+ \alpha _k(q_{k}^{\prime }-q_{k-1}^{\prime })-q_{k-1}^{\prime }\Vert \nonumber \\&\leqslant \Vert q_{k}^{\prime }-q_{k-1}^{\prime }\Vert + \alpha _k\Vert q_{k}^{\prime }-q_{k-1}^{\prime }\Vert \nonumber \\&=d(q_{k}, q_{k-1}) + \alpha _k d(q_{k}, q_{k-1})\nonumber \\&=(1+ \alpha _k)d(q_{k}, q_{k-1}). \end{aligned}$$

(33)

By definition of $z_{k},$ (32) and (33), we get

$$\begin{aligned} d(z_k, p)&=\Vert z_{k}^{\prime }-p^{\prime }\Vert \nonumber \\&=\Vert w_{k}^{\prime } + \theta _k(w_{k}^{\prime }-q_{k-1}^{\prime })-p^{\prime }\Vert \nonumber \\&\leqslant \Vert w_{k}^{\prime }-p^{\prime }\Vert + \theta _k\Vert w_{k}^{\prime }-q_{k-1}^{\prime }\Vert \nonumber \\&=d(w_{k}, p) + \theta _k d(w_k, q_{k-1})\nonumber \\&\leqslant d(q_{k}, p) + \alpha _k d(q_{k}, q_{k-1}) + \theta _k(1+\alpha _k)d(q_{k}, q_{k-1})\nonumber \\&=d(q_{k}, p) + (\alpha _k + \theta _k(1+ \alpha _k))d(q_{k}, q_{k-1}). \end{aligned}$$

(34)

Since $\lim \limits _{k \rightarrow \infty }\big (1-\mu ^2\frac{\rho _k^{2}}{\rho _{k+1}^2}\big ) =1-\mu ^2 > 0,$ this implies that there exists $N> 0$ such that $1-\mu ^2 \frac{\rho _k^{2}}{\rho _{k+1}^2} > 0, \forall ~k \geqslant \mathbb {N}.$

From (31) and (34), we deduce that

$$\begin{aligned} d(q_{k+1}, p)&\leqslant d(z_{k}, p)\nonumber \\&\leqslant d(q_{k}, p) + (\alpha _k + \theta _k(1+ \alpha _k))d(q_{k}, q_{k-1})\nonumber \\&\leqslant d(q_k, p) + (\alpha _k + \theta _k(1+ \alpha _k))\big (d(q_{k}, p) + d(q_{k-1}, p)\big )\nonumber \\&=(1+ \alpha _k + \theta _k(1+ \alpha _k))d(q_{k}, p) + (\alpha _k+ \theta _k(1+ \alpha _k))d(q_{k-1}, p). \end{aligned}$$

(35)

By applying Lemma 7, we obtain that

$$\begin{aligned} d(q_{k+1}, p) \leqslant M \cdot \prod _{j=1}^{k} (1+ 2(\alpha _j+ \theta _j(1+\alpha _j))), \end{aligned}$$

(36)

where $M=\max \{d(q_1, p), d(q_2, p)\}$. Hence, the proof completes.

To establish the second part of the proof, we need to show that $\{q_k\}$ converges to a point in $\Omega .$ Since $\sum \limits _{k=1}^{\infty }\alpha _k < + \infty$ and $\sum \limits _{k=1}^{\infty }\theta _k < + \infty$, by Lemma 7 and (36), the sequence $\{q_k\}$ is bounded. This also implies that $\sum \limits _{k=1}^{\infty }\alpha _k d(q_{k},q_{k-1}) < + \infty$ and $\sum \limits _{k=1}^{\infty }\theta _k d(q_{k},q_{k-1}) < + \infty .$ Using Lemma 8 in (35), we can claim that $\lim \limits _{k \rightarrow \infty } d(q_{k}, p)$ exists. We have from Lemma 5 (ii) and Proposition 4 that

$$\begin{aligned} d^2(w_k, p)&=\Vert w_{k}^{\prime }-p^{\prime }\Vert ^2\nonumber \\&=\Vert q_{k}^{\prime }+ \alpha _k(q_{k}^{\prime }-q_{k-1}^{\prime })-p^{\prime }\Vert ^2\nonumber \\&=\Vert (1+ \alpha _k)(q_{k}^{\prime }-p^{\prime })-\alpha _k(q_{k-1}^{\prime }-p^{\prime })\Vert ^2\nonumber \\&=(1+\alpha _k)d^2(q_{k}, p)-\alpha _kd^2(q_{k-1}, p) + \alpha _k(1+\alpha _k)d^2(q_{k}, q_{k-1}). \end{aligned}$$

(37)

We also consider

$$\begin{aligned} d^2(w_{k}, q_{k-1})&=\Vert w_{k}^{\prime }-q_{k-1}^{\prime }\Vert ^2\nonumber \\&=\Vert q_{k}^{\prime }+ \alpha _k(q_{k}^{\prime }-q_{k-1}^{\prime })-q_{k-1}^{\prime }\Vert ^2\nonumber \\&=\Vert q_{k}^{\prime }-q_{k-1}^{\prime }\Vert ^2 + 2 \langle q_{k}^{\prime }-q_{k-1}^{\prime }, \alpha _k(q_{k}^{\prime }-q_{k-1}^{\prime })\rangle \nonumber \\ {}&\quad + \alpha _k^2\Vert q_{k}^{\prime }-q_{k-1}^{\prime }\Vert ^2. \end{aligned}$$

(38)

But from (14), we have

$$\begin{aligned} \langle q_{k}^{\prime }-q_{k-1}^{\prime }, q_{k}^{\prime }-q_{k-1}^{\prime }\rangle&\leqslant \langle \exp _{q_{k-1}}^{-1}q_{k}, \exp _{q_{k-1}}^{-1}q_k\rangle \nonumber \\&=\Vert \exp _{q_{k-1}}^{-1}q_k\Vert ^2\nonumber \\&=d^2(q_{k}, q_{k-1}). \end{aligned}$$

(39)

On substituting (39) into (38), we get

$$\begin{aligned} d^2(w_k, q_{k-1})&\leqslant d^2(q_{k}, q_{k-1}) + 2 \alpha _k d^2(q_{k}, q_{k-1}) + \alpha _k^2 d^2(q_{k}, q_{k-1})\nonumber \\&=(1+ \alpha _k)^2d^2(q_{k}, q_{k-1}). \end{aligned}$$

(40)

We deduce from Lemma 5, (37) and (40) that

$$\begin{aligned} d^2(z_{k}, p)&=\Vert z_{k}^{\prime }-p^{\prime }\Vert ^2\nonumber \\&=\Vert w_{k}^{\prime }+ \theta _k(w_{k}^{\prime }-q_{k-1}^{\prime })-p^{\prime }\Vert ^2\nonumber \\&=\Vert (1+ \theta _k)(w_{k}^{\prime }-q_{k-1}^{\prime })-\theta _k(q_{k-1}^{\prime }-p^{\prime })\Vert ^2\nonumber \\&=(1+ \theta _k)d^2(w_{k}, q_{k-1})-\theta _kd^2(q_{k-1}, p) + \theta _k(1+ \theta _k)d^2(w_k, q_{k-1})\nonumber \\&=(1+ \theta _k)\big ((1+ \alpha _k)d^2(q_{k}, p)-\alpha _k d^2(q_{k-1}, p) + \alpha _k(1+ \alpha _k)d^2(q_{k}, q_{k-1})\big )\nonumber \\&\quad -\theta _k d^2(q_{k-1}, p) + \theta _k(1+ \theta _k)d^2(w_k, q_{k-1})\nonumber \\&\leqslant (1+ \theta _k)\big (d^2(q_k, p) + \alpha _k\big (d^2(q_{k}, p)-d^2(q_{k-1}, p)\big ) + \alpha _k(1+ \alpha _k)d^2(q_{k}, q_{k-1})\big )\nonumber \\&\quad -\theta _k d^2(q_{k-1}, p) + \theta _k(1+ \theta _k)(1+ \alpha _k)^2 d^2(q_{k}, q_{k-1})\nonumber \\&=d^2(q_{k}, p) + \big (\theta _k + (1+ \theta _k)\alpha _k\big )\big (d^2(q_{k}, p)-d^2(q_{k-1}, p)\big )\nonumber \\&\quad + \alpha _k(1+\alpha _k)(1+ \theta _k)d^2(q_{k}, q_{k-1}) + \theta _k(1+ \theta _k)(1+\alpha _k)^2d^2(q_{k}, q_{k-1}). \end{aligned}$$

(41)

On substituting (41) into (31), we obtain

$$\begin{aligned} d^2(q_{k+1}, p)&\leqslant d^2(q_{k}, p) + (\theta _k + (1+ \theta _k)\alpha _k)\big (d^2(q_{k}, p)-d^2(q_{k-1}, p)\big )\nonumber \\&\quad + \alpha _k(1+ \alpha _k)(1+ \theta _k)d^2(q_{k}, q_{k-1}) + \theta _k(1+\theta _k)(1+ \alpha _k)^2d^2(q_{k}, q_{k-1})\nonumber \\&\quad -\big (1-\mu ^2 \frac{\rho _{k}^2}{\rho _{k+1}^2}\big )d^2(t_k, z_k). \end{aligned}$$

(42)

The last inequality yields

$$\begin{aligned}&\big (1-\mu ^2 \frac{\rho _{k}^2}{\rho _{k+1}^2}\big )d^2(t_k, z_k) \leqslant d^2(q_{k}, p)+ (\theta _k + (1+ \theta _k)\alpha _k)\big (d^2(q_k, p)-d^2(q_{k-1}, p)\big )\nonumber \\&\quad \quad + \alpha _k(1+ \alpha _k)(1+ \theta _k)d^2(q_{k}, q_{k-1})+\theta _k(1+ \theta _k)(1+ \alpha _k)^2d^2(q_{k}, q_{k-1})\nonumber \\&\quad \quad -d^2(q_{k+1}, p)\nonumber \\&\quad =\big (d^2(q_k, p)-d^2(q_{k+1}, p)\big ) + (\theta _k + (1+ \theta _k)\alpha _k)\big (d^2(q_{k}, p)-d^2(q_{k-1}, p)\big )\nonumber \\&\quad \quad + \alpha _k(1+\alpha _k)(1+\theta _k)d^2(q_{k}, q_{k-1}) + \theta _k(1+ \theta _k)(1+ \alpha _k)^2d^2(q_k, q_{k-1}). \end{aligned}$$

(43)

Since $\lim \limits _{k \rightarrow \infty }d(q_{k}, p)$ exists, $\sum \limits _{k=1}^{\infty }\alpha _k< + \infty$ and $\sum \limits _{k=1}^{\infty }\theta _k < + \infty$. It follows from (43) that

$$\begin{aligned} \lim _{k \rightarrow \infty } d(t_k, z_k)=0. \end{aligned}$$

(44)

Note that

$$\begin{aligned} d(w_k, q_k)&=\Vert w_{k}^{\prime }-q_{k}^{\prime }\Vert \nonumber \\&=\Vert q_{k}^{\prime } + \alpha _k(q_{k}^{\prime }-q_{k-1}^{\prime })-q_{k}^{\prime }\Vert \nonumber \\&=\alpha _kd(q_{k}, q_{k-1}) \rightarrow 0,~k \rightarrow \infty . \end{aligned}$$

(45)

From (45), we get

$$\begin{aligned} d(z_k, q_k)&=\Vert z_{k}^{\prime }-q_{k}^{\prime }\Vert \nonumber \\&=\Vert w_k^{\prime } + \theta _k(w_{k}^{\prime }-q_{k-1}^{\prime })-q_{k}^{\prime }\Vert \nonumber \\&\leqslant \Vert w_{k}^{\prime }-q_{k}^{\prime }\Vert + \theta _k\Vert q_{k}^{\prime } + \alpha _k(q_{k}^{\prime }-q_{k-1}^{\prime })-q_{k-1}^{\prime }\Vert \nonumber \\&\leqslant d(w_k, q_k) + \theta _k d(q_{k}, q_{k-1}) + \theta _k \alpha _k d(q_{k}, q_{k-1}) \rightarrow 0,~k \rightarrow \infty . \end{aligned}$$

(46)

From (44) and (46), we have

$$\begin{aligned} \lim \limits _{k \rightarrow \infty }d(t_k, q_k)=0. \end{aligned}$$

(47)

Using (45) and (46), we deduce that

$$\begin{aligned} \lim _{k \rightarrow \infty }d(z_k, w_k)=0. \end{aligned}$$

(48)

Since $\{q_k\}$ is bounded, there exists a subsequence $\{q_{k_l}\}$ which converges to a cluster point $\overline{p}$. Also, from (47), there exists a subsequence $\{t_{k_l}\}$ of $\{t_k\}$ which converges weakly to $\overline{p} \in \mathbb {P}$. By (17), we deduce that

$$\begin{aligned} \Upsilon _{k_l}=-\Gamma _{t_{k_l}, z_{k_l}} \Phi (z_{k_l})-\frac{1}{\rho _{k_l}}\exp _{t_{k_l}}^{-1}z_{k_l} \in \Psi (t_{k_l}). \end{aligned}$$

(49)

Thus, by applying (44), we have

$$\begin{aligned} \lim \limits _{l \rightarrow \infty }\frac{1}{\rho _{k_l}} \Vert \exp _{t_{k_l}}^{-1}z_{k_l}\Vert =\lim _{l \rightarrow \infty } \frac{1}{\rho _{k_l}}d(t_{k_l}, z_{k_l})=0, \end{aligned}$$

hence,

$$\begin{aligned} \lim _{l \rightarrow \infty } \frac{1}{\rho _{k_l}} \exp _{t_{k_l}}^{-1}z_{k_l}=0. \end{aligned}$$

(50)

Since $\Phi$ is a Lipschitz continuous vector field and $z_{k_{l}} \rightarrow \overline{p}$ as $l \rightarrow \infty .$ Combining (49) and (50), we obtain

$$\begin{aligned} \lim _{l \rightarrow \infty } \Upsilon _{k_l}=-\Gamma (\overline{p}). \end{aligned}$$

(51)

Also, using the fact that $\Psi$ is a maximal monotone vector field, so it is upper Kuratowski semicontinuous. Thus $-\Gamma (\overline{p}) \in \Psi (\overline{p}),$ which implies that $\overline{p}$ solves $\Omega$. Lastly by Lemma 1, we obtain that $\{q_k\}$ converges to a point in $\Omega .$

4 Numerical Example

Example 1

Let $\mathbb {R}_{++}=\{x \in \mathbb {R}: x > 0 \}$ and $\mathbb {P}=(\mathbb {R}_{++}, \langle \cdot ,\cdot \rangle )$ be the Riemannian manifold with Riemannian metric defined by $\langle p,q\rangle =\frac{1}{x^2}pq\; \in \mathbb {R}_{++}, \; p,q \in T_{x}\mathbb {P}.$ The Riemannian distance $d: \mathbb {P} \times \mathbb {P} \rightarrow \mathbb {R}_{+}$ is given by $d(x,y)=|\ln \frac{y}{x}|$ for all $x,y \in \mathbb {P}.$ Let $x \in \mathbb {P},$ then the exponential map $\exp _{x}:T_x \mathbb {P} \rightarrow \mathbb {P}$ is defined by $\exp _{x} sq=x\textrm{e}^{\frac{qs}{x}}$ for all $q \in T_x \mathbb {P}.$ The inverse of the exponential map, $\exp _{x}^{-1}: \mathbb {P} \rightarrow T_x \mathbb {P}$ is defined by $\exp _{x}^{-1}y=x\ln \frac{y}{x}$ for all $x,y \in \mathbb {P}.$ The parallel transport is the identity on $T\mathbb {P}.$ Let $\mathcal {K}=(0,1],$ $\Psi :\mathcal {K} \rightarrow \mathbb {R}$ and $\Phi : \mathcal {K} \rightarrow T\mathbb {P}$ be defined by $\Psi (x)=x\ln x$ and $\Phi (x)=x(1+\ln x)$, respectively. Then, $\Psi$ is maximal monotone on $\mathcal {K}$ and $\Phi$ is a continuous and monotone vector field on $\mathcal {K}.$ By simple calculation, we obtain that $t_k$ in Algorithm 19 can be expressed as

$$\begin{aligned} t_k=\left( \frac{z_k}{\textrm{e}^{\rho _k}}\right) ^{\frac{1}{1+\rho _k}},\; \rho _k >0, \end{aligned}$$

and $(\Phi +\Psi )^{-1}(0)=\frac{1}{\sqrt{\textrm{e}}}.$ We choose $\alpha _{k}=\frac{1}{k+1},$ $\theta _k=\frac{1}{2n+3},$ $\lambda _k=\frac{1}{k\sqrt{k}},$ $\mu =\frac{1}{2}$ and $\rho _{0}=0.3.$ We terminate the execution of the process at $E_k=d(x_{k+1},x_k)=10^{-3}$ and make a comparison of Algorithm 19 with a step inertial and non-accelerated versions of the Algorithm. We test the convergence of the method with some initial values of $x_0$ and $x_1.$ The result of this experiment is shown in Fig. 1.

Case I::

$x_0=0.1$ and $x_1=0.18.$

Case II::

$x_0=0.9$ and $x_1=0.5.$

Fig. 1

Numerical report for Example 2

Example 2

Let $\mathbb {R}^{3}_{++}=\{x=(x_1,x_2,x_3) \in \mathbb {R}^3: x_i >0, i=1,2,3\},$ $\mathbb {P}=(\mathbb {R}^{3}_{++},\langle \cdot ,\cdot \rangle )$ be the Riemannian manifold with the Riemannian metric is defined by

$$\begin{aligned} \langle p,q\rangle =pG(x)q^\textrm{T}, \quad x\in \mathbb {R}_{++}^{3}, ~p,q \in T_{x}\mathbb {R}^{3}_{++}=\mathbb {R}^3, \end{aligned}$$

where G(x) is a diagonal matrix defined $G(x)=\textrm{diag}(x_{1}^{-2},x_{2}^{-2},x_{3}^{-2}).$ The Riemannian $d: \mathbb {P} \times \mathbb {P} \rightarrow \mathbb {R}_{+}$ is defined by

$$\begin{aligned} d(x,y)=\sqrt{\left( \sum \limits _{i=1}^{3}\ln ^2\frac{x_i}{y_i}\right) ,} \; \forall ~x,y \in \mathbb {P}. \end{aligned}$$

The sectional curvature of the Riemannian manifold $\mathbb {P}$ is 0. Thus $\mathbb {P}=(\mathbb {R}_{++}^{3},\langle \cdot ,\cdot \rangle )$ is a Hadamard manifold. Let $x=(x_1,x_2,x_3) \in \mathbb {P}.$ Then, the exponential map $\exp _{x}: T_x \mathbb {P} \rightarrow \mathbb {P}$ is defined by

$$\begin{aligned} \exp _x (p)=\left( x_1 \textrm{e}^{\frac{p_1}{x_1}},x_2 \textrm{e}^{\frac{p_2}{x_2}},x_3 \textrm{e}^{\frac{p_3}{x_3}}\right) \end{aligned}$$

for all $p=(p_1,p_p,p_3) \in T_x \mathbb {P}.$ The inverse of the exponential map, $\exp _{x}^{-1}: \mathbb {P}\rightarrow T_x \mathbb {P}$ is defined by

$$\begin{aligned} \exp _{x}^{-1}y=\left( x_1\ln \frac{y_1}{x_1},x_2\ln \frac{y_2}{x_2},x_3\ln \frac{y_3}{x_3}\right) \end{aligned}$$

for all $x,y \in \mathbb {P}.$ The parallel transport $\Gamma _{y,x}: T_x \mathbb {P} \rightarrow T_y \mathbb {P}$ is defined by

$$\begin{aligned} P_{y,x}(p)=\left( p_1\frac{y_1}{x_1},p_2\frac{y_2}{x_2},p_3\frac{y_3}{x_3}\right) \end{aligned}$$

for all $p=(p_1,p_2,p_3) \in T_x \mathbb {P}.$ Let $\mathcal {K}=\{x=(x_1,x_2,x_3) \in \mathbb {P}: 0 < x_i \leqslant 1, ~~\text{ for }~~i=1,2,3 \}$ be the geodesic convex subset of $\mathbb {P}.$ Let $\Phi :\mathbb {M} \rightarrow T\mathbb {P}$ be defined by

$$\begin{aligned} \Psi (x)=(-x_1,x_2\ln x_2,3x_3), \; \forall ~ (x_1,x_2,x_3) \in \mathbb {P}, \end{aligned}$$

and $\Phi :\mathbb {M} \rightarrow T\mathbb {P}$ be defined by

$$\begin{aligned} \Phi (x_1,x_2,x_3)=(x_1+x_1\ln x_1,x_2,-3x_1+2x_3\ln 2x_3), \; \forall ~(x_1,x_2,x_3) \in M. \end{aligned}$$

Then, $\Psi$ is maximal monotone vector field on $\mathcal {K}$ and $\Phi$ is continuous and monotone vector field on $\mathcal {K}$ (see [8, Example 1]). By simple calculation, we see that $t_k$ in Algorithm 19 can be expressed as

$$\begin{aligned} t_k=\left( t_{k}^1 \textrm{e}^{\rho _k},(t_{k}^2)^{\frac{1}{1+\rho _{k}}},t_{k}^3\textrm{e}^{-3\rho _{k}}\right) . \end{aligned}$$

Note that $(\Psi +\Phi )^{-1}(0)=\{(1,\frac{1}{\textrm{e}},\frac{1}{2})\}.$ Let $\alpha _{k}=\frac{1}{k+1},$ $\theta =\frac{1}{2k+3},$ $\lambda _k=\frac{1}{k\sqrt{k}},$ $\mu =\frac{1}{2}$ and $\rho _0=0.9.$ We terminate the execution of the process at $E_k=d(x_{k+1},x_k)=10^{-4}$ and make a comparison of Algorithm 19 with one inertial and a non-accelerated versions of the Algorithm. The result of this experiment is shown in Fig. 2 for two initial values of $x_0$ and $x_1.$

Case 1::

$x_0=[1.5,1.5,1.5]'$ and $x_1=[1.3,1.2,1.1]'.$

Case 2::

$x_0=[1.8,1.8,1.8]'$ and $x_1=[1.5,1.5,1.6]'.$

Fig. 2

Numerical report for Example 2

5 Conclusion

In this manuscript, we proposed double inertial methods with a forward–backward method for solving variational inclusion problem in the settings of a Hadamard manifold. We establish a convergence result for solving variational inclusion problem and illustrate some numerical examples to show the performance of our method in comparison with some related ones in the literature. It can be seen from our figures that the two steps inertial extrapolation method illustrated in our manuscript converges faster that the one step inertial method and the non-inertial iterative method. This result discussed in this manuscript is new in the settings of a Hadamard manifold.