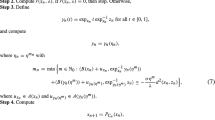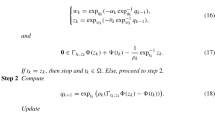Abstract
The main purpose of this paper is to introduce a new iterative algorithm to solve inclusion problems in Hadamard manifolds. Moreover, applications to convex minimization problems and variational inequality problems are studied. A numerical example also is presented to support our main theorem.
Similar content being viewed by others
1 Introduction
Let H be a Hilbert space, \(A: H \to H\) an operator and \(B: H \to 2^{H}\) a multivalued operator. The inclusion problem is to find \(p^{*} \in H\) such that
If \(A =0\), then the problem (1) becomes the inclusion problem introduced by Rockafellar [1]. Several nonlinear problems such as optimization problems, variational inequality problems, DEs [2–6] and economics can be formulated to find a singularity of the problem (1). The problem (1) is highly considered by many authors who performed dedicated work to theoretical results as well as iterative procedures; see, for instance [7–10] and the references therein.
In 1979, Lions and Mercier [11] showed that the problem (1) is equivalent to find fixed points of the mapping \(J^{B}_{\lambda }(I - \lambda A)\), that is, \(p^{*} = J^{B}_{\lambda }(p^{*} - \lambda A(p^{*})) \Leftrightarrow 0 \in (A+B)(p^{*})\), where \(J^{B}_{\lambda }= (I + \lambda B)^{-1}\). Owing to the fixed point formulation, Lions and Mercier [11] presented the following proximal point method: let \(p_{0} \in H\) be an initial point and
where \(\lambda > 0\). The proximal point method (2) has been extensively studied with many authors; see, e.g. [8, 12–17]. In particular, Chen and Rockafellar [14] studied convergence rates of the method (2). Afterwards, Tseng [15] proposed the modification for approximating singularities of the inclusion problem (1), also known as Tseng’s splitting algorithm. In 2012, Takahashi et al. [16] introduced an iterative scheme to solve the problem (1) by combining Mann-type and Halpern-type algorithms with the proximal point method. Recently, Lorenz and Pock [13] have defined an iterative algorithm related to the inertial extrapolation technique.
Over the past year, many significant techniques, concepts of nonlinear and analytical optimization that fit in Euclidean spaces have been extended to Riemannian manifolds. From the Riemannian geometry point of view, some non-convex constrained optimization problems can be viewed as convex unconstrained optimization problems by the introduction of a suitable Riemannian metric (see, e.g. [18–26] and the references therein).
In recent years, several researchers have extended the relevance of inclusion theory from linear spaces to the Riemannian context. For instance, Ferreira et al. [27] considered inclusion problem (1) in the setting of Hadamard manifolds. Later on, Ansari et al. [28] introduced Korpelevich’s algorithm to solve the inclusion problem (1) and discussed its convergence. Moreover, they [28] obtained the relationship between the set of singularities of inclusion problems and fixed points of the resolvent of maximal monotone vector fields in Hadamard manifolds. In 2019, Al-Homidan et al. [29] presented Halpern-type and Mann-type iterative methods for approximating singularities of the inclusion problem (1) in the framework of Hadamard manifolds. Very recent, Ansari and Babu [30] presented the proximal point method for finding singularities of the inclusion problem (1) on Hadamard manifolds. The authors [30] also devoted their results to convex minimization problems and variational inequality problems.
Inspired by the work mentioned above, the purpose of this paper is to introduce a new class of inverse-strongly-monotone operators, and then develop a new class of iterative algorithms to solve the problem of finding singularities defined by the sum of an inverse-strongly-monotone vector field and a multivalued maximal monotone vector field in Hadamard manifolds.
The paper is organized as follows: In the next section, we give some fundamental concepts of geometry and nonlinear analysis in Riemannian manifolds. In Sect. 3, we construct the inclusion problem (1) in the setting of Hadamard manifolds and exhibit the concept of monotonicity for single-valued as well as for multivalued vector fields. Some fundamental realized results identified with the monotone vector fields are additionally mentioned. In Sect. 4, we present the Mann-type splitting method and establish convergence theorems of any sequence generated by the proposed algorithm converges to a solution of the proposed problem in Hadamard manifolds. In Sect. 5, an application of this results to solve the convex minimization problems and variational inequality in Hadamard manifolds were presented. In Sect. 6, we provide a numerical example to support the Mann-type splitting method.
2 Preliminaries
Let M be a connected finite-dimensional Riemannian manifold, ∇ a Levi-Civita connection, and χ a smooth curve on M. F is the unique vector field such that \(\nabla _{\chi ^{\prime }}F ={\mathbf{0}}\) for all \(t \in [a,b]\), where 0 is the zero section of the tangent bundle TM. Then the parallel transport \(\mathrm{P}_{{\chi },{\chi (b)},{\chi (a)}}: T_{\chi (a)}M \to T_{\chi (b)}M\) on the tangent bundle TM along \(\chi : [a,b] \to \mathbb{R}\) is defined by
If χ is a minimizing geodesic joining p to q, then we write \(\mathrm{P}_{q,p}\) instead of \(\mathrm{P}_{\chi ,q,p}\). Note that, for every \(a,b,b_{1},b_{2} \in \mathbb{R,}\) we have
Also, \(\mathrm{P}_{\chi (b),\chi (a)}\) is an isometry from \(T_{\chi (a)}M\) to \(T_{\chi (b)}M\), that is, the parallel transport preserves the inner product,
for all \(\upsilon , \nu \in T_{\chi (a)}M\).
A Riemannian manifold is complete if for any \(p \in M\) all geodesic emanating from p are defined for all \(t \in \mathbb{R}\).
Let M be a complete Riemannian manifold and \(p \in M\). The exponential map \(\exp _{p} : T_{p}M \to M\) is defined as \(\exp _{p}\nu = \chi _{\nu }(1,p)\), then, for any value of t, we have \(\exp _{p}t\nu = \chi _{\nu }(t,p)\). Note that the mapping \(\exp _{p}\) is differentiable on \(T_{p}M\) for every \(p \in M\). The exponential map has inverse \(\exp ^{-1}_{p} : M \to T_{p}M\). Moreover, for any \(p,q \in M\), we have \(d(p,q) = \|\exp _{p}^{-1}q\|\), where \(d(\cdot ,\cdot )\) is a Riemannian distance.
A complete simply connected Riemannian manifold of nonpositive sectional curvature is said to be an Hadamard manifold. Throughout, M always denotes a finite-dimensional Hadamard manifold. The following proposition is outstanding and will be helpful.
Proposition 1
([31])
Let \(p \in M\). The \(\exp _{p} : T_{p}M \to M\) is a diffeomorphism, and for any two points \(p,q \in M\) there exists a unique normalized geodesic joining p to q, which is can be expressed by the formula
A geodesic triangle \(\triangle (p_{1},p_{2},p_{3})\) of a Riemannian manifold M is a set consisting of three points \(p_{1}\), \(p_{2}\) and \(p_{3}\), and three minimizing geodesics joining these points.
Proposition 2
([31])
Let \(\triangle (p_{1},p_{2},p_{3})\) be a geodesic triangle. Then
and
Moreover, if θ is the angle at \(p_{1}\), then we have
The following relation between geodesic triangles in Riemannian manifolds and triangles in \(\mathbb{R}^{2}\) can be found in [32].
Lemma 1
([32])
Let \(\triangle (p_{1},p_{2},p_{3})\) be a geodesic triangle in a Hadamard manifold M. Then there exists a triangle \(\triangle (\overline{p_{1}}, \overline{p_{2}}, \overline{p_{3}})\) for \(\triangle (p_{1},p_{2},p_{3})\) such that \(d(p_{i},p_{i+1}) = \|\overline{p_{i}} - \overline{p_{i+1}}\|\), with the indices taken modulo 3; it is unique up to an isometry of \(\mathbb{R}^{2}\).
The triangle \(\triangle (\overline{p_{1}}, \overline{p_{2}}, \overline{p_{3}})\) in Lemma 1 is said to be a comparison triangle for \(\triangle (p_{1},p_{2},p_{3})\). The points \(\overline{p_{1}}\), \(\overline{p_{2}}\), \(\overline{p_{3}}\) are called comparison points to the points \(p_{1}\), \(p_{2}\), \(p_{3}\), respectively.
Lemma 2
Let \(\triangle (p_{1},p_{2},p_{3})\) be a geodesic triangle in M and \(\triangle (\overline{p_{1}}, \overline{p_{2}}, \overline{p_{3}})\) be its comparison triangle.
-
(i)
Let \(\theta _{1}\), \(\theta _{2}\), \(\theta _{3}\) (respectively, \(\overline{\theta _{1}}\), \(\overline{\theta _{2}}\), \(\overline{\theta _{3}}\)) be the angles of \(\triangle (p_{1},p_{2},p_{3})\) (respectively, \(\triangle (\overline{p_{1}}, \overline{p_{2}}, \overline{p_{3}})\)) at the vertices \(p_{1}\), \(p_{2}\), \(p_{3}\) (respectively, \(\overline{p_{1}}\), \(\overline{p_{2}}\), \(\overline{p_{3}}\)). Then
$$ \theta _{1} \leq \overline{\theta _{1}}, \qquad \theta _{2} \leq \overline{\theta _{2}} \quad \textit{and} \quad \theta _{3} \leq \overline{\theta _{3}}. $$ -
(ii)
Let q be a point on the geodesic joining \(p_{1}\) to \(p_{2}\) and q̅ its comparison point in the interval \([\overline{p_{1}}, \overline{p_{2}}]\). If \(d(p_{1},q) = \| \overline{p_{1}} -\overline{q} \|\) and \(d(p_{2},q) = \| \overline{p_{2}} - \overline{q} \|\), then \(d(p_{3},q) \leq \|\overline{p_{3}} - \overline{q}\|\).
Definition 1
A subset Γ in a Hadamard manifold M is called geodesic convex if for all p and q in Γ, and for any geodesic \(\chi : [a,b] \to M\), \(a,b \in \mathbb{R}\) such that \(p = \chi (a)\) and \(q = \chi (b)\), one has \(\chi ((1-t)a + tb) \in \Gamma \) for all \(t \in [0,1]\).
Definition 2
A function \(\phi : M \to \mathbb{R}\) is called geodesic convex if for any geodesic χ in M, the composition function \(\phi \circ \chi : [a,b] \to \mathbb{R}\) is convex, that is,
Proposition 3
([31])
Let \(d : M \times M \to \mathbb{R}\) be the distance function. Then \(d(\cdot ,\cdot )\) is a geodesic convex function with respect to the product Riemannian metric, that is, for any pair of geodesics \(\chi _{1} : [0,1] \to M\) and \(\chi _{2} : [0,1] \to M\) the following inequality holds:
Particularly, for all \(q \in M\), the function \(d(\cdot ,q) : M \to \mathbb{R}\) is a geodesic convex function.
We now present the results of parallel transport which will be helpful in the sequel.
Remark 1
([24])
If \(p,q \in M\) and \(\nu \in T_{p}M\), then
Remark 2
([33])
Let \(p,q,r \in M\) and \(\nu \in T_{p}M\), and using (5) and Remark 1,
Let us end the preliminary section with the following results, which are important in establishing our convergence theorem.
Definition 3
([19])
Let Γ be a nonempty subset of M and \(\{p_{n}\}\) be a sequence in M. Then \(\{p_{n}\}\) is said to be Fejér monotone with respect to Γ if for all \(q \in \Gamma \) and \(n \in \mathbb{N}\),
Lemma 3
([19])
Let Γ be a nonempty subset of M and \(\{p_{n}\} \subset M\) be a sequence in M such that \(\{p_{n}\}\) is a Fejér monotone with respect to Γ. Then the following hold:
-
(i)
for every \(q \in \Gamma \), \(\{d(p_{n},q)\}\) converges;
-
(ii)
\(\{p_{n}\}\) is bounded;
-
(iii)
assume that any cluster point of \(\{p_{n}\}\) belongs to Γ, then \(\{p_{n}\}\) converges to a point in Γ.
3 Problem formulations
Given Γ is a nonempty subset of a Hadamard manifold M. Let \(\Psi (\Gamma )\) denote the set of all single-valued vector fields \(A : \Gamma \to TM\) such that \(A(p) \in T_{p}M\), for each \(p \in \Gamma \). \(\mathfrak{X}(\Gamma )\) denote the set of all multivalued vector fields \(B: \Gamma \to 2^{TM}\) such that \(B(p) \subseteq T_{p}M\) for all \(p \in \Gamma \), and denote \(D(B)\) the domain of B defined by \(D(B) = \{p \in \Gamma : B(p) \neq \emptyset \}\).
Let a vector field \(A \in \Psi (\Gamma )\) and a vector field \(B \in \mathfrak{X}(\Gamma )\). In this paper, we consider the following inclusion problem: find \(p^{*} \in \Gamma \) such that
We denote by \((A+B)^{-1}({\mathbf{0}})\) the set of singularities of the problem (8).
In this article we work mainly with specific classes of vector fields which are defined in the following.
Definition 4
A vector field \(A \in \Psi (\Gamma )\) is called
-
(i)
monotone if
$$ \bigl\langle A(p), \exp ^{-1}_{p}q\bigr\rangle \leq \bigl\langle A(q), - \exp ^{-1}_{q}p \bigr\rangle , \quad \forall p,q \in \Gamma ; $$ -
(ii)
β-strongly monotone if there is \(\beta > 0\) such that
$$ \bigl\langle A(p), \exp ^{-1}_{p}q\bigr\rangle + \bigl\langle A(q), \exp ^{-1}_{q}p \bigr\rangle \leq -\beta d^{2}(p,q) , \quad \forall p,q \in \Gamma ; $$ -
(iii)
K-Lipschitz continuous if there is \(K>0\) such that
$$ \bigl\Vert \mathrm{P}_{p,q}A(q)-A(p) \bigr\Vert \leq Kd(p,q), \quad \forall p,q \in \Gamma . $$
Definition 5
([36])
A vector field \(B \in \mathfrak{X}(\Gamma )\) is called
-
(i)
monotone if for all \(p,q \in D(B)\)
$$ \bigl\langle \upsilon, \exp ^{-1}_{p}q\bigr\rangle \leq \bigl\langle \nu, - \exp ^{-1}_{q}p \bigr\rangle , \quad \forall \upsilon \in B(p) \ \text{and} \ \forall \nu \in B(q); $$ -
(ii)
maximal monotone if it is monotone and for all \(p \in \Gamma \) and \(\upsilon \in T_{p}\Gamma \), the condition
$$ \bigl\langle \upsilon, \exp ^{-1}_{p}q\bigr\rangle \leq \bigl\langle \nu, - \exp ^{-1}_{q}p \bigr\rangle , \quad \forall q \in D(B) \ \text{and} \ \forall \nu \in B(q), $$implies that \(\upsilon \in B(p)\).
The concept of the resolvent for multivalued vector fields and firmly nonexpansive mappings on Hadamard manifolds was introduce by Li et al. [24] and reads as follows.
Definition 6
([37])
Let a vector field \(B \in \mathfrak{X}(\Gamma )\) and \(\lambda \in (0,\infty )\). The λ-resolvent of B is multivalued map \(J^{B}_{\lambda } : \Gamma \to 2^{\Gamma }\) defined by
Definition 7
([37])
Let \(T : \Gamma \subseteq M \to M\) be a mapping. Then T is said to be firmly nonexpansive if for any two points \(p,q \in \Gamma \), the function \(\Theta : [0,1] \to [0, + \infty ]\) defined by
is nonincreasing.
Let \(T: \Gamma \to \Gamma \) be a nonexpansive mapping, i.e., \(d(T(p),T(q)) \leq d(p,q)\) for all \(p,q \in \Gamma \). By Definition 7, it is clear that any firmly nonexpansive mapping T is nonexpansive. In particular, the monotonicity and nonexpansivity are firmly related.
Theorem 1
([37])
Let a vector field \(B \in \mathfrak{X}(\Gamma )\) is monotone if and only if \(J^{B}_{\lambda }\) is single-valued and firmly nonexpansive.
Let Γ be a nonempty closed geodesic convex subset of M. The projection operator \(P_{\Gamma}(\cdot) : M \to \Gamma\) is defined for any \(p \in M\) by \(P_{\Gamma}(p) := \{r : d(p,r) \leq d(p,q), \forall q \in \Gamma \}\). The projection operator \(P_{\Gamma}\) is firmly nonexpansive as described in the following proposition [37].
Proposition 4
([37])
Let Γ be a nonempty closed geodesic convex subset of M. Then the following assertions holds:
-
(i)
\(P_{\Gamma}\) is single-valued and firmly nonexpansive;
-
(ii)
For all \(p \in M\), \(r = P_{\Gamma}(p)\) if and only if \(\langle \exp_{r}^{-1}p, \exp^{-1}_{r}q\rangle \leq 0\), for all \(q \in \Gamma\).
Recently, Ansari et al. [28] obtained the relationship between a fixed point of \(T^{A,B}_{\lambda }\) (see Lemma 5) and a singularity of the inclusion problem (8) as follows.
Proposition 5
([28])
For each \(p \in \Gamma \), the following assertions are equivalent:
-
(i)
\(p \in (A + B)^{-1}({\mathbf{0}})\);
-
(ii)
\(p = T^{A,B}_{\lambda }(p)\), \(\forall \lambda \in (0,\infty )\).
Moreover, they [28] also provided the following lemma which is useful in establishing the convergence result of the inclusion problem (8).
Lemma 4
([29])
Let Γ be a nonempty closed subset of a Hadamard manifold M and \(B \in \mathfrak{X}(\Gamma )\) a maximal monotone. Let \(\{\lambda _{n}\} \subset (0,\infty )\) with \(\lim_{n \to \infty }\lambda _{n} = \lambda >0\) and a sequence \(\{p_{n}\} \subset \Gamma \) with \(\lim_{n \to \infty }p_{n} = p \in \Gamma \) such that \(\lim_{n \to \infty }J^{B}_{\lambda _{n}}(p_{n}) = q\). Then \(q = J_{\lambda }^{B}(p)\).
Next, let us introduce the concept of an inverse-strongly-monotone vector field in Hadamard manifolds.
Definition 8
A vector \(A \in \Psi (\Gamma )\) is said to be inverse-strongly-monotone if there exists \(\alpha > 0\) such that
In this case α-inverse-strongly-monotone. The reason for us to provide this definition is that β-strongly monotone and K-Lipschitz continuous vector field must be \(\frac{\beta }{K^{2}}\)-inverse-strongly-monotone. (It is seen from the definition.) Moreover, we can see that if A is α-inverse-strongly-monotone, then it is \(\frac{1}{\alpha }\)-Lipschitz continuous.
Indeed, let A be α-inverse-strongly-monotone, then by the definition we have
this implies that
for all \(p,q \in \Gamma \), where \(\alpha >0\). Thus, A is \(\frac{1}{\alpha }\)-Lipschitz continuous.
Conversely, let A be \(\frac{1}{\alpha }\)-Lipschitz continuous, then by the definition we have
for all \(p,q \in \Gamma \), where \(\alpha >0\). Thus, A is α-inverse-strongly-monotone.
Now, we provide some examples of inverse-strongly-monotone vector fields.
Example 1
Let \(\mathbb{R}^{++}_{n}\) is the product space of \(\mathbb{R}^{++}\), that is, \(\mathbb{R}^{++}_{n} = \{p = (p_{1},p_{2},\ldots ,p_{n})\in \mathbb{R}^{n} : p_{i} >0, \ i = 1,\ldots ,n\}\). Let \(M = (\mathbb{R}^{++}_{n}, \langle \cdot , \cdot \rangle )\) with metric defined by \(\langle \upsilon , \nu \rangle := \upsilon ^{T}G(p)\nu \), for \(p \in \mathbb{R}_{n}^{++}\) and \(\upsilon , \nu \in T_{p}\mathbb{R}_{n}^{++} \) where \(G(p)\) is a diagonal metric defined by \(G(p) = \operatorname{diag} (p_{1}^{-2},p_{2}^{-2},\ldots ,p_{n}^{-2} )\). Specially, \(M = (\mathbb{R}^{++}_{n}, \langle \cdot , \cdot \rangle ) \) is a Hadamard manifold with sectional curvature zero (see [18]).
Let \(A : \mathbb{R}^{++}_{n} \to T\mathbb{R}^{++}_{n}\) be a single-valued vector field defined by
where \(a_{i}, b_{i}, d_{i} \in \mathbb{R}^{+}\) and \(c_{i} \in \mathbb{R}^{++}\) satisfy \(c_{i} > a_{i}\). Hence, A is a K-Lipschitz continuous with \(K < \sum_{i=1}^{n}(a_{i} + 2c_{i})^{2}\); for more details see [22]. Thus, we see that A is \(\frac{1}{K}\)-inverse-strongly-monotone where \(K < \sum_{i=1}^{n}(a_{i} + 2c_{i})^{2}\).
Example 2
Let \(n= 1\) in Example 1 and \(A : \mathbb{R}^{++} \to T\mathbb{R}^{++}\) be a single-valued vector field defined by
Hence, A is a \(\frac{33}{32}\)-Lipschitz continuous; for further details see [38]. Thus, we see that A is \(\frac{32}{33}\)-inverse-strongly-monotone.
We have the following lemma.
Lemma 5
Let \(A \in \Psi (\Gamma )\) be an α-inverse-strongly-monotone vector field, where \(\alpha > 0\), and \(B \in \mathfrak{X}(\Gamma )\) a maximal monotone vector field. Then the following properties hold:
-
(i)
for each \(\lambda \in [0,2\alpha ]\), the mapping \(W_{\lambda }: \Gamma \to \Gamma \) defined by \(W_{\lambda }(p) = \exp _{p}-\lambda A(p)\) is nonexpansive;
-
(ii)
for each \(\lambda > 0\), the mapping \(T^{A,B}_{\lambda }: \Gamma \to \Gamma \) defined by \(T^{A,B}_{\lambda }(p) = J^{B}_{\lambda }(W_{\lambda }(p))\) is well defined and \((A+B)^{-1}({\mathbf{0}}) = \operatorname{Fix} (T^{A,B}_{\lambda } )\), where \(\operatorname{Fix} (T^{A,B}_{\lambda } )\) is the set of fixed points of \(T^{A,B}_{\lambda } \);
-
(iii)
for each \(\lambda \in (0,2\alpha ]\), \(T^{A,B}_{\lambda }\) is nonexpansive.
Proof
Conclusion (ii) follows from Proposition 5 and the maximal monotonicity of B.
In order to prove (i), let \(\triangle (p,W_{\lambda }(p),W_{\lambda }(q)) \subseteq M\) be a geodesic triangle with vertices p, \(W_{\lambda }(p)\) and \(W_{\lambda }(q)\), and \(\triangle (\overline{p},\overline{W_{\lambda }(p)}, \overline{W_{\lambda }(q)} ) \subseteq \mathbb{R}^{2}\) is the corresponding comparison triangle. Then we have \(d(p,W_{\lambda }(p)) = \Vert \overline{p} - \overline{W_{\lambda }(p)} \Vert \), \(d(W_{\lambda }(p),W_{\lambda }(q)) = \Vert \overline{W_{\lambda }(p)} - \overline{W_{\lambda }(q)} \Vert \), and \(d(W_{\lambda }(q),p) = \Vert \overline{W_{\lambda }(q)} - \overline{p} \Vert \). Again, letting \(\triangle (p,q,W_{\lambda }(q)) \subseteq M\) be a geodesic triangle with vertices p, q and \(W_{\lambda }(q)\), and \(\triangle (\overline{p},\overline{q},\overline{W_{\lambda }(q)} ) \subseteq \mathbb{R}^{2}\) be the corresponding comparison triangle, one obtains
Now,
Let θ, θ̅ be the angles at the vertices q, q̅. By (i) of Lemma 2, we get \(\theta \leq \overline{\theta } \). Besides, by Proposition 2, we have
Repeating the argument above gives
Moreover, we have
Consider
Repeating the argument above yields
and
Substituting (14) and (15) into (13) gives
Noting Remarks 1 and 2 in the last inequality, we get
Substituting (16) into (12) yields
Combining (9), (10), (11) and (17), we obtain
From Remarks 1 and 2, the last inequality becomes
So,
Since A is an α-inverse-strongly-monotone, we get
Substituting (20) into (19), we deduce that
From the fact the \(\lambda \in [0,2\alpha ]\)
hence \(W_{\lambda }(p)\) is nonexpansive. To prove (iii), notice that B is maximal monotone and so the resolvent \(J^{B}_{\lambda }\) is firmly nonexpansive. It follows immediately from (i) that \(T^{A,B}_{\lambda }(x) = J^{B}_{\lambda }(W_{\lambda }(x))\) is nonexpansive. □
4 Mann-type splitting method
In this section, we present the conditions that guarantee the convergence of the Mann-type splitting method in Hadamard manifolds and the proof.
Theorem 2
Let Γ be a nonempty, closed and geodesic convex subset of a Hadamard manifold M. Let \(A \in \Psi (\Gamma )\) be an α-inverse-strongly-monotone vector field, where \(\alpha >0\), and \(B \in \mathfrak{X}(\Gamma )\) a maximal monotone vector field with \((A+B)^{-1}({\mathbf{0}}) \neq \emptyset \). Choose \(p_{0} \in \Gamma \) and define \(\{q_{n}\}\) and \(\{p_{n}\}\) as follows:
for all \(n \in \mathbb{N} \), where \(\{\gamma _{n}\}\) is a sequence in \((0,1)\) and \(\{\lambda _{n}\}\) is a real positive sequence satisfying the following conditions:
-
(i)
\(0 < \gamma _{1} \leq \gamma _{n} \leq \gamma _{2} < 1\), \(\forall n \in \mathbb{N}\),
-
(ii)
\(0 < \hat{\lambda } \leq \lambda _{n} \leq 2\alpha < \infty \), \(\forall n \in \mathbb{N}\).
Then \(\{p_{n}\}\) is convergent to a solution of the inclusion problem (8).
Proof
Let \(x \in (A+B)^{-1}({\mathbf{0}})\). From (ii) of Lemma 5, we have \(x = T^{A,B}_{\lambda _{n}}(x) = J^{B}_{\lambda }(W_{\lambda }(x))\). By the nonexpansiveness of \(J^{B}_{\lambda _{n}}\) and \(W_{\lambda _{n}}\), gives
Let \(\chi : [0,1] \to M\) be geodesic joining \(p_{n}\) to \(q_{n}\). Thus, (21) can be written as \(p_{n+1} = \chi (1-\gamma _{n})\), respectively. By using the geodesic convexity of Riemannian distance, we have
Hence, \(\{p_{n}\}\) is Fejér monotone with respect to \((A+B)^{-1}({\mathbf{0}})\). By (ii) of Lemma 3, \(\{p_{n}\}\) is bounded. Hence, there exists a subsequence \(\{p_{n_{k}}\}\) of \(\{p_{n}\}\) which converges to a cluster point y of \(\{p_{n}\}\). Next, we show that
Fix \(n \in \mathbb{N}\) and for \(x \in (A+B)^{-1}({\mathbf{0}})\). Let \(\triangle (p_{n},q_{n},x) \subseteq M\) be a geodesic triangle with vertices \(p_{n}\), \(q_{n}\) and x, and \(\triangle (\overline{p_{n}},\overline{q_{n}},\overline{x} ) \subseteq \mathbb{R}^{2}\) be the corresponding comparison triangle, one obtains
Let \(\overline{p_{n+1}} = \gamma _{n} \overline{p_{n}} + (1-\gamma _{n}) \overline{q_{n}}\) be the comparison point of \(p_{n+1}\). Using (ii) of Lemma 2 and (22),
which implies that
From the fact that \(0 < \gamma _{1} \leq \gamma _{n} \leq \gamma _{2} < 1\), we have \(\gamma _{1}(1-\gamma _{2}) \leq \gamma _{n}(1-\gamma _{n})\) for all \(n \in \mathbb{N}\). Summing (23) from \(i=0\) to \(i =n\), we obtain
Letting \(n \to \infty \), we have
Hence,
Next, we prove \(y \in (A+B)^{-1}({\mathbf{0}})\). Since \(\hat{\lambda } \leq \lambda _{n} \leq 2\alpha \), we may assume without the loss of generality that \(\lim_{k \to \infty }\lambda _{n_{k}} = \lambda \) for some \(\lambda \in [\hat{\lambda }, 2\alpha ]\). Recall that \(q_{n} = J^{B}_{\lambda _{n}}(\exp _{p_{n}}(- \lambda _{n} A(p_{n})))\). Then, by (24) and Lemma 4, we obtain \(\lim_{k \to \infty } q_{n_{k}} = y\) and that \(y = J_{\lambda }^{B}(\exp _{y}(-\lambda A(y)))\). It indicates that \(y \in (A+B)^{-1}({\mathbf{0}})\) by applying (ii) of Lemma 5. By (iii) of Lemma 3, the sequence \(\{p_{n}\}\) converges to a singularity of the inclusion problem (8). Therefore, the proof is completed. □
In the order to present an example in support of our main theorem, we need the following results.
Let \(\mathcal{M}\) be a Riemannian manifold and \(\phi : \mathcal{M} \to \mathbb{R}\) a differentiable function. The directional derivative of ϕ at p in direction \(\nu \in T_{p}\mathcal{M}\) is
The gradient of ϕ at \(p \in \mathcal{M}\) [39] is given by \(\langle \operatorname{grad}\phi (p), \nu \rangle := \phi ^{\prime }( p;\nu )\) for all \(\nu \in T_{p}\mathcal{M}\). If \(\phi : \mathcal{M} \to \mathbb{R}\) is a twice differentiable function, then the Hessian of ϕ at \(p \in \mathcal{M}\) [40], denoted by Hessϕ, is defined by
where ∇ is the Riemannian connection of \(\mathcal{M}\).
The norm of the Hessian, hess ϕ, at \(p \in \mathcal{M}\) is given by
Proposition 6
([20])
Let M be an Hadamard manifold and \(\phi : M \to \mathbb{R}\) a twice continuously differentiable function. If Hessϕ is bounded, then the gradient vector field gradϕ is K-Lipschitz continuous.
Definition 9
([31])
Let \(\varphi : \Gamma \to \mathbb{R}\) be a geodesic convex function. Take \(p \in \Gamma \), a vector \(\nu \in T_{p}M\) is said to be a subgradient of φ at p if and only if
The set of all subgradients of φ, denoted by \(\partial \varphi (p)\) is said to be the subdifferential of φ at p, which is a closed geodesic convex (possibly empty) set.
Lemma 6
([24])
Let \(\varphi : \Gamma \to \mathbb{R} \cup \{+ \infty \}\) be a proper, lower semicontinuous and geodesic convex function and \(D(\varphi ) = \Gamma \). Then the subdifferential ∂φ of φ is a maximal monotone vector field.
Next, we present an example in the cone of the positive semidefinite matrices with other metrics.
Example 3
Let \(\mathbb{S}^{n}\) be the set of symmetric matrices, \(\mathbb{S}^{n}_{+}\) be the cone of the symmetric positive semidefinite matrices and \(\mathbb{S}^{n}_{++}\) be the cone of the symmetric positive-definite matrices both \(n \times n\). \(X, Y \in \mathbb{S}^{n}_{+}\), \(X\succeq X \) (or \(X \preceq Y\)) means that \(Y-X \in \mathbb{S}^{n}_{+}\) and \(X \succ Y\) (or \(X \prec Y\)) means that \(Y - X \in \mathbb{S}^{n}_{++}\).
Following Rothaus [41], let \(M := (\mathbb{S}^{n}_{++},\langle \cdot , \cdot \rangle )\) be the Riemannian manifold endowed with the Riemannian metric defined by
where \(\operatorname{Tr}(X)\) denotes the trace of matrix \(X \in \mathbb{S}^{n}\) and \(T_{X}M \approx \mathbb{S}^{n}\), with the corresponding norm denoted by \(\|\cdot \|\). The gradient and the Hessian of a twice differentiable function \(\phi : \mathbb{S}^{n}_{++} \to \mathbb{R}\) are given by
where \(V \in T_{X}M\), and \(\phi ^{\prime }(X)\) and \(\phi ^{\prime \prime }(X)\) are the Euclidian gradient and Hessian of ϕ at X, respectively.
In fact, M is a Hadamard manifold with curvature is not identically zero; see [42, Theorem 1.2. p. 325] for further details. The unique geodesic segment connecting any \(X,Y \in M\) is given by
see, for example [43]. From the last equation
Thus, for all \(X \in M\), \(\exp ^{-1}_{X} : M \to T_{X}M\) and \(\exp _{X} : T_{X}M \to M\) are defined, respectively, by
Now, since the Riemannian distance d is given by \(d(X,Y) = \|\exp ^{-1}_{X}Y\|\), from (27), along with first expression in (30), we have
where \(\eta _{i} (X^{-1/2}YX^{-1/2} )\) denotes the ith eigenvalue of the symmetric matrix \(X^{-1/2}YX^{-1/2}\).
Following [22], let the function \(\phi : \mathbb{S}_{++}^{n} \to \mathbb{R}\) defined by
where \(a >0\). The Euclidian gradient and Hessian of ϕ are given, respectively, by
where \(X \in \mathbb{S}_{++}^{n}\) and \(V \in \mathbb{S}^{n}\).
By combining (28), (29), (33) and (34), we obtain, after some calculations,
for all \(X \in M\) and \(V \in T_{X}M\). We further have \(\langle \operatorname{hess}\phi (X)V, V \rangle = 2a\operatorname{Tr}(X^{-1}V)^{2} \geq 0\). Thus, ϕ is geodesic convex in M. Moreover, (27) together with (36) gives \(\|\operatorname{hess}\phi (X)V\| = 2a \operatorname{Tr}(X^{-1}V)\) for all \(X \in M\) and \(V \in T_{X}M\). If we assume that \(\|V\|^{2} = \operatorname{Tr}(VX^{-1}VX^{-1}) = 1\), then \(\operatorname{Tr}(X^{-1}V) \leq \sqrt{n}\). Hence,
Therefore, (25) and Proposition 6 imply that gradϕ is Lipschitz with constant \(K \leq 2a \sqrt{n}\). We also have gradϕ is \(\frac{1}{K}\)-inverse-strongly-monotone vector field with constant \(K \leq 2a \sqrt{n}\).
Let \(\Gamma = \{X \in \mathbb{S}_{++}^{n}: \eta _{\min }(X) \geq 1\}\), where \(\eta _{\min }(X)\) denotes the minimum eigenvalue of the matrix X, be a nonempty, closed and geodesic convex subset of M and \(\varphi : \Gamma \to \mathbb{R}\cup \{+\infty \}\) be a proper, lower semicontinuous and geodesic convex defined by
where \(\eta _{i}(X^{-1})\) is the ith eigenvalue of the matrix \(X^{-1}\). One can see that I is a minimizer of φ, where I denotes the identity matrix. By Definition 9, the subdifferential of φ at X is defined by
The subdifferential ∂φ of φ is a maximal monotone vector field, according to Lemma 6. Moreover, we have
Since the minimizer of φ is I, it is easy to see that \({\mathbf{0}} \in \partial \varphi (I)\).
Let \(A : \Gamma \to \mathbb{S}^{n}\) is a \(\frac{1}{K}\)-inverse-strongly-monotone vector field defined by
where \(K \leq 2 \sqrt{n}\), and \(B : \Gamma \to 2^{\mathbb{S}^{n}}\) be a maximal monotone multivalued field defined by
We see that \((A+B)^{-1}({\mathbf{0}}) = \{I\}\). Choose initial point \(X_{0} \in \Gamma \), then Theorem 2 is applicable leading us to conclude that any sequence generated by Eq. (21) converges to a singularity of the inclusion problem (8).
Remark 3
It is worth noting that ϕ is non-convex with non-Lipschitz continuous gradient on \(\mathbb{S}_{++}^{n}\) endowed with the Euclidean metric. Thus we cannot apply existence results, e.g. [8, 16], to solve the corresponding inclusion problem in the Euclidean setting.
5 Applications
In this section, we shall utilize the Mann-type splitting method presented in the paper to study the convex minimization problems and variational inequality problems.
5.1 Convex minimization problems
Let \(\phi ,\varphi : \Gamma \to \mathbb{R} \cup \{+\infty \}\) are proper, lower semicontinuous and geodesic convex functions such that ϕ is differentiable. We consider the problem of finding \(p^{*} \in \Gamma \) such that
The problem is said to be a convex minimization problem. We denote S by the set of minimizers of the problem (37), that is, \(S:= \{p \in \Gamma : \phi (p) + \varphi (p) \leq \phi (q) + \varphi (q), \forall q \in \Gamma \}\). It is to see that the problem (37) is equivalent to the following inclusion problem: find \(p \in \Gamma \) such that \({\mathbf{0}} \in \operatorname{grad}f(p) +\partial g(p)\), that is,
For further details see [30].
If \(\phi : \Gamma \to \mathbb{R} \cup \{+\infty \}\) is a proper, twice continuously differentiable and geodesic convex function such that Hessϕ is bounded, then, by Proposition 6, gradϕ is K-Lipschitz continuous vector field. Then gradϕ is \(\frac{1}{K}\)-inverse-strongly-monotone vector field. Moreover, from Lemma 6, ∂φ is a maximal monotone vector field. By replacing A and B by gradϕ and ∂φ, respectively, in Theorem 2, we get the following result for convex minimization problem (37).
Theorem 3
Suppose that \(S \neq \emptyset \). Let Γ be a nonempty, closed and geodesic convex subset of a Hadamard manifold M. Let \(\phi : \Gamma \to \mathbb{R} \cup \{+ \infty \}\) be a proper, differentiable and geodesic convex function such that Hessϕ is bounded, \(\varphi : \Gamma \to \mathbb{R} \cup \{+\infty \}\) a proper, lower semicontinuous and geodesic convex function such that \(D(\varphi ) = \Gamma \). Choose \(p_{0} \in \Gamma \) and define \(\{p_{n}\}\) as follows:
for all \(n \in \mathbb{N} \), where \(\{\gamma _{n}\}\) is a sequence in \((0,1)\) and \(\{\lambda _{n}\}\) is a real positive sequence satisfying the following conditions:
-
(i)
\(0 < \gamma _{1} \leq \gamma _{n} \leq \gamma _{2} < 1\), \(\forall n \in \mathbb{N}\),
-
(ii)
\(0 < \hat{\lambda } \leq \lambda _{n} \leq 2\alpha < \infty \), \(\forall n \in \mathbb{N}\).
Then \(\{p_{n}\}\) is convergent to a solution of the convex minimization problem (37).
Proof
By replacing A and B by gradϕ and ∂φ, respectively, in Theorem 2, we get the required result. □
5.2 Variational inequalities
A monotone variational inequality problem (VIP) on a Hadamard manifold was initially studied by Németh [44]. Then the problem is to find \(p^{*} \in \Gamma \) such that
where \(V : \Gamma \to TM\) is a single-valued vector field. \(VIP(V,\Gamma )\) denotes the set of solutions of the problem (39). Let \(N_{\Gamma }(p)\) denote the normal cone of the set Γ at \(p \in \Gamma \):
Let \(\delta _{\Gamma }\) be the indicator function of Γ, that is,
It is easy to see that \(\delta _{\Gamma }\) is a proper, lower semicontinuous and geodesic convex function on a Hadamard manifold M. By Lemma 6, \(\partial \delta _{\Gamma }\) is a maximal monotone multivalued vector field.
From (40), \(\delta _{\Gamma }(p) = 0\) for all \(p \in \Gamma \), and therefore, from (26), we get
Thus, \(\partial \delta _{\Gamma }(p) = N_{\Gamma }(p)\). For every \(p \in \Gamma \) and \(V \in \Psi (\Gamma )\), using (41),
The resolvent operator \(J_{\lambda }^{{\partial \delta _{\Gamma }}}\) of \(\partial \delta _{\Gamma }\) for \(\lambda > 0\) is given by
For every \(p \in \Gamma \), we get
We replace B and \(J_{\lambda }\) by \(\partial \delta _{\Gamma }\) and \(P_{\Gamma }\), respectively, in Theorem 2, then we get the following result for variational inequality problem (39).
Theorem 4
Let Γ be a nonempty, closed and geodesic convex subset of a Hadamard manifold M. Let \(V \in \Psi (\Gamma )\) be an α-inverse-strongly-monotone vector field, where \(\alpha >0\) such that \(VIP(V,\Gamma ) \neq \emptyset\). Choose \(p_{0} \in \Gamma \) and define \(\{p_{n}\}\) as follows:
for all \(n \in \mathbb{N} \), where \(\{\gamma _{n}\}\) is a sequence in \((0,1)\) and \(\{\lambda _{n}\}\) is a real positive sequence satisfying the following conditions:
-
(i)
\(0 < \gamma _{1} \leq \gamma _{n} \leq \gamma _{2} < 1\), \(\forall n \in \mathbb{N}\),
-
(ii)
\(0 < \hat{\lambda } \leq \lambda _{n} \leq 2\alpha < \infty \), \(\forall n \in \mathbb{N}\).
Then \(\{p_{n}\}\) is convergent to a solution of the variational inequality problem (39).
Proof
By replacing B by \(\partial \delta _{\Gamma }\), in Theorem 2, we get the required result. □
6 Numerical example
We present an illustrative example in Hadamard manifolds to show the applicability of the Mann-type splitting method in this section. All the program are written in Matlab R2016b and computed on PC Intel(R) Core(TM) i5 @1.80 GHz, Ram 8.00 GB.
Let \(M := \mathbb{R}^{++} = \{p \in \mathbb{R} : p >0\}\) and \(\mathbb{R}^{+} = \{p \in \mathbb{R} : p \geq 0\}\). Following [20, Example 1], let \((\mathbb{R}^{++},\langle \cdot , \cdot \rangle )\) be the Riemannian manifold, and \(\langle \cdot , \cdot \rangle \) the Riemannian metric defined by
The Riemannian distance \(d: M \times M \to \mathbb{R}^{+} \) is defined by
for further details see [39]. Then \((\mathbb{R}^{++},\langle \cdot , \cdot \rangle )\) is a Hadamard manifold and the unique geodesic \(\chi : \mathbb{R} \to M\) starting from \(\chi (0) = p\) with \(\nu = \chi ^{\prime }(0) \in T_{p}M\) is defined by \(\chi (t) := p e^{(\nu t/p)}\). Therefore,
The inverse of exponential map is defined by
Example 4
Let \(\Gamma = [1,+\infty )\) be a closed and geodesic convex subset of \(\mathbb{R}^{++}\) and \(A: \Gamma \to \mathbb{R}\) a single-valued vector field defined by
This is 1-Lipschitz continuous vector field, that is,
for all \(p,q \in \Gamma \); see [30] for more details. Hence, A is a 1-inverse strongly monotone vector field. Indeed, let \(x,y \in \Gamma \), we obtain
Let \(\varphi : \Gamma \to \mathbb{R} \cup \{+\infty \}\) be a proper, lower semicontinuous and geodesic convex function defined by
From Definition 9, we have
Lemma 6 shows that the subdifferential ∂φ of φ is a maximal monotone vector field. Now, consider the maximal monotone vector field B by ∂φ. Moreover, we have
It is clear that \(\{1\} = (A+B)^{-1}({\mathbf{0}})\).
Setting \(\gamma _{n} = \lambda _{n} = \frac{1}{2}+\frac{1}{n+4}\), so the sequences \(\{\gamma _{n}\}\) and \(\{\lambda _{n}\}\) satisfied the conditions (i) and (ii) of Theorem 2. With initial point \(x_{0} =2\) and \(x_{0} = 3\), we show the numerical behaviour of Mann-type splitting method in Table 1 and Fig. 1.
7 Concluding remarks
The problem of finding singularities of inclusion problems, which is defined by the sum of an inverse-strongly-monotone vector field and a multivalued maximal monotone vector field on a Hadamard manifold, is examined in this paper. A Mann-type splitting method is proposed for solving this problem. Under suitable conditions, the convergence theorem for sequences generated by the presented methods was established. We gave an example that demonstrates the usefulness of the Mann splitting method’s generalization from Hilbert spaces to Hadamard manifolds, in the sense that it must help in the explanation of some previously unconsidered situations. Furthermore, our algorithm was used to solve convex minimization problems and variational inequalities.
Availability of data and materials
Not applicable.
References
Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 14(5), 877–898 (1976)
You, X.X., Ali, M.A., Budak, H., Agarwal, P., Chu, Y.M.: Extensions of Hermite–Hadamard inequalities for harmonically convex functions via generalized fractional integrals. J. Inequal. Appl. 2021, Paper No. 102 (2021). https://doi.org/10.1186/s13660-021-02638-3
Ali, M.A., Abbas, M., Budak, H., Agarwal, P., Murtaza, G., Chu, Y.M.: New quantum boundaries for quantum Simpson’s and quantum Newton’s type inequalities for preinvex functions. Adv. Differ. Equ. 2021, Paper No. 64, 21 (2021). https://doi.org/10.1186/s13662-021-03226-x
Kadakal, M., İşcan, I., Agarwal, P., Jleli, M.: Exponential trigonometric convex functions and Hermite-Hadamard type inequalities. Math. Slovaca 71(1), 43–56 (2021). https://doi.org/10.1515/ms-2017-0410
Mehrez, K., Agarwal, P.: New Hermite-Hadamard type integral inequalities for convex functions and their applications. J. Comput. Appl. Math. 350, 274–285 (2019). https://doi.org/10.1016/j.cam.2018.10.022
Agarwal, P., Tariboon, J., Ntouyas, S.K.: Some generalized Riemann-Liouville k-fractional integral inequalities. J. Inequal. Appl. 2016, Paper No. 122, 13 (2016). https://doi.org/10.1186/s13660-016-1067-3
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd edn. CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC. Springer, Cham (2017) With a foreword by Hédy Attouch
Kitkuan, D., Kumam, P., Martínez-Moreno, J.: Generalized Halpern-type forward–backward splitting methods for convex minimization problems with application to image restoration problems. Optimization 69(7–8), 1557–1581 (2020)
Tibshirani, R.: Regression shrinkage and selection via the lasso: a retrospective. J. R. Stat. Soc., Ser. B, Stat. Methodol. 73(3), 273–282 (2011)
Sahu, D.R., Yao, J.C., Verma, M., Shukla, K.K.: Convergence rate analysis of proximal gradient methods with applications to composite minimization problems. Optimization 70(1), 75–100 (2021)
Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16(6), 964–979 (1979)
Boţ, R.I., Csetnek, E.R.: An inertial forward–backward–forward primal–dual splitting algorithm for solving monotone inclusion problems. Numer. Algorithms 71(3), 519–540 (2016)
Lorenz, D.A., Pock, T.: An inertial forward–backward algorithm for monotone inclusions. J. Math. Imaging Vis. 51(2), 311–325 (2015)
Chen, G.H.G., Rockafellar, R.T.: Convergence rates in forward–backward splitting. SIAM J. Optim. 7(2), 421–444 (1997)
Tseng, P.: A modified forward–backward splitting method for maximal monotone mappings. SIAM J. Control Optim. 38(2), 431–446 (2000)
Takahashi, W., Wong, N.C., Yao, J.C.: Two generalized strong convergence theorems of Halpern’s type in Hilbert spaces and applications. Taiwan. J. Math. 16(3), 1151–1172 (2012)
Shehu, Y.: Iterative approximations for zeros of sum of accretive operators in Banach spaces. J. Funct. Spaces 2016, Art. ID 5973468, 9 (2016)
Da Cruz Neto, J.X., Ferreira, O.P., Pérez, L.R.L., Németh, S.Z.: Convex- and monotone-transformable mathematical programming problems and a proximal-like point method. J. Glob. Optim. 35(1), 53–69 (2006)
Ferreira, O.P., Oliveira, P.R.: Proximal point algorithm on Riemannian manifolds. Optimization 51(2), 257–270 (2002)
Bento, G.C., Ferreira, O.P., Oliveira, P.R.: Proximal point method for a special class of nonconvex functions on Hadamard manifolds. Optimization 64(2), 289–319 (2015)
Li, C., López, G., Martín-Márquez, V.: Iterative algorithms for nonexpansive mappings on Hadamard manifolds. Taiwan. J. Math. 14(2), 541–559 (2010)
Ferreira, O.P., Louzeiro, M.S., Prudente, L.F.: Gradient method for optimization on Riemannian manifolds with lower bounded curvature. SIAM J. Optim. 29(4), 2517–2541 (2019)
Wang, X., López, G., Li, C., Yao, J.C.: Equilibrium problems on Riemannian manifolds with applications. J. Math. Anal. Appl. 473(2), 866–891 (2019)
Li, C., López, G., Martín-Márquez, V.: Monotone vector fields and the proximal point algorithm on Hadamard manifolds. J. Lond. Math. Soc. (2) 79(3), 663–683 (2009)
Khammahawong, K., Kumam, P., Chaipunya, P.: Splitting algorithms of common solutions between equilibrium and inclusion problems on Hadamard manifolds. Linear Nonlinear Anal. 6(2), 227–243 (2020)
Khammahawong, K., Kumam, P., Chaipunya, P., Martínez-Moreno, J.: Tseng’s methods for inclusion problems on Hadamard manifolds. Optimization 1–35 (2021). https://doi.org/10.1080/02331934.2021.1940179
Ferreira, O.P., Jean-Alexis, C., Piétrus, A.: Metrically regular vector field and iterative processes for generalized equations in Hadamard manifolds. J. Optim. Theory Appl. 175(3), 624–651 (2017)
Ansari, Q.H., Babu, F., Li, X.B.: Variational inclusion problems in Hadamard manifolds. J. Nonlinear Convex Anal. 19(2), 219–237 (2018)
Al-Homidan, S., Ansari, Q.H., Babu, F.: Halpern- and Mann-type algorithms for fixed points and inclusion problems on Hadamard manifolds. Numer. Funct. Anal. Optim. 40(6), 621–653 (2019)
Ansari, Q.H., Babu, F.: Proximal point algorithm for inclusion problems in Hadamard manifolds with applications. Optim. Lett. 15, 901–921 (2021)
Sakai, T.: Riemannian Geometry. Translations of Mathematical Monographs, vol. 149. Am. Math. Soc., Providence (1996) Translated from the 1992 Japanese original by the author
Bridson, M.R., Haefliger, A.: Metric Spaces of Non-positive Curvature. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 319. Springer, Berlin (1999)
Chen, J., Liu, S., Chang, X.: Modified Tseng’s extragradient methods for variational inequality on Hadamard manifolds. Appl. Anal. 100(12), 2627–2640 (2019)
Németh, S.Z.: Monotone vector fields. Publ. Math. (Debr.) 54(3–4), 437–449 (1999)
Wang, J.H., López, G., Martín-Márquez, V., Li, C.: Monotone and accretive vector fields on Riemannian manifolds. J. Optim. Theory Appl. 146(3), 691–708 (2010)
da Cruz Neto, J.X., Ferreira, O.P., Lucambio Pérez, L.R.: Monotone point-to-set vector fields. Balk. J. Geom. Appl. 5(1), 69–79 (2000). Dedicated to Professor Constantin Udrişte
Li, C., López, G., Martín-Márquez, V., Wang, J.H.: Resolvents of set-valued monotone vector fields in Hadamard manifolds. Set-Valued Var. Anal. 19(3), 361–383 (2011)
Van Nguyen, L., Thu, N.T., An, N.T.: Variational inequalities governed by strongly pseudomonotone vector fields on Hadamard manifolds (2021)
do Carmo M.Pa.: Riemannian Geometry. Mathematics: Theory & Applications. Birkhäuser Boston, Boston (1992) Translated from the second Portuguese edition by Francis Flaherty
Udrişte, C.: Convex Functions and Optimization Methods on Riemannians Manifolds. Mathematics and Its Applications, vol. 297. Kluwer Academic, Dordrecht (1994)
Rothaus, O.S.: Domains of positivity. Abh. Math. Semin. Univ. Hamb. 24, 189–235 (1960)
Lang, S.: Fundamentals of Differential Geometry. Graduate Texts in Mathematics, vol. 191. Springer, New York (1999)
Nesterov, Y.E., Todd, M.J.: On the Riemannian geometry defined by self-concordant barriers and interior-point methods. Found. Comput. Math. 2(4), 333–361 (2002)
Németh, S.Z.: Variational inequalities on Hadamard manifolds. Nonlinear Anal. 52(5), 1491–1498 (2003)
Acknowledgements
The second author is supported by Postdoctoral Fellowship from King Mongkut’s University of Technology Thonburi (KMUTT), Thailand. The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. Moreover, this research project is supported by Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2021 under project number 64A306000005.
Funding
Postdoctoral Fellowship from King Mongkut’s University of Technology Thonburi (KMUTT), Thailand. Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2021 under project number 64A306000005. The Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT, Thailand.
Author information
Authors and Affiliations
Contributions
All authors contributed equally in writing this article. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chaipunya, P., Khammahawong, K. & Kumam, P. Iterative algorithm for singularities of inclusion problems in Hadamard manifolds. J Inequal Appl 2021, 147 (2021). https://doi.org/10.1186/s13660-021-02676-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-021-02676-x