Low-Thrust Lunar Capture Leveraging Nonlinear Orbit Control

Abstract

Nonlinear orbit control with the use of low-thrust propulsion is proposed as an effective strategy for autonomous guidance of a space vehicle directed toward the Moon. Orbital motion is described in an ephemeris model, with the inclusion of the most relevant perturbations. Unfavorable initial conditions, associated with weak, temporary lunar capture, are considered, as representative conditions that may be encountered in real mission scenarios. These may occur when the spacecraft is released in nonnominal flight conditions, which would naturally lead it to impact the Moon or escape the lunar gravitational attraction. To avoid this, low-thrust propulsion, in conjunction with nonlinear orbit control, is employed, to drive the space vehicle toward two different, prescribed, low-altitude lunar orbits. Nonlinear orbit control leads to identifying a saturated feedback law (for the low-thrust magnitude and direction) that is proven to enjoy global stability properties. The guidance strategy at hand is successfully tested on three different mission scenarios. Then, the capture region is identified, and includes a large set of initial conditions for which nonlinear orbit control with low-thrust propulsion is effective to achieve lunar capture and final orbit acquisition. For the purpose of achieving lunar capture, low-thrust propulsion is shown to be more effective if ignited at aposelenium.

1 Introduction

Low energy missions to the Moon have attracted a great interest, for decades. In general, orbital motion in the Earth-Moon system has a chaotic nature, although several dynamical structures, such as periodic orbits and invariant manifolds, were proven to exist in the framework of the circular restricted three-body problem (CR3BP), which is usually employed for preliminary analysis. Some missions were already carried out, on the basis of early studies on low-energy trajectories in multibody environments. Examples are the European Smart-1 mission [1], the Japanese Hiten mission [2], and the NASA missions Genesis [3], Artemis [4], and GRAIL [5]. These missions exploit special classes of unstable periodic orbits that are proven to exist in the context of the CR3BP. Exterior and interior transfers to the Moon include transits through the regions located in the proximity of the collinear libration points. Former studies [6] established that the invariant manifolds associated with planar Lyapunov orbits play the role of separatrices. This means that in the phase space, the stable invariant manifold converging into the Lyapunov orbit separates the trajectories that transit from the Earth to the Moon from those that approach the interior collinear libration point and then return toward the Earth. Closely related to this, lunar capture dynamics represents a challenging and very significant problem of practical interest. In fact, a great deal of effort was dedicated to the identification and topological description of (non-periodic) lunar capture orbits, since the 60 s [7,8,9,10,11,12]. A fundamental conjecture dates back to the 60 s and is due to Conley [11], who stated that “if a crossing asymptotic orbit exists, then near any such there is a capture orbit”. In the subsequent decades, different methodologies were proposed, with the intent of obtaining lunar capture orbits. A popular approach, followed by a successful application in a real mission scenario, is due to Belbruno and Miller [12], and employs the concept of ballistic capture, leveraging the Sun gravitational influence. More recently, the senior author investigated lunar capture dynamics using isomorphic mapping [13], with the intent of relating capture orbits to asymptotic trajectories.

In the last decades, low-thrust electric propulsion has attracted an increasing interest by the scientific community, and already found application in a variety of mission scenarios, e.g. the NASA Deep Space 1 [14] and the ESA Smart-1 [1] missions. Thanks to high values of the specific impulse, low-thrust propulsion allows substantial propellant savings, at the price of increasing—even considerably—the time of flight. In a very recent publication, Cox et al. [15] focus on transit and capture in the planar three-body problem, using low-thrust dynamical structures. In fact, under certain assumptions, periodic orbits and invariant manifolds can be proven to subsist even if low thrust is ignited.

The present research focuses on low-thrust lunar capture dynamics and orbit acquisition, leveraging nonlinear orbit control. Orbital motion is described in an ephemeris model, and modified equinoctial elements are employed, for the purpose of describing the spacecraft trajectory relative to the Moon. All the relevant perturbations, i.e. third body gravitational attraction due to the Sun and the Earth, as well as several relevant harmonics of the selenopotential, are included in the dynamical modeling. Initial spacecraft positions and velocities, associated with weak, temporary lunar capture, are selected, as representative conditions that may be encountered in real mission scenarios, e.g. when a space vehicle is released in nonnominal flight conditions. In the absence of any corrective maneuver, these conditions lead to either (i) escape the Moon realm or (ii) impact with the lunar surface. This work is intended to prove that low-thrust propulsion, in conjunction with nonlinear orbit control, can drive the spacecraft toward a stable, specified orbit about the Moon (e.g., a low-altitude polar orbit), even in the presence of very unfavorable initial conditions. To do this, a saturated feedback law for the low-thrust magnitude and direction—with an upper bound on magnitude—is described and employed. In a previous work [16], a similar approach was employed for Earth orbits, for the purpose of orbit correction (at injection) and subsequent maintenance. Low-thrust nonlinear orbit control was shown to be effective both in driving the spacecraft toward the target trajectory and for orbit maintenance, starting from initial conditions sufficiently close to the desired ones. Instead, this research applies nonlinear orbit control in the presence of challenging (off nominal) initial conditions, far from the target orbit. More precisely, two types of target lunar orbits are considered: (a) polar circular orbit with specified radius and (b) polar elliptic orbit with a minimum value of periselenium radius and a maximum value of aposelenium radius. The mentioned nonlinear feedback law is proposed as an autonomous real-time guidance strategy, and its effectiveness is being tested in the presence of three different, challenging conditions at spacecraft release. Then, a large set of initial conditions are being considered, to investigate and characterize the effectiveness of low-thrust propulsion and nonlinear orbit control in leading the spacecraft toward the desired operational conditions. The final purpose is in identifying the capture region, i.e. the set of initial conditions compatible with low-thrust lunar capture and orbit acquisition.

In conclusion, the primary objectives of this study are (i) proposing a saturated nonlinear feedback control law based on nonlinear orbit control as an autonomous spacecraft guidance strategy to achieve lunar capture, (ii) providing an exhaustive stability analysis of the feedback law at hand, by completing the analysis presented in Ref. 16, (iii) testing its effectiveness in three challenging mission scenarios, in which an unpowered vehicle would impact the Moon or escape its realm, and (iv) identifying the capture region, i.e. a set of initial conditions for which low thrust propulsion and nonlinear orbit control represent an effective strategy for lunar capture and final orbit acquisition, while providing a concise and convenient two-dimensional representation of this region.

2 Orbit Dynamics

This study considers low-thrust propulsion with nonlinear orbit control, for the purpose of driving and maintaining a weakly-captured space vehicle in the proximity of some desired stable operational conditions about the Moon. The spacecraft of interest is mainly affected by the lunar gravitational field, and its orbital motion can be appropriately investigated by employing a perturbed two-body-problem model. As a first perturbing action, the lunar gravitational potential differs to some extent from that generated by a spherical mass distribution. As a result, some significant harmonics of the selenopotential are to be included in the dynamical model, in order to yield more realistic results from simulations. Other than lunar asphericity, the third-body perturbation due to the gravitational attraction of the Sun and the Earth represents an additional contribution. Steerable, throttleable low-thrust propulsion is used for orbit correction and maintenance maneuvers.

The remainder of this section describes the governing equations for orbit dynamics, as well as the orbit perturbations included in the dynamical modeling. As a preliminary step, some useful reference frames are introduced.

2.1 Reference Frames

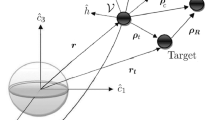
The Earth-centered inertial frame (ECI) and the Moon-centered inertial frame (MCI) are defined in relation to the heliocentric inertial frame (HCI). The latter reference system is associated with the right-hand sequence of unit vectors $\left( {\hat{c}_{1} ,\hat{c}_{2} ,\hat{c}_{3} } \right)$, where $\hat{c}_{1}$ is the vernal axis (corresponding to the intersection of the ecliptic plane with the Earth equatorial plane) and $\hat{c}_{3}$ points toward the Earth orbit angular momentum. Vectrix $\underline{\underline{{\text{S}}}}$ is introduced, $\underline{\underline{{\text{S}}}} \,: = \,\left[ {\hat{c}_{1} \quad \hat{c}_{2} \quad \;\hat{c}_{3} } \right]$.

The Earth-Centered inertial frame (ECI) has origin at the Earth’s center and is associated with vectrix $\underline{\underline{{\text{E}}}} \, = \,\left[ {\hat{c}_{1}^{\left( E \right)} \quad \hat{c}_{2}^{\left( E \right)} \quad \hat{c}_{3}^{\left( E \right)} } \right]$, where unit vectors $\hat{c}_{1}^{\left( E \right)}$ and $\hat{c}_{2}^{\left( E \right)}$ lie on the Earth’s mean equatorial plane. In particular, $\hat{c}_{1}^{\left( E \right)}$ is the vernal axis, while $\hat{c}_{3}^{\left( E \right)}$ points toward the Earth rotation axis. The ECI-frame and the HCI-frame are related through the ecliptic obliquity angle $\left( {\varepsilon = 23.4{\text{ deg}}} \right)$,

$$\underline{\underline{{\text{E}}}}^{T} \, = \,{\varvec{\textrm{R}}}_{1} \left( { - \varepsilon } \right)\underline{\underline{{\text{S}}}}^{T}$$

(1)

where ${\varvec{\textrm{R}}}_{j} \left( \xi \right)$ denotes an elementary counterclockwise rotation about axis j by a generic angle $\xi$.

According to the Cassini’s laws, the Moon rotation axis is coplanar with the Moon orbit angular momentum ${\mathbf{\mathop{h}\limits_{\rightarrow} }}_{M}$ and the normal to the ecliptic plane $\hat{c}_{3}$. The two vectors $\hat{z}_{M}$ and ${\mathbf{\mathop{h}\limits_{\rightarrow} }}_{M}$ are located at opposite sides of the ecliptic pole $\hat{c}_{3}$, and both of them are subject to clockwise precession due to the Sun, with a period of 18.6 years. Hence, axis $\hat{c}_{3}^{\left( M \right)}$ of MCI can be properly identified as the rotation axis $\hat{z}_{M}$ at a reference epoch $t_{ref}$, $\hat{c}_{3}^{\left( M \right)} = \hat{z}_{M} \left( {t_{ref} } \right)$. If $\psi_{M}$ and $\delta_{M}$ denote respectively the precession angle and the Moon equator obliquity (separating $\hat{c}_{3}^{\left( M \right)}$ from $\hat{c}_{3}$), then

$$\underline{\underline{{\text{M}}}}^{T} \, = \,{\varvec{\textrm{R}}}_{1} \left( {\delta_{M} } \right){\varvec{\textrm{R}}}_{3} \left( {\psi_{M}^{{\left( {ref} \right)}} } \right)\underline{\underline{{\text{S}}}}^{T}$$

(2)

where $\psi_{M}^{{\left( {ref} \right)}}$ represents the precession angle at $t_{ref}$, whereas $\underline{\underline{{\text{M}}}} : = \left[ {\begin{array}{*{20}c} {\hat{c}_{1}^{\left( M \right)} } & {\hat{c}_{2}^{\left( M \right)} } & {\hat{c}_{3}^{\left( M \right)} } \\ \end{array} } \right]$ identifies the MCI-frame.

The local horizontal frame (LH) represents a useful reference system that rotates together with the space vehicle. It is associated with $\underline{\underline{{\text{R}}}}_{LH} \,: = \,\left[ {\hat{r}\quad \hat{E}\quad \hat{N}} \right]$, where $\hat{r}$ is aligned with the spacecraft position vector ${\mathbf{\mathop{r}\limits_{\rightarrow} }}$ (taken from the center of the Moon), $\hat{E}$ is directed along the local east direction, and $\hat{N}$ is aligned with the local north direction. The LH-frame is related to the MCI-frame through the absolute longitude $\lambda_{a}$ and the latitude $\phi$,

$$\underline{\underline{{\text{R}}}}_{LH}^{T} = {\varvec{\textrm{R}}}_{2} \left( { - \phi } \right){\varvec{\textrm{R}}}_{3} \left( {\lambda_{a} } \right)\underline{\underline{{\text{M}}}}^{T}$$

(3)

If $\lambda_{a}^{{\left( {ref} \right)}}$ denotes the absolute longitude (taken counterclockwise from $\hat{c}_{1}^{\left( B \right)}$) of the reference meridian, then the satellite absolute longitude is $\lambda_{a} = \lambda_{a}^{{\left( {ref} \right)}} + \lambda_{g}$, where $\lambda_{g}$ is the spacecraft geographical longitude. The local horizontal local vertical frame (LVLH) is another useful reference system that rotates together with the space vehicle. It is associated with $\underline{\underline{{\text{R}}}}_{LVLH} : = \,\left[ {\hat{r}\quad \hat{\theta }\quad \hat{h}} \right]$, where $\hat{\theta }$ is aligned with the projection of the spacecraft velocity ${\mathbf{\mathop{v}\limits_{\rightarrow} }}$ into the local horizontal plane, whereas $\hat{h}$ points toward its angular momentum. The last two reference systems are related through the heading angle $\zeta$,

$$\underline{\underline{{\text{R}}}}_{LVLH}^{T} = {\varvec{\textrm{R}}}_{1} \left( \zeta \right)\underline{\underline{{\text{R}}}}_{LH}^{T}$$

(4)

Let a, e, i, $\Omega$, $\omega$, and f represent respectively the instantaneous (osculating) semimajor axis, eccentricity, inclination, right ascension of the ascending node (RAAN), argument of periselenium, and true anomaly of the space vehicle; $\theta$ denotes its argument of latitude, $\theta : = \omega + f$. The three angles $\lambda_{a}$, $\phi$, and $\zeta$ can be obtained as functions of the osculating orbit elements [17],

$$\phi = \arcsin \left( {\sin \theta \sin i} \right)$$

(5)

$$\lambda_{a} = 2\arctan \left( {\frac{\cos \theta \sin \Omega + \sin \theta \cos i\cos \Omega }{{\sqrt {1 - \left( {\sin \theta \sin i} \right)^{2} } + \cos \theta \cos \Omega - \sin \theta \cos i\sin \Omega }}} \right)$$

(6)

$$\zeta = 2\arctan \left( {\frac{\cos \theta \sin i}{{\sqrt {1 - \left( {\sin \theta \sin i} \right)^{2} } + \cos i}}} \right)$$

(7)

2.2 Equations of Motion

Orbit dynamics can be described using either osculating orbit elements or spherical coordinates. However, the Gauss equations [18] for the time derivatives of the orbit elements become singular if a circular or equatorial orbit is encounterd (or if an elliptic orbit transitions to a hyperbola). For these reasons, the modified equinoctial orbit elements (MEE) [19] l, m, n, s, and q are employed, together with the semilatus rectum (parameter) p, used in place of a. The six elements p, l, m, n, s, and q are defined as [19, 20]

$$\begin{aligned}&p = a\left( {1 - e^{2} } \right) \quad l = e\cos \left( {\Omega + \omega } \right) \quad m = e\sin \left( {\Omega + \omega } \right) \\ &n = \tan \frac{i}{2}\cos \Omega \quad s = \tan \frac{i}{2}\sin \Omega \quad q = \Omega + \omega + f\end{aligned}$$

(8)

These elements are nonsingular for all Keplerian trajectories, with the only exception of equatorial retrograde orbits ($i = \pi$). The osculating orbit elements can be retrieved by inverting Eq. (8). If $\eta : = 1 + l\cos q + m\sin q$, the spacecraft instantaneous radius $r \, \left( { = \left| {{\mathbf{\mathop{r}\limits_{\rightarrow} }}} \right|} \right)$) is given by $r = {p \mathord{\left/ {\vphantom {p \eta }} \right. \kern-0pt} \eta }$. Letting $x_{6} \equiv q$ and ${\mathbf{z}}: = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } & {x_{4} } & {x_{5} } \\ \end{array} } \right]^{T} \equiv \left[ {\begin{array}{*{20}c} p & l & m & n & s \\ \end{array} } \right]^{T}$, the governing equations for MEE can be written as

$${\dot{\mathbf{z}}} = {\varvec{\textrm{G}}}\left( {{\mathbf{z}},x_{6} } \right){\mathbf{a}}$$

(9)

$$\dot{x}_{6} = \sqrt {\frac{{\mu_{M} }}{{x_{1}^{3} }}} \eta^{2} + \sqrt {\frac{{x_{1} }}{{\mu_{M} }}} \frac{{x_{4} \sin x_{6} - x_{5} \cos x_{6} }}{\eta }a_{h}$$

(10)

where $\mu_{M}$ represents the lunar gravitational parameter, whereas

$${\varvec{\textrm{G}}}\left( {{\mathbf{z}},x_{6} } \right) = \sqrt {\frac{{x_{1} }}{{\mu_{M} }}} \left[ {\begin{array}{*{20}c} 0 & {\frac{{2x_{1} }}{\eta }} & 0 \\ {{\text{sin }}x_{6} } & {\frac{{\left( {\eta + 1} \right){\text{cos }}x_{6} + x_{2} }}{\eta }} & { - \frac{{x_{4} {\text{sin }}x_{6} - x_{5} {\text{cos }}x_{6} }}{\eta }x_{3} } \\ { - {\text{cos }}x_{6} } & {\frac{{\left( {\eta + 1} \right){\text{sin }}x_{6} + x_{3} }}{\eta }} & {\frac{{x_{4} {\text{sin }}x_{6} - x_{5} {\text{cos }}x_{6} }}{\eta }x_{2} } \\ 0 & 0 & {\frac{{1 + x_{4}^{2} + x_{5}^{2} }}{2\eta }{\text{cos }}x_{6} } \\ 0 & 0 & {\frac{{1 + x_{4}^{2} + x_{5}^{2} }}{2\eta }{\text{sin }}x_{6} } \\ \end{array} } \right]$$

(11)

Vector a is a $\left( {3 \times 1} \right)$-vector that includes the components of the non-Keplerian acceleration that affects the spacecraft motion. These components, denoted with $\left( {a_{r} ,a_{\theta } ,a_{h} } \right)$, are the projections of a into the LVLH-frame. Vector a includes both the thrust acceleration and the perturbing acceleration inherent to the space environment. It is convenient to distinguish these two contributions, therefore ${\mathbf{a}} = {\mathbf{a}}_{T} + {\mathbf{a}}_{P}$, where subscripts T and P refer to thrust and perturbations, respectively.

Let $T_{max}$ and $m_{0}$ denote the maximum available thrust magnitude and the initial mass. If $x_{7}$ represents the mass ratio and T the instantaneous thrust magnitude, then $x_{7}$ obeys the following equation:

$$\dot{x}_{7} : = \frac{{\dot{m}}}{{m_{0} }} = - \frac{{u_{T} }}{c}{\text{ with }}0 \le u_{T} \le u_{T}^{{\left( {max} \right)}} \, \left( {u_{T} : = \frac{T}{{m_{0} }}{\text{ and }}u_{T}^{{\left( {max} \right)}} : = \frac{{T_{max} }}{{m_{0} }}} \right)$$

(12)

where c is the (constant) effective exhaust velocity of the propulsion system. The magnitude of the instantaneous thrust acceleration is ${{a_{T} = u_{T} m_{0} } \mathord{\left/ {\vphantom {{a_{T} = u_{T} m_{0} } m}} \right. \kern-0pt} m} = {{u_{T} } \mathord{\left/ {\vphantom {{u_{T} } {x_{7} }}} \right. \kern-0pt} {x_{7} }}$ and varies in the interval $0 \le a_{T} \le a_{T}^{{\left( {max} \right)}}$, where $a_{T}^{{\left( {max} \right)}} = {{u_{T}^{{\left( {max} \right)}} } \mathord{\left/ {\vphantom {{u_{T}^{{\left( {max} \right)}} } {x_{7} }}} \right. \kern-0pt} {x_{7} }}$. Moreover, the thrust acceleration is ${\mathbf{a}}_{T} = {{{\mathbf{u}}_{T} } \mathord{\left/ {\vphantom {{{\mathbf{u}}_{T} } {x_{7} }}} \right. \kern-0pt} {x_{7} }}$, where ${\mathbf{u}}_{T}$ has magnitude constrained to $\left[ {0,u_{T}^{{\left( {max} \right)}} } \right]$.

In conclusion, orbit dynamics is described by the time evolution of the state vector ${\mathbf{x}}: = \left[ {\begin{array}{*{20}c} {{\mathbf{z}}^{T} } & {x_{6} } & {x_{7} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } & {x_{4} } & {x_{5} } & {x_{6} } & {x_{7} } \\ \end{array} } \right]^{T}$, whereas the control vector is ${\mathbf{u}}_{T}$, directly related to the thrust acceleration. Equations (9), (10), and (12) represent the state equations.

2.3 Harmonics of the Selenopotential

Currently, some accurate models exist for the Moon gravitational fields, i.e. (a) Goddard gravity model 3 (GLGM3150) and (b) Lunar Prospector models. This research employs the Lunar Prospector GLGM3150 model [21], which supplies a large number of coefficients of zonal, tesseral, and sectorial harmonics of the Moon gravitational field. These coefficients ($J_{l,m}$ and $\lambda_{lm}$) appear in the classical equation of planetary gravitational potentials (per mass unit), written in terms of Legendre polynomials $P_{lm}$,

$$U = \frac{{\mu_{M} }}{r} - \frac{{\mu_{M} }}{r}\sum\limits_{l = 2}^{\infty } {\left( {\frac{{R_{M} }}{r}} \right)^{l} J_{l} P_{l0} \left( {\sin \phi } \right)} + \frac{{\mu_{M} }}{r}\sum\limits_{l = 2}^{\infty } {\sum\limits_{m = 1}^{l} {\left( {\frac{{R_{M} }}{r}} \right)^{l} J_{l,m} P_{lm} \left( {\sin \phi } \right)\cos \left[ {m\left( {\lambda_{g} - \lambda_{lm} } \right)} \right]} }$$

(13)

where $R_{M}$ is the lunar equatorial radius.

In the LH-frame, the gravitational acceleration due to the Moon is given by

$${\mathbf{\mathop{G}\limits_{\rightarrow} }} = \nabla U{\text{ where }}\nabla = \hat{r}\frac{\partial }{\partial r} + \frac{{\hat{E}}}{r\cos \phi }\frac{\partial }{{\partial \lambda_{g} }} + \frac{{\hat{N}}}{r}\frac{\partial }{\partial \phi }$$

(14)

The previous expression, together with Eqs. (4)-(7) leads to obtaining the three components $\left( {G_{r} ,G_{\theta } ,G_{h} } \right)$ of the gravitational acceleration in the LVLH-frame, as a function of the instantaneous orbit elements. Because $G_{r}$ includes the main gravitational term, the related perturbing accelerations are $a_{P,r}^{\left( H \right)} = G_{r} + {{\mu_{M} } \mathord{\left/ {\vphantom {{\mu_{M} } {r^{2} }}} \right. \kern-0pt} {r^{2} }}$, $a_{P,\theta }^{\left( H \right)} = G_{\theta }$, and $a_{P,h}^{\left( H \right)} = G_{h}$. These components are incorporated in the $\left( {3 \times 1} \right)$-vector ${\mathbf{a}}_{P}^{\left( H \right)} = \left[ {\begin{array}{*{20}c} {a_{P,r}^{\left( H \right)} } & {a_{P,\theta }^{\left( H \right)} } & {a_{P,h}^{\left( H \right)} } \\ \end{array} } \right]^{T}$.

This works considers the first nine zonal harmonics of the selenopotential, i.e. $J_{1}$ through $J_{9}$.

2.4 Third Body Perturbation

The Earth and Sun gravitational influence on the space vehicle while this orbits the Moon can be modeled as a third body perturbation. In general, the perturbing acceleration due to a third body can be expressed as

$${\mathbf{\mathop{a}\limits_{\rightarrow} }}_{P}^{{\left( {3B} \right)}} = - \frac{{\mu_{3} }}{{s_{3}^{3} \left( {1 + q_{3} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}\left[ {{\mathbf{\mathop{r}\limits_{\rightarrow} }} + {}^{M}{\mathbf{\mathop{r}\limits_{\rightarrow} }}^{B} q_{3} \frac{{3 + 3q_{3} + q_{3}^{2} }}{{1 + \left( {1 + q_{3} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}} \right]{\text{, with }}q_{3} : = \frac{{r^{2} - 2{\mathbf{\mathop{r}\limits_{\rightarrow} }} \cdot {}^{M}{\mathbf{\mathop{r}\limits_{\rightarrow} }}^{B} }}{{r_{3B} }}$$

(15)

where $\mu_{3}$ denotes the gravitational parameter of the third body, ${}^{M}{\mathbf{\mathop{r}\limits_{\rightarrow} }}^{B}$ ($B = E{\text{ or }}B = S$, E and S standing for Earth and Sun) represents the position vector of the third body relative to the main body (i.e., the Moon), and $r_{3B} = \left| {{}^{M}{\mathbf{\mathop{r}\limits_{\rightarrow} }}^{B} } \right|$. The previous expression makes use of the Battin-Giorgi [18, 22] approach to the Encke’s method for orbit perturbations.

In the ECI-frame, the instantaneous position vectors of both the Sun and the Moon with respect to the Earth center, denoted respectively with $\mathop {{}^{E}{\mathbf{r}}^{S} }\limits_{ \to }$ and $\mathop {{}^{E}{\mathbf{r}}^{M} }\limits_{ \to }$, can be derived through interpolation of the ephemerides, using the approach described in Ref. [23]. Letting

$$\mathop {{}^{E}{\mathbf{r}}^{S} }\limits_{ \to } = \left[ {\begin{array}{*{20}c} {x_{S} } & {y_{S} } & {z_{S} } \\ \end{array} } \right]\underline{\underline{{\text{E}}}}^{T} \quad{\text{ and }}\quad\mathop {{}^{E}{\mathbf{r}}^{M} }\limits_{ \to } = \left[ {\begin{array}{*{20}c} {x_{M} } & {y_{M} } & {z_{M} } \\ \end{array} } \right]\underline{\underline{{\text{E}}}}^{T}$$

(16)

the two relative position vectors $\mathop {{}^{M}{\mathbf{r}}^{E} }\limits_{ \to }$ and $\mathop {{}^{M}{\mathbf{r}}^{S} }\limits_{ \to }$, which appear in Eq. (15), are given by

$$\mathop {{}^{M}{\mathbf{r}}^{E} }\limits_{ \to } = - \mathop {{}^{E}{\mathbf{r}}^{M} }\limits_{ \to }\quad {\text{ and }}\quad\mathop {{}^{M}{\mathbf{r}}^{S} }\limits_{ \to } = - \left( {\mathop {{}^{S}{\mathbf{r}}^{E} }\limits_{ \to } + \mathop {{}^{E}{\mathbf{r}}^{M} }\limits_{ \to } } \right) = \mathop {{}^{E}{\mathbf{r}}^{S} }\limits_{ \to } - \mathop {{}^{E}{\mathbf{r}}^{M} }\limits_{ \to }$$

(17)

Equations (15–17), in conjunction with Eqs. (1–4) lead to obtaining the three componemts of the third body perturbing acceleration due to both the Earth $\left( {a_{P,r}^{\left( E \right)} ,a_{P,\theta }^{\left( E \right)} ,a_{P,h}^{\left( E \right)} } \right)$ and the Sun $\left( {a_{P,r}^{\left( S \right)} ,a_{P,\theta }^{\left( S \right)} ,a_{P,h}^{\left( S \right)} } \right)$. These components are incorporated in the perturbing accelerations ${\mathbf{a}}_{P}^{\left( E \right)} = \left[ {\begin{array}{*{20}c} {a_{P,r}^{\left( E \right)} } & {a_{P,\theta }^{\left( E \right)} } & {a_{P,h}^{\left( E \right)} } \\ \end{array} } \right]^{T}$ and ${\mathbf{a}}_{P}^{\left( S \right)} = \left[ {\begin{array}{*{20}c} {a_{P,r}^{\left( S \right)} } & {a_{P,\theta }^{\left( S \right)} } & {a_{P,h}^{\left( S \right)} } \\ \end{array} } \right]^{T}$.

3 Nonlinear Orbit Control

Previous research [24] has shown that any state (associated with elliptic orbits) is accessible when the spacecraft dynamics is subject to the Gauss equations for classical orbit elements. However, the same property also holds for equinoctial elements [24]. This represents the theoretical premise for applying nonlinear techniques to orbital control.

In Sect. 2.2, the spacecraft motion was shown to be governed by Eqs. (9), (10), and (12). In particular, Eq. (9) can be rewritten as

$${\dot{\mathbf{z}}} = {\varvec{\textrm{G}}}\left( {{\mathbf{z}},x_{6} } \right)\left( {\frac{{{\mathbf{u}}_{T} }}{{x_{7} }} + {\mathbf{a}}_{P} } \right)$$

(18)

where the perturbing acceleration ${\mathbf{a}}_{P}$ includes several contributions, related to the space environment, namely harmonics of the selenopotential (term ${\mathbf{a}}^{\left( H \right)}$) and third body gravitational attraction due to both the Earth (${\mathbf{a}}_{P}^{\left( E \right)}$) and the Sun (${\mathbf{a}}_{P}^{\left( S \right)}$). Thus, ${\mathbf{a}}_{P} = {\mathbf{a}}_{P}^{\left( H \right)} + {\mathbf{a}}_{P}^{\left( E \right)} + {\mathbf{a}}_{P}^{\left( S \right)}$. It is worth noticing that Eq. (18) assumes a control-affine form in the absence of perturbing accelerations (${\mathbf{a}}_{P} = {\varvec{0}}$). For systems governed by Eq. (18) with ${\mathbf{a}}_{P} = {\varvec{0}}$, the Jurdjevic-Quinn theorem [25, 26] provides a feedback control law that can drive the dynamical system to an arbitrary target state, making the controlled system Lyapunov-stable.

In practical mission scenarios, orbit maintenance regards some (or all) of the following orbit elements: semimajor axis a, eccentricity e, inclination i, right ascension of the ascending node (RAAN) $\Omega$, and argument of periapse $\omega$. These identify the orbit size, shape, and orientation in space. Under the assumption that the target trajectory is defined in terms of these orbit elements only, the desired operational conditions depend only on ${\mathbf{z}}$ and can be formally defined by

$${{\varvec{\uppsi}}}\left( {\mathbf{z}} \right) = {\varvec{0}}$$

(19)

The previous vector equation is problem-dependent and corresponds to $q \, \left( { \le 5} \right)$ relations that involve equinoctial elements $x_{1}$ through $x_{5}$. If $q < 5$, Eq. (19) identifies a target set that is assumed to be a connected and differentiable manifold.

3.1 Feedback Control Law and Related Lyapunov Stability

This section is specifically devoted to defining a feedback control law capable of driving the dynamical system at hand (associated with Eqs. (10), (12), and (18)) toward the target conditions identified by Eq. (19). To do this, the following candidate Lyapunov function is introduced:

$$V = \frac{1}{2}{{\varvec{\uppsi}}}^{T} {\varvec{\textrm{K}}}{{\varvec{\uppsi}}}$$

(20)

where K denotes a diagonal matrix with constant, positive elements, which play the role of arbitrary weights. These are selected a priori in relation to the application of interest. It is immediate to recognize that $V > 0$ unless ${{\varvec{\uppsi}}} = {\varvec{0}}$. Yet, further conditions are required in order that V be an actual Lyapunov function. This issue is being addressed in the following three propositions, all proven in Ref. [16].

Proposition 1. Let ${\mathbf{b}}: = {\varvec{\textrm{G}}}^{T} \left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\mathbf{z}}}}} \right. \kern-0pt} {\partial {\mathbf{z}}}}} \right)^{T} {\varvec{\textrm{K}}}{{\varvec{\uppsi}}}$. If and ${{\varvec{\uppsi}}}$ and $\left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\mathbf{z}}}}} \right. \kern-0pt} {\partial {\mathbf{z}}}}} \right)$ are continuous, $\left| {\mathbf{b}} \right| > 0$ unless ${{\varvec{\uppsi}}} = {\varvec{0}}$, and $u_{T}^{{\left( {max} \right)}} \ge x_{7} \left| {{\mathbf{b}} + {\mathbf{a}}_{P} } \right|$, then the feedback control law,

$${\mathbf{u}}_{T} = - x_{7} \left( {{\mathbf{b}} + {\mathbf{a}}_{P} } \right)$$

(21)

leads a dynamical system governed by Eqs. (10), (12), and (18) to converge asymptotically to the target set associated with Eq. (19).

The previous proposition includes the condition $u_{T}^{{\left( {max} \right)}} \ge x_{7} \left| {{\mathbf{b}} + {\mathbf{a}}_{P} } \right|$. If this inequality is violated, the feedback law (21) is infeasible, because $\left| {{\mathbf{u}}_{T} } \right| = x_{7} \left| {{\mathbf{b}} + {\mathbf{a}}_{P} } \right|$ exceeds the maximum value $u_{T}^{{\left( {max} \right)}}$. In this case, an alternative feedback law can be employed, in place of Eq. (21).

Proposition 2. Let ${\mathbf{b}}: = {\varvec{\textrm{G}}}^{T} \left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\mathbf{z}}}}} \right. \kern-0pt} {\partial {\mathbf{z}}}}} \right)^{T} {\varvec{\textrm{K}}}{{\varvec{\uppsi}}}$. If and ${{\varvec{\uppsi}}}$ and $\left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\mathbf{z}}}}} \right. \kern-0pt} {\partial {\mathbf{z}}}}} \right)$ are continuous, $\left| {\mathbf{b}} \right| > 0$ unless ${{\varvec{\uppsi}}} = {\varvec{0}}$, $u_{T}^{{\left( {max} \right)}} < x_{7} \left| {{\mathbf{b}} + {\mathbf{a}}_{P} } \right|$, and ${\mathbf{b}}^{T} {\mathbf{a}}_{P} \le 0$, then the feedback control law

$${\mathbf{u}}_{T} = - u_{T}^{{\left( {max} \right)}} \frac{{{\mathbf{b}} + {\mathbf{a}}_{P} }}{{\left| {{\mathbf{b}} + {\mathbf{a}}_{P} } \right|}}$$

(22)

leads a dynamical system governed by Eqs. (10), (12), and (18) to converge asymptotically to the target set associated with Eq. (19).

The preceding proposition requires the sufficient condition ${\mathbf{b}}^{T} {\mathbf{a}}_{P} \le 0$ to guarantee $\dot{V} < 0$. However, ${\mathbf{b}}^{T} {\mathbf{a}}_{P}$ usually assumes both positive and negative values, depending on the specific time evolution of the dynamical system at hand. An additional sufficient condition that ensures $\dot{V} < 0$ even if ${\mathbf{b}}^{T} {\mathbf{a}}_{P} > 0$, regardless of the particular time evolution, is provided by the following:

Proposition 3. Let ${\mathbf{b}}: = {\varvec{\textrm{G}}}^{T} \left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\mathbf{z}}}}} \right. \kern-0pt} {\partial {\mathbf{z}}}}} \right)^{T} {\varvec{\textrm{K}}}{{\varvec{\uppsi}}}$. If and ${{\varvec{\uppsi}}}$ and $\left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\mathbf{z}}}}} \right. \kern-0pt} {\partial {\mathbf{z}}}}} \right)$ are continuous, $\left| {\mathbf{b}} \right| > 0$ unless ${{\varvec{\uppsi}}} = {\varvec{0}}$, and $x_{7} \left| {{\mathbf{a}}_{P} } \right| < u_{T}^{{\left( {max} \right)}} < x_{7} \left| {{\mathbf{b}} + {\mathbf{a}}_{P} } \right|$, then the feedback control law (23) leads a dynamical system governed by Eqs. (10), (12), and (18) to converge asymptotically to the target set associated with Eq. (19).

The two feedback laws (20) and (23) can be written in compact form as

$${\mathbf{u}}_{T} = - u_{T}^{{\left( {max} \right)}} \frac{{x_{7} \left( {{\mathbf{b}} + {\mathbf{a}}_{P} } \right)}}{{\max \left\{ {u_{T}^{{\left( {max} \right)}} ,x_{7} \left| {{\mathbf{b}} + {\mathbf{a}}_{P} } \right|} \right\}}}$$

(23)

Equation (23) incorporates the saturation condition on ${\mathbf{u}}_{T}$, i.e. $\left| {{\mathbf{u}}_{T} } \right| \le u_{T}^{{\left( {max} \right)}}$, and provides a control law that can be actuated using steerable and throttleable thrust (with time-varying magnitude and direction).

If the perturbing acceleration is negligible compared to the thrust acceleration $\left( {\left| {{\mathbf{a}}_{P} } \right| \ll {{u_{T}^{{\left( {max} \right)}} } \mathord{\left/ {\vphantom {{u_{T}^{{\left( {max} \right)}} } {x_{7} }}} \right. \kern-0pt} {x_{7} }}} \right)$, then the control law (22) can be regarded as nearly-Lyapunov-optimal. Proposition 3 provides a very useful sufficient condition that has a straightforward physical interpretation: if the thrust acceleration magnitude, ${{u_{T}^{{\left( {max} \right)}} } \mathord{\left/ {\vphantom {{u_{T}^{{\left( {max} \right)}} } {x_{7} }}} \right. \kern-0pt} {x_{7} }}$, exceeds the perturbation acceleration magnitude, $a_{P}$, then $\dot{V} < 0$ (unless ${{\varvec{\uppsi}}} = {\varvec{0}}$).

It is worth remarking that Propositions 1 through 3 represent sufficient conditions for stability. This circumstance implies that the assumptions of Propositions 1 through 3 can be violated, without necessarily compromising asymptotic stability toward the desired final condition, associated with Eq. (19).

3.2 Nonlinear Control for Semimajor Axis, Eccentricity, and Inclination of Lunar Orbits

The previous stability properties refer to the spacecraft dynamics, governed by Eqs. (10), (12), and (18). The desired operational conditions are defined by Eq. (19), which is problem-dependent and identifies the target set.

In this research, the desired lunar orbit is specified in terms of target values of semimajor axis, eccentricity, and inclination, denoted respectively with $a_{d}$, $e_{d}$, and $i_{d}$. Thus, due to Eq. (8), the desired operational conditions are

$$x_{1} - p_{d} = 0$$

(24)

$$x_{2}^{2} + x_{3}^{2} - e_{d}^{2} = 0$$

(25)

$$x_{4}^{2} + x_{5}^{2} - \tan^{2} \frac{{i_{d} }}{2} = 0$$

(26)

where $p_{d} = a_{d} \left( {1 - e_{d}^{2} } \right)$ and $e_{d} < 1$. The left-hand sides of Eqs. (24–26) form vector ${{\varvec{\uppsi}}}$, whose components are denoted with $\left( {\psi_{1} ,\psi_{2} ,\psi_{3} } \right)$.

The preceding section supplies three sets of sufficient conditions (stated in Propositions 1 through 3) that guarantee asymptotic stability, i.e. convergence toward the target set, identified by Eqs. (24–26). This subsection is intended to analyze these conditions, for the $\left( {3 \times 1} \right)$-vector ${{\varvec{\uppsi}}}$ defined by Eqs. (24–26).

As first steps, both ${{\varvec{\uppsi}}}$ and $\left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\mathbf{z}}}}} \right. \kern-0pt} {\partial {\mathbf{z}}}}} \right)$ turn out to be continuous in the entire domain where equinoctial elements are defined (i.e., $i \ne \pi$).

Then, vector b, whose components are $\left\{ {b_{1} ,b_{2} ,b_{3} } \right\}$, is derived analytically for the problem at hand,

$$b_{1} = - 2k_{2} \sqrt {\frac{{x_{1} }}{{\mu_{E} }}} \left( {x_{3} \cos x_{6} - x_{2} \sin x_{6} } \right)\psi_{2}$$

(27)

$$b_{2} = \frac{2}{\eta }\sqrt {\frac{{x_{1} }}{{\mu_{E} }}} \left\{ {k_{1} x_{1} \psi_{1} + k_{2} \psi_{2} \left( {\eta^{2} + x_{2}^{2} + x_{3}^{2} - 1} \right)} \right\}$$

(28)

$$b_{3} = \frac{{k_{3} }}{\eta }\sqrt {\frac{{x_{1} }}{{\mu_{E} }}} \left( {x_{4} \cos x_{6} + x_{5} \sin x_{6} } \right)\psi_{3} \left( {x_{4}^{2} + x_{5}^{2} + 1} \right)$$

(29)

The attracting set collects all the dynamical states that fulfill $\dot{V} = 0$. In fact, out of the attracting set $\dot{V} < 0$. The latter condition is met if ${\mathbf{b}} = {\varvec{0}}$, i.e. if the three components $\left\{ {b_{1} ,b_{2} ,b_{3} } \right\}$ equal 0, for any choice of the positive coefficients $\left\{ {k_{1} ,k_{2} ,k_{3} } \right\}$. It is straightforward to recognize that $x_{1} = 0$ yields $b_{1} = b_{2} = b_{3} = 0$. Other than this solution, from inspection of Eq. (33), $b_{2} = 0$ regardless of $\left\{ {k_{1} ,k_{2} } \right\}$ if ($\psi_{1} = 0$ and $\psi_{2} = 0$) or ($\psi_{1} = 0$ and $x_{2} = x_{3} = 0$). The term $\left( {\eta^{2} + x_{2}^{2} + x_{3}^{2} - 1} \right)$ can equal 0 also at specific values of $x_{6}$, but this circumstance is ruled out because $x_{6}$ is time-varying. Then, $b_{1} = 0$ if either $\psi_{2} = 0$ or $x_{2} = x_{3} = 0$. Lastly, $b_{3} = 0$ if either $\psi_{3} = 0$ or $x_{4} = x_{5} = 0$. In short, the attracting set includes the following five subsets:

• 1. $x_{1} = 0$ (rectilinear trajectories);

• 2. $x_{1} = p_{d} ,\,x_{2}^{2} + x_{3}^{2} = e_{d}^{2} ,\,x_{4}^{2} + x_{5}^{2} = 0$ (equatorial elliptic orbits with semilatus rectum $p_{d}$ and eccentricity $e_{d}$);

• 3. $x_{1} = p_{d} ,\,x_{2}^{2} + x_{3}^{2} = 0,\,x_{4}^{2} + x_{5}^{2} = \tan^{2} \left( {{{i_{d} } \mathord{\left/ {\vphantom {{i_{d} } 2}} \right. \kern-0pt} 2}} \right)$ (circular orbits with radius $p_{d}$ and inclination $i_{d}$);

• 4. $x_{1} = p_{d} ,\,x_{2}^{2} + x_{3}^{2} = 0,\,x_{4}^{2} + x_{5}^{2} = 0$ (circular equatorial orbits with radius $p_{d}$);

• 5. $x_{1} = p_{d} ,\,x_{2}^{2} + x_{3}^{2} = e_{d}^{2} ,\,x_{4}^{2} + x_{5}^{2} = \tan^{2} \left( {{{i_{d} } \mathord{\left/ {\vphantom {{i_{d} } 2}} \right. \kern-0pt} 2}} \right)$ (target set).

This analysis identifies two further subsets (3 and 4), which were not detected in Ref. [16]. Because the attracting set contains subsets other than the target set (which coincides with subset 5), asymptotic stability at the desired conditions is only local, based on Lyapunov’s theorem [27]. However, the LaSalle’s principle [27] can be used to rule out, if possible, subsets 1 through 4. Because ${{\varvec{\uppsi}}}$ is continuous and $\dot{V} < 0$ (except in the attracting set, denoted with A henceforth), the condition $V\left( {\mathbf{z}} \right) \le V\left( {{\mathbf{z}}_{0} } \right)$ (where ${\mathbf{z}}_{0}$ is z evaluated at the initial time) defines a compact set C. The invariant set must be sought in ${\text{A}} \cap {\text{C}}$, i.e. in the portion of the attracting set contained in C. By definition, the invariant set collects all the dynamical states (in the attracting set of z) that remain unchanged when ${\mathbf{a}} \equiv {\varvec{0}}$. This implies that if the invariant set is reached, then ${\mathbf{b}} \equiv {\varvec{0}}$ at future times, which implies ${\dot{\mathbf{b}}} \equiv {\varvec{0}}$ while ${\mathbf{a}} \equiv {\varvec{0}}$.

For the application at hand, the time derivatives of the three components of b are given by

$$\dot{b}_{j} = \frac{{\partial b_{j} }}{{\partial {\mathbf{z}}}}{\dot{\mathbf{z}}} + \frac{{\partial b_{j} }}{{\partial x_{6} }}\dot{x}_{6} = \frac{{\partial b_{j} }}{{\partial {\mathbf{z}}}}{\varvec{\textrm{G}}}\left( {{\mathbf{z}},x_{6} } \right){\mathbf{a}} + \frac{{\partial b_{j} }}{{\partial x_{6} }}\left[ {\sqrt {\frac{{\mu_{E} }}{{x_{1}^{3} }}} \eta^{2} + \sqrt {\frac{{x_{1} }}{{\mu_{E} }}} \frac{{x_{4} \sin x_{6} - x_{5} \cos x_{6} }}{\eta }a_{h} } \right]$$

(30)

where $j = 1,2,3$. The previous expression, evaluated at ${\mathbf{a}} \equiv {\varvec{0}}$ reduces to

$$\dot{b}_{j} = \frac{{\partial b_{j} }}{{\partial x_{6} }}\sqrt {\frac{{\mu_{E} }}{{x_{1}^{3} }}} \eta^{2} \, \left( {j = 1,2,3} \right)$$

(31)

Equations (27) through (29), in conjunction with Eq. (31), lead to

$$\dot{b}_{1} = \frac{{2k_{2} }}{{x_{1} }}\left( {x_{2} \cos x_{6} + x_{3} \sin x_{6} } \right)\psi_{2}$$

(32)

$$\dot{b}_{2} = \frac{2}{{x_{1} }}\left( {x_{2} \sin x_{6} - x_{3} \cos x_{6} } \right)\left\{ {k_{1} x_{1} \psi_{1} + k_{2} \psi_{2} \left( { - \eta^{2} + x_{2}^{2} + x_{3}^{2} - 1} \right)} \right\}$$

(33)

$$\dot{b}_{3} = \frac{{k_{3} }}{{x_{1} }}\psi_{3} \left( {x_{4}^{2} + x_{5}^{2} + 1} \right)\left( {x_{2} x_{5} - x_{3} x_{4} + x_{5} \cos x_{6} - x_{4} \sin x_{6} } \right)$$

(34)

Inspection of Eqs. (32–34) reveals that subset 1 ($x_{1} = 0$) does not belong to the invariant set, therefore convergence toward rectilinear trajectories is ruled out. Instead, subsets 2 thorugh 5 form the invariant set for the problem at hand.

Actually, convergence toward subsets 2 through 4 is only theoretical. In fact, the Lyapunov function can be rewritten in terms of orbit elements as

$$V = \frac{1}{2}\left[ {k_{1} \left( {p - p_{d} } \right)^{2} + k_{2} \left( {e^{2} - e_{d}^{2} } \right)^{2} + k_{3} \left( {\tan^{2} \frac{i}{2} - \tan^{2} \frac{{i_{d} }}{2}} \right)^{2} } \right]$$

(35)

where p, e, and i are the instantaneous semilatus rectum, eccentricity, and inclination. Function V, written in the form of Eq. (35) and evaluated at $p = p_{d}$, can be regarded as a function of two variables, i.e. e and i. It is relatively straightforward to prove that subset 5, i.e. the target set, corresponds to the global minimum of V, whereas the remaining subsets that form the invariant set are associated with unstable equilibrium conditions. In fact, the partial derivatives of V with respect to e and i are

$$\frac{\partial V}{{\partial e}} = 2k_{2} e\left( {e^{2} - e_{d}^{2} } \right)$$

(36)

$$\frac{\partial V}{{\partial i}} = 2k_{3} \tan \frac{i}{2}\left( {1 + \tan^{2} \frac{i}{2}} \right)\left( {\tan^{2} \frac{i}{2} - \tan^{2} \frac{{i_{d} }}{2}} \right)$$

(37)

$$\frac{{\partial^{2} V}}{{\partial e^{2} }} = 2k_{2} \left( {3e^{2} - e_{d}^{2} } \right)$$

(38)

$$\frac{{\partial^{2} V}}{{\partial i^{2} }} = - \frac{{k_{3} }}{2}\left( {1 + \tan^{2} \frac{i}{2}} \right)\left[ {3\tan^{2} \frac{i}{2}\left( {\tan^{2} \frac{{i_{d} }}{2} - 1} \right) - 5\tan^{4} \frac{i}{2} + \tan^{2} \frac{{i_{d} }}{2}} \right]$$

(39)

$$\frac{{\partial^{2} V}}{\partial e\partial i} = 0$$

(40)

Because ${{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial e}}} \right. \kern-0pt} {\partial e}} = 0$ at $e = 0{\text{ and }}e = e_{d}$ and ${{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial i}}} \right. \kern-0pt} {\partial i}} = 0$ at $i = 0{\text{ and }}i = i_{d}$, V is stationary in all the subsets that form the invariant set, which in fact includes all the equilibrium conditions. However, using Eqs. (36–39), in.

$${\text{subset 2}}:\,{{\partial^{2} V} \mathord{\left/ {\vphantom {{\partial^{2} V} {\partial e^{2} }}} \right. \kern-0pt} {\partial e^{2} }} > 0{\text{ and }}{{\partial^{2} V} \mathord{\left/ {\vphantom {{\partial^{2} V} {\partial i^{2} }}} \right. \kern-0pt} {\partial i^{2} }} < 0,\,{\text{while holding}}\quad{{\partial^{2} V}}/\left({\partial i \partial e }\right) = 0$$

(41)

$${{{\text{subset 3}}:\,\partial^{2} V} \mathord{\left/ {\vphantom {{{\text{subset 3}}:\,\partial^{2} V} {\partial e^{2} }}} \right. \kern-0pt} {\partial e^{2} }} < 0{\text{ and }}{{\partial^{2} V} \mathord{\left/ {\vphantom {{\partial^{2} V} {\partial i^{2} }}} \right. \kern-0pt} {\partial i^{2} }} > 0,\,{\text{while holding}}\quad{{\partial^{2} V}}/\left({\partial i \partial e }\right) = 0$$

(42)

$${{{\text{subset 4}}:\,\partial^{2} V} \mathord{\left/ {\vphantom {{{\text{subset 4}}:\,\partial^{2} V} {\partial e^{2} }}} \right. \kern-0pt} {\partial e^{2} }} < 0{\text{ and }}{{\partial^{2} V} \mathord{\left/ {\vphantom {{\partial^{2} V} {\partial i^{2} }}} \right. \kern-0pt} {\partial i^{2} }} < 0,\,{\text{while holding}}\quad{{\partial^{2} V}}/\left({\partial i \partial e }\right) = 0$$

(43)

$${\text{subset 5}}:\,{{\partial^{2} V} \mathord{\left/ {\vphantom {{\partial^{2} V} {\partial e^{2} }}} \right. \kern-0pt} {\partial e^{2} }} > 0{\text{ and }}{{\partial^{2} V} \mathord{\left/ {\vphantom {{\partial^{2} V} {\partial i^{2} }}} \right. \kern-0pt} {\partial i^{2} }} > 0,\,{\text{while holding}}\quad{{\partial^{2} V}}/\left({\partial i \partial e }\right) = 0$$

(44)

The preceding inequalities prove that (a) subsets 2 and 3 correspond to saddle points for V, (b) subset 4 is associated with a local maximum of V, and (c) subset 5, i.e. the target set, corresponds to the global minimum of V, and is the only stable equilibrium condition. This circumstance has the remarkable practical consequence that—from the numerical point of view—the dynamical system of interest enjoys global convergence toward the desired operational conditions, provided that the control law (23) is adopted, while holding the assumptions of either Proposition 1, 2, or 3.

It is worth remarking that the feedback law addressed in this section considers a target orbit with specified values of semilatus rectum, eccentricity, and inclination. Extension to more general Keplerian orbits is relatively straightforward using the definitions of MEE. As a further generalization, Ref. [28] considers a target orbit with prescribed, time-varying RAAN.

4 Low-Thrust Lunar Capture and Orbit Acquisition

This study considers a spacecraft equipped with a low-thrust propulsion system, tailored to achieving and maintaining a specified desired orbit about the Moon, in spite of unfavorable initial conditions. The propulsive performance is defined by the maximum value of $u_{T}^{{}}$, denoted with $u_{T}^{{\left( {max} \right)}}$, and the effective exhaust velocity c,

$$c = 30 \, {{{\text{km}}} \mathord{\left/ {\vphantom {{{\text{km}}} {\sec {\text{ and }}}}} \right. \kern-0pt} {\sec {\text{ and }}}}u_{T}^{{\left( {max} \right)}} = 5 \cdot 10^{ - 5} {\text{ g}}_{0} \, \left( {{\text{g}}_{0} = 9.8 \, {{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\sec^{2} }}} \right. \kern-0pt} {\sec^{2} }}} \right)$$

(45)

The reference epoch, corresponding to the initial time of the numerical simulations, is set to June 6, 2021 at 12:00 UTC. The numerical simulations are performed using canonical units. The distance unit (DU) equals the lunar radius, whereas the time unit (TU) is such that $\mu_{M} = 1 \, {{{\text{DU}}^{3} } \mathord{\left/ {\vphantom {{{\text{DU}}^{3} } {{\text{TU}}^{2} }}} \right. \kern-0pt} {{\text{TU}}^{2} }}$. Moreover, the following weighting coefficient are used, after extensive trial-and-attempt tuning: $k_{1} = 1$, $k_{2} = 1000$, and $k_{3} = 1$. These values turn out to be effective to drive the space vehicle toward the target orbit in the three illustrative examples being described. However, in a particular mission scenario, if the spacecraft initial conditions are specified (or predicted with sufficient advance), then gain tuning can allow selecting even more appropriate values of constants $\left( {k_{1} ,k_{2} ,k_{3} } \right)$, i.e. values that minimize the time of flight while using the feedback law (23). This approach was proven to be effective in Ref. [28], and led to finding near-optimal gains, associated with a time of flight close to the actual optimal (minimum-time) solution.

Two operational conditions are defined: (a) polar circular orbit at altitude of 550 km and (b) polar elliptic orbit with specified values of the minimum periselenium and maximum aposelenium radii, denoted respectively with $r_{P}^{{\left( {min} \right)}}$ and $r_{A}^{{\left( {max} \right)}}$. In this work, $r_{P}^{{\left( {min} \right)}} = R_{M} + 100{\text{ km}}$ and $r_{A}^{{\left( {max} \right)}} = R_{M} + 1000{\text{ km}}$. In the (e, p)-plane, orbit (a) corresponds to a point, whereas (b) is associated with a triangular region, idenitified by the inequalitites

$$r_{P} = \frac{p}{1 + e} \ge r_{P}^{{\left( {min} \right)}} \, \Rightarrow \, p \ge r_{P}^{{\left( {min} \right)}} \left( {1 + e} \right)$$

(46)

$$r_{A} = \frac{p}{1 - e} \le r_{A}^{{\left( {max} \right)}} \, \Rightarrow \, p \le r_{A}^{{\left( {max} \right)}} \left( {1 - e} \right)$$

(47)

Initial spacecraft positions and velocities, associated with weak, temporary lunar capture, are selected, as representative conditions that may be encountered in real mission scenarios, e.g. when a space vehicle is released in nonnominal flight conditions. In the absence of any corrective maneuver, these conditions very often lead to either (i) escape the Moon realm or (ii) impact with the lunar surface. Low-thrust propulsion, in conjunction with the feedback control law (23), is used, with the intent of driving the spacecraft toward either condition (a) or condition (b). In both cases the target set is defined by Eqs. (24–26), with $p_{d} = R_{M} + 550{\text{ km}}$, $e_{d} = 0$, and $i_{d} = 90{\text{ deg}}$. However, if the operational condition (b) is pursued, low thrust is turned off when both inequalitites (42) and (43) are fulfilled, while holding

$$\left| {\psi_{3} } \right| = \left| {\tan^{2} \frac{i}{2} - \tan^{2} \frac{{i_{d} }}{2}} \right| < 10^{ - 5}$$

(48)

4.1 Illustrative Examples

This subsection considers 3 illustrative examples of the use low-thrust propulsion in conjunction with nonlinear orbit control, for the purpose of driving the spacecraft of interest toward the operational conditions (a) and (b), also termed “target point” and “target region” henceforth, with reference to the respective representartions in the $\left( {e,p} \right)$-plane. Orbit propagations cover a duration of 3 years, starting from the initial epoch $t_{0}$. Three unfavorable initial conditions (with subscript 0), reported in Table 1 in terms of osculating orbit elements, are assumed, which would lead the spacecraft to either impact the Moon or escape the lunar gravitational attraction.

Table 1 Initial orbit elements for the 3 mission scenarios

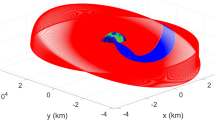
In the first mission scenario, the space vehicle would impact the lunar surface in about 4 days, in the absence of any control action. In Fig. 1, the related path in the $\left( {e,p} \right)$-plane is portrayed in red and denoted with “no control”. Instead, low-thrust propulsion and nonlinear orbit control are proven to be able to drive the spacecraft toward either the target region or the target point. Figure 2a illustrates the related paths in the $\left( {e,p} \right)$-plane, with a zoom on the terminal arc leading to the target point. The two paths associated with operational conditions (a) and (b) overlap until the target region is entered. Then, low thrust is switched off if the target region is pursued (condition (b)), whereas it remains on if the target point represents the final objective (cyan arc). For the former case, Fig. 2b shows that the osculating elements $\left( {e,p} \right)$ are kept in close proximity of the boundary of the target region, for the entire residual mission duration. Figure 3 depicts the mass ratio time histories. Pursuing the target region (final orbit (b)) implies saving a moderate yet relevant propellant amount with respect to point targeting (final orbit (a)). Nevertheless, the propellant consumption associated with the target point strategy is completely compatible with a mission duration of 3 years (cf. Table 2 and Fig. 3a). With reference to the latter strategy, Fig. 4b portrays the inclination time history, and points out that 87.5 days are needed to enter the desired polar orbit plane. Finally, Fig. 4a illustrates the low-thrust trajectory, for the entire time of flight.

Fig. 1

Mission scenario 1: orbit evolution with no control (red) and with nonlinear orbit control (blue and cyan) (Color figure online)

Fig. 2

Mission scenario 1: zoom on the terminal arcs in the (e,p)-plane: target point (a) and target region (b)

Fig. 3

Mission scenario 1: mass ratio time histories, associated with target point (a) and target region (b)

Table 2 Final mass ratio for the 3 mission scenarios, with reference to the two operational conditions

Fig. 4

Mission scenario 1, target point: trajectory and inclination time history (orbit acquisition phase)

In the second mission scenario, the space vehicle would escape the lunar realm, in the absence of any control action. The related path in the $\left( {e,p} \right)$-plane is portrayed in red and denoted with “no control”. Escape corresponds to reaching eccentricity greater than 1. Instead, low thrust propulsion and nonlinear orbit control are able to drive the spacecraft toward either the target region or the target point. Figure 5 illustrates the related paths in the $\left( {e,p} \right)$-plane, whereas Fig. 6a shows a zoom on the terminal arc leading to the target point. Also in this case, the two paths associated with operational conditions (a) and (b) overlap until the target region is entered. Figures 5 through 8 are the counterparts of Figs. 1 through 4 for case 1, and similar considerations apply (Fig. 7). With reference to the target point strategy, Fig. 8b portrays the inclination time history, showing that 58.6 days are needed to enter the desired polar orbit plane. Finally, Fig. 8a illustrates the low-thrust trajectory, for the entire time of flight.

Fig. 5

Mission scenario 2: orbit evolution with no control (red) and with nonlinear orbit control (blue and cyan) (Color figure online)

Fig. 6

Mission scenario 2: zoom on the terminal arcs in the (e,p)-plane: target point (a) and target region (b)

Fig. 7

Mission scenario 2: mass ratio time histories, associated with target point (a) and target region (b)

Fig. 8

Mission scenario 2, target point: (a) trajectory and (b) inclination time history (orbit acquisition phase)

In the third mission scenario, the space vehicle would travel in close proximity of the Moon before escaping the lunar realm, in the absence of any control action. This circumstance is apparent by inspecting Figs. 9 and 10, which illustrate the ballistic path in red. The constraint on the minimum periapse radius is violated while the space vehicle is far from its periselenium. As a result, no lunar impact occurs, although the spacecraft approaches the Moon up to a minimum altitude of 511 km before escaping its gravitational attraction. Instead, low-thrust propulsion and nonlinear orbit control are able to drive the spacecraft toward either the target region or the target point. Figure 11a illustrates a zoom on the terminal arc leading to the target point. Also in this case, the two paths associated with operational conditions (a) and (b) overlap until the target region is entered (Fig. 12). Figures 9 and 11 through 13 are the counterparts of Figs. 1 through 4 for case 1, and similar considerations apply. With reference to the target point strategy, Fig. 13b portrays the inclination time history, showing that 79.7 days are needed to enter the desired polar orbit plane. Finally, Fig. 13a illustrates the low-thrust trajectory, for the entire time of flight.

Fig. 9

Mission scenario 3: orbit evolution with no control (red) and with nonlinear orbit control (blue and cyan) (Color figure online)

Fig. 10

Mission scenario 3: zoom on the initial arcs in the (e,p)-plane

Fig. 11

Mission scenario 3: zoom on the terminal arcs in the (e,p)-plane: target point (a) and target region (b)

Fig. 12

Mission scenario 3: mass ratio time histories, associated with target point (a) and target region (b)

Fig. 13

Mission scenario 3, target point: a trajectory and b inclination time history (orbit acquisition phase)

From inspection of Figs. 3, 7, and 12 it is apparent that two phases exist: (i) orbit acquisition, corresponding to the maximum thrust magnitude (and faster mass decrease), followed by (ii) orbit maintenance, associated with intermediate, time-varying thrust magnitude (and reduced mass depletion, compared to the preceding phase). These two phases are encountered regardless of the final operational condition.

4.2 Capture Region

The preceding methodology is then applied to a large set of initial conditions. A number of different values are considered for the initial eccentricity $e_{0}$ and semilatus rectum $p_{0}$. More specifically, equally-spaced values are assumed for both elements, with spacing set to 0.01 for $e_{0}$ and 1000 km for $p_{0}$. Elements $i_{0}$, $\Omega_{0}$, and $\omega_{0}$ are identical to those reported in Table 1, for all cases. Moreover, two different initial conditions are assumed for the initial true anomaly, i.e. $f_{0} = 0$ or $f_{0} = 180{\text{ deg}}$. The natural orbit dynamics is considered first, then low-thrust propulsion with nonlinear orbit control is employed, for an overall time of flight of 3 years.

Figure 14a illustrates—with different colors—the regions corresponding to lunar capture (for at least 3 years), impact, or escape (before 3 years have elapsed), under the assumption that the spacecraft is at periselenium at $t_{0}$ ($f_{0} = 0$). Figure 14b portrays the corresponding orbit evolution when low thrust and nonlinear orbit control are used. The line that appears in the lower part is associated with the minimum periselenium altitude, set to 100 km. It is apparent that the low-thrust capture region includes a large portion of initial conditions that would otherwise lead an unpowered space vehicle to impact the Moon or escape its realm.

Fig. 14

Orbit evolution in the (e, p)-plane, with initial condition at periselenium. a Natural dynamics: capture region (green), impact region (yellow), escape region (red). b Powered dynamics: capture region (green), escape region (red) (Color figure online)

Similarly, Fig. 15a illustrates—with different colors—the regions corresponding to lunar capture (for at least 3 years), impact, or escape (before 3 years have elapsed), under the assumption that the spacecraft is at aposelenium at $t_{0}$ ($f_{0} = 180{\text{ deg}}$). Figure 15b portrays the corresponding orbit evolution when low-thrust and nonlinear orbit control are used. It is apparent that the capture region includes again a large portion of initial conditions that would otherwise lead an unpowered space vehicle to impact the Moon or escape its realm.

Fig. 15

Orbit evolution in the (e, p)-plane, with initial condition at aposelenium. a Natural dynamics: capture region (green), impact region (yellow), escape region (red). b Powered dynamics: capture region (green), escape region (red) (Color figure online)

Comparison of the preceding figures reveals that the use of low-thrust propulsion and nonlinear orbit control is more advantageous if it is ignited when the spacecraft is at aposelenium at the initial epoch. In fact, in the $\left( {e_{0} ,p_{0} } \right)$-plane the region associated with lunar capture when $f_{0} = 180{\text{ deg}}$ is much larger than that corresponding to $f_{0} = 0$. Enhanced effectiveness of low-thrust nonlinear orbit control, if it is ignited at aposelenium, represents a remarkable finding, which deserves further analysis. As a first outcome of this study, orbit propagations point out that escape takes place in the very early phases after the spacecraft is released, i.e. before completing the first orbit about the Moon. This behavior occurs both for unpowered spacecraft and for those initial conditions that yield escape in spite of the use of low-thrust propulsion. This fact implies that if nonlinear orbit control avoids escape in the very early phases of spaceflight, then the space vehicle remains captured in the proximity of the Moon, so that low-thrust propulsion can successfully drive it toward the final desired operational conditions. Therefore, for the purpose of avoiding escape after spacecraft release, it is vital that low thrust be able to promptly reduce the orbit eccentricity. Ignition at aposelenium can be shown to be more effective than ignition at periselenium through the approximate analysis that follows. If $\left( {a_{r} ,a_{\theta } ,a_{h} } \right)$ represent the components of the non-Keplerian acceleration in the LVLH-frame, then the Gauss equations for the orbit eccentricity and the true anomaly are [29]

$$\dot{e} = a_{r} \sqrt {\frac{p}{{\mu_{M} }}} \sin f + a_{\theta } \sqrt {\frac{p}{{\mu_{M} }}} \frac{{e + e\cos^{2} f + 2\cos f}}{1 + e\cos f}$$

(49)

$$\dot{f} = \sqrt {\frac{{\mu_{M} }}{{p^{3} }}} \left( {1 + e\cos f} \right)^{2} + a_{r} \sqrt {\frac{p}{{\mu_{M} }}} \frac{\cos f}{e} + a_{\theta } \sqrt {\frac{p}{{\mu_{M} }}} \sin f\frac{ - 2 - e\cos f}{{e\left( {1 + e\cos f} \right)}} \simeq \sqrt {\frac{{\mu_{M} }}{{p^{3} }}} \left( {1 + e\cos f} \right)^{2}$$

(50)

where in the last step the right-hand side of Eq. (46) is reduced to the first term, which prevails over the remaining ones. Using these relations, the derivative of e with respect to f, denoted with $e^{\prime}$, is obtained,

$$e^{\prime} = a_{r} \frac{{p^{2} }}{{\mu_{M} }}\frac{\sin f}{{\left( {1 + e\cos f} \right)^{2} }} + a_{\theta } \frac{{p^{2} }}{{\mu_{M} }}\frac{{e + e\cos^{2} f + 2\cos f}}{{\left( {1 + e\cos f} \right)^{3} }}$$

(51)

The thrust control law that minimizes $e^{\prime}$ is sought, under the assumption that $\left( {a_{r} ,a_{\theta } ,a_{h} } \right)$ only include the contribution due to propulsion. First, the two components $\left( {a_{r} ,a_{\theta } } \right)$, which appear in Eq. (47), are expressed in terms of acceleration magnitude $a_{T}$ and angle $\alpha$,

$$a_{r} = a_{T} \sin \alpha \,{\text{ and }}\,a_{\theta } = a_{T} cos\alpha$$

(52)

and Eq. (47) is rewritten as

$$e^{\prime} = a_{T} \frac{{p^{2} }}{{\mu_{M} \left( {1 + e\cos f} \right)^{2} }}\left[ {\begin{array}{*{20}c} {\sin \alpha } & {\cos \alpha } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\sin f} & {\frac{{e + e\cos^{2} f + 2\cos f}}{1 + e\cos f}} \\ \end{array} } \right]^{T}$$

(53)

Then, minimization of $e^{\prime}$ leads to

$$\sin \alpha = - \frac{\sin f}{{\sqrt {\sin^{2} f + \left( {\frac{{e + e\cos^{2} f + 2\cos f}}{1 + e\cos f}} \right)^{2} } }}\,{\text{ and }}\,\cos\alpha = - \frac{{\frac{{e + e\cos^{2} f + 2\cos f}}{1 + e\cos f}}}{{\sqrt {\sin^{2} f + \left( {\frac{{e + e\cos^{2} f + 2\cos f}}{1 + e\cos f}} \right)^{2} } }}$$

(54)

and the minimum value of $e^{\prime}$ is

$$e^{\prime} = - a_{T} \frac{{p^{2} }}{{\mu_{M} \left( {1 + e\cos f} \right)^{2} }}\sqrt {\sin^{2} f + \left( {\frac{{e + e\cos^{2} f + 2\cos f}}{1 + e\cos f}} \right)^{2} }$$

(55)

The preceding expression provides an indication on the sensitivity of $e^{\prime}$ with respect to the true anomaly f, when the thrust acceleration is chosen with the intent of minimizing e, which is the key requirement in the early phases of spaceflight, to avoid escape. Figure 16 portrays the auxiliary function $g\left( {f,e} \right): = {{\left( {\mu_{M} e^{\prime}} \right)} \mathord{\left/ {\vphantom {{\left( {\mu_{M} e^{\prime}} \right)} {\left( {p^{2} a_{T} } \right)}}} \right. \kern-0pt} {\left( {p^{2} a_{T} } \right)}}$, for different values of e (= 0.6, 0.7, 0.8, 0.9). Inspection of this figure points out that for all values of e, function g has minimum values at $f = \pi$, and this means that the effect of low thrust is amplified at aposelenium if compared to what occurs at periselenium. Although orbit perturbations are neglected, the preceding analysis provides a justification of the enhanced effectiveness of low-thrust propulsion in avoiding escape, when ignition occurs at aposelenium.

Fig. 16

Function g( f,e), related to the sensitivity of e’ with respect to f when low thrust minimizes e’

As a final remark, it is worth noticing that in all cases, if low-thrust propulsion is ignited, then no impact with the lunar surface occurs (cf. Figures 14b and 15b).

5 Concluding Remarks

Nonlinear orbit control with the use of low-thrust propulsion is proposed as an effective strategy for autonomous guidance of a space vehicle directed toward the Moon. Orbital motion is described in an ephemeris model, and modified equinoctial elements are employed, for the purpose of describing the spacecraft dynamics relative to the Moon. All the relevant perturbations, i.e. third body gravitational attraction due to the Sun and the Earth, as well as several relevant harmonics of the selenopotential, are included in the dynamical modeling. Unfavorable initial conditions, associated with weak, temporary lunar capture, are considered, as representative conditions that may be encountered in real mission scenarios. These may occur when the spacecraft is released in nonnominal flight conditions, which would naturally lead it to impact the Moon or escape the lunar gravitational attraction. Instead, low-thrust propulsion, in conjunction with nonlinear orbit control, is proven to be an effective strategy to drive the spacecraft toward a stable, specified orbit about the Moon (e.g., a low-altitude polar orbit). To do this, a saturated feedback law for the low-thrust magnitude and direction—with an upper bound on magnitude—is described and applied, and is demonstrated to enjoy quasi-global analytical stability properties. Moreover, the operational conditions are proven to correspond to the only stable equilibrium of the closed-loop dynamical system, and this ensures numerical convergence toward the target orbit (in global sense). The sufficient conditions for asymptotic stability consider the perturbing acceleration term, and lead to identifying two types of arcs: (i) maximum-thrust arcs and (ii) time-varying, intermediate-thrust arcs. The feedback control law at hand does not require any offline reference trajectory. Therefore, it is effective as an autonomous real-time guidance strategy, even in the presence of unpredictable nonnominal flight conditions. Two types of target orbits are assumed: (a) polar circular orbit with specified radius, and (b) polar elliptic orbit with a minimum value of periselenium radius and a maximum value of aposelenium radius. These two final conditions can be represented in the (e,p)-plane, where p and e denote the orbit semilatus rectum and eccentricity, respectively. Three illustrative examples are considered, corresponding to different initial conditions, associated with a variety of uncontrolled trajectory evolutions. In all of these cases, orbit propagations demonstrate that low-thrust nonlinear orbit control represents an effective real-time feedback strategy for achieving lunar capture ad convergence toward an operational orbit, even starting from unfavorable initial conditions that would naturally lead the space vehicle to impact the Moon or escape the lunar gravitational attraction. Driving the spacecraft toward orbit (b) and the subsequent maintenance maneuvers require about 15% of the initial mass, for a mission duration of 3 years. If orbit (a) is pursued, propellant consumption increases, but the mass budget is still favorable and completely compatible with a 3-year mission. Then, a large set of initial conditions was considered. In most cases, the spacecraft would naturally impact the Moon or escape its gravitational attraction. Instead, if nonlinear orbit control with low-thrust propulsion is employed, impact is avoided and the capture region is enlarged considerably, especially if the thrust is ignited when the spacecraft is at aposelenium. The numerical results over a large set of initial conditions represent a further confirmation on the utility and effectiveness of low-thrust nonlinear orbit control in achieving lunar capture and final orbit acquisition. Extension of this study may be pursued with the aim of identifying a feedback control law able to drive the space vehicle toward non-Keplerian orbits, associated with time-varying orbit elements. As a remarkable example of current interest, the operational path of the Lunar Gateway is a non-Keplerian near rectilinear Halo orbit, and generalization of nonlinear orbit control to target this type of trajectory would certainly represent a valuable extension of this research, worth of future investigation.