Mars Constellation Design and Low-Thrust Deployment Using Nonlinear Orbit Control

Abstract

This research addresses the design of a Mars constellation composed of 12 satellites and devoted to telecommunications. While 3 satellites travel areostationary orbits, the remaining 9 satellites are placed in three distinct quasi-synchronous, inclined, circular orbits. The constellation at hand provides continuous global coverage, over the entire Martian surface. The use of 4 carrier vehicles, departing from a 4-sol orbit, is proposed as an affordable option for the purpose of deploying the entire constellation, even starting from dispersed initial conditions. Each carrier is driven toward the respective operational orbit using steerable and throttleable low-thrust propulsion, in conjunction with nonlinear orbit control. Lyapunov stability analysis leads to defining a feedback law that enjoys quasi-global stability properties. Orbit phasing concludes the constellation deployment, and is carried out by each satellite. The tradeoff between phasing time and propellant expenditure is characterized.

1 Introduction

Mars represents a major target for planetary exploration in the decades to come. Several scientific missions are already planned, and the prospect of carrying out the first human mission is becoming more and more concrete. A variety of objects, ranging from rovers to scientific instrumentation for environmental analyses, were (and are being) released in different locations on the Martian surface. A satellite constellation aimed at providing continuous, global coverage over the great majority of the red planet could serve as a communications relay system and would certainly represent a valuable asset for future missions. In fact, such a constellation would significantly facilitate the communications among orbiters, probes and instruments located on the surface, and Earth ground stations. This would also lead to extending the existing capabilities of NASA’s Deep Space Network, as remarked in Ref. [1]. Several goals were defined [1] for a satellite constellation about Mars:

• (a) global coverage over a prescribed time span,

• (b) communication support of the equatorial region, also as a support to human missions,

• (c) maximization of the communication and navigation performance across all latitudes and longitudes,

• (d) minimization of the variations of the navigation and communication performance,

• (e) redundant coverage in case of loss of any single satellite, and

• (f) minimization of the coverage variability due to long-term orbit perturbations, with special reference to the orbit plane precession.

Depending on the specific tasks, several types of orbits may be suitable for the purpose of designing and deploying a constellation around Mars [2, 3]. Bell et al. [2] proposed 4 distinct constellation configurations of microsatellites that travel low-altitude, inclined orbits and ensure satisfactory global communication and navigation performance, with special regard to the equatorial region. Each configuration includes 6 satellites with different inclinations. Yet, for all configurations the maximum revisit time ranges from 1 to 8 h, and exceeds 2 h over the great majority of the Martian surface. Nann et al. [4] focused on precise characterization of the Martian atmosphere for future missions, and designed a constellation of 8 satellites suitable for the purpose of performing radio occultation measurements. The same constellation can be reconfigured, to provide (discontinuous) navigation services. Most recently, Kelly and Bevilacqua [5] proposed a constellation of 15 satellites that ensures global and continuous coverage of the entire Martian surface, using 5 equally spaced, inclined orbit planes.

Release of multiple satellites from a single carrier spacecraft would be an attractive and affordable option for constellation deployment. However, this objective is rather challenging, especially if the constellation configuration is designed to include different orbit planes with large angular displacements. Former contributions in the scientific literature were mainly focused on deployment strategies for Earth constellations [6–9]. In 2006, the FORMOSAT-3/COSMIC constellation [7] was released from a single launch vehicle. Each of the 6 satellites raised its orbit, and leveraged the differential precessional motion due to the Earth oblateness, with the final aim of achieving the desired orbit plane. This well-known effect was also investigated by Crisp et al. [8] In addition, they designed a second strategy, based on the temporary release of the spacecraft in the proximity of the interior libration point of the Earth-Moon system. Most recently, Lee et al. [9] focused on a flexible deployment strategy in response to the possible evolution of the Earth regions of interest, whereas Pontani and Teofilatto [10] focused on low-thrust deployment of a low-Earth-orbit constellation tailored to polar ice monitoring.

This research considers a constellation composed of 12 satellites released in 4 distinct orbit planes about Mars. While 3 satellites travel an areostationary orbit, the remaining 9 satellites are released in three repeating, circular, quasi-synchronous, inclined orbits. This configuration is aimed at guaranteeing global and continuous coverage, while ensuring repetition and predictability of the visible passes as well as visibility of multiple satellites. This work also addresses the problem of deploying all the satellites using 4 carrier vehicles, released by the mother spacecraft. The latter orbits a highly elliptical path, i.e. the ESA 4-sol orbit [11], which is entered after planetary capture. Orbit dynamics about Mars is modeled with the inclusion of the most relevant perturbations, i.e. several harmonics of the areopotential, together with the gravitational pull due to the Sun as a third body. Each carrier embarks 3 satellites and employs steerable and throttleable low-thrust propulsion for the purpose of driving them toward the respective operational orbit. Nonlinear orbit control is proposed as a suitable strategy for autonomous real-time guidance, even in the presence of nonnominal flight conditions, e.g. if the initial highly elliptical orbit is significantly different from the expected one, due to injection errors at the planetary capture. Numerical simulations are intended to prove that the approach at hand is effective and accurate for releasing 4 carrier vehicles in the respective operational orbits. Phasing represents the last phase of deployment, and is performed by each satellite. The final goal is in gaining the correct angular position, without leaving the desired orbit plane. To this end, both internal phasing (using an intermediate orbit with shorter period) and external phasing (using an intermediate orbit with longer period) are being considered.

In short, the present research has the following objectives: (i) design a constellation of 12 satellites, capable of guaranteeing continuous global coverage of the entire Martian surface, with simultaneous visibility of multiple satellites, (ii) propose the use of 4 carrier vehicles for the release of the 12 satellites in 4 distinct orbit planes, (iii) use an effective low-thrust deployment strategy based on nonlinear orbit control, in the presence of nominal and nonnominal initial conditions, and (iv) describe the phasing maneuver, performed by each satellite, while providing a comprehensive analysis of the tradeoff between overall velocity change and phasing time.

2 Constellation Configuration

This research proposes a satellite constellation about Mars tailored to telecommunications. Global coverage of the Martian surface is sought, using 12 satellites placed in 4 distinct orbit planes, i.e. 3 satellites in areostationary orbit, and 9 satellites in 3 quasi-synchronous, circular, repeating-ground-track, inclined orbits. High-altitude orbits are considered, and no atmospheric drag is encountered. For the purpose of constellation design, the solar radiation pressure and the third body gravitational pull due to the Sun are negligible as well. In contrast, the Mars oblateness ($J_{2}$ zonal harmonic) produces significant effects on the orbit elements and is considered in the model.

Desirable features of a satellite constellation are (a) repetitiveness, which implies predictability of the performance, and (b) invariance with respect to the $J_{2}$ perturbation. The use of circular orbits is a common and convenient requirement, specifically related to onboard sensors. In fact, if the altitude is constant, the sensor performance and operational modality does not change.

2.1 Coverage Analysis for 3 Satellites in Areostationary Orbit

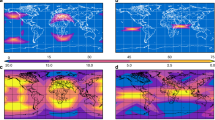
The first three satellites that form the constellation travel areostationary orbits, at equally-spaced geographical longitudes. However, similarly to what occurs for geostationary satellites, areostationary spacecraft are subject to the perturbation related to harmonic $J_{2,2}$ of the areopotential. This term is responsible for the existence of two stable and two unstable geographical longitudes for an aerostationary satellite. The two unstable Martian longitudes equal − 105° and 75° [12]. Therefore, the following equally-spaced geographical longitudes are chosen for the three satellites placed in areostationary orbit: − 135°, − 15°, 105°. These values correspond to maximizing the angular separation of the subsatellite points from the unstable longitudes. The visible regions from each satellite are portrayed in Fig. 1, with different colors associated with distinct elevation angles. The black curves represent the bound of the visible regions with elevation $\varepsilon \ge \varepsilon_{min} = 0^{ \circ }$, whereas the blue and red curves correspond to $\varepsilon_{min} = 20^{ \circ }$ and 40°, respectively. Inspection of Fig. 1 points out that only a limited latitudinal range (i.e. [− 14.6, 14.6]°) is continuously covered with an elevation $\varepsilon \ge 20^{ \circ }$. Not surprisingly, polar coverage is poor. In fact, no location with latitude $\phi$ such that $\left| \phi \right| > 61.1^{ \circ }$ is visible with elevation $\varepsilon \ge 20^{ \circ }$. A greater number of satellites in areostationary orbits would certainly widen the latitudinal range associated with coverage with $\varepsilon \ge \varepsilon_{min} = 20^{ \circ }$, but would not alter the latitudinal intervals (in the two hemispheres) where no satellite is visible with $\varepsilon \ge \varepsilon_{min} = 20^{ \circ }$.

Fig. 1

Regions covered by three areostationary satellites (black: $\varepsilon \ge \varepsilon_{min} = 0^{ \circ }$; blue: $\varepsilon \ge \varepsilon_{min} = 20^{ \circ }$; red: $\varepsilon \ge \varepsilon_{min} = 40^{ \circ }$)

In conclusion, 3 satellites placed in areostationary orbits, at equally-spaced longitudes, represent a viable option to continuously cover the equatorial region. Nevertheless, the use of inclined orbits for global continuous coverage is ineludible.

2.2 Quasi-synchronous, Circular, Repeating-Ground-Track, Inclined Orbits

While 3 satellites are placed in an equatorial areostationary orbit, the remaining 9 satellites travel equally-inclined circular orbits with an identical altitude. On average, oblateness effects ($J_{2}$ zonal harmonic perturbation) yield the following time derivatives [13] of the right ascension of the ascending node (RAAN) $\Omega$, argument of periapse $\omega$, and mean anomaly M:

$$\dot{\Omega }\left( {a,e,i} \right) = - \frac{3}{2}J_{2} \frac{{R_{M}^{2} \sqrt {\mu_{M} } }}{{a^{3.5} \left( {1 - e^{2} } \right)^{2} }}\cos i$$

(1)

$$\dot{\omega }\left( {a,e,i} \right) = \frac{3}{2}J_{2} \frac{{R_{M}^{2} \sqrt {\mu_{M} } }}{{a^{3.5} \left( {1 - e^{2} } \right)^{2} }}\left( {2 - \frac{5}{2}\sin^{2} i} \right)$$

(2)

$$\dot{M}\left( {a,e,i} \right) = \frac{3}{2}J_{2} \frac{{R_{M}^{2} \sqrt {\mu_{M} } }}{{a^{3.5} \left( {1 - e^{2} } \right)^{3.5} }}\left( {1 - \frac{3}{2}\sin^{2} i} \right) + \sqrt {\frac{{\mu_{M} }}{{a^{3} }}}$$

(3)

In Eqs. (1)–(3) $R_{M}$, $\mu_{M}$, and $J_{2}$ are the mean equatorial radius, gravitational parameter, and oblateness coefficient, whereas a, e, and i are the orbit semimajor axis (SMA), eccentricity, and inclination, respectively. Due to Eqs. (1)–(3), the time histories of $\Omega$, $\omega$, and M are linear with time.

For circular orbits only the argument of latitude $\theta = \omega + M$ is meaningful, because the periapse is not defined. Therefore, if $\Omega_{ref}$, $\omega_{ref}$, and $\theta_{ref}$ are the values of the respective variables at the reference time $t_{ref}$, the time-varying (average) orbital elements $\Omega \left( t \right)$ and $\theta \left( t \right)$ are given by

$$\Omega \left( t \right) = \Omega_{ref} + \dot{\Omega }\left( {a,i} \right)\left( {t - t_{ref} } \right)\,\,{\text{ and }}\,\,\theta \left( t \right) = \theta_{ref} + \dot{\theta }\left( {a,i} \right)\left( {t - t_{ref} } \right)$$

(4)

where $\dot{\theta }\left( {a,i} \right) = \dot{\omega }\left( {a,i} \right) + \dot{M}\left( {a,i} \right){\text{ and }}\theta_{ref} = \omega_{ref} + M_{ref}$. All the satellites are assumed to have identical inclination and SMA (or altitude H for circular orbits) in order to avoid differential actions due to the $J_{2}$ perturbation. This circumstance would cause a substantial alteration of the performance attainable by the constellation.

An orbit is termed repeating when phased with the planet rotation, i.e. when the ground track is periodically repeated. This occurs if the satellite completes $N_{t}$ orbits in m nodal days,

$$mD_{n} \left( {a,i} \right) = N_{t} T_{n} \left( {a,i} \right)$$

(5)

In Eq. (5) $T_{n} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {\dot{\theta }}}} \right. \kern-\nulldelimiterspace} {\dot{\theta }}}$ is the nodal orbital period (i.e., the time interval between two consecutive ascending node crossings) and $D_{n} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {\left( {\omega_{M} - \dot{\Omega }} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\omega_{M} - \dot{\Omega }} \right)}}$ is the nodal day (i.e. the time required for Mars to make a complete rotation with respect to the orbital plane; $\omega_{M}$ denotes the Mars rotation rate). Both $T_{n}$ and $D_{n}$ depend on a and i (whereas $e = 0$). This fact implies that the ratio $r_{t} = {{N_{t} } \mathord{\left/ {\vphantom {{N_{t} } m}} \right. \kern-\nulldelimiterspace} m}$, which represents the number of orbits per nodal day, depends on a and i.

Quasi-synchronous satellites are stationary with respect to a specific location on the Martian surface. This location is selected as the one corresponding to the maximum latitude flown by the satellite, denoted with $\phi_{M}$. For direct orbits, the eastward component of the velocity at the maximum (and minimum) latitude coincides with the orbital velocity, i.e. $\sqrt {{{\mu_{M} } \mathord{\left/ {\vphantom {{\mu_{M} } R}} \right. \kern-\nulldelimiterspace} R}}$. Quasi-synchronism holds if the angular rate of an observer at latitude $\phi_{M}$ equals the eastward angular velocity of the satellite, i.e.

$$\sqrt {\frac{{\mu_{M} }}{{R^{3} }}} = \omega_{M} \cos \phi_{M} \, \Rightarrow \, R = \frac{{\mu_{M}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} }}{{\left( {\omega_{M} \cos i} \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}} }}$$

(6)

In the last step, $\phi_{M} \equiv i$ was used. Figure 2 portrays the radius of quasi-synchronous circular orbits as a function of inclination (in blue), together with the related number of orbits per nodal days $q: = {{N_{t} } \mathord{\left/ {\vphantom {{N_{t} } m}} \right. \kern-\nulldelimiterspace} m}$ (orange curve). Each point along the blue curve corresponds to a circular orbit whose motion is synchronous with the planet rotation rate, when the satellite is located at the maximum or minimum latitude. It is apparent that all these orbits have periods greater than one nodal day. The quasi-synchronous orbit associated with $N_{t} = 1$ and $m = 2$ ($q = 0.5$) is selected, and corresponds to $R = 32427{\text{ km}}$ and $i = 60.0^{ \circ }$. This choice corresponds to a supersynchronous orbit, and is motivated by the reasonable values of its inclination and radius, together with the short repetition period, i.e. 2 nodal days. Figure 3 depicts the ground tracks of three satellites placed along 3 distinct orbits, with the preceding values of R and i and right ascension separation of 120°. It is worth noticing that each ground track has cusps at the extremal latitudes. This is a typical feature of orbits that are synchronous with the planet rotation at specific points, corresponding to the cusps of the ground track.

Fig. 2

Quasi-synchronous circular orbits: radius as a function of inclination and related number of orbits per nodal day

Fig. 3

Ground tracks associated with 3 quasi-synchronous circular orbits; “o” and “x” denote symmetry points with respect to the ground track

2.3 Coverage Analysis for 9 Satellites in Quasi-synchronous Orbits

Overall, 9 satellites are placed in the inclined quasi-synchronous circular orbits described in the preceding subsection. Each orbit is traveled by 3 satellites, with angular separation of 120°. As a result, any point along the ground track is flown over by satellite 2 and 3, with delays equal to ${{T_{n} } \mathord{\left/ {\vphantom {{T_{n} } 3}} \right. \kern-\nulldelimiterspace} 3}$ and ${{2T_{n} } \mathord{\left/ {\vphantom {{2T_{n} } 3}} \right. \kern-\nulldelimiterspace} 3}$ with respect to satellite 1.

While coverage of the 3 areostationary satellites is identified by the regions portrayed in Fig. 1, the analysis for the remaining 9 satellites is more complicated. In a repetition period, for a given location on the Martian surface, the minimum elevation of visibility is to be determined. To do this, the scheduling of the visible passes of all the 9 satellites must be obtained and inspected. However, due to the symmetry properties of the ground track, identifying the minimum elevation angle of a limited number of locations suffices to supply precise information on the global coverage properties. These sample locations are portrayed in Fig. 3, and lie along the symmetry meridians of the ground track. In fact, let $\varepsilon_{min} \left( {\lambda_{g} ,\phi } \right)$ denote the minimum elevation angle over a repetition period, as a function of latitude, $\phi$, and geographical longitude, $\lambda_{g}$. If $\phi$ is set to a specific value $\overline{\phi }$, $\varepsilon_{min} \left( {\lambda_{g} ,\overline{\phi }} \right)$ becomes a function of a single variable, which is continuous and locally even with respect to six values of $\lambda_{g}$, i.e. $\lambda_{g} = - 180^{ \circ }, - 120^{ \circ }, - 60^{ \circ },\,0^{ \circ },\,60^{ \circ },\,120^{ \circ }$. These values correspond to the symmetry meridians of the ground track. This implies that the function $\varepsilon_{min} \left( {\lambda_{g} ,\overline{\phi }} \right)$ must have extremal values, i.e. maxima and minima, at these values of $\lambda_{g}$. As a result, for a given latitude $\overline{\phi }$, the minimum and maximum values of $\varepsilon_{min} \left( {\lambda_{g} ,\overline{\phi }} \right)$ can be identified by considering only a pair of locations, e.g. those marked with “o” and “x” in Fig. 3. The coverage properties of the south hemisphere are identical to those of the northern hemisphere, due to nodal symmetry of the ground tracks.

Using the previously mentioned symmetry properties, the extremal values of $\varepsilon_{min} \left( {\lambda_{g} ,\overline{\phi }} \right)$ were identified, for different latitudes. They are collected in Table 1. It is apparent that the 9 satellites placed in inclined orbits can guarantee global and continuous coverage of the Martian surface with an elevation angle never lower than 20.1°. Figures 4 and 5 depict the elevation and azimuth time histories of all the satellites over two distinct sites on the planet surface. Inspection of these figures reveals that multiple satellites are visible during the entire repetition period.

Table 1 Extremals of the minimum elevation, depending on the latitude on the Martian surface

Fig. 4

Elevation and azimuth angles over a specific location ($\lambda_{g} = 0^{ \circ }$ and $\phi = 80^{ \circ }$)

Fig. 5

Elevation and azimuth angles over a specific location ($\lambda_{g} = 60^{ \circ }$ and $\phi = 80^{ \circ }$)

3 Low-Thrust Orbit Dynamics

In recent years, low thrust propulsion has attracted a strong interest in the scientific community, and has already been used in several space missions, e.g. the NASA Deep Space 1 and the ESA Smart-1 missions [14, 15], to name a few. Low-thrust propulsion leads to substantial propellant savings, at the price of increasing (even considerably) the time of flight. Recently, nonlinear control was proven to be an effective option for real-time feedback guidance in Earth orbit transfers, as well as for orbit maintenance [10, 16–18]

This section is focused on low-thrust orbit dynamics, using the modified equinoctial elements to describe the dynamics of 4 carrier vehicles, modeled as point masses. Orbital motion of each carrier is mainly affected by the Martian gravitational field. Therefore, the spacecraft dynamics can be investigated appropriately by employing a perturbed two-body-problem model. The most relevant orbit perturbations are included in this dynamical framework, i.e. (i) some harmonics of the areopotential (i.e., $J_{2}$, $J_{3}$, and $J_{4}$) and (ii) third body gravitational pull due to the Sun. These 4 spacecraft depart from a specified parking orbit, and drive the 12 satellites that form the constellation toward their orbits. More specifically, each carrier vehicle contains 3 satellites, and delivers all of them in the respective orbit, either the aerostationary orbit or one of the 3 quasi-synchronous, inclined, circular orbits. Steerable, throttleable low-thrust propulsion actuates the orbit injection maneuvers of the 4 carriers. After delivery from the carrier vehicle, each satellite performs phasing maneuvers, using its own chemical propulsion system, with the final aim of reaching the correct argument of latitude along the operational orbit.

The spacecraft dynamics can be described using the osculating orbit elements, i.e. semimajor axis a, eccentricity e, inclination i, right ascension of the ascending node (RAAN) $\Omega$, argument of periapse $\omega$, and true anomaly f. However, the Gauss equations [19], which govern the time evolution of the orbit elements, become singular while approaching a circular or equatorial orbit and when the eccentricity tends to 1. For these reasons, the modified equinoctial elements (MEE) [19] l, m, n, s, and q are employed, together with the semilatus rectum (parameter) p, used in place of a. The five elements l, m, n, s, and q are defined as [19]

$$l = e\cos \left( {\Omega + \omega } \right) \quad m = e\sin \left( {\Omega + \omega } \right) \quad n = \tan \frac{i}{2}\cos \Omega \quad s = \tan \frac{i}{2}\sin \Omega \quad q = \Omega + \omega + f$$

(7)

These elements are nonsingular for all trajectories, with the only exception of equatorial retrograde orbits ($i = \pi$). If $\eta : = 1 + l\cos q + m\sin q$, the orbit (instantaneous) radius equals $r = {p \mathord{\left/ {\vphantom {p \eta }} \right. \kern-\nulldelimiterspace} \eta }$. The governing equations for the modified equinoctial elements are [17, 19, 20]

$${\dot{\varvec{z}}} = {\mathbf{G}}\left( {{\varvec{z}},x_{6} } \right){\varvec{a}}$$

(8)

$$\dot{x}_{6} = \sqrt {\frac{{\mu_{M} }}{{x_{1}^{3} }}} \eta^{2} + \sqrt {\frac{{x_{1} }}{{\mu_{M} }}} \frac{{x_{4} \sin x_{6} - x_{5} \cos x_{6} }}{\eta }a_{h}$$

(9)

where $x_{6} \equiv q$ and $\varvec{z}: = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } & {x_{4} } & {x_{5} } \\ \end{array} } \right]^{T} \equiv \left[ {\begin{array}{*{20}c} p & l & m & n & s \\ \end{array} } \right]^{T}$, whereas $\mu_{M}$ represents the Mars gravitational parameter and

$${\mathbf{G}} \left( {{\varvec{z}},x_{6} } \right) = \sqrt {\frac{{x_{1} }}{{\mu_{M} }}} \left[ {\begin{array}{*{20}c} 0 & {\frac{{2x_{1} }}{\eta }} & 0 \\ {{\text{sin }}x_{6} } & {\frac{{\left( {\eta + 1} \right){\text{cos }}x_{6} + x_{2} }}{\eta }} & { - \frac{{x_{4} {\text{sin }}x_{6} - x_{5} {\text{cos }}x_{6} }}{\eta }x_{3} } \\ { - {\text{cos }}x_{6} } & {\frac{{\left( {\eta + 1} \right){\text{sin }}x_{6} + x_{3} }}{\eta }} & {\frac{{x_{4} {\text{sin }}x_{6} - x_{5} {\text{cos }}x_{6} }}{\eta }x_{2} } \\ 0 & 0 & {\frac{{1 + x_{4}^{2} + x_{5}^{2} }}{2\eta }{\text{cos }}x_{6} } \\ 0 & 0 & {\frac{{1 + x_{4}^{2} + x_{5}^{2} }}{2\eta }{\text{sin }}x_{6} } \\ \end{array} } \right]$$

(10)

Vector a is a $\left( {3 \times 1} \right)$-vector that collects the components of the non-Keplerian acceleration that affects the spacecraft motion. These are denoted with $\left( {a_{r} ,a_{\theta } ,a_{h} } \right)$ and refer to the local vertical local horizontal (LVLH) rotating frame aligned with $\left( {\hat{r},\hat{\theta },\hat{h}} \right)$, where unit vector $\hat{r}$ is directed toward the instantaneous position vector r (taken from the Mars center), whereas $\hat{h}$ is aligned with the spacecraft angular momentum. Vector a includes both the thrust acceleration ${\varvec{a}}_{T}$ and the perturbing acceleration ${\varvec{a}}_{P}$ inherent to the space environment. Thus ${\varvec{a}} = {\varvec{a}}_{T} + {\varvec{a}}_{P}$. The perturbing acceleration (due to harmonics of the areopotential and third body gravitational attraction) are then projected in the LVLH-frame. It is worth remarking that the preceding equations of motion reduce to $\dot{x}_{1} = \ldots = \dot{x}_{5} = 0$ and $\dot{x}_{6} = \dot{f} = \left( {1 + l\cos q + m\sin q} \right)^{2} \sqrt {{{\mu_{M} } \mathord{\left/ {\vphantom {{\mu_{M} } {x_{1}^{3} }}} \right. \kern-\nulldelimiterspace} {x_{1}^{3} }}}$ if ${\varvec{a}} = {\varvec{a}}_{T} + {\varvec{a}}_{P} = {\varvec{0}}$ (Keplerian motion). This means that 5 out of 6 MEE remain constant along Keplerian paths, similarly to what occurs if classical orbit elements are used.

Let $T_{max}$ and $m_{0}$ denote the maximum available thrust magnitude and the initial mass. If $x_{7}$ represents the mass ratio and T the thrust magnitude, the following equation holds for $x_{7}$:

$$\dot{x}_{7} : = \frac{{\dot{m}}}{{m_{0} }} = - \frac{{u_{T} }}{c}{\text{ where }}0 \le u_{T} \le u_{T}^{{\left( {max} \right)}} \, \left( {u_{T} : = \frac{T}{{m_{0} }}{\text{ and }}u_{T}^{{\left( {max} \right)}} : = \frac{{T_{max} }}{{m_{0} }}} \right)$$

(11)

where c represents the effective exhaust velocity of the propulsion system. The magnitude of the instantaneous thrust acceleration is ${{a_{T} = u_{T} m_{0} } \mathord{\left/ {\vphantom {{a_{T} = u_{T} m_{0} } m}} \right. \kern-\nulldelimiterspace} m} = {{u_{T} } \mathord{\left/ {\vphantom {{u_{T} } {x_{7} }}} \right. \kern-\nulldelimiterspace} {x_{7} }}$ and is constrained to $0 \le a_{T} \le a_{T}^{{\left( {max} \right)}}$, where $a_{T}^{{\left( {max} \right)}} = {{u_{T}^{{\left( {max} \right)}} } \mathord{\left/ {\vphantom {{u_{T}^{{\left( {max} \right)}} } {x_{7} }}} \right. \kern-\nulldelimiterspace} {x_{7} }}$. Moreover, the thrust acceleration is ${\varvec{a}}_{T} = {{{\varvec{u}}_{T} } \mathord{\left/ {\vphantom {{{\varvec{u}}_{T} } {x_{7} }}} \right. \kern-\nulldelimiterspace} {x_{7} }}$, where ${\varvec{u}}_{T}$ has magnitude constrained to the interval $\left[ {0,u_{T}^{{\left( {max} \right)}} } \right]$.

In conclusion, the spacecraft dynamics is described in terms of the state vector ${\varvec{x}}: = \left[ {\begin{array}{*{20}c} {{\varvec{z}}^{T} } & {x_{6} } & {x_{7} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } & {x_{4} } & {x_{5} } & {x_{6} } & {x_{7} } \\ \end{array} } \right]^{T}$, whereas the control vector is ${\varvec{u}}_{T}$, directly related to the thrust acceleration. Equations (8)–(11) represent the governing equations.

4 Nonlinear Orbit Control for Low-Thrust Deployment

In this section, a nonlinear technique is described, aimed at identifying the thrust direction and magnitude for a carrier spacecraft tailored to constellation deployment and equipped with a low-thrust propulsion system. The initial parking orbit is a typical ESA 4-sol orbit [11], associated with the following orbit elements:

$$a = 51545{\text{ km }}\quad e = 0.928 \quad i = 92.3{\text{ deg }} \quad \Omega = 64.7{\text{ deg }}\quad\omega = 342.4{\text{ deg }}$$

(12)

At the initial epoch $t_{0}$, set to 19 April 2023 at 0:00 UTC, the true anomaly is assumed to equal 180°.

4.1 Deployment Conditions

Each carrier must deploy 3 satellites in the respective desired orbit, identified by semimajor axis, eccentricity, inclination, and RAAN. On average, only the latter element changes in time due to $J_{2}$ (cf. Eq. (1)). This means that for satellite k the desired RAAN $\Omega_{d}^{\left( k \right)}$ is time-varying, i.e. $\Omega_{d}^{\left( k \right)} = \Omega_{k} \left( {t_{0} } \right) + \dot{\Omega }\left( {a_{d} ,e_{d} ,i_{d} } \right)\left( {t - t_{0} } \right)$ $\left( {k = 1, \ldots ,12} \right)$, where $\dot{\Omega }\left( {a_{d} ,e_{d} ,i_{d} } \right)$ is given by Eq. (1) and subscript d refers to the specified (nominal) value of the respective variable. Letting $p_{d} : = a_{d} \left( {1 - e_{d}^{2} } \right)$, the desired deployment conditions for a and e, in terms of equinoctial elements, are

$$x_{1} - p_{d} = 0\quad{\text{ and }}\quad x_{2}^{2} + x_{3}^{2} - e_{d}^{2} = 0$$

(13)

The remaining conditions regard the (time-varying) orbit plane orientation, defined by $i_{d}$ and $\Omega_{d}^{\left( k \right)}$. Omitting the superscript (k) hence forward, these conditions are enforced by requiring that the instantaneous angular momentum, with direction aligned with $\hat{h}$, point toward the desired direction, denoted with $\hat{h}_{d}$. Unit vector $\hat{h}$ can be written in terms of $\Omega$ and i, i.e. $\hat{h} = \hat{c}_{1} \sin \Omega \sin i + \hat{c}_{2} \cos \Omega \sin i + \hat{c}_{3} \cos i$. [13] The alignment condition is

$$\hat{h} \cdot \hat{h}_{d} = 1 \, \Rightarrow \, \sin \Omega \sin i\sin \Omega_{d} \sin i_{d} + \cos \Omega \sin i\cos \Omega_{d} \sin i_{d} + \cos i \cos i_{d} = 1$$

(14)

After some steps, omitted for the sake of brevity, the preceding relation leads to the following equality:

$$2x_{5} \sin \Omega_{d} \sin i_{d} + 2x_{4} \cos\Omega_{d} \sin i_{d} + \left( {1 - x_{4}^{2} - x_{5}^{2} } \right)\cos i_{d} - \left( {1 + x_{4}^{2} + x_{5}^{2} } \right) = 0$$

(15)

The final conditions for deployment (13) and (15) can be incorporated as the three components $\left\{ {\psi_{1} ,\psi_{2} ,\psi_{3} } \right\}$ of vector ${{\varvec{\uppsi}}}$ and finally expressed in compact form as

$${{\varvec{\uppsi}}}\left( {{\varvec{z}},t} \right) = {\varvec{0}}$$

(16)

It is worth remarking that ${{\varvec{\uppsi}}}$ is time-varying due to $\Omega_{d}^{\left( k \right)}$. For the 3 inclined orbits, the initial values of $\Omega_{k} \left( {t_{0} } \right)$ are

$$\Omega_{1} \left( {t_{0} } \right) = - 120^{ \circ }\quad\Omega_{2} \left( {t_{0} } \right) = 0^{ \circ }\quad\Omega_{3} \left( {t_{0} } \right) = 120^{ \circ }$$

(17)

4.2 Feedback Law and Stability Analysis

In a preceding section, the spacecraft motion was shown to be governed by Eqs. (8)–(10). In particular, Eq. (8) can be rewritten as

$${\dot{\varvec{z}}} = {\mathbf{G}}\left( {{\varvec{z}},x_{6} } \right)\left( {\frac{{{\varvec{u}}_{T} }}{{x_{7} }} + {\varvec{a}}_{P} } \right)$$

(18)

where the perturbing acceleration ${\varvec{a}}_{P}$ includes several contributions, related to the space environment, i.e. harmonics of the areopotential and third body gravitational attraction due to the Sun. In this research, orbit perturbations are assumed to be perfectly known, for the purpose of applying the feedback laws described in this section. For systems governed by Eq. (18) with ${\varvec{a}}_{P} = {\varvec{0}}$, the Jurdjevic–Quinn theorem [21] provides a feedback control law that drives the dynamical system to an arbitrary target state, making the controlled system Lyapunov-stable. This subsection outlines the fundamental steps needed to identify a saturated feedback control law for low-thrust orbit injection of the four carrier vehicles. Further details and proofs are contained in a recent publication [10], which adopts a similar approach for a completely different constellation about Earth.

The three (scalar) deployment conditions are written in the compact form (16), which defines the target set. Due to Eqs. (13) and (15), this is a connected and differentiable manifold. Nonlinear orbit control is aimed at defining a feedback control law capable of driving the dynamical system at hand (associated with Eqs. (9), (11), and (18)) toward the target conditions identified by Eq. (16). To do this, the following candidate Lyapunov function is introduced:

$$V = \frac{1}{2}{{\varvec{\uppsi}}}^{T} {\mathbf{K}}{{\varvec{\uppsi}}}$$

(19)

where K denotes a diagonal matrix with constant, positive elements, which play the role of arbitrary weights. These are selected a priori. It is obvious that $V > 0$ unless ${{\varvec{\uppsi}}} = {\varvec{0}}$. Yet, further conditions are required in order that V be an actual Lyapunov function [22]. As a preliminary steps, the following auxiliary vectors are introduced:

$${\varvec{b}}: = {\mathbf{G}}^{T} \left( {\frac{{\partial {{\varvec{\uppsi}}}}}{{\partial {\varvec{z}}}}} \right)^{T} {\mathbf{K}}{{\varvec{\uppsi}}}\quad{\text{ and }}\quad{\varvec{d}}: = {\varvec{a}}_{P} + \left[ {\frac{{\partial {{\varvec{\uppsi}}}}}{{\partial {\varvec{z}}}}{\mathbf{G}}} \right]^{ - 1} \frac{{\partial {{\varvec{\uppsi}}}}}{\partial t}$$

(20)

Two propositions establish the conditions for V to be a Lyapunov function, and lead to identifying a saturated feedback law.

Proposition 1

If ${{\varvec{\uppsi}}}$ and $\left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\varvec{z}}}}} \right. \kern-\nulldelimiterspace} {\partial {\varvec{z}}}}} \right)$ are continuous, $\left[ {\left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\varvec{z}}}}} \right. \kern-\nulldelimiterspace} {\partial {\varvec{z}}}}} \right){\mathbf{G}}} \right]^{ - 1} \left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}} \right)$ is finite, $\left| {\varvec{b}} \right| > 0$ unless ${{\varvec{\uppsi}}} = {\varvec{0}}$, and $u_{T}^{{\left( {max} \right)}} \ge x_{7} \left| {{\varvec{b}} + {\varvec{d}}} \right|$, then the feedback control law

$${\varvec{u}}_{T} = - x_{7} \left( {{\varvec{b}} + {\varvec{d}}} \right)$$

(21)

leads a dynamical system governed by Eqs. (9), (11), and (18) to converge asymptotically to the target set associated with Eq. (16).

Proof of Proposition 1 is reported in Ref. [10]. This proposition includes the assumption $u_{T}^{{\left( {max} \right)}} \ge x_{7} \left| {{\varvec{b}} + {\varvec{d}}} \right|$. If this inequality is violated, the feedback control law (21) is infeasible, because $\left| {{\varvec{u}}_{T} } \right| = x_{7} \left| {{\varvec{b}} + {\varvec{d}}} \right|$ would exceed the maximal value $u_{T}^{{\left( {max} \right)}}$. In this case, in place of (21), an alternative feedback law can be used.

Proposition 2

If and ${{\varvec{\uppsi}}}$ and $\left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\varvec{z}}}}} \right. \kern-\nulldelimiterspace} {\partial {\varvec{z}}}}} \right)$ are continuous, $\left[ {\left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\varvec{z}}}}} \right. \kern-\nulldelimiterspace} {\partial {\varvec{z}}}}} \right){\mathbf{G}}} \right]^{ - 1} \left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}} \right)$ is finite, $\left| {\varvec{b}} \right| > 0$ unless ${{\varvec{\uppsi}}} = {\varvec{0}}$, and $x_{7} \left| {\varvec{d}} \right| < u_{T}^{{\left( {max} \right)}} < x_{7} \left| {{\varvec{b}} + {\varvec{d}}} \right|$, then the feedback control law

$$ {\varvec{u}}_{T} = - u_{T} \frac{{{\varvec{b}} + {\varvec{d}}}}{{\left| {{\varvec{b}} + {\varvec{d}}} \right|}},{\text{ with }}\left\{ \begin{gathered} {\text{(a) }}u_{T} = 0,\qquad \qquad \quad\, \; \; \; \qquad{\text{ if }}{\varvec{b}}^{T} {\varvec{b}} + {\varvec{b}}^{T} {\varvec{d}} < 0 \hfill \\ {\text{(b) }}x_{7} \left| {\varvec{d}} \right| < u_{T} \le u_{T}^{{\left( {max} \right)}} ,\qquad{\text{ if }}{\varvec{b}}^{T} {\varvec{b}} + {\varvec{b}}^{T} {\varvec{d}} \ge 0 \hfill \\ \end{gathered} \right. $$

(22)

leads a dynamical system governed by Eqs. (9), (11), and (18) to converge asymptotically to the target set associated with Eq. (16).

Proof of Proposition 2 is reported in Ref. [10]. Actually, Eqs. (21) and (22) provide a straightforward indication on the value of $u_{T}$ that minimizes $\dot{V}$. In fact, selection of $u_{T} = u_{T}^{{\left( {max} \right)}}$ corresponds to the least value of $\dot{V}$. In short, due to the last consideration, the two feedback laws (21) and (22) can be written in compact form as

$$ {\varvec{u}}_{T} = - u_{T} \frac{{{\varvec{b}} + {\varvec{d}}}}{{\left| {{\varvec{b}} + {\varvec{d}}} \right|}},{\text{ with }}u_{T} = \left\{ \begin{gathered} x_{7} \left| {{\varvec{b}} + {\varvec{d}}} \right|,\,{\text{ if }}x_{7} \left| {{\varvec{b}} + {\varvec{d}}} \right| \le u_{T}^{{\left( {max} \right)}} \hfill \\ 0,\quad \quad \quad \quad{\text{ if }}x_{7} \left| {{\varvec{b}} + {\varvec{d}}} \right| > u_{T}^{{\left( {max} \right)}} \quad{\text{ and }}{\varvec{b}}^{T} {\varvec{b}} + {\varvec{b}}^{T} {\varvec{d}} < 0 \hfill \\ u_{T}^{{\left( {max} \right)}} ,\quad\quad {\text{ if }}x_{7} \left| {{\varvec{b}} + {\varvec{d}}} \right| > u_{T}^{{\left( {max} \right)}} \quad{\text{ and }}{\varvec{b}}^{T} {\varvec{b}} + {\varvec{b}}^{T} {\varvec{d}} \ge 0 \hfill \\ \end{gathered} \right. $$

(23)

Equation (23) incorporates the saturation condition on ${\varvec{u}}_{T}$, i.e. $\left| {{\varvec{u}}_{T} } \right| \le u_{T}^{{\left( {max} \right)}}$, and provides a control law that can be actuated using steerable and throttleable propulsive thrust (with time-varying magnitude and direction).

It is worth remarking that Propositions 1 and 2 provide some sufficient conditions for stabilizing the dynamical system of interest. This circumstance implies that the assumptions of Propositions 1 and 2 can be violated (in some time intervals), without necessarily compromising asymptotic convergence to the desired final condition identified by Eq. (16).

Moreover, some assumptions regard vectors $\left[ {\left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\varvec{z}}}}} \right. \kern-\nulldelimiterspace} {\partial {\varvec{z}}}}} \right){\mathbf{G}}} \right]^{ - 1} \left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}} \right)$ and b. Vector b has components, denoted with $\left\{ {b_{1} ,b_{2} ,b_{3} } \right\}$, whose expressions are reported in Ref. [10]. The attracting set collects all the dynamical states that fulfill $\dot{V} = 0$. The latter condition is met if ${\varvec{b}} = {\varvec{0}}$, i.e. if the three components $\left\{ {b_{1} ,b_{2} ,b_{3} } \right\}$ equal 0, for any choice of the positive coefficients $\left\{ {k_{1} ,k_{2} ,k_{3} } \right\}$. The analysis reported in Ref. [10] leads to identifying the following three subsets, which form the attracting set:

• 1. $x_{1} = 0$ (rectilinear trajectories);

• 2. $\psi_{1} = \psi_{3} = 0$, $x_{2} = x_{3} = 0$ (circular orbit with radius $p_{d}$ and desired i and $\Omega$);

• 3. $\psi_{1} = \psi_{2} = \psi_{3} = 0$ (target set).

Because the attracting set contains other subsets other than the target set, the asymptotic convergence toward the desired conditions is only local, based on Lyapunov’s stability theorem. However, the equality ${\varvec{b}} = {\varvec{0}}$ can be considered again, to rule out, if possible, subsets 1 and 2. The condition ${\varvec{b}} = {\varvec{0}}$ implies ${\dot{\varvec{b}}} = {\varvec{0}}$, i.e. $\dot{b}_{1} = \dot{b}_{2} = \dot{b}_{3} = 0$, where

$$\dot{b}_{j} = \frac{{\partial b_{j} }}{{\partial x_{6} }}\sqrt {\frac{{\mu_{M} }}{{x_{1}^{3} }}} \eta^{2} + \frac{{\partial b_{j} }}{{\partial \Omega_{d} }}\dot{\Omega }\left( {a_{d} ,e_{d} ,i_{d} } \right) \quad \left( {j = 1,2,3} \right)$$

(24)

Equation (24) yields three relations. Inspection of their closed-form expressions [10] leads to ruling out subset 1. Therefore, only subsets 2 and 3 correspond to equilibria.

Actually, the possible convergence toward subset 2 is only theoretical. In fact, using $x_{2}^{2} + x_{3}^{2} = e^{2}$ in the expression of $\psi_{2}$, the Lyapunov function can be rewritten as

$$V = \frac{1}{2}\left[ {k_{1} \psi_{1}^{2} + k_{2} \left( {e^{2} - e_{d}^{2} } \right)^{2} + k_{3} \psi_{3}^{2} } \right]$$

(25)

where e is the instantaneous eccentricity. Because $\psi_{1}$ and $\psi_{3}$ are independent of $x_{2}$ and $x_{3}$, the partial derivative of V with respect to e is ${{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial e}}} \right. \kern-\nulldelimiterspace} {\partial e}} = 2k_{2} e\left( {e^{2} - e_{d}^{2} } \right)$. It is apparent that ${{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial e}}} \right. \kern-\nulldelimiterspace} {\partial e}} = 0$ (i.e. V is stationary) at $e = 0$, which is consistent with the fact that subset 2 corresponds to an equilibrium condition. However, if $e = e_{\varepsilon } > 0$ (with $e_{\varepsilon }$ arbitrarily small), then ${{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial e}}} \right. \kern-\nulldelimiterspace} {\partial e}} < 0$, and the reduction of V leads e to increasing up to the desired value $e_{d}$, which is associated with subset 3, i.e. the target set. This means that the latter corresponds to a stable equilibrium, unlike subset 2. This circumstance has the very interesting practical consequence that—from the numerical point of view—the dynamical system of interest enjoys global convergence toward the desired operational conditions, provided that the control law (23) is adopted, while holding the assumptions of Propositions 1 or 2.

As a final step, vector $\left[ {\left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial {\varvec{z}}}}} \right. \kern-\nulldelimiterspace} {\partial {\varvec{z}}}}} \right){\mathbf{G}}} \right]^{ - 1} \left( {{{\partial {{\varvec{\uppsi}}}} \mathord{\left/ {\vphantom {{\partial {{\varvec{\uppsi}}}} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}} \right)$, which appears in the definition of d, can be obtained for the deployment problem at hand. Its first two components are identically 0, whereas the third component is proven to be finite almost everywhere [10]. This circumstance, in conjunction with Eq. (23) (that includes the case $\left| {{\varvec{b}} + {\varvec{d}}} \right| > u_{T}^{{\left( {max} \right)}}$), ensures that the feedback law (23) is feasible.

5 Low-Thrust Constellation Deployment

Electric propulsion requires onboard electrical power in order to operate. In some cases, this can be provided only when the space vehicle is illuminated. However, in this subsection, electric propulsion is assumed to be able to operate regardless of the spacecraft lighting conditions. On the other hand, it is worth remarking the carrier vehicles encounter eclipse conditions only in the last portion of the transfer path, therefore the preceding assumption is reasonable. The overall propulsive performance is identified by the following parameters:

$$c = 30 \, {{{\text{km}}} \mathord{\left/ {\vphantom {{{\text{km}}} {{\text{s}} {\text{ and }}}}} \right. \kern-\nulldelimiterspace} {{\text{s}}\quad {\text{ and }}}}\quad n_{T}^{{\left( {max} \right)}} = 5 \cdot 10^{ - 5} {\text{ g}}_{0} \, \left( {{\text{g}}_{0} = 9.8 \, {{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {{\text{s}}^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{s}}^{2} }}} \right)$$

(26)

The numerical simulations are performed using canonical units. The distance unit (DU) equals the Martian radius, whereas the time unit (TU) is such that $\mu_{M} = 1 \, {{{\text{DU}}^{3} } \mathord{\left/ {\vphantom {{{\text{DU}}^{3} } {{\text{TU}}^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{TU}}^{2} }}$. The reference epoch is set to April 19, 2023. Specific tolerances are allowed on the desired final conditions, associated with Eqs. (13) and (15), and this allows avoiding an excessive propellant expenditure. In particular, if the three constraints are met to a prescribed accuracy, then the respective weight is set to zero, i.e.

$$\left| {\psi_{1} } \right| < 30{\text{ km}} \Rightarrow k_{1} = 0, \, \left| {\psi_{2} } \right| < 10^{ - 5} \Rightarrow k_{2} = 0, \, \left| {\psi_{3} } \right| < 10^{ - 6} \Rightarrow k_{3} = 0$$

(27)

For each satellite, orbit injection is achieved when the three conditions of Eq. (26) are met. Four distinct final orbits are considered. For each of them, numerical search on the weighting coefficients leads to identifying the respective values that minimize the time of flight (cf. Appendix).

In the numerical simulations, the following perturbations are modeled: (i) some harmonics of the areopotential (i.e., $J_{2}$, $J_{3}$, and $J_{4}$) and (ii) third body gravitational pull due to the Sun. As a preliminary step, the inequality $u_{T}^{{\left( {max} \right)}} > \left| {\varvec{d}} \right|$ is checked. Using the spacecraft data (i.e. propulsion and mass), the minimum available thrust acceleration $u_{T}^{{\left( {max} \right)}}$ turns out to exceed the maximal magnitude of the perturbing acceleration. As a result, the feedback law guarantees the convergence toward the desired operational conditions, associated with the four final orbits. The numerical propagations are run up to reaching the desired tolerances (27).

5.1 Nominal Initial Conditions

This subsection considers the low-thrust orbit transfers using nonlinear orbit control, leading the carrier spacecraft to inject into the four operational orbits, i.e. the areostationary orbit and the 3 distinct quasi-synchronous, inclined orbits. Subsequent phasing is performed by each satellite that forms the constellation (cf. Section 6). The initial (nominal) orbit is a typical ESA 4-sol orbit [11], associated with the orbit elements reported in Eq. (12). The numerical results point out that orbit insertion occurs after

• 36.2 days (quasi-synchronous orbit 1), with final mass ratio equal to 0.949

• 47.8 days (quasi-synchronous orbit 2), with final mass ratio equal to 0.933

• 34.5 days (quasi-synchronous orbit 3), with final mass ratio equal to 0.951

• 39.1 days (areostationary orbit), with final mass ratio equal to 0.946

Figures 6, 7, and 8 portray the transfer paths leading to delivering the carrier vehicles in quasi-synchronous, inclined orbits 1, 2, and 3, together with the corresponding time histories of SMA, inclination, eccentricity, and RAAN. It is worth remarking that the latter has a desired value that is time-varying. Figure 9 depicts the transfer trajectory toward the areostationary orbit, accompanied by the time histories of semimajor axis, eccentricity, and inclination. In all cases, low-thrust propulsion is turned off when the tolerances (27) are met.

Fig. 6

Deployment into quasi-synchronous inclined orbit orbit 1: orbit elements and low-thrust transfer trajectory

Fig. 7

Deployment into quasi-synchronous inclined orbit orbit 2: orbit elements and low-thrust transfer trajectory

Fig. 8

Deployment into quasi-synchronous inclined orbit orbit 3: orbit elements and low-thrust transfer trajectory

Fig. 9

Deployment into areostationary orbit: orbit elements and low-thrust transfer trajectory

5.2 Nonnominal Initial Conditions

Nonlinear orbit control appears as particularly appropriate as a feedback strategy for autonomous guidance when nonnominal flight conditions occur. This section considers the problem of driving the carrier spacecraft toward the respective operational orbits in the presence of large dispersions on the initial orbit elements. These displacements are simulated stochastically in a Monte Carlo campaign composed of 100 simulations, by assuming Gaussian distribution for all the orbit elements, with mean value equal to the nominal value of the 4-sol orbit (cf. Eq. (12)) and standard deviations reported in Table 2. However, to avoid unrealistic values and hyperbolic trajectories, the limiting bounds reported in Table 2 are assumed for each orbit element.

Table 2 Nominal values, standard deviations, and limiting values of the initial orbit elements

Each simulation ends when the required tolerances (27) are met. Table 3 reports the average values (denoted with the upper bar) and the standard deviation (superscript $\left( \sigma \right)$) for the time of flight and the final mass ratio, as well as the correlation coefficients between either the time of flight and the initial inclination ($\varsigma_{i}$) or the time of flight and the initial RAAN ($\varsigma_{\Omega }$). Figures 10, 11, 12, 13, 15, 16, 17, 18, 20, 21, 22, and 23 portray the time histories of the semimajor axis, eccentricity, inclination, and RAAN for the 3 quasi-synchronous inclined orbits. Figures 14, 19, and 24 illustrate the time of flight as a function of the initial inclination and RAAN, for the 3 orbits of interest. It is apparent that a correlation $\varsigma_{\Omega }$ exists for deployment into 2 quasi-synchronous orbits out of 3. Instead, the transfer paths leading to quasi-synchronous orbit 1 exhibit weak correlation $\varsigma_{\Omega }$. This is due to the time evolution of the RAAN, shown in Fig. 13. In fact, in this case two subsets of transfer trajectories exist: in subset 1, the RAAN increases, whereas in subset 2 the RAAN reduces, with convergence toward the final desired value in both cases. For this orbit, correlation $\varsigma_{i}$ is greater than for the remaining 2 quasi-synchronous orbits. Figures 25, 26, 27, and 28 depict the time histories of the semimajor axis, eccentricity, and inclination referred to the final areostationary orbit, as well as the time of flight as a function of the initial inclination and RAAN. In this case, a correlation emerges between the time of flight and the initial inclination, testified by the value of $\varsigma_{i}$. This means that the transfer time needed to converge to the final areostationary (equatorial) orbit is substantially affected by the initial inclination. In all cases, in spite of largely dispersed initial conditions, the time of flight has an average value close to the nominal one and standard deviations between 5.5 and 13.5 days. The final mass ratio has average values ranging from 0.931 (quasi-synchronous orbit 2) to 0.950 (quasi-synchronous orbit 3), with modest standard deviations, never exceeding 1.3 e−2.

Table 3 Results of the Monte Carlo campaign

Fig. 10

Quasi-synchronous orbit 1: time history of the semimajor axis (MC campaign)

Fig. 11

Quasi-synchronous orbit 1: time history of eccentricity (MC campaign)

Fig. 12

Quasi-synchronous orbit 1: time history of inclination (MC campaign)

Fig. 13

Quasi-synchronous orbit 1: time history of RAAN (MC campaign)

Fig. 14

Quasi-synchronous orbit 1: time of flight vs. initial inclination (left) and RAAN (right)

Fig. 15

Quasi-synchronous orbit 2: time history of the semimajor axis (MC campaign)

Fig. 16

Quasi-synchronous orbit 2: time history of eccentricity (MC campaign)

Fig. 17

Quasi-synchronous orbit 2: time history of inclination (MC campaign)

Fig. 18

Quasi-synchronous orbit 2: time history of RAAN (MC campaign)

Fig. 19

Quasi-synchronous orbit 2: time of flight vs. initial inclination (left) and RAAN (right)

Fig. 20

Quasi-synchronous orbit 3: time history of the semimajor axis (MC campaign)

Fig. 21

Quasi-synchronous orbit 3: time history of eccentricity (MC campaign)

Fig. 22

Quasi-synchronous orbit 3: time history of inclination (MC campaign)

Fig. 23

Quasi-synchronous orbit 3: time history of RAAN (MC campaign)

Fig. 24

Quasi-synchronous orbit 3: time of flight vs. initial inclination (left) and RAAN (right)

Fig. 25

Areostationary orbit: time history of the semimajor axis (MC campaign)

Fig. 26

Areostationary orbit: time history of eccentricity (MC campaign)

Fig. 27

Areostationary orbit: time history of inclination (MC campaign)

Fig. 28

Areostationary orbit: time of flight vs. initial inclination (left) and raan (right)

6 Orbit Phasing

The first phase of constellation deployment ends with orbit injection of each carrier, which corresponds to achieving the desired orbit plane, with zero eccentricity and the prescribed orbit radius. Then, the satellites are released, and each of them performs corrective phasing maneuvers, with the use of chemical propulsion. Usually, this implies very short ignitions, and the impulsive thrust approximation can be adopted as a result [23, 24]. The methodology for phasing described in this section resembles the one described in Ref. [10] for Earth orbits.

Orbit phasing is performed by placing the space vehicle in a parking elliptic orbit. Two options are investigated:

• (1) internal phasing: a braking horizontal velocity change injects the spacecraft into an inner elliptic orbit; after a certain phasing time, a second velocity variation (at apoapse) inserts the satellite into the final orbit;

• (2) external phasing: an accelerating horizontal velocity change injects the spacecraft into an outer elliptic orbit; after a certain phasing time, a second velocity variation (at periapse) inserts the satellite into the final orbit.

In both cases the two velocity changes have the same magnitude. The initial and final orbit are identical, but the spacecraft is shifted along the orbit, to reach the desired position, as a result of the phasing maneuver. In the context of orbit phasing, harmonic $J_{2}$ of the areopotential (related to the Martian oblateness) is the only perturbing action included in the model, because it is largely dominant if compared to the remaining orbit perturbations.

After the first velocity variation $\Delta v_{\theta } \hat{\theta }$ (either in case (a) or in case (b)), the parking elliptic orbit has semimajor axis $a_{PH}$ and eccentricity $e_{PH}$. The satellite completes $n_{PH}$ parking orbits (from either apoapse to apoapse, case (1), or periapse to periapse, case (2)) in a time interval

$$\Delta t_{PH} = \frac{{2\pi n_{PH} }}{{\dot{f}}},{\text{ with }}\dot{f} = \sqrt {\frac{{\mu_{E} }}{{a^{3} }}} + \frac{3}{2}J_{2} \frac{{R_{E}^{2} \sqrt {\mu_{E} } }}{{a^{3.5} \left( {1 - e^{2} } \right)^{2} }}\left( {\frac{3}{2}\sin^{2} i - 1} \right)$$

(28)

where $\, \dot{f}$ represents the average time derivative of the true anomaly [25]. Along the parking orbit, the RAAN is subject to natural drift due to Mars oblateness (harmonic $J_{2}$) that differs from the desired one. The displacement $\Delta \Omega_{PH}$ between the desired change of RAAN and the actual variation is

$$\Delta \Omega_{PH} = - \frac{3}{2}R_{M}^{2} J_{2} \sqrt {\mu_{M} } \cos i\left[ {\frac{1}{{R^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-\nulldelimiterspace} 2}}} }} - \frac{1}{{a_{PH}^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-\nulldelimiterspace} 2}}} \left( {1 - e_{PH}^{2} } \right)}}} \right]\Delta t_{PH}$$

(29)

where $\Delta t_{PH}$ is given by Eq. (29). To compensate this undesired drift, an out-of-plane velocity change $\Delta v_{h} \hat{h}$ is applied when the argument of latitude equals 90°, to avoid any alteration of the orbit inclination i. [19] To do this, the out-of-plane velocity change has component

$$\Delta v_{h} = \Delta \Omega_{PH} \sin i\sqrt {\frac{{\mu_{M} }}{R}}$$

(30)

However, the out-of-plane velocity variation has the undesired effect of altering the argument of latitude along the circular orbit [19],

$$\Delta \theta = - \Delta v_{h} \frac{\cos i}{{\sin i}}\sqrt {\frac{R}{{\mu_{M} }}}$$

(31)

To address this issue, a virtual vehicle is introduced, with argument of latitude $\theta_{d}$ corresponding to the desired angular position; $\theta_{d,0}$ denotes the value of $\theta_{d}$ when the phasing maneuver begins. Instead, the actual argument of latitude along the parking orbit is $\theta$, with initial value $\theta_{0}$ (when the first velocity change is applied). Let $\Delta \alpha : = \theta_{d,0} - \theta_{0}$ denote the phasing angle, i.e. the difference between the desired and the actual argument of latitude when the phasing maneuver starts. After two in-plane velocity changes and the final out-of-plane velocity variation (cf. Eq. (32)) the final argument of latitude equals

$$\theta_{f} = \theta_{0} + \dot{\theta }\Delta t_{PH} + \Delta \theta ,{\text{ with }}\dot{\theta } = \dot{\omega } + \dot{f}$$

(32)

Equation (33) includes also the variation due to the out-of-plane velocity change $\Delta \theta$ (cf. Equation (32)). In the last relation the average time derivatives $\dot{\omega }$ and $\dot{f}$ are given by Eqs. (2) and (29), respectively. The condition that ensures correct phasing is

$$\theta_{d,f} - \theta_{f} = 2k\pi \, \Rightarrow \, \left( {\theta_{d,0} + \dot{\theta }_{d} \Delta t_{PH} } \right) - \left( {\theta_{0} + \dot{\theta }\Delta t_{PH} + \Delta \theta } \right) = 2k\pi$$

(33)

with either $k = 0$ (internal phasing) or $k = 1$ (external phasing). The symbol $\dot{\theta }_{d}$ represents the average time derivative of the argument of latitude of the virtual vehicle. Using the definition of $\Delta \alpha \, \left( {: = \theta_{d,0} - \theta_{0} } \right)$, the phasing Eq. (34) becomes

$$\Delta \alpha - \Delta \theta + \left( {\dot{\theta }_{d} - \dot{\theta }} \right)\Delta t_{PH} - 2k\pi = 0$$

(34)

In short, three velocity changes (two in-plane changes and a single out-of-plane velocity variation) allow performing the phasing maneuver. For a specified $n_{PH}$ and a specified (desired) angular displacement $\Delta \alpha$, the following steps lead to identifying $\Delta v_{\theta }$ and $\Delta v_{h}$:

• (a) the semimajor axis and eccentricity of the parking orbit are expressed as functions of $\Delta v_{\theta }$, using the specific angular momentum, in conjunction with the vis viva equation for the specific energy;

• (b) the time spent in the parking orbit is found, using Eq. (29);

• (c) the displacement $\Delta \Omega_{PH}$ is found through Eq. (30);

• (d) the out-of-plane velocity change, $\Delta v_{h} \hat{h}$, is evaluated by means of Eq. (31);

• (e) the value of $\Delta \theta$, related to the out-of-plane velocity change, is obtained through Eq. (32);

• (f) phasing, i.e. Eq. (34), is enforced.

In the end, the preceding steps allow placing the satellite at the correct angular position, while taking into account the coupled effects of in-plane and out-of-plane velocity changes.

Figure 29 portrays the overall velocity change needed for phasing as a function of $\Delta \alpha$, along the quasi-synchronous inclined orbit, whereas Fig. 30 depicts the corresponding in-plane and out-of-plane velocity variations. Different numbers of orbits (i.e. 10, 20, 30, 40, and 50) along the parking path are considered, and correspond to the durations reported in the right inset. Only the most convenient option between internal and external phasing is depicted. It is apparent that for values of $\Delta \alpha$ larger than 180°, external phasing is more convenient in terms of overall velocity change. Conversely, internal transfers are preferable if the satellite must be moved ahead of its initial position by an angle that does not exceed 180°. Not surprisingly, larger durations correspond to reduced propellant budgets. In particular, Fig. 29 points out that the overall velocity change reduces to modest values if the time spent in the parking orbit exceeds 80 days. As a further remark, the comparison of in-plane and out-of-plane velocity changes reveals that the latter have negligible values if compared to in-plane velocity variations. Moreover, the out-of-plane velocity change turns out to be relatively independent of the phasing duration.

Fig. 29

Quasi-synchronous inclined orbit: overall velocity change for orbit phasing

Fig. 30

Quasi-synchronous orbit: in-plane (a) and out-of-plane (b) velocity change for orbit phasing

Figure 31 depicts the overall velocity change as a function of $\Delta \alpha$, along the areostationary orbit. It is worth remarking that in this case no out-of-plane velocity change is required. Also in this case, longer durations correspond to reduced velocity variations needed to complete orbit phasing, with modest values if the time spent in the parking orbit exceeds 50 days.

Fig. 31

Areostationary orbit: overall velocity change for orbit phasing

7 Concluding Remarks

In this research, a satellite constellation that guarantees global continuous coverage over Mars is designed. This could serve as a communications relay system and would certainly represent a valuable asset for future missions. While 3 satellites travel an areostationary orbit, the remaining 9 satellites are released in three repeating-ground-track, circular, quasi-synchronous, inclined orbits. This configuration guarantees global and continuous coverage, while ensuring repetition and predictability of the visible passes and simultaneous visibility of multiple satellites. Moreover, this work addresses the problem of deploying the 12 satellites using 4 carrier vehicles, released by the mother spacecraft. The latter orbits a highly elliptical path, i.e. the ESA 4-sol orbit, which is entered after planetary capture. Orbit dynamics about Mars is modeled with the inclusion of the most relevant perturbations, i.e. several harmonics of the areopotential, together with the gravitational pull due to the Sun as a third body. Each carrier embarks 3 satellites and employs steerable and throttleable low-thrust propulsion for the purpose of driving them toward the respective operational orbit. A saturated feedback law for the low-thrust magnitude and direction—with an upper bound on magnitude—is described and used, and enjoys global stability properties. In particular, some sufficient conditions for the asymptotic convergence toward the operational conditions are stated. These conditions include the perturbing acceleration term, and lead to identifying three types of transfer arcs: (a) maximum-thrust arcs, (b) time-varying, intermediate-thrust arcs, and (c) coast arcs. The numerical simulations demonstrate that the low-thrust deployment strategy based on nonlinear orbit control is effective, and needs a limited amount of propellant. Moreover, the feedback control law at hand does not require any offline reference trajectory. Therefore, it is effective as an autonomous real-time guidance strategy, even in the presence of nonnominal flight conditions. With this regard, a Monte Carlo campaign proves that orbit injection is successfully completed even starting from dispersed initial conditions, which can be regarded as representative of initial elliptical orbits significantly different from the expected one, due to injection errors at the planetary capture. Orbit phasing represents the last phase of deployment, and is performed by each satellite. Both internal and external phasing are considered. A simple and effective strategy is described that includes out-of-plane and in-plane velocity changes and avoids leaving the operational orbit plane. The tradeoff between overall propellant expenditure and phasing time is identified.

Appendix

This appendix is concerned with the gain selection for the feedback law (23). For each final orbit, a systematic search was performed, by assuming $k_{1} = 1$, $k_{2} = 10^{3} ,10^{4} ,10^{5} ,10^{6}$ $k_{3} = 10^{3} ,10^{4} ,10^{5} ,10^{6}$. Because the weights $k_{2}$ and $k_{3}$ relative to $k_{2}$ are meaningful, $k_{1}$ was set to 1, and different values were assumed only for $k_{2}$ and $k_{3}$. Overall, 16 simulations were run for each final orbit, under the assumption of neglecting orbit perturbations, with the results collected in Tables 4, 5, 6, 7, 8, 9, 10 and 11, in terms of time of flight and final mass ratio. Inspection of Tables 4, 5, 6, 7, 8, 9, 10, and 11 leads to choosing the most appropriate gains for each case, i.e.,

• areostationary orbit: $k_{1} = 1, \, k_{2} = 10^{4} , \, k_{3} = 10^{6}$

• quasi-synchronous orbit 1: $k_{1} = 1, \, k_{2} = 10^{4} , \, k_{3} = 10^{6}$

• quasi-synchronous orbit 2: $k_{1} = 1, \, k_{2} = 10^{4} , \, k_{3} = 10^{5}$

• quasi-synchronous orbit 3: $k_{1} = 1, \, k_{2} = 10^{4} , \, k_{3} = 10^{6}$

Table 4 Areostationary orbit: time of flight (days) as a function of gains k₂ and k₃

Table 5 Areostationary orbit: final mass ratio as a function of gains k₂ and k₃

For the case of final areostationary orbit, the result attained after gain tuning was compared to the minimum-time orbit transfer, detected with the use of the indirect heuristic method [26]. It is worth remarking that the latter approach is computationally intensive and cannot be performed in real time. Moreover, optimal control does not provide a feedback law capable of compensating for nonnominal flight conditions and orbit perturbations. Nevertheless, the minimum-time transfer is useful for the purpose of comparing the numerical results found with nonlinear orbit control and optimal control. For the case at hand (final areostationary orbit), the following results were obtained:

• optimal control: $t_{f} = 33.4{\text{ days, }}x_{7,f} = 0.953$

• nonlinear feedback control: $t_{f} = 39.1{\text{ days, }}x_{7,f} = 0.946$

These results provide a clear indication on the capability of approaching the performance obtained with optimal control, through proper selection of $k_{1}$, $k_{2}$, and $k_{3}$.

Table 6 Quasi-synchronous orbit 1: time of flight (days) as a function of gains k₂ and k₃

Table 7 Quasi-synchronous orbit 1: final mass ratio as a function of gains k₂ and k₃

Table 8 Quasi-synchronous orbit 2: time of flight (days) as a function of gains k₂ and k₃

Table 9 Quasi-synchronous orbit 2: final mass ratio as a function of gains k₂ and k₃

Table 10 Quasi-synchronous orbit 3: time of flight (days) as a function of gains k₂ and k₃

Table 11 Quasi-synchronous orbit 3: final mass ratio as a function of gains k₂ and k₃