Abstract
Background
An immediate loss of strength follows virtually all types of muscle injury but there is debate whether the initial strength loss is maximal or if a secondary loss of strength occurs during the first 3 days post-injury.
Objective
The objective of this analysis was to conduct a systematic review and meta-analysis of the research literature to determine if a secondary loss of strength occurs after an injurious initiating event.
Methods
Literature searches were performed using eight electronic databases (e.g., PubMed, Cochrane Library). Search terms included skeletal muscle AND (injur* OR damage*) AND (strength OR force OR torque). The extracted strength data were converted to a standard format by calculating the standardized mean difference, which is reported as the effect size (ES) along with its 95 % confidence interval (CI). The calculation of ES was designed so that a negative ES that was statistically less than zero would be interpreted as indicating a secondary loss of strength.
Results
A total of 223 studies with over 4000 human and animal subjects yielded data on 262 independent groups and a total of 936 separate ESs. Our overall meta-analysis yielded a small-to-medium, positive overall ES that was statistically greater than zero (overall ES = +0.34, 95 % CI 0.27–0.40; P < 0.00000001). Considerable variation in ES was observed among studies (I 2 = 86 %), which could be partially explained by the research group conducting the study, sex of the subject, day of post-injury strength assessment, whether fatigue was present immediately post-injury, and the muscle group injured. From the subgroup meta-analyses probing these variables, 36 subgroup ESs were calculated and none were statistically less than zero.
Conclusion
Overall, our findings do not support the presence of a secondary loss of strength following an acute muscle injury, and strongly suggest that strength, on average, recovers steadily over the first 3 days post-injury.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
On average, strength does not deteriorate in the first 3 days after a muscle injury. |
Care should be taken when debating the use of therapeutic interventions designed to prevent or attenuate a strength loss associated with secondary muscle injury. |
1 Introduction
Injury to skeletal muscle induced by work, exercise, and most traumatic means (e.g., crush, laceration, penetration, blast, freezing) results in an immediate loss of strength. Depending on the means for inducing injury, this strength loss can be attributed to a disruption of the excitation–contraction coupling process and/or frank damage to force-generating or -transmitting structures within the muscle [1–3]. We and others have hypothesized that the initial injury can start a cascade of events that leads to additional injury in the ensuing hours and days [3, 4]. This cascade has been thought to begin with a loss of intracellular calcium homeostasis within the damaged muscle fibers that is brought on by a loss of plasmalemmal integrity. The loss of calcium homeostasis may then lead to activation of several degradative pathways intrinsic to muscle that are referred to as autogenetic mechanisms [4]. These calcium-sensitive pathways include calcium-activated neutral proteases and those of the phospholipase A2 cascade, which produce arachidonic acid, prostaglandins, and leukotrienes that may further damage cell membranes. Elevated intracellular calcium may also disrupt mitochondrial respiration and result in sarcomeric contracture. The autogenetic mechanisms for inducing damage are thought to be followed by an inflammatory phase, beginning 2–6 h after the initiating event [4]. In this phase, neutrophils and macrophages invade the damaged tissue and are primarily responsible for removal of that tissue over the next several days. It is believed that this inflammatory response may induce additional injury by spillover of inflammation, including reactive oxygen species, from damaged tissue onto adjacent tissue that was initially undamaged (i.e., the so-called bystander injury) [5].
If the autogenetic mechanisms and inflammatory response contribute to an additional (or secondary) injury in the hours and days following the initiating event, the damage should be measurable using standard markers of muscle injury. Such markers include histopathology, soreness, blood levels of muscle proteins, limb range of motion, and strength. We and others have reasoned that muscle strength, measured during either maximal voluntary or electrically elicited contractions, provides the single-best assessment of the extent of muscle injury regardless of injury type. This is because strength comes closest to evaluating the overall functional capacity of the tissue [3, 6]. Strength is also quantifiable in both human and animal injury models whereas many other measures are not feasible or practical in all models (e.g., quantitative histopathology in human models) and/or are only semi-quantitative (e.g., blood levels of muscle proteins).
The earliest suggestion for a secondary loss of strength following an initiating injurious event came from John Faulkner and colleagues in a narrative review article published over 20 years ago [3]. They specifically argued that a secondary strength loss occurs in the first 3 days after injury. Since then, others have acknowledged that such a strength loss is likely [7, 8], but the direct evidence for the loss has been mixed (e.g., Brooks and Faulkner [9] and Roche et al. [10]). It is important to determine whether a secondary strength loss occurs because this information can affect if and how muscle injuries should be treated, specifically whether interventions such as anti-inflammatory medications, cryotherapy, or antioxidants should be used to block autogenetic pathways or minimize the inflammatory response. It is possible that these cellular events are more associated with repair and regeneration of the damaged tissue than with inducing an additional (or secondary) injury. If this is the case, the above interventions may have no beneficial effects at best and adverse effects at worst.
Because of the apparent discrepant evidence in the literature for the presence of a secondary strength loss, we felt that a rigorous, quantitative analysis of the literature was warranted. Our objective was to conduct a systematic review combined with a meta-analytic approach to determine whether over the first 3 days following an injurious event to muscle, there is a strength loss above and beyond the initial loss (Fig. 1). Such a loss would constitute a secondary strength loss and a secondary muscle injury. We are unaware of any previous attempt to address this issue using this methodology. We also sought to explain the disparate findings in the literature by examining the effects of various experimental factors (e.g., subject type [animal vs. human], sex of the subject, type of injury, muscle group injured, day of post-injury strength assessment) that have varied among studies.
2 Methods
2.1 Systematic Review
2.1.1 Selection of Studies
A thorough systematic search of the research literature was performed conforming to the PRISMA statement [11] to determine if a secondary loss of strength occurs over the first 3 days after a muscle injury. Our literature search began in January 2011 and continued through to December 2012. The databases that were searched include PubMed, SPORTDiscus, ISI Web of Knowledge, CINAHL, Cochrane Library, OpenSIGLE, ProQuest Dissertation and Theses, and the American College of Sports Medicine database of annual meeting proceedings. The search terms used were skeletal muscle AND (injur* OR damage*) AND (strength OR force OR torque). Reference lists from fully evaluated publications were also examined for studies not found with the online database searches.
2.1.2 Study Inclusion and Exclusion Criteria
Studies meeting the following criteria were considered for review: (1) muscle injury had to be induced experimentally by exercise or work biased to the performance of eccentric contractions or by trauma (e.g., crush, laceration, penetration, blast, freezing, myotoxin injection, ischemia–reperfusion); (2) strength in the injured muscle group had to be assessed immediately post-injury (i.e., within the first 6 h) in addition to at least one assessment performed between 24 and 72 h post-injury; and (3) isometric, isokinetic, and/or isotonic strength was assessed using maximal voluntary and/or electrically elicited contractions. Studies or study subgroups were excluded for the following reasons. First, subjects performed non-damaging exercise (e.g., isometric or concentric contractions) in addition to or in lieu of eccentric contractions or eccentric contraction-biased exercise. Second, drugs, ergogenic drink/food, or supplements were ingested or administered prior to, during, or after injury. However, if one or more independent groups of subjects from a study met the above criteria for inclusion (e.g., a control group whose muscles were injured but received sham treatment in an interventional study), their data were included in the analysis. Third, a therapeutic modality such as massage, heat, ice, transcutaneous electrical nerve stimulation, ultrasound, or hyperbaric oxygen was applied prior to, during, or after injury. Fourth, for studies inducing injury by eccentric contractions, a bout of eccentric contractions had been performed in the previous 3 months; in other words, the second bout in repeated-bout studies was excluded. Fifth, animal strains modeling a disease were used (e.g., the mdx mouse, which is a model for Duchenne muscular dystrophy). Sixth, if there were insufficient data reported in a study to calculate an effect size (ES) for the change of strength over the first 3 days post-injury, the study was excluded. Before excluding such studies, we attempted to retrieve the necessary data by contacting the corresponding author by e-mail and/or telephone.
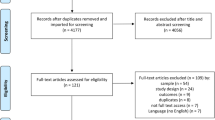
A total of 5525 non-duplicate studies were originally identified through the database searches and review of article reference lists. Of those, 3685 were initially excluded on the basis of reviewing the title and abstract. At this point, 1840 were fully evaluated via a careful review of the full-text article. Using the inclusion and exclusion criteria, 1617 studies were excluded, leaving a total of 223 studies to be included in the meta-analyses. The review and selection processes for the studies in the systematic review are summarized in Fig. 2. Each step of the review and selection processes was conducted independently by at least two of the authors. If there was disagreement among the two authors, a third author was recruited to settle the dispute.
2.1.3 Data Extraction and Assessment of Study Quality or Bias
For calculation of study ESs to be used in the meta-analysis, strength data were extracted in the form of means, sample sizes, and standard deviations (SDs) or standard errors (SEs) for all post-injury timepoints, strength measures, and subject groups meeting our criteria. In studies that did not report all three descriptors, the following were extracted: (1) means, sample sizes, and P value; or (2) effect direction, sample sizes, and P value. If available for repeated-measures design studies, individual subject data were also extracted so that between-trial correlations for the strength measures (i.e., correlation between that measured immediately and day 1–3 post-injury) could be calculated. Study quality and/or bias was not formally assessed in the 223 studies because there were no studies whose objective was to examine the existence of a secondary strength loss, which was the objective of the present analysis. Thus, if a study’s quality was poor or if study bias existed with regard to a study’s objective, this should not have a systematic influence on a study’s ES in our meta-analysis.
2.2 Meta-Analysis
The extracted strength loss data were converted to a standard format by calculating the standardized mean difference, which will be referred to as the ES. The standardized mean difference calculation was set up so that a negative value would indicate a secondary strength loss. For studies in which the immediate and day 1–3 post-injury strength measures were taken on the same subjects and also means, SDs, and sample sizes were reported (i.e., the most common scenario; n = 197 studies), the paired difference (i.e., day 1–3 post-injury strength mean − immediate post-injury strength mean), paired difference SD [i.e., (“day 1–3” SD2 + “immediate” SD2 − 2 × between-trial correlation × “day1–3” SD × “immediate” SD)½], and paired difference SE (i.e., paired difference SD/n½) were initially calculated. These were then used to calculate the standardized mean difference [i.e., paired difference × (2 × (1 − between-trial correlation))½/paired difference SD] and standardized mean difference SE [i.e., (1/n + standardized mean difference2/2n)½ × (2 × (1 − between-trial correlation))½]. Because between-trial correlations could be calculated for only 14 independent groups, the median between-trial correlation (0.803) was substituted in the calculations for studies without correlations. For the studies in which independent groups of subjects were used within a study for measurements at the different timepoints (i.e., n = 26 studies), standardized mean differences were calculated as detailed previously [12].
When a study measured strength under multiple conditions (e.g., measured both isokinetic and isometric strength or measured strength multiple times over the first 3 days post-injury) using the same group of subjects, the standardized mean differences and variances were calculated for each condition level and then averaged across the different condition levels for the group. When a study had more than one independent group of subjects that met the criteria for assessing secondary strength loss, a standardized mean difference and variance was calculated for each group. Then, in the calculation of the overall standardized mean difference, these groups were treated as if they were independent studies [12]. Though 223 studies were used in the meta-analysis, these studies yielded 262 independent groups of subjects and a total of 936 separate ESs.
Meta-analyses were run using a random-effects model that accounts for true between-study variation in effects as well as for random error within each study. A random-effects model was chosen over a fixed-effect model because of the wide variation in experimental factors (e.g., use of humans vs. animals, different means of inducing injury) among studies. Between-study variation in true ES, or heterogeneity, was assessed by Q and I 2 statistics. Because heterogeneity was found to be high, meta-regressions utilizing a method-of-moments approach and subgroup meta-analyses utilizing a Q-test based on ANOVA were used to investigate potential moderator variables (experimental factors) as possible explanations for the heterogeneity. The potential moderator variables examined were (1) study publication year; (2) subject type (human vs. animal); (3) subject sex; (4) subject age; (5) day of post-injury assessment of muscle strength (day 1 vs. day 2 vs. day 3); (6) for human studies, the muscle group injured (e.g., elbow flexors vs. knee extensors); (7) for animal studies, the type of rodent (rat vs. mouse); (8) for animal studies, the muscle injured (ankle dorsiflexor vs. plantarflexor); (9) for animal studies, the type of injury (eccentric contractions vs. traumatic); (10) presence of fatigue immediately post-injury; (11) magnitude of the immediate strength loss; (12) type of contraction used to assess strength; and (13) research group conducting a study.
It was important to determine whether fatigue was present in a study because it might explain some of the between-study variation in ES. If fatigue was present after injurious work or exercise, the immediate post-injury strength would be lower than it should be. As a result, the study ES would be inflated and possibly positive when it should have been negative. To determine whether fatigue was present in a study, we examined the methods for each study to see if (1) there was a comparable control group (e.g., using isometric or concentric contractions as a control for injury induced by eccentric contractions); or (2) multiple strength measurements were made in the 0–6 h post-injury period so that strength changes over this period could be assessed. If the strength loss in a control group was apparent as compared with that for an eccentric contraction-injured group or if recovery of strength was apparent in the eccentric contraction-injured group over 0–6 h post-injury, fatigue was said to be present immediately post-injury in that study. For studies without these controls but in which (1) the injury was traumatic in nature (i.e., no contractions were performed during injury induction); or (2) the immediate post-injury measure of strength was performed relatively late after the eccentric contraction injury protocol (i.e., 0.5–6 h post-injury), we assumed that fatigue was not present immediately post-injury. For all other studies, the presence of fatigue immediate post-injury was listed as unknown.
To determine if the research group conducting a study might also explain some of the between-study variation in ES, we designated research groups using the following procedure. First, we identified authors of studies from our meta-analysis that had conducted five or more studies. These authors were then cross-referenced with each other to identify collaborative groups (e.g., relationships between an advisor and his/her current or former students, post-doctoral fellows, or colleagues). Each collaborative group was required to have ten or more independent groups for which an ES was calculated in the meta-analysis. We identified five research groups that met these criteria. Studies not belonging to a research group were placed in a group labeled “All other studies.”
For all subgroup meta-analyses, each subgroup was required to have a minimum of five studies, with the exception as noted in the previous paragraph. In studies that had more than one level of the experimental factor being evaluated (e.g., a study measuring strength loss in both a group of men and a group of women in the subgroup meta-analysis evaluating the effect of subject sex), an ES was calculated for each level and each ES was treated as if it originated from an independent study.
Meta-analyses, subgroup meta-analyses, and meta-regressions were performed using the Comprehensive Meta-Analysis software (version 3.3; Biostat Inc., Englewood, NJ, USA). ESs of 0.2, 0.5, and 0.8 were considered to be small, medium, and large, respectively [13]; an ES of 0.1 was considered to be trivial. An α level of 0.05 was used in all analyses except in subgroup meta-analyses where more than two levels of a moderator variable existed and the overall Q-test yielded a significant P value. In this situation, a Benjamini and Hochberg false discovery rate adjustment was applied to the α level to correct for multiple post hoc pairwise comparisons using Q-tests. As for study quality and bias as mentioned above, the effect of publication bias on the meta-analysis was not assessed because no studies in the meta-analysis had a research objective matching that of the present analysis. Though unpublished studies meeting our inclusion/exclusion criteria are likely, these should not be biased towards exhibiting a secondary strength loss or not.
3 Results
3.1 Description of Included Studies
In total, 223 studies, along with data for 262 independent groups of subjects, were published between 1985 and 2012, and these were included in the meta-analysis investigating secondary strength loss. Briefly, there were 184 human and 39 animal studies. For the human studies, there were a total of 3413 subjects, with the average age for a study ranging from 18 to 70.5 years. These studies contained 111 independent groups that were male only and 22 that were female only. For the human studies, strength was reported both immediately and at day 1, day 2, or day 3 post-injury in 192, 188, and 163 independent groups, respectively. Eccentric contraction-biased exercise or eccentric contractions were used to induce injury in all human studies. For the animal studies, there were a total of 664 rodents, with the average age for a study ranging from 2 to 27 months. These studies contained 24 independent groups that were male only and 11 that were female only. For the animal studies, strength was reported both immediately and at day 1, day 2, or day 3 post-injury in 14, 11, and 40 independent groups, respectively. Animal studies employed several injury models (i.e., eccentric contraction-induced injury, downhill walking/running, blunt-impact injury, ischemia–reperfusion injury, and freeze injury).
3.2 Meta-Analysis of Secondary Strength Loss
Considerable variation in ES was observed among studies, with ES ranging from −2.46 [9] to +6.29 [14] (Electronic Supplementary Material Figure S1). As illustrated in the forest plot, 67 of the 262 independent groups exhibited a negative ES, which supports a secondary loss of strength occurring at 1–3 days post-injury. Conversely, 195 independent groups exhibited a positive ES, indicating an absence of secondary strength loss in those studies. With all independent groups included, the meta-analysis yielded a small-to-medium overall ES that was positive and statistically greater than zero (overall ES = +0.336, 95 % confidence interval [CI] 0.270–0.401; P < 0.00000001; Electronic Supplementary Material Figure S1), indicating that, on average, muscle strength improves over the first 3 days post-injury. As one would expect, there was no one study that dominated the overall ES. The study of Rodenburg et al. [15] had the single largest effect on the overall ES. If this study was removed from the meta-analysis, the overall ES would only fall to +0.326 and the effect would still be statistically greater than zero (P < 0.00000001).
The overall ES was also calculated using the most liberal scenario for possibly detecting a secondary strength loss. Because multiple ESs were calculated for most studies, we opted to run the primary meta-analysis using the single smallest (or most negative) ES determined for each independent group or study. The overall effect (ES = +0.067; 95 % CI 0.004–0.130; P = 0.036) when calculated this way was still positive, albeit trivial in magnitude, and was significantly greater than zero. Thus, this analysis also does not provide support for the occurrence of a secondary strength loss.
Tests of heterogeneity were performed to assess the extent of between-study variation in the ES. Because heterogeneity was large and statistically significant (I 2 = 86 %; Q = 1900, P < 0.00000001), moderator variables that could potentially explain this heterogeneity were investigated using subgroup meta-analysis and meta-regression. With the exception of one moderator variable, Table 1 summarizes the findings of the subgroup meta-analyses. Subject type was not a significant moderator variable as there was no statistical difference in ES between studies using humans and those using animals. Likewise, within animal studies, there was no significant difference in ES between studies using rats and those using mice. The sex of the subject was, however, able to explain a significant portion of the heterogeneity (P = 0.02). Interestingly, the ES determined for studies using males was more than twice that for studies using females, suggesting that males may recover strength faster after injury.
The day of post-injury strength assessment was a significant moderator variable. In the analysis examining all studies (Table 1) and in the analysis examining human studies only (Fig. 3a), studies making measurements of strength at day 3 post-injury had an ES that was greater than that for studies taking measurements at day 2 post-injury, which in turn was greater than that for studies taking measurements at day 1 post-injury. The moderator variable’s effect was different when analyzing animal studies only (Fig. 3b). Only animal studies taking measurements at day 3 post-injury had an ES that was significantly less than the ES for studies taking measurements at day 2 post-injury (+0.44 vs. +1.19; P = 0.02). More importantly, the ES for each of the day subgroups were positive and statistically greater than zero. When the analysis was run using only studies, including human and animal studies, that took measurements on all 3 days, the findings were identical to those for all studies and the human-only studies (Fig. 3c).
Forest plots depicting the effect of day of post-injury strength assessment on effect size: a studies using human subjects; b studies using animal subjects; c studies with data for all 3 days. The center of a diamond represents the subgroup effect size for a given day. Diamond width represents the 95 % confidence interval for the subgroup effect size. The number of independent groups contributing to a subgroup effect size is listed within the parentheses. An asterisk indicates a significant difference between subgroups analyzed using post hoc pairwise comparisons and a Benjamini and Hochberg false discovery rate-adjusted α level. CI confidence interval, ES effect size
To determine if the muscle group injured could explain some of the between-study variation in ES, subgroup meta-analyses were performed separately for human and animal studies (Table 1). For humans, the ESs from studies injuring elbow flexors, knee extensors, and/or knee flexors were compared. For animals, ankle plantarflexor muscles were contrasted against ankle dorsiflexor muscles. The muscle group tested was a significant moderator variable for both the human and animal studies. The ES for the group of studies injuring the elbow flexors was three to four times greater than the ES for the groups of studies injuring the knee extensors or flexors. These data suggest that the strength recovery over the first 3 days post-injury may be greater for the elbow flexors than for either the knee extensors or flexors. In the animal studies using the ankle plantarflexors, the ES was approximately three times greater than the ES for the studies using the dorsiflexors. This suggests that the plantarflexors may recover strength faster following injury.
The injury induced in all human studies was induced using eccentric contractions or eccentric contraction-biased exercise but several injury models were employed in the animal studies including eccentric contraction-induced injury, freeze injury, crush injury, and ischemia–reperfusion injury. To determine if the type of injury could explain some of the between-study variation in the ES, a subgroup meta-analysis was performed for animal studies comparing eccentric contraction-induced injury models with traumatic injury models (i.e., freeze, crush, and ischemia–reperfusion models combined). However, injury type was not found to be a significant moderator variable (P = 0.78) (Table 1). In addition, the type of contraction used to assess strength (i.e., isometric vs. isokinetic or isotonic) was unable to explain any heterogeneity (P = 0.67).
The presence of fatigue in a study at the time of the immediate post-injury assessment was able to explain a significant amount of the between-study variation in ES (P = 0.03) (Table 1). When fatigue was present, the study ES was greater than when the fatigue state in a study was unknown (+0.62 vs. +0.30). Similarly, when fatigue was present, the study ES approached being significantly greater than the ES from studies where fatigue was not present or unlikely to be present (+0.62 vs. +0.32; P = 0.054).
A subgroup meta-analysis conducted to determine if the research group performing a study could explain some of the between-study variation in ES yielded statistically significant results (P = 0.001) (Fig. 4). Research group ES values ranged from −0.11 for the “J. A. Faulkner and S. V. Brooks” group to +0.47 for the “P.M. Clarkson, T. C. Chen, and K. Nosaka” group. The “J. A. Faulkner and S. V. Brooks” group was the only research group to have a negative ES, though it was not statistically less than zero. Post hoc testing revealed that there were three pairs of groups, with one group being significantly different from the other (Fig. 4).
Forest plot depicting the effect of research group on effect size. The center of a diamond represents the effect size for a given research group. Diamond width represents the 95 % confidence interval for the subgroup effect size. Research group assignments were made after careful cross-of all studies to detect collaborations (e.g., co-authorships) and shared research approaches (e.g., same or similar experimental model). For consideration as a group for the subgroup meta-analysis, each research group had to have a minimum of ten independent groups of subjects included in the overall meta-analysis. Studies not assigned to a research group were lumped together in the “All other studies” group. The number of independent groups contributing to a subgroup effect size is listed within the parentheses. An asterisk indicates a significant difference between subgroups analyzed using post hoc pairwise comparisons and a Benjamini and Hochberg false discovery rate-adjusted α level. CI confidence interval, ES effect size
Meta-regression analysis was used to determine if two continuous variables, study publication year and subject age, could explain any of the between-study variation in ES. There was no significant (P = 0.17) linear relationship between the year a study was published and its ES (slope = +0.008 year−1; 95 % CI −0.004 to 0.021). The analysis of subject age was run separately for human and animal studies. There was no significant (P ≥ 0.16) linear relationship between mean subject age in years and study ES when analyzing either human studies (slope = +0.006 year−1; 95 % CI −0.005 to 0.017) or animal studies (slope = −0.319 year−1; 95 % CI −0.766 to 0.129).
Meta-regression was also used to determine the relationship between the mean immediate post-injury strength loss (%) and study ES. One might hypothesize that a secondary strength loss would be more likely to occur with a greater initial injury. Figure 5 illustrates the relationship for both the studies using humans (Fig. 5a) and those using animals (Fig. 5b). Surprisingly, the relationship was positive in the human studies (P < 0.000000001) but negative in the animal studies (P = 0.02). More importantly, predicted study ES was only negative when the immediate post-injury strength loss was small (i.e., <13 %) in the human studies. In contrast, the predicted study ES in the animal studies was never less than zero. The smallest predicted ES would be +0.19, occurring at a 100 % immediate post-injury strength loss. If the studies exhibiting fatigue at the time of the immediate post-injury measurement were removed from the analyses, the relationship between the immediate post-injury strength loss and study ES was lost in the animal studies but remained unchanged in the human studies.
Meta-regression analysis of the relationship between the magnitude of the immediate post-injury strength loss (%) and study (or independent group) effect size for human-only studies (a) and animal-only studies (b). Each study or independent group is represented by a circle and the size of a circle reflects the degree of weighting for that datapoint. There are 334 and 88 datapoints in (a) and (b), respectively. These outnumber the numbers of studies and independent groups because many studies measured strength in more than one fashion. In (a) and (b), the straight line reflects the line of best fit and is surrounded by two curvilinear lines representing the 95 % confidence interval. The statistical significance of the relationships in (a) and (b) are P < 0.000000001 and P = 0.02, respectively
4 Discussion
Overall, we found 262 independent groups of subjects from 223 studies in which strength was measured immediately post-injury and again at 1, 2, and/or 3 days post-injury. Our analysis was based on a total of 936 ESs, which were calculated from a total of over 4000 human and animal subjects. The calculation of the ES was designed so that a negative ES would be interpreted as supporting a secondary strength loss. Furthermore, in order to establish a significant secondary strength loss, a negative ES had to be statistically less than zero. Our meta-analysis of the data from the 223 studies yielded a small-to-medium, positive overall ES that was statistically greater than zero (P < 0.00000001) (Electronic Supplementary Material Figure S1), indicating that strength in the typical study recovers during the first 3 days after injury. However, there was a large variation in ES among studies (i.e., I 2 = 86 %). Experimental factors that could explain the variability, at least partially, included the sex of the subject, the day of post-injury strength assessment, whether fatigue was present immediately post-injury, the muscle group injured, the research group conducting the study, and the magnitude of the immediate post-injury strength loss (Table 1; Figs. 3, 4, 5).
4.1 Technical Limitations of the Analysis
Potential technical limitations of our systematic review and meta-analysis include (1) the likelihood of our review having missed studies; and (2) failure to know the between-trial correlations in many studies utilizing a repeated-measures research design. We performed an extensive literature search for studies conducted in 2011 or before. We did not exclude unpublished studies, non-English studies, or studies based on geographical location. However, it is doubtful that our systematic review retrieved all relevant studies and therefore our analysis probably consists of a random subset of all relevant studies. While failure to include all possible studies can affect meta-analysis statistical power and ES CIs, we do not believe that this limitation had a significant impact on the overall ES [12]. An Orwin’s Fail-Safe N test was used to determine how many missing studies would have to exist in order to bring the overall ES down to a level indicating a secondary strength loss [16]. We sought to identify the number of missing studies that would need to be found to produce a negative, albeit trivial, overall effect (i.e., ES = −0.1) that would be statistically less than zero. Assuming that the missing studies had a mean ES of −0.5, we determined that 234 missing studies would have to be found and added to our meta-analysis before we could conclude that, on average, a secondary strength loss occurs following injury. This number of missing studies is almost equal to the total number of independent groups that we did find. Furthermore, only 8 % of the 262 independent groups we retrieved had an ES of −0.5 or less. We believe it is highly unlikely that we missed 234 or more studies with a mean ES of –0.5 and thus this analysis is consistent with the argument that a secondary strength loss does not occur in the typical study.
The other technical limitation of our systematic review and meta-analysis was not knowing the between-trial correlations (i.e., that between immediate post-injury and the day 1–3 post-injury measures) in most of the studies employing a repeated-measures research design. We were only able to calculate correlations for 14 independent groups and used the median of those 14 correlations (i.e., 0.803) as the correlation for the groups for which a correlation could not be calculated. The inability to calculate between-trial correlations is a common issue for data extraction from primary research studies but the effect of this limitation can be addressed by performing a sensitivity analysis [12]. We performed a sensitivity analysis by allowing the assumed correlation to vary between what we considered to be the extreme possibilities for the correlation. By varying the correlation between 0 and 0.95, the overall ES varied minimally from +0.299 to +0.339 while remaining statistically greater than zero (P < 0.00000001) in all instances. Therefore, our sensitivity analysis indicates that not knowing the between-trial correlations for all studies most likely had minimal effect on the overall ES and its qualitative label as a small-to-medium, positive effect.
4.2 Evidence For and Against Secondary Strength Loss
There was minimal evidence in our analysis supporting a secondary strength loss after muscle injury, even when considering the potential moderator variables that might explain some of the marked between-study variation in ES. For example, the subgroup meta-analysis probing how the day of post-injury assessment affected study ESs showed that for both all studies and the human-only studies, the ES for the subgroup of studies measuring strength at 3 days post-injury was significantly larger than that for the subgroup measuring strength at 2 days post-injury, which in turn was larger than that for the subgroup measuring strength at 1 day post-injury (Table 1; Fig. 3a). These results were the same as when we conducted a subgroup meta-analysis using only studies that made measurements on all 3 days (Fig. 3c). While causal conclusions cannot be made from subgroup meta-analyses, this particular analysis presents the strongest case for the interpretation that muscle strength is steadily recovering over the first 3 days post-injury.
Overall, we looked at ten moderator variables using the subgroup meta-analysis procedure. This generated a total of 36 subgroups and there was only one subgroup with a negative ES, and that ES was not statistically less than zero (Table 1; Figs. 3, 4). Moreover, of the 35 subgroups with positive ESs, all but six were statistically greater than zero. From the 223 studies included in our review, we also conducted an overall meta-analysis using the smallest (or most negative) ES from each study and still observed a positive overall effect (ES = +0.067), which was statistically greater than zero. Given the criterion to establish a secondary strength loss (i.e., a negative ES that was statistically less than zero), this “smallest ES” analysis approach was biased towards finding a secondary strength loss but still failed to do so. Also, the mean immediate post-injury strength loss among the 223 studies varied substantially, and one might posit that greater initial injury would coincide with the appearance of a secondary strength loss. However, the relationships between mean immediate post-injury strength loss and study ESs determined by meta-regressions were not predictive of a secondary strength loss in the case of the animal-only studies or were only predictive of a secondary strength loss at relatively small immediate post-injury strength losses in the human-only studies (Fig. 5). Collectively, we found minimal evidence to support a statistically significant secondary strength loss.
4.3 Explanations for Between-Study Variance in Effect Size
Over the past 30 years, a number of research groups have made significant contributions to the understanding of muscle injury and repair. It is not surprising that differences in ES were observed among the five research groups in our “research group” analysis because these groups have used different experimental models and had differing research objectives. For example, of the five groups, the “J. A. Faulkner and S. V. Brooks” and “R. B. Armstrong, C. P. Ingalls, and G. L. Warren” groups primarily used rodent models, with the former group utilizing an in situ model for inducing injury versus an in vivo model being used by the latter group. The three other research groups primarily used human subjects, with the “P. M. Clarkson, T. C. Chen, and K. Nosaka” studies typically injuring the elbow flexors while the “A. E. Donnelly” and “R. G. Eston and M. P. McHugh” studies typically injured the knee extensors and/or flexors. It is important to remind the reader that in a separate subgroup meta-analysis we found human studies injuring the elbow flexors to have an ES that was much greater than that for studies injuring the knee extensors. However, it is not possible to determine if this muscle group difference is truly a muscle group difference or if it occurred due to other experimental differences among the “P. M. Clarkson, T. C. Chen, and K. Nosaka,” “A. E. Donnelly,” and “R. G. Eston and M. P. McHugh” research groups. This emphasizes why causal conclusions cannot be made from the results of subgroup meta-analyses or meta-regressions. However, what is clear from this “research group” analysis is that no single subgroup ES was statistically less than zero, which argues against a secondary loss of strength occurring.
In a narrative review discussing secondary strength loss, Faulkner and associates [3] wrote that the magnitude of the primary injury can be determined by measuring strength loss at 3 h post-injury to rule out any contribution to strength loss arising from fatigue. While both injury and fatigue can cause an immediate loss of muscle strength, fatigue is characterized by the reversal of strength loss with rest, whereas muscle injury requires muscle fiber repair and/or regeneration and strength recovery is more prolonged. Per our inclusion criteria, we accepted studies with strength measurements up to 6 h post-injury for our “immediate post-injury” timepoint. We subsequently performed a subgroup meta-analysis to determine the potential impact that fatigue could have had on the study ES. Specifically, if fatigue contributed to the immediate post-injury strength loss, this would make it more difficult to detect a secondary strength loss because the ES would be inflated. Indeed, the ES for studies where fatigue was present was twofold greater than the ES for all other studies (i.e., +0.62 vs. +0.30–0.32). More importantly, this subgroup meta-analysis also showed that when fatigue was not present or not likely to be present, there was still a positive ES that was statistically greater than zero (Table 1). We concluded that fatigue can confound the strength loss immediately post-injury in eccentric contraction-induced injury studies and thus inflate the associated ES. However, fatigue appears to have occurred in a minority of studies and thus it is unlikely to have substantially affected our overall finding and interpretation of that finding.
The results of our “day of post-injury strength assessment” subgroup meta-analysis conducted on animal-only studies (Fig. 3b) may lead some to suggest that we should give consideration to calculating the ES for strength data collected after 3 days post-injury. This is because the studies taking measurements of strength at 3 days post-injury had a significantly lower ES than that of studies taking measurements at 2 days. One might hypothesize that the ES could decline further over the next few days post-injury, eventually becoming negative. However, using data collected after 3 days post-injury is outside the time frame originally proposed for when a secondary strength loss occurs [3]. Furthermore, as compared with the analysis using human-only studies, there were far fewer independent groups contributing to the animal-only subgroup meta-analysis (i.e., 11–40 vs. 163–192 studies per timepoint). With far fewer studies in the animal-only analysis, it is more likely for a subgroup ES to be influenced by a particular research group’s approach or methodology. For example, 15 of the 40 “3 days post-injury” ESs came from the “J. A. Faulkner and S. V. Brooks” research group, whereas only one of the 11 “2 days post-injury” ESs came from that group. This is noteworthy because the “J. A. Faulkner and S. V. Brooks” studies tended to have negative ESs (Fig. 4), and thus this might help explain why the “3 days post-injury” ES was lower than that for 2 days post-injury.
The present analysis provides insight for future research directions. In particular, studies exploring subject sex differences or muscle group differences in the strength recovery from muscle injury would be warranted (Table 1). One interpretation from the “subject sex” subgroup meta-analysis is that males recover faster than females. Alternatively, males could be more susceptible to muscle injury (i.e., greater immediate strength loss) and if males and females recovered to a similar percentage of initial strength by 3 days post-injury, the rate of strength recovery would appear to be greater for males. This theory would tend to agree with our meta-regression analysis showing a positive relationship between immediate strength loss and the study ES in the human-only studies (Fig. 5a). However, assumptions on sex differences in susceptibility or recovery from injury are not supported by a cursory review of the literature, at least for human studies [17]. Similar to subject sex differences in ES, the greater ES for human studies employing the elbow flexors may simply reflect how the ES is calculated because the elbow flexors appear to be more susceptible to eccentric contraction-induced injury than are the knee extensors [18–20]; the immediate strength loss for the elbow flexors is ~50 % greater on average [18]. A possible alternative explanation for the muscle group difference is that the elbow flexors may be more fatigable than the knee extensors during the performance of eccentric contractions. However, in our analysis of the incidence of fatigue, the association of fatigue with studies using the elbow flexors was no different from that for studies using the knee extensors (P = 0.92).
4.4 Practical and Clinical Implications
A primary motivation for this meta-analysis was to determine if a secondary loss of strength occurs after the initiating injurious event so that one can make more informed decisions about if and how to treat muscle injuries. Specifically, the autogenetic and inflammatory phases following injury have been directly implicated as causing a secondary deleterious event in skeletal muscle leading to a secondary loss of strength [3, 14, 21, 22]. If such a secondary strength loss occurs, then pharmacological, dietary, and therapeutic interventions to block autogenetic pathways and/or inflammation in the first few days post-injury might be efficacious. On the other hand, if there is no secondary strength loss, more caution should be employed for such interventions because they might impair the recovery process. The results of our systematic review and meta-analysis may suggest why pharmacological, dietary, and therapeutic interventions have not been generally effective [23, 24], i.e., because there is minimal, if any, evidence for a secondary injury, at least not an injury resulting in an additional strength loss. This could be because the autogenetic and inflammatory phases may be constrained to lie within the initially damaged tissue and thus may be thought of as parts of the tissue repair and regeneration processes rather than degeneration processes that cause additional damage.
We can also envision a scenario in which secondary injury occurs but a secondary strength loss does not. We have shown that in the first few days after the initiation of eccentric contraction-induced injury, most (i.e., 50–75 %) of the strength loss is attributable to a failure in the excitation–contraction (E-C) coupling process, with the remainder of the strength loss being due to physical disruption of force-bearing elements within the muscle [25]. The strength loss attributable to E-C uncoupling is recovered more rapidly than that associated with physical disruption. We have hypothesized that the former recovery process is more of a repair process and does not require degeneration and subsequent regeneration of muscle fibers, whereas recovery of strength from physical disruption would require degeneration, including inflammation, and regeneration [26]. We theorize that it is possible to have some damaged muscle fibers recovering from E-C uncoupling at the same time that other damaged fibers, although fewer in number, are engulfed in inflammatory infiltrate to the extent that adjacent, but previously undamaged, fibers incur a bystander injury. In this scenario, strength measured at the whole muscle level could be recovering but locally, initially uninjured fibers could be undergoing damage by the inflammation but not to the extent that the muscle strength recovery is blunted or noticeably slowed. Support for such a hypothesis comes from a study by Pizza and colleagues [27] in which eccentric contraction-induced injury was induced in muscles of wild-type mice and mice with a genetic deletion that blunts neutrophil accumulation in injured muscle. There was no evidence of a secondary strength loss in either strain of mice, i.e., strength recovered steadily over time after injury, but strength recovered faster in the mice with a reduced neutrophil accumulation in the injured muscle. The scenario of having a secondary injury without a secondary strength loss can easily be envisioned when the mechanisms for injury, and the recovery from it, are not homogenous, either temporally or spatially, within the muscle.
5 Conclusions
A robust systematic review and meta-analysis was conducted utilizing data from 262 independent groups of subjects reported in 223 studies with over 4000 subjects and 936 separate ESs. Our findings do not support the presence of a secondary strength loss following an initial injurious event in skeletal muscle. In fact, our findings suggest that, on average, strength recovers steadily over the first 3 days post-injury, particularly in humans. Moving forward, we recommend that future studies no longer use secondary strength loss as a foundation on which to justify a study. Furthermore, careful thought should be applied before initiating a study using an intervention (e.g., dietary, pharmacological, therapeutic) to block or attenuate inflammatory or autogenetic processes when recovery of muscle strength is desired.
References
Friden J, Lieber RL. Structural and mechanical basis of exercise-induced muscle injury. Med Sci Sports Exerc. 1992;24(5):521–30.
Warren GL, Ingalls CP, Lowe DA, et al. What mechanisms contribute to the strength loss that occurs during and in the recovery from skeletal muscle injury? J Orthop Sports Phys Ther. 2002;32(2):58–64. doi:10.2519/jospt.2002.32.2.58.
Faulkner JA, Brooks SV, Opiteck JA. Injury to skeletal muscle fibers during contractions: conditions of occurrence and prevention. Phys Ther. 1993;73(12):911–21.
Armstrong RB, Warren GL, Warren JA. Mechanisms of exercise-induced muscle fibre injury. Sports Med. 1991;12(3):184–207.
Tidball JG. Inflammatory processes in muscle injury and repair. Am J Physiol Regul Integr Comp Physiol. 2005;288(2):R345–53. doi:10.1152/ajpregu.00454.2004.
Warren GL, Lowe DA, Armstrong RB. Measurement tools used in the study of eccentric contraction-induced injury. Sports Med. 1999;27(1):43–59.
Morton JP, Kayani AC, McArdle A, et al. The exercise-induced stress response of skeletal muscle, with specific emphasis on humans. Sports Med. 2009;39(8):643–62. doi:10.2165/00007256-200939080-00003.
Smith C, Kruger MJ, Smith RM, et al. The inflammatory response to skeletal muscle injury: illuminating complexities. Sports Med. 2008;38(11):947–69. doi:10.2165/00007256-200838110-00005.
Brooks SV, Faulkner JA. Contraction-induced injury: recovery of skeletal muscles in young and old mice. Am J Physiol. 1990;258(3 Pt 1):C436–42.
Roche JA, Lovering RM, Roche R, et al. Extensive mononuclear infiltration and myogenesis characterize recovery of dysferlin-null skeletal muscle from contraction-induced injuries. Am J Physiol Cell Physiol. 2010;298(2):C298–312. doi:10.1152/ajpcell.00122.2009.
Moher D, Liberati A, Tetzlaff J, et al. Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. BMJ. 2009;339:b2535. doi:10.1136/bmj.b2535.
Borenstein M, Hedges LV, Higgins JPT, et al. Introduction to meta-analysis (Statistics in Practice). Chichester: Wiley; 2009.
Cohen J. Statistical power analysis for the behavioral sciences. 2nd ed. Hillsdale: Lawrence Erlbaum; 1988.
Lapointe BM, Frenette J, Cote CH. Lengthening contraction-induced inflammation is linked to secondary damage but devoid of neutrophil invasion. J Appl Physiol. 2002;92(5):1995–2004. doi:10.1152/japplphysiol.00803.2001.
Rodenburg JB, Steenbeek D, Schiereck P, et al. Warm-up, stretching and massage diminish harmful effects of eccentric exercise. Int J Sports Med. 1994;15(7):414–9. doi:10.1055/s-2007-1021080.
Becker BJ. Failsafe n or file-drawer number. In: Rothstein HR, Borenstein M, editors. Publication bias in meta-analysis. West Sussex: Wiley; 2005. p. 111–25.
Hubal MJ, Clarkson PM. Counterpoint: estrogen and sex do not significantly influence post-exercise indexes of muscle damage, inflammation, and repair. J Appl Physiol. 2009;106(3):1012–4. doi:10.1152/japplphysiol.90848.2008a.
Warren GL, Palubinskas LE. Human and animal experimental muscle injury models. In: Tiidus PM, editor. Skeletal muscle damage and repair. Champaign: Human Kinetics; 2008. p. 13–36.
Chen TC, Lin KY, Chen HL, et al. Comparison in eccentric exercise-induced muscle damage among four limb muscles. Eur J Appl Physiol. 2011;111(2):211–23. doi:10.1007/s00421-010-1648-7.
Jamurtas AZ, Theocharis V, Tofas T, et al. Comparison between leg and arm eccentric exercises of the same relative intensity on indices of muscle damage. Eur J Appl Physiol. 2005;95(2–3):179–85. doi:10.1007/s00421-005-1345-0.
Zerba E, Komorowski TE, Faulkner JA. Free radical injury to skeletal muscles of young, adult, and old mice. Am J Physiol. 1990;258(3 Pt 1):C429–35.
Van Der Meulen JH, McArdle A, Jackson MJ, et al. Contraction-induced injury to the extensor digitorum longus muscles of rats: the role of vitamin E. J Appl Physiol. 1997;83(3):817–23.
Baldwin Lanier A. Use of nonsteroidal anti-inflammatory drugs following exercise-induced muscle injury. Sports Med. 2003;33(3):177–85.
Teixeira VH, Valente HF, Casal SI, et al. Antioxidants do not prevent postexercise peroxidation and may delay muscle recovery. Med Sci Sports Exerc. 2009;41(9):1752–60. doi:10.1249/MSS.0b013e31819fe8e3.
Warren GL, Ingalls CP, Lowe DA, et al. Excitation-contraction uncoupling: major role in contraction-induced muscle injury. Exerc Sport Sci Rev. 2001;29(2):82–7.
Rathbone CR, Wenke JC, Warren GL, et al. Importance of satellite cells in the strength recovery after eccentric contraction-induced muscle injury. Am J Physiol Regul Integr Comp Physiol. 2003;285(6):R1490–5. doi:10.1152/ajpregu.00032.2003.
Pizza FX, Peterson JM, Baas JH, et al. Neutrophils contribute to muscle injury and impair its resolution after lengthening contractions in mice. J Physiol. 2005;562(Pt 3):899–913. doi:10.1113/jphysiol.2004.073965.
Kerksick C, Lt Taylor, Harvey A, et al. Gender-related differences in muscle injury, oxidative stress, and apoptosis. Med Sci Sports Exerc. 2008;40(10):1772–80. doi:10.1249/MSS.0b013e31817d1cce.
Brown SJ, Child RB, Day SH, et al. Exercise-induced skeletal muscle damage and adaptation following repeated bouts of eccentric muscle contractions. J Sports Sci. 1997;15(2):215–22. doi:10.1080/026404197367498.
Newton M, Nosaka K, Sacco P. Relationship between force and histological changes in mouse anterior crural muscles following eccentric exercise. Basic Appl Myol. 2000;10(5):225–9.
Skurvydas A, Kamandulis S, Stanislovaitis A, et al. Leg immersion in warm water, stretch-shortening exercise, and exercise-induced muscle damage. J Athl Train. 2008;43(6):592–9. doi:10.4085/1062-6050-43.6.592.
McCully KK, Faulkner JA. Injury to skeletal muscle fibers of mice following lengthening contractions. J Appl Physiol. 1985;59(1):119–26.
Paschalis V, Nikolaidis MG, Giakas G, et al. Beneficial changes in energy expenditure and lipid profile after eccentric exercise in overweight and lean women. Scand J Med Sci Sports. 2010;20(1):e103–11. doi:10.1111/j.1600-0838.2009.00920.x.
Ingalls CP, Warren GL, Armstrong RB. Dissociation of force production from MHC and actin contents in muscles injured by eccentric contractions. J Muscle Res Cell Motil. 1998;19(3):215–24.
McHugh MP, Connolly DA, Eston RG, et al. Electromyographic analysis of exercise resulting in symptoms of muscle damage. J Sports Sci. 2000;18(3):163–72. doi:10.1080/026404100365063.
Hortobagyi T, Houmard J, Fraser D, et al. Normal forces and myofibrillar disruption after repeated eccentric exercise. J Appl Physiol. 1998;84(2):492–8.
Tsatalas T, Giakas G, Spyropoulos G, et al. The effects of muscle damage on walking biomechanics are speed-dependent. Eur J Appl Physiol. 2010;110(5):977–88. doi:10.1007/s00421-010-1589-1.
Lovering RM, De Deyne PG. Contractile function, sarcolemma integrity, and the loss of dystrophin after skeletal muscle eccentric contraction-induced injury. Am J Physiol Cell Physiol. 2004;286(2):C230–8. doi:10.1152/ajpcell.00199.2003.
Skurvydas A, Sipaviciene S, Krutulyte G, et al. Dynamics of indirect symptoms of skeletal muscle damage after stretch-shortening exercise. J Electromyogr Kinesiol. 2006;16(6):629–36. doi:10.1016/j.jelekin.2005.11.002.
Jackman SR, Witard OC, Jeukendrup AE, et al. Branched-chain amino acid ingestion can ameliorate soreness from eccentric exercise. Med Sci Sports Exerc. 2010;42(5):962–70. doi:10.1249/MSS.0b013e3181c1b798.
Crameri RM, Aagaard P, Qvortrup K, et al. Myofibre damage in human skeletal muscle: effects of electrical stimulation versus voluntary contraction. J Physiol. 2007;583(Pt 1):365–80. doi:10.1113/jphysiol.2007.128827.
Jakeman JR, Byrne C, Eston RG. Efficacy of lower limb compression and combined treatment of manual massage and lower limb compression on symptoms of exercise-induced muscle damage in women. J Strength Cond Res. 2010;24(11):3157–65. doi:10.1519/JSC.0b013e3181e4f80c.
Jakeman JR, Byrne C, Eston RG. Lower limb compression garment improves recovery from exercise-induced muscle damage in young, active females. Eur J Appl Physiol. 2010;109(6):1137–44. doi:10.1007/s00421-010-1464-0.
Aminian-Far A, Hadian MR, Olyaei G, et al. Whole-body vibration and the prevention and treatment of delayed-onset muscle soreness. J Athl Train. 2011;46(1):43–9. doi:10.4085/1062-6050-46.1.43.
Chleboun GS, Howell JN, Conatser RR, et al. Relationship between muscle swelling and stiffness after eccentric exercise. Med Sci Sports Exerc. 1998;30(4):529–35.
McHugh MP, Connolly DA, Eston RG, et al. Electromyographic analysis of repeated bouts of eccentric exercise. J Sports Sci. 2001;19(3):163–70. doi:10.1080/026404101750095295.
Pizza FX, Baylies H, Mitchell JB. Adaptation to eccentric exercise: neutrophils and E-selectin during early recovery. Can J Appl Physiol. 2001;26(3):245–53.
McLoughlin TJ, Snyder AR, Brolinson PG, et al. Sensory level electrical muscle stimulation: effect on markers of muscle injury. Br J Sports Med. 2004;38(6):725–9. doi:10.1136/bjsm.2003.007401.
Brown SJ, Child RB, Day SH, et al. Indices of skeletal muscle damage and connective tissue breakdown following eccentric muscle contractions. Eur J Appl Physiol Occup Physiol. 1997;75(4):369–74. doi:10.1007/s004210050174.
Chapman DW, Newton M, McGuigan MR, et al. Comparison between old and young men for responses to fast velocity maximal lengthening contractions of the elbow flexors. Eur J Appl Physiol. 2008;104(3):531–9. doi:10.1007/s00421-008-0806-7.
Hilbert JE, Sforzo GA, Swensen T. The effects of massage on delayed onset muscle soreness. Br J Sports Med. 2003;37(1):72–5.
Skurvydas A, Brazaitis M, Kamandulis S. Prolonged muscle damage depends on force variability. Int J Sports Med. 2010;31(2):77–81. doi:10.1055/s-0029-1241213.
Prasartwuth O, Allen TJ, Butler JE, et al. Length-dependent changes in voluntary activation, maximum voluntary torque and twitch responses after eccentric damage in humans. J Physiol. 2006;571(Pt 1):243–52. doi:10.1113/jphysiol.2005.101600.
Nosaka K, Sakamoto K, Newton M, et al. Influence of pre-exercise muscle temperature on responses to eccentric exercise. J Athl Train. 2004;39(2):132–7.
Skurvydas A, Brazaitis M, Kamandulis S, et al. Muscle damaging exercise affects isometric force fluctuation as well as intraindividual variability of cognitive function. J Mot Behav. 2010;42(3):179–86. doi:10.1080/00222891003751835.
Day SH, Donnelly AE, Brown SJ, et al. Electromyogram activity and mean power frequency in exercise-damaged human muscle. Muscle Nerve. 1998;21(7):961–3.
Buford TW, Cooke MB, Redd LL, et al. Protease supplementation improves muscle function after eccentric exercise. Med Sci Sports Exerc. 2009;41(10):1908–14. doi:10.1249/MSS.0b013e3181a518f0.
Paddon-Jones D, Keech A, Lonergan A, et al. Differential expression of muscle damage in humans following acute fast and slow velocity eccentric exercise. J Sci Med Sport. 2005;8(3):255–63.
Warren GL, Hulderman T, Jensen N, et al. Physiological role of tumor necrosis factor alpha in traumatic muscle injury. FASEB J. 2002;16(12):1630–2. doi:10.1096/fj.02-0187fje.
Miyama M, Nosaka K. Protection against muscle damage following fifty drop jumps conferred by ten drop jumps. J Strength Cond Res. 2007;21(4):1087–92. doi:10.1519/R-21056.1.
Corona BT, Rouviere C, Hamilton SL, et al. FKBP12 deficiency reduces strength deficits after eccentric contraction-induced muscle injury. J Appl Physiol. 2008;105(2):527–37. doi:10.1152/japplphysiol.01145.2007.
Mackey AL, Donnelly AE, Turpeenniemi-Hujanen T, et al. Skeletal muscle collagen content in humans after high-force eccentric contractions. J Appl Physiol. 2004;97(1):197–203. doi:10.1152/japplphysiol.01174.2003.
Child RB, Brown SJ, Day SH, et al. Manipulation of knee extensor force using percutaneous electrical myostimulation during eccentric actions: effects on indices of muscle damage in humans. Int J Sports Med. 1998;19(7):468–73. doi:10.1055/s-2007-971946.
Lockhart NC, Baar K, Mazzeo RS, et al. Activation of Akt as a potential mediator of adaptations that reduce muscle injury. Med Sci Sports Exerc. 2006;38(6):1058–64. doi:10.1249/01.mss.0000222832.43520.27.
Chatzinikolaou A, Fatouros IG, Gourgoulis V, et al. Time course of changes in performance and inflammatory responses after acute plyometric exercise. J Strength Cond Res. 2010;24(5):1389–98. doi:10.1519/JSC.0b013e3181d1d318.
McHugh MP, Nesse M. Effect of stretching on strength loss and pain after eccentric exercise. Med Sci Sports Exerc. 2008;40(3):566–73. doi:10.1249/MSS.0b013e31815d2f8c.
Warren GL, Summan M, Gao X, et al. Mechanisms of skeletal muscle injury and repair revealed by gene expression studies in mouse models. J Physiol. 2007;582(Pt 2):825–41. doi:10.1113/jphysiol.2007.132373.
Kinugasa R, Kuchiki K, Tono T, et al. Superficial cooling inhibits force loss in damaged muscle. Int J Sports Med. 2008;29(9):726–31. doi:10.1055/s-2008-1038345.
Racz IB, Illyes G, Sarkadi L, et al. The functional and morphological damage of ischemic reperfused skeletal muscle. Eur Surg Res. 1997;29(4):254–63.
Paddon-Jones D, Muthalib M, Jenkins D. The effects of a repeated bout of eccentric exercise on indices of muscle damage and delayed onset muscle soreness. J Sci Med Sport. 2000;3(1):35–43.
Kamandulis S, Skurvydas A, Brazaitis M, et al. The repeated bout effect of eccentric exercise is not associated with changes in voluntary activation. Eur J Appl Physiol. 2010;108(6):1065–74. doi:10.1007/s00421-009-1219-y.
Sayers SP, Clarkson PM. Force recovery after eccentric exercise in males and females. Eur J Appl Physiol. 2001;84(1–2):122–6. doi:10.1007/s004210000346.
Teague BN, Schwane JA. Effect of intermittent eccentric contractions on symptoms of muscle microinjury. Med Sci Sports Exerc. 1995;27(10):1378–84.
Gulbin JP, Gaffney PT. Identical twins are discordant for markers of eccentric exercise-induced muscle damage. Int J Sports Med. 2002;23(7):471–6. doi:10.1055/s-2002-35076.
McHugh MP, Tetro DT. Changes in the relationship between joint angle and torque production associated with the repeated bout effect. J Sports Sci. 2003;21(11):927–32. doi:10.1080/0264041031000140400.
Harrison AJ, Gaffney SD. Effects of muscle damage on stretch-shortening cycle function and muscle stiffness control. J Strength Cond Res. 2004;18(4):771–6. doi:10.1519/14343.1.
Ingalls CP, Warren GL, Williams JH, et al. E-C coupling failure in mouse EDL muscle after in vivo eccentric contractions. J Appl Physiol. 1998;85(1):58–67.
Ring SM, Dannecker EA, Peterson CA. Vitamin D status is not associated with outcomes of experimentally-induced muscle weakness and pain in young, healthy volunteers. J Nutr Metab. 2010;2010:674240. doi:10.1155/2010/674240.
Kilmer DD, Aitkens SG, Wright NC, et al. Response to high-intensity eccentric muscle contractions in persons with myopathic disease. Muscle Nerve. 2001;24(9):1181–7.
Nottle C, Nosaka K. Changes in power assessed by the Wingate Anaerobic Test following downhill running. J Strength Cond Res. 2007;21(1):145–50. doi:10.1519/R-17425.1.
Eston RG, Finney S, Baker S, et al. Muscle tenderness and peak torque changes after downhill running following a prior bout of isokinetic eccentric exercise. J Sports Sci. 1996;14(4):291–9. doi:10.1080/02640419608727714.
Gibala MJ, MacDougall JD, Tarnopolsky MA, et al. Changes in human skeletal muscle ultrastructure and force production after acute resistance exercise. J Appl Physiol. 1995;78(2):702–8.
Saxton JM, Donnelly AE. Length-specific impairment of skeletal muscle contractile function after eccentric muscle actions in man. Clin Sci (Lond). 1996;90(2):119–25.
Hedayatpour N, Falla D, Arendt-Nielsen L, et al. Effect of delayed-onset muscle soreness on muscle recovery after a fatiguing isometric contraction. Scand J Med Sci Sports. 2010;20(1):145–53. doi:10.1111/j.1600-0838.2008.00866.x.
McHugh MP, Pasiakos S. The role of exercising muscle length in the protective adaptation to a single bout of eccentric exercise. Eur J Appl Physiol. 2004;93(3):286–93. doi:10.1007/s00421-004-1196-0.
Cleak MJ, Eston RG. Muscle soreness, swelling, stiffness and strength loss after intense eccentric exercise. Br J Sports Med. 1992;26(4):267–72.
Fredsted A, Clausen T, Overgaard K. Effects of step exercise on muscle damage and muscle Ca2+ content in men and women. J Strength Cond Res. 2008;22(4):1136–46. doi:10.1519/JSC.0b013e318173db9b.
Bottas R, Miettunen K, Komi PV, et al. Disturbed motor control of rhythmic movement at 2 h and delayed after maximal eccentric actions. J Electromyogr Kinesiol. 2010;20(4):608–18. doi:10.1016/j.jelekin.2009.11.010.
Paddon-Jones D, Keech A, Jenkins D. Short-term beta-hydroxy-beta-methylbutyrate supplementation does not reduce symptoms of eccentric muscle damage. Int J Sport Nutr Exerc Metab. 2001;11(4):442–50.
Park ND, Maresca RD, McKibans KI, et al. Caffeines enhancement of maximal voluntary strength and activation in uninjured but not injured muscle. Int J Sport Nutr Exerc Metab. 2008;18(6):639–52.
Brown SJ, Child RB, Donnelly AE, et al. Changes in human skeletal muscle contractile function following stimulated eccentric exercise. Eur J Appl Physiol Occup Physiol. 1996;72(5–6):515–21.
Nosaka K, Clarkson PM. Influence of previous concentric exercise on eccentric exercise-induced muscle damage. J Sports Sci. 1997;15(5):477–83. doi:10.1080/026404197367119.
Lee J, Goldfarb AH, Rescino MH, et al. Eccentric exercise effect on blood oxidative-stress markers and delayed onset of muscle soreness. Med Sci Sports Exerc. 2002;34(3):443–8.
Warren JA, Jenkins RR, Packer L, et al. Elevated muscle vitamin E does not attenuate eccentric exercise-induced muscle injury. J Appl Physiol. 1992;72(6):2168–75.
Paddon-Jones D, Abernethy PJ. Acute adaptation to low volume eccentric exercise. Med Sci Sports Exerc. 2001;33(7):1213–9.
Geronilla KB, Miller GR, Mowrey KF, et al. Dynamic force responses of skeletal muscle during stretch-shortening cycles. Eur J Appl Physiol. 2003;90(1–2):144–53. doi:10.1007/s00421-003-0849-8.
Nottle C, Nosaka K. The magnitude of muscle damage induced by downhill backward walking. J Sci Med Sport. 2005;8(3):264–73.
Brooks SV. Rapid recovery following contraction-induced injury to in situ skeletal muscles in mdx mice. J Muscle Res Cell Motil. 1998;19(2):179–87.
Zainuddin Z, Sacco P, Newton M, et al. Light concentric exercise has a temporarily analgesic effect on delayed-onset muscle soreness, but no effect on recovery from eccentric exercise. Appl Physiol Nutr Metab. 2006;31(2):126–34. doi:10.1139/h05-010.
Nosaka K, Newton M, Sacco P, et al. Partial protection against muscle damage by eccentric actions at short muscle lengths. Med Sci Sports Exerc. 2005;37(5):746–53.
Saxton JM, Donnelly AE. Light concentric exercise during recovery from exercise-induced muscle damage. Int J Sports Med. 1995;16(6):347–51. doi:10.1055/s-2007-973018.
Hubal MJ, Devaney JM, Hoffman EP, et al. CCL2 and CCR2 polymorphisms are associated with markers of exercise-induced skeletal muscle damage. J Appl Physiol. 2010;108(6):1651–8. doi:10.1152/japplphysiol.00361.2009.
Miyama M, Nosaka K. Influence of surface on muscle damage and soreness induced by consecutive drop jumps. J Strength Cond Res. 2004;18(2):206–11. doi:10.1519/R-13353.1.
Donnelly AE, Maughan RJ, Whiting PH. Effects of ibuprofen on exercise-induced muscle soreness and indices of muscle damage. Br J Sports Med. 1990;24(3):191–5.
Chapman DW, Newton MJ, Zainuddin Z, et al. Work and peak torque during eccentric exercise do not predict changes in markers of muscle damage. Br J Sports Med. 2008;42(7):585–91. doi:10.1136/bjsm.2007.037929.
Prasartwuth O, Taylor JL, Gandevia SC. Maximal force, voluntary activation and muscle soreness after eccentric damage to human elbow flexor muscles. J Physiol. 2005;567(Pt 1):337–48. doi:10.1113/jphysiol.2005.087767.
Jakeman JR, Macrae R, Eston R. A single 10-min bout of cold-water immersion therapy after strenuous plyometric exercise has no beneficial effect on recovery from the symptoms of exercise-induced muscle damage. Ergonomics. 2009;52(4):456–60. doi:10.1080/00140130802707733.
Nosaka K, Chapman D, Newton M, et al. Is isometric strength loss immediately after eccentric exercise related to changes in indirect markers of muscle damage? Appl Physiol Nutr Metab. 2006;31(3):313–9. doi:10.1139/h06-005.
Hammond JW, Hinton RY, Curl LA, et al. Use of autologous platelet-rich plasma to treat muscle strain injuries. Am J Sports Med. 2009;37(6):1135–42. doi:10.1177/0363546508330974.
Chen TC, Hsieh SS. The effects of repeated maximal voluntary isokinetic eccentric exercise on recovery from muscle damage. Res Q Exerc Sport. 2000;71(3):260–6. doi:10.1080/02701367.2000.10608906.
Davies RC, Rowlands AV, Poole DC, et al. Eccentric exercise-induced muscle damage dissociates the lactate and gas exchange thresholds. J Sports Sci. 2011;29(2):181–9. doi:10.1080/02640414.2010.526626.
Martin V, Millet GY, Lattier G, et al. Effects of recovery modes after knee extensor muscles eccentric contractions. Med Sci Sports Exerc. 2004;36(11):1907–15.
Clarkson PM, Nosaka K, Braun B. Muscle function after exercise-induced muscle damage and rapid adaptation. Med Sci Sports Exerc. 1992;24(5):512–20.
Mekjavic IB, Exner JA, Tesch PA, et al. Hyperbaric oxygen therapy does not affect recovery from delayed onset muscle soreness. Med Sci Sports Exerc. 2000;32(3):558–63.
Ingalls CP, Warren GL, Zhang JZ, et al. Dihydropyridine and ryanodine receptor binding after eccentric contractions in mouse skeletal muscle. J Appl Physiol. 2004;96(5):1619–25. doi:10.1152/japplphysiol.00084.2003.
Milias GA, Nomikos T, Fragopoulou E, et al. Effects of eccentric exercise-induced muscle injury on blood levels of platelet activating factor (PAF) and other inflammatory markers. Eur J Appl Physiol. 2005;95(5–6):504–13. doi:10.1007/s00421-005-0031-6.
Starbuck C, Eston RG. Exercise-induced muscle damage and the repeated bout effect: evidence for cross transfer. Eur J Appl Physiol. 2012;112(3):1005–13. doi:10.1007/s00421-011-2053-6.
Black CD, McCully KK. Muscle injury after repeated bouts of voluntary and electrically stimulated exercise. Med Sci Sports Exerc. 2008;40(9):1605–15. doi:10.1249/MSS.0b013e3181788dbe.
Donnelly AE, Clarkson PM, Maughan RJ. Exercise-induced muscle damage: effects of light exercise on damaged muscle. Eur J Appl Physiol Occup Physiol. 1992;64(4):350–3.
Byrne C, Eston R. The effect of exercise-induced muscle damage on isometric and dynamic knee extensor strength and vertical jump performance. J Sports Sci. 2002;20(5):417–25. doi:10.1080/026404102317366672.
Koh TJ, Brooks SV. Lengthening contractions are not required to induce protection from contraction-induced muscle injury. Am J Physiol Regul Integr Comp Physiol. 2001;281(1):R155–61.
Barroso R, Roschel H, Ugrinowitsch C, et al. Effect of eccentric contraction velocity on muscle damage in repeated bouts of elbow flexor exercise. Appl Physiol Nutr Metab. 2010;35(4):534–40. doi:10.1139/H10-042.
Michaut A, Pousson M, Ballay Y, et al. Short-term changes in the series elastic component after an acute eccentric exercise of the elbow flexors. Eur J Appl Physiol. 2001;84(6):569–74.
Chen TC, Nosaka K. Responses of elbow flexors to two strenuous eccentric exercise bouts separated by three days. J Strength Cond Res. 2006;20(1):108–16. doi:10.1519/R-16634.1.
Chen TC, Hsieh SS. Effects of a 7-day eccentric training period on muscle damage and inflammation. Med Sci Sports Exerc. 2001;33(10):1732–8.
Hamlin MJ, Quigley BM. Quadriceps concentric and eccentric exercise 2: differences in muscle strength, fatigue and EMG activity in eccentrically-exercised sore and non-sore muscles. J Sci Med Sport. 2001;4(1):104–15.
Hutchins MO, Skjonsby HS, Brazeau GA, et al. Weakness in mouse masticatory muscles by repetitive contractions with forced lengthening. J Dent Res. 1995;74(2):642–8.
Davies RC, Rowlands AV, Eston RG. Effect of exercise-induced muscle damage on ventilatory and perceived exertion responses to moderate and severe intensity cycle exercise. Eur J Appl Physiol. 2009;107(1):11–9. doi:10.1007/s00421-009-1094-6.
Kerksick CM, Kreider RB, Willoughby DS. Intramuscular adaptations to eccentric exercise and antioxidant supplementation. Amino Acids. 2010;39(1):219–32. doi:10.1007/s00726-009-0432-7.
Hubal MJ, Rubinstein SR, Clarkson PM. Mechanisms of variability in strength loss after muscle-lengthening actions. Med Sci Sports Exerc. 2007;39(3):461–8. doi:10.1249/01.mss.0000247007.19127.da.
Black CD, Elder CP, Gorgey A, et al. High specific torque is related to lengthening contraction-induced skeletal muscle injury. J Appl Physiol. 2008;104(3):639–47. doi:10.1152/japplphysiol.00322.2007.
Balnave CD, Thompson MW. Effect of training on eccentric exercise-induced muscle damage. J Appl Physiol. 1993;75(4):1545–51.
Nosaka K, Newton M. Is recovery from muscle damage retarded by a subsequent bout of eccentric exercise inducing larger decreases in force? J Sci Med Sport. 2002;5(3):204–18.
Savage KJ, Clarkson PM. Oral contraceptive use and exercise-induced muscle damage and recovery. Contraception. 2002;66(1):67–71.
Chen TC. Effects of a second bout of maximal eccentric exercise on muscle damage and electromyographic activity. Eur J Appl Physiol. 2003;89(2):115–21. doi:10.1007/s00421-002-0791-1.
Nguyen D, Brown LE, Coburn JW, et al. Effect of delayed-onset muscle soreness on elbow flexion strength and rate of velocity development. J Strength Cond Res. 2009;23(4):1282–6. doi:10.1519/JSC.0b013e3181970017.
Newton MJ, Morgan GT, Sacco P, et al. Comparison of responses to strenuous eccentric exercise of the elbow flexors between resistance-trained and untrained men. J Strength Cond Res. 2008;22(2):597–607. doi:10.1519/JSC.0b013e3181660003.
Vissing K, Overgaard K, Nedergaard A, et al. Effects of concentric and repeated eccentric exercise on muscle damage and calpain-calpastatin gene expression in human skeletal muscle. Eur J Appl Physiol. 2008;103(3):323–32. doi:10.1007/s00421-008-0709-7.
Stupka N, Tarnopolsky MA, Yardley NJ, et al. Cellular adaptation to repeated eccentric exercise-induced muscle damage. J Appl Physiol. 2001;91(4):1669–78.
Black CD, McCully KK. Force per active area and muscle injury during electrically stimulated contractions. Med Sci Sports Exerc. 2008;40(9):1596–604. doi:10.1249/MSS.0b013e3181757182.
Bloomer RJ, Falvo MJ, Schilling BK, et al. Prior exercise and antioxidant supplementation: effect on oxidative stress and muscle injury. J Int Soc Sports Nutr. 2007;4:9. doi:10.1186/1550-2783-4-9.
Chapman DW, Newton M, McGuigan M, et al. Effect of lengthening contraction velocity on muscle damage of the elbow flexors. Med Sci Sports Exerc. 2008;40(5):926–33. doi:10.1249/MSS.0b013e318168c82d.
Newham DJ, Jones DA, Ghosh G, et al. Muscle fatigue and pain after eccentric contractions at long and short length. Clin Sci (Lond). 1988;74(5):553–7.
Lowe DA, Warren GL, Ingalls CP, et al. Muscle function and protein metabolism after initiation of eccentric contraction-induced injury. J Appl Physiol. 1995;79(4):1260–70.
Lavender AP, Nosaka K. Comparison between old and young men for changes in makers of muscle damage following voluntary eccentric exercise of the elbow flexors. Appl Physiol Nutr Metab. 2006;31(3):218–25. doi:10.1139/h05-028.
Rawson ES, Gunn B, Clarkson PM. The effects of creatine supplementation on exercise-induced muscle damage. J Strength Cond Res. 2001;15(2):178–84.
Byrne C, Eston RG, Edwards RH. Characteristics of isometric and dynamic strength loss following eccentric exercise-induced muscle damage. Scand J Med Sci Sports. 2001;11(3):134–40.
Turner TS, Tucker KJ, Rogasch NC, et al. Impaired neuromuscular function during isometric, shortening, and lengthening contractions after exercise-induced damage to elbow flexor muscles. J Appl Physiol. 2008;105(2):502–9. doi:10.1152/japplphysiol.90421.2008.
Barnes JN, Trombold JR, Dhindsa M, et al. Arterial stiffening following eccentric exercise-induced muscle damage. J Appl Physiol. 2010;109(4):1102–8. doi:10.1152/japplphysiol.00548.2010.
Peake JM, Nosaka K, Muthalib M, et al. Systemic inflammatory responses to maximal versus submaximal lengthening contractions of the elbow flexors. Exerc Immunol Rev. 2006;12:72–85.
Miles MP, Andring JM, Pearson SD, et al. Diurnal variation, response to eccentric exercise, and association of inflammatory mediators with muscle damage variables. J Appl Physiol. 2008;104(2):451–8. doi:10.1152/japplphysiol.00572.2007.
Nosaka K, Newton M, Sacco P. Muscle damage and soreness after endurance exercise of the elbow flexors. Med Sci Sports Exerc. 2002;34(6):920–7.
Mair J, Koller A, Artner-Dworzak E, et al. Effects of exercise on plasma myosin heavy chain fragments and MRI of skeletal muscle. J Appl Physiol. 1992;72(2):656–63.
Buckley JD, Thomson RL, Coates AM, et al. Supplementation with a whey protein hydrolysate enhances recovery of muscle force-generating capacity following eccentric exercise. J Sci Med Sport. 2010;13(1):178–81. doi:10.1016/j.jsams.2008.06.007.
Ahmadi S, Sinclair PJ, Davis GM. Muscle oxygenation after downhill walking-induced muscle damage. Clin Physiol Funct Imaging. 2008;28(1):55–63. doi:10.1111/j.1475-097X.2007.00777.x.
Saxton JM, Clarkson PM, James R, et al. Neuromuscular dysfunction following eccentric exercise. Med Sci Sports Exerc. 1995;27(8):1185–93.
Rinard J, Clarkson PM, Smith LL, et al. Response of males and females to high-force eccentric exercise. J Sports Sci. 2000;18(4):229–36. doi:10.1080/026404100364965.
Chapman D, Newton M, Sacco P, et al. Greater muscle damage induced by fast versus slow velocity eccentric exercise. Int J Sports Med. 2006;27(8):591–8. doi:10.1055/s-2005-865920.
Nosaka K, Clarkson PM. Effect of eccentric exercise on plasma enzyme activities previously elevated by eccentric exercise. Eur J Appl Physiol Occup Physiol. 1994;69(6):492–7.
Dartnall TJ, Rogasch NC, Nordstrom MA, et al. Eccentric muscle damage has variable effects on motor unit recruitment thresholds and discharge patterns in elbow flexor muscles. J Neurophysiol. 2009;102(1):413–23. doi:10.1152/jn.91285.2008.
Nosaka K, Newton MJ, Sacco P. Attenuation of protective effect against eccentric exercise-induced muscle damage. Can J Appl Physiol. 2005;30(5):529–42.
Nikolaidis MG, Paschalis V, Giakas G, et al. Decreased blood oxidative stress after repeated muscle-damaging exercise. Med Sci Sports Exerc. 2007;39(7):1080–9. doi:10.1249/mss.0b013e31804ca10c.
Rader EP, Song W, Van Remmen H, et al. Raising the antioxidant levels within mouse muscle fibres does not affect contraction-induced injury. Exp Physiol. 2006;91(4):781–9. doi:10.1113/expphysiol.2005.033043.
Howatson G, Gaze D, van Someren KA. The efficacy of ice massage in the treatment of exercise-induced muscle damage. Scand J Med Sci Sports. 2005;15(6):416–22. doi:10.1111/j.1600-0838.2005.00437.x.
Close GL, Ashton T, Cable T, et al. Eccentric exercise, isokinetic muscle torque and delayed onset muscle soreness: the role of reactive oxygen species. Eur J Appl Physiol. 2004;91(5–6):615–21. doi:10.1007/s00421-003-1012-2.
Chapman DW, Newton MJ, McGuigan MR, et al. Effect of slow-velocity lengthening contractions on muscle damage induced by fast-velocity lengthening contractions. J Strength Cond Res. 2011;25(1):211–9. doi:10.1519/JSC.0b013e3181bac2bd.
Madden MC, Byrnes WC, Lebin JA, et al. Plasma matrix metalloproteinase-9 response to eccentric exercise of the elbow flexors. Eur J Appl Physiol. 2011;111(8):1795–805. doi:10.1007/s00421-010-1806-y.
Ahmadi S, Sinclair PJ, Foroughi N, et al. Monitoring muscle oxygenation after eccentric exercise-induced muscle damage using near-infrared spectroscopy. Appl Physiol Nutr Metab. 2008;33(4):743–52. doi:10.1139/h08-048.
Paddon-Jones DJ, Quigley BM. Effect of cryotherapy on muscle soreness and strength following eccentric exercise. Int J Sports Med. 1997;18(8):588–93. doi:10.1055/s-2007-972686.
Nosaka K, Newton M, Sacco P. Responses of human elbow flexor muscles to electrically stimulated forced lengthening exercise. Acta Physiol Scand. 2002;174(2):137–45. doi:10.1046/j.1365-201X.2002.00936.x.
Kamandulis S, Skurvydas A, Masiulis N, et al. The decrease in electrically evoked force production is delayed by a previous bout of stretch-shortening cycle exercise. Acta Physiol (Oxf). 2010;198(1):91–8. doi:10.1111/j.1748-1716.2009.02041.x.
Nosaka K, Clarkson PM. Changes in plasma zinc following high force eccentric exercise. Int J Sport Nutr. 1992;2(2):175–84.
Chen TC, Chen HL, Lin MJ, et al. Potent protective effect conferred by four bouts of low-intensity eccentric exercise. Med Sci Sports Exerc. 2010;42(5):1004–12. doi:10.1249/MSS.0b013e3181c0a818.
Muthalib M, Lee H, Millet GY, et al. Comparison between maximal lengthening and shortening contractions for biceps brachii muscle oxygenation and hemodynamics. J Appl Physiol. 2010;109(3):710–20. doi:10.1152/japplphysiol.01297.2009.
Linnamo V, Bottas R, Komi PV. Force and EMG power spectrum during and after eccentric and concentric fatigue. J Electromyogr Kinesiol. 2000;10(5):293–300.
Dundon JM, Cirillo J, Semmler JG. Low-frequency fatigue and neuromuscular performance after exercise-induced damage to elbow flexor muscles. J Appl Physiol. 2008;105(4):1146–55. doi:10.1152/japplphysiol.01339.2007.
Tokmakidis SP, Kokkinidis EA, Smilios I, et al. The effects of ibuprofen on delayed muscle soreness and muscular performance after eccentric exercise. J Strength Cond Res. 2003;17(1):53–9.
Nosaka K, Newton M. Difference in the magnitude of muscle damage between maximal and submaximal eccentric loading. J Strength Cond Res. 2002;16(2):202–8.
Jonhagen S, Ackermann P, Eriksson T, et al. Sports massage after eccentric exercise. Am J Sports Med. 2004;32(6):1499–503. doi:10.1177/0363546503262196.
Nosaka K, Newton M, Sacco P. Delayed-onset muscle soreness does not reflect the magnitude of eccentric exercise-induced muscle damage. Scand J Med Sci Sports. 2002;12(6):337–46.
Dartnall TJ, Nordstrom MA, Semmler JG. Motor unit synchronization is increased in biceps brachii after exercise-induced damage to elbow flexor muscles. J Neurophysiol. 2008;99(2):1008–19. doi:10.1152/jn.00686.2007.
Lauritzen F, Paulsen G, Raastad T, et al. Gross ultrastructural changes and necrotic fiber segments in elbow flexor muscles after maximal voluntary eccentric action in humans. J Appl Physiol. 2009;107(6):1923–34. doi:10.1152/japplphysiol.00148.2009.
Lavender AP, Nosaka K. Changes in markers of muscle damage of middle-aged and young men following eccentric exercise of the elbow flexors. J Sci Med Sport. 2008;11(2):124–31. doi:10.1016/j.jsams.2006.11.004.
Sbriccoli P, Felici F, Rosponi A, et al. Exercise induced muscle damage and recovery assessed by means of linear and non-linear sEMG analysis and ultrasonography. J Electromyogr Kinesiol. 2001;11(2):73–83.
Bryer SC, Goldfarb AH. Effect of high dose vitamin C supplementation on muscle soreness, damage, function, and oxidative stress to eccentric exercise. Int J Sport Nutr Exerc Metab. 2006;16(3):270–80.
Byrne C, Eston R. Maximal-intensity isometric and dynamic exercise performance after eccentric muscle actions. J Sports Sci. 2002;20(12):951–9. doi:10.1080/026404102321011706.
Chen TC. Variability in muscle damage after eccentric exercise and the repeated bout effect. Res Q Exerc Sport. 2006;77(3):362–71. doi:10.1080/02701367.2006.10599370.
Faulkner JA, Jones DA, Round JM. Injury to skeletal muscles of mice by forced lengthening during contractions. Q J Exp Physiol. 1989;74(5):661–70.
van Someren KA, Edwards AJ, Howatson G. Supplementation with beta-hydroxy-beta-methylbutyrate (HMB) and alpha-ketoisocaproic acid (KIC) reduces signs and symptoms of exercise-induced muscle damage in man. Int J Sport Nutr Exerc Metab. 2005;15(4):413–24.
Chen TC, Chen HL, Lin MJ, et al. Muscle damage responses of the elbow flexors to four maximal eccentric exercise bouts performed every 4 weeks. Eur J Appl Physiol. 2009;106(2):267–75. doi:10.1007/s00421-009-1016-7.
Lavender AP, Nosaka K. A light load eccentric exercise confers protection against a subsequent bout of more demanding eccentric exercise. J Sci Med Sport. 2008;11(3):291–8. doi:10.1016/j.jsams.2007.03.005.
Kyparos A, Matziari C, Albani M, et al. A decrease in soleus muscle force generation in rats after downhill running. Can J Appl Physiol. 2001;26(4):323–35.
Nosaka K, Sakamoto K, Newton M, et al. The repeated bout effect of reduced-load eccentric exercise on elbow flexor muscle damage. Eur J Appl Physiol. 2001;85(1–2):34–40.
McNeil CJ, Allman BL, Symons TB, et al. Torque loss induced by repetitive maximal eccentric contractions is marginally influenced by work-to-rest ratio. Eur J Appl Physiol. 2004;91(5–6):579–85. doi:10.1007/s00421-003-0996-y.
Piitulainen H, Komi P, Linnamo V, et al. Sarcolemmal excitability as investigated with M-waves after eccentric exercise in humans. J Electromyogr Kinesiol. 2008;18(4):672–81. doi:10.1016/j.jelekin.2007.01.004.
Warren GL, Hermann KM, Ingalls CP, et al. Decreased EMG median frequency during a second bout of eccentric contractions. Med Sci Sports Exerc. 2000;32(4):820–9.
Raastad T, Owe SG, Paulsen G, et al. Changes in calpain activity, muscle structure, and function after eccentric exercise. Med Sci Sports Exerc. 2010;42(1):86–95. doi:10.1249/MSS.0b013e3181ac7afa.
Chen TC, Nosaka K. Effects of number of eccentric muscle actions on first and second bouts of eccentric exercise of the elbow flexors. J Sci Med Sport. 2006;9(1–2):57–66. doi:10.1016/j.jsams.2006.03.012.
Lavender AP, Nosaka K. Responses of old men to repeated bouts of eccentric exercise of the elbow flexors in comparison with young men. Eur J Appl Physiol. 2006;97(5):619–26. doi:10.1007/s00421-006-0224-7.
Walker JA, Cerny FJ, Cotter JR, et al. Attenuation of contraction-induced skeletal muscle injury by bromelain. Med Sci Sports Exerc. 1992;24(1):20–5.
Reisman S, Allen TJ, Proske U. Changes in passive tension after stretch of unexercised and eccentrically exercised human plantarflexor muscles. Exp Brain Res. 2009;193(4):545–54. doi:10.1007/s00221-008-1657-5.
Brockett CL, Morgan DL, Proske U. Human hamstring muscles adapt to eccentric exercise by changing optimum length. Med Sci Sports Exerc. 2001;33(5):783–90.
Kaufman T, Burke JR, Davis JM, et al. Exercise-induced neuromuscular dysfunction under reflex conditions. Eur J Appl Physiol. 2001;84(6):510–20.
Nosaka K, Sakamoto K. Effect of elbow joint angle on the magnitude of muscle damage to the elbow flexors. Med Sci Sports Exerc. 2001;33(1):22–9.
Lavender AP, Nosaka K. Changes in fluctuation of isometric force following eccentric and concentric exercise of the elbow flexors. Eur J Appl Physiol. 2006;96(3):235–40. doi:10.1007/s00421-005-0069-5.
Murayama M, Nosaka K, Yoneda T, et al. Changes in hardness of the human elbow flexor muscles after eccentric exercise. Eur J Appl Physiol. 2000;82(5–6):361–7. doi:10.1007/s004210000242.
Green MS, Corona BT, Doyle JA, et al. Carbohydrate-protein drinks do not enhance recovery from exercise-induced muscle injury. Int J Sport Nutr Exerc Metab. 2008;18(1):1–18.
Paschalis V, Nikolaidis MG, Giakas G, et al. The effect of eccentric exercise on position sense and joint reaction angle of the lower limbs. Muscle Nerve. 2007;35(4):496–503. doi:10.1002/mus.20723.
Chen TC, Nosaka K, Wu CC. Effects of a 30-min running performed daily after downhill running on recovery of muscle function and running economy. J Sci Med Sport. 2008;11(3):271–9. doi:10.1016/j.jsams.2007.02.015.
Bowers EJ, Morgan DL, Proske U. Damage to the human quadriceps muscle from eccentric exercise and the training effect. J Sports Sci. 2004;22(11–12):1005–14.
Gleeson N, Eston R, Marginson V, et al. Effects of prior concentric training on eccentric exercise induced muscle damage. Br J Sports Med. 2003;37(2):119–25 (discussion 25).
Falvo MJ, Schilling BK, Bloomer RJ, et al. Efficacy of prior eccentric exercise in attenuating impaired exercise performance after muscle injury in resistance trained men. J Strength Cond Res. 2007;21(4):1053–60. doi:10.1519/R-21406.1.
Corona BT, Rouviere C, Hamilton SL, et al. Eccentric contractions do not induce rhabdomyolysis in malignant hyperthermia susceptible mice. J Appl Physiol. 2008;105(5):1542–53. doi:10.1152/japplphysiol.90926.2008.
Warren GL, Ingalls CP, Shah SJ, et al. Uncoupling of in vivo torque production from EMG in mouse muscles injured by eccentric contractions. J Physiol. 1999;515(Pt 2):609–19.
Semmler JG, Tucker KJ, Allen TJ, et al. Eccentric exercise increases EMG amplitude and force fluctuations during submaximal contractions of elbow flexor muscles. J Appl Physiol. 2007;103(3):979–89. doi:10.1152/japplphysiol.01310.2006.
Whitehead NP, Weerakkody NS, Gregory JE, et al. Changes in passive tension of muscle in humans and animals after eccentric exercise. J Physiol. 2001;533(Pt 2):593–604.
Paoni NF, Peale F, Wang F, et al. Time course of skeletal muscle repair and gene expression following acute hind limb ischemia in mice. Physiol Genomics. 2002;11(3):263–72. doi:10.1152/physiolgenomics.00110.2002.
Rowlands AV, Eston RG, Tilzey C. Effect of stride length manipulation on symptoms of exercise-induced muscle damage and the repeated bout effect. J Sports Sci. 2001;19(5):333–40. doi:10.1080/02640410152006108.
Cleary MA, Sitler MR, Kendrick ZV. Dehydration and symptoms of delayed-onset muscle soreness in normothermic men. J Athl Train. 2006;41(1):36–45.
Paulsen G, Lauritzen F, Bayer ML, et al. Subcellular movement and expression of HSP27, alphaB-crystallin, and HSP70 after two bouts of eccentric exercise in humans. J Appl Physiol. 2009;107(2):570–82. doi:10.1152/japplphysiol.00209.2009.
Crisco JJ, Jokl P, Heinen GT, et al. A muscle contusion injury model. Biomechanics, physiology, and histology. Am J Sports Med. 1994;22(5):702–10.
Paulsen G, Crameri R, Benestad HB, et al. Time course of leukocyte accumulation in human muscle after eccentric exercise. Med Sci Sports Exerc. 2010;42(1):75–85. doi:10.1249/MSS.0b013e3181ac7adb.
Newham DJ, Jones DA, Clarkson PM. Repeated high-force eccentric exercise: effects on muscle pain and damage. J Appl Physiol. 1987;63(4):1381–6.
Whitehead NP, Allen TJ, Morgan DL, et al. Damage to human muscle from eccentric exercise after training with concentric exercise. J Physiol. 1998;512(Pt 2):615–20.
Murphy RM, Goodman CA, McKenna MJ, et al. Calpain-3 is autolyzed and hence activated in human skeletal muscle 24 h following a single bout of eccentric exercise. J Appl Physiol. 2007;103(3):926–31. doi:10.1152/japplphysiol.01422.2006.
Child RB, Saxton JM, Donnelly AE. Comparison of eccentric knee extensor muscle actions at two muscle lengths on indices of damage and angle-specific force production in humans. J Sports Sci. 1998;16(4):301–8. doi:10.1080/02640419808559358.
Corona BT, Balog EM, Doyle JA, et al. Junctophilin damage contributes to early strength deficits and EC coupling failure after eccentric contractions. Am J Physiol Cell Physiol. 2010;298(2):C365–76. doi:10.1152/ajpcell.00365.2009.
Bloomer RJ, Goldfarb AH, McKenzie MJ, et al. Effects of antioxidant therapy in women exposed to eccentric exercise. Int J Sport Nutr Exerc Metab. 2004;14(4):377–88.
Larsen RG, Ringgaard S, Overgaard K. Localization and quantification of muscle damage by magnetic resonance imaging following step exercise in young women. Scand J Med Sci Sports. 2007;17(1):76–83. doi:10.1111/j.1600-0838.2006.00525.x.
Sesto ME, Radwin RG, Block WF, et al. Anatomical and mechanical changes following repetitive eccentric exertions. Clin Biomech (Bristol, Avon). 2005;20(1):41–9. doi:10.1016/j.clinbiomech.2004.09.002.
Staples JR, Clement DB, Taunton JE, et al. Effects of hyperbaric oxygen on a human model of injury. Am J Sports Med. 1999;27(5):600–5.
Nosaka K, Newton M. Repeated eccentric exercise bouts do not exacerbate muscle damage and repair. J Strength Cond Res. 2002;16(1):117–22.
Proske U, Gregory JE, Morgan DL, et al. Force matching errors following eccentric exercise. Hum Mov Sci. 2004;23(3–4):365–78. doi:10.1016/j.humov.2004.08.012.
Rodenburg JB, Bar PR, De Boer RW. Relations between muscle soreness and biochemical and functional outcomes of eccentric exercise. J Appl Physiol. 1993;74(6):2976–83.
Barash IA, Mathew L, Ryan AF, et al. Rapid muscle-specific gene expression changes after a single bout of eccentric contractions in the mouse. Am J Physiol Cell Physiol. 2004;286(2):C355–64. doi:10.1152/ajpcell.00211.2003.
Carter GT, Kikuchi N, Abresch RT, et al. Effects of exhaustive concentric and eccentric exercise on murine skeletal muscle. Arch Phys Med Rehabil. 1994;75(5):555–9.
Peters D, Barash IA, Burdi M, et al. Asynchronous functional, cellular and transcriptional changes after a bout of eccentric exercise in the rat. J Physiol. 2003;553(Pt 3):947–57. doi:10.1113/jphysiol.2003.048462.
Cutlip RG, Geronilla KB, Baker BA, et al. Impact of muscle length during stretch-shortening contractions on real-time and temporal muscle performance measures in rats in vivo. J Appl Physiol. 2004;96(2):507–16. doi:10.1152/japplphysiol.00046.2003.
Costello JT, Algar LA, Donnelly AE. Effects of whole-body cryotherapy (−110 degrees C) on proprioception and indices of muscle damage. Scand J Med Sci Sports. 2012;22(2):190–8. doi:10.1111/j.1600-0838.2011.01292.x.
Nakazato K, Ochi E, Waga T. Dietary apple polyphenols have preventive effects against lengthening contraction-induced muscle injuries. Mol Nutr Food Res. 2010;54(3):364–72. doi:10.1002/mnfr.200900145.
Shafat A, Butler P, Jensen RL, et al. Effects of dietary supplementation with vitamins C and E on muscle function during and after eccentric contractions in humans. Eur J Appl Physiol. 2004;93(1–2):196–202. doi:10.1007/s00421-004-1198-y.
Acknowledgments
We thank Samuel R. Coley, Jennifer L. Miller, Clint W. Satterfield, and Christopher D. Vlahos for their assistance in extracting study data during the early stages of our study.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Funding
No sources of funding were used to assist in the preparation of this article.
Conflicts of interest
Gordon Warren, Jarrod Call, Amy Farthing, and Bemene Baadom-Piaro declare that they have no conflicts of interest relevant to the content of this review.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Warren, G.L., Call, J.A., Farthing, A.K. et al. Minimal Evidence for a Secondary Loss of Strength After an Acute Muscle Injury: A Systematic Review and Meta-Analysis. Sports Med 47, 41–59 (2017). https://doi.org/10.1007/s40279-016-0528-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40279-016-0528-7