Abstract
Background and Objectives
The kidney is a major drug-eliminating organ. Renal impairment or concomitant use of transporter inhibitors may decrease active secretion and increase exposure to a drug that is a substrate of kidney secretory transporters. However, prediction of the effects of patient factors on kidney transporters remains challenging because of the multiplicity of transporters and the lack of understanding of their abundance and specificity. The objective of this study was to use physiologically based pharmacokinetic (PBPK) modelling to evaluate the effects of patient factors on kidney transporters.
Methods
Models for three renally cleared drugs (oseltamivir carboxylate, cidofovir and cefuroxime) were developed using a general PBPK platform, with the contributions of net basolateral uptake transport (Tup,b) and apical efflux transport (Teff,a) being specifically defined.
Results and Conclusion
We demonstrated the practical use of PBPK models to: (1) define transporter-mediated renal secretion, using plasma and urine data; (2) inform a change in the system-dependent parameter (≥10-fold reduction in the functional ‘proximal tubule cells per gram kidney’) in severe renal impairment that is responsible for the decreased secretory transport activities of test drugs; (3) derive an in vivo, plasma unbound inhibition constant of Tup,b by probenecid (≤1 μM), based on observed drug interaction data; and (4) suggest a plausible mechanism of probenecid preferentially inhibiting Tup,b in order to alleviate cidofovir-induced nephrotoxicity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Despite their often secondary role, compared with the liver’s capacity to eliminate drugs, the kidneys should not be overlooked. In fact, approximately 30 % of approved drugs show renal clearance as their main route of elimination [1, 2].
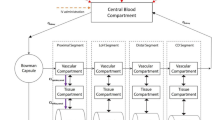
Renal clearance is a net result of glomerular filtration, reabsorption and secretion. Secretion is the transport of substances from the renal blood to the lumen of the nephron. It occurs predominantly in the proximal tubules, via transporters on the basolateral and apical membranes to facilitate the uptake and efflux, respectively, of substances into urine. Using a generic physiologically based pharmacokinetic (PBPK) model structure (Fig. 1), one can visualize the contributions of both passive and active processes in drug movement across the basolateral membrane (between blood and cells) and apical membrane (between cells and urine) of a proximal tubule epithelial cell to drug distribution and elimination in the kidneys.
Passive and active processes of drug movement across the basolateral and apical membranes of kidney proximal tubule cells. a For all drug models in this study, a full physiologically based pharmacokinetic (PBPK) model in Simcyp Simulator® was used. The kidney compartment used a ‘mechanistic kidney module’ with major transporters [1], which has been simplified in the figure with urine, tubule cell and blood compartments to illustrate the three major renal clearance processes: passive diffusion clearance (CLpd, on both membranes), net uptake of the drug into tubule cells from the blood (intrinsic transporter clearance, CLint,T), and net efflux of drug into the urine from the cells (efflux intrinsic transporter clearance, CLint,efflux). b Net basolateral uptake and apical efflux are represented by ‘lumped’ transporter processes Tup,b and Teff,a; each is composed of different transporters that move drugs in different directions at each side of the tubular cell. ADME absorption, distribution, metabolism, and excretion, B/P blood to plasma partition ratio, CLint,T,eff efflux transporter-mediated intrinsic clearance, CLint,T,up uptake transporter-mediated intrinsic clearance, CLiv in vivo clearance, CLr renal clearance, CLr,T renal clearance mediated by a transporter, fa fraction available from dosage form, fu,p fraction unbound in plasma, ka first-order absorption rate constant, LogP partition coefficient, MW molecular weight, Peff,man effective permeability, pKa dissociation constant, Vss volume of distribution at steady state
Renal clearance of drugs may be significantly affected by intrinsic and extrinsic patient factors, such as renal impairment and/or drug–drug interactions (DDIs). When active secretion represents a major contributor to a drug’s total clearance, the effects of these patient factors on renal transporter function and overall renal clearance can cause significant changes in the disposition of the affected drug.
The objective of this study was to explore the utility of PBPK modelling to evaluate the effects of renal impairment and transporter-interacting drugs on drug exposure and safety. Specifically, we aimed to (1) demonstrate the use of PBPK to model renal active secretion by transporters; (2) explore how a system-dependent parameter may be associated with renal impairment; (3) evaluate the utility of PBPK to predict the effect of competitive transporter inhibition via the interacting drug probenecid on the pharmacokinetics of three renally eliminated drugs; and (4) identify the roles of renal transporters and inhibitors in nephrotoxicity associated with renally cleared drugs.
2 Methods
2.1 Model Drugs
PBPK models of oseltamivir carboxylate, cidofovir and cefuroxime were built using the population-based PBPK software Simcyp Simulator® (version 12.1; Simcyp Ltd, Sheffield, UK). All three drugs are predominantly renally cleared (cidofovir ~90 %) or exclusively renally cleared (oseltamivir carboxylate and cefuroxime ~100 %) (see Table 1).
Drug-dependent parameters for oseltamivir carboxylate, cidofovir and cefuroxime PBPK models were derived from a variety of sources (Table 1). In addition to in vitro and in vivo data, in silico predictions of certain physicochemical properties, including the partition coefficient (LogP), compound type, dissociation constant (pKa) and blood to plasma partition ratio (B/P), were made using data from the following publicly available sources: ChemSpider, the free chemical database (http://www.chemspider.com; Royal Society of Chemistry, Cambridge, UK), ADMET Predictor™ version 6 (Simulations Plus, Inc., Lancaster, CA, USA) and PubChem (http://pubchem.ncbi.nlm.nih.gov; National Institutes of Health, Bethesda, MD, USA). Distribution parameters, including the volume of distribution at steady state (Vss) and tissue-to-plasma partition coefficient (Kp), were predicted [3, 4] and, if necessary, optimized using the Kp scalar function based on cited in vivo human data. Cidofovir and cefuroxime were both dosed intravenously, whereas oseltamivir carboxylate, the active metabolite, was formed from orally administered oseltamivir phosphate. To approximate the rate and extent of the appearance of oseltamivir carboxylate in plasma, oral parameters fa (fraction absorbed) and ka (first-order absorption rate constant) were used to represent the rate and extent of conversion from the parent drug to oseltamivir carboxylate. Detailed PBPK model development for each substrate can be found in the Electronic Supplementary Material, including the use of various techniques (e.g. retrograde calculation, parameter estimation and sensitivity analysis methods of the software). When needed, mean plasma or serum concentration–time data points from cited observed studies were digitized using GetData Graph Digitizer software (http://getdata-graph-digitizer.com).
The system-dependent parameters used in our models were based on existing population data [5] in Simcyp®. The mechanistic kidney model within the simulator was used to capture the differential processes relating to renal clearance [1]. Briefly, the model described the necessary processes governing drug transfer from blood to the urine through kidney cells, including passive diffusion, basolateral transporters (i.e. blood ↔ cell), apical transporters (i.e. cell ↔ tubule) and the glomerular filtration rate (GFR). A Cockcroft–Gault equation based on predefined creatinine clearances in the existing Simcyp population data was used to calculate the GFR. This mechanistic kidney model was then connected to the whole-body PBPK model structure through blood flow terms as illustrated in Fig. 1. The major assumptions made for this work are discussed below.
2.1.1 Negligible Passive Diffusion for Highly Hydrophilic Drugs
Since model substrate drugs are all hydrophilic and are generally ionized at physiological pH, the basolateral passive diffusion clearance (i.e. blood ↔ cell) and the apical passive diffusion clearance (i.e. cell ↔ tubule) were deemed negligible and were thus assumed to be zero. Accordingly, passive reabsorption was also assumed to be negligible.
2.1.2 Use of ‘Global’ Basolateral Uptake and Apical Efflux Transporters
In the absence of convincing transporter specificity data to properly define secretion of these drugs, a ‘global’ basolateral uptake transporter and a ‘global’ apical efflux transporter were assumed to be responsible for drug transport. This allowed the model to cover the ‘net’ transporter-mediated clearances on both membranes (Fig. 1). Technically, a basolateral transporter in the software was assumed to capture net uptake (Tup,b, uptake transporter on basolateral membrane), and an apical transporter was assumed to capture net efflux (Teff,a, efflux transporter on apical membrane).
2.1.3 Same Transporter Activity for Each Functional Proximal Tubular Cell in Patients with Severe Renal Impairment
The effect of severe renal impairment on renal transporters was modelled by decreasing the absolute number of functional tubular cells via the system-dependent parameter PTCPGK (proximal tubular cells per gram kidney). This parameter extrapolates transporter activity at the cellular level to that of the whole organ (see Sect. 2.3).
The transporter-mediated intrinsic clearance (CLint,T) for Tup,b was determined via parameter estimation against plasma/serum drug concentration–time profile data observed clinically, using the software’s ‘Healthy Volunteers’ population. Once this parameter was established, the CLint,T for Teff,a was optimized using sensitivity analysis to match the simulated drug accumulation in the urine to that observed in the same published study. A higher-fold CLint,T was then assumed to assure appropriate efflux of the drug into urine (see sections 1.1–1.3 in the Electronic Supplementary Material). It has to be noted that the CLint,T for Teff,a was generally unidentifiable with the available data for each substrate.
2.2 The Inhibitor Drug
Probenecid was selected as the perpetrator drug to inhibit Tup,b defined in the PBPK models of each drug, because Tup,b is the rate-determining process affecting systemic exposure to these drugs. In addition, probenecid appears to be a much stronger inhibitor of basolateral uptake transporters (University of Washington Metabolism and Transporter database: http://www.druginteractioninfo.org). Inhibition of Teff,a by probenecid was explored in simulation of cidofovir-induced nephrotoxicity (Sect. 2.5 below). Section 2 in the Electronic Supplementary Material summarizes the model development for probenecid.
2.3 Simulation of Renal Impairment
The software’s pre-existing populations of ‘RenalGFR_less_30’ and ‘Healthy Volunteers’, which included known physiological differences between healthy and renal impairment populations [6], were used for the severe renal impairment and healthy virtual subject simulations, respectively. Within the software’s PBPK framework, kidney transporter activity, or drug intrinsic clearance at the level of the transporter protein, is scaled to whole organ clearance according to Eq. 1 [1].
where CLr,T is renal clearance mediated by a transporter with a unit of litres per hour, CLint,T is intrinsic clearance of Tup,b or Teff,a with a unit of microlitres per minute per million tubule cells, PTCPGK has a unit of million proximal tubular cells per gram kidney (default healthy = 60 million PTCPGK) and kidney weight has a unit of grams. Kidney CLint,T for Tup,b or Teff,a is therefore parameterized with system-dependent parameters (i.e. PTCPGK and kidney weight) and a drug-dependent parameter (i.e. intrinsic clearance) at the level of the transporter protein (Eq. 1).
The default value of PTCPGK in ‘RenalGFR_less_30’ is the same as that in ‘Healthy Volunteers’ (60 million PTCPGK). In order to assess the effect of severe renal impairment on transporter activities, a sensitivity analysis of a range of PTCPGK values (0.1–60 million; kidney weight was assumed to be unchanged) was conducted to compare the predicted area under the concentration–time curve ratio (AUCR) between subjects with severe renal impairment (RI) and those with normal renal function (AUCRRI/Normal) and the AUCR values observed in renal impairment studies involving each of the three drugs. While the values of the unbound plasma fraction (fu,p) of oseltamivir carboxylate and cefuroxime remained unchanged in the renal impairment population [7, 8], the fu,p of cidofovir was decreased from 0.90 in the healthy population to 0.56 in the renal impairment population [9]. The fu,p = 0.56 was then used in the renal impairment simulations for cidofovir.
2.4 Simulation of Renal Drug–Drug Interaction
The effect of co-administration of oral probenecid on each substrate drug was simulated. Probenecid was assumed to only inhibit Tup,b. The inhibition mechanism assumed reversible inhibition according to Eq. 2:
where [I] is the plasma unbound inhibitor concentration and Ki is the plasma unbound reversible inhibition constant [1].
Considering the reported in vitro IC50 and Ki values of probenecid, which ranged from 1 to 30 μM, with different organic anion transporter (OAT) substrates [10–12], a sensitivity analysis using a range of Ki values (0.1–100 μM) was performed to compare the predicted AUCR (with and without an inhibitor, AUCR+inhibitor/−inhibitor) with AUCR values observed in DDI studies involving probenecid and each of the three drugs. The software’s ‘Healthy Volunteers’ population was used in these simulations.
2.5 Simulation of Potential Nephrotoxicity
Cidofovir has known nephrotoxic effects and is prescribed with probenecid as a preventive measure [13, 14]. To assess the amount of cidofovir within kidney cells, simulations were conducted in which cidofovir was administered alone or in combination with probenecid (using a Ki of 1 μM; see Sect. 3). The effects of differential and simultaneous inhibition of Tup,b and Teff,a by probenecid on intracellular exposure to cidofovir were explored.
2.6 PBPK Simulation Design
The dosage designs all mimicked those described in the referenced observed studies. Unless specified otherwise, all simulations were deterministic in order to illustrate the effects of patient factors. Deterministic simulations were accomplished using the ‘Population Representative’ feature of the software.
2.7 Approximation of the Standard Deviation of the Observed Mean AUC Ratio
In the referenced renal impairment and DDI studies, the observed results were reported as mean area under the concentration–time curve (AUC) values with corresponding variance for each study condition (control versus renal impairment population or DDI arm). The AUCR values were calculated and standard deviations were approximated using corresponding variance expression for the ratio of two independent variables based on the bivariate first-order Taylor expansion [15].
3 Results
3.1 Can PBPK Modelling Describe Kidney Drug Transport for Compounds that Undergo Active Renal Secretion?
Three model drugs—oseltamivir carboxylate, cidofovir and cefuroxime—were chosen on the basis of the criteria that they are all predominantly renally cleared, with sufficient plasma/serum and urinary drug concentration–time profiles, and that systemic exposure to each of these drugs has been shown to be altered in subjects with renal impairment and when co-administered with probenecid. Using a PBPK framework integrated with a mechanistic kidney structure [1] (Fig. 1), we developed models for each of the model drugs and estimated the contribution of both Tup,b and Teff,a transporter(s) to active secretion. Plasma pharmacokinetic data were used to determine CLint,T for Tup,b. Although CLint,T for Teff,a remains unidentifiable even after CLint,T for Tup,b is defined (Fig. 1), urine excretion profiles (e.g. the amount excreted over time) were used to suggest a plausible value of CLint,T for Teff,a for each drug. These PBPK models included detailed physiological determinants describing the dynamics of drug disposition, and could be used to predict and evaluate the impact of renal impairment or co-administration of the transporter inhibitor probenecid (an intrinsic patient factor and an extrinsic factor, respectively) on systemic drug levels and urinary excretion profiles (see the Electronic Supplementary Material).
3.2 Can Changes in Transporter Activity by Severe Renal Impairment be Derived Using PBPK Modelling?
Initially, when the PBPK drug models only considered GFR changes in subjects with severe renal impairment (CLCR <30 mL/min, software ‘RenalGFR_less_30’ population), the plasma AUCRRI/Normal values were only predicted to be 3 to 5.5-fold, considerably lower than mean AUCR values of 7.5, 9.8 and 13-fold observed for cidofovir, cefuroxime and oseltamivir carboxylate, respectively. In order to reflect the effect of severe renal impairment on active transport processes, a sensitivity analysis of PTCPGK, a system-dependent parameter, was performed in subjects with severe renal impairment. The predicted AUCRRI/Normal values for each compound were plotted against PTCPGK values ranging from 0.1 × 106 to the default 60 million PTCPGK [1] and compared with the observed AUCR values (Fig. 2).
Evaluation of the effects of theoretical changes in the number of proximal tubular cells per gram kidney (PTCPGK) on plasma exposure changes (AUCR, severe renal impairment versus normal renal function) in severe renal impairment. The dashed lines represent the simulated AUCR, and the solid lines ± shade represent observed the mean ± SD AUCR. The tested PTCPGK values ranged from 0.1 to 60 million proximal tubular cells per gram of kidney. a Oseltamivir carboxylate: 100 mg oral multiple dose (single dose on day 1, twice daily on days 2–5, single dose on day 6) in subjects with severe renal impairment and healthy subjects [7]. b Cidofovir: 0.5 mg/kg intravenous infusion over 1 h in subjects with severe renal impairment and healthy subjects [9, 30] (note: in both simulated and observed studies, cidofovir was co-administered with oral probenecid to reduce nephrotoxicity). c Cefuroxime: 750 mg intravenous bolus dose over 2 min in subjects with severe renal impairment and healthy subjects [8]
Both oseltamivir carboxylate and cefuroxime required more than a ten-fold downgrade from the baseline PTCPGK value in subjects with severe renal impairment to predict their respective observed AUCR values. A fifteen-fold reduction in PTCPGK (to 4 million PTCPGK; Fig. 2a) in the severe renal impairment population in the oseltamivir carboxylate PBPK model resulted in a simulated AUC that was 10.0-fold higher than that in healthy subjects, similar to an observed mean AUC increase of 10.3-fold. Likewise, for cefuroxime, a 15-fold reduction in PTCPGK resulted in a simulated AUC that was 9.1-fold higher than that in healthy subjects, comparable to a mean AUC increase of 9.8-fold observed in severe renal impairment (Fig. 2c).
For cidofovir, both healthy subjects and those with severe renal impairment were concomitantly dosed with oral probenecid to reduce the drug’s nephrotoxicity. In these studies, the active secretion process would have been largely inhibited by probenecid (see Sect. 3.3 below), resulting in an apparent lack of response to decreasing PTCPGK values in subjects with severe renal impairment (Fig. 2b). The model predicted a 5.5-fold increase in the AUC in subjects with severe renal impairment, regardless of the PTCPGK value defined in this population. The observed mean AUC increase was 7.5-fold.
3.3 Can the In Vivo Inhibition Potency of Probenecid on Renal Transporters Be Derived Using PBPK Modelling?
In vitro information is limited for probenecid with regard to its inhibition potency and specificity towards renal transporters. We conducted PBPK modelling to derive the apparent in vivo Ki of probenecid by assuming reversible inhibition on Tup,b of the substrate drugs. A sensitivity analysis was conducted over a range of Ki values in the probenecid PBPK model, targeting Tup,b. A Ki value in the range of 0.1 to 10 μM appeared to predict the observed mean AUCR for oseltamivir carboxylate. For example, at Ki = 1 μM, the PBPK predicted exposure change for oseltamivir carboxylate was 2.2-fold when oseltamivir phosphate was co-administered with probenecid, and the observed mean AUCR for oseltamivir carboxylate was 2.5-fold (Fig. 3a). For cidofovir, the predicted AUCR was not sensitive to the in vivo Ki value. At a >1,000-fold range of Ki values (0.1–100 μM), the predicted exposure changes for cidofovir were between 1.1 and 1.4, and the observed mean AUCR was 1.3 (Fig. 3b). For cefuroxime, a Ki value around 10 μM predicted the observed mean AUCR values (1.6 and 1.4 for the predicted and observed AUCR values, respectively; Fig. 3c). As the Ki value decreased, the model appeared to overpredict the AUC increase for cefuroxime.
Evaluation of the effects of use of different probenecid inhibition constant (Ki) values on simulated plasma exposure changes of test substrates (AUCR, with and without inhibitor). The dashed lines represent the simulated AUCR, and the solid lines ± shade represent the observed mean ± SD AUCR. a Oseltamivir carboxylate: 150 mg single oral dose with and without probenecid [12]. b Cidofovir: 3.0 mg/kg intravenous infusion over 1 h with and without probenecid [9]. c Cefuroxime: 750 mg intravenous infusion over 20 min with and without probenecid [31]
3.4 Can PBPK Modelling Be Used to Evaluate the Role of Renal Transporters on Drug Exposure in Kidney Cells, With or Without Co-administration of a Transporter Inhibitor?
Since cidofovir accumulation in kidney cells is believed to correlate with its nephrotoxicity under clinical dosing [13, 14], we investigated the hypothetical effect of differential and simultaneous inhibition of the net basolateral uptake and apical efflux transporters (Fig. 1) by probenecid, using PBPK. Maximal cidofovir exposure in kidney cells after an intravenous drug infusion was simulated in different inhibition scenarios (Table 2). A Ki value of 1 μM in the probenecid PBPK model was chosen for Tup,b on the basis of the analyses in Sect. 3.3. When the model assumed inhibition on Tup,b only, the simulated amount of cidofovir in kidney cells decreased substantially, compared with cidofovir administration alone. In contrast, kidney cells were exposed to significantly greater amount of cidofovir when the model assumed inhibition of Teff,a only. When simultaneous inhibition of Tup,b and Teff,a was assumed to be inhibited by probenecid, using Ki = 1 μM for both, the predicted kidney exposure was about 40 % lower than the condition without inhibition. The simulated 24 h time profile of the drug amount in kidney cells from these simulations can be found in Fig. S6 in the Electronic Supplementary Material.
4 Discussion
This study provides a framework for modelling active drug secretion in the kidneys, using PBPK. With consideration of detailed drug disposition mechanisms in the kidney, we addressed each of the questions posed in Sect. 3.
4.1 Can PBPK Modelling Describe Kidney Drug Transport for Compounds that Undergo Active Renal Secretion?
In order to successfully predict the effects of patient factors on drug pharmacokinetics, the quantitative contribution of each disposition pathway and the effects of patient factors on the pathway need to be defined a priori. Specifically for drug transporters, there is often a lack of information regarding transporter specificity between a substrate (which is often mediated by multiple transporters) and a perpetrator drug (which often inhibits multiple transporters). Present knowledge gaps in system-dependent parameters (e.g. the effect of renal impairment on drug transporters and absolute transporter abundance) further hinder the prediction. However, using a PBPK model with sufficient mechanistic complexity, supported by suitable sets of in vivo data, one can discern the impact of patient factors on a specific pathway to identify or even fill the knowledge gaps.
4.2 Can Changes in Transporter Activity by Severe Renal Impairment Be Derived Using PBPK Modelling?
We and others have used PBPK modelling to hypothesize that severe kidney dysfunction significantly affects hepatic uptake transporters [6, 16]. In this study, we extended the use of PBPK modelling to quantify the effect of renal impairment on renal transporter activities, using model compounds. Initially, the use of a predefined severe renal impairment population, assuming unchanged intrinsic renal secretion, underestimated the exposure changes in our test compounds. The predicted AUC increase in this population versus the population with normal renal function was at most 3-fold for drugs such as oseltamivir carboxylate and cefuroxime, whereas 9.8- to 10-fold increases had been observed, suggesting a potential effect of decreased renal function also on the non-filtration pathway (Fig. 2). Decreased renal function is known to correlate with pathological changes in the glomerulus and tubular interstitium of the kidney [17, 18], and conditions such as albuminuria have been hypothesized to induce scar damage [19–22]. As such, a common end result of chronic kidney disease is renal fibrosis, characterized by significant tissue scarring, leading to total damage of kidney parenchyma [23] and thereby affecting both filtration and secretion elimination pathways. Additionally, kidney disease, such as bilateral ureteral obstruction, is known to correlate with downregulation of the uptake transporters OAT1 and OAT3 in proximal tubule cells in rats [24]. According to Eq. 1, PTCPGK is a key system-scaling factor for determining the contribution of a transporter to renal clearance. We conducted sensitivity analyses by predicting the AUCRRI/Normal over a range of PTCPGK values under the assumption that the other two parameters remain unchanged in subjects with renal impairment. The results of our simulations showed that a decrease of at least ten-fold in the PTCPGK value from the baseline (i.e. from 60 million to ≤ 6 million) was necessary to predict the observed AUC changes in subjects with severe renal impairment. It is important to emphasize that we are not proposing the PTCPGK drop as an unequivocal mechanistic explanation for renal impairment, but as a practical singular means of simulating renal impairment affecting the secretion pathway, using PBPK.
The effect on alteration of PTCPGK in renal impairment cannot be derived for cidofovir, because of the presence of probenecid in its renal impairment study to reduce nephrotoxicity, which in theory would have abolished the secretion pathway (Fig. 2b showed the insensitivity of the plasma exposure in renal impairment with the changes in PTCPGK). However, the cidofovir simulations represented a good example of using PBPK modelling to simulate the dynamic effects of both renal impairment and DDI on multiple disposition processes of a drug.
This >10-fold reduction in PTCPGK allows us to predict the effect of severe renal impairment on the active transport component of renal clearance for an investigational drug, using the PBPK approach. Studies are underway to confirm the extrapolation capability of this finding, using other renally eliminated drugs.
4.3 Can the In Vivo Inhibition Potency of Probenecid on Renal Secretion Be Derived Using PBPK Modelling?
Both oseltamivir carboxylate and cidofovir are substrates of OAT1 in vitro [10, 12]. The reported in vitro probenecid Ki values against OAT1 were 1–30 μM [10–12, 25, 26]. In this study, inhibition of Teff,a was not considered, as it would not affect plasma pharmacokinetics when the passive process was assumed to be negligible (see Sect. 2). In vivo probenecid Ki values towards Tup,b appear to be ≤1 μM for oseltamivir carboxylate and ~10 μM for cefuroxime in order to predict the observed AUCR. Cidofovir is not sensitive to a range of Ki values tested, likely because of a much smaller contribution of secretion clearance to its total renal clearance (<40 %; Table 1).
Increased cefuroxime systemic exposure in the presence of probenecid could be predicted by PBPK simulations only when Ki is between 10 and 100 μM. Use of probenecid Ki ≤1 μM (as for oseltamivir carboxylate simulations) overpredicted the AUCR value for cefuroxime. One plausible explanation may be that specific inhibition of different uptake transporters for each test substrate was not captured in the model (the contribution of a specific transporter to total Tup,b for cefuroxime that could be inhibited by probenecid was unknown).
Currently, if an investigational drug (in particular, an organic anion) is found to be significantly secreted in the kidney, a clinical study using probenecid may be recommended to determine the effect of co-adminnistration with probenecid and/or other inhibitors of renal basolateral organic anion transporters. In the absence of transporter specificity information, our simulations suggest a practical use of PBPK to assess the risk of interaction with probenecid. The developed probenecid PBPK model with an unbound Ki value of ≤1 μM on net Tup,b would provide an initial estimate of AUCR values in the presence of probenecid.
4.4 Can PBPK Modelling Be Used to Evaluate the Role of Renal Transporters on Drug Exposure in Kidney Cells, With or Without Co-administration of a Transporter Inhibitor?
Using PBPK models, the effect of transporter inhibition by probenecid on cidofovir kidney cell exposure was simulated (Table 2). Simulations showed that probenecid likely inhibits kidney uptake transporter(s) and decreases exposure to cidofovir in kidney cells. Inhibition of only apical efflux of cidofovir would cause significant accumulation of the drug in kidney cells, which would greatly exacerbate cidofovir’s known nephrotoxic effects.
4.5 Limitations of the Current Study
Though the current study demonstrated important uses of PBPK modelling in predicting the effects of patient factors on systemic and renal drug levels and on DDIs, some limitations should be noted. First, the three drugs used in the study are all organic anions. Therefore, it is not known whether the conclusion based on the developed PBPK model would apply to organic cations, which are eliminated by a different set of renal transporters with distinct mechanisms. Second, the drugs used in the study were eliminated in large part by secretion in the kidney. Further research is needed to evaluate the utility of this PBPK approach for drugs with smaller components of secretion, whose renal elimination is sensitive to urine pH and flow, and which undergo reabsorption, or drugs which undergo significant elimination by renal and hepatic pathways.
5 Conclusion
This study demonstrated the practical use of PBPK modelling, with a clearly defined mechanistic kidney model, to evaluate the effects of patient factors on kidney uptake and efflux transporters, using three predominantly renally cleared model drugs. The results showed that for an investigational drug whose filtration and active secretion pathways are quantitatively known, one can use PBPK approaches to (1) practically define transporter-mediated renal secretion, using plasma and urine data; (2) predict the effect of severe renal impairment on the exposure change of the drug, assuming a 10-fold reduction in functional tubule cells in conjunction with a reduced filtration rate in the model; (3) predict the effect of inhibition of kidney uptake transport by probenecid, using a conservative in vivo Ki (≤1 μM); and (4) evaluate the effect of transporter inhibition on drug exposure in kidney cells. These findings could be confirmed with future PBPK modelling of other drugs that undergo renal elimination.
Abbreviations
- AUC:
-
Area under the concentration–time curve
- B/P :
-
Blood to plasma partition ratio
- CLCR :
-
Creatinine clearance
- CLint,T :
-
Transporter-mediated intrinsic clearance
- CLiv :
-
In vivo clearance
- CLpd :
-
Passive diffusion clearance
- CLr :
-
Renal clearance
- CLr,T :
-
Renal clearance mediated by a transporter
- DDI:
-
Drug–drug interaction
- f a :
-
Fraction available from dosage form
- f u,p :
-
Fraction unbound in plasma
- GFR:
-
Glomerular filtration rate
- [I]:
-
Plasma unbound inhibitor concentration
- k a :
-
First-order absorption rate constant
- K i :
-
Reversible inhibition constant
- K p :
-
Tissue-to-plasma partition coefficient
- LogP :
-
Partition coefficient
- OAT:
-
Organic anion transporter
- pKa:
-
Dissociation constant
- PBPK:
-
Physiologically based pharmacokinetic modelling
- PTCPGK:
-
Proximal tubular cells per gram kidney
- RI:
-
Renal impairment
- T eff,a :
-
Efflux transporter on apical membrane
- T up,b :
-
Uptake transporter on basolateral membrane
- V ss :
-
Volume of distribution at steady state
References
Neuhoff S, Gaohua L, Burt H, Jamei M, Li L, Tucker GT, Rostami-Hodjegan A. Accounting for transporters in renal clearance: towards a mechanistic kidney model (Mech KiM). In: Steffanson B, Sugiyama Y, editors. Transporters in drug discovery, development, and use. New York: Springer; 2013 (in press).
Varma MV, Feng B, Obach RS, Troutman MD, Chupka J, Miller HR, El-Kattan A. Physicochemical determinants of human renal clearance. J Med Chem. 2009;52:4844–52.
Rodgers T, Leahy D, Rowland M. Physiologically based pharmacokinetic modeling 1: predicting the tissue distribution of moderate-to-strong bases. J Pharm Sci. 2005;94:1259–76.
Rodgers T, Rowland M. Physiologically based pharmacokinetic modelling 2: predicting the tissue distribution of acids, very weak bases, neutrals and zwitterions. J Pharm Sci. 2006;95:1238–57.
Jamei M, Dickinson GL, Rostami-Hodjegan A. A framework for assessing inter-individual variability in pharmacokinetics using virtual human populations and integrating general knowledge of physical chemistry, biology, anatomy, physiology and genetics: a tale of ‘bottom-up’ vs ‘top-down’ recognition of covariates. Drug Metab Pharmacokinet. 2009;24:53–75.
Rowland Yeo K, Aarabi M, Jamei M, Rostami-Hodjegan A. Modeling and predicting drug pharmacokinetics in patients with renal impairment. Expert Rev Clin Pharmacol. 2011;4:261–74.
Multiple ascending oral dose study of the pharmacokinetics, tolerability, and safety of the neuraminidase inhibitor Ro 64-0796 in subjects with renal impairment. Clinical Pharmacology and Biopharmaceutics Review from Drugs@FDA; 1999.
Bundtzen RW, Toothaker RD, Nielson OS, Madsen PO, Welling PG, Craig WA. Pharmacokinetics of cefuroxime in normal and impaired renal function: comparison of high-pressure liquid chromatography and microbiological assays. Antimicrob Agents Chemother. 1981;19:443–9.
Cundy KC. Clinical pharmacokinetics of the antiviral nucleotide analogues cidofovir and adefovir. Clin Pharmacokinet. 1999;36:127–43.
Chu XY, Bleasby K, Yabut J, Cai X, Chan GH, Hafey MJ, Xu S, Bergman AJ, Braun MP, Dean DC, Evers R. Transport of the dipeptidyl peptidase-4 inhibitor sitagliptin by human organic anion transporter 3, organic anion transporting polypeptide 4C1, and multidrug resistance P-glycoprotein. J Pharmacol Exp Ther. 2007;321:673–83.
Cutler MJ, Urguhart BL, Velenosi TJ, Meyer zu Schwabedissen HE, Dresser GK, Leake BF, Tirona RG, Kim RB, Freeman DJ. In vitro and in vivo assessment of renal drug transporters in the disposition of mesna and dimesna. J Clin Pharmacol. 2012;52:530–42.
Hill G, Cihlar T, Oo C, Ho ES, Prior K, Wiltshire H, Barrett J, Liu B, Ward P. The anti-influenza drug oseltamivir exhibits low potential to induce pharmacokinetic drug interactions via renal secretion-correlation of in vivo and in vitro studies. Drug Metab Dispos. 2002;30:13–9.
Cidofovir (US label); 2013. http://www.accessdata.fda.gov/drugsatfda_docs/label/1999/020638s003lbl.pdf.
Cidofovir (EMA summary for the public); 2013. http://www.ema.europa.eu/docs/en_GB/document_library/EPAR_-_Summary_for_the_public/human/000121/WC500052073.pdf.
Stuart & Ord. Kendall’s advanced theory of statistics, 6th ed. London: Arnold; 1998.
Zhao P, Vieira Mde L, Grillo JA, Song P, Wu TC, Zheng JH, Arya V, Berglund EG, Atkinson Jr AJ, Sugiyama Y, Pang KS, Reynolds KS, Abernethy DR, Zhang L, Lesko LJ, Huang SM. Evaluation of exposure change of nonrenally eliminated drugs in patients with chronic kidney disease using physiologically based pharmacokinetic modeling and simulation. J Clin Pharmacol. 2012;52:91S–108S.
Bohle A, Christ H, Grund KE, Mackensen S. The role of the interstitium of the renal cortex in renal disease. Contrib Nephrol. 1979;16:109–14.
Dixon RJ, Young K, Brunskill NJ. Lysophosphatidic acid-induced calcium mobilization and proliferation in kidney proximal tubular cells. Am J Physiol. 1999;276:F191–8.
Burton C, Harris KP. The role of proteinuria in the progression of chronic renal failure. Am J Kidney Dis. 1996;27:765–75.
Eddy AA. Interstitial nephritis induced by protein-overload proteinuria. Am J Pathol. 1989;135:719–33.
Eddy AA, Giachelli CM. Renal expression of genes that promote interstitial inflammation and fibrosis in rats with protein-overload proteinuria. Kidney Int. 1995;47:1546–57.
Thomas ME, Schreiner GF. Contribution of proteinuria to progressive renal injury: consequences of tubular uptake of fatty acid bearing albumin. Am J Nephrol. 1993;13:385–98.
Liu Y. Renal fibrosis: new insights into the pathogenesis and therapeutics. Kidney Int. 2006;69:213–7.
Villar SR, Brandoni A, Anzai N, Endou H, Torres AM. Altered expression of rat renal cortical OAT1 and OAT3 in response to bilateral ureteral obstruction. Kidney Int. 2005;68:2704–13.
Hashimoto T, Narikawa S, Huang XL, Minematsu T, Usui T, Kamimura H, Endou H. Characterization of the renal tubular transport of zonampanel, a novel alpha-amino-3-hydroxy-5-methylisoxazole-4-propionic acid receptor antagonist, by human organic anion transporters. Drug Metab Dispos. 2004;32:1096–102.
Takeda M, Narikawa S, Hosoyamada M, Cha SH, Sekine T, Endou H. Characterization of organic anion transport inhibitors using cells stably expressing human anion transporters. Eur J Pharmacol. 2001;419:113–20.
Parrott N, Davies B, Hoffman G, Koerner A, Lave T, Prinssen E, Theogaraj E, Singer T. Development of a physiologically based model for oseltamivir and simulation of pharmacokinetics in neonates and infants. Clin Pharmacokinet. 2011;50:613–23.
Foord RD. Cefuroxime: human pharmacokinetics. Antimicrob Agents Chemother. 1976;9:741–7.
Study of the pharmacokinetics and absolute bioavailability of the neuraminidase inhibitor Ro 64-0796/Ro 64-0802 (Protocol NP15719). Clinical Pharmacology and Biopharmaceutics Review from Drugs@FDA; 1999.
Brody SR, Humphreys MH, Gambertoglio JG, Schoenfeld P, Cundy KC, Aweeka FT. Pharmacokinetics of cidofovir in renal insufficiency and in continuous ambulatory peritoneal dialysis or high-flux hemodialysis. Clin Pharmacol Ther. 1999;65:21–8.
Garton AM, Rennie RP, Gilpin J, Marrelli M, Shafran SD. Comparison of dose doubling with probenecid for sustaining serum cefuroxime levels. J Antimicrob Chemother. 1997;40:903–6.
Acknowledgments
The authors gratefully acknowledge Professor Amin Rostami-Hodjegan (from the University of Manchester, Manchester, UK) and Drs Sibylle Neuhoff and Masoud Jamei (from Simcyp Ltd, Sheffield, UK) for their scientific input. This research was supported by the US Food and Drug Administration’s (FDA’s) Medical Countermeasures initiative. Dr Vicky Hsu was supported in part by an appointment to the Research Participation Program at the Center for Drug Evaluation and Research, administered by the Oak Ridge Institute for Science and Education through an interagency agreement between the US Department of Energy and the FDA. No official support or endorsement by the FDA or the Medical Products Agency is intended or should be inferred.
Conflicts of Interest
The authors have declared no conflict of interest.
Author Contributions
Vicky Hsu, Manuela de L. T. Vieira and Ping Zhao designed the research, performed the research, analysed the data, contributed new reagents/analytical tools and participated in the writing of the manuscript. Lei Zhang, Jenny Huimin Zheng, Anna Nordmark, Eva Gil Berglund, Kathleen M. Giacomini and Shiew-Mei Huang analysed the data and participated in the writing of the manuscript. All authors read and approved the final manuscript.
Author information
Authors and Affiliations
Corresponding author
Electronic Supplementary Material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this license, visit (http://creativecommons.org/licenses/by-nc-nd/2.5/)
About this article
Cite this article
Hsu, V., de L. T. Vieira, M., Zhao, P. et al. Towards Quantitation of the Effects of Renal Impairment and Probenecid Inhibition on Kidney Uptake and Efflux Transporters, Using Physiologically Based Pharmacokinetic Modelling and Simulations. Clin Pharmacokinet 53, 283–293 (2014). https://doi.org/10.1007/s40262-013-0117-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40262-013-0117-y