Introduction

As the backbone of the global economy, contemporary SCs encounter substantial risks and vulnerabilities due to the instability of the operational environment and major disruptions that make it increasingly complicated to plan for the future effectively (Juan et al., 2022a, 2022b; Klibi et al., 2018). The COVID-19 pandemic fundamentally changed the SC landscape, resulting in a “new normal” of constant flux. This new state has been shaped by a series of disruptions caused by this pandemic (Rahman et al., 2022). Given the persistent nature of the challenges posed by this state, it is critical to consider the application of dynamic resilience measurement in the new phase of the SC during the post-pandemic and companies should immunise their SC by taking behavioural biases and social effects into account and re-evaluating their contractual responsibilities (Asian et al., 2020). Moreover, in the post-pandemic, companies make every attempt to restore their profitability (Wided, 2023). With its adaptability capacity, SCRes can prove highly effective in dealing with ongoing challenges (Settembre-Blundo et al., 2021). By incorporating elements of avoidance, absorption, and elasticity, a SC can be designed to be dynamically resilient and better equipped to cope with the new normal (Mithani, 2020). If the industry and its SCs cannot adapt to new situations after disruption, making strategic decisions to improve resiliency is necessary to prevent resulting shortages (Singh et al., 2021a, 2021b; Tucker et al., 2020). Hence, SCNs should be sufficiently robust and resilient to ensure ongoing operations even in the event of disruptions. (Dixit et al., 2020b).

SCRes is described as “the adaptive capability of the SC to prepare for unexpected events, respond to disruptions, and recover from them by maintaining continuity of operations at the desired level of connectedness and control over structure and function” (Ponomarov & Holcomb, 2009, p. 131). Market volatility and supply interruptions resulted in significant decrease in the short-term and long-term revenues of many organisations with worldwide supply networks (Asian & Nie, 2014; S. Singh et al., 2021a, 2021b). A SC's design and structure substantially affect its resilience, which determines the impact of the disruption (Ojha et al., 2018; Rezaei Somarin et al., 2018). For example, the undesirable effects of disruptions on SCNs with many locally located nodes are much higher than those on networks with nodes that are scattered across a larger distance. In addition, when a specific node aggregates supplies and feeds the demand of several other nodes, then any disruption of this central node makes the whole SC defected and non-operational (Dixit et al., 2020b). Longer and larger SCs with more tiers and depth make the partnering companies more vulnerable to disruptions (Alfarsi et al., 2019; Paul et al., 2019).

Many historical disruptions have exposed SCs to risks. For instance, when the Tohoku earthquake hit Japan in 2011, it not only disrupted the Japanese and Asian SCs but also resulted in shortages in the SC of associated industries in Europe (Scholten et al., 2014). So, SCRes is viewed as a risk mitigation strategy in response to disruptions and to deal with an unstable operational environment (Alfarsi et al., 2019). SCNs become more resilient through proactive strategies such as efficient collaborations among firms, higher visibility, more flexibility (Chowdhury & Quaddus, 2016; Klibi et al., 2018), multiple sourcing to increase redundancy and back-up suppliers, holding extra safety stocks, and growing capacity of facilities (e.g. manufacturing, warehousing, logistics and transportation) (Klibi et al., 2018; Salehi Sadghiani et al., 2015). However, responsiveness and recovery are the reactive strategies to improve the resiliency of the SCs (Kamalahmadi & Mellat-Parast, 2015). After defining flexibility, visibility, and resilience, it is important to understand their effects within a SC (Dolgui & Ivanov, 2022; Singh et al., 2019a, 2019b). These three attributes enhance the chain's resilience and robustness (Mackay et al., 2020). Flexibility facilitates swift adaptation to unexpected circumstances, while visibility provides real-time insights into operations, enabling better decision-making (Dubey et al., 2021). Resilience embodies the ability of the SC to recover from disruptions quickly, a trait bolstered by flexibility and visibility (Juan et al., 2022a, 2022b).

Enhancing SCRes through over-increasing capacity and boundless redundancy becomes a very expensive decision (Sokolov et al., 2015). Therefore, measuring SCRes using data analytics is crucial to analysing the efficacy of different strategies for improving resilience (Kaur & Singh, 2022; Klibi et al., 2018). Analysing the resilience of the entire SCN enables practising SC managers to clearly understand the weaknesses of the network and address those shortcomings by implementing suitable strategies and warning every firm in the network about the risks and vulnerabilities that they encounter in their business environment (Li & Zobel, 2020). The improved knowledge of the business environment in which the firms function enables them to devise more effective responses to disruptions through informed investment decisions (Juan et al., 2022a, 2022b).

Along with the increase in the current global use of natural gas, which composes 25% of the energy mix (International Energy Agency, 2016), the intensity and frequency of disruptive risks to the energy sector and natural gas in particular are increasing (Ding et al., 2020) which can be the result of natural disasters, economic risks, geopolitical risks, maritime transportation risk and so on (Geng et al., 2017). Studies on energy security most often concentrate on the vulnerability of a nation to supply shortages. To some extent, they have recommended solutions to mitigate the impacts of disruptions and crises by focusing on solutions to decrease the frequency and intensity of disruptions (pre-disruption mitigation). However, they have not elaborated on the role of efficient use of resources in lowering the vulnerability of SCs through post-disruption resilience (Rose et al., 2018).

Thus, the efficiency of SCNs in terms of resilience and capacity to recover after disruptions necessitates more research. This study adopts data envelopment analysis (DEA) to bridge this gap and examine the resiliency of SCNs. DEA is a mathematical approach based on linear programming that uses multiple inputs and outputs to evaluate the efficiency of homogeneous decision-making units (DMUs) (Kiani Mavi et al., 2021). DEA shines in its versatility and adaptability. Unlike simulation and optimisation models that require a predefined objective function and assumptions about the distribution of data, DEA does not demand such preconditions, granting it more flexibility. It uses empirical data to construct a piecewise linear surface to envelop the data points, creating an efficiency frontier to evaluate other units against (Jradi & Ruggiero, 2023). The ability of DEA to work with multiple inputs and outputs simultaneously without any need to specify weights in advance is its key advantage over most statistical methods (Goker & Karsak, 2021). Therefore, DEA is exceptionally well suited for assessing complex systems like SCs where numerous elements interact and influence one another.

Since the traditional models of DEA are flexible in attributing weights to input and output variables to measure efficiency (Jahanshahloo et al., 2011; Tavana et al., 2015), they produce a different weighting scheme for each DMU to maximise its efficiency score. This weighting scheme results in several DMUs becoming efficient. The common set of weights (CSW) analysis overcomes this shortcoming by evaluating the efficiency of all DMUs consistently (Kiani Mavi et al., 2019a, 2019b). This study performs a common weights analysis using the ideal point method. The advantage of the ideal point method is in determining the amount of improvement for inefficient DMUs (Kiani Mavi et al., 2019a, 2019b). This research significantly contributes to advancing resilience strategies in the Pacific region, particularly in the SCNs domain. The proposed model contributes to the exploration of a strategic approach towards resilience by analysing the distinct obstacles and potential advantages of SCRes in the Pacific region. The incorporation of non-discretionary and non-controllable inputs within the CSW model demonstrates the interplay between economic, social, environmental, and political elements that influence resilience in the Pacific region.

Complexity theories, particularly complex adaptive systems (CAS) and complexity thinking (CT), have assisted supply chains practitioners to better analyse their intricate dynamics (Rebs et al., 2019; Tsolakis et al., 2021; Wieland et al., 2023; Wilden et al., 2022). Nilsson and Gammelgaard (2012) provided a paradigmatic reflection on these approaches, contrasting them with the traditional systems approach which has long dominated SCM and logistics research. They argue that current challenges of organisational complexity in supply chain management, such as those related to innovation, learning, and sense-making, can be effectively investigated through the fundamental assumptions of CAS and CT which are centred around adaptation, emergent behaviour, and nonlinear interactions. This perspective is echoed by Elias et al. (2021), who apply systems thinking to analyse sustainable wood supply chains in Amazon, showcasing the applicability of these approaches in diverse and complex contexts. The inclusion of complexity approaches in the broader discourse of SCM provides valuable alternative perspectives that complement and enrich the understanding of the supply chain dynamics. Acknowledging these theories not only aligns with the current trajectory of the field but also opens up avenues for future research to analyse the multifaceted nature of supply chains through various theoretical lenses (Naim et al., 2019; Waller et al., 2015).

This paper is structured as follows: Sect. "Literature Review" reviews the literature on SCN resilience, approaches to analyse it, and common weight analysis in DEA. In Sect. "Proposed ideal Point Common Weights Model with Non-discretionary and Non-controllable Inputs", the developed common set of weights model is presented. Sect. "Case Study: LPG Supply Chain" illustrates a case study in the LPG sector and discusses the results. Finally, Sect. "Conclusion" provides the concluding remarks.

Literature Review

Supply Cain Resilience

Statistics show that over 75% of firms experience a type of disruption yearly (Scholten et al., 2019). SC disruptions impose risk to the SCs besides other negative impacts such as reduced operational and financial performance (Lotfi & Saghiri, 2018), a higher number of customer complaints, and longer lead times (Al Naimi et al., 2021; Kinra et al., 2019). As a result of the globalisation of business and the industry's adoption of new business practises, such as lean manufacturing, rapid response programmes, and effective customer service, the market has grown more volatile, which has resulted in an increased need for SC adjustments (Rao et al., 2013; Singh et al., 2019a, 2019b). In response to disruptions, SC managers must decide on and implement strategies through SCRes to speed up recovery from disruptions and to continue the normal operations of SCs (Al Naimi et al., 2021; Ali et al., 2017). SCRes (SCRes) is the capacity of an organisation to bounce back to its normal conditions after disruptive events by minimising instabilities (Bag et al., 2023). In addition to the capacity of the system to predict the risk and minimising its disruptive impacts (Day, 2014), resilient organisations not only respond to a disruption in a better way but also try to take advantage of disruptions to the benefit of the organisation (Brandon-Jones et al., 2014). SCRes has the potential to support various departments in aligning with market expectations, thereby gaining a competitive edge. If there is a change in the market, resilient aspects of a SC can facilitate rapid growth. Additionally, these features can assist businesses in improving their cash flow cycle and reducing the expenses that are incurred (Modgil et al., 2021). Anticipation (forward-thinking ideas and plans), resistance (continued structural and functional factors), and recovery and responsiveness are the three possible stages of SCRes which is rapid and efficient. SCRes, in its broadest sense, refers to the methods used to mitigate interruptions in the SC so that information, products, and money can continue to move without disruption (Gu et al., 2021).

Resilience involves averting known risks and accomplishing the expected performance by meeting business objectives (Aslam et al., 2020; Sawyerr & Harrison, 2020). SCRes has two major pillars: (1) capacity to resist (resistance capacity) which is the ability of an SC to prevent or lessen the adverse effects of a disruption by avoiding it completely or by reducing the time between disruption occurrence and beginning the process of recovery; and (2) capacity to recover (recovery capacity) which is the ability of an SC to restore the functionality after a disruption happened (Melnyk et al., 2014). The ability of a firm to manage and restructure its resources (Ambulkar et al., 2015) and to enhance the cooperation and coordination among SC actors by immediate information sharing and long-term planning (Chandra & Grabis, 2009) help in boosting SCRes. On the other hand, innovation helps firms and their SCs become more resilient facing disruptions (Sabahi & Parast, 2019). Besides, the severity of the effects of a disruption in a SC is heavily influenced by the design of the network. Thus, it has been acknowledged that SCN structural factors significantly influence resilience (Dixit et al., 2020a; Ivanov & Ivanov, 2018).

Shashi et al. (2019) identified four principles of SCRes; (1) SC engineering, (2) collaboration, (3) agility, and (4) risk management culture, which SCs cannot become resilient without them. Several factors enable building resiliency in the SCs. Along with non-industry-specific enablers such as redundancy, flexibility, visibility, and collaboration (Purvis et al., 2016; Scholten et al., 2019), different enablers lead to higher resiliency in various industries. To ensure resilience in oil and gas SCs, it is important to adopt flexible contracting, diversify portfolios, plan transportation, and maintain an additional safety stock (Urciuoli et al., 2014). Conversely, automotive SCs should focus on multiple sourcing and establishing a flexible supplier base with a high level of visibility (Azevedo et al., 2013). Holding fewer inventories, utilising information technology, and multiple sourcing are building resiliency in electronic SCs (Sodhi & Lee, 2007).

Redundancy is the deliberate and judicious use of extra capacity and inventory that could be called upon to address a disaster, such as demand spikes or supply disruptions. Redundancy is an efficient method for fostering resilience and accelerating recovery from disturbances (Parast & Shekarian, 2018). Implementing three different types of redundancy methods (keeping extra inventory, identifying backup suppliers, and establishing a group of protected suppliers) may enhance a company's performance in a volatile and complicated business environment that necessitates reducing the consequences of SC interruption (Shekarian & Mellat Parast, 2021). Maintaining stock levels, engaging in negotiations with alternative suppliers, and investing in supplier security represent the most popular redundancy strategies (Kamalahmadi et al., 2022; Knemeyer et al., 2009). SC flexibility is the capability of an SC to modify its operations, resources, design, and institutional arrangements within a predetermined scope in response to fluctuations in production quantity and product variability (Novais et al., 2019). To remain competitive in today's market, many businesses realise that SC flexibility is a key factor that needs decisive management action (Shekarian & Mellat Parast, 2021). Flexibility indicates a company's ability to adjust its supply chain design in response to long-term or systemic changes in the supply chain and industry trends (Engelhardt-Nowitzki, 2012). This metric demonstrates a company's responsiveness to changes in the market, demand, supply, and technology (Gupta et al., 2019; Siagian et al., 2021). For example, emergency replenishment strategy as a strategic flexibility guarantees that companies and governments have contingency plans in place to prevent SC disruptions and unanticipated occurrences that might impair the availability of essential resources (Rezaei Somarin et al., 2018).

Supply chain visibility is characterised by the degree to which participants in the supply chain have access to timely and accurate information that they consider crucial or valuable for their operations (Barratt & Barratt, 2011; Somapa et al., 2018). To be more particular, it relates to the visibility of information about demand and inventory throughout the SC as a whole (Silva et al., 2017). Improved visibility into customer requirements and inventory levels enhances demand forecasting, expedites the process of adjusting production plans to meet changing demand, improves the delivery process, and decreases the quantity of stock on hand at all SC tiers (Juan et al., 2022a, 2022b; Småros et al., 2003). Collaboration entails numerous enterprises or independent business organisations cooperating in a partnership with the objective of sharing enhanced results and advantages (Soosay & Hyland, 2015). To accomplish these performance enhancements, the corporate entities must create an adequate degree of trust, communicate vital information, make shared decisions, and, if required, integrate SC activities (Min et al., 2005). Collaboration in the SC is typically characterised as two or more firms collaborating in order to generate a competitive advantage and better profits than can be gained by operating independently (Sudusinghe & Seuring, 2021). Collaboration may also be described as a connection between autonomous businesses marked by transparency and trust in which risks, benefits, and expenses are shared (Duong & Chong, 2020).

Businesses need to perform SCRes evaluations to improve their awareness of the risks inherent in their SCs and assess their capacity for bouncing back from disasters and their strategies for mitigating those risks (Soni et al., 2014). Risks of SCN design are generally categorised into two groups: (1) operational risks which arise because of lack of knowledge about variables such as demand, processing duration, and operation costs and (2) disruption risks which are the result of natural disasters such as earthquake, and man-made crises such as war and failure of the machinery (Arabsheybani & Khasmeh, 2021). Operational risks are potential disruptions to the normal operations of SC, including alterations to lead-time and demand. Disruption risks, though less frequent, can have a greater impact, e.g. natural disasters (El Baz & Ruel, 2021).

To quickly recover from disruptions, firms must forecast and be prepared to meet unforeseeable demand to achieve competitive advantages (Ali et al., 2021). Integrating the whole supply network and increasing transparency and visibility among SC actors can help mitigate or eliminate such risks, bolstering SCRes (Namdar et al., 2018). Furthermore, to survive post-COVID-19, resilient SCNs must transform by integrating SCRes with SC viability measures (Sarkar et al., 2022; Zaoui et al., 2023). in the post-COVID-19 age, businesses throughout the globe confront several significant obstacles to social sustainability impeding the accomplishment of sustainable development objectives (Dwivedi et al., 2021; Sarker et al., 2021).

Measuring SCRes

The proactive development of a strategy for future major disruptions relies heavily on the accurate measurement of SCRes (Moosavi & Hosseini, 2021). Different methodologies have been employed to study the resilience of SCs. Some scholars created conceptual frameworks to build resilience in a variety of contexts, while others adopted empirical approaches and case studies. Quantitative methods (mathematical modelling and statistical analysis) have gained more interest from SC scholars (Gao et al., 2021; Sharma et al., 2023). Here, we dive into quantitative studies in SCRes and classify them into five major categories.

Statistical Analysis of SCRes

This category includes studies that investigated the association between SCRes and other relevant variables using statistical analyses. These studies have often considered SCRes as the dependent variable which is influenced by several independent variables. Aslam et al. (2020) defined SC ambidexterity as the concurrent utilisation of SC adaptability and SC alignment and studied the effects of SC-ambidexterity on SCRes. Using structural equation modelling (SEM), they uncovered that the agility of the SC plays a decisive role in the positive relationship between SC ambidexterity and SCRes. Conducting the partial least squares structural equation modelling (PLS-SEM), Bag et al. (2023) found that big data analytics tools can enhance the resiliency of SCs. In another study, Balakrishnan and Ramanathan (2021) performed structural equation modelling to measure the impacts of digital SC technologies on SC resilience. They realised that the use of digital technologies improves SC performance, either directly or through SCRes. They also uncovered the stronger positive impact of digital technology use on SC resilience and performance after COVID-19 crises compared to before that.

Optimisation for SCRes

The studies in this category have extended linear, mix-integer and nonlinear programming models to optimise SCRes to achieve different objectives, such as maximising service level and minimising unfulfilled demand, during and post-disruption (Paul & Chowdhury, 2020). In other words, for most of the SCRes optimisation models, financial gain is the primary goal, such as minimising the total cost or maximising overall profit. Second, the SC's efficiency or service loss owing to the disruption is quantified by the vulnerability goal variables (—for example, inventory capacity, lead time delay, stock out rate, replenishment). Third, exposure and recovery are two sides of SCRes in terms of recovery time and resource consideration. In most cases, the primary goal of the optimisation models is to accelerate the rate at which a disrupted company's production or supply capacity can be restored. In light of this, some scholars see SCR's main goal as increasing the degree of recovery after a disruption or decreasing the amount of time needed to go back to normal (Hosseini et al., 2019).

Arabsheybani and Khasmeh (2021) proposed a robust bi-objective multi-product optimisation model to evaluate the resiliency of multi-period and multi-item SCN designs. They used multi-criteria decision-making techniques to obtain the weight of influencing variables. Dixit et al. (2016) developed a multi-objective stochastic mixed-integer programming (MOS-MIP) model to minimise the unfulfilled demand and the total transportation cost post-disaster. Zahiri et al. (2017) developed a mixed integer linear programming model with multiple objectives integrating sustainability and resilience to design a pharmaceutical SCN under uncertainty. To handle the uncertainty of the model, they proposed a novel fuzzy possibilistic-stochastic programming approach. Alikhani et al. (2023) developed a multi-method strategy, on the basis of resource dependence theory and two-stage stochastic programming, for selecting the most appropriate resilience strategies, taking into account their positive and negative synergistic impacts under resource constraints. They proposed an unique method for identifying the optimal combination of potential techniques with regard to these synergistic effects. Their results revealed the significance of evaluating synergistic impacts amongst SCRes strategies in the face of budgetary constraints.

Simulation of SCRes

Simulation techniques make it possible to experiment with a real-world process when there is not sufficient data to study it, the process/event is more complex and conventional approaches cannot handle it, or the researcher wants to discover answers to the “what-if” questions by flexibly testing the isolated/simulated system at different scales. Because of the dynamics in business environments with many complex and sometimes unquantifiable relations, evaluating SCRes becomes challenging (Priya Datta et al., 2007). Wu et al. (2013) conducted an agent-based simulation, examining the prevalence of stockouts among retailers dealing with heterogeneous products. Utilising downstream market share as a performance metric, they reported that customer type, initial market share, and the length of the stockout all contributed to the resiliency of the retailers. Priya Datta et al. (2007) developed an agent-based computational framework to enhance the operational resilience of a multi-product, multi-country SC when demand changes and manufacturing and distribution capacity is constrained. Given the dynamic behaviour of SCs, Spiegler et al. (2012) developed a system dynamics model to characterize SCs. They introduced a new metric, “the Integral of the Time Absolute Error (ITAE)”, to evaluate the resiliency of SCs in terms of inventory levels and delivery rates. They found that a robust SC that maintains performance and functionality events in disruption might not necessarily be resilient. Azadeh et al. (2014) performed a simulation to develop different scenarios and different strategies to improve the resiliency of transportation systems. They used DEA to choose the most preferred scenario. Recently, Burgos and Ivanov (2021) explored the implications of COVID-19 on the resilience of food retail SCs. They established a discrete-event simulation model to analyse the operations of SCs and corresponding performance metrics. They indicated that demand spikes and supplier closures had the most significant effect on SC operations and performance, whereas transportation disruptions had a relatively minor effect.

Graph/Network Theory for SCRes

Based on complex network theory, studies in this category consider the SCN as a system consisting of several nodes and paths and model it. Researchers who studied SCRes using graph theory have often used simulation techniques for their analysis. Tan et al. (2019) used graph theory to propose a SCN conceptual model. Mapping the redundant relations between plants and materials, they found that increased structural redundancy of the SCN improves SCRes. Viewing the SCN as a dynamic and complex adaptive system (CAS) that is composed of several firms and demand–supply relationships among them, (Hou et al., 2018) characterised an SCN as a direct graph in which the overall behaviour of the network follows the interactions of firms’ micro-level behaviours. Conduction a multi-agent simulation, they found that trust-based supplier selection is highly robust against occasional and targeted disruptions. Adopting complex network theory, Hearnshaw and Wilson (2013) found that efficient SCs have a “scale-free” structure. They ascertained that aspects like a succinct characteristic path length, a substantial clustering coefficient, and a power-law connectivity distribution can significantly enhance the resilience of the SC. Agarwal et al. (2022) sought to establish a methodology for quantifying SCRes as a value. Graph theoretic approach (GTA) is utilised to assess a firm's SCRes index, and their findings demonstrated that the strategic level component of drivers contributes more to SCRes.

Multi-criteria Analysis of SCRes

Studies that use multi-criteria decision-making (MCDM) techniques rely on expert opinions to analyse the impacts, relations, or weights of different variables associated with SCRes. Kumar and Singh (2022) used the best–worst method (BWM) to determine the weight of variables influencing the resiliency of the SC in the agri-food sector. They implemented quality function deployment (QFD) to evaluate the strategies for enhancing SCRes. In the same context, Shanker et al. (2022) used the grey decision-making trial and evaluation laboratory (DEMATEL) and analytic network process (ANP) methods to improve the resiliency of perishable food SCs. Ekanayake et al. (2022) identified critical SC vulnerabilities and used fuzzy synthetic evaluation (FSE) to analyse them. They found that industrial construction SCs in Hong Kong are very vulnerable to disruptions, and top management support is needed to overcome those vulnerabilities. López and Ishizaka (2019) used a hybrid fuzzy cognitive map (FCM) and analytic hierarchy process (AHP) to forecast the ramifications of offshore outsourcing location decisions on SCRes. They found that the right supplier can preserve the SCRes and improve it. Vergara et al. (2023) offered novel ideas and techniques towards environmental protection and social welfare; modifications have been made to fit SC to the needs of contemporary manufacturing processes. Their study aimed to provide a system for determining the performance levels in sustainable SCRes that blends multicriteria analysis approaches with fuzzy logic. Workplace culture and corporate social responsibility were shown to have the largest impact on SC performance, confirming the framework's emphasis on social dimensions.

Data Envelopment Analysis and SCRes

Implementing resilience strategies improves the ability of SCs to respond to and recover from unforeseen events effectively. SCRes effectively manages and adapts to uncertainties and disruptions such as natural disasters, and promptly restores regular operations (Karbassi Yazdi et al., 2022).

Data envelopment analysis (DEA) is shown to be one of the most popular mathematical approaches to measure the relative efficiency of decision-making units (DMUs) that produce multiple outputs using multiple inputs (Kazemi et al., 2021). DEA has been widely used across different industries, such as evaluating the efficiency of bank branches (Kazemi et al., 2021; Kiani Mavi et al., 2015), sustainability and environmental assessment (Albertini et al., 2021; Wu et al., 2021), energy (Bhunia et al., 2021; Mavi & Mavi, 2019; G. Singh et al., 2021a, 2021b), agriculture and food (Hesampour et al., 2022), healthcare (Gerami et al., 2023), production and distribution planning (Nishizaki et al., 2022), higher education (Tavares et al., 2021), and eco-innovation analysis (Kiani Mavi & Kiani Mavi, 2021; Kiani Mavi & Standing, 2016, 2017) among many other contexts. In the SC and logistics domain, scholars use DEA for evaluating sustainability, eco-efficiency (Alvarez-Rodriguez et al., 2020), supplier and third-party logistics provider selection (Torres-Ruiz & Ravindran, 2019), performance measurement (Wong et al., 2015), and SC risk (Azadeh & Alem, 2010). However, through superb logistics operations, firms with logistics innovation capacity could be able to control SC risks (Wang et al., 2020).

The linkage between DEA and SCRes is comprehended through performance evaluation and enhancement. Using DEA to examine the relative efficiency of decision-making units within a SC, specifically during unpredicted circumstances, provides crucial insight. This process underscores inefficient DMUs and those units showing resilience, which can guide strategic planning within the SC (Azadi et al., 2022). By numerically representing the efficiency of various DMUs within a SC (such as logistic hubs, manufacturing units, etc.), DEA equips the management team to locate inefficiencies, identify potential enhancements, and distribute resources to maximise total efficiency. This process bolsters the SC's resilience level, allowing it to resist and rebound from adversities more effectively (Kraude et al., 2022; Mohammadnazari et al., 2023). The forecasting capability of DEA supports the development of strategies to mitigate risks, enhancing the SC's capacity to adjust and bounce back from unforeseen incidents, e.g. environmental calamities, a vendor closing shop, or drastic demand variations, and in turn amplifying its resilience (Heidari et al., 2017).

Measuring the sustainability and resilience of SCNs is difficult for many decision-makers. The increasing complexity of SCs has made them increasingly vulnerable to disruptions in the business environment. SC resilience is strategic planning over disruption periods to mitigate SC vulnerabilities and speed recovery. Pourhejazy et al. (2017) employed data envelopment analysis to assess the resilience of SCNs. They used topological and operational variables to evaluate the resiliency of liquefied petroleum gas (LPG) companies. Kazemi Matin et al. (2022) developed a network DEA model to evaluate the sustainability and resilience of blood SCNs. Given the presence of undesirable factors, such as waste of donated blood, they included undesirable outputs in their model. Yazdanparast et al. (2018) used a hybrid approach consisting of Z-number DEA and a neural network to evaluate the resiliency of automotive SCs in terms of resilience enablers.

The major shortcoming of traditional DEA models for efficiency analysis is that they allow each DMU to freely choose a weight for the input and output variables in order to maximise its relative efficiency (Hatami-Marbini & Saati, 2018). The common set of weight (CSW) models have been developed to address this shortcoming by evaluating all DMUs using a consistent and identical weights vector (Heidary Dahooie et al., 2021).

Scholars have adopted several approaches to develop a CSW. Jahanshahloo et al. (2011) employed the Zionts–Wallenius technique to generate a common set of weights in which decision-makers' preferences have been considered. The capacity of goal programming (GP) to minimising undesirable deviations from multiple objective functions has made it a suitable technique for developing a common set of weights in DEA (Gharakhani et al., 2018; Makuei et al., 2008; Omrani et al., 2019). Adopting an efficiency-fitting perspective, Wang et al. (2011) used regression analysis to propose the common set of weights model. Their target efficiencies were the conventional DEA efficiencies that DMUs tried to achieve using common weights. Chiang et al. (2011) used a separation vector to transform the multiple objectives fractional linear programming problem (MOFP) into a single objective linear program in order to generate common weights. They implemented their proposed CSW for analysing Beijing Olympic Games. Using mixed-integer linear programming (MILP), Özsoy et al. (2021) proposed a CSW model to identify the most efficient DMU. They performed a simulation and showed that the proposed CSW's discrimination power is high enough to distinguish the most efficient DMU. While many CSW models have been proposed for a specific point in time, Kiani Mavi and Kiani Mavi (2019) developed a CSW model for the Malmquist productivity index (MPI) using the ideal point method to evaluate the efficiency of DMUs over time. More recently, Wang et al. (2021) suggested a common weight analysis using the bargaining game theory. They proposed a secondary goal to minimise the sum of differences between the self-assessment efficiency and the peer-assessment efficiency of each DMU. Abedian et al. (2023) introduced an integrated decision-making system that utilised fuzzy set theory and the DEA methodology for supplier selection. Their strategy for selecting suppliers is based on generic, resilient, and environmentally friendly criteria. In addition, fuzzy set theory was used to assess and categorise the performance of suppliers and to evaluate the weights of their criteria. In addition, its proposed model can be built to accommodate any number of suppliers and metrics.

Research Gap

The extant literature on SCRes has provided valuable insights. However, a significant research gap exists in effectively measuring and enhancing resilience in SCNs, particularly in the Pacific region. It is imperative for companies to have an optimal balance between operational efficiency and organisational flexibility to hedge uncertainty and mitigate disruptions arising from unpredictability. From a methodological perspective, existing approaches to assess the resilience of SCs frequently exhibit limitations in their ability to consider non-discretionary and non-controllable variables and their capacity to offer a comprehensive ranking of SCNs based on the metrics that define the notion of resilience. On the other hand, the existing body of literature on SCRes in the Pacific region is limited, particularly in strategies that consider distinctive regional characteristics such as population density and the geographical distances between supply and demand nodes. There is an apparent necessity for developing an evaluation framework that specifically targets the deficiencies in assessing SCRes. This framework provides valuable insights to SC managers in the Pacific region.

Proposed Ideal Point Common Weights Model with Non-discretionary and Non-controllable Inputs

Charnes et al. (1978) crafted the CCR model to measure the relative efficiency of similar DMUs. Under constant returns to scale (CRS), the relative efficiency of DMUp is obtained by Program (1).

$$ \begin{aligned} & E_{p}^{{{\text{CCR}}}} = {\text{Max}} \mathop \sum \limits_{r = 1}^{s} u_{r} y_{rp} \\ & {\text{Subject }}\,{\text{to}} \\ & \quad \quad \mathop \sum \limits_{r = 1}^{s} u_{r} y_{rj} - \mathop \sum \limits_{i = 1}^{m} v_{i} x_{ij} \le 0;\,\quad j = 1,2, \ldots ,n \\ & \quad \quad \mathop \sum \limits_{i = 1}^{m} v_{i} x_{ip} = 1 \\ & \quad \quad u_{r} , v_{i} \ge 0; r = 1,2, \ldots ,s;\quad i = 1,2, \ldots ,m \\ \end{aligned} $$
(1)

If \({E}_{p}^{*}=1\), then \({{\text{DMU}}}_{p}\) is called efficient; otherwise, when \({E}_{p}^{*}<1,\) it is referred to as an inefficient DMU.

In real-world settings, managers are not able to control non-discretionary and non-controllable inputs that are exogenously fixed (Lotfi et al., 2007). By extending the CCR model, therefore, we propose Program (2) to evaluate the efficiency of DMUs when they are operating with discretionary (D), non-discretionary (ND), and non-controllable (NC) inputs under CRS conditions. We distinguish between the non-controllable and non-discretionary inputs, assuming that no slack is allowed for non-controllable inputs (Cooper et al., 2007).

$$ \begin{aligned} & E_{p}^{{{\text{CCR}}}} = {\text{Max}} \mathop \sum \limits_{r = 1}^{s} u_{r} y_{rp} - \mathop \sum \limits_{k = 1}^{l} f_{k} z_{kp} - \mathop \sum \limits_{c = 1}^{b} h_{c} d_{cp} \\ & {\text{Subject}}\,{\text{ to}}: \\ & \quad \quad \mathop \sum \limits_{r = 1}^{s} u_{r} y_{rj} - \mathop \sum \limits_{k = 1}^{l} f_{k} z_{kj} - \mathop \sum \limits_{c = 1}^{b} h_{c} d_{cj} - \mathop \sum \limits_{i = 1}^{m} v_{i} x_{ij} \le 0;\quad { }j = 1,2, \ldots ,n \\ & \quad \quad \mathop \sum \limits_{i = 1}^{m} v_{i} x_{ip} = 1 \\ & \quad \quad u_{r} ,v_{i} \ge 0{ }\quad \quad i = 1, \ldots .,m{ };{ }r = 1, \ldots .,s \\ & \quad \quad f_{k} > 0\quad \quad \quad k = 1, \ldots ,l \\ & \quad \quad h_{c} \to {\text{free}} \quad c = 1, \ldots ,b{ } \\ \end{aligned} $$
(2)

where \({x}_{ij},i=1,\dots ,m\) are the discretionary inputs of \({DMU}_{j}\), \({z}_{kj}, k=1,\dots ,l\) are the non-discretionary inputs of \({DMU}_{j}\), and \({d}_{cj}, c=1,\dots ,b\) are the non-controllable inputs of \({DMU}_{j}\).

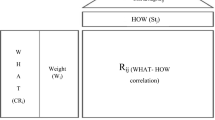
The principal advantage of producing a common weights vector is restricting the weight flexibility of original DEA models to provide a consistent and identical basis to evaluate all DMUs (Shabani et al., 2019). Conducting CSW analysis, all DMUs do not get the full efficiency score (Hosseinzadeh Lotfi et al., 2013). Regardless of the approach to generating CSW, the common set of weights models enable managers and policymakers to evaluate the performance of all DMUs on a consistent basis to enunciate strategies to enhance the performance of inefficient ones. The rationale of the deal point method is minimising the distance between every DMU and the ideal or the best DMU with the lowest amount of inputs and the highest amount of outputs (Sun et al., 2013). Thus, \({DMU}_{I}\), the ideal DMU, is defined as Eq. 3:

$${{\text{DMU}}}_{I}=\left({X}_{{\text{min}}},{Y}_{{\text{max}}}\right)$$
(3)

where \({{\text{x}}}_{i ({\text{min}})}={\text{min}}\left\{\left.{x}_{ij}\right|j=1,\dots ,n\right\}, \left(i=1,\dots ,m\right)\mathrm{ and }{{\text{y}}}_{r ({\text{max}})}={\text{max}}\left\{\left.{y}_{rj}\right|j=1,\dots ,n\right\}, \left(r=1,\dots ,s\right)\). In Eq. 3, \({X}_{{\text{min}}}\) denotes the vector of inputs and \({Y}_{{\text{max}}}\) denotes the vector of outputs of the ideal DMU.

Since the ideal point model tries to minimise the distance between each DMU and the ideal DMU, then Model (4) meets this objective and gives a CSW (Sun et al., 2013).

$$ \begin{aligned} & {\text{Min}}\,{ }Z = \mathop \sum \limits_{j = 1}^{n} \left( {\mathop \sum \limits_{r = 1}^{s} u_{r} y_{{r\left( {\max } \right)}} - \mathop \sum \limits_{r = 1}^{s} u_{r} y_{rj} } \right) + \mathop \sum \limits_{j = 1}^{n} \left( {\mathop \sum \limits_{i = 1}^{m} v_{i} x_{ij} - \mathop \sum \limits_{i = 1}^{m} v_{i} x_{{i\left( {\min } \right)}} } \right) \\ & {\text{Subject to}}: \\ & \quad \quad \mathop \sum \limits_{r = 1}^{s} u_{r} y_{rj} - \mathop \sum \limits_{i = 1}^{m} v_{i} x_{ij} \le 0;{ }\quad \quad j = 1,2, \ldots ,n \\ & \quad \quad \mathop \sum \limits_{i = 1}^{m} v_{i} x_{{i\left( {{\text{min}}} \right)}} = 1 \\ & \quad \quad \mathop \sum \limits_{r = 1}^{s} u_{r} y_{{r\left( {{\text{max}}} \right)}} = 1{ } \\ & \quad \quad u_{r} ,v_{i} \ge \varepsilon > 0,\quad i = 1, \ldots .,m,\quad r = 1, \ldots .,s \\ \end{aligned} $$
(4)

The objective function in Model (4) minimises the total distance between each DMU and the ideal DMU. The first set of constraints guarantee that the relative efficiency of DMUs do not exceed unity. The second and third constraints determine weights of inputs and outputs to ensure that the ideal DMU lie on the efficiency frontier.

Implementing the ideal point method to generate a common set of weights for Model (2) results in the common weights Model (5):

$$ \begin{aligned} & {\text{Min}} \,Z = \mathop \sum \limits_{j = 1}^{n} \left( {\left[ {\mathop \sum \limits_{r = 1}^{s} u_{r} y_{{r\left( {\max } \right)}} - \mathop \sum \limits_{k = 1}^{l} f_{k} z_{{k\left( {\min } \right)}} - \mathop \sum \limits_{c = 1}^{b} h_{c} d_{{c\left( {\min } \right)}} } \right] - \left[ {\mathop \sum \limits_{r = 1}^{s} u_{r} y_{rj} - \mathop \sum \limits_{k = 1}^{l} f_{k} z_{kj} - \mathop \sum \limits_{c = 1}^{b} h_{c} d_{cj} } \right]} \right) + \mathop \sum \limits_{j = 1}^{n} \left( {\mathop \sum \limits_{i = 1}^{m} v_{i} x_{ij} - \mathop \sum \limits_{i = 1}^{m} v_{i} x_{{i\left( {\min } \right)}} } \right) \\ & {\text{Subject }}\,{\text{to:}} \\ & \quad \quad \mathop \sum \limits_{r = 1}^{s} u_{r} y_{rj} - \mathop \sum \limits_{k = 1}^{l} f_{k} z_{kj} - \mathop \sum \limits_{c = 1}^{b} h_{c} d_{cj} - \mathop \sum \limits_{i = 1}^{m} v_{i} x_{ij} \le 0; \quad j = 1,2, \ldots ,n \\ & \quad \quad \mathop \sum \limits_{i = 1}^{m} v_{i} x_{{i\left( {\min } \right)}} = 1 \\ & \quad \quad n\mathop \sum \limits_{r = 1}^{s} u_{r} y_{{r\left( {\max } \right)}} - \mathop \sum \limits_{j = 1}^{n} \mathop \sum \limits_{k = 1}^{l} f_{k} z_{kj} - \mathop \sum \limits_{j = 1}^{n} \mathop \sum \limits_{c = 1}^{b} h_{c} d_{cj} = n \\ & \quad \quad u_{r} ,v_{i} \ge \varepsilon > 0 \quad i = 1, \ldots .,m ; r = 1, \ldots .,s \\ & \quad \quad f_{k} > 0 \quad k = 1, \ldots ,l \\ & \quad \quad h_{c} \to {\text{free}} \quad c = 1, \ldots ,b \\ \end{aligned} $$
(5)

Model (5) determines the common set of weights for inputs (including non-discretionary and non-controllable) and outputs to minimise the overall distance between all DMUs and the idel DMU. Model (5) distinguishes from Model (4) by modelling the non-discretionary and non-controllbale inputs. Because managers do not have control over these variables, they negatively contribute to the outputs \(\left[\sum_{r=1}^{s}{u}_{r}{y}_{rj}-\sum_{k=1}^{l}{f}_{k}{z}_{kj}-\sum_{c=1}^{b}{h}_{c}{d}_{cj}\right]\) of DMUs. The first set of constraints in Model (5) ensures that the relative efficiency of each DMU remains in the range (0,1] given that \({h}_{c}\) is a non-constrained-in-sign variable. The second and third constraints position the ideal DMU on the efficiency frontier.

The optimal solution of Model (5), \(\left({u}_{r}^{*},{v}_{i}^{*},{f}_{k}^{*},{h}_{c}^{*}\right),\) will be the common set of weights to evaluate the relative efficiency of DMUs which is obtained by Eq. 6, where \({E}_{p}^{*}\) is the efficiency of \({DMU}_{p}\) calculated by the common set of weights.

$${E}_{p}^{*}=\frac{\left[\sum_{r=1}^{s}{u}_{r}^{*}{y}_{rp}-\sum_{k=1}^{l}{f}_{k}^{*}{z}_{kp}-\sum_{c=1}^{b}{h}_{c}^{*}{d}_{cp}\right]}{\sum_{i=1}^{m}{v}_{i}^{*}{x}_{ip}} $$
(6)

Case Study: LPG Supply Chain

There has been a notable shift towards using LPG in the energy domain, notably in Pacific region, motivated mainly by its limited or absence of subsidies. LPG has emerged as a viable option that is not only economically accessible and environmentally friendly but also demonstrates superior distribution capabilities. This practical energy source is both cost-effective and easily transportable. Additionally, it establishes a sustainable trajectory for attaining environmental goals by significantly reducing home and industrial pollutants. This is especially evident when it replaces more carbon-intensive fuels like firewood or kerosene in various applications (Abhimanyu Bhuchar, 2020). LPG is progressively emerging as a cost-effective and environmentally friendly intermediate alternative during the shift from conventional liquid petroleum fuels to renewable energy sources. LPG is now used by Pacific Island governments and territories, mainly for domestic culinary activities. If the use of LPG were to be extended to replace all cooking kerosene and biomass throughout the Pacific area, it is plausible that the existing demand may see a twofold increase. The rationale for advocating for this modification is grounded on health considerations, environmental sustainability, and potential cost reductions for individual homes. Nevertheless, it is reasonable to anticipate that the rise in demand will lead to varying degrees of improved economies of scale across Pacific Island Countries and Territories. The potential escalation in volume may prompt some Pacific Island Countries and Territories to transition towards bulk distribution methods, hence potentially exerting a substantial influence on the price at which goods are transported. The use of LPG in transportation or the implementation of local piped gas networks might potentially lead to an additional rise in volumes and perhaps result in improved economic benefits associated with bulk imports. The ongoing experimentation in Fiji involves the use of LPG in heavy-duty vehicles and the amalgamation of LPG with other fuel sources for power production, drawing upon existing commercial technologies present in Australia. In 2050, although LPG continues to have a restricted use in cooking within some rising markets and developing nations, the predominant sources catering to 95% of cooking energy requirements are electricity and contemporary bioenergy (Morgan & Atkinson, 2016). Therefore, all the processes that are related to LPG have emerged as key elements of their economic framework. Due to the intricate and expensive nature of installing infrastructure for LPG, it is essential to consider numerous factors. Additionally, given the potential disruptions and risks across every stage of the process, effective management is crucial to enhance the resilience of the system. Energy SCs are of huge significance for societies. Any disruption in the energy sector and its associated SCs might have devastating economic impacts on companies dealing with producing and distributing energy products (Urciuoli et al., 2014).

Many factors, such as supply and demand nodes and their available capacity, are important for assessing the resilience of SCNs, as any disruption in those variables results in the uncertainty and vulnerability of the SCN (Alikhani et al., 2021; Lu et al., 2018). The inputs and outputs for measuring supply chain resilience using common weight DEA model are explained below:

Outputs:

Node degree and clustering coefficient: These are topographical measurements emphasising the SCN's structural design and connectivity. High connectivity typically suggests enhanced resilience as suppliers with extensive connections have various alternatives to supply goods, thereby reducing disruption risks (Pourhejazy et al., 2017; Zhao et al., 2011). These parameters comprise the average node degree (the mean number of connections per node) and the average clustering coefficient (a measure of the degree of mutual connectivity among nodes).

Both node degree (Chen & Lin, 2012; Hearnshaw & Wilson, 2013; Kim et al., 2015; Sahlmueller & Hellingrath, 2022; Xia, 2020; Xu et al., 2016) and clustering coefficient (Geng et al., 2014; Hearnshaw & Wilson, 2013; Li et al., 2020; Mari et al., 2015; Xia, 2020) have positive impacts on supply chain resilience by showing how SC nodes are interconnected.

The average node degree (AND) shows the average number of connections for every node and is obtained by Eq. 7;

$${\text{AND}}=\frac{1}{N}\sum_{i=1}^{N}{k}_{i}$$
(7)

where N is the total number of nodes in the network and \({k}_{i}\) represents the number of connections between node i and the reset of the network.

In addition, the average clustering coefficient (ACC) evaluates the degree of mutual exchange connections between the nodes in the network. ACC is calculated by Eq. 8;

$${\text{ACC}}=\frac{1}{N}\sum_{i=1}^{N}\frac{{N}_{i}}{{k}_{i}({k}_{i}-1)/2}$$
(8)

where \({N}_{i}\) is the number of immediately connected neighbours of node i.

Inputs:

Number of supply nodes: This parameter, another topographical measure, indicates the quantity of supply points in the SCN. A lower figure implies a more centralised network, which might result in slower recovery post-disturbances. The number of supply nodes also impacts the scale of potential disruptions, with a decentralised system typically yielding less severe impacts due to the distributed nature of the supply nodes. The number of supply nodes can enhance the capacity of the SCN, better accommodating demand than before. This can be equated with supplier diversity; a greater number of nodes may bolster flexibility (Etemadnia et al., 2015; Khan et al., 2021; Lam, 2021; Wang et al., 2015; Zhao et al., 2022). The density of a supply network means that a higher number of nodes are located at short distances. In case of local disruptions such as natural disasters, a higher density increases the vulnerability of the SCN and, as a result, decreases the SCRes (Dixit et al., 2020b).

Available capacity: This operational metric reveals the presence of spare supply capacity within the network. It is deduced through the complete potential supply ability across the network and an availability ratio. This measure provides a lucid indication of the network's robustness in handling disruptions. Available capacity serves as a resilient strategy for networks. While increasing capacity may escalate costs, particularly holding and warehousing expenses, it can strengthen the network against disruptions (Hosseini et al., 2019; Mohammed et al., 2023; Shashi et al., 2020; Tan et al., 2020).

Total distance: As an operational parameter, total distance signifies the cumulative distance between demand and supply nodes. The distance between nodes has implications for lead times, transportation expenditures, and vulnerability to disruptions. Minimising this distance can shield the SCN from potential disruptions and uncertainties (Chen & Lin, 2012; Djomo et al., 2023; Hearnshaw & Wilson, 2013; Xu et al., 2016; Zahraee et al., 2022). Lesser total distance generally contributes to increased resilience as it reduces logistical complexities and facilitates more efficient demand–supply balancing.

Population density: This societal factor assesses the populace concentration around supply facilities. Higher densities indicate heightened societal risk if a supply facility hazard occurs. This measure provides an insight into potential societal impact and can influence risk management strategies. This metric is paramount in evaluating network resilience, with denser areas indicating heightened potential societal impacts (Cooper et al., 2007; Gružauskas, 2020; Gružauskas & Burinskienė, 2022; Haeri et al., 2020; Liu & Zhao, 2015). This study considers population density a non-controllable input (Cooper et al., 2007), as SC managers and decision-makers do not control it.

Data for the SCNs are shown in Table 1, which are adopted from Pourhejazy et al. (2017).

Table 1 LPG SC data
Full size table

Running MATLAB R2016b to solve Models (2) and (5) gives the efficiency score of SCNs. This study assumes that outputs change at the same ratio that inputs change and vice versa, so it employs the CCR model for efficiency analysis. As mentioned, Model (2) provides different sets of weights for each SCN. For example, Table 2 shows the weights of inputs and outputs for SCN-1 and SCN-2 with the highest and lowest ranks, respectively.

Table 2 Weights of inputs and outputs using Model (2)
Full size table

As the number of nodes in a network grows, the network's vulnerability becomes magnified, thereby exacerbating the potential for susceptibility (Alikhani et al., 2023). This is because disruptions at any one node may create delays and disruptions in manufacturing, distribution, and customer service across the whole SC (Sawik, 2022). A SC's resilience can be enhanced by fortifying its nodes to totally or partially shield facilities against threats (Sawik, 2022).

Organisations seeking to increase their resilience to the impact of disruptions might consider investing in the available capacity and diversifying their supply sources to swiftly adjust to unanticipated shifts in demand or supply (Goldbeck et al., 2020). When dealing with disruptions, a SC with excess capacity is stronger than one without (Riccardo et al., 2021). This is because a "buffer" created by the excess capacity can accommodate swings in demand or supply. Therefore, the availability of backup capacity is also crucial since it helps mitigate the impact of disruptions (Hosseini et al., 2019). Back-up capacity helps speed up the SC's recovery after disruptions (Ivanov, 2019).

Distance, in this context, refers to the physical separation between the SC's various nodes, such as suppliers, manufacturers, distributors, and warehouses (Birkie & Trucco, 2020).

Transportation costs, lead times, and vulnerability to disruptions all rise in direct proportion to the distance and separation of these nodes (Li et al., 2017; Musazzi et al., 2020).

SC management faces difficulties in communication and coordination due to the inherent complexity that distance adds to the process (Li et al., 2017). There are a number of ways in which physical separation weakens SCs. For instance, as lead times are extended, SCs may be more susceptible to disruptions since delays at any point in the chain might have a ripple effect on the other parts (Sawik, 2023). In addition, transportation costs may rise with increasing distance, cutting into SC profits (Mohammed et al., 2019). Finally, as SCs get more complicated, it might be more difficult to effectively coordinate and communicate with other levels (Pimenta et al., 2022). However, geographical diversification of suppliers is one method through which businesses can mitigate the detrimental effects of distance on SCRes (Li et al., 2017). By doing so, businesses continue to provide a consistent supply of products and services despite disruptions at a single site. They could become more resilient and competitive as a result.

Population density may have a substantial effect on SCRes since it can alter the availability and efficacy of resources and transportation networks (Salama & McGarvey, 2021). Population density can have a significant impact on distribution strategies, as it can influence the availability and efficiency of transportation systems, the cost of resources, and the complexity of the SCN. The allocation of resources in low-density areas may be more challenging and require different distribution strategies than those in high-density areas (Gružauskas & Burinskienė, 2022). Population density can impact the efficiency of transportation networks since excessive traffic volume and congestion can cause delays and interruptions in the transfer of products. This may affect the speed and dependability of delivery, which in turn can affect SCRes (Gružauskas, 2020).

Node degree, when discussing SCNs, measures how many connections an individual node has to other nodes (Xia, 2020). The degree of a node is a topological indicator that provides insight into the interconnectedness and complexity of a SCN, both of which are vital in determining the network's resilience (Zhao et al., 2011). Most SC partners choose the company with the highest capacity, and this is reflected in the node degree. Manufacturers and distributors with a higher degree indicate stronger buying power and a wider reach to potential clients, while suppliers with a higher degree indicate a more robust supply capacity. Hence, the new node is added to the network according to the current nodes and a probability that is proportionate to the degree of the existing nodes. Therefore, in addition to indicating the node's relative relevance in the network, a node's degree may provide insight into its practical capabilities (Geng et al., 2013).

A node's tendency to cluster with others is quantified by its clustering coefficient. Each node's clustering may be thought of as the percentage of all potential triangles (3 loops) that pass through that node (Li et al., 2020). A high clustering coefficient enhances the SC's susceptibility (Brandon-Jones et al., 2015). The development of SCNs is intricately linked to the manner in which levels engage with each other through interconnections and interactions. In this regard, the clustering coefficient serves as an invaluable metric for measuring the level of connectivity within such networks. By capturing the extent to which nodes are interconnected within the network, the clustering coefficient offers a powerful tool for evaluating the evolution of SC systems (Geng et al., 2014).

The flexibility of weights and choosing different weighting schemes by the conventional CCR model results in having 13 efficient SCNs with an efficiency score of 1. When 59% of SCNs are identified as efficient, discriminating them for complete ranking is almost impossible. The proposed CSW model resolves this issue by generating a common set of weights to analyse the resilience of SCNs as follows:

$$ \begin{array}{*{20}c} {u_{1}^{*} = 0.4742 ; } & {u_{2}^{*} = 2.0673e - 17} \\ {v_{1}^{*} = 7.0303e - 13 ; } & {v_{2}^{*} = 1.8867e - 5} \\ {f_{1}^{*} = 9.9404e - 18 ;} & {h_{1}^{*} = 3.5688e - 17} \\ \end{array} $$

Using Eq. 6, the efficiency score of SCNs in terms of resiliency is obtained, as shown in Table 3. The projection of discretionary inputs on the CCR efficiency frontier (4th and 5th columns) shows that SCNs can reduce their inputs to the projected values to produce the same outputs in order to become efficient (resilient). On the other hand, the projection of outputs on the CCR efficiency frontier (6th and 7th columns) show that SCNs can become efficient/resilient by expanding their clustering coefficient and node degree while using the same amount of inputs. Findings show that the CCR model identifies 13 efficient SCNs with an average efficiency score of 0.9468, while the proposed CSW model identifies one SCN with the highest efficiency score with the average of 0.7335. Therefore, the proposed CSW model ensures complete ranking of DMUs with a higher discrimination power.

Table 3 Resilience score of LPG SCNs
Full size table

Findings show the resilience score of 22 SCNs, indicating that SCN-1 has the highest resilience score (0.9459) and SCN-10 has the lowest resilience score (0.5813). Comparing the configuration of SCN-1 and SCN-3, the two top SCNs show that SCN-1 has yielded fewer outputs using fewer discretionary inputs. While their first outputs are close to each other, the clustering coefficient of SCN-1 is ten times smaller than that of SCN-3. The higher resilience score of SCN-1 can be attributed to inputs, both discretionary inputs (number of supply nodes and available capacity) and non-discretionary inputs (total distance) and non-controllable inputs (population density). SCN-1 has technically operated very well as it has used fewer resources compared to SCN-3. While SCN-1 has a better status than SCN-3 in terms of population density (less population density increases SCRes), it suffers from a long geographical distance to demand nodes which reduces its capability to respond to disruptions and be resilient. The optimal solution shows that the average node degree is the most important output variable (\({u}_{1}^{*}=0.4742\)) in determining the resilience of SCNs. This variable measures the connectivity of elements of the SCN, and higher connectivity means that knowledge sharing among the nodes is higher, so they have a common understanding of the disruptive situations and are better prepared to respond to them.

Comparing SCN-1 as the highly resilient and SCN-10 as the least resilient SCN shows that SCN-10 has produced much higher outputs with significantly higher amounts of discretionary inputs. While SCN-10 enjoys a shorter distance (over 34% shorter), its population density is over 200% more than that of SCN-1, which reduces its capacity to respond to disruptions and recover from them after any disruption occurs. As the technical efficiency of SCN-10 is 0.5813, so, 0.4187 parts of the discretionary inputs are not efficiently used to contribute to its resilience. In order to improve its resilience and operate as a fully resilient SCN, while it is operating under a 106,870 km distance and 13,895 population density, SCN-10 can reduce its discretionary inputs from (5, 87,422.7) to \(\left(2.9065\approx 3, 50818.82\right)\) to yield the same outputs (2.022, 1.6). To improve the market share and SC surplus, SCNs tend to expand their outputs instead of reducing the inputs. Focusing on SCN-10 from the output perspective reveals that if this SCN makes more connections with other networks and increases the outputs from (2.022, 1.600) to (3.4784, 2.7525), can position itself on the efficiency frontier and become a resilient network. These benchmarking practices help SCNs to focus on their capabilities to enhance their resilience.

Conclusion

Results show that various configurations of SCNs can impact the resilience level. For the Pacific region, this could imply that optimal planning and management of the number of supply nodes, their capacities, and their geographical locations could enhance the resilience of their LPG SCs. Managers can easily control discretionary inputs such as the number of supply bases and the network's available capacity in supplying the items during recovery. While increasing the capacity and adding to the supply nodes are costly for the SCN, these practices increase the resilience of SCNs, and if required, managers implement strategies to accomplish them.

The LPG SCs in the Pacific region are recommended to increase capacity and diversify supply sources to improve SCRes. Table 3 implies that LPG SCs should invest in infrastructures to increase capacity and diversify sources of LPG to react expeditiously to changing demand and supply. On the other hand, we found that non-discretionary inputs such as total distance among the supply and demand nodes and population density greatly impact the resilience of SCNs. Since manipulating non-controllable inputs such as population density is impossible and changing some non-discretionary inputs such as total distance among the supply and demand nodes is extremely costly (and even in many cases, the losses of the SCN because of longer distances are less than the cost of moving supply nodes to geographically closer locations), managers must formulate strategies to minimise the negative impacts of disruptions. Provided the above-mentioned non-discretionary inputs, holding extra inventories in the supply bases and securing multiple supply sources improves the resilience of SCNs. Given the unique geographical dispersion of the Pacific Islands, the distance between SC nodes could impact SCRes. Therefore, determining the supply node's optimal and strategic location and focusing on efficient transportation is important in helping managers make optimal decisions. Besides, key nodes, i.e. major distribution centres or suppliers, should have strong connections to other nodes to react to disruptions appropriately. The Pacific Island nations can enhance the resilience of their SCs by increasing the clustering coefficient and node degree of their SCNs by building more connections with other SCs, thus ensuring smoother operations during disruptions.

Given the flow of materials, cash, and information between the SC partners, it is expected that the information flow experiences a higher clustering coefficient compared to the other flows in the efficient SCs. The drawback of having a low clustering coefficient is that it might result in more inefficiencies due to the higher difficulty of coordination and collaboration throughout the network (Hearnshaw & Wilson, 2013). Thus, to improve the efficiency and therefore the resilience of supply networks, SC managers can build more social connections with other members of the network to increase the mutual flow of materials and information. Furthermore, in the post-pandemic era, good resilient strategies involve proactive strategies that anticipate changes and reactive strategies that respond to new challenges.

SCs are constantly exposed to disruptions, including natural disasters and man-made disruptive events. SCs need to improve their capabilities to proactively and reactively respond to disruptions through risk mitigation and devising business continuity plans. In the post-pandemic period, the issue of SCRes is to adapt to new and unanticipated disruptions while maintaining a balance between efficiency and adaptability. The pandemic has shown the weaknesses and interdependencies of global SCs, requiring companies to engage in resilience-building strategies such as supplier diversity, enhanced visibility and transparency, and the use of new technology. Nonetheless, these solutions may need substantial expenditures and may have an effect on the cost and pace of operations, resulting in a trade-off between resilience and profitability. In this context, SC finance emerges as a critical lever to balance this trade-off. By providing more efficient financing options, it enhances SC cost optimisation, thereby reducing the cost burden of resilience strategies. Additionally, it can mitigate SCRes risks by ensuring more robust financial flows, contributing to SCRes through enhanced financial stability, which is vital in periods of disruption. Moreover, the strategic use of SC finance is instrumental in enhancing SC performance by aligning financial flows with operational needs, ensuring that SCs are not only resilient but also financially optimised. The SCRes of 22 LPG SCs has been measured and analysed in this study. Given the presence of several non-discretionary and non-controllable factors and their impacts (which are more likely negative) on the resilience of SCs, we developed a common set of weights model with non-discretionary and non-controllable inputs to evaluate the resilience of SCNs. The proposed model has the capability to provide SC managers with the complete ranking of the SCNs and highlight the best practices by solving only one linear program. SCNs are able to determine their excess inputs and try to minimise them to increase resilience. Looking at the population density and total distance among supply and demand nodes, holding extra inventories and extending the supplier base are two suitable strategies that speed up the recovery from disruptions. Despite the provided strengths of the proposed model, it does not look at the outputs and how much they should increase to make the network efficient. Future studies can extend the proposed methodology to non-oriented DEA models to assess the resilience of SCNs to offer a wider view of SCRes and the needed output upswing for peak operations. Secondly, investigating the changing nature of SCs can delve deeper into resilient responses to evolving situations. Lastly, studying the effects of technologies like artificial intelligence and blockchain on SCRes can shed light on the influence of digital evolution on SC efficiency and adaptability.