Introduction

In this paper, we consider nonhomogeneous differential equation with variable delays in the form [3, 5, 10, 12, 23, 30, 37, 38].

$$\begin{aligned} y'\left( t\right) =P_{o} (t)+P_{1} (t)y(t)+\sum _{j=2}^{m}P_{j} (t)y\left( t-\tau _{j} (t)\right) \end{aligned}$$
(1)

under the initial condition \(y(a)=\lambda\), where the coefficients \(P_{j}(t)\) and the delays \(\tau _{j}\) are continuous functions on the interval \(0\le a\le j\le b\) and the delays are nonnegative, \(\tau _{j} \left( t\right) \ge 0\) for \(t\ge a\).

Delay differential equations of the type 1 arise in a variety of applications including control systems, electrodynamics, mixing liquids, neutron transportation, population models, physiological processes and conditions including production of blood cells [1, 14, 23, 25, 27, 28, 34, 37].

In the case of bounded delays, many authors using standard techniques [3, 10, 20, 27, 34, 37] have studied the asymptotic behavior of solutions, the asymptotic stability in equations and the existence of positive periodic solutions of delay equations. However, most of the mentioned type delay equations have not analytical and numerical solutions; therefore, numerical methods are required to obtain approximate solutions. For this purpose, by means of the matrix method based on collocation points which have been given by Sezer and coworkers [2, 6, 16, 17, 21, 26, 29, 36], we develop a novel matrix technique to find the approximate solution of Eq. 1 under the initial condition \(y(a)=\lambda\) in the truncated Morgan–Voyce series form

$$\begin{aligned} y\left( t\right) \cong y_{N} \left( t\right) =\sum _{n=0}^{N}y_{n} b_{n} (t) ,\; \; a\le t\le b \end{aligned}$$
(2)

where \(y_{n},\;n=0,1,\ldots ,N\) are coefficients to be determined; \(b_{n}, n=0,1,\ldots ,N\) are the first kind Morgan–Voyce polynomials defined by [11, 32, 33]

$$\begin{aligned} b_{n} \left( t\right) =\sum _{j=0}^{n}\left( \begin{array}{c} {n+j} \\ {n-j} \end{array}\right) \, t^{j} ,\quad n\in {\mathrm{N}},\; \; a\le t\le b \end{aligned}$$
(3)

Here, the set of polynomials \(\left\{ b_{n} \left( t\right) \right\}\) has the following properties [11, 15, 19, 32]

  1. 1.

    The polynomials \(b_{n} \left( t\right)\) defined by 3 are recursively given by the relation

    $$\begin{aligned} b_{n} \left( t\right) =\left( t+2\right) b_{n-1} \left( t\right) -b_{n-2} \left( t\right) ,\quad n\ge 2 \end{aligned}$$

    with \(b_{o} \left( t\right) =1\) and \(b_{n} \left( t\right) =t+1\).

  2. 2.

    The polynomials \(y=b_{n} \left( t\right) ,\; n=0,1,\ldots\) are solutions of the differential equation

    $$\begin{aligned} t\left( t+4\right) y''+2\left( t+1\right) y'-n\left( n+1\right) y=0. \end{aligned}$$
  3. 3.

    The first four Morgan–Voyce polynomials of the first kind are obtained from 3 as

    $$\begin{aligned} b_{o} \left( t\right)= & 1,\; b_{1} \left( t\right) =t+1,\; b_{2} \left( t\right) =t^{2} +3t+1,\; \\ b_{3} \left( t\right)= & t^{3} +5t^{2} +6t+1,\ldots \end{aligned}$$

Fundamental matrix relations

In this section, we compose the matrix relations of Eq. 1 and its solution Eq. 2. For this aim, we first write the matrix form of the finite Morgan–Voyce series Eq. 2 as

$$\begin{aligned} y\left( t\right) \cong y_{N} \left( t\right) ={ b}\left( t\right) { Y} \end{aligned}$$
(4)

so that

$$\begin{aligned} { b}\left( t\right) = & \left[ b_{o} \left( t\right) ,b_{1} \left( t\right) ,\ldots ,b_{N} \left( t\right) \right] \\ { Y}= & \left[ y_{o} ,y_{1} ,\ldots ,y_{N} \right] ^{T} ; \end{aligned}$$

then, by using the Morgan–Voyce polynomials Eq. 3, we obtain the matrix form \({ b}\left( t\right)\) as follows

$$\begin{aligned} { b}\left( t\right) = { X}\left( t\right) { M} \end{aligned}$$
(5)

where

$$\begin{aligned} { X}\left( t\right) =\left[ 1,t,t^{2} ,\ldots ,t^{N} \right] \end{aligned}$$

and

$$\begin{aligned} { M}=\left[ \begin{array}{ccccc} {\left( \begin{array}{c} {0} \\ {0} \end{array}\right) } &{\left( \begin{array}{c} {1} \\ {1} \end{array}\right) } &{\left( \begin{array}{c} {2} \\ {2} \end{array}\right) } &{\cdots } &{\left( \begin{array}{c} {N} \\ {N} \end{array}\right) } \\ {0} &{\left( \begin{array}{c} {2} \\ {0} \end{array}\right) } &{\left( \begin{array}{c} {3} \\ {1} \end{array}\right) } &{\cdots } &{\left( \begin{array}{c} {N+1} \\ {N-1} \end{array}\right) } \\ {0} &{0} &{\left( \begin{array}{c} {4} \\ {0} \end{array}\right) } &{\cdots } &{\left( \begin{array}{c} {N+2} \\ {N-2} \end{array}\right) } \\ {\vdots } &{\vdots } &{\vdots } &&{\vdots } \\ {0} &{0} &{0} &{\cdots } &{\left( \begin{array}{c} {2N} \\ {0} \end{array}\right) } \end{array}\right] \end{aligned}$$

Besides, the relation between the matrix and its derivative \({ X}'\left( t\right)\) can be written in the form [13, 18, 22, 24]

$$\begin{aligned} X'\left( t\right) =X\left( t\right) T \end{aligned}$$
(6)

where

$$\begin{aligned} T=\left[ \begin{array}{ccccc} {\;0\;} &{\;1\;} &{\;0\;} &{\; \ldots \; } &{\;0\;} \\ {0} &{0} &{2} &{\ldots } &{0} \\ {\vdots } &{\vdots } &{\vdots } &&{\vdots } \\ {0} &{0} &{0} &{\ldots } &{N} \\ {0} &{0} &{0} &{\ldots } &{0} \end{array}\right] . \end{aligned}$$

Then, by means of the matrix relations Eqs. 4, 5, and 6, we obtain

$$\begin{aligned} y\left( t\right)\cong & y_{N} (t) = { b}\left( t\right) { Y} \nonumber \\= & { X}\left( t\right) { MY} \end{aligned}$$
(7)

and

$$\begin{aligned} y^{'} \left( t\right)\cong & y_{N}^{'} (t)\,=\, { X}^{'} \left( t\right) { MY} \nonumber \\= & { X}\left( t\right) { TMY} \end{aligned}$$
(8)

By putting \(t\rightarrow t-\tau _{j} \left( t\right)\) in Eq. 7, we gain the recurrence relation [13, 18, 22, 24]

$$\begin{aligned} y\left( t-\tau _{j} (t)\right) \cong y_{N} (t) = & \, X\left( t-\tau _{j} (t)\right) { MY} \nonumber \\= & { X}\left( t\right) L\left( -\tau _{j} (t)\right) { MY} \end{aligned}$$
(9)

so that

$$\begin{aligned} L\left( \tau _{j} \left( t\right) \right) = \left[ \begin{array}{ccccl} {\left( \begin{array}{c} {0}\\ {0}\end{array}\right) \left( -\tau _{j} \left( t\right) \right) ^{0} } &{\left( \begin{array}{c} {1}\\ {0}\end{array}\right) \left( -\tau _{j} \left( t\right) \right) ^{1}} &{\left( \begin{array}{c} {2}\\ {0}\end{array}\right) \left( -\tau _{j} \left( t\right) \right) ^{2} } &{\cdots } &{\left( \begin{array}{c} {N}\\ {0}\end{array}\right) \left( -\tau _{j} \left( t\right) \right) ^{N} } \\ {0} &{\left( \begin{array}{c} {1} \\ {1} \end{array}\right) \left( -\tau _{j} \left( t\right) \right) ^{0} } &{\left( \begin{array}{c} {2} \\ {1} \end{array}\right) \left( -\tau _{j} \left( t\right) \right) ^{1} } &{\cdots } &{\left( \begin{array}{c} {N} \\ {1} \end{array}\right) \left( -\tau _{j} \left( t\right) \right) ^{N-1} } \\ {0} &{0} &{\left( \begin{array}{c} {2} \\ {2} \end{array}\right) \left( -\tau _{j} \left( t\right) \right) ^{0} } &{\cdots } &{\left( \begin{array}{c} {N} \\ {2} \end{array}\right) \left( -\tau _{j} \left( t\right) \right) ^{N-2} } \\ {\vdots } &{\vdots } &{} {\vdots } &{} {} &{} {\quad \; \vdots } \\ {0} &{} {0} &{} {0} &{} {\cdots } &{} {\left( \begin{array}{c} {N} \\ {N} \end{array}\right) \left( -\tau _{j} \left( t\right) \right) ^{0} } \end{array}\right] \end{aligned}$$

Note that the matrix \({ X}\left( t-\tau _{j} (t)\right)\) can be written as

$$\begin{aligned} { X}\left( t-\tau _{j} (t)\right) ={ X}\left( t\right) { L}\left( -\tau _{j} (t)\right) \end{aligned}$$

By substituting the relations Eqs. 7, 8, and 9 into Eq. 1, we have the matrix equation

$$\left[{ X}\left( t\right) T-P_{1}\left( t\right) X\left( t\right) -\sum _{j=2}^{m}P_{j} \left( t\right) X\left( t\right) L\left( -\tau _{j}\left( t\right) \right) \right]MY=P_{o} \left( t\right)$$
(10)

and by placing the collocation points defined by

$$\begin{aligned} t_{i} =a+\frac{b-a}{N} i,\quad i=0,1,\ldots ,N. \end{aligned}$$

in Eq. 10, the compact form of the obtained matrix equations system

$$\left[XT-P_{1}X-\sum _{j=2}^{m}P_{j} \left( t\right) \bar{X} \bar{L}\left( -\tau _{j} \right) \right]MY=P_{o}$$
(11)

where

$$\begin{aligned} { X}= & \left[ \begin{array}{c} {{ X}\left( t_{o} \right) } \\ {{ X}\left( t_{1} \right) } \\ {\vdots } \\ {{ X}\left( t_{N} \right) } \end{array}\right] =\left[ \begin{array}{ccccc} {1} &{} {t_{o} } & {t_{o}^{2} } & {\cdots } & {t_{o}^{N} } \\ {1} & {t_{1} } & {t_{1}^{2} } & {\cdots } & {t_{1}^{N} } \\ {\vdots } & {\vdots } & {\vdots } & & {\vdots } \\ {1} & {t_{N} } & {t_{N}^{2} } & {\cdots } & {t_{N}^{N} } \end{array}\right] , \\ { P}_{o}= & \left[ \begin{array}{c} {{ P}_{o} (t_{o} )} \\ {{ P}_{o} (t_{1} )} \\ {\vdots } \\ {{ P}_{o} (t_{N} )} \end{array}\right] , \; \bar{{ L}}\left( -\tau _{j} \right) =\left[ \begin{array}{c} {{ L}\left( -\tau _{j} \left( t_{o} \right) \right) } \\ {{ L}\left( -\tau _{j} \left( t_{1} \right) \right) } \\ {\vdots } \\ {{ L}\left( -\tau _{j} \left( t_{N} \right) \right) } \end{array}\right] \\ { P}_{o}= & diag\left[ { P}_{j} (t_{o} ),{ P}_{j} (t_{1} ),\ldots ,{ P}_{j} (t_{N})\right] , j=1,2,\ldots ,m\\ \bar{{ X}}= & diag\left[ { X}(t_{o} ),{ X}(t_{1} ),\ldots ,{ X}(t_{N} )\right] , \end{aligned}$$

Morgan–Voyce matrix method

The fundamental matrix Eq. 11 of Eq. 1 can be expressed in the form

$${ WY}={ P}_{o} \, \Leftrightarrow \, \left[ { W};{\mathrm{P}}_{o} \right]$$
(12)

where

$$\begin{aligned} W= & \left[ w_{pq} \right] =\left[XT-{ P}_{1} { X}-\sum _{j=2}^{m}{} { P}_{j} \left( t\right) \bar{{ X}} \bar{{ L}}\left( -\tau _{j} \right) \right]{ M} \\&p,q=0,1,\ldots { ,N}. \end{aligned}$$

By using the relation Eq. 7, we obtain the corresponding matrix form to the initial condition \(y(a)=\lambda\) as

$$\begin{aligned} U{ Y}=\lambda \, \Leftrightarrow \, \left[ U;{ Y}\right] \end{aligned}$$
(13)

such that

$$\begin{aligned} U={ X}(a){ M}=\left[ u_{00} ,u_{01} ,\ldots ,u_{0N} \right] \end{aligned}$$

Consequently, in order to get the approximate solution of Eq. 1 subject to \(y(a)=\lambda\), we replace the row matrix in Eq. 13 by the last row(or any row) of the augmented matrix in Eq. 12; then, we obtain the result matrix

$$\left[ \tilde{W};\tilde{P}_{o} \right] \, \Leftrightarrow \, \tilde{W}Y=\tilde{P}_{o}$$
(14)

If \({\text {rank}}\, \tilde{{ W}} = {\text {rank}}\left[ \tilde{{ W}};\tilde{{ P}}_{o} \right] =N+1\), then we can write, \(Y= \left( \tilde{{ W}}\right) ^{-1} \tilde{P}_{o}\). Thus the matrix, Y (thereby the Morgan–Voyce coefficients \(y_{o} ,y_{1} ,\ldots ,y_{N}\)) is uniquely determined; thus Eq. 1 has a unique solution.

Error analysis

In this section, an error analysis will be presented for the Morgan–Voyce polynomial solution in Eq. 16 with the residual error function [4, 8, 9, 13, 21, 22, 28, 31, 36]. In addition, we will improve the Morgan–Voyce polynomial solution \(y_{N} \left( t\right)\) with the aid of the residual error function.

Firstly, we consider the operator Eq. 1, under the initial condition \(y(a)=\lambda\),

$$\begin{aligned} L\left[ y\left( t\right) \right]= & g(t)\nonumber \\ L\left[ y(t)\right]= & y'\left( t\right) -P_{o} (t)-P_{1} (t)y(t)-\sum _{j=2}^{m}P_{j} (t)y\left( t-\tau _{j} (t)\right) . \end{aligned}$$
(15)

Here, \(y_{N} (t)\) is the approximate solution of the problem and satisfies the problem

$$\begin{aligned} \left\{ \begin{array}{l} {L[y_{N} (t)]=g(t)+R_{N} (t),\quad a\le t\le b,} \\ {y_{N} (t)=\lambda .} \end{array}\right. \end{aligned}$$
(16)

Also, the residual function of the Morgan–Voyce polynomial approximation \(y_{N} \left( t\right)\)is defined as

$$\begin{aligned} R_{N} (t)=L[y_{N} (t)]-g(t). \end{aligned}$$
(17)

If we know the exact solution \(y\left( t\right)\), then the error function is calculated as the difference between the approximate and the exact solutions defined by

$$\begin{aligned} e_{N} \left( t\right) =y\left( t\right) -y_{N} \left( t\right) . \end{aligned}$$
(18)

By using the Eqs. 15, 16, 17 and 18, we get the error problem

$$\begin{aligned} L[e_{N} (t)]= & {} L[y(t)]-L[y_{N} (t)] = -R_{N} (t).\nonumber \\ e_{N}\left( a\right)= & {} 0. \end{aligned}$$
(19)

By solving the error problem in Eq. 19 with the method presented in Sect. 3, we get the approximation \(e_{N,M} (t)\) to \(e_{N} (t)\) as follows

$$\begin{aligned} e_{N,M} (t)=\sum _{n=0}^{M}a_{n}^{*} b_{n} (t) , \; \; \; (M\ge N). \end{aligned}$$

Consequently, by means of the polynomials \(y_{N} (t)\) and \(e_{N,M} (t)\), \((M\ge N)\), we obtain the corrected Morgan–Voyce polynomial solution \(y_{N,M} (t)=y_{N} (t)+e_{N,M} (t)\). Here, \(e_{N} (t)=y(t)-y_{N} (t)\), \(E_{N,M} (t)=e_{N} (t)-e_{N,M} (t)=y(t)-y_{N,M} (t)\) and \(e_{N,M} (t)\) denote the error function, the corrected error function and the estimated error function, respectively.

If the exact solution of Eq. 1 can not been known, then the absolute errors \(\left| e_{N} (t_{i} )\right| =\left| y(t_{i} )-y_{N} (t_{i} )\right|\), (\(a\le t_{i} \le b\)) are not computed. However, the absolute errors \(\left| e_{N} (t_{i} )\right| =\left| y(t_{i} )-y_{N} (t_{i} )\right|\), (\(a\le t_{i} \le b\)) can be estimated by using the absolute error function \(\left| e_{N,M} (t)\right|\).

Numerical examples

Example 1

Consider the differential equation with variable delay \(t^{2} +1\)

$$\begin{aligned} y'(t) = & {} 3t-t^{2} +t^{2} y(t)-y(t-t^{2} )+ty(t-t^{2} -1)\nonumber \\&0\le t\le 1 \end{aligned}$$
(20)

subject to the initial condition \(y(0)=-1\). The exact solution of this equation is \(y(t)=t-1\). First of all, let us determine the collocation points by the formula \(t_{i} = a+\frac{b-a}{N} i,\;i=0,1,\ldots ,N\) for \(a=0\), \(b=1\), and \(m=3, N=2\). Therefore the collocation points are obtained as \(t_{o} =0,\, \, t_{1} ={\textstyle \frac{1}{2}} ,\, \, t_{2} =1\). By Eq. 11, the fundamental matrix equation of this problem is written as

$$\begin{aligned} \left [{ XT}-{ P}_{1} { X}-\sum _{j=2}^{3}{} { P}_{j} \left( t\right) \bar{{ X}} \bar{{ L}}\left( -\tau _{j} \right) \right ]MY={ P}_{o} \end{aligned}$$

where

$$\begin{aligned} P_{o}\;= & {} \left[ \begin{array}{c} {\;0\;} \\ {{\textstyle \frac{5}{4}} } \\ {2} \end{array}\right] ,\;\; P_{1} =\left[ \begin{array}{ccc} {\;0\;} &{} {\;0\;} &{} {\;0\;} \\ {0} &{} {{\textstyle \frac{1}{4}} } &{} {0} \\ {0} &{} {0} &{} {1} \end{array}\right] ,\;\;P_{2} =\left[ \begin{array}{ccc} {-1} &{} {0} &{} {0} \\ {0} &{} {-1} &{} {0} \\ {0} &{} {0} &{} {-1} \end{array}\right] ,\;\;P_{3} =\left[ \begin{array}{ccc} {\;0\;} &{} {\;0\;} &{} {\;0\;} \\ {\;0\;} &{} {{\textstyle \frac{1}{2}} } &{} {0} \\ {\;0\;} &{} {0} &{} {1} \end{array}\right] \\ X\left( t\right)= & {} \left[ \begin{array}{ccc} {1}&{\quad t}&{\quad t^{2}}\end{array}\right] \\ T= & {} \left[ \begin{array}{ccc} {0} &{} {1} &{} {0} \\ {0} &{} {0} &{} {2} \\ {0} &{} {0} &{} {0} \end{array}\right] ,\; M=\left[ \begin{array}{ccc} {1} &{} {1} &{} {1} \\ {0} &{} {1} &{} {3} \\ {0} &{} {0} &{} {1} \end{array}\right] ,\; X=\left[ \begin{array}{c} {X\left( 0\right) } \\ {X\left( {\textstyle \frac{1}{2}} \right) } \\ {X\left( 1\right) } \end{array}\right] =\left[ \begin{array}{ccc} {\;1\;} &{} {\;0\;} &{} {\;0\;} \\ {1} &{} {{\textstyle \frac{1}{2}} } &{} {{\textstyle \frac{1}{4}} } \\ {1} &{} {1} &{} {1} \end{array}\right] \\ \bar{X}= & {} \left[ \begin{array}{ccc} {X\left( 0\right) } &{} {0} &{} {0} \\ {0} &{} {X\left( {\textstyle \frac{1}{2}} \right) } &{} {0} \\ {0} &{} {0} &{} {X\left( 1\right) } \end{array}\right] =\left[ \begin{array}{ccccccccc} {\;1\;} &{} {\;0\;} &{} {\;0\;} &{} {\;0\;} &{} {\;0\;} &{} {\;0\;} &{} {\;0\;} &{} {\;0\;} &{} {\;0\;} \\ {0} &{} {0} &{} {0} &{} {1} &{} {{\textstyle \frac{1}{2}} } &{} {{\textstyle \frac{1}{4}} } &{} {0} &{} {0} &{} {0} \\ {0} &{} {0} &{} {0} &{} {0} &{} {0} &{} {0} &{} {1} &{} {1} &{} {1} \end{array}\right] \\ \bar{{ L}}\left( -\tau _{2} (t_{i} )\right)= & {} \left[ \begin{array}{ccc} {\;\;1\;\;} &{} {\;\;0\;\;} &{} {\;\;0\;\;} \\ {0} &{} {1} &{} {0} \\ {0} &{} {0} &{} {1} \\ {1} &{} {-{\textstyle \frac{1}{4}} } &{} {{\textstyle \frac{1}{16}} } \\ {0} &{} {1} &{} {-{\textstyle \frac{1}{2}} } \\ {0} &{} {0} &{} {1} \\ {1} &{} {-1} &{} {1} \\ {0} &{} {1} &{} {-2} \\ {0} &{} {0} &{} {1} \end{array}\right] ,\;\;\bar{{ L}}\left( -\tau _{3} (t_{i} )\right) =\left[ \begin{array}{ccc} {\;\;1\;\;} &{} {\;\;-1\;\;} &{} {\;\;1\;\;} \\ {0} &{} {1} &{} {-2} \\ {0} &{} {0} &{} {1} \\ {1} &{} {-{\textstyle \frac{5}{4}} } &{} {{\textstyle \frac{25}{16}} } \\ {0} &{} {1} &{} {-{\textstyle \frac{5}{2}} } \\ {0} &{} {0} &{} {1} \\ {1} &{} {-2} &{} {4} \\ {0} &{} {1} &{} {-4} \\ {0} &{} {0} &{} {1} \end{array}\right] . \end{aligned}$$

The augmented matrix of the fundamental matrix equation is computed as

$$\begin{aligned} \left[ { W};{ P}_{o} \right] =\left[ \begin{array}{ccc} {1} &{} {2} &{} {4} \\ {\;0.25\;} &{} {\;1.75\;} &{} {\;5.46875\;} \\ {-1} &{} {0} &{} {2} \end{array}\left| \begin{array}{c} {0} \\ {\;1.25\;} \\ {-1} \end{array}\right. \right] \end{aligned}$$

and the augmented matrix for initial condition is obtained as

$$\begin{aligned} \left[ U;\lambda \right] =\left[ \left. \begin{array}{ccc} {1}&{1}&{1} \end{array}\right| -1\right] . \end{aligned}$$

By using the procedure in Sect. 3, we obtain the approximate solution as

$$\begin{aligned} \, y_{2} (t)=t-1 \end{aligned}$$

which is the exact solution.

Example 2

Consider the differential equation with variable delay \(t^{2}\)

$$\begin{aligned} 2y'(t)-ty(t)+te^{2t^{2} } y(t-t^{2} )=4e^{2t} ,\quad 0\le t\le 1 \end{aligned}$$

subject to the initial condition \(y(0)=1\). The exact solution of this equation is \(y(t)=e^{2t}\). The fundamental matrix equation is

$$\begin{aligned} \left [XT-P_{1}X-P_{2} \bar{X} \bar{L}\left( -\tau _{2} \left( t_{i} \right) \right) \right ]MY=P_{o}. \end{aligned}$$

After the collocation points substituted into this matrix equation, we solve the system and we obtain the solutions in the form 4 of Example 2 for \(N=3,4,12\) in the interval \(\left[ 0,1\right]\) Table 1.

Table 1 Numerical results of the exact, approximate and corrected solutions of Example 2 for some N values
Full size table

Now, we will give the exact, approximation, and corrected solutions of Example 2 for \(N=3,\ 4\) in Figs. 1 and 2, respectively.

Fig. 1
figure 1

Exact, approximate and corrected solutions of Example 2 for \(N=3\)

Full size image
Fig. 2
figure 2

Exact, approximate and corrected solutions of Example 2 for \(N=4\)

Full size image
Table 2 Comparison of the absolute errors and corrected absolute errors of Example  2
Full size table

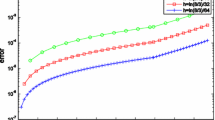
The absolute and corrected errors of Example 2 in Table 2 are compared for \(N=3,\ 4\) in Figs. 3 and 4, respectively.

Fig. 3
figure 3

Comparison of the absolute error with the corrected absolute error for \(N=3\)

Full size image
Fig. 4
figure 4

Comparison of the absolute error with the corrected absolute error for \(N=4\)

Full size image

Example 3

Consider the delay differential equation having variable delays \(\ln \left( t+1\right)\) and \(t^{2}\)

$$\begin{aligned} y'(t)=\left( t^{2} +t-1\right) e^{-t} -ty\left( t-\ln \left( t+1\right) \right) -e^{-t^{2} } y\left( t-t^{2} \right) +y(t),\quad 0\le t\le 1 \end{aligned}$$

subject to the initial condition \(y(0)=1\). The exact solution of this equation is \(y(t)=e^{-t}\). The fundamental matrix equation is

$$\begin{aligned} \left [XT-P_{1} X-P_{2} \bar{X} \bar{L}\left( -\tau _{2} \left( t_{i}\right) \right) -P_{3} \bar{X} \bar{L}\left( -\tau _{3} \left( t_{i} \right) \right) \right ]MY=P_{o}. \end{aligned}$$

After the collocation points substituted into this matrix equation, we can solve the system and we obtain the solutions in the form 4 of Example 3 for \(N=3,\ 4,\ 12\) in the interval \(\left[ 0,1\right]\) Table 3.

Table 3 Numerical results of the exact, approximate and corrected solutions of Example 3 for some N values
Full size table

All exact, approximation, and corrected solutions of Example 3 for \(N=3, 4\) are given in Fig. 5 and 6, respectively. The absolute and corrected errors of Example 3 in Table 4 are compared for \(N=3,\ 4\) in Figs. 7 and 8, respectively.

Fig. 5
figure 5

Exact, approximate and corrected solutions of Example 3 for \(N=3\)

Full size image
Fig. 6
figure 6

Exact, approximate and corrected solutions of Example 3 for \(N=4\)

Full size image
Table 4 Comparison of the absolute errors and corrected absolute errors of Example  3
Full size table
Fig. 7
figure 7

Comparison of the absolute error with the corrected absolute error for \(N=3\)

Full size image
Fig. 8
figure 8

Comparison of the absolute error with the corrected absolute error for \(N=4\)

Full size image

Example 4

Consider the following delay differential equation [7] having variable delay \(\ln \left( t^{2}+1\right)\)

$$\begin{aligned} y'(t)=\left( t^{2} +1\right) e^{-t} -y\left( t-\ln \left( t^{2}+1\right) \right) -y(t),\quad 0\le t\le 2 \end{aligned}$$

subject to the initial condition \(y(0)=1\). The exact solution of this equation is \(y(t)=e^{-t}\).

Similarly, we can solve this problem by present method and we obtain the solutions in the form 4 of Example 4 for \(N=6\) in the interval \(\left[ 0,2\right]\). Then, we also compare the present solutions and Hybrid Taylor-Lucas Method [7] (HTL) solutions in Table 5. The present method has been shown to be suitable as graphically for nonhomogeneous differential equation with variable delays in Fig. 9.

Table 5 Numerical results of the Exact, Present and HTL solutions of Example 4 for \(N=6\) value
Full size table
Fig. 9
figure 9

Comparison of the exact, present and HTL solutions of Example 4 for \(N=6\) value

Full size image

In order to better define the solution space of the problems of Examples 2,  3 and  4 described above, the N value has been scanned up 1 to 100. The root-mean-square error (RMSE) value of the solution obtained for each N value is calculated and shown in Fig. 10. When \(N>12\), the RMSE values of the solutions of both problems are oscillated between \({10}^{-10}\) and \({10}^{-16}\). The reason of these oscillations is the truncation errors in the calculations.

Fig. 10
figure 10

RMSE values for \(\hbox {N}=1,2, \ldots , 100\) for Examples 2,  3 and  4

Full size image

Conclusion

A new approach using the Morgan–Voyce polynomials to solve numerically the first-order nonhomogeneous differential equations with variable delays is presented in this study. An error analysis technique based on residual function is also developed our problems. If the exact solution of the problem is not known, by using this technique it is possible to estimate the error function and also to reduce the error due to the residual function. It is seen that, the accuracy improves, when N is increased. To compute our solutions and error functions, we have written a code in Matlab and calculated all computations by means of this code.

Consequently, the present method has been shown to be convenient, reliable and effective for solving the first-order nonhomogeneous differential equation with variable delays.