Introduction

Load forecasting is a method to predict future load demands by analyzing historical data and finding dependency patterns of its time-step observations. It has many applications in power system operation and planning including demand response, scheduling, unit commitment, energy trading, system planning, and energy policy [1]. Accurate load forecasting helps power companies and decision-makers to make a balance between supply and demand, prevent power interruptions due to load shedding, and avoid excess reserve of power generation. Load forecasting problem is a challenging task due to its complexity, uncertainty, and variety of factors affecting the prediction. It is considered as a type of time-series problems that needs a special solution. Depending on its application, load forecasting can be classified into: very–short load forecasting (VSTLF), short–term load forecasting (STLF), medium–term load forecasting (MTLF), and long–term load forecasting (LTLF). VSTLF is used in the problems of demand response and real-time operation that require a time horizon of a few minutes to several hours ahead. Forecasting the load demand from one day to several days ahead is called STLF, whereas forecasting from 1 week to several weeks ahead is known as MTLF. These two types of forecasting cover the majority of load-forecasting studies in the literature and are mainly used in scheduling, unit commitment, and energy marketing. Lastly, LTLF refers to the forecasting with a time frame of up to serval years ahead and it is useful for planning and energy-trading purposes. [1, 2].

Several recent studies have comprehensively reviewed the state-of-the-art techniques used in load forecasting [3,4,5,6,7,8,9,10,11,12]. These techniques can be mainly classified into two groups: statistical and machine learning. Statistical methods are classical models that map the input data to the output. Autoregressive integrated moving average (ARIMA), linear regression, and exponential smoothing are examples of this kind of load forecasting. Statistical techniques are relatively fast, easy to set up, and computationally inexpensive. However, they suffer from uncertainty and low accuracy with high nonlinear systems. On the other hand, techniques based on machine learning such as artificial neural networks, deep learning, and recurrent neural networks have more complex setup and expensive training-time but they are relatively more accurate and perform better. Among the second-type approaches, the long short-term memory (LSTM) and its newer version named gated recurrent unit (GRU) are very popular techniques and widely used in the recent studies [13, 14]. In [14], a deep neural network and historical data augmentation (DNN–HDA) is proposed for data with a high correlation which shows a great improvement in the accuracy. The method is based on dividing the input data into multiple sequences, each sequence represents a dataset for 1 year. However, when data is divided into multiple parts, information about the connection between the end of one part and the beginning of the next part is missing. For some data and load forecasting problems, this could be unproblematic as shown in the paper. However, when the nature of data changes and includes high uncertainty and fluctuations in the time step information, this approach was found struggling to predict future load demand, especially for long-term forecasting.

In [15], a sequence-to-sequence recurrent neural network approach is proposed to capture time dependencies of input data. References [16,17,18,19], proposed multi-channels and features to extract useful information from the historical data. Most recent studies in [13, 20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45] use LSTM as a main deep neural network or in a hybrid model to develop a better STLF load forecasting network. Some of these studies [33] added the impact of COVID-19 on load forecasting using lockdown information as another sequence input. Others [40] use bidirectional LSTM as a learning component. Concerning the previous studies applied to the test data of Kurdistan regional load demand, several studies [46, 47] are present. The methods used in these papers are either statistical approaches or simple models of neural networks.

It should be noted that all the denoting studies use mainly MATLAB to implement the proposed models. We know that Simulink is a visualized version of MATLAB and is bidirectionally connected to MATLAB. It has several advantages over MATLAB. For instance, you can see how the algorithm works through looking into the block diagram shown as a flow chart for the problem. You can easily set up a new built-in or customizable component and add it to the model. The blocks and the signals can hold values in the form of scalars or vectors. In addition, we can replace the for-loop required to update the network at each time step in MATLAB with a vectorized model without the need of for-loops.

This study proposes a reform in the forecasting input data to obtain a better performance and solve certain complex problems that the 1-year data-augmentation approach fails to predict accurately. Not only a one-day or week-day ahead forecasting is addressed, but a 365-day ahead prediction is introduced. Five scenarios are used for comparison including classical single-variable input one-day ahead, single-variable input 365-day ahead, single-variable multi-sequence inputs 365-day ahead, classical multi-variable input 365-day ahead, and multi-variable multi-sequence per variable inputs 365-day ahead. This paper also fills the gap in the current programs used for load forecasting by introducing the Simulink model of prediction.

The rest of the paper is organized as follows. In the next section, a theoretical background is presented on the long short-term memory and gated reset unit neural networks. In Sect. 3, the dataset under study is analyzed using a correlation function of input time-series observations. The forecasting methodology used in this study is described in Sect. 4, whereas the Simulink program developed for this work is introduced in Sect. 5. The results are discussed in Sect. 6. Finally, the conclusion is presented in Sect. 7.

Theoretical background on LSTM and GRU

Conventional neural networks such as multilayer perceptron (MLP) can be applied to sequence-based and time-series problems but in practice, it has multiple major limitations. Its stateless structure, messy scaling, fixed-sized inputs and outputs, and unawareness of time-related structure are some of these limitations [48]. A better alternative neural network for these types of problems is the recurrent neural network (RNN). RNN is a feedforward multineural network with additional feedback cycles from previous time steps used to store temporal information as internal states. A recurrent network adds a memory state to learn the sequence order of input data and extracts the dependencies among the input observations. However, almost all RNNs are nowadays replaced with the long-short-term memory (LSTM) or gated reset unit (GRU) to solve major shortcomings in the RNNs: vanishing and exploding gradients. When the RNN weights are updated, it quickly results in either too small changes in the weights (vanishing gradient) or too large changes (exploding). The result is a short-term memory which is extremely hard for the RNN to learn and determine the dependencies among observations from earlier time steps to the later ones.

LSTM

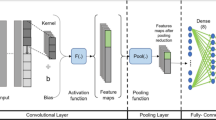
The LSTM model is developed to overcome the drawback of the RNNs by adding a memory or cell state to the network. The cell state is responsible for adding or removing past information based on its relevance and importance to make the prediction. The structure of LSTM is more complex than the RNN. It has \(S\) cell-blocks connected in series, where \(S\) is the total time-steps or length of input data. Figure 1 shows the architecture of an LSTM with \(C\) features and \(D\) hidden units, the former is equivalent to the number of neurons in the classical neural network. Each LSTM cell consists of three adjusting-gate blocks to regulate its state. The gates are simple neural networks composed of weights, biases, and activation functions. The LSTM gates can be described as follows:

  1. 1.

    Forget gate: This gate determines what information from the cell state \({c}_{t-1}\) (the top horizontal line in Fig. 2 colored in orange) should be thrown away using information from the previous hidden state \({h}_{t-1}\) and the current input \({x}_{t}\). The current cell input \({x}_{t}\) is multiplied by the weight matrix \({W}_{f}\) whereas the previous hidden-state \({h}_{t-1}\) is multiplied by the recurrent weight matrix \({R}_{f}\). The resulting output of these products are added to a bias vector \({b}_{f}\). Finally, a sigmoid function \({\sigma }_{g}\) is activated to get the output vector \({f}_{t}\) that has values varying between 0 and 1. The value “0” means no information from the previous time-step of cell state is allowed to flow (not important information), whereas the value “1” means all previous information of the memory is allowed to flow (extremely important). If the information is partially relevant, the function outputs a value between “0” and “1”. Mathematically, this description can be written as follows:

    $${f}_{t}={\sigma }_{g}\left({W}_{f}{x}_{t}+{R}_{f}{h}_{t-1}+{b}_{f}\right)$$
    (1)

    where \({\sigma }_{g}\) denotes the gate’s activation function, and all the other parameters and variables are defined above. If the input variable \({x}_{t}\) is a vector of sequences with \(C\) features, and each cell has \(D\) hidden units, then the weights \({W}_{f}\) and \({R}_{f}\) are matrices with the dimensions of \(DxC\) and \(DxD\), respectively, whereas the bias \({b}_{f}\) is a vector with \(D\) elements. As a result, the output of the gate \({f}_{t}\) is a vector with \(D\) elements.

  2. 2.

    Update gate: This gate is used to update the cell state or memory that was regulated by the forget gate in the previous step. It is composed of two parts of neural networks: input gate \({i}_{t}\) and candidate cell \({g}_{t}\), and are fed with the same inputs used for the forget-gate (\({h}_{t-1}\) and \({x}_{t}\)). However, the weights, biases, and activation functions of \({i}_{t}\) and \({g}_{t}\) branches are different. For the input-gate branch– \({i}_{t}\), we have the input variables \({x}_{t}\) and \({h}_{t-1}\) weighted by the matrices \({W}_{i}\) and \({R}_{i}\), respectively and biased with \({b}_{i}\), and finally activated using a sigmoid function \({\sigma }_{g}\).

    The same is repeated for the candidate-state branch– \({g}_{t}\) using the denoting letter \(i\) instead of \(g\), and replacing the sigmoid function \({\sigma }_{g}\) with a tan hyperbolic (tanh or \({\sigma }_{s}\)) to squishes the data between − 1 and 1. The input branch is used to control the output of the squished data–the candidate state. Finally, the outputs of these two neural networks \({f}_{t}\) and \({g}_{t}\) are multiplied to produce the output of the update gate.

    Mathematically, the two networks can be written as follows:

    $${i}_{t}={\sigma }_{g}\left({W}_{i}{x}_{t}+{R}_{i}{h}_{t-1}+{b}_{i}\right)$$
    (2)
    $${g}_{t}={\sigma }_{s}\left({W}_{g}{x}_{t}+{R}_{g}{h}_{t-1}+{b}_{g}\right)$$
    (3)

    where \({\sigma }_{s}\) denotes the state activation function.

  3. 3.

    Output gate: This gate is used to compute the current hidden state \({h}_{t}\). We pass a copy of the combined input (\({x}_{t}\) and \({h}_{t-1}\)) to a sigmoid function \({\sigma }_{g}\) after multiplied with the respective weights \({W}_{o}\) and \({R}_{o}\), and added to the bias \({b}_{o}\). The resulting output \({o}_{t}\) is multiplied with the current cell state \({c}_{t}\) after squished to the range [-1, 1] using the tanh function \({\sigma }_{s}\). Mathematically, the output gate can be described as follows:

    $${o}_{t}={\sigma }_{g}\left({W}_{o}{x}_{t}+{R}_{o}{h}_{t-1}+{b}_{o}\right)$$
    (4)

    The equations of the new cell-state \({c}_{t}\) and hidden-state \({h}_{t}\) are:

    $${c}_{t}={f}_{t}.*{c}_{t-1}+{i}_{t}.*{g}_{t}$$
    (5)
    $${h}_{t}={o}_{s}.*{\sigma }_{s}\left({c}_{t}\right)$$
    (6)

    where the operator \(.*\) refers to the Hadamard multiplication (element-wise or pointwise operation). Since we use MATLAB to train our network, the same variable and parameter names used by the software are employed here in this study.

    To summarize, the forget gate determines what information from the old memory is relevant to keep and forget the irrelevant ones. The input gate is used to update the relevant memory and generate the current memory used in the next block. The output gate is used to compute the output of the current block and the next hidden-state. We should note that all the gates have the same inputs consisting of three copies of the previous hidden state and the current input combined (the bottom line in Fig. 2). The top of Fig. 2 is the LSTM memory or cell state that is used by the network to learn about the sequence order of input data.

Fig. 1
figure 1

An LSTM layer with multi-inputs and multi-outputs (created for this study)

Full size image
Fig. 2
figure 2

Internal structure of an LSTM cell (created for this study)

Full size image
Fig. 3
figure 3

Internal structure of a GRU cell (created for this study)

Full size image

GRU

GRU model (Fig. 3) is a simplified and newer version of LSTM. It is composed of two gates and one candidate-state network, namely: reset gate \({r}_{t}\), update gate \({z}_{t}\), and candidate state \({\tilde{h }}_{t}\). The update gate used by the GRU is equivalent to the forget and input gates in the LSTM model combined as a single network. It is used to determine what information to remove or add. The reset gate is used to determine how much information from the previous state to forget. In contrast to the LSTM, there is no cell state in the GRU network. In other words, the cell state can be seen as the previous hidden state \({h}_{t-1}\). The network parameters of the GRU are less than those in LSTM and hence the network requires less training time to learn about dependencies among the time-step observations or sequence data. Mathematically, the following equations are used for the reset and update gates, candidate state, and the hidden state, respectively:

$${r}_{t}={\sigma }_{g}\left({W}_{r}{x}_{t}+{b}_{r}+{R}_{r}{h}_{t-1}\right)$$
(7)
$${z}_{t}={\sigma }_{g}\left({W}_{z}{x}_{t}+{b}_{z}+{R}_{z}{h}_{t-1}\right)$$
(8)
$${\tilde{h }}_{t}={\sigma }_{s}\left({W}_{\tilde{h }}{x}_{t}+{b}_{\tilde{h }}+{r}_{t}{R}_{\tilde{h }}{h}_{t-1}\right)$$
(9)
$${h}_{t}=\left(1-{z}_{t}\right).*{\tilde{h }}_{t}+{z}_{t}.*{h}_{t-1}$$
(10)

Dataset correlation: a research motivation

In this study, a historical dataset is collected for Kurdistan regional power system containing load profiles for each governorate for the range of years 2015–2020 [49, 50]. The map of this region is shown in Fig. 4. The data is divided into two subsets: training and test subsets. The first five years of the data are used for training the network, whereas the last year of the data is used for testing the trained network. We call these two datasets \(XTrain\) and \(XTest\), respectively, which represent the predictors or independent variables for the respective training and test datasets. The predictors are moved by one-time step to generate the response or dependent variables for the respective training and test datasets \(YTrain\) and \(YTest\).

Fig. 4
figure 4

Map of Kurdistan region of Iraq

Full size image

In order to see how the dataset for one year is correlated to another yearly dataset of the same time-series sequence, a correlation analysis is conducted on the sample data. Figure 5 shows the correlation among pairs of time-series variables that express the daily load demand of Kurdistan region–Erbil governorate for 6 years. The diagonal plots in Fig. 5 display the histograms of data, whereas the off-diagonal figures exhibit the scatter plots of pair variables. The correlation coefficients for each pair of variables are highlighted on the graph and listed in Table 1. It can be observed from these plots and the table that the input loads used in this study are highly correlated. The minimum and maximum correlation coefficients are 0.777 and 0.9167, respectively, and the average of these off-diagonal values is 0.8991. The implicit relationships motivate us to investigate the use of this nature in the historical data to improve the load forecasting. As mentioned earlier, one recent study [14] observed this correlation using another dataset and introduces the concept of historical data augmentation (HDA). However, for high uncertainty data with fast changes in the time step information, the use of 1-year data for training a long-term dataset is a challenging problem; the data corresponding to the end of one year has no connection with the beginning of the next year dataset. In fact, if the starting day of a historical data marks the first day of a year which is common, then the data starts in the middle of a winter season which has a similar load-profile shape with respect to the loads obtained for the end of the previous year. Therefore, in the results section, a simple modification of this method is proposed to remove this shortcoming and accelerate the process.

Fig. 5
figure 5

Correlation analysis of the input data

Full size image
Table 1 Numerical values for the correlation analysis
Full size table

Forecast methodology

To predict the future values of load demands, we can implement one time-step ahead forecasting (OTSAF) or multiple time-steps ahead forecasting (MTSAF). For their future prediction, both approaches use an initial value computed from the last time-step of the historical load demands. However, the difference between OTSAF and MTSAF is in the way the network is updated for the next predictions. OTSAF updates the network using the current value of the test data, whereas MTSAF updates the network from the current predicted value. In other words, in MTSAF, the test dataset is not used anymore for future time-step prediction except for the first one. For the rest of remaining predictions, we loop over the predicted values once at a time until the end of the time-step sequence. It should be noted that for the OTSAF, the network state needs to be reset to prevent the influence of past predictions on new data forecasting.

In this study, several scenarios for the forecasting are considered including single-sequence and multi-sequence input–output forecasting. For the single sequence prediction, the input is the historical load demands. For the multi-sequence, the inputs consist of load demands, weather data, week-day and holiday information. In addition to the classical method of data inputting with a full sequence of time steps, a modification on the input data is proposed by dividing the data into several subsets by considering a two-year period per each subset instead of only one-year dataset. The results are presented and compared in the following sections.

Simulink models

This section presents the Simulink models developed for load forecasting and applied to both the OTSAF and MTSAF methods. Figures 6a, b show the block diagrams of each of these models. Since in the OTSAF, a variable from the test dataset is required for each time step to predict the next load demand, the network will have a vector of test inputs (or matrix in the case of multiple sequences), and there is no feedback loop from the output of the prediction block to its input. However, as it can be observed in Fig. 6b, the current output is fed to the input of the prediction block to be used for forecasting the next time step of load demand. By doing this loop, we are actually replacing the for-loop command required by MATLAB to achieve this task pragmatically. It is more useful to see visually how the algorithm works by showing the main steps in blocks connected to each other. From the figure, we can see three main steps in the program: standardization, prediction, and un-standardization. For the MTSAF, in addition to these three steps, we have an updating loop signal. To avoid an algebraic loop in the model, a memory block is added between the two ends of the prediction block. For multiple-sequence problems, we can keep all output sequences unchanged and plot the results, or we can evaluate a statistical value for these outputs such as their average, minimum, or maximum. A clock and switch blocks are added to switch the input from a first-time-step value obtained from the test data to the next values obtained from the prediction.

Fig. 6
figure 6

a Simulink program for the OTSAF model developed for this study. b Simulink program for the MTSAF model developed for this study

Full size image

Results

This study includes several different models with separate network training settings. The models are decided empirically starting from a single LSTM model with default values. The number of recurrent neural networks is increased gradually until a satisfying result is obtained. Most of the models need at least three blocks of LSTM, GRU, or a combination of them with a fully connected layer to get an acceptable accuracy. The gradient threshold is set to 1.0 to avoid any exploding in the network update. The initial value of the learning rate is chosen to be in the range 0.001–0.01 to balance between training time and model accuracy. Reducing this value increases the training time but might reduce the error. The maximum number of epochs is not fixed here and it varies from a network to network according to the complexity of the model and pattern of the input data.

OTSAF approach

We first start with the results obtained from the classical OTSAF model where the input data are given as a single set of time-series load demands without dividing it into subsets of data, and without considering other input variables such as weather or calendrical data. Figure 7a shows the training data in blue for the years from 2015 to 2019, followed by the 2020 test-data, and finally, the forecasting values are plotted over the test data for comparison. The \(x-\) axis is the day index starting from day-one which marks 01-Jan-2015 and ending on 31-Dec-2020, whereas the \(y-\) axis is the load demands in MW. The network which is selected empirically is a deep neural network with three LSTM layers and 128 hidden units per each which is a default setting. Figure 7b shows the observed and predicted results for the last year of the dataset –that is, 2020– showing the difference errors in MW. The root means square error (RMSE) for this scenario is computed to be 83.0345 MW and the relative percentage error is 83.0345/2696 or 3.08%. Note that both the MATLAB and Simulink programs give the same results. For a network with OTSAF, a maximum number of 100 epochs (Fig. 7c) was found to be sufficient to reach the above accuracy. The algorithm required around four minutes to train the network on a regular computer.

Fig. 7
figure 7

a Load forecasting–OTSAF Model, b Model output errors–OTSAF, c Training and loss function errors–OTSAF Model

Full size image

MTSAF approach

Next, we implement the MTSAF approach on the same data and design a network to learn from the five-year training data and predict load demands for the next year. The network architecture is selected experimentally and it consists of two layers of LSTM on the top connected to two layers of GRU on the bottom. The number of hidden units for these layers are chosen empirically to be 128, 64, 32, and 16, respectively. A maximum number of 1500-epochs is chosen to train the network with a learning rate of 0.01 reduced to accelerate the training process. The results shown in Fig. 8a–c show that the network learned from training the data and predicted the next-year forecasting given only a single-day initial value and loop over until the end of the year. Compared to the case of OTSAF, the relative RMSE error is 215.4212/2696 or 7.99% which is higher than the previous case. This is expected as we know that OTSAF is a one-day ahead forecasting whereas MTSAF here is a 365-day ahead forecasting. It is worth pointing out that this method of updating network parameters requires a relatively long training time. Compared to OTSAF, MTSAF consumes around eight times more time to train the network, though the learning rate has been already reduced.

Fig. 8
figure 8

a Load forecasting–MTSAF Model, b Model output errors–MTSAF, c Training and loss function errors–MTSAF Model

Full size image

Single-variable data-reshaping approach

The next scenario is for the case when the input data is divided into multiple subsets, each subset is for two consecutive-year periods (or one year repeated twice) so that it relates to the two ends of the year. As a result, we have a model with five-sequence inputs and five-sequence outputs. An LSTM-GRU hybrid network is chosen for this scenario in which its number of layers and hidden units are selected empirically as in the previous cases. The errors for the five sequences are evaluated to be 434.2163, 287.8786, 174.3753, 186.2802, and 243.1786 MW, respectively, and their corresponding relative errors are 16.11%, 10.68%, 6.47%, 6.91%, and 9.02%. We see that the third subset has the lowest error (6.47%) which is smaller than the error in the previous single-sequence case (7.99%). Not only the error is lower but also the training time is much less than in the previous case. The results are plotted and shown in Fig. 9a–c. It is worth mentioning that the previous forecasting method used for the data augmentation failed here to learn from the data and predict the next 365-day demands using the exact training settings and network structure above. The gap of information between the starting and ending points of the yearly dataset had a significant impact on model accuracy.

Fig. 9
figure 9

a Load forecasting– single-variable multi-sequence, b Model output errors– single-variable multi-sequence, c Training and loss errors– single-variable multi-sequence

Full size image

Multi-variable data-reshaping approach

Single sequence per variable

So far, the input variable used for prediction is the load demands. The network can be trained using multi-variable inputs including weather data, weekday, and weekend information. The necessary data for the average daily temperature for the region is collected and preprocessed. The one-hot encoding technique is used for the calendrical variables so that it does not give more weights to week-day variables. However, the weekend days have different one-hot values owing to the reduction in power consumption during these days. The network is trained with the above four input-variables which are augmented into 11 input sequences: one sequence for each of demands and temperature variables, seven sequences for the weekday variable, and two sequences for the weekend days. The corresponding errors for the output variables are 206.5580, 3.6647, 0.5346, 0.5345, 0.5347, 0.5350, 0.5347, 0.5356, 0.5349, 0.5355, and 0.5321, respectively. The relative percentage error for the load demand is calculated to be 7.66%, and the results are plotted and displayed in Fig. 10a–c.

Fig. 10
figure 10

a Load forecasting– multi-variables single-sequence per variable, b Model output errors– multi-variables single-sequence per variable, c Training and loss function error, multi-variables single-sequence per variable

Full size image

Multi-sequence per variable

We can also forecast future load demands using multi-input data augmentation by dividing the demand sequence into several training yearly subsets. The same input variables used in the previous scenario are employed for this case study. The input variables are load demand, averaged-daily temperature, weekday information, and weekend days data. The total input sequences are 20 sequences, five per each input variable representing the 5-year training sets. The network is trained and simulated with the test data. The sequence errors are computed to be 429.2631, 288.5629, 174.6432, 191.2456, 239.1730, 0.0872, 2.4136, 3.1355, 3.4470, 3.4504, 0.0141, 0.5271, 0.7512, 0.7502, 0.7543, 3.7824, 4.3455, 5.1981, 3.7032, and 3.8014, respectively. The load demand error for the sequences is 174.64/2696 or 6.48% which is lower than the corresponding one with classical inputting described in the previous model. The results of training the network and model analysis for this scenario are plotted and shown in Fig. 11a–c.

Fig. 11
figure 11

a Load forecasting, multi-variables multi-sequence per variable, b Model errors– multi-variables multi-sequence per variable, c Training and loss function errors– multi-variables multi-sequence per variable

Full size image

Load forecasting with different sampling-rates

All the networks designed so far are for input data with a sampling rate of one prediction per day. It will be useful to investigate the problem with the same input data but considering different sampling rates, such as one prediction per week. For comparison reasons, the data is smoothed using Gaussian function in MATLAB. The OTSAF example analyzed previously is repeated here with the new sampling rate and smoothed data. The network is a deep learning with the same structure as the one used for the OTSAF, and the results are shown in Fig. 12a–c. The relative error is computed to be 0.3485%, which is quite small and sufficient for an accurate load forecasting. The same procedure can be repeated for the other models in this study. It should be noted that in Fig. 12, we see the load demand is increasing from one year to another by an average scale value computed for the length of data to be 12.35%.

Fig. 12
figure 12

a Load forecasting, smoothed weekly data, b Forecasted errors– smoothed weekly data, c Training and loss function errors– smoothed weekly data

Full size image

Speed and error analysis

In this section, the different models we discussed so far are compared with respect to their errors and training times. The OTSAF model requires less time for training the network compared to the same network using the MTSAF approach owing to its forecasting time window. The ratio factor is 270/2053 which is around 13%. Error ratio is also different for these methods with a percentage of 3.08% for OTSAF and 7.99% for MTSAF. However, when the data is smoothed and the sampling ratio is changed from one-day to one-week per prediction, additional improvements in training time and model error of OTSAF are obtained which are found to be 93 s (it was 270 s) and 0.3485% (it was 3.08%). However, for the rest of the models, the data is decided to remain unchanged to reflect the original data received from the source. Next, we compare the classical method of data inputting as one sequence and the proposed data augmentation technique. The main difference is in the training time where the proposed model requires only 26% (551/2053) of the training time of the classical model. The error is also improved by 23.5% (7.99/6.47). Another significant improvement in the model is that the previous model in the literature with the one-year data division fails to accurately predict the 365-day ahead demand this dataset. For the multi-variable models, the proposed data augmentation improves the accuracy with 18% less error (7.66/6.48) and accelerates the learning process 236% times faster than the classical inputting with one sequence per variable.

Conclusion

This paper presented an improved historical data-augmentation approach proposed to enhance the load forecasting performance, accuracy, and training-time speed. Deep learning networks are used using LSTM and GRU techniques, which are the state-of-the-art approaches for time series and sequence-based problems. Multiple input sequences are employed to increase the generality of the model including load demands, temperature data, and important calendrical data such as weekday and weekend information. While the literature uses mainly MATLAB coding for forecasting load demands, this study introduces MATLAB and Simulink programs to present the algorithm in a visualized way. The test data employed in this paper is the load profile for the Kurdistan regional power system. The relationship between observations in the input data is conducted using correlation analysis which showed a high correlation value among the time-series observations. While the previous data augmentation approach was unsuccessful to train the network for several cases, the proposed method demonstrates its ability to forecast the future next 365-day load demands in a comparatively short training time and with better accuracy.