Evaluating wind speed probability distribution models with a novel goodness of fit metric: a Trinidad and Tobago case study

Abstract

Wind energy has been explored as a viable alternative to fossil fuels in many small island developing states such as those in the Caribbean for a long time. Central to evaluating the feasibility of any wind energy project is choosing the most appropriate wind speed model. This is a function of the metric used to assess the goodness of fit of the statistical models tested. This paper compares a number of common metrics then proposes an alternative to the application-blind statistical tools commonly used.Wind speeds at two locations are considered: Crown Point, Tobago; and Piarco, Trinidad. Hourly wind speeds over a 15-year period have been analyzed for both sites. The available data is modelled using the Birnbaum–Saunders, Exponential, Gamma, Generalized Extreme Value, Generalized Pareto, Nakagami, Normal, Rayleigh and Weibull probability distributions. The distributions were compared graphically and their parameters were estimated using maximum likelihood estimation. Goodness of fit was assessed using the normalised mean square error testing, Chi-squared testing, Kolmogorov–Smirnov, R-squared, Akaike information criteria and Bayesian information criteria tests and the distributions ranked. The distribution ranking varied widely depending on the test used highlighting the need for a more contextualized goodness of fit metric. With this in mind, the concept of application-specific information criteria (ASIC) for testing goodness of fit is introduced. This allows distributions to be ranked by secondary features which are a function of both the primary data and the application space.

Introduction

Electricity costs in most Caribbean Small Island Developing States (SIDS) are amongst the highest in the world [1] with majority of electrical energy being produced from imported fossil fuels [2]. As a result, wind energy is increasingly being explored as an alternative source of energy [3] with feasibility studies showing great potential for various islands [4,5,6,7]. Conversely, the Caribbean countries are amongst the most wind storm-prone regions in the world suffering from 26 storm impacts in the last 4 years alone [8,9,10]. These storms have an acute impact on the economies of these small states [11]. Additionally, wind speeds can even impact upon the region’s flora and fauna [12].

Given the importance of wind to Caribbean SIDS, it is necessary for the characteristics of the wind be studied closely. Energy studies, storm risk studies and aviation considerations, among others, require the wind to be modelled as accurately and comprehensively as possible. Many studies have aimed at characterizing or comparing wind speed distributions at different locations [13,14,15,16,17,18,19,20,21]. Several emphasize seasonal variations while diurnal variations have also been examined [5]. However, these have either been located outside the Caribbean or have been limited in their exploration of candidate distributions. Furthermore, there is no consensus on the goodness of fit criterion which is most suitable for evaluating the appropriateness of the distribution to a particular application [22].

The paper examines the applicability of probability distributions commonly used to model wind speeds to data available from two locations in Trinidad and Tobago. The relative performance of these distributions is compared using goodness of fit tests. Additionally, the concept of application-specific information criteria (ASIC), is introduced as an improved method for distribution ranking in the case of wind energy studies. Section 2, “Description of Data,”describes the data used for this study, investigates the basic statistical properties and outlines the pre-processing required before utilisation of the data. Section 3, “Methodology” describes the candidate distributions, goodness-of-fit criteria used and the method for parameter estimation. Section 4, “Results and Discussion” displays the fit of the candidate distributions to the data graphically. Several goodness-of-fit tests are used to rank the performance of the distributions. In addition, expected wind energy output from a turbine is estimated and compared to the energy output calculated using the actual wind data. Finally, concluding remarks are given in Sect. 5.

Description of data

General

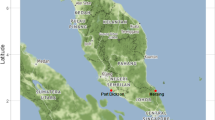
The locations given in Fig. 1, provide a useful opportunity for comparison as they are both greeted by the same north-easterly trade wind system [23], but are located at sites with differing geography. Crown Point is on a sheltered coast while Piarco is located in-land in an open plain. Piarco also receives some degree of sheltering by mountains to the North.

Table 1 Coordinates of wind measurement locations

Fig. 1

Map of Trinidad and Tobago illustrating measurement locations [24]

The dataset consists of the mean hourly wind speeds at Crown Point, Tobago and Piarco, Trinidad (locations indicated in Table 1 for the years 2000–2015, provided by the meteorological offices at airports at both locations and does not include wind direction or peak gust speed. The speeds were recorded in knots, rounded to the nearest knot, and are given in intervals of 1 h for each hour of the 24-h day for every day of the month. It should be noted that there are data points missing from both datasets. For Piarco, Trinidad, approximately 19 days of data from October 21 to November 9, 2009 are missing. There are also missing data points for a number of hours on other days. The total number of measurements is 133,083 out of a maximum possible number of 133,656 (0.4% missing data). For Crown Point, the data for the months of July to September, 2001, and August, 2011, are missing. Additionally, some days are missing data for an hour or a few hours. The total number of measurements is 123,429 out of a maximum possible number of 133,656 (7.7% missing data).

Basic statistics

Before any pre-processing, the data were described by the statistics given in Tables 2 and 3. Data pre-processing included data inspection for possibly erroneous values:

Table 2 Basic statistics of wind speeds at Piarco before pre-processing

Table 3 Basic statistics of wind speeds at Crown Point before pre-processing

• As seen in Table 2, at Piarco, the maximum wind speed recorded is 196 knots at 9:00 a.m. on July 3, 2014. The maximum wind speed on that day otherwise was 16 knots, and the average was 8 knots. A wind speed of 196 knots (363 km/h) is the equivalent of a Category 5 hurricane [25]. 196 knots surpasses the sustained wind speeds of the strongest hurricane on record, Hurricane Patricia in October 2015 [26]. Records from satellite-based models available online [27] confirm that the measurement is erroneous.

• Similarly, a speed of 94 knots was recorded as the maximum wind speed in 2009. This peak wind speed was recorded on June 12 at 11:00 a.m., followed by a measurement of 84 knots at 12:00 p.m.. The average wind speed on that day without these two measurements was 5.9 knots. These two wind speeds are the equivalent of a Category 2 Hurricane according to the Saffir–Simpson scale [25]. However, review of archived daily newspapers, for the next day make no mention of the event [28]. Again, no corroborating records were found to confirm these wind speeds [14] and as such, they were deemed erroneous.

• On February 16, 2015 a wind speed of 40 knots was noted at 9:00 a.m. This would be classified as tropical storm wind speeds according to the Saffir–Simpson scale. Online records corroborate the data for the rest of the day.

• At Crown Point, Tobago a maximum wind speed of 264 knots is recorded on November 9, 2001 at 11:00 p.m. This wind speed exceeds the world record maximum 3 second surface wind gust of 220 knots. As such, it can safely be concluded that this is an erroneous record. Online records corroborate the data for the rest of the day.

• Similar methods to those utilised above were used to identify 214 knots recorded on November 20, 2005 at 2:00 p.m., 187 knots on April 20, 2001, 96 knots July 17, 2005, 70 knots at 9:00 p.m. on June 20, 2006, 62 knots on March 20, 2001, 45 knots January 3, 2004 and 39 knots on January 2, 2002 at 11:00 a.m.

All noted erroneous measurements were replaced with null values. Tables 4 and 5 reflects the wind statistics after pre-processing.

Table 4 Basic statistics of wind speeds at Piarco after pre-processing

Table 5 Basic Statistics of Wind Speeds at Crown Point after pre-processing

Fig. 2

Histogram of wind speeds at Piarco

Fig. 3

Histogram of wind speeds at Crown Point

Methodology

Distribution fitting

Typically, wind data is modelled as a Weibull distribution, especially when the aim is to characterise the annual resource [5, 15, 29,30,31,32], however, a number of other candidate distributions have been catalogued [33]. For other applications such as statistical analysis of extreme wind speeds, the Weibull (or reverse Weibull) has also been recommended [34] while other distributions such as the generalised extreme value distribution [17] and the generalised pareto [19] have been explored. Agustin [20] encouraged using mixed distributions while confirming the applicability of Weibull. Sarkar et al. [35] identified the weakness of the Weibull distribution as its failure to describe the upper tail. The Rayleigh distribution has also been used as a probability model for wind speed [31], although some applications have found Weibull to be more accurate [32, 36]. Recent studies found autoregressive models [37] and maximum entropy distributions [38] to be better suited to wind speed applications than Weibull or Rayleigh. Alavi et al.  [39] found that the Nakagami distribution performed well when compared to other distributions frequently used to model wind speed. Additionally, the Normal and Exponential Distributions were identified as potential candidates via visual inspection of the histogram shape. The Birnbaum–Saunders and Gamma distributions performed well when goodness of fit was assessed using the Akaike information criterion (AIC) and the Bayesian information criterion (BIC) criteria, and were thus included in the comparative analysis (Figs. 2, 3).

Review of probability distribution functions

The equations defining the probability density functions (PDFs) for various candidate distributions of interest are given below. While by no means exhaustive, the distributions represent those commonly used in the literature.

Birnbaum–Saunders

$$\begin{aligned} f(x) = \frac{\sqrt{\frac{x-\mu }{\beta }} + \sqrt{\frac{\beta }{x-\mu }}}{2\gamma (x-\mu )}\Phi \left( \frac{\sqrt{\frac{x-\mu }{\beta }} - \sqrt{\frac{\beta }{x-\mu }}}{\gamma }\right) , \quad x>\mu , \end{aligned}$$

(1)

where $\mu$ is the location parameter, $\gamma >0$ is the shape parameter, $\beta >0$ is the scale parameter and $\Phi (t) = \frac{1}{\sqrt{2\pi }}\mathrm{e}^{\frac{t^2}{2}}$ [40].

Exponential

$$\begin{aligned} f(x) = \lambda \mathrm{e}^{-\lambda x},\quad x\ge 0, \end{aligned}$$

(2)

where $\lambda >0$ is the rate parameter [41].

Gamma

$$\begin{aligned} f(x) = \frac{x^{k-1}\mathrm{e}^{-\frac{x}{\theta }}}{\theta ^k\Gamma (k)},\quad x\ge 0, \end{aligned}$$

(3)

where $k,~\theta \ge 0$, and $\Gamma (k)=(k-1)!$ is the gamma function [42, 43].

Generalized extreme value

$$\begin{aligned} f(x) = \frac{1}{\sigma }t(x)^{\xi + 1}\mathrm{e}^{-t(x)} \end{aligned}$$

(4)

where

$$\begin{aligned} t(x) = {\left\{ \begin{array}{ll} \left( 1+\left( \frac{x-\mu }{\sigma }\xi \right) \right) ^{-\frac{1}{\xi }},&{}\quad \xi \ne 0, \\ \mathrm{e}^{-\frac{x-\mu }{\sigma }},&{}\quad \xi = 0, \end{array}\right. } \end{aligned}$$

(5)

where $\mu \in {\mathbf {R}}$ is the location parameter, $\sigma >0$ is the scale parameter and $\xi \in {\mathbf {R}}$ is the shape parameter [44].

Generalized Pareto

$$\begin{aligned} f(x) = \frac{1}{\sigma }\left( 1+\frac{x-\mu }{\sigma }\xi \right) ^{-\left( \frac{\xi + 1}{\xi }\right) } \end{aligned}$$

(6)

where $\mu \in {\mathbf {R}}$ is the location parameter, $\sigma >0$ is the scale parameter and $\xi \in {\mathbf {R}}$ is the shape parameter [45].

Nakagami

$$\begin{aligned} f(x) = 2\left( \frac{\mu }{\omega } \right) ^{\mu } \frac{1}{\Gamma (\mu )}x^{(2\mu -1)}\mathrm{e}^{-\frac{\mu }{\omega }x^2} \end{aligned}$$

(7)

where $\mu$ is the shape parameter and $\omega$ is the spread parameter, for $x>0$ [46].

Normal

$$\begin{aligned} f(x) = \frac{1}{\sigma \sqrt{2\pi }}\mathrm{e}^{-\frac{(x-\mu )^2}{2\sigma ^2}}, \end{aligned}$$

(8)

where $\mu$ is the mean and $\sigma$ is the standard deviation [45].

Rayleigh

$$\begin{aligned} f(x) = \frac{x}{\sigma ^2}\mathrm{e}^{\frac{-x^2}{2\sigma ^2}}, \end{aligned}$$

(9)

where $\sigma$ is the scale parameter [47].

Weibull

$$\begin{aligned} f(x) = {\left\{ \begin{array}{ll} \frac{k}{\lambda }\left( \frac{x}{\lambda }\right) ^{k-1}\mathrm{e}^{-\left( \frac{x}{\lambda }\right) ^k}&{}\quad x \ge 0 \\ 0,&{}\quad x < 0, \end{array}\right. } \end{aligned}$$

(10)

where $k>0$ is the shape parameter and $\lambda >0$ is the scale parameter [48].

Parameter estimation

Several techniques exist for parameter estimation (e.g., [22]). In this work, the parameters for these various distributions were estimated using the maximum likelihood method, which selects as its estimate the parameter value that maximizes the probability of the observed data [49]. This method is popularly used since the resulting estimators are generally asymptotically unbiased and consistent. They also offer the advantage of simplicity in implementation. While this method can be limited through the need to determine closed-form estimator solutions, for the distributions of interest in this work, these can be readily obtained [22].

Goodness of fit

After plotting the distributions using the estimated parameters, the goodness of fit of the distributions to the data profile were assessed using the following metrics:

• Normalised mean square error (NMSE).

• Chi-squared statistic.

• Two sample.

• Kolmogorov–Smirnov.

• Coefficient of determination ($R^2$).

• Akaike information criterion (AIC).

• Bayseian information criterion (BIC).

The normalised mean square error (NMSE)

The NMSE was calculated using the previous method with the following equation:

$$\begin{aligned} \mathrm{NMSE} =1-\sum _{i=1}^{n} \left( \frac{y_i-f_i}{y_i-\hat{f}_i } \right) ^2 \end{aligned}$$

(11)

Where $y_n$ are the modelled values and $f_n$ are the reference data.

The returned value varies between $-\infty$ (bad fit) to 1 (perfect fit) [50, 51].

The Chi-squared statistic

For testing the goodness of fit, the Chi-squared was used. The Chi-square statistic ($\chi ^2$) is calculated as follows:

$$\begin{aligned} \chi ^2= \sum _{i=1}^{N}\frac{\left( O_i- E_i\right) ^2}{E_i}, \end{aligned}$$

(12)

where $O_i$ are the observed counts and $E_i$ are the expected counts [49]. $O_i$ was the estimated sample datasets calculated using the estimated pdf of each distribution. $E_i$ was derived via the frequency histogram based on the measured data. N was determined by the number of bins used in the frequency histogram. A smaller Chi-squared statistic indicates a better fit.

The two-sample Kolmogorov–Smirnov test

The two-sample Kolmogorov–Smirnov test statistic was calculated as follows:

$$\begin{aligned} D^*= \max \limits _{x}(|F_1 (x)-F_2 (x)|) \end{aligned}$$

(13)

where $F_1(x)$ is the proportion of x1 values less than or equal to x, and $F_2(x)$ is the proportion of x2 values less than or equal to x. The smaller the test statistic the better the fit [52].

Co-efficient of determination, $R^2$

The $R^2$ statistic was calculated as follows:

$$\begin{aligned} R^2 = 1-\frac{SS_\mathrm{res}}{SS_\mathrm{tot}}, \end{aligned}$$

(14)

where,

$$\begin{aligned} SS_\mathrm{res} = \sum _i\left( y_i-f_i\right) ^2, \end{aligned}$$

(15)

and,

$$\begin{aligned} SS_\mathrm{res} = \sum _i \left( y_i - \bar{y}\right) ^2, \end{aligned}$$

(16)

where $y_i$ represents the dataset and $f_i$ represents the modelled values. R$^2$ varies between − Inf (bad fit) to 1 (perfect fit) [53].

Akaike information criterion

The AIC statistic was calculated as follows:

$$\begin{aligned} \mathrm{aic}= -2\mathrm{log}L(\theta ) +2k, \end{aligned}$$

(17)

where $\mathrm{log}L(\theta )$ denotes the value of the maximized loglikelihood objective function for a model with k parameters. A smaller AIC statistic value indicates a better fit [54].

Bayesian information criterion

The BIC statistic was calculated as follows:

$$\begin{aligned} \mathrm{bic}= -2\mathrm{log}L(\theta )+k\mathrm{log}(N), \end{aligned}$$

(18)

where $\mathrm{log}L(\theta )$ denotes the value of the maximized loglikelihood objective function for a model with k parameters fit to N data points. A smaller BIC statistic value indicates a better fit [54] (Figs. 4, 5, 6, 7).

Results and discussion

Fig. 4

Wind distribution at Crown Point

Fig. 5

Wind distribution at Piarco

Fig. 6

Wind distribution at Crown Point (Bin Size 3)

Fig. 7

Wind distribution at Piarco (Bin Size 3)

The estimated parameters for each distribution are shown in the Appendix. The performance of these distributions were compared using the goodness of fit metrics described in Sect. 3.4 (Tables 6, 7, 8, 9).

Table 6 Distribution ranking for Crown Point data (Bin Size 1)

Table 7 Distribution ranking for Piarco data (Bin Size 1)

Table 8 Distribution ranking for Crown Point data (Bin Size 3)

Table 9 Distribution ranking for Piarco data (Bin Size 3)

As evident, rankings varied depending on the goodness of fit metric used. Although in some other studies goodness of fit metrics corroborated each other [32, 38, 39], similar variability was observed in [55].

Figures 8, 9, 10, 11, 12, 13, 14, 15, 16 and 17 show the details for each goodness of fit metric. This is particularly evident in Figs.  8 and 9 which show rankings by NMSE and Chi-squared metrics, where the Birnbaum–Sanders distribution was particularly ill fitted as compared to Figs.  11 and 12 in which it is comparable when evaluated using the $R^2$, and AIC and BIC criteria, respectively.

Fig. 8

Crown Point—NMSE

Fig. 9

Crown Point—Chi Squared

Fig. 10

Crown Point—KS

Fig. 11

Crown Point—R Squared

Fig. 12

Crown Point—Log Likelihood, AIC and BIC

Fig. 13

Piarco—NMSE

Fig. 14

Piarco—Chi Squared

Fig. 15

Piarco—ranked by KS

Fig. 16

Piarco—Chi Squared

Fig. 17

Piarco—Log-Likelihood, AIC and BIC

The variability in rankings raises the question of suitability of any given metric to the application. Consequently, some method of determining which goodness-of-fit criterion is best suited to the application has to be found or a new application-specific information criterion (ASIC) has to be formulated.

Application-specific information criterion

Wind models are used to calculate the expected energy generated by wind turbines. In this case, expected energy output over a particular time would be an important consideration in design and investment decisions. The ability of the distribution to accurately estimate this value is crucial.

Consider a wind turbine modeled as a 3MW unit using a piecewise linear model with a cut-in speed (cis) of 3.5 ms$^{-1}$, rated speed (rs) of 14 ms$^{-1}$ and cut-out speed ($\cos$) of 25 ms$^{-1}$ as shown in Fig. 18.

The expected energy output of the turbine over a given period of time is calculated according to Eq. 19.

$$\begin{aligned} E = \mathrm{hrs}\times \int ^{\cos }_\mathrm{cis}P(v)\times \,f(v)\,\mathrm{d}v \end{aligned}$$

(19)

where P(v) is the turbine power vs speed characteristic (Fig. 18) and f(v) is the distribution function used to model the data.

For this work, the proposed ASIC is defined as a normalized weighted error function (in this case normalized error in expected energy is used), with the weightings defined by the turbine characteristic.

$$\begin{aligned} \mathrm{ASIC}&= \frac{\mathrm{hrs}\times \left[ \int ^{\cos }_\mathrm{cis}P(v)\times \,\hat{f}(v)\,\mathrm{d}v - \int ^{\cos }_\mathrm{cis}P(v)\times \,f(v)\,\mathrm{d}v\right] }{\mathrm{hrs}\times \int ^{\cos }_\mathrm{cis}P(v)\times \,f(v)\,\mathrm{d}v},\nonumber \\&=\frac{\int ^{\cos }_\mathrm{cis}P(v)\times \,\left( \hat{f}(v)-f(v)\right) }{\int ^{\cos }_\mathrm{cis}P(v)\times \,f(v)\,\mathrm{d}v}\,\mathrm{d}v \end{aligned}$$

(20)

where $\hat{f}(v)$ is the estimated distribution function.

Fig. 18

Wind turbine power characteristic

Using this approach, sections of the distribution which contribute more to the application are more heavily weighted than those that do not. In this case, the fit of the distributions below wind speeds of 3.5 ms$^{-1}$ or above 25 ms$^{-1}$ are not as important since the wind turbine does not output any power for those conditions. Using the chosen ASIC, the fit of the data over the range of power producing speeds of the turbine is assessed. This marks a departure from the philosophy behind other goodness-of-fit tests which equally weight all sections of a distribution or weight them based on probability and do not consider any external information in the determination of goodness of fit.

The actual energy output for Piarco was calculated as approximately 112 GWh, while the value for Crown Point was 155 GWh. Tables 10 and 11 show the percentage difference in energy predicted by the models as compared to the energy derived directly from the wind data. As evident, the results did not match any ranking derived from the conventional goodness-of-fit metrics.

Among the traditional goodness-of-fit tests, the Chi-squared and Kolmogorov–Smirnov tests produced similar results to the ASIC in that they placed similar candidate distributions within the top four ranked distributions, albeit with a different order. This indicates that they may be better suited as goodness-of-fit tests for the purpose of wind energy studies than the other traditional goodness of fit metrics utilised in this paper. Given that the application space is known, however, using an ASIC would still be preferrable since rankings are made according to a parameter (energy in this case) which is meaningful to users of the data.

Finally, it is also noteworthy that the Weibull distribution, which is traditionally used in wind modelling in the Caribbean, performed poorly for both datasets using all the metrics investigated. This is likely due to the large amount of low to zero wind speed measurements. Castellanos [37] has also noted that the Weibull distribution performs poorly when the data contains a large proportion of low wind speeds (Figs. 19, 20; Table 12).

Table 10 Expected energy at Crown Point by distribution

Table 11 Expected energy predicted at Piarco by distribution

Table 12 Parameter Estimates for distributions

Fig. 19

Crown Point ranked by expected energy

Fig. 20

Piarco ranked by expected energy

Conclusions

The Weibull distribution was found to perform relatively poorly as a wind probability model for both sites. The Rayleigh distribution performed consistently better than the Weibull but was still ill suited as a model for the data.

The inconsistency in results for the goodness of fit led to the conceptualization of application-specific information criteria (ASIC) as a more meaningful approach for assessment of goodness of fit in cases where the secondary, application-specific features must be calculated from the primary data.

For the application in question, the normalized error in expected energy is used as a goodness-of-fit metric to rank candidate distributions. The advantage of this technique is that the distributions can be examined in terms of over-estimation or under-estimation of expected energy as well as the magnitude of deviation while using a metric that is meaningful in the context of the intended application space.