1 Introduction

1.1 Historical development of wind speed modeling with probability distributions

Mid 20th Century was an epoch when the world started exploring the wind energy potential. With its emerging demand for power and vulnerability to oil crises, India started its wind energy program in 1983–84. The success of the wind energy program lies in the accuracy of the assessment of wind flow patterns at a potential site. Wind energy is a site-specific and intermittent source of power. Therefore, an extensive wind resources assessment is an essential prerequisite for harnessing the wind power potential at a given site. Wind resource assessment estimates wind flow patterns based on several factors: available wind data, topographical conditions, meteorological conditions, etc. This necessitates the involvement of statistics in evaluating wind flow patterns, which is critical in designing mega-structures and optimizing energy generation from the wind. In statistical terms, the wind flow pattern is not stable in the short term. Nonetheless, it exhibits a consistent and stable pattern over the long term (except for radical and lasting changes due to climate change, which can be spotted by statistical approaches such as change-point detection Aminikhanghahi and Cook (2017)). According to Zhang (2015), wind statistics is a scientific field that examines the wind patterns over a significant duration. Wind data is viewed as a continuous random variable, leading to the use of continuous probability distributions to model the predictable wind pattern. Since the 1940s till today, several papers have been published that used different continuous probability distributions to describe the wind speed, including (Akpinar and Akpinar 2004a, 2009; Jaramillo and Borja 2004; Carta and Ramirez 2007a, b; Carta and Mentado 2007; Gokcek et al. 2007; Vicente 2008; Akdağ et al. 2010; Fyrippis et al. 2010; Safari and Gasore 2010; Chang 2011b; Morgan et al. 2011; Safari 2011; Soukissian 2013; Zhang et al. 2013; Alavi et al. 2016; Hu et al. 2016; Jung et al. 2017; Kantar et al. 2018) and Mohammadi et al. (2017). Distributions with up to 2 parameters were used to model unimodal data, while data exhibiting bimodality have been modeled using multi-parameter distributions, in particular as mixtures of 2-parameter distributions.

Sherlock (1951) recommended utilizing the Pearson type III distribution which is essentially the Gamma distribution, due to its successful and widespread use. The distribution employs two parameters, a scale parameter and a shape parameter and performs well in modeling natural phenomena specificity velocity data.

Luna and Church (1974) used the 2-parameter log-normal distribution for studying air pollution level. The same distribution was implemented by Kaminsky (1977) and Justus (1978) for wind speed analyses, but since then it has only very rarely been considered for fitting this type of data (Tar 2008; Garcia et al. 1998; Bogardi and Matyasovzky 1996).

In the 1970s, the Rayleigh (R) and Weibull (W) distributions entered the scene to model the wind speed (Hennessey Jr 1978). Until the late 1990s, the Weibull distribution proves to be superior to earlier distributions with a low (\(<=2\)) number of parameters (Morgan 1995; Akpinar and Akpinar 2004b, 2005; Pishgar-Komleh et al. 2015; Pishgar-Komleh and Akram 2017). Therefore, it has been a part of widely used computer modeling softwares such as HOMER (Rehman et al. 2007; Van Alphen et al. 2007) and WASP (Hunter and Elliot 1994; Sahin et al. 2005). For instance, the Weibull distribution showed better fitting than Rayleigh (Bidaoui et al. 2019), exponential, square root normal, log-normal and Gamma distributions (Chang 2011b). However, it is well known that the Weibull distribution is not suitable for fitting bimodal data or data with high volume (\(>15\) % of total wind data set) of low wind speed (meaning 0 m/s) (Carta and Ramírez 2007a, b). Therefore a lot of research efforts have been oriented to find alternatives for and modifications to the Weibull distribution (e.g., Chadee and Sharma (2001); Carta and Mentado (2007); Bali and Theodossiou (2008); Akpinar and Akpinar (2009); Akdağ et al. (2010); Chang (2011b); Chellali et al. (2012); Akgül et al. (2016); Bracale et al. (2017); Aries et al. (2018)). A 3-parameter Weibull distribution with an added location parameter is another suitable alternative to fit wind data of low wind speed (Chalamcharla and Doraiswamy 2016). However, Chadee and Sharma (2001) noted that including the extra location parameter in the estimation process creates challenges, and a positive value for this parameter results in an unrealistic condition of zero probability of wind speeds less than the parameter value. To address high probabilities of zero wind speeds, Carta et al. (2008) proposed using a singly truncated normal (TN) distribution. In cases where wind speed data has infrequent low speeds, Bardsley (1980) recommended the use of the inverse Gaussian distribution as a viable alternative to the 3-parameter Weibull distribution with a positive location parameter. Bivona et al. (2003) fitted all non-zero wind speeds with the Weibull distribution and treated zero wind speeds separately. Table 1 shows comparative studies of the most classical 2-parameter distributions for wind speed modeling.

As there was no universal acceptance of the Weibull distribution (Carta et al. 2009), the search for other distributions intensified, leading to numerous studies, and new distributions were developed. Ouarda et al. (2016) revealed the importance of skewness and kurtosis while modeling the data sets. Some new distributions which were earlier used in other applications were also tested for goodness-of-fit of wind speed data. Soukissian (2013) has introduced the 4-parameter Johnson \(S_B\) distribution for wind speed data modeling and compared it with the Weibull distribution. He revealed that indiscriminate use of the Weibull distribution is unjustified and found that the Johnson \(S_B\) distribution is a much more suitable model for 11 and 8 buoys of Eastern and Western Mediterranean Sea, respectively.

Various authors have proposed using two-component mixture distributions with different weight proportions to model bimodal wind speed data. Most proposed mixture distributions comprise a Weibull component (Jaramillo and Borja 2004; Carta and Ramírez 2007a;b; Akpinar and Akpinar 2009; Akdağ et al. 2010; Shin et al. 2016) and are typically of the type Weibull–Weibull, truncated normal-Weibull, and Gamma-Weibull. Table 2 provides a summary of articles in which mixture models have been applied for wind speed modeling.

1.2 Review of methods used for parameter estimation in continuous probability distributions

There exist numerous different methods to estimate the parameters of continuous probability distributions, such as for instance the method of moments (MoM), the least square method (LSM), the L-moment method and the maximum likelihood method (ML). Various articles have compared distinct methods in the context of wind data modeling, including (Akdağ and Dinler 2009; Carta et al. 2009; Bagiorgas et al. 2011; Chang 2011a; Morgan et al. 2011; Saleh et al. 2012; Arslan et al. 2014; Azad et al. 2014; De Andrade et al. 2014; Akdağ and Güler 2015; Mohammadi et al. 2016). In the next paragraph we shall briefly point out the pros and cons of these methods, and refer the reader to Gugliani et al. (2018) for a more detailed analysis.

For the LSM, the best estimator is the one that minimizes the sum of squared errors between the observed and the corresponding theoretical values from the distribution. The LSM thus is based on the cumulative distribution function (cdf) of a continuous random variable, function which describes the probability for this random variable to be smaller than a given value. This can lead to complex calculations, in which case it is recommended to solve the equation using a nonlinear technique such as Levenberg–Marquardt (Akdağ et al. 2010).

The MoM is the simplest computational method as it estimates the distribution’s parameters using the sample moments. In this way, the parameters are estimated by equating the theoretical moments with the sample moments. However, the method has certain drawbacks (e.g., it can lack robustness), as pointed out in Akdağ and Dinler (2009).

Hosking (1990) proposed the L-moment as another important parameter estimation method. The L-moments are more robust than conventional moments to outliers in the data and enable more secure inferences to be made from small samples about an underlying probability distribution. They are less susceptible to sampling variability, which makes it more suitable for modeling extreme data. Several authors (Gubareva 2011; Murshed et al. 2011; Strupczewski et al. 2011; Papalexiou and Koutsoyiannis 2013; Rutkowska et al. 2017; Ul Hassan et al. 2019; Nerantzaki and Papalexiou 2022) have utilized this method to fit generalized extreme value distributions to rainfall, flood, streamflow data across various parts of the world. Comparative studies of this method with other two methods, viz., MLE and MoM reveals that it is equivalently good as compared to MLE (Rowinski et al. 2002; Gubareva and Gartsman 2010; Hu et al. 2020) and outperforms MoM in parameter estimation (Murshed et al. 2011; Vivekanandan 2015).

The ML method selects those values of parameters that maximize the probability under that distribution of obtaining the randomly observed sample. Suppose \((v_1, v_2, \ldots , v_n)\) is the vector of the observations and \(\varvec{\theta }\) is the vector of the parameters. The likelihood function is defined as the product of probability density functions (pdfs), which we denote here as f, evaluated at each individual observation

$$\begin{aligned} L=\prod _{i=1}^n f\left( v_i ;\, \varvec{\theta }\right) . \end{aligned}$$

Subsequently, the log-likelihood function is obtained as

$$\begin{aligned} \ln L=\sum _{i=1}^n \ln f\left( v_i ;\, \varvec{\theta }\right) . \end{aligned}$$

By setting the partial derivatives of the log-likelihood function with respect to \(\varvec{\theta }\) to zero

$$\begin{aligned} \frac{\partial }{\partial \varvec{\theta }}\ln L=0, \end{aligned}$$

the maximum likelihood estimates (MLEs) of the parameters are obtained by solving the system of equations, however solving the likelihood equations can be tricky and require numerical methods (Chang 2011a).

1.3 Model selection criteria

In the statistical literature, there exist various criteria to identify the best-fitting distribution for a given data set. In studies about wind speed data, the most commonly used are the coefficient of determination (\(R^2\)), the root mean square error (RMSE) (Akdağ et al. 2010; Aries et al. 2018), the chi-square (\(\chi ^2\)) (Akpinar and Akpinar 2009) and the Kolmogorov–Smirnov (K–S) goodness-of-fit tests (Ayyub and McCuen 2016; Chang 2011a).

In this paper, the K–S goodness-of-fit test has been used to measure the closeness of the fitted cdf with the cumulative relative frequency of the sample wind speed data and to indicate whether or not a distribution is suitable to fit a given data set. The K–S test is defined as the max-error between two cumulative distribution functions

$$\begin{aligned} Q=\max |F(v)-G(v)| \end{aligned}$$

where F(v) is a fitted cdf and G(v) is the cumulative relative frequency of a sample.

However, among all acceptable distributions, they do not tell which one fits best (p-values only serve to reject a distribution for fit or not, but one should not compare p-values among themselves to rank distributions). Such a ranking is provided by information criteria such as the Akaike Information Criterion (AIC) which is based on a compromise between the goodness-of-fit of a distribution in terms of the likelihood function and the number of parameters to estimate, and this compromise is obtained via a penalization on that number. The mathematical expression for AIC is given as

$$\begin{aligned} AIC= 2N-2log(L) \end{aligned}$$

where L is the likelihood and N is the number of parameters of the model. The smallest AIC value indicates the most suitable distribution. This distribution, however, is not guaranteed to give a reasonable fit (the AIC would also choose the best among bad-fitting distributions). Therefore the best strategy is to first compare distributions via the AIC and then test the best-fitting distribution through the K–S goodness-of-fit test.

1.4 Contribution of the present paper

Given the plethora of different proposals of distributions for modeling wind speed, it is not obvious to know which one to use. As indicated in Tables 1 and 2, comparisons have already been made, but so far no paper has done a really exhaustive comparison taking also mixture components into account. Moreover, the comparison of distributions in the literature is mostly along the coastal line of countries, and often a single distribution performs better than others for all the locations under consideration. However, this factor is not valid for a vast country like India. The main land of India is full of various hills across its geography. These hilly regions also have the capability to harness the wind energy potential. The additional advantage of these hilly regions is that they are not prone to cyclones thanks to their higher topography compared to surrounding land. Once wind turbines have been installed, they can operate at their full capacity producing uninterrupted power supply, without the fear of damage to the power plant. Therefore, in this study, we have taken as many as seventeen locations covering the main land, western coastal region, and eastern coastal region of India, so that the manufacturers can identify the most suitable distributions for their probable site before installing the power plant.

The wind speed data utilized in this study were recorded at a height of \(10 \mathrm {~m}\) by the Indian Meteorological Department (IMD), Pune, assuming no density variation occurs vertically with height for long slender structures. The vertical change in wind speed with altitude typically follows the power law. Upon estimating the mean wind speed at a height of \(10 \mathrm {~m}\) using parameters from the most appropriate distribution, the mean wind speed at higher altitudes will be computed using the power law. This computation will enable a judicious selection of the type of wind turbine required for installation at a specific height. Consequently, a comparative evaluation of various distributions is necessary to assess the most suitable distribution for site-specific wind speed data. This evaluation is crucial in determining the appropriate wind turbine for optimal performance at different altitudes.

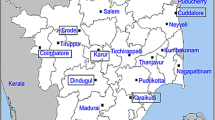
Following these motivations, in this paper we review and compare various probability distributions that have been suggested over the years by different researchers for wind resources assessment. Moreover, we shall also include some novel distributions that have primarily been used in other domains such as economics and reliability analysis or financial assessment. Many more (too many) probability distributions exist for describing positive data, see Sinner et al. (2022) for an overview. We restrict to those fourteen that we judge most important for modeling wind speed (see Sect. 2), and we estimate their parameters by the ML method, yielding precise estimates with minimal variance. The ML method allows us to use the AIC as criterion to compare the distributions. According to Ley et al. (2021), a good probability distribution should both be versatile, i.e. fit various distinct shapes, and parameter parsimonious, hence ideally not have too many parameters as this complicates interpretation and can lead to overfitting. Therefore, we choose the AIC as a goodness-of-fit criterion and the Kolmogorov–Smirnov test as a goodness-of-fit test. As case study we consider long-term wind speed data of seventeen onshore locations in India, which are described in Sect. 3. Nine sites lie in the seven windy states of India, and eight sites are from the state with zero wind power generation (as per physical report published by the Ministry of New & Renewable Energy). See Fig. 1. The results are presented and discussed in Sect. 4, while Sect. 5 provides a conclusion.

Fig. 1
figure 1

The locations of the seventeen considered stations in India (https://www.surveyofindia.gov.in/pages/outline-maps-of-india)

Full size image
Table 1 Comparative studies of the most classical 2-parameter distributions for wind speed modeling, where * indicates particularly relevant distributions for the considered study
Full size table
Table 2 Overview of papers that have used mixture models for representing wind speed data, where the number of *’s indicates the most relevant distributions for the considered study
Full size table

2 Overview of the considered continuous distributions

The distributions relevant for this study are briefly described in what follows. We start from 1- and 2-parameter distributions and end with 4- and 5-parameter distributions.

2.1 Weibull distribution

The 2-parameter Weibull distribution (W) is a classical distribution for wind speed data analysis, in particular unimodal frequency distributions. Originally the Weibull-distribution has 3 parameters, the third being known as the location parameter used for defining the lowest value in a data set. Since for wind speed this corresponds to 0, the location parameter can be dropped (or, say, implicitly equated to 0) and the 3-parameter Weibull distribution simplifies to the 2-parameter Weibull distribution. This 2-parameter Weibull distribution has been extensively employed to estimate the wind power potential or, to be more specific, in the estimation of wind characteristics, see e.g. Bivona et al. (2003); Akpinar and Akpinar (2004a, 2005); Gokcek et al. (2007); Fyrippis et al. (2010); Safari and Gasore (2010); Dursun et al. (2011); Baseer et al. (2017). The pdf and cdf of the 2-parameter Weibull distribution are respectively given by

$$\begin{aligned} f(v;\,k,s)=\left( \frac{k}{s}\right) {\left( \frac{v}{s}\right) }^{k-1}{\exp \left[ -{\left( \frac{v}{s}\right) }^k\right] \ }, v,k,s>0, \end{aligned}$$
(1)

and

$$\begin{aligned} F\left( v;k,s\right) =1-{\exp \left[ -{\left( \frac{v}{s}\right) }^k\right] \ }\ , \end{aligned}$$

where k is the non-dimensional shape parameter and s the scale parameter whose dimension is the same as that of the variable v. For clarification purposes we mention that the variable v stands for the wind speed that we wish to model. Besides a reasonably good fit to wind speed data, there are two further reasons for the popularity of the Weibull distribution: (a) there exist formulas that allow a vertical extrapolation of the wind characteristics (Tar 2008; Safari and Gasore 2010), and (b) it is very practical for calculating the capacity factor, power coefficient, and output power of wind turbines (Jangamshetti and Rau 1999; Dursun et al. 2011; Gugliani et al. 2021).

2.2 Rayleigh distribution

The Rayleigh (R) distribution is a 1-parameter distribution that arises as a special case of the Weibull distribution whose shape parameter is fixed to 2. Consequently, the expression of pdf and cdf of the Rayleigh distribution are given as

$$\begin{aligned} f(v;\,s)=\frac{2v}{s^2}{\exp \left[ -{\left( \frac{v}{s}\right) }^2\right] \ }, v,s>0 , \end{aligned}$$

and

$$\begin{aligned} F\left( v;\,s\right) =1-{\exp \left[ \frac{-v^2}{s^2}\right] \ }. \end{aligned}$$

2.3 Birnbaum–Saunders distribution

The 2-parameter Birnbaum–Saunders (BS) distribution is known as fatigue life distribution and was promoted in the two papers Birnbaum and Saunders (1969a, b). It has been developed by making a monotonic transformation of the standard normal random variable. The pdf and cdf of the BS distribution are given as

$$\begin{aligned} f(v;\,\alpha ,\beta )= & {} \frac{1}{2\sqrt{2\pi }\alpha \beta }\left[ {\left( \frac{\beta }{v}\right) }^{1/2}+{\left( \frac{\beta }{v}\right) }^{3/2}\right] \\{} & {} \times {\exp \left[ -\frac{1}{2{\alpha }^2}\left( \frac{v}{\beta }+\frac{\beta }{v}-2\right) \right] \ }, v,\alpha ,\beta >0, \end{aligned}$$

and

$$\begin{aligned} F\left( v;\,\alpha ,\beta \right) =\Phi \left[ \frac{1}{\alpha }\left\{ {\left( \frac{v}{\beta }\right) }^{{1}/{2}}-{\left( \frac{\beta }{v}\right) }^{{1}/{2}}\right\} \right] , \end{aligned}$$

where \(\beta\) is a scale parameter, \(\alpha\) is a shape parameter and \(\Phi\) (.) is the standard normal cdf.

2.4 Gamma distribution

The Gamma (G) distribution is a 2-parameter distribution whose curve drops off much more gradually than that of the exponential distribution for shape parameters \(\zeta\) > 1 and more quickly for \(\zeta\)< 1. The pdf and cdf are

$$\begin{aligned} f(v;\,\zeta ,\beta ) =\frac{v^{\zeta -1}}{\beta ^\zeta \Gamma (\zeta )}\exp \left[ -\frac{v}{\beta }\right] , v,\beta ,\zeta >0 , \end{aligned}$$
(2)

and

$$\begin{aligned} F\left( v;\,\zeta ,\beta \right) =\int ^v_0{\frac{x^{\zeta -1}}{{\beta }^{\zeta }\Gamma \left( \zeta \right) }}{\exp \left[ -\frac{x}{\beta }\right] \ }dx, \end{aligned}$$

where \(\zeta\) and \(\beta\) are the shape and scale parameters, respectively, and \(\Gamma (.)\) is the gamma function. The chi-squared distribution is a special case of the Gamma corresponding to \(\beta =2\) and \(\zeta =k/2\) for some positive integer k.

2.5 Nakagami distribution

The 2-parameter Nakagami (Na) distribution is strongly related to the G distribution (Nakagami 1960) and it is extensively used in communication engineering (Pajala et al. 2006; Beaulieu and Cheng 2005). Suppose V has the G distribution in (2), then \(\sqrt{V/\zeta }\) follows the Na distribution. The pdf and cdf of the Nakagami distribution are given as

$$\begin{aligned} f\left( v;\, \zeta ,\beta \right) =\frac{2\zeta ^\zeta }{{\beta }^\zeta \Gamma \left( \zeta \right) }v^{2\zeta -1}{\exp \left( -\frac{\zeta }{\beta }v^2\right) \ }, \zeta> 1/2,\ v,\beta >0, \end{aligned}$$

and

$$\begin{aligned} F\left( v;\,\zeta ,\beta \right) =\frac{P\left( \zeta ,\frac{\zeta }{\beta }v^2\right) }{\Gamma \left( \zeta \right) }, \end{aligned}$$

where P and \(\Gamma\) are the upper incomplete gamma and gamma functions, respectively.

2.6 Log-normal distribution

If a random variable V follows the log-normal (LN) distribution, then \(Y = \ln V\) has the normal distribution. The expressions for the pdf and cdf of the log-normal distribution are

$$\begin{aligned} f(v;\,\mu ,\sigma )=\frac{1}{v\sigma \sqrt{2\pi }}{\exp \left[ -\frac{({{\textrm{ln}} v\ }-\mu )^2}{2\sigma ^2}\right] \ }, v,\sigma { >}0,\mu \in {\mathbb {R}}, \end{aligned}$$

and

$$\begin{aligned} F\left( v;\,\mu ,\sigma \right) =\frac{1}{2}+\frac{1}{2}erf\left[ \frac{{{\textrm{ln}} v }-\mu }{\sqrt{2}\sigma }\right] . \end{aligned}$$

2.7 Truncated normal distribution

If the support of the density of a normal random variable Y is truncated on the left at zero, the resulting truncated random variable \(V > 0\) follows the truncated normal (TN) distribution with pdf and cdf

$$\begin{aligned} f\left( v;\,\mu ,\sigma \right) =\frac{1}{\Phi \left( \mu /\sigma \right) \sigma \sqrt{2\pi }}{\exp \left[ -\frac{(v-\mu )^2}{2{\sigma }^2}\right] \,}, v,\mu , \sigma >0, \end{aligned}$$
(3)

and

$$\begin{aligned} F(v;\,\mu ,\sigma )=\frac{1}{\Phi (\mu /\sigma )}\left\{ \frac{1}{2}+\frac{1}{2}erf\left[ \frac{v-\mu }{\sqrt{2}\sigma }\right] -\Phi (-\mu /\sigma )\right\} . \end{aligned}$$

2.8 Inverse Gaussian distribution (Wald distribution)

The inverse Gaussian (IG) is a skewed, 2-parameter distribution which is similar to the Gamma distribution with greater skewness and a sharper peak. The name is misleading in the sense that an IG random variable is not obtained as inverse of a normal random variable, but it is related to two distinct quantities of Brownian motions that the IG and normal describe. This distribution is suitable to fit unimodal and positively skewed data sets. The pdf of the IG is given as

$$\begin{aligned} f(v;\,\mu ,\lambda )=\left( \frac{ \lambda }{2 \pi v^3}\right) ^{\frac{1}{2}} \exp \left[ \frac{- \lambda (v-\mu )^2}{2\mu ^2v}\right] , v>0, \end{aligned}$$

where \(\mu\) 0 is the mean and \(\lambda\) 0 is the shape parameter. The cdf can be expressed in terms of the standard normal distribution function \(\Phi (.)\) by

$$\begin{aligned} F\left( v;\,\mu ,\lambda \right)\,= \,& {} \Phi \left( {\left( \frac{\lambda }{v}\right) }^{\frac{1}{2}}\left( -1+\frac{v}{\mu }\right) \right) \\{} & {} +{\exp \left( \frac{2\lambda }{\mu }\right) \ }\Phi \left( -{\left( \frac{\lambda }{v}\right) }^{\frac{1}{2}}\left( 1+\frac{v}{\mu }\right) \right) . \end{aligned}$$

The IG has the property that if a random variable V follows the inverse Gaussian distribution with parameters \(\mu\) and \(\lambda\), then a scalar multiple cV with \(c>0\) follows the same distribution with parameters \(c\mu\) and \(c\lambda\), respectively.

2.9 Johnson S\({}_{B}\) distribution

The Johnson S\({}_{B}\) (JSB) distribution is one of the Johnson distributions (Johnson 1949) and remarkably flexible. This flexibility is owed to the presence of 4 parameters; as of now, we move indeed from 2-parameter distributions to distributions with 4 or more parameters. The pdf and cdf of the JSB distribution are given by

$$\begin{aligned} f(v;\,\gamma ,\delta ,\xi ,\lambda )= & {} \frac{\delta \lambda }{\sqrt{2\pi }(v-\xi )(\xi +\lambda -v)}\\{} & {} \times \exp \left\{ -\frac{1}{2}{\left[ \gamma +\delta {\ln \left( \frac{v-\xi }{\xi +\lambda -v}\right) \ }\right] }^2\right\} , \end{aligned}$$

and

$$\begin{aligned} F\left( v;\gamma ,\delta ,\xi ,\lambda \right) =\Phi \left( \gamma +\delta {\ln \left( \frac{v-\xi }{\xi +\lambda -v}\right) \ }\right) , \end{aligned}$$

where \(\xi \le v\le \xi +\lambda\), \(\xi\) is the location parameter, \(\lambda\)> 0 is the scale parameter and \(\gamma\) and \(\delta\) > 0 are shape parameters. The JSB distribution actually also has been derived from a normal distribution. Indeed, if a random variable V follows the JSB distribution, then \(Z=\gamma +\delta \ln \left( \frac{Y}{1-Y}\right)\) with \(Y=(V-\xi )/\lambda\) follows the standard normal distribution.

2.10 Generalized beta distribution of the second kind

The generalized beta distribution of the second kind (GB2) introduced by McDonald and Xu (1995) is a 4-parameter flexible distribution which is mostly applied as a size distribution of income in economics. The pdf of the GB2 is given by

$$\begin{aligned} f(v;\,a,b,p,q)=\frac{av^{ap-1}}{b^{ap}B(p,q)\left( 1+\left( \frac{v}{b}\right) ^a\right) ^{p+q}}, \, v>0, \end{aligned}$$

where \(a,p,q>0\) are shape parameters, \(b>0\) is a scale parameter and \(B(p,q)=\frac{\Gamma (p)\Gamma (q)}{\Gamma (p+q)}\) is the beta function. The cdf of the GB2 is

$$\begin{aligned} F\left( v;\,a,b,p,q\right) =1-I_{\left( 1+\left( \frac{v}{b}\right) ^a\right) ^{-1}}(p,q), \end{aligned}$$
(4)

where \(I_{x}(p,q)=\frac{B_x(p,q)}{B(p,q)}\) is the incomplete beta function.

2.11 Generalized hyperbolic distribution

The generalized hyperbolic (GH) distribution is a 5-parameter distribution introduced by Barndorff-Nielsen (1978) and contains numerous well-known special cases such as variance-gamma, Laplace, hyperbolic, Student’s t, Cauchy, normal inverse Gaussian and normal distributions. It can model skew as well as light- and heavy-tailed data. Through a location-scale transformation, the pdf of the GH distribution is given as

$$\begin{aligned}{} & {} f(v;\,\lambda ,\alpha ,\beta ,\mu ,\sigma )\\{} & {} \quad =\frac{\sqrt{\alpha }{\left( 1-{\beta }^2\right) }^{\frac{\lambda }{2}-\frac{1}{4}}}{\sqrt{2\pi }\delta \sigma K_{\lambda }(\alpha )}{\left[ {\left( \frac{v-\mu }{\delta \sigma }\right) }^2+1\right] }^{\frac{\lambda }{2}-\frac{1}{4}}\\{} & {} \quad \quad \times K_{\lambda -1/2}\left( \frac{\alpha }{\sqrt{1-{\beta }^2}}\sqrt{{\left( \frac{v-\mu }{\delta \sigma }\right) }^2+1}\right) \\{} & {} \quad \quad {\exp \left[ \frac{\alpha \beta }{\sqrt{1-{\beta }^2}}\left( \frac{v-\mu }{\delta \sigma }\right) \right] }, v>0, \end{aligned}$$

with

$$\begin{aligned} \delta ={\left[ \frac{K_{\lambda +1}(\alpha )}{\alpha K_{\lambda }(\alpha )}+\frac{{\beta }^2}{1-{\beta }^2}\left( \frac{K_{\lambda +2}(\alpha )}{K_{\lambda }(\alpha )}-\frac{K_{\lambda +1}(\alpha )^2}{K_{\lambda }(\alpha )^2}\right) \right] }^{-\frac{1}{2}}, \end{aligned}$$

and

$$\begin{aligned} \mu =m-\delta \sigma \frac{\beta }{\sqrt{1-{\beta }^2}}\frac{K_{\lambda +1}\left( \alpha \right) }{K_{\lambda }\left( \alpha \right) }, \end{aligned}$$

where m and \(\delta\) are the mean and variance of the distribution, respectively, where \(K{}_{\lambda }\)(.) denotes the modified Bessel function of the third kind with order \(\lambda\) \(\in {\mathbb {R}}\) , \(\lambda\) and \(\alpha\) > 0 are shape parameters, |\(\beta\)|< 1 is a skewness parameter, \(\sigma\) > 0 a scale parameter and \(\mu\) \(\in {\mathbb {R}}\) a location parameter.

2.12 Mixture distributions

Consider a finite set of pdfs \(f_1(v),..., f_k(v)\) and weights \(w_1,..., w_k\) such that \(w_i \ge 0\) and \(\sum _{i=1}^{k} w_i = 1\). A mixture distribution f(v) is then represented by

$$\begin{aligned} f(v)=\sum _{i=1}^{k} w_{i}f_{i}(v). \end{aligned}$$

Mixture distributions are useful for modeling heterogeneous wind data, see, e.g., Jaramillo and Borja (2004); Carta and Ramírez (2007a, b); Akpinar and Akpinar (2009); Akdağ et al. (2010); Qin et al. (2009, 2012) or Alonzo et al. (2017). The following mixture distributions are investigated in this paper as two-component mixture models (\(k=2\) in (4)).

2.12.1 Weibull–Weibull distribution

The Weibull–Weibull distribution (WW) consists of two Weibull components with different weight proportions. Jaramillo and Borja (2004) used this distribution for the first time for wind speed data analysis of La Ventosa, Mexico, while Akdağ et al. (2010) analyzed the wind speed data of nine buoys located in the Ionian and Aegean Sea (Eastern Mediterranean) with the WW distribution and compared it with the conventional Weibull distribution.

2.12.2 Truncated normal-Weibull distribution

The truncated normal-Weibull distribution (TNW) is based on the truncated normal (3) and the Weibull (1) distributions. Carta and Ramírez (2007a, b) analyzed the wind speed data of 16 locations of the Canarian Archipelago that comprised both unimodal and bimodal distributions with the TNW, WW and W distributions.

2.12.3 Truncated normal-Gamma distribution

The truncated normal-Gamma distribution (TNG) is a mixture of the truncated normal (3) and the Gamma (2) distributions. Gugliani et al. (2017) found this distribution to model best the wind speed data at the Trivandrum site in India.

3 Data description

We have considered long-term wind speed data from the Indian Meteorology Department Pune, IMD, that has a significant number of weather stations across India. Dyne pressure tube anemometer is the instrument employed by IMDs to record wind speed data. It is located at the height of 10 m above the mean ground level at a position utterly free from obstructions to the airflow. Typically, these observatories are established near airports to take advantage of open terrain. In this paper, wind speed data of seventeen stations, namely Bangalore, Dolphin Nose, Amritsa, Palam, New Delhi, Jaipur, Lucknow, Allahabad, Gaya, New Kandla, Ahmedabad, Bhopal, Indore, Jamshedpur, Calcutta, Hyderabad and Tuticorin, have been considered for the case study (see Fig. 1). Table 3 provides some information about the geographical coordinates of stations and the wind speed observations for each station. In this study, the impact of null wind speed has been checked and found to be occurring in less than 15\(\%\) of the cases. This is considered to be marginally low (Takle and Brown 1978; Razika and Marouane 2014), therefore any null values have been removed from the hourly data series.

Table 4 shows the statistical description of wind speed data for the seventeen considered locations in India. From Table 4 it has been revealed that New Kandla and Calcutta have maximum wind speed. The two stations are located in India’s western and eastern offshore and near the Arabian Sea and Bay of Bengal, respectively. The New Kandla and Indore are two stations showing mean and median wind speed well above the cut-in (2–3 m/s) wind speed of wind turbines at 10 m height, followed by Tuticorin. These sites are therefore the most probable sites for installing a wind farm. Tuticorin has the smallest skewness (in absolute value), whereas Bangalore has the highest among all stations. The Dolphin Nose exhibits negative skewness, however this might be associated with the fact that we have less than 10,000 observations at that station. The kurtosis of all stations is higher than 3 except for Indore which is a land lock fastest growing city. The high kurtosis value reveals that all the stations’ wind speed histogram is leptokurtic except for Indore. Furthermore, the CV is maximum for Allahabad, followed by Calcutta and Amritsar, and least for Indore. A high CV value means a wide variation in wind speed from the mean wind speed.

Table 3 Geographical coordinates, number of wind speed observations, observation period, and missing years for the selected reference stations in India (IMD, Pune)
Full size table
Table 4 Statistical description of wind speed data for the seventeen considered locations in India
Full size table

4 Result and discussions

The ML method was used to estimate the parameters of the fourteen distributions analyzed in the seventeen locations in India. To compare the performance of different models, we used the AIC as a goodness-of-fit criterion and the Kolmogorov–Smirnov (K–S) test as a goodness-of-fit test. Tables 6 and 7 in the Appendix contain the estimated values of the parameters for the fourteen distributions in the seventeen locations, while Table 8 in the Appendix shows the AIC values. The distribution with minimum AIC is the most suitable distribution for the given data set. Among 5-parameter distributions, the truncated normal-Gamma distribution outperforms all other distributions at four locations, followed by the Weibull–Weibull distribution at three stations, the generalized hyperbolic distribution at two locations and the truncated normal-Weibull at one location. At four locations the 4-parameter generalized beta distribution of second kind has the best performance as a wind speed model. At three locations have 2-parameter distributions come out as most suitable, twice the Birnbaum–Saunders distribution and once the Gamma distribution. If we compare only 2-parameter distributions among themselves, then the Gamma is judged the most suitable six times, the Birnbaum–Saunders four times, the Weibull distribution three times, and the Nakagami and the truncated normal distributions respectively two times. Note however that the Weibull is sometimes only beaten by a very small margin, in particular by the Nakagami distribution. Nevertheless, these findings reveal the interesting fact that one should not blindly use the Weibull distribution out of convenience, as better choices are definitely available, even among 2-parameter distributions. For each station, the best fitted model along with the corresponding AIC, the p-value of the K–S test, the coefficient of determination \(R^2\) and RMSE are summarized in Table 5. We see that, at \(5\%\) level, only 4 best-fitting distributions would be rejected, while none would be rejected at \(3\%\) level, showing, especially at such a high number of observations, that the selected distributions are very suitable models for the data under investigation.

For visual inspection, we provide the wind speed histograms and empirical cdfs along with pdfs and cdfs of the best fitted models for four locations in India, namely Bangalore, Hyderabad, Jaipur and New Kandla, see Figs. 2 and 3. The plots for other distributions and stations are of course available upon request, as we did not want to render the paper unnecessarily long. Note that we chose as class width for the bins 2 km/h following the recent suggestions by Deep et al. (2020), who illustrated the appropriateness of a 2 km/h class width for removing the sampling error. As general conclusion, we find that, for highly skewed and leptokurtic histograms, distributions with more than 2 parameters are more suitable, which explains why multiparameter or mixture models are such good choices. The reader is referred to Gugliani et al. (2018) to calculate the wind power density by knowing the pdf of different distributions.

Table 5 The best fitted model with the corresponding p-value of the K–S test, the AIC, \(R^2\) and the RMSE for the seventeen considered locations in India
Full size table
Fig. 2
figure 2

Wind speed histograms and empirical cdfs at a Banglore and b Jaipur stations along with the pdfs and cdfs of the best fitted distributions

Full size image
Fig. 3
figure 3

Wind speed histograms and empirical cdfs at c Hyderabad and d New Kandla stations along with the pdfs and cdfs of the best fitted distributions

Full size image

5 Conclusions

Fourteen continuous probability distributions have been reviewed and compared for modeling wind speed data at seventeen locations in India covering the east and west offshore corner and the mainland of India, hence a large variety of distinct climatological situations. Our aim was to identify the site-specific best distribution that can model the wind speed data with minimum amount of parameters and maximum agreement with the given wind data set. The Maximum Likelihood method has been used to estimate the parameters of the distributions. We determined the most suitable distribution by means of the AIC and checked the suitability with the Kolmogorov–Smirnov test. We found that out of the seventeen locations, four wind speed sites have been best modeled by the truncated normal-Gamma distribution, four by the generalized beta distribution of second kind, three by the Weibull–Weibull distribution, two respectively by the generalized hyperbolic and the Birnbaum–Saunders distributions, and one respectively by the truncated normal-Weibull distribution and Gamma distribution.

Our study reveals two main important messages, namely (i) that wind speed varies quite a lot within India from one location to another and that one should treat each geographic situation individually for best wind power generation, and (ii) that the wide acceptance of the Weibull distribution should at least be questioned, as it cannot perfectly represent all the wind regimes for wind speed modeling, especially wind regimes with heterogeneous data sets exhibiting multimodality, high levels of skewness and/or kurtosis. Instead, more suitable probability distributions such as those presented in this paper should be selected for each wind regime to minimize errors in the estimation of the wind energy potential at a given site. Our study shows that mixture distributions are very good candidates.