Self-focusing of a high-intensity laser pulse by a magnetized plasma lens in sub-relativistic regime

Abstract

Interaction of high power circularly polarized short laser pulses with a cold underdense magnetized thin plasma lens is analyzed in the sub-relativistic regime. The magnetic field is applied along the direction of the laser field propagation. The evolution equation of the beam spot size is derived and solved by making use of the variational principle approach method. The theoretical investigations reveal that not only the magnetized plasma lens more sufficiently decreases the laser spot size, but also the left-handed circularly polarized beam is more effectively focused by a magnetized plasma lens compared to the right-handed circularly polarized beam.

Introduction

Studying the evolution of high-intensity laser pulses propagating through underdense plasmas is an active area of research due to its importance to plasma accelerators [1], radiation schemes [2], X-ray lasers [2, 3], and etc. The problem of self-focusing of laser light in collisionless plasmas has been the subject of intense study in last years [4, 6]. However; laser pulse interaction with magnetized plasmas is, respectively, new and of interest to researchers and therefore the related physical processes have been studied. It has been seen that intense magnetic fields are generated in the laser plasma interaction [5]. These self-generated (or externally applied) transverse and axial magnetic fields affect the propagation of laser pulses in plasmas since the canonical momentum in a magnetized plasma is not conserved [6, 7]. Furthermore, laser pulse interaction with magnetized plasmas finds various applications for different branches such as: nonlinear interaction [8], wakefield excitation [9], modulation instability [10, 11], laser fusion schemas [12, 13], and fast ignition schemes in inertial confinement fusion (ICF) [14]. Moreover, self-generated magnetic fields in the corona region have been studied for intense laser pulse interaction with magnetized plasmas.

Self-focusing in plasma can occur through thermal, relativistic and ponderomotive effects [15]. Thermal self-focusing is due to collisional heating of plasma exposed to electromagnetic radiation and the rise in temperature induces a hydrodynamic expansion, which leads to an increase in the index of refraction and further heating [18]. Relativistic self-focusing is caused by the mass increase in electrons traveling at speed approaching the speed of light which modifies the plasma refraction index [4, 6, 19]. Ponderomotive self-focusing is caused by the ponderomotive force, which pushes electrons away from the region where the laser beam is more intense, therefore increasing the refraction index and inducing the focusing effect [20].

In the present paper we analyze this problem with the assumption that the plasma is cold so that before the passage of the laser radiation, the plasma electrons are at rest and the magnetic field does not affect them [21, 22]. Clearly, the ponderomotive force [23] tries to expel electrons; however, since the ions are assumed motionless (because of their inertia and the shortness of the pulse), expelled electrons lead to a charge imbalance, creating an electrostatic field which attracts the electrons back into this channel. The balance between the radial electrostatic and ponderomotive forces determines the electron density within the channel. In our study it will be assumed that the electrons are cold. This is justified if the quiver velocity of the electron motion in the wave is large compared to the electron thermal speed [24]. In additional, we consider the effect of nonlinear electric field in the dielectric function of plasma. It arises on account of redistribution of electron density in the transverse direction. Also because of the time duration of the laser pulse is shorter than the electrons plasma relaxation time $(t \prec t_{\varepsilon } )$, we only consider the relativistic self-focusing nonlinearity. To investigate nonlinear interplay instabilities in the laser–plasma interaction it is desirable to obtain differential equations for the evolution of the macroscopic quantities that characterize the laser beam profile [25, 26], including the amplitude, spot size, phase, curvature radius, and centroid. There are various methods for attempting to obtain such envelope equations, including the variation method [27], the moment method [28], and the source dependent expansion (SDE) technique [29]. We can use these mentioned techniques to study the nonlinear relativistic self-focusing phenomena with taking into account the relativistic mass corrections. Relativistic self-focusing is caused by the mass increase of the electrons traveling at speed and approaching the speed of light which modifies the plasma refractive index [4, 6, 30,31,32,33,34,35,36,37,38]. As we know, the propagation of a laser beam without diffraction is an essential factor to get better application [39]. According to this reason, in this work we use a thin magnetized plasma lens to compress and focus a laser beam outside of the plasma in the vacuum region. The plasma lens is a thin plasma layer used to focus particle beams and laser pulses. By making use of a thin plasma lens, it is possible to compress and focus a laser beam outside of the plasma in the vacuum region. Plasma lens is not damaged by an intense laser beam which is an advantage of the plasma lens compared with an optical lens [40]. Here, we show that for high-intensity laser pulses propagating in the underdense magnetized plasma lens, in the sub-relativistic regime, the magnetic field sufficiently decreases the minimum spot size of the radiation field and increases the focal length of the laser beam for the circular polarization. The focal length is defined as the distance between the plasma lens and the laser beam focus point.

Using the magnetized plasma as a thin lens for focusing high-intensity lasers, we extend the variation principal technique to solve the nonlinear wave equation and analyze the self-focusing phenomenon in the presence of the static magnetic field. The focusing of intense laser beam in magnetized plasma lens has been studied by Jha et al. in [35]. Here, the propagation of an intense circularly polarized laser beam in axially magnetized plasma is analyzed. In this reference plasma is assumed to be cold so that before the passage of the laser radiation, the plasma electrons are at rest and the magnetic field does not affect them. Here, the effect of an axial magnetic field on the self-focusing property of the laser beam is discussed and an expression for the circular power for self-focusing is obtained. To compare our current work with this reference it should be noted that we consider the dependence of a laser pulse trial function on the group velocity dispersion in our calculation and by considering the circular polarization for the laser beam propagating through a magnetized plasma and taking into account the sub-relativistic effects, we obtain the modified laser spot size, minimum laser spot size, and the focal length parameters with the variations of the external magnetic field for right- and left-handed circular polarizations. It is important to note that in Jha et al. [35] only the variations of the normalized spot size versus normalized propagation distance for a constant laser pulse strength in right- and left-handed polarizations were presented. As a comparison, in our current work by considering the group velocity dispersion effect in our calculation the variations of the normalized beam spot size as a function of the normalized cyclotron frequency for different laser pulse strength in right- and left-handed circular polarizations are obtained. It is clear that in left-hand circular polarization, the normalized beam spot size decreased more with increasing the laser pulse strength. It should be noted that in our current work and in the Jha et al. [35], the pulse dimension is in the order of plasma wavelength and it assure us to neglect the instability effect [41].

This paper is arranged as follows: in “Analytical analysis”, the current density generated in the plasma lens due to the interaction of the intense laser beam with an axially magnetized plasma is obtained. In “Spot size evolution”, by making use of the variation principal approach, the envelope equation for laser spot size is solved, and the minimum spot size and focal length are obtained. Finally a summery and conclusion is presented in “Summery and conclusion”.

Analytical analysis

We assume the laser beam propagating through magnetized plasma has circular polarization. In this case, the electric radiation field is given by:

$$ \varvec{E} = (\varvec{e}_{\varvec{x}} \pm i\varvec{e}_{\varvec{y}} )\left( {E(r,z,t) e^{i(kz - \omega t)} + {\text{c}} . {\text{c}}.} \right), $$

(1)

where $\varvec{e}_{\varvec{x}}$ and $\varvec{e}_{\varvec{y}}$ refer to the unit vectors in $x$ and $y$ directions, $E(r,z,t),k$ and $\omega$ are amplitude, wave number, and laser field frequency, respectively. Furthermore, the sings + and − are used to define the left and right-handed circularly polarized beams. In addition, c.c. denotes the complex conjugate. The equations of electrons motion in the presence of the external magnetic field $B_{0}$ in x and y directions are:

$$ \frac{{{\text{d}}v_{x} }}{{{\text{d}}t}} = - \frac{{eE_{x} }}{{m_{e} }} - \frac{{eB_{0} }}{{m_{e} c}}v_{y} , $$

(2)

$$ \frac{{dv_{y} }}{dt} = - \frac{{eE_{y} }}{{m_{e} }} + \frac{{eB_{0} }}{{m_{e} c}}v_{x} . $$

(3)

Here, the direction of the external magnetic field is along the z axis ($\varvec{B} = B_{0} \hat{\varvec{z}}$). Also, m, and $c$ are the electron mass and the light speed, respectively. Assuming that the growth rate is slow compared to the pulse frequency, we find:

$$ V_{ \bot x} = \frac{ie}{{m_{e} \omega }}\left( {E_{x} + i\left( {\frac{{\omega_{ce} }}{\omega }} \right)E_{y} } \right)\left( {1 - \left( {\frac{{\omega_{ce} }}{\omega }} \right)^{2} } \right)^{ - 1} , $$

(4)

$$ V_{ \bot y} = \frac{ie}{{m_{e} \omega }}\left( {E_{y} - i\left( {\frac{{\omega_{ce} }}{\omega }} \right)E_{x} } \right)\left( {1 - \left( {\frac{{\omega_{ce} }}{\omega }} \right)^{2} } \right)^{ - 1} , $$

(5)

where $\omega_{ce} = \frac{{eB_{0} }}{{m_{e} }}$ is the electron cyclotron frequency. Now, using the Maxwell equation, the wave equation of the electric field is obtained as follows:

$$ \left( {\nabla^{2} - \frac{1}{{c^{2} }}\frac{{\partial^{2} }}{{\partial t^{2} }}} \right){\mathbf{E}}_{{\mathbf{ \bot }}} = \frac{4\pi }{{c^{2} }}\frac{{\partial {\mathbf{J}}_{{\mathbf{ \bot }}} }}{\partial t}, $$

(6)

where ${\mathbf{J}}_{{\mathbf{ \bot }}} = - ne{\mathbf{v}}_{{\mathbf{ \bot }}}$ is the plasma transverse current density with respect to ${\mathbf{E}}$, ${\mathbf{v}}$ and $n$ are the electron velocity and density.

Here, by defining the normalized laser pulse strength as ${\mathbf{A}}_{{\mathbf{ \bot }}} = \frac{{e\varvec{E}_{{\mathbf{ \bot }}} }}{{m_{e} \omega c}}$ and by considering the transverse electrons velocity as ${\mathbf{v}}_{{\mathbf{ \bot }}} = \varvec{e}_{\varvec{x}} v_{x} + \varvec{e}_{\varvec{y}} v_{y} ,\left( {v_{ \bot } = \sqrt {v_{x}^{2} + v_{y}^{2} } } \right)$ in Eq. (6), then the equation of the laser vector potential is obtained as:

$$ \nabla^{2} \varvec{A}_{ \bot } - \frac{1}{{c^{2} }}\frac{{\partial^{2} }}{{\partial t^{2} }}\varvec{A}_{ \bot } = \frac{{\omega_{pe}^{2} }}{{c^{2} }}\frac{1}{\gamma }\left( {\frac{\omega }{{\omega \pm \omega_{ce} }}} \right)\varvec{A}_{ \bot } , $$

(7)

where $\omega_{pe} = (4\pi ne^{2} /m)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$ is the electron plasma frequency and $\gamma = \left( {1 + \frac{{P_{ \bot }^{2} }}{{m_{e}^{2} c^{2} }}} \right)^{{\frac{1}{2}}}$ is the relativistic factor. It should be noted that in this equation the laser vector potential ($\varvec{A}_{ \bot }$) is normalized to $m_{e} c^{2} /e$.

It is obvious when the laser pulse strength magnitude is rather near to unity, the sub-relativistic effects should be taken into account and the plasma particles will experience a sub-relativistic nonlinear force. Here, the strength of wake field can exceed to $10^{9} \frac{v}{m}$ and we have:

$$ \frac{1}{\gamma } \cong 1 - \frac{{v_{ \bot }^{2} }}{{c^{2} }} \cong 1 - \frac{{\left| {A_{ \bot } } \right|^{2} }}{2}\left( {\frac{\omega }{{\omega \pm \omega_{ce} }}} \right)^{2} . $$

(8)

Then the final equation will be:

$$ \nabla^{2} \varvec{A}_{ \bot } - \frac{1}{{c^{2} }}\frac{{\partial^{2} }}{{\partial t^{2} }}\varvec{A}_{ \bot } = \frac{{\omega_{pe}^{2} }}{{c^{2} }}\left( {1 - \frac{{\left| {A_{ \bot } } \right|^{2} }}{2}\left( {\frac{\omega }{{\omega \pm \omega_{c} }}} \right)^{2} } \right)\left( {\frac{\omega }{{\omega \pm \omega_{ce} }}} \right)\varvec{A}_{ \bot } . $$

(9)

Now, we can write the transverse normalized potential vector $\varvec{A}_{ \bot }$ as the product of an envelope and a phase,

$$ \varvec{A} = (\varvec{e}_{\varvec{x}} \pm i\varvec{e}_{\varvec{y}} )\left( {\frac{a}{2} e^{i(kz - \omega t)} + {\text{c}} . {\text{c}} .} \right), $$

(10)

where $a = \frac{{e\left| {E_{ \bot } } \right|}}{{m_{e} \omega c}}$ is the magnitude of laser pulse strength; $\omega ,k$ satisfy the circularly polarized wave dispersion relation as:

$$ \frac{{\omega^{2} }}{{c^{2} }} - k^{2} = \frac{{\omega_{pe}^{2} /c^{2} }}{{1 \pm \omega_{ce} /\omega }}. $$

(11)

Using a mathematical transformation from the coordinate variables $(t,z)$ to variables $(\psi ,\tau )$ in which $\tau = z$ and $\psi = t - z/v_{\text{g}} ,$ where $v_{\text{g}}$ is the group velocity of the radiation field, the envelope equation of $a(\psi ,\tau )$ reduces to:

$$ 2ik\frac{\partial a}{\partial \tau } + \nabla^{2}_{ \bot } a - \frac{{\omega_{pe}^{2} /c^{2} }}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)}}\left( {1 - \frac{{\left| a \right|^{2} /4}}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)^{2} }}} \right)a + \left( {\frac{1}{{v_{g}^{2} }} - \frac{1}{{c^{2} }}} \right)\frac{{\partial^{2} a}}{{\partial \psi^{2} }} - \frac{2}{{v_{g} }}\frac{{\partial^{2} a}}{\partial \psi \partial \tau } + \left( {\frac{{\omega^{2} }}{{c^{2} }} - k^{2} } \right)a + \left( {\frac{2i\omega }{{c^{2} }} - \frac{2ik}{{v_{g} }}} \right)\frac{\partial a}{\partial \psi } + \frac{{\partial^{2} a}}{{\partial \tau^{2} }} = 0. $$

(12)

In this equation, both the first and second terms are related to the diffraction of the pulse. The third term represents the reaction of the plasma and the features of the medium. This term shows the relativistic effects in the dispersion relation of the plasma. The other terms denote the group velocity dispersion. In this equation, the group velocity is obtained by:

$$ v_{\text{g}} = c\frac{{\sqrt {\omega^{2} + (\omega /\omega_{ce} )\omega_{pe}^{2} } }}{{\omega + \omega_{pe}^{2} /2\omega_{ce} }} \cong c\frac{{\sqrt {1 + \omega_{pe}^{2} /\omega \omega_{ce} } }}{{1 + \omega_{pe}^{2} /2\omega \omega_{ce} }}. $$

(13)

Note that in Eq. (12), in the term $\frac{{\omega_{pe}^{2} /c^{2} }}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)}}\left( {1 - \frac{{\left| a \right|^{2} /4}}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)^{2} }}} \right)a,$ the second part has large value and we can neglect the first part. Therefore, the simplest equation including self-focusing in the magnetized plasma is:

$$ \begin{aligned} 2ik_{{}} \frac{\partial a}{\partial \tau } + \frac{{\varepsilon^{2} }}{{c^{2} }}\frac{{\partial^{2} a}}{{\partial \psi^{2} }} + \nabla^{2}_{ \bot } a + \left( {\frac{2i\omega }{{c^{2} }} - \frac{{2ik_{{}} }}{{v_{g} }}} \right)\frac{\partial a}{\partial \psi } + \frac{{\omega_{pe}^{2} }}{{c^{2} }}\frac{{\left| a \right|^{2} /4}}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)^{3} }}a = 0, \hfill \\ \hfill \\ \end{aligned} $$

(14)

where $\varepsilon = \frac{1}{{c^{2} }}\frac{{\left\{ {\omega_{pe}^{4} /4\omega \omega_{ce} } \right\}}}{{(\omega_{pe}^{2} + \omega \omega_{ce} )}}$. This equation can be approximately solved by using the variational principle [24]. It is done by writing down the Lagrangian density $(l)$ for Eq. 14 as follows:

$$ \begin{aligned} l = & \,ik\left( {a\frac{{\partial a^{ * } }}{\partial \tau } - a^{ * } \frac{\partial a}{\partial \tau }} \right) + \frac{{\varepsilon^{2} }}{{c^{2} }}\frac{{\partial a^{ * } }}{\partial \psi }\frac{\partial a}{\partial \psi } \\ & + \nabla_{ \bot } a^{ * } .\nabla_{ \bot } a - i\left( {\frac{\omega }{{c^{2} }} - \frac{k}{{v_{g} }}} \right)\left( {a\frac{{\partial a^{ * } }}{\partial \psi } - a^{ * } \frac{\partial a}{\partial \psi }} \right) - \frac{{\omega_{pe}^{2} }}{{8c^{2} }}\frac{{a^{2} a^{ * 2} }}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)^{3} }}, \\ \end{aligned} $$

(15)

i.e., Eq. (12) is the Euler–Lagrange equation. With this equation we can minimize the action integral $S = \int {ld\tau dx_{ \bot } } d\psi$ for variations of $a^{ * }$ and $a$. Next we use the following trial function:

$$ a = a(\tau )e^{ - i\varphi (\tau )} e^{{i\psi^{{^{2} }} /\eta (\tau )}} e^{{ - \psi^{{^{2} }} /L^{{^{2} }} }} e^{{ik_{0} r^{{^{2} }} /2R(\tau )}} e^{{ - r^{{^{2} }} /W^{{^{2} }} }} . $$

(16)

Here, $L,W,a,\phi ,\eta ,$ and $R$, being real quantities, are the pulse length, spot size, amplitude, phase, chirp, and radius of curvature of the Gaussian laser beam, respectively. Substituting this trial function into Eq. (15) and integrating over $\psi$ and $x_{ \bot } ({\text{d}}x_{ \bot } = r{\text{d}}r)$, we obtain the reduced Lagrangian density:

$$ \begin{aligned} l \equiv & \,\frac{4}{\sqrt \pi }\int\limits_{0}^{ + \infty } {rdr\int\limits_{ - \infty }^{ + \infty } {ld\psi = - \sqrt 2 } } a^{2} k\left( {\frac{d\varphi }{d\tau } + \frac{{L^{2} }}{{4\eta^{2} }}\frac{d\eta }{d\tau } + \frac{{kW^{2} }}{{4R^{2} }}\frac{dR}{d\tau }} \right) \\ & + \frac{{\varepsilon^{2} }}{{c^{2} }}\frac{{a^{2} }}{\sqrt 2 }\left( {\frac{1}{{L^{2} }} + \frac{{L^{2} }}{{\eta^{2} }}} \right) + \frac{{a^{2} }}{\sqrt 2 }\left( {\frac{2}{{W^{2} }} + \frac{{k^{2} W^{2} }}{{2R^{2} }}} \right) - \frac{{a^{4} }}{{32W^{2} L}}\frac{{\omega_{pe}^{2} /c^{2} }}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)^{3} }}. \\ \end{aligned} $$

(17)

Spot size evolution

We use the Euler–Lagrange equations of the reduced Lagrangian density to drive the evolution of $W$ in τ. We consider the ideal case where a thin magnetized plasma lens with a thickness $\Delta$ is placed at the vacuum waist (τ = 0) of a Gaussian laser pulse with the spot size W ₀. The laser exits the plasma at τ = Δ and reaches to its focus, where it has the minimum spot size $W_{\hbox{min} }$, at τ = f. If the pulse is assumed to remain Gaussian and finite pulse length effects are neglected, i.e., L, and $\eta$ are assumed to remain fixed, then the evolution equation for spot size W inside the plasma can be derived from the reduced Lagrangian given by Eq. (17). Varying $\varphi$ leads to power conservation,

$$ \frac{{da^{2} }}{d\tau } = 0. $$

(18)

Furthermore, varying $R$ relates $R$ and ${\text{d}}W/{\text{d}}\tau$ as:

$$ \frac{W}{R} = \frac{{{\text{d}}W}}{{{\text{d}}\tau }}, $$

(19)

and varying $W$ gives another equation for $R$ and $W$ as:

$$ - \frac{{k^{2} }}{\sqrt 2 }\frac{{a^{2} W}}{{R^{2} }}\frac{dR}{d\tau } + \frac{{a^{2} }}{\sqrt 2 }\left( {\frac{ - 4}{{W^{3} }} + \frac{{k^{2} W}}{{R^{2} }}} \right) + \frac{{\omega_{pe}^{2} /c^{2} }}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)^{3} }}\frac{{a^{4} }}{{16W^{3} L}} = 0. $$

(20)

Combining Eqs. (19) and (20), we can obtain the evolution equation for the laser beam spot size $W$ as:

$$ \frac{{{\text{d}}^{2} W}}{{{\text{d}}\tau^{2} }} = - \frac{4}{{k^{2} W^{3} }}\left( {\frac{{P/P_{c} }}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)^{3} }} - 1} \right), $$

(21)

where $P/P_{c} = \sqrt 2 a^{2} \omega_{pe}^{2} W_{0}^{2} /(64c^{2} )$ is independent of $\tau .$ The solution of Eq. (21) with the initial condition of $W = W_{0}$ and ${\text{d}}W/{\text{d}}\tau = 0$ at $\tau = 0,$ gives laser beam spot size inside the magnetized plasma lens as:

$$ W = W_{0} \sqrt {1 - \left( {\frac{{P/P_{c} }}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)^{3} }} - 1} \right)\left( {\frac{{\tau^{2} }}{{\tau_{R}^{2} }}} \right)} , $$

(22)

where τ _R  ≡ kW ² ₀ /2 is the vacuum Raleigh length of the laser pulse. It is found that spot size will eventually go to zero if P/Pc > 1. When the laser beam exits the plasma, spot size evolves as:

$$ \frac{{{\text{d}}^{2} W}}{{{\text{d}}\tau^{2} }} = \frac{4}{{k^{2} W^{3} }}. $$

(23)

If the laser beam is focused in the focal length $f$, and the minimum spot size $W_{\hbox{min} }$, we can obtain laser spot size outside of the plasma lens in the vacuum region by solving Eq. (23) as:

$$ W = W_{\hbox{min} } \sqrt {1 + \left( {\frac{\tau - f}{{\tau_{R} }}} \right)^{2} \frac{{W_{0}^{4} }}{{W_{\hbox{min} }^{4} }}}. $$

(24)

By matching $W$ and ${\text{d}}W/{\text{d}}\tau$ from Eqs. (22) and (24), we can obtain the minimum spot size $W_{\hbox{min} }$ and focal length $f$ as follows:

$$ W_{\hbox{min} } = W_{0} \sqrt {\frac{{1 - \delta^{2} }}{{1 + \left( {\frac{{P/P_{c} }}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)^{3} }} - 1} \right)\delta^{2} }}} , $$

(25)

$$ f = \Delta \frac{{\frac{{P/P_{c} }}{{(1 \pm \omega_{c} /\omega )^{3} }}}}{{1 + \left( {\frac{{P/P_{c} }}{{\left( {1 \pm \frac{{\omega_{ce} }}{\omega }} \right)^{3} }} - 1} \right)\delta^{2} }}, $$

(26)

where $\delta = (\Delta /\tau_{R} )(P/P_{c} - 1)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$ is the normalized lens thickness.

Although some methods have been already studied to obtain the variations of laser spot size with plasma distance such as SDE (source dependence expansion) [35, 36], but these methods present only the variation of laser spot size with distance. In the present method (Lagrangian density), as we see, other parameters such as the variation of laser spot size with the variations of the plasma distance and the external magnetic field for right and left-handed circular polarizations are obtained. Furthermore, the variations of the minimum laser spot size and laser focal length versus the variations of the external magnetic field and laser pulse strength for right and left-handed circular polarizations are presented. Also, it is noticeable to note that we can study evaluation of spot size versus other parameter such as external magnetic field, propagation length and plasma density through SDE method.

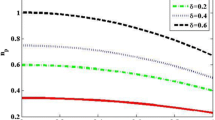
Figure 1 shows the plot of the normalized beam spot size $\frac{W}{{W_{0} }}$ as a dimensionless parameters $\omega_{ce} /\omega_{0}$ for right and left circular polarizations at the fixed point $\frac{\tau }{{\tau_{R} }} = 0.03$ inside the plasma lens. The laser source is Nd:Yag with frequency $f_{0} = 1.88 \times 10^{15} {\text{s}}^{ - 1}$, wavelength $\lambda$ = 1 μm, and initial beam spot size W ₀ = 100 μm. This figure predicts that the self-focusing property is enhanced by increasing the external magnetic field for left-handed circular polarization. In this figure we see that the maximum reduction for the left-handed circularly polarized beam propagating through the magnetized pure electron plasma lens is smaller than $0.15W_{0}$. On the other hand, this figure shows that the right-handed circularly polarized beam diffraction is increased slightly by increasing the magnetic field.

Fig. 1

Variation of the normalized spot size $\frac{W}{{W_{0} }}$ as a dimensionless parameter $\omega_{ce} /\omega_{0}$ for right (solid line) and left circular polarized (dashed line) laser beams. The parameters are chosen as $\omega_{p} /\omega_{0} = 0.09,$ W ₀ = 100 μm, $\omega_{0} = 1.88 \times 10^{15} \,{\text{s}}^{ - 1} ,$ laser wavelength λ = 1 μm and $a = 0.7$, for a fix point $\frac{\tau }{{\tau_{R} }} = 0.03$ inside the plasma lens with thickness $\Delta = 1\,{\text{mm}}$

Figure 2 illustrates the normalized beam spot size $\frac{W}{{W_{0} }}$ as a function of the dimensionless parameter $\frac{{\omega_{ce} }}{{\omega_{0} }}$ for different laser pulse strength with the right-handed circular polarization at the fixed point $\frac{\tau }{{\tau_{R} }} = 0.03$ inside the plasma lens. It is clear that the diffraction property of the laser beam is enhanced strongly with increasing the strength of the external magnetic field. In Fig. 3 the normalized spot size $\frac{W}{{W_{0} }}$ is plotted as a function of the normalized parameter $\frac{{\omega_{ce} }}{{\omega_{0} }}$ for different laser pulse strength with left-handed circular polarization. It is seen, in contrast to the right-handed circularly polarized beam, the normalized beam spot size decreases with increasing the strength of the external magnetic field. In the above figures, it should be noted that the application of external magnetic field enhances the quality of self-focusing for left-hand polarization and reduces it for right-hand polarization. Physically, the left-hand wave drives electrons in the direction of their cyclotron motion. In this polarization the increase in magnetic field causes the increase in transverse velocity of electrons and it leads to increase in nonlinear current density or nonlinearity of plasma. Furthermore, the rotation sense of the right-hand polarization is opposite to the electrons cyclotron motion and the velocity of the electrons or consequently, the nonlinearity of plasma medium decreases with increase in external magnetic field. Finally, we conclude that, self-focusing for left-handed circularly laser light in magnetized plasma is stronger toward the right-handed circular polarization.

Fig. 2

Variation of normalized spot size $\frac{W}{{W_{0} }}$ as a dimensionless parameter $\omega_{ce} /\omega_{0}$ for right circularly polarized laser beam with different laser pulses strength ($a = 0.25$ dotted line), ($a = 0.5$ dashed line) and ($a = 0.7$ solid line), in the fix point $\frac{\tau }{{\tau_{R} }} = 0.03$ inside the plasma lens. The other parameters are chosen as Fig. 1

Fig. 3

Variation of normalized spot size $\frac{W}{{W_{0} }}$ as a dimensionless parameter $\omega_{ce} /\omega_{0}$ for left circularly polarized laser beam with different laser pulses strength ($a = 0.25$ dotted line), ($a = 0.5$ dashed line) and ($a = 0.7$ solid line), in the fix point $\frac{\tau }{{\tau_{R} }} = 0.03$ inside plasma lens. The other parameters are chosen as Fig. 1

Figures 4 and 5 show the normalized minimum spot size $\frac{{W_{\hbox{min} } }}{{W_{0} }}$ of a laser beam as a function of the dimensionless parameter $\frac{{\omega_{ce} }}{{\omega_{0} }}$ for different laser pulse strength with right and left-handed circular polarizations, respectively. It is shown that by increasing laser pulse strength the initial minimum spot size is decreased for the left-handed circular polarization, while it is increased for the right-handed circular polarization. Figures 6 and 7 show the plot of the normalized focal length variations as a function of the normalized parameter $\frac{{\omega_{ce} }}{{\omega_{0} }}$ for different laser pulse strength with right and left-handed circular polarizations, respectively. These figures show that we can focus a weakly relativistic $(a < 1)$ right-handed circularly polarized laser beam to a long focal length by applying an external magnetic field, while it is plausible to focus a rather strong ($a \approx 1$) left-handed circularly polarized beam to a long focal length by making use of a magnetized plasma lens.

Fig. 4

Variation of the minimum normalized spot size $\frac{{W_{\hbox{min} }^{{}} }}{{W_{0} }}$ as a dimensionless parameter $\omega_{ce} /\omega_{0}$ for right circularly polarized laser beam with different strengths ($a = 0.25$ dotted line), ($a = 0.5$ dashed line) and ($a = 0.7$ solid line) with plasma lens thickness $\Delta = 1 \,{\text{mm}}$. The other parameters are chosen as Fig. 1

Fig. 5

Variation of the minimum normalized spot size $\frac{{W_{\hbox{min} }^{{}} }}{{W_{0} }}$ as a dimensionless parameter $\omega_{ce} /\omega_{0}$ for left circularly polarized laser beam with different strengths ($a = 0.25$ dotted line), ($a = 0.5$ dashed line) and ($a = 0.7$ solid line) with plasma lens thickness $\Delta = 1 {\text{mm}}$. The other parameters are chosen as Fig. 1

Fig. 6

Variation of the normalized focal length $\frac{f}{\Delta }$ as a dimensionless parameter $\omega_{ce} /\omega_{0}$ for right circularly polarized laser beam with different strengths ($a = 0.25$ dotted line), ($a = 0.5$ dashed line) and ($a = 0.7$ solid line) with plasma lens thickness $\Delta = 1 {\text{mm}}$. The other parameters are chosen as Fig. 1

Fig. 7

Variation of the normalized focal length $\frac{f}{\Delta }$ as a dimensionless parameter $\omega_{ce} /\omega_{0}$ for left circularly polarization laser beam with different strengths ($a = 0.25$ dotted line), ($a = 0.5$ dashed line) and ($a = 0.7$ solid line) with plasma lens thickness $\Delta = 1 \,{\text{mm}}$. The other parameters are chosen as Fig. 1

Summary and conclusion

We have derived analytical formulas for the spot size evolution of a high-intensity laser pulse propagating in a thin magnetized plasma lens in the sub-relativistic regime. Our results show that how $W_{\hbox{min} }$ and $f$ depend on plasma lens thickness and the normalized laser power $P/P_{c}$. Clearly, the magnetic field modifies the plasma density and intensifies the nonlinear effects. In such a case, the self-focusing of the left-handed circularly polarized beam is enhanced by increasing the external magnetic field, while this property is diminished for the right-handed circularly polarized beam. The analytical investigation predicts the increase of the laser beam focal length and the decrease of the minimum spot size by increasing the external magnetic field for a left-handed circularly polarized case. As a final conclusion, we can focus a strong left-handed circularly polarized laser beam to a long focal length by applying the external magnetic field on the plasma lens.