A study on dust acoustic traveling wave solutions and quasiperiodic route to chaos in nonthermal magnetoplasmas

Abstract

Bifurcations and chaotic behaviors of dust acoustic traveling waves in magnetoplasmas with nonthermal ions featuring Cairns–Tsallis distribution is investigated on the framework of the further modified Kadomtsev–Petviashili (FMKP) equation. The FMKP equation is derived employing the reductive perturbation technique (RPT). Bifurcations of dust acoustic traveling waves of the FMKP equation is presented. Using the bifurcation theory of planar dynamical systems, two new analytical traveling wave solutions for solitary and periodic waves are derived depending on the parameters $\alpha , \alpha _1, q, l$ and U. Considering an external periodic perturbation, the chaotic behavior of dust acoustic traveling waves is investigated through quasiperiodic route to chaos. The parameter q significantly affects the chaotic behavior of the perturbed FMKP equation.

Introduction

The physics of dusty plasmas is an important topic of growing research which has gained more and more interest over the last few decades not only from the academic point of view, but also from the view of its new aspects [1] in space and modern astrophysics, semiconductor technology, fusion devices, plasma chemistry, crystal physics, and biophysics. In 1989, Goertz [2] discussed collective effects in dusty plasmas which affect various waves, such as density waves in planetary rings and low-frequency plasma waves. The authors described briefly the possibility of charged grains forming a Coulomb lattice. Low temperature dusty plasmas is used in manufacturing of chips and material processing [3, 4] in industry, which is one of the greatest impacts on our everyday lives. Recently, a number of laboratory experiments [5–7] have demonstrated that highly ordered dust structures, i.e., dusty plasma crystals are formed when $\Gamma _\mathrm{c}\ge 170$. Because of different types of dust charged grains in a plasma, a number of different wave modes are introduced, for example, dust acoustic mode [8], dust ion acoustic mode [9], dust lattice mode [10], Shukla–Varma mode [11], dust Berstain–Green–Kruskal mode [12] and dust drift mode [13]. Rao et al. [8] investigated the existence of a new extremely low-phase velocity dust acoustic waves (DAW) in an unmagnetized dusty plasma. Many experimental and theoretical observations performed by Angelo [14], Barkan et al. [15, 16], Nakamuro et al. [17] have confirmed the linear and nonlinear phenomena of both DAW and DIAW. Tomar et al. [18] studied the reflection of ion acoustic soliton in an inhomogeneous dusty plasma having two temperature electrons. Sabetkar and Dorranian [19] investigated the effect of obliqueness and external magnetic field on the characteristics of dust acoustic solitary waves in dusty plasma with two temperature nonthermal ions. El-Hanbaly et al. [20] studied the propagation of linear and nonlinear dust acoustic waves in a homogeneous unmagnetized, collisionless and dissipative dusty plasma consisted of extremely massive, micron-sized, negative dust grains. Tomar et al. [21] also investigated the evolution of solitons and their reflection and transmission in a plasma having negatively charged dust grains. Sabetkar and Dorranian [22] investigated the nonextensive effects on the characteristics of dust acoustic solitary waves in magnetized dusty plasma with two temperature isothermal ions. Dorranian and Sabetkar [23] studied the nonlinear dust acoustic solitary waves in a dusty plasma with two nonthermal ion species at different temperatures. The authors showed the effects of nonthermal coefficient, ions temperature, and ions number density on the amplitude and width of soliton in dusty plasma. Shahmansouri and Tribeche [24] investigated nonlinear dust acoustic (DA) shock waves in a nonextensive charge varying complex plasma and found that the influence of nonextensive particles and dust charge fluctuation affect the basic properties of the collisionless DA shock wave drastically. Shahmansouri and Mamun [25] carried out a theoretical investigation to study the basic properties of dust acoustic (DA) shock waves in a magnetized nonthermal dusty plasma containing cold viscous dust fluid, nonthermal ions, and nonthermal electrons. Shahmansouri and Borhanian [26] reported the nonlinear aspects of nonplanar dust acoustic (DA) solitary waves in an unmagnetized complex plasma comprising of cold dust grains, kappa-distributed ions as well as electrons.

There are some astrophysical and space plasmas environments containing particles with distribution functions which are quasi-Maxwellian up to the mean thermal velocities and present non-Maxwellian nonthermal tails when the particles gain high velocities and energies [27–29]. These types of plasmas are known as nonthermal plasmas which are observed in Mercury, in the solar wind, Saturn and in the Magnetospheres of the Earth [29, 30]. Tribeche et al. [31] generalized the model of Cairns et al. [32] and outlined a physically meaningful nonextensive nonthermal velocity distribution. They [31] studied the ion acoustic solitary waves in a plasma with nonthermal electrons featuring Tsallis distribution (Cairns–Tsallis). Recently, Williams and Kourakis [33] re-examined the Cairns–Tsallis model for ion acoustic solitons and concluded that the parameters q and $\alpha$ must be in the ranges $0\le \alpha <0.25$ and $0.6<q<1$ subject to the physical cutoff imposed by the monotonicity condition $\alpha =\frac{(2q-1)}{4}$.

There are many important nonlinear dynamical systems in physics, chemistry and biology which clearly display different types of regular and chaotic behaviors depending upon the strength of control parameters, initial conditions, nature of external perturbation, and so on. Thus, to identify whether a given motion of a dynamical system is periodic or quasiperiodic or chaotic, one needs to perform quantitative measures in addition to the various qualitative features. Using numerical computations, some perturbed nonlinear evolution equations (Sine-Gordon, KdV and Schrodinger equations) have been investigated [34, 35]. But it is important to note that the presence of external perturbations introduces different dynamic behaviors like quasiperiodic behavior and chaotic behavior. Thus, addition of an external perturbation to a nonlinear integrable wave equation may provide quasiperiodic and chaotic motions. Considering an external perturbation, many authors have investigated chaos through different routes, such as, period doubling route [36] to chaos, quasiperiodic route [37] to chaos, crisis route [38] to chaos and intermittency route [39] to chaos.

Recently, Samanta et al. [40] studied bifurcations of dust ion acoustic traveling waves in a magnetized dusty plasma with a q-nonextensive electron velocity distribution using bifurcation theory of planar dynamical systems for the first time in the literature. Later on, a number works [41–45] on bifurcations of nonlinear waves in plasmas have been reported through perturbative and nonperturbative approaches. Saha and Chatterjee [46] studied propagation and interaction of dust acoustic multi-soliton in dusty plasmas with q-nonextensive electrons and ions. Very recently, Saha et al. [47] investigated the dynamic behavior of ion acoustic waves in electron–positron–ion magnetoplasmas with superthermal electrons and positrons in the framework of perturbed and non-perturbed Kadomtsev–Petviashili (KP) equations. Ghosh et al. [48] investigated the dynamic structures of ion acoustic waves in an unmagnetized plasma with q-nonextensive electrons and positrons applying the bifurcation theory of planar dynamical systems. Sahu et al. [49] studied the quasiperiodic behavior in quantum plasmas due to the presence of bohm potential. Zhen et al. [50] studied dynamic behavior of the quantum ZK equation in dense quantum magnetoplasma. But bifurcation and chaotic behaviors of nonlinear waves in plasmas on the framework of FMKP equation have not been reported to the best of our knowledge.

In this work, our aim is to investigate the bifurcation and chaotic behaviors of dust acoustic traveling waves in magnetoplasmas with nonthermal ions featuring Cairns–Tsallis distribution on the framework of FMKP equation using bifurcation theory of planar dynamical systems. We derive two new analytical solutions for solitary and periodic waves of the FMKP equation. Considering an external periodic perturbation, we study the chaotic behaviors of the perturbed FMKP equation through quasiperiodic route to chaos in the mentioned plasmas. In this case, we restrict the parameter ranges $0\le \alpha <0.25$ and $0.6<q<1$ based on the study [33].

The remaining part of the paper is organized as follows. In the next section, we consider model equations and then derive the FMKP equation. Following this, we obtain a dynamical system of the FMKP equation after which bifurcations of phase portraits are obtained. In the subsequent section, two analytical traveling wave solutions of the FMKP equation are derived. Before the concluding section, we discuss the chaotic behavior of the perturbed FMKP equation. The study is concluded in the final section.

Basic equations

We consider a plasma model whose constituents are dynamic dust particles and nonthermal cold ions featuring Tsallis distribution in the presence of an external static magnetic field $M=\hat{x}M_0$ acting along the x-axis, where $\hat{x}$ is an unit vector along the x-axis. The normalized continuity, momentum and Poisson’s equations are as follows:

$$\begin{aligned} \frac{\partial n}{\partial t}+\nabla .(n\tilde{U})= & {} 0,\end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial \tilde{U}}{\partial t}+(\tilde{U}.\nabla )\tilde{U}= & {} \nabla \phi -\tilde{U}\times \hat{x},\end{aligned}$$

(2)

$$\begin{aligned} \nabla ^2 \phi= & {} \alpha _1(n-n_i), \end{aligned}$$

(3)

where $\alpha _1=\frac{r^2}{\lambda ^2}$, $r=\frac{C_s}{\Omega }$ is the dust gyroradius, $\lambda =\sqrt{T_i/4\pi e^2 n_0z_{d0}}$ is the Debye length, $C_s=(T_i/m)^{1/2}$ is the dust acoustic velocity, $\Omega =\frac{eM_0}{m c}$ is the dust gyrofrequency, c is the speed of the light, m is the mass of dusts and $z_\mathrm{d}$ is the number of the charge residing on the dust grains, so that the charge of the dust $q_\mathrm{d}=-ez_\mathrm{d}$ with e is the elementary charge. $\phi$ is the plasma potential. n and $\tilde{U}$ denote number density and velocity of dust particles, respectively. We assume that the wave is propagating in the xy-plane. Here, $n_{i0}$, and $n_0$ are, respectively, the unperturbed number densities of ions and dust particles. The dust velocity $\tilde{U}=(u,v,w)$ is normalized to dust acoustic speed $C_s=\sqrt{\frac{T_i}{m}}$ and plasma potential $\phi$ is normalized to $T_i/e$. Space variables and time are normalized to the dust gyroradius r and inverse of the dust gyrofrequency $\Omega$, respectively.

The nonextensive nonthermal velocity distribution [31] function is given by:

$$\begin{aligned} f_i(v_x)=C_{q,\alpha } \left( 1+\alpha \frac{v_x^4}{v_{ti}^4}\right) \left\{ 1-(q-1)\frac{v_x^2}{2v_{ti}^2}\right\} ^{\frac{1}{q-1}}, \end{aligned}$$

where $v_{ti}=(T_i/m_i)^{1/2}$ is the ion thermal velocity, $T_i$ is the ion temperature, $m_i$ is its mass, and $C_{q,\alpha }$ is the constant of normalization which is given by the following expressions:

$$\begin{aligned} C_{q,\alpha } = n_{i0} \sqrt{\frac{m_i}{2\pi T_i}} \frac{\Gamma (\frac{1}{1-q})(1-q)^{5/2}}{\Gamma (\frac{1}{1-q} -\frac{5}{2})[3\alpha +(\frac{1}{1-q} -\frac{3}{2})(\frac{1}{1-q} -\frac{5}{2})(1-q)^2]}\quad \hbox {for } -1<q<1, \end{aligned}$$

and

$$\begin{aligned} C_{q,\alpha } = n_{i0} \sqrt{\frac{m_i}{2\pi T_i}} \frac{\Gamma (\frac{1}{q-1}+\frac{3}{2})(q-1)^{5/2}(\frac{1}{q-1} + \frac{3}{2})(\frac{1}{q-1}+\frac{5}{2})}{\Gamma (\frac{1}{q-1}+1)[3\alpha +(\frac{1}{q-1} +\frac{3}{2})(\frac{1}{q-1}+\frac{5}{2})(q-1)^2]}\quad \hbox {for } q>1. \end{aligned}$$

Here, $\alpha$ is a parameter determining the number of nonthermal ions present in the model, q stands for the strength of nonextensivity, and $\Gamma$ is the standard Gamma function. For $q>1$, the distribution function exhibits a thermal cutoff on the maximum value allowed for the velocity of the ions, given by

$$\begin{aligned} v_\mathrm{max}=\sqrt{\frac{2T_i}{m_i(q-1)}}, \end{aligned}$$

beyond which no probable states exist.

Integrating the nonthermal velocity distributed function $f_i(v_x)$ over all velocity space, one can obtain the ion density [31] as:

$$\begin{aligned} n_i=n_{i0}\left( 1-M\left( \frac{e\phi }{T_i}\right) +N\left( \frac{e\phi }{T_i}\right) ^2\right) \left\{ 1-(q-1)\left( \frac{e\phi }{T_i}\right) \right\} ^{\frac{1}{q-1}+\frac{1}{2}}, \end{aligned}$$

where $M=-\frac{16\alpha q}{(5q-3)(3q-1)+12\alpha }$ and $N=\frac{16\alpha q(2q-1)}{(5q-3)(3q-1)+12\alpha }.$

In the limiting case, when $q\rightarrow 1$, the above ion density reduces to the nonthermal ion density of Cairns et al. [32] as $n_i=n_{i0}\left(1+\frac{4\alpha }{1+3\alpha }\left(\frac{e\phi }{T_i}\right)+\frac{4\alpha }{1+3\alpha }\left(\frac{e\phi }{T_i}\right)^2\right)\times \exp \left(-\frac{e\phi }{T_i}\right),$ and in the case, when $\alpha =0$, the ion density reduces to the nonextensive ion density [51] as

$$\begin{aligned} n_i=n_{i0}\left\{ 1-(q-1)\left( \frac{e\phi }{T_i}\right) \right\} ^{\frac{1}{q-1}+\frac{1}{2}}. \end{aligned}$$

The normalized ion number density [31] is given by

$$\begin{aligned} n_i=(1-M\phi +N\phi ^2)\{1-(q-1)\phi \}^{\frac{1}{q-1}+\frac{1}{2}}, \end{aligned}$$

where $M=-\frac{16\alpha q}{(5q-3)(3q-1)+12\alpha }$ and $N=\frac{16\alpha q(2q-1)}{(5q-3)(3q-1)+12\alpha }.$

Equations (1)–(3) can be written in components form as:

$$\begin{aligned} \frac{\partial n}{\partial t}+\frac{\partial (nu)}{\partial x}+\frac{\partial (nv)}{\partial y}&= 0,\end{aligned}$$

(4)

$$\begin{aligned} \frac{\partial u}{\partial t}+\left( u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}\right) u= & {} \frac{\partial \phi }{\partial x} ,\end{aligned}$$

(5)

$$\begin{aligned} \frac{\partial v}{\partial t}+\left( u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}\right) v= & {} \frac{\partial \phi }{\partial y}-w,\end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial w}{\partial t}+\left( u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}\right) w= v, \end{aligned}$$

(7)

$$\begin{aligned} \left( \frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}\right) \phi =\alpha _1\left[ n-(1-M\phi +N\phi ^2)\{1-(q-1)\}^{\frac{1}{q-1}+\frac{1}{2}}\right] . \end{aligned}$$

(8)

Derivation of the FMKP equation

We employ the reductive perturbation technique (RPT) to derive the Kadomtsev–Petviashili(KP) equation. According to the RPT, the independent variables are stretched as:

$$\begin{aligned} \left\{ \begin{array}{l} Y = \epsilon ^2 y,\\ \eta = \epsilon (x-Vt),\\ \tau = \epsilon ^3 t, \end{array} \right. \end{aligned}$$

(9)

where V denotes the phase velocity of dust acoustic wave along the x-axis in magnetoplasmas with nonthermal ions featuring Tsallis distribution, and $\epsilon$ is a small parameter which characterizes the strength of the nonlinearity. The dependent variables in the above relations are expanded as:

$$\begin{aligned} \left\{ \begin{array}{l} n = 1+\epsilon ^2 n_1+\epsilon ^4 n_2+\cdots \\ u = \epsilon ^2 u_1+\epsilon ^4 u_2+\cdots \\ v = \epsilon ^3 v_1+\epsilon ^5 v_2+\cdots \\ w = \epsilon ^3 w_1+\epsilon ^5 w_2+\cdots \\ \phi = \epsilon ^2\phi _1+\epsilon ^4\phi _2+\cdots \end{array} \right. \end{aligned}$$

(10)

Substituting the Eqs. (9)–(10) into the system of Eqs. (4)–(8) and equating the coefficient of lowest order of $\epsilon$, one can obtain the phase velocity as

$$\begin{aligned} V^2= & {} \frac{1}{(a+M)}, \end{aligned}$$

(11)

where $a=\frac{q+1}{2}$.

Considering the coefficient of next order of $\epsilon$, we obtain the KP equation as:

$$\begin{aligned} \frac{\partial }{\partial \eta } \left[ \frac{\partial \phi _1}{\partial \tau }-A \phi _1\frac{\partial \phi _1}{\partial \eta }+B \frac{\partial ^3 \phi _1}{\partial \eta ^3}\right] +C\frac{\partial ^2 \phi _1}{\partial Y^2}&= 0, \end{aligned}$$

(12)

where $A=\frac{V}{2P}[3P^2-2Q],\quad B=\frac{V}{2P\alpha _1},$ $\quad C=\frac{V}{2},$ with $P=a+M$, $b=\frac{(q+1)(3-q)}{8}$ and $Q=b+N+aM.$

Fig. 1

A is a function of q when $\alpha =0.1$

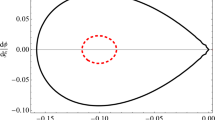
The KP equation (12) depends on A which is a function of $\alpha$ and q. In Fig. 1, it is shown that A may be positive or negative depending on different values of q with fixed value of $\alpha =0.1$, but there is a critical point at which $A=0,$ which can provide an infinite growth of the amplitude of the solitary wave solutions and periodic wave solutions of Eq. (12) which breaks down the validity of the RPT. In this case, q is called the critical parameter with critical value $q\simeq 0.8751$. Thus, the exact solutions of the Eq. (12) do not exist at the points which are very near to the critical values of the critical parameters. In this situation, the KP equation is unable to describe the nonlinear wave phenomena in this dusty plasma. So to describe the nonlinear wave features near or around or at $A=0$, we extend the study and want to obtain satisfactory solutions near and around the critical value. Therefore, we consider more higher order nonlinear equation to achieve the desired results.

We proceed for the modified Kadomtsev–Petviashili (MKP) equation by considering higher order coefficients of $\epsilon$. We consider the same set of stretched coordinates but the previous expansions of the dependent variables are not valid. Therefore, we consider a set of new expansions of the dependent variables as follows:

$$\begin{aligned} \left\{ \begin{array}{l} n = 1+\epsilon n_1+\epsilon ^2 n_2+\epsilon ^3 n_3+\cdots \\ u =\epsilon u_1+\epsilon ^2 u_2+\epsilon ^3 u_3+\ldots \\ v = \epsilon ^2 v_1+\epsilon ^3 v_2+\epsilon ^4 v_3+\ldots \\ w = \epsilon ^2 w_1+\epsilon ^4 w_2+\epsilon ^6 w_3+\ldots \\ \phi = \epsilon \phi _1+\epsilon ^2\phi _2+\epsilon ^3\phi _3+\ldots . \end{array} \right. \end{aligned}$$

(13)

Substituting the above expansions (13) along with the same stretched coordinates (9) into Eqs. (4)–(8) and equating the coefficients of different powers of $\epsilon$ and eliminating $n_3, w_3$ and $\phi _3$, one can obtain the following equation:

$$\begin{aligned} \frac{\partial }{\partial \eta } \left[ \frac{\partial \phi _1}{\partial \tau }-A\frac{\partial (\phi _1 \phi _2)}{\partial \eta }- D\phi _1^2\frac{\partial \phi _1}{\partial \eta }+B \frac{\partial ^3\phi _1}{\partial \eta ^3}\right] +C\frac{\partial ^2 \phi _1}{\partial Y^2} = 0, \end{aligned}$$

(14)

where the coefficients A, B and C are same as the coefficients of the KP equation and $D=\frac{3V}{2P}(R+2P^3-3PQ)$ with $R=K+bM+aN$. It is clear that for the critical values of the parameters A may equal to zero and the Eq. (14) reduces to the following MKP equation:

$$\begin{aligned} \frac{\partial }{\partial \eta } \left[ \frac{\partial \phi _1}{\partial \tau }- D\phi _1^2\frac{\partial \phi _1}{\partial \eta }+B \frac{\partial ^3\phi _1}{\partial \eta ^3}\right] +C\frac{\partial ^2 \phi _1}{\partial Y^2} = 0, \end{aligned}$$

(15)

If A is at the same order of $\epsilon$, but not zero, we derive the FMKP equation using the same stretched coordinates and same expansions as the MKP equation:

$$\begin{aligned} \frac{\partial }{\partial \eta } \left[ \frac{\partial \phi _1}{\partial \tau }-A\phi _1\frac{\partial \phi _1}{\partial \eta }- D\phi _1^2\frac{\partial \phi _1}{\partial \eta }+B \frac{\partial ^3\phi _1}{\partial \eta ^3}\right] +C\frac{\partial ^2 \phi _1}{\partial Y^2} = 0. \end{aligned}$$

(16)

Formation of dynamical system

To investigate all traveling wave solutions of the FMKP equation (16), we transform it to a dynamical system by introducing a new variable $\chi$ as follows:

$$\begin{aligned} \chi = (l\eta +mY-U\tau ), \end{aligned}$$

(17)

where l and m are the cosines of the angles made by wave propagation with $\eta$-axis and Y-axis, respectively. Here, U is the speed of dust acoustic traveling wave. Substituting $\psi (\chi )= \phi _1(\eta ,Y,\tau )$ into the FMKP equation (16) and then integrating twice, the FMKP equation (16) takes the form

$$\begin{aligned} Bl^{4} \frac{\mathrm{d}^ {2}\psi }{\mathrm{d} \chi ^{2}} + (Cm^{2} - lU)\psi -\frac{Al^{2}}{2}\psi ^{2}-\frac{Dl^{2}}{3}\psi ^{3}= 0. \end{aligned}$$

(18)

Then, Eq. (18) can be written as the following dynamical system:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d}\psi }{\mathrm{d} \chi }=z, \\ \frac{\mathrm{d}z}{\mathrm{d} \chi }=\frac{(lU-C(1-l^2)+\frac{Al^{2}}{2}\psi +\frac{Dl^{2}}{3}\psi ^2)\psi }{Bl^{4}}. \end{array} \right. \end{aligned}$$

(19)

The system (19) represents a planar Hamiltonian system with the following Hamiltonian function:

$$\begin{aligned} H(\psi ,z)=\frac{z^2}{2}-\frac{1}{12 Bl^{4}} \left( 6(lU-C(1-l^2))+2Al^{2}\psi +Dl^2\psi ^2 \right) \psi ^2. \end{aligned}$$

(20)

The system (19) is a planar dynamical system with parameters $\alpha , \alpha _1, q, l$ and U. It is interesting to note that the phase orbits defined by the vector fields of Eq. (19) determine all traveling wave solutions of the FMKP equation (16). Thus, we investigate bifurcations of phase portraits of Eq. (19) in the $(\psi ,z)$ phase plane as the parameters $\alpha , \alpha _1, q, l$ and U are varied. In this case, we consider a physical system for which only bounded traveling wave solutions are meaningful. Therefore, our attention is to study only bounded traveling wave solutions of the FMKP equation (16). It is known that a solitary wave solution of Eq. (16) corresponds to a homoclinic orbit of Eq. (19). A periodic orbit of Eq. (19) corresponds to a periodic traveling wave solution of Eq. (16). The bifurcation theory of planar dynamical systems [52, 53] plays an important role in this study.

Phase plane analysis

In this section, we investigate the bifurcations of phase portraits of Eq. (19). When $AB\beta l\ne 0$ and $lU\ne C(1-l^2)$, then there are three equilibrium points at $E_0(\psi _0,0)$, $E_1(\psi _1,0)$ and $E_2(\psi _2,0)$, where $\psi _0=0$, $\psi _1=\frac{3}{2Dl^2}\{\frac{-Al^2}{2}+\sqrt{\frac{A^2l^4}{2}-\frac{4Dl^2}{3}(lU-C(1-l^2))}\}$ and $\psi _2=\frac{3}{2Dl^2}\{\frac{-Al^2}{2}-\sqrt{\frac{A^2l^4}{2}-\frac{4Dl^2}{3}(lU-C(1-l^2))}\}$.

Let $M(\psi _i,0)$ be the coefficient matrix of the linearized system of Eq. (19) at an equilibrium point $E_i(\psi _i,0)$. Then, we have

$$\begin{aligned} J=\mathrm{det}M(\psi _i,0)=\frac{(C(1-l^2)-lU)}{Bl^{4}}-\frac{1}{Bl^{2}}\{A\psi _i+D\psi _i^2\}. \end{aligned}$$

(21)

By the theory of planar dynamical systems [52, 53], we know that the equilibrium point $E_i(\psi _i,0)$ of the planar dynamical system (19) is a saddle point when $J<0$ and the equilibrium point $E_i(\psi _i,0)$ of the planar dynamical system (19) is a center when $J>0.$

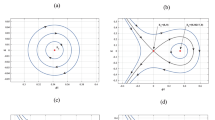
If $2lU>V(1-l^2), \; 3P^2<2Q$, $R+2P^3<3PQ$, $\frac{5}{7}<q<1,$ $0\le \alpha <0.25,$ $0<l<1$, and $\alpha _1>0$, then the system (19) has three equilibrium points at $E_0(\psi _0,0)$, $E_1(\psi _1,0)$ and $E_2(\psi _2,0)$, where $\psi _0=0$, $\psi _1>0$ and $\psi _2<0.$ The equilibrium point $E_0(\psi _0,0)$ is a saddle point, $E_1(\psi _1,0)$ and $E_2(\psi _2,0)$ are centers. There is a pair of homoclinic orbits at $E_0(\psi _0,0)$ surrounding the centers $E_1(\psi _1,0)$ and $E_2(\psi _2,0)$ (see Fig. 2).

Using the above analysis, we have shown the phase portrait of Eq. (19) in Fig. 2 depending on some special values of the parameters $\alpha , \alpha _1, q, l$ and U. It is seen that there is a pair of homoclinic orbits at the equilibrium point $E_0(\psi _0,0)$ surrounding two centers at the equilibrium points $E_1(\psi _1,0)$ and $E_2(\psi _2,0)$ in Fig. 2. For these pair of homoclinic orbits of the dynamical system (19), the FMKP equation has dust acoustic compressive and rarefactive solitary wave solutions.

Fig. 2

Phase portrait of Eq. (19) for $l=0.7, \alpha =0.1, \alpha _1=0.1, q=0.8$ and $U=1$

Fig. 3

Phase projection of system (19) with the same values of parameters as Fig. 2

Fig. 4

Periodicity of Z based on system (19) with the same values of parameters as Fig. 2

Fig. 5

Periodicity of $\psi$ based on system (19) with the same values of parameters as Fig. 2

In Fig. 3, we have presented one limit cycle about the center $E_1(\psi _1,0)$ of the dynamical system (19) for $l=0.7, \alpha =0.1, \alpha _1=0.1, q=0.8$ and $U=1$. Corresponding to the limit cycles about the center $E_1(\psi _1,0)$ of the dynamical system (19), we get a family of periodic wave solutions of the FMKP equation (16). In Fig. 4, we have presented the periodicity of Z based on system (19) with the same values of parameters as Fig. 2 and in Fig. 5, we have shown the periodicity of $\psi$ based on system (19) with the same values of parameters as Fig. 2. We can obtain similar results in case of equilibrium point $E_2(\psi _2,0)$.

Analytical traveling wave solutions

In this section, using the planar dynamical system Eq. (19) and the Hamiltonian function Eq. (20), we derive analytical traveling wave solutions for solitary waves and periodic waves of the FMKP equation (16) depending on the parameters $\alpha , \alpha _1, q, l$ and U. It should be noted that $cn(\Omega _1 \xi , k_1)$ is the Jacobian elliptic function [54] with the modulo $k_1$.

• (1) Corresponding to the pair of homoclinic orbits at $E_0(\psi _0,0)$ surrounding the centers $E_1(\psi _1,0)$ and $E_2(\psi _2,0)$ (see Fig. 2), the FMKP equation (16) has a pair of the solitary wave solutions (compressive and rarefactive types):

  $$\begin{aligned} \psi (\chi )=\pm \frac{1}{\sqrt{2\left(1-\frac{b_1^2}{9a_1c_1}\right)}\;\sin \left(2\sqrt{\frac{a_1}{c_1}}\chi \right )+\frac{b_1}{6a_1}}, \end{aligned}$$

  (22)

  where $a_1=\frac{lU-C(1-l^2)}{Bl^4}$, $b_1=\frac{A}{2Bl^2}$ and $c_1=\frac{D}{3Bl^2}$.

• (2) Corresponding to the family of periodic orbits about $E_2(\psi _2,0)$ (see Fig. 2), the FMKP equation (16) has a family of the periodic traveling wave solutions:

  $$\begin{aligned} \psi (\chi )=\frac{\alpha _2B_1+\beta _2A_1-(\alpha _2B_1-\beta _2A_1)cn(\Omega _1\chi ,k_1)}{B_1+A_1-(B_1-A_1)cn(\Omega _1\chi ,k_1)}, \end{aligned}$$

  (23)

  where $A_1=\alpha _2^2+\alpha _2\gamma _2+\delta _2, B_1=\beta _2^2+\beta _2\gamma _2+\delta _2, \Omega _1=\sqrt{-\frac{D}{6Bl^2}}$ and $k_1=\frac{(\alpha _2-\beta _2)^2-(A_1-B_1)^2}{4A_1B_1}$ with $\alpha _2, \beta _2, \gamma _2$ and $\delta _2$ are roots of the equation $h+\frac{1}{12 Bl^{4}} (6(lU-C(1-l^2))+2Al^{2}\psi +Dl^2\psi ^2)\psi ^2= -\frac{D}{12Bl^2}(\alpha _2-\psi )(\psi -\beta _2)(\psi ^2+\gamma _2\psi +\delta _2)$, satisfying $\alpha _2>\beta _2,$ and $\gamma _2^2-4\delta _2<0, h\in (h_2,0)$, $h_2=H(\psi _2,0)$.

Sabetkar and Dorranian [22] investigated dust acoustic solitary waves (DASWs) in a magnetized four component dusty plasma and showed that due to electron nonextensivity, their dusty plasma model admitted positive potential as well as negative potential solitons. Dorranian and Sabetkar [23] also investigated the dust acoustic solitary waves in a dusty plasma on the frameworks of the KP and modified KP equations. The authors obtained the compressive and rarefactive solitary wave solutions in terms of $\mathrm{sech}(\frac{\chi }{w})$ for some special values of the physical parameters. But in this work, we have obtained a new form of the compressive and rarefactive solitary wave solutions (22) and periodic wave solution (23) in terms of the Jacobean elliptic function. Thus, the dust acoustic compressive and rarefactive solitary waves of our work have been supported by the works [22, 23] reported in the literature.

Quasiperiodic route to chaos

In this section, we study the quasiperiodic and chaotic behaviors of the perturbed system given by:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\mathrm{d}\psi }{\mathrm{d} \chi }=z, \\ \frac{\mathrm{d}z}{\mathrm{d} \chi }=\frac{\left(lU-C(1-l^2)+\frac{Al^{2}}{2}\psi +\frac{Dl^{2}}{3}\psi ^2\right)\psi }{Bl^{4}}+f_0\;\cos (\omega \chi ), \end{array} \right. \end{aligned}$$

(24)

where $f_0\;\cos (\omega \chi )$ is an external periodic perturbation, $f_0$ is the strength of the periodic perturbation and $\omega$ is the frequency. It is to be noted that the difference between system (19) and system (24) is that only external periodic perturbation is added with system (24). Furthermore, existence of $f_0~\cos (\omega \chi )$ in system (24) is a root that can turn system (19) into the chaotic state.

Fig. 6

Phase portrait of the perturbed system (24) for $l=0.7, \alpha =0.1, \alpha _1=0.1, q=0.8, U=1$,  $f_0=0.02$ and $\omega =1$ with initial condition $(\psi _0, z_0)=(1.72,0.0001)$

Fig. 7

Quasiperiodicity of Z based on system (24)

Fig. 8

Quasiperiodicity of $\psi$ based on system (24)

Fig. 9

Phase portrait of the perturbed system (24) for $l=0.7, \alpha =0.1, \alpha _1=0.1, q=0.8, U=1$, $f_0=1$ and $\omega =1$ with initial condition $(\psi _0, z_0)=(1.72,0.0001)$

Fig. 10

Chaotic motions of Z based on system (24)

Fig. 11

Chaotic motions of $\psi$ based on system (24)

In Fig. 6, we have presented phase portrait of the perturbed system (24) for $l=0.7, \alpha =0.1, \alpha _1=0.1, q=0.8, U=1$, $f_0=0.02$ and $\omega =1$ with initial condition $(\psi _0, z_0)=(1.72,0.0001).$ It is found that the perturbed system (24) has quasiperiodic motion even if the external periodic perturbation is considered. Thus, a quasiperiodic motion of the system (24) is observed with incommensurable periodic motions and the trajectory in the phase space winds around torus filling its surface densely. In Figs. 7 and 8, we have presented the quasiperiodicity of Z and $\psi$, respectively, based on the system (24) with the same values of parameters as Fig. 6. If we increase strength of the periodic perturbation and consider $f_0=1$ with the same values of other parameters, then the perturbed system (24) shows chaotic motions. In Fig. 9, we have presented the phase portrait of the perturbed system (24) for $l=0.7, \alpha =0.1, \alpha _1=0.1, q=0.8, U=1$,  $f_0=1$ and $\omega =1$ with same initial condition as Fig. 6. In Figs. 10 and 11, we have presented the chaotic motions of Z and $\psi$, respectively, based on the system (24) with same values of parameters as Fig. 9. Thus, the developed chaotic motions occur (see Figs. 9, 10, 11) and the solutions ignore the periodic motions and represent random sequences of uncorrelated oscillations. Hence, the strength of the periodic perturbation plays a crucial role for the development of the quasiperiodic motion of the perturbed system (24) and transition from quasiperiodic motion to chaotic motion of the system (24). Thus, it is observed that the perturbed plasma system shows chaotic behavior through quasiperiodic route to chaos which is an important observation in this study.

Conclusions

In this paper, we have derived the FMKP equation for dust acoustic waves in magnetoplasmas with nonthermal ions featuring Cairns–Tsallis distribution. Applying the bifurcation theory of planar dynamical systems to the FMKP equation, we have presented the existence of solitary and periodic traveling waves through phase plane analysis. Two new analytical solutions for the solitary waves (compressive and rarefactive) and periodic waves are obtained depending on parameters $\alpha , \alpha _1, q, l$ and U. Considering an external periodic perturbation, the quasiperiodic and chaotic behaviors of dust acoustic waves are studied through numerical computations. The presence of the parameters $q, \alpha ,$ and $\alpha _1$ affects significantly on bifurcation of traveling wave solutions of the FMKP equation, the quasiperiodic and chaotic behaviors of the perturbed FMKP equation. It should be noted that for same set of values of parameters $\alpha , \alpha _1, q, l$ and U, the unperturbed FMKP equation has solitary and periodic wave solutions, but the perturbed FMKP equation shows the quasiperiodic and chaotic behaviors based on the strength of the external periodic perturbation. It is also important to note that the dust acoustic waves of the perturbed FMKP equation represent the chaotic motions through quasiperiodic route to chaos.