Introduction

The nineteenth century and half of twentieth century can be viewed as the triumph of linear physics, which started with Maxwell’s equations, based on a linear formalism emphasizing a superposition principle. But the physicists had noticed the importance of nonlinear phenomena which appeared in the momentum balance equation of electro-hydrodynamics, gravitational theory, etc. The importance of an intrinsic analysis of nonlinear phenomena has been gradually understood, and led to two concepts, the strange attractor and the soliton. Both are related to astonishing properties of nonlinear systems, the strange attractor is linked to the idea of chaos [1] in a system with small number of degree of freedom, while the solitons appear in the systems with the large number of degree of freedom. The study of interesting solitonic structures, periodic solution, and chaotic structures [2–5] in plasma dynamics is very important and curious. Therefore, the investigation of various structures like solitonic, periodic, quasi-periodic, and chaotic in nonlinear plasma dynamics is a growing research field of plasma physics. Some of the nonlinear evolution equations like Kortewg-de Vries (KdV), Kortewg-de Vries Burgers (KdVB), etc., arisen from many physical fields are completely integrable [6, 7]. It is known that a completely integrable nonlinear system possesses some nice properties like the Lax pair, N-soliton solutions, infinite conservation laws, Painlev property and bi-Hamiltonian structure. However, there often exist various perturbations in many real physical processes [8–10]. The addition of a perturbation or forcing term to an integrable equation can lead to chaotic dynamics [1], while deterministic chaos is one of the most interesting nonlinear phenomena. In the present paper, we want to study dramatic changes of structures from periodic to chaotic or solitonic to chaotic of ion acoustic waves in electron–positron–ion plasmas through direct approach. Indeed electrons are often accelerated to energies of tens of MeV by the electric field induced during the disruptive instability in tokamaks [11]. The resulting beam of runway electrons can carry up to about half of the original plasma current. At these high energies, electron–positron pairs can be created in collisions between the runaway electrons and background plasma ions and electrons. Helander and Ward [12] estimated the number of such pairs and discussed the fate of the positrons created in this way. The experiments [13–16] have established the possibility of creating a nonrelativistic electron–positron plasma in the laboratory. There are at least two schemes in which the nonrelativistic electron–positron plasma can be produced in the laboratory. In one scheme, a relativistic electron beam impinges on a high-Z target, where positrons are produced copiously. The relativistic pair plasma is then trapped in a magnetic mirror and is expected to cool rapidly by radiation [17]. In another scheme, positrons are accumulated from a radioactive source [15]. The production of pure positron plasmas [13, 15, 18] now makes it possible to perform laboratory experiments on electron–positron plasmas. A natural extension of this research is to learn how to accumulate and store sufficient numbers of positrons so that they behave as a collective, many-body system. Surko et al. [15] have developed a method to accumulate and store positrons in an electrostatic trap using a tungsten moderator and inelastic collisions with nitrogen gas. The resulting positron gas fulfills the requirements on density n and temperature T for it to act collectively as a classical, single-component positron plasma. The electron–positron plasmas occur in many astrophysical environments such as the inner regions of the accretion disks surrounding black holes [19], the center of our galaxy [20], the early universe [21], the polar regions of neutron stars [22], active galactic nuclei [23], or pulsar magnetosphere [24], and in solar atmosphere [25] together with small number of ions. These types of three-component e–p–i plasmas can also be found in the laboratory plasma, for example, during the propagation of a short relativistic strong laser pulse in matter, and photo production of pairs due to the photon scattering by nuclei can lead to the formation of e–p–i plasmas [26, 27]. Indeed, electron–positron plasmas represent a large class of equal-mass plasmas, a class of plasmas that may offer plasma physical properties quite different from those of conventional ion–electron plasmas. Clearly, the properties of wave motions in an electron–positron–ion plasma should be different from those in two-component electron–positron plasmas. A great deal of attention has been paid to study the electron–positron–ion plasmas during the last three decades [28–34].

Out of the existence of electron–positron–ion plasmas in various physical plasma situations, nonextensive electron–positron–ion plasmas is the most studied research field due to the limitation of proper implementation of Maxwell distribution in long-range interactions in unmagnetized collision less plasma where the nonequilibrium stationary state exists. Space plasma observations clearly indicate the presence of ion and electron populations that are far away from their thermodynamic equilibrium [35–39]. A new statistical approach, [40] namely nonextensive statistics or Tsallis statistics based on the derivation of Boltzmann–Gibbs–Shannon (BGS) entropic measure, [41] is proposed to the study the cases where Maxwell distribution is considered inappropriate. This was first acknowledged by Reni [40] and afterward proposed by Tsallis [41], where the entropic index q characterized the degree of non extensivity of the considered system. The parameter q that underpins the generalized entropy of Tsallis is linked to the underlying dynamics of the system and measures the amount of its nonextensivity. In statistical mechanics and thermodynamics, systems characterized by the property of nonextensivity are systems for which the entropy of the whole is different from the sum of the entropies of the respective parts. In other words, the generalized entropy of the whole is greater than the sum of the entropies of the parts if \(q <1\) (superextensivity), whereas the generalized entropy of the system is smaller than the sum of the entropies of the parts if \(q >1\) (subextensivity). In accordance with the evidences found earlier [40–52], the q-entropy may provide a convenient frame for the analysis of many astrophysical scenarios, such as stellar poly tropes, solar neutrino problem, and peculiar velocity distribution of galaxy cluster. To study all possible astrophysical scenarios, it is wise to follow the nonextensive distribution. As electrons and positrons have the same mass but opposite charge, it is expected that they will be described by a similar distribution. Shahmansouri and Alinejad [53] studied the effect of electron nonextensivity on oblique propagation of arbitrary ion acoustic waves in a magnetized plasma. Shahmansouri and Astaraki [54] investigated the transverse perturbation on three-dimensional ion acoustic waves in electron–positron–ion plasma with high-energy tail electron and positron distribution. Shahmansouri and Alinejad [55] also investigated arbitrary amplitude electron acoustic (EA) solitary waves in a magnetized nonextensive plasma comprising cool fluid electrons, hot nonextensive electrons, and immobile ions. Sabetkar and Dorranian [56] studied the nonextensive effects on the characteristics of dust-acoustic solitary waves in magnetized dusty plasma with two-temperature isothermal ions.

Recently, Samanta et al. [57] studied bifurcations of dust-ion acoustic traveling waves in a magnetized dusty plasma with a q-nonextensive electron velocity distribution using bifurcation theory of planar dynamical systems for the first time in the literature. A number works [58–66] on bifurcations of nonlinear waves in plasmas have been reported through perturbative and nonperturbative approaches. Saha and chatterjee [67] studied propagation and interaction of dust-acoustic multi-soliton in dusty plasmas with q-nonextensive electrons and ions. Very recently, Saha et al. [2] investigated the dynamic behavior of ion acoustic waves in electron–positron–ion magnetoplasmas with superthermal electrons and positrons. Sahu et al. [3] studied the quasi-periodic behavior in quantum plasmas due to the presence of bohm potential. Zhen et al. [4] studied dynamic behavior of the quantum ZK equation in dense quantum magnetoplasma. Zhen et al. [5] also studied soliton solution and chaotic motion of the extended ZK equations in a magnetized dusty plasmas with Maxwellian hot and cold ions.

The remaining part of the paper is organized as follows: In "Basic equations" section, we consider basic equations. In "Planar dynamical system and phase portraits" section, we obtain a planar dynamical system and corresponding phase portraits. New solitary and periodic wave solutions are derived in "New solitary and periodic wave solutions" section. We present the chaotic behavior of the perturbed system in "Chaos in the perturbed system" and "Conclusions" sections are kept for conclusions.

Basic equations

In this work, we consider a three-component collisionless unmagnetized plasma containing inertial ions, and q-nonextensive velocity distributed electrons and positrons. In equilibrium, the charge neutrality condition is \(n_{e0}=n_{p0}+n_0,\) where \(n_{e0}, n_{p0}\) and \(n_0\) are the unperturbed number densities of electron, positron and ion, respectively. The dynamics of nonlinear ion acoustic waves in such plasma is described by the following normalized equations:

$$\begin{aligned} \frac{\partial n}{\partial t}+\frac{\partial (nu)}{\partial x} = 0,\end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x} = -\frac{\partial \phi }{\partial x},\end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial ^2 \phi }{\partial x^2} = n_e-n_p-n. \end{aligned}$$
(3)

The density of the q-nonextensive electrons and positrons are given by

$$\begin{aligned} n_e=\frac{1}{1-p}\{1+(q-1)\phi \}^{\frac{1}{q-1}+\frac{1}{2}},\end{aligned}$$
(4)
$$\begin{aligned} n_p=\frac{p}{1-p}\{1-(q-1)\sigma \phi \}^{\frac{1}{q-1}+\frac{1}{2}}, \end{aligned}$$
(5)

where \(n_e, n_p, \) and n are the number densities of electrons, positrons and ions, respectively, normalized by their unperturbed densities. In this case, u and \(\phi \) are the ion fluid velocity and electrostatic potential, respectively, normalized by the ion acoustic speed \(c=(T_e /m )^{1/2}\), and \(T_e /e\), where e is the electron charge and m is the mass of ions. The time variable is normalized by inverse of ion plasma frequency \(\omega ^{-1}=(m/4\pi n_0e^2)^{1/2}\) and the space variable is normalized by the Debye length \(=(T_e/4\pi n_0 e^2 )^{1/2}\), respectively. Here \(p = n_{p0} /n_{e0}\), and \(\sigma = T_e /T_p\).

The state of a plasma is kinetically characterized by the one-particle distribution function \(f(\overrightarrow{x}, \overrightarrow{v}, t)\). The quantity \(f(\overrightarrow{x}, \overrightarrow{v}, t)d^3x d^3v\) gives, at each time t, the number of particles in the volume element \(d^3x d^3v\) around the particle position \(\overrightarrow{x}\) and velocity \(\overrightarrow{v}\). In principle [46], this distribution function verifies the q-nonextensive Boltzmann transport equation or Vlasov equation

$$\begin{aligned} \frac{\partial f}{\partial t}+v\frac{\partial f}{\partial x}+ \frac{k}{m_e}\frac{\partial f}{\partial v}=C_q(f), \end{aligned}$$

where \(C_q\) denotes the q-collisional term. Here, nonextensivity effects can be incorporated only through the collisional term under the consideration that the \(C_q\) is consistent with the energy, momentum, and particle number conservation laws. To generalize the usual Boltzmann–Gibbs thermostatics according to the demand of thermodynamical or statistical description of nonextensive systems, the standard Boltzmann–Gibbs approach based on the extensive entropy measure \(S=-k\sum _i p_ilnp_i \), where k is the Boltzmann constant and \({p_i}\) denotes the probabilities of microscopic configurations modified by Tsallis [41, 42] in the following nonextensive form of entropy \(S_q=k\frac{1-\sum _i P_i^q}{q-1}\), where q is a parameter quantifying the degree of nonextensivity. Also Tsallis [41, 42] measure verifies \(S_q(A+B)=S_q(A)+S_q(B)+(1-q)S_q(A)S_q(B)\). In the limit \(q\rightarrow 1\), \(S_q\) reduces to the standard logarithmic measure and the usual additivity of the entropy is recovered. Advancing in this manner [45], one can get the following q-distribution function

$$\begin{aligned} f_e(v)=C_q\left\{ 1+(q-1)\left[ \frac{m_ev^2}{2T_e}-\frac{e\phi }{T_e}\right] \right\} ^{\frac{1}{q-1}}. \end{aligned}$$

The variables or parameters have their usual meaning. It may be noted that \(f_e(v)\) is the particular distribution that maximizes the Tsallis entropy and therefore conforms to the laws of thermodynamics. The normalization constant \(C_q\) is given by

$$\begin{aligned} C_q=n_{e0}\frac{\Gamma \big (\frac{1}{1-q}\big )}{\Gamma \big (\frac{1}{1-q}-\frac{1}{2}\big )}\sqrt{\frac{m_e(1-q)}{2\pi T_e}}\quad \text {for}\quad -1<q<1; \end{aligned}$$
$$\begin{aligned} C_q=n_{e0}\Big (\frac{1+q}{2}\Big )\frac{\Gamma \Big (\frac{1}{q-1}+\frac{1}{2}\Big )}{\Gamma \big (\frac{1}{q-1}\big )}\sqrt{\frac{m_e(q-1)}{2\pi T_e}}\quad \text {for}\quad q>1; \end{aligned}$$

where the parameter q stands for the strength of nonextensivity. It may be useful to note that \(q<-1\), the q-distribution is unnormalizable. It should be noted that for \(q>1\), the q-distribution function exhibits a thermal cutoff on the maximum value allowed for the velocity of the particles, which is given by

$$\begin{aligned} v_\mathrm{max}=\sqrt{\frac{2T_e}{m_e}\left( \frac{e\phi }{T_e}+\frac{1}{q-1}\right) }; \end{aligned}$$

we get

$$\begin{aligned} n_e(\phi )=\int _{-\infty }^{\infty }f_e(v)\mathrm{d}v,\quad \text {for}\quad -1<q<1; \end{aligned}$$
$$\begin{aligned} n_e(\phi )=\int _{-v\mathrm{max}}^{+v_\mathrm{max}}f_e(v)\mathrm{d}v,\quad \text {for}\quad q>1. \end{aligned}$$

The derivation of nonextensive distribution from the density function gives

$$\begin{aligned} n_e=[1+(q-1)\phi ]^{\frac{1+q}{2(q-1)}}. \end{aligned}$$

In stead of gaussian profile one, q-nonextensive electrons satisfy a power law distribution which reduces to the Maxwellian distribution as \(q\rightarrow 1\). It should be emphasized that the physical state described by the q-distribution is not the thermodynamic equilibrium. The nonextensive parameter q was proved to relate to the temperature gradient and the potential energy of the system in terms of the formula \(k_\mathrm{B}\nabla T_e+(1-q)Q\nabla \phi =0\). Thus, the deviation of q from unity qualifies the degree of the inhomogeneity of temperature or the deviation from the equilibrium [69]. It is shown clearly from the above formula that the nonextensive parameter is \(q \ne 1\) if and only if the temperature gradient is \(\nabla T \ne 0\), which gives a clear physics of \(q \ne 1\) with regard to the nature of nonisothermal configurations of plasma systems with the Coulombian long-range interactions. The above formula is a mathematical expression of the nonextensive parameter q, and it gives a clearly physical meaning of \(q \ne 1\) about temperature gradient and the Coulombian force on an electron in the nonisothermal plasma. If \(\nabla T = 0\), the system becomes isothermal, and we have \(q = 1\), which corresponds to the thermal equilibrium state for which B–G statistics has presented well description. While if \(\nabla T \ne 0\), then \(q \ne 1\), which corresponds to the case of Tsallis statistics. We therefore conclude that Tsallis statistics can deal with the nonisothermal nature in plasma systems with the Coulombian long-range interactions [68, 69]. The physical meaning of nonextensive parameter of electron (q) different from 1 can be explained [69], respectively, by the relations, \((1-q)e\nabla \phi =k_\mathrm{B}\nabla T_e\).

Planar dynamical system and phase portraits

In this section, we transform our model equations into a planar dynamical system. To do so, we introduce a new variable \(\xi =x-vt,\) where v is the velocity of the ion acoustic traveling wave. Substituting the new variable \(\xi \) into Eqs. (1) and (2) and using the initial condition \(u=0,n=1\) , and \(\phi =0\), we can express the ion number density as

$$\begin{aligned} n= \frac{v}{\sqrt{v^2-2\phi }}. \end{aligned}$$
(6)

Substituting Eqs. (4), (5), and (6) into Eq. (3) and considering the terms involving \(\phi \) up to third degree, we have

$$\begin{aligned} \frac{\mathrm{d}^2 \phi }{\mathrm{d}\xi ^2}=a\phi +b\phi ^2+c\phi ^3, \end{aligned}$$
(7)

where \(a=\frac{(q+1)(1+p\sigma )}{2(1-p)}-\frac{1}{v^2}\), \(b=\frac{(q+1)(3-q)(1-p\sigma ^2)}{8(1-p)}-\frac{3}{2v^4}\), and \(c=\frac{(q+1)(3-q)(5-3q)(1+p\sigma ^3)}{48(1-p)}-\frac{5}{2v^6}\).

Then, Eq. (7) is equivalent to the following planar dynamical system:

$$\left\{ \begin{array}{ll} \frac{\mathrm{d}\phi }{\mathrm{d} \xi }=z, \\ \frac{\mathrm{d}z}{\mathrm{d} \xi }=a\phi +b\phi ^2+c\phi ^3. \end{array} \right.$$
(8)

It is important to note that a system of planar equations \(\frac{\mathrm{d}\phi }{\mathrm{d}\xi }=f_1(\phi , z)\), \(\frac{\mathrm{d}z}{\mathrm{d}\xi }=f_2(\phi , z)\) is called a Hamiltonian system (in classical mechanics) if there exists a function \(H(\phi ,z)\) such that \(f_1=\frac{\partial H}{\partial z}\) and \(f_2=-\frac{\partial H}{\partial \phi }\). A necessary and sufficient condition for a planar system \(\frac{\mathrm{d}\phi }{\mathrm{d}\xi }=f_1(\phi , z)\), \(\frac{\mathrm{d}z}{\mathrm{d}\xi }=f_2(\phi , z)\) to be Hamiltonian is that \(\frac{\partial f_1}{\partial \phi }+\frac{\partial f_2}{\partial z}=0\).

The system (8) is a planar Hamiltonian system with Hamiltonian function:

$$\begin{aligned} H(\phi ,z)=\frac{z^2}{2}-a\frac{\phi ^2}{2}- b\frac{\phi ^3}{3}-c\frac{\phi ^4}{4}=h,\text {say}. \end{aligned}$$
(9)

The system Eq. (8) is a planar dynamical system with parameters \(q, p, \sigma \) and v. It is clear that the phase orbits defined by the vector fields of Eq. (8) will determine all traveling wave solutions of Eq. (7). We will study the bifurcations of phase portraits of Eq. (8) in the \((\phi ,z)\) phase plane depending on the parameters. A homoclinic orbit of Eq. (8) gives a solitary wave solution of Eq. (7). Similarly, a periodic orbit of Eq. (8) gives a periodic traveling wave solution of Eq. (7).

We study the bifurcation set and phase portraits of the planar dynamical system (8). Clearly, on the \((\phi ,z)\) phase plane, the abscissas of equilibrium points of system (8) are the zeros of \(f(\phi )=\phi (\phi ^2+\frac{b}{c}\phi +\frac{a}{c})\). Let \(E_i(\phi _i,0)\) be an equilibrium point of the dynamical system (8) where \(f(\phi _i)=0.\) When \(b^2-4ac>0, \) there exist three equilibrium points at \(E_0(\phi _0,0)\), \(E_1(\phi _1,0)\), and \(E_2(\phi _2,0)\), where \(\phi _0=0\), \(\phi _1=\frac{-b+\sqrt{b^2-4ac}}{2c}\) , and \(\phi _2=\frac{-b-\sqrt{b^2-4ac}}{2c}\). If \(M(\phi _i,0)\) is the coefficient matrix of the linearized system of the dynamical system (8) at an equilibrium point \(E_i(\phi _i,0)\), then we get

$$\begin{aligned} J=\mathrm{det}M(\phi _i,0)=-cf^{'}(\phi _i). \end{aligned}$$
(10)

By the theory of planar dynamical systems [70, 71], it is clear that the equilibrium point \(E_i(\phi _i,0)\) of the planar dynamical system 8 is a saddle point when \(J\,<\,0\) and the equilibrium point \(E_i(\psi _i,0)\) of the planar dynamical system (8) is a center when \(J>0.\)

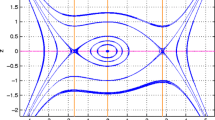
Applying the systematic analysis of parameters \(q, p, \sigma ,\) and v, we have presented the phase portrait of the system (8) in Figs. 1 and 2. In Fig. 1, we have presented the phase portrait of the system (8) for \(q=-0.8, p=0.5, \sigma =0.6,\) and \(v=1.6\). Thus, the velocity of the ion acoustic traveling wave is sonic. There are three equilibrium points of the system (8) at \(E_0(\phi _0,0),\) \(E_1(\phi _1,0),\) and \(E_2(\phi _2,0)\) with \(\phi _2 <0<\phi _1\). The equilibrium points \(E_1(\phi _1,0)\), \(E_2(\phi _2,0)\) are saddle points and \(E_0(\phi _0,0)\) is a center. There is a homoclinic orbit at the equilibrium point \(E_2(\phi _1,0)\) enclosing the center at \(E_0(\phi _0,0)\) which is surrounded by a family of periodic orbits. In Fig. 2, we have shown the phase portrait of the system (8) for \(q=0.1, p=0.5, \sigma =0.6\) and \(v=1\). In this case, there are three equilibrium points of the system (8) at \(E_0(\phi _0,0),\) \(E_1(\phi _1,0),\) and \(E_2(\phi _2,0)\) with \(\phi _1 <0<\phi _2\). The equilibrium points \(E_1(\phi _1,0)\), \(E_2(\phi _2,0)\) are centers and \(E_0(\phi _0,0)\) is a saddle point. There is a pair of homoclinic orbits at the equilibrium point \(E_0(\phi _1,0)\) enclosing the centers at \(E_1(\phi _1,0)\) and \(E_2(\phi _2,0)\) which are surrounded by a family of periodic orbits.

Fig. 1
figure 1

Phase portrait of Eq. (8) for \(q=-0.8, p=0.5, \sigma =0.6\) and \(v=1.6\)

Full size image
Fig. 2
figure 2

Phase portrait of Eq. (8) for \(q=0.1, p=0.5, \sigma =0.6\) , and \(v=1\)

Full size image

It is to be noted that for \(q>1\) with fixed values of other parameters (\(p=0.5, \sigma =0.6\) , and \(v=1\)), the type of the phase portrait is same as Fig. 2. So the phase portrait for \(q>1\) is not presented.

New solitary and periodic wave solutions

In this section, we present solitary wave solutions and periodic wave solutions with the help of the dynamical system (8) and the Hamiltonian function (9). It is important to note that if a phase portrait of a dynamical system has a homoclinic orbit at an equilibrium point of the system, then the system has a solitary wave solution corresponding to the homoclinic orbit at that point. If a phase portrait of a dynamical system has a family of periodic orbits about an equilibrium point of the system, then the system has a family of periodic wave solutions corresponding to the family of periodic orbits about that point. It should be noted that \(\mathrm{sn}(\Omega \xi , k)\) is the Jacobian elliptic function [72] with the modulo k.

  1. (1)

    The dynamical system (8) has a family of periodic orbits about the equilibrium point \(E_0(\phi _0,0)\) in Fig. 1 described by \(H(\phi ,z)=h\), \(h\in (h_2,0)\), where \(h_2=H(\phi _2,0)\). Corresponding to this family of periodic orbits about \(E_0(\phi _0,0)\), our system has a family of periodic wave solutions:

    $$\begin{aligned} \phi (\xi )=\frac{(\beta _1-\gamma _1)\delta _1 \mathrm{sn}^2(\Omega \xi , k)-\gamma _1(\beta _1-\delta _1)}{(\beta _1-\gamma _1)\mathrm{sn}^2(\Omega \xi , k)-(\beta _1-\delta _1)}, \end{aligned}$$
    (11)

    with \(\Omega =\sqrt{-\frac{c}{8}(\beta _1-\delta _1)(\gamma _1-\alpha _1)}\), \(k=\sqrt{\frac{(\alpha _1-\delta _1)(\beta _1-\gamma _1)}{(\alpha _1-\gamma _1)(\beta _1-\delta _1)}}\), where \(\alpha _1,\beta _1,\gamma _1\) , and \(\delta _1\) are roots of the equation \(h+\frac{c}{4}\phi ^4+\frac{b}{3}\phi ^3+\frac{a}{2}\phi ^2=0\), with \(\alpha _1>\beta _1>\gamma _1>\delta _1\), \(h\in (h_2,0)\).

  2. (2)

    The dynamical system (8) has a pair of homoclinic orbits about the equilibrium point \(E_0(\phi _0,0)\) in Fig. 2 described by \(H(\phi ,z)=0\). Corresponding to this pair of homoclinic orbits at \(E_0(\phi _0,0)\), our system has both compressive and rarefactive solitary wave solutions:

    $$\begin{aligned} \phi (\xi )=\pm \frac{1}{\sqrt{2\Big (1-\frac{b^2}{9ac}\Big )}\mathrm{sin}\left( 2\sqrt{\frac{a}{c}}\xi \right) +\frac{b}{6a}}. \end{aligned}$$
    (12)

It is important to note that one can obtain solitary wave solution corresponding to the homoclinic orbit at \(E_2(\phi _2,0)\) in Fig. 1. Similarly, one can obtain two families of periodic wave solutions corresponding to two families of periodic orbits about \(E_1(\phi _1,0)\) and \(E_2(\phi _2,0)\) in Fig. 2. In the work [61], the authors derived compressive solitary wave solution involving \(\mathrm{sec}h^2\xi \) corresponding to the homoclinic orbit at the saddle point (see Fig. 4 in [61]) and periodic wave solutions involving \(\mathrm{sec}^2\xi \) corresponding to the periodic orbits about the center (see Fig. 2 in [61]) of the dynamical system. But, in the present work, we obtain a family of periodic wave solutions (11) involving Jacobian elliptic function \(\mathrm{sn}^2(\Omega \xi , k)\) corresponding to the family of periodic orbits about the center \(E_0(\phi _0,0)\) in Fig. 1. We also obtain both compressive and rarefactive solitary wave solutions (12) corresponding to the pair of homoclinic orbits at the saddle point \(E_0(\phi _0,0)\) in Fig. 2.

Chaos in the perturbed system

In this section, we will discuss the chaotic behavior of the following perturbed system:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d}\phi }{\mathrm{d} \xi }=z, \\ \frac{\mathrm{d}z}{\mathrm{d} \xi }=a\phi +b\phi ^2+c\phi ^3+f_0~\mathrm{cos}(\omega \xi ), \end{array} \right. \end{aligned}$$
(13)

where \(f_0 \mathrm{cos}(\omega \xi )\) is the external periodic perturbation, \(f_0\) is strength of the external perturbation, and \(\omega \) is the frequency. The difference between the system (8) and the system (13) is that only external periodic perturbation is added with the system (8). The system (13) depends on six independent parameters \(q, p, \sigma , v, f_0,\) and \(\omega \). An investigation of such a system for complete range of parametric space or the influence of each parameter is complicated and difficult. To simplify the analysis, all parameters are kept as constants except q to be changed. In order to explore the possible chaotic structure of the perturbed system (13), we consider special values of the parameter q with fixed values of \(p,\, \sigma ,\, v,\, f_0,\) and \(\omega \) in three possible regimes \(-1<q<0, 0<q<1\) and \(q>1\). We could in fact vary any of the other parameters, but this does not give us any significant different qualitative results.

Fig. 3
figure 3

Phase portrait of the perturbed system (13) for \(q=-0.01,\, p=0.5,\,\sigma =0.6,\, v=1,\, f_0=1\) and \(\omega =1\) (initial condition \(\phi =0.23, z=0.1\))

Full size image
Fig. 4
figure 4

Phase portrait of the perturbed system (13) for \(q=0.1\) with same values of other parameters as Fig. 3 (initial condition \(\phi =0.3, z=0.1\))

Full size image
Fig. 5
figure 5

Phase portrait of the perturbed system (13) for \(q=2\) with same values of other parameters as Fig. 3 (initial condition \(\phi =1, z=0.8\))

Full size image
Fig. 6
figure 6

Plot of z versus \(\xi \) of the perturbed system (13) for same values of parameters as Fig. 3

Full size image
Fig. 7
figure 7

Plot of z versus \(\xi \) of the perturbed system (13) for same values of parameters as Fig. 4

Full size image
Fig. 8
figure 8

Plot of z versus \(\xi \) of the perturbed system (13) for same values of parameters as Fig. 5

Full size image

In Figs. 3, 4, and 5, we have presented phase portraits of the perturbed dynamical system (13) for different values of q (\(-0.01\) (see Fig. 3), 0.1 (see Fig. 4), 2 (see Fig. 5)) with fixed values of other parameters \(p=0.5, \sigma =0.6, f_0=1, \omega =1,\) and \(v=1\). In this case, the velocity of the perturbed traveling wave is sonic. It is clear that the perturbed system (13) shows chaotic oscillations. Any periodic or quasi-periodic behaviors are not observed in Figs. 3, 4, and 5 even if the external periodic perturbation is considered. Furthermore, the developed chaotic motions occur (see Figs. 3, 4, and 5) and the solutions ignore the periodic motions and represent random sequences of uncorrelated oscillations. For different ranges of the nonextensive parameter q, different developed chaotic motions(see Figs. 3, 4, and 5) are presented with suitable initial conditions. In Figs. 6, 7, and 8, we have plotted z vs. \(\xi \) for the perturbed system (13) for different values of q (\(-0.01\) (see Fig. 6), 0.1 (see Fig. 7), 2 (see Fig. 8)) with same values of other parameters as Fig. 3. In other words, the perturbed system (13) shows chaotic behavior when electrons or positrons evolve away from their Maxwell–Boltzmann equilibrium. It is easily seen that chaotic behavior is visible in the system (13) for different values of q.

Conclusions

We have addressed the dynamic structures of ion acoustic waves in an unmagnetized plasma with q-nonextensive electrons and positrons using the bifurcation theory of planar dynamical systems through direct approach. We have transformed the model equations into a planar dynamical system using a traveling wave transformation. Using the bifurcations of planar dynamical system, we have presented the existence of solitary and periodic waves through phase portrait analysis. We have derived new analytical forms for solitary and periodic waves depending on parameters \(q, p, \sigma, \) and v. Considering an external periodic perturbation, chaotic structure of ion acoustic waves has been presented. Depending upon different regimes of the nonextensive parameter q, we have shown the effect of q on chaotic structures of ion acoustic waves with fixed values of other parameters \(p,\sigma \) and v. It has been observed that the unperturbed system has the solitary and periodic wave solutions, but the perturbed dynamical system has chaotic structures for same values of parameters \(q, p, \sigma,\) and v. Our present study could be helpful in understanding the solitary, periodic, and chaotic structures of ion acoustic nonlinear waves in space plasmas [19–25] as well as in laboratory plasmas [26, 27], where q-nonextensive electrons and positrons are present.