Introduction

The study of networks is of great importance for such areas as freight and passenger transportation, telecommunication, postal services and rapid transit systems.

The objects enumerated above can be presented as a set of nodes connected by edges. Meanwhile, a large amount of nodes are not connected with each other due to the physical limitations. That means that the several nodes have to be served using intermediate nodes with additional properties like consolidation and distribution possibility. The organization of special nodes as hubs produces savings by consolidation and reduces the total operational cost to service processes. Hub location problem (HLP) is directed to determine hubs and network operation processes in a most efficient way.

The epoch of huge amount of works carrying out in HLP area has been started from the seminal work of O’kelly (1986). The initial stages of HLP theory are associated with problems formulation (p-hub median problems, capacitated/uncapacitated HLPs, single or multiple hubs location, allocation possibilities, etc.), general assumptions, introduction of rules (flows are allowed to go through hub facilities, hubs are facilities to be located, all commodities must be routed, discount factor, hubs network is a complete graph, etc.) which allow to classify networks design decisions. The deep review of HLP progress is discussed by Campbell and O’Kelly (2012) and Contreras (2015). The latest works present modifications of the initial assumptions and characterize the new features intercalation adapted to real-world needs and problems complexity reduction. These approaches are based on achievements in discrete and computational mathematics.

The modern planning systems deal with the approximated data which tend to realize the expectations of the expert and bring it as close as possible to reality. Because of the ambiguity of the future, large amount of unpredictable participants and factors in the hub networks (users, traffic jams, breakdowns, service time, seasons, competitors, prices, etc.), the uncertainties in the data are caused. The network design is the part of the strategic planning where the decisions are made on prospect of development and striving for improvements. The most profitable solutions are also sufficiently risky what makes to take into account several scenarios in decision process.

From the other side, the network design at most is modeled using precise optimization approaches (mixed integer programming MIP, quadratic programming, nonlinear programming) sensible to the input data: the minor changes in the data cause the significant differences in final solutions. Consideration of several alternatives becomes a necessity for solution stability in different implementations.

To overcome this issue, different robust HLP formulations of various uncertainty sources are discussed in the last ten years research in facility location area. Following Alumur et al. (2012), the data ambiguity in the decision-making process may be divided into two directions: the first one, which this work adhere to, when the uncertainties in the data are weighted via the known probability distribution and the second one, where the uncertainties without probabilistic laws or uniformly distributed possible situations are considered. Besides, the M/D/c queuing system is used in Marianov and Serra (2003) and Kahag et al. (2019) to obtain the number of the customers in the network with the estimated probabilities for hub capacities evaluation. The stochastic programming formulations (Contreras et al. 2011; Sim et al. 2009; Yang 2009) use the scenarios with probabilistic assessment for expected total costs minimization. In Yahyaei and Bashiri (2017), the authors propose the stochastic formulation with hub disruption risks where the sample average approximation algorithm is applied to reduce the complexity of the problem. The reliability of the solution based on the worst-case scenario belongs to the second one. The minmax regret formulation of hub setup costs uncertainty paired with the stochastic model of demand uncertainties (Alumur et al. 2012; Boukani et al. 2016) aligns with the second uncertainty type too. The popular way to take demand uncertainty into consideration is to use the hose model where the demand has polyhedral uncertainty. The possible demand maximization under hose approach and total transportation costs minimization problem are offered in Meraklı and Yaman (2016) to generate robust hub network. Uncertainties budget model is described in Zetina et al. (2017) where the limits for demand interval uncertainties (known as lower and upper bounds) are set. The budget constraint in robust HLP formulation is discussed in de Sá et al. (2018) where the total cost for infrastructure development and activities scheduling is limited.

In this work, the demand uncertainty in uncapacitated multiple allocation hub location problem is considered and analyzed. The feature of present article consists of uncertainty representation in the mathematical formulation where the network design robustness is positioned as follows: the total transportation costs for each demand scenario should strive to be equal and lowest as far as a hub installation costs allow cost minimization. The trade-off between transportation costs minimization and equalization in the context of scenarios is the core point of the study. The hub network for different demand scenarios quantifies the lowest reliable upper bound of transportation costs and provides an opportunity to reduce them by node-hub re-allocation on separate scenario and estimated hub network. The node-hub re-binding is postponed to the later planning levels when the demand scenario becomes clear. The hub location in proposed robust HLP formulation reduces the transportation costs fluctuations among the demand scenarios and provides the reliable solution.

To the best of authors' knowledge, the transportation costs equalization approach under the scenarios in hub location problem was not considered before. The new robust uncapacitated multiple allocation hub location problem under demand uncertainties is formulated. Initially, the proposed problem is formulated as a nonlinear problem because of absolute deviation of transportation costs inclusion. To avoid nonlinearity. the equivalent linear problem is provided. The scenario set introduction into the model entails an increase in the problem complexity. Therefore, Bender’s decomposition and improved Bender’s cuts (Pareto-optimal cuts) are selected to simplify and reduce the complexity of the problem.

The work is organized as follows: basic and stochastic formulations of UMAHLP are described in the “Basic definitions and notation” section, robust approach for solving of hub location problem is proposed in the “Robust hub location problem concept” section, Benders decomposition and Pareto-optimal cuts are presented in the “Benders decomposition” section. Computational experiments and results’ analysis are discussed in the “Computational experiments” section.

Basic definitions and notation

In this section, notations and the mathematical problems’ formulation as a reference point of the analysis are presented. Moreover, it should be stressed that special type of the HLP described here could be replaced by another one, because general approach discussed later does not depend on the formulation type. The uncapacitated multiple allocation hub location problem (UMAHLP) is considered as a base model (see Hamacher et al. 2004), where non-hub node could be allocated with more than one hub. The model is constructed under following assumptions: (1) The hub network represents complete graph where links between non-hub nodes are forbidden; (2) the capacities of hub facilities are unlimited; (3) shipment costs represent costs for collection, transfer and distribution; (4) transshipment is allowed only on hubs (i.e., only three actions are permitted: flow from spoke nodes to hub, flow between hubs, flow from hub to spoke.)

Hereinafter, the notation is used: \(N=\{1, \ldots , n\}\) is the set of nodes which could send or receive a traffic; \(K \subset N\) is the set of hub candidates; \(d_{ij}\) is the distance between i and j where \(i, j \in N\) and \(a_k\) is fixed hub setup cost for hub node candidate \(k \in K\); \(\alpha \), \(\chi \) and \(\delta \) are transfer, collection and distribution costs per unit flow and per unit distance, respectively; \(w_{ij}\) is a flow originated from node \(i \in N\) that is destined to node \(j \in N\).

As it was mentioned previously, the traffic is routed at least through the one hub and in most cases, two hubs are enough in UMAHLP for consideration (Campbell and O’Kelly 2012; Contreras 2015). Therefore, the transportation costs routed via one or two hubs are denoted as follows: \(c_{ijkm}=\chi c_{ik}+\alpha c_{km} + \delta c_{mj}\), that is transportation cost per unit flow from \(i \in N\) to \(j \in N\) routed via hubs \(k \in K\) and \(m \in K\), where \(k = m\) is the flow routed via one hub.

UMAHLP

The mathematical formulation of the nominal UMAHLP uses the following decision variables:

\(y_k\)

Binary variable indicates that node \(k \in K\) is chosen to be a hub

\(x_{ijkm}\)

Continuous variable which corresponds to the flow from node \(i \in N\) to \(j \in N\) routed through hubs \(k, m \in K\)

Using the aforementioned notation, the UMAHLP can be stated as follows:

$$\begin{aligned}& {{\mathbf {min}}} \quad \sum _{k \in K} a_k y_k + \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x_{ijkm} \end{aligned}$$
(1)
$$\begin{aligned}&{{\mathrm{S.t.}}} \quad \sum _{m \in K, m\ne k} x_{ijmk} + \sum _{m \in K} x_{ijkm}\nonumber \\&\quad \le w_{ij} y_k \quad {i, j \in N, k \in K} \end{aligned}$$
(2)
$$\begin{aligned}&\sum _{k \in K} \sum _{m \in K} x_{ijkm} = w_{ij} \quad i,j \in N \end{aligned}$$
(3)
$$\begin{aligned}&x_{ijkm} \ge 0 \quad i,j \in N, k,m \in K \end{aligned}$$
(4)
$$\begin{aligned}&y_k \in \{0, 1\} \quad k \in K \end{aligned}$$
(5)

The objective function (1) represents the total costs to be minimized. Constraints (2) state that flow is routed via operating hubs. Constraints (3) ensure flow \(i-j\) routing exactly via hubs. Finally, (4) and (5) are domain constraints.

The UMAHLP consists of locating a set of hubs, assigning and routing the commodities flows through hubs without hub capacity constraints with objective function to minimize hub setup and transportation costs; therefore, the problem always will have a solution if K is not an empty set. Nonetheless, this formulation is not suitable for the real life, since the solution is very sensitive for the input data scenario and could be notably changed due to flow variation. For the strategic planning, the variation should be taken in account by using stochastic formulation.

Stochastic formulation of UMAHLP

The UMAHLP model (1)–(5) is extended on stochastic case where uncertainty of demand is introduced. The discrete set of scenarios \(S=\{1, \dots , f\}\) accounts the possible traffic changes with certain probability \(p_s\) for \(s \in S\). The demand associated with each scenario is \(w^s_{ij}\), i.e., flow originated from node \(i \in N\) which is destined to node \(j \in N\) in scenario \(s \in S\).

Uncertainty representation via a set of scenarios with occurrence probabilities is called to emphasize the most realistic situations which have great impact on the decision-making process. The normalized weights of scenario influence power characterize their occurrence probabilities; thus, it is assumed that \(\sum _{s \in S} p_s = 1\).

So that, an additional index should be added to the flow variables:

\(x^s_{ijkm}\)

Flow from node \(i \in N\) to \(j \in N\) which is routed through hubs \(k, m \in K\) in scenario \(s\in S\)

The stochastic formulation of the model is following:

$$\begin{aligned} {{\mathbf{min}}} \quad \sum _{k \in K} a_k y_k + \sum _{s \in S} p_s \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^s_{ijkm} \end{aligned}$$
(6)

      S.t.    (5)

$$\begin{aligned}&\sum _{m \in K, m\ne k} x^s_{ijmk} + \sum _{m \in K} x^s_{ijkm} \nonumber \\&\quad \le w^s_{ij} y_k \quad {i, j \in N, k \in K, s \in S} \end{aligned}$$
(7)
$$\begin{aligned}&\sum _{k \in K} \sum _{m \in K} x^s_{ijkm} = w^s_{ij} \quad i,j \in N, s \in S \end{aligned}$$
(8)
$$\begin{aligned}&x^s_{ijkm} \ge 0 \quad i,j \in N, k,m \in K, s \in S \end{aligned}$$
(9)

The objective function (6) represents the hub installation costs and expected transportation costs to be minimized under set of scenarios S. The constraints (7)–(9) correspond to deterministic case constraints (2)–(4) for each scenario \(s \in S\). The solution of the stochastic problem will be used as a referent plan further.

Robust hub location problem concept

In this section, the methodological concept of a robust hub network design is described. The expected transportation costs do not make the influence on the hub robustness evaluation, since it is the “optimal mean” between scenarios. The main feature of new approach is an inclusion of the absolute deviation between expected solution and every scenario into the objective function of stochastic HLP. This addend serves as a measure of transportation cost equalization on scenario set.

The new robust HLP concept is based on the UMAHLP case with stochastic demand as uncertainty source. The introduced problem formulation averages the weighted absolute differences among considered scenarios and thereby assures the resistance to expected changes in the demand. Thus, hubs location result is substantial for strategic planning.

Robust UMAHLP formulation

Thereby, the stochastic formulation of the problem to find a robust solution is given as:

$$\begin{aligned}&{{\mathbf{min}}} \quad \sum _{k \in K} a_k y_k\nonumber \\&\quad + \sum _{s \in S} p_s \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^s_{ijkm} \nonumber \\&\quad + \lambda \sum _{s \in S} p_s |\sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^s_{ijkm} \nonumber \\&\quad - \sum _{s' \in S} p_{s'} \left( \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^{s'}_{ijkm}\right) | \end{aligned}$$
(10)

S.t. (5), (7)–(9)

We propose the stochastic programming model where the robust hub location remains “close” to optimal for each scenario \(s \in S\). The problem is abbreviated as StHLPAD that means stochastic hub location problem with absolute deviation.

The first term in (10) represents the hub setup costs, the second addend in the goal function is the expected transportation costs, and the third addend is the weighted mean absolute deviation of the transportation costs. The parameter \(\lambda \) can be regarded as risk trade-off factor between expected costs and deviation.

Nonlinearity elimination

The objective function (10) contains absolute value function which adds some complexity into the model. The literature proposes the efficient linearization approach in application of robust optimization with mean absolute deviation. We use the Yu and Li (2000) results for (10) reformulation.

Theorem 1

(Yu and Li 2000) A problem Minimize\(Z= |f(X) - g|\), subject to\(X \in F\) (Fis a feasible set), can be linearized by using the following formulation:

$$\begin{aligned}& {{\mathrm {min}}} \quad f(X) - g + 2\delta \end{aligned}$$
(11)
$$\begin{aligned}&\textit{S.t.} \quad g - f(X) - \delta \le 0 \end{aligned}$$
(12)
$$\begin{aligned}&\delta \ge 0 \end{aligned}$$
(13)
$$\begin{aligned}&X \in F \end{aligned}$$
(14)

The multiple application of Yu and Li (2000) theorem to the third term of (10) converts the robust hub location problem with absolute deviation into the mixed integer programming task:

$$\begin{aligned}& {{\mathbf {min}}} \quad \sum _{k \in K} a_k y_k + \sum _{s \in S} p_s \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^s_{ijkm} \nonumber \\&\quad + \lambda \sum _{s \in S} p_s \left( \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^s_{ijkm} \right. \nonumber \\&\quad \left. - \sum _{s' \in S} p_{s'} \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^{s'}_{ijkm} + 2z^s\right) \end{aligned}$$
(15)

S.t. (5), (7)–(9)

$$\begin{aligned}&\sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^s_{ijkm} \nonumber \\&\quad - \sum _{s' \in S} p_{s'} \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^{s'}_{ijkm} \nonumber \\&\quad + z^s \ge 0 \quad \forall {s \in S} \end{aligned}$$
(16)
$$\begin{aligned}&z^s \ge 0, \forall s \in S \end{aligned}$$
(17)

The \(z^s\) is an absolute value linearization auxiliary nonnegative continuous variable for any scenario \(s \in S\). The (15) is a linear objective function with the constraints (16) and (17) which collectively are equivalent to (10). The constraints (16) and (17) correspond to (12) and (13).

The third term of (16) by the means of using the scenario occurrence integrality constraint \(\sum _{s \in S} p_s = 1\) is simplified:

$$\begin{aligned} {{\mathbf{min}}} \quad \sum _{k \in K} a_k y_k + \sum _{s \in S} p_s \left[ \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^s_{ijkm} + 2\lambda z^s\right] \end{aligned}$$
(18)

Benders decomposition

The Benders decomposition method is the procedure of partitioning linear and nonlinear integer programming problems with a stair-case matrix structure introduced by Bender (1962). The partitioning method relies on projections usage in combination with dual problem and relaxation stages. In this section, decomposition parts formulation for problem (5), (7)–(9), (16)–(18) are offered. The new smaller subproblems as original problem splitting result are described in “SP formulation” and “Master problem MP” sections, respectively, subproblem (SP) and master problem (MP).

SP formulation

By fixing the integer variables \(y_k=y^h_k\) at iteration h calculated in MP optimization stage, we obtain the primal linear SP:

$$\begin{aligned}& {{\mathbf{min}}} \quad \sum _{s \in S} p_s \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^s_{ijkm} \nonumber \\&\quad + 2\lambda \sum _{s \in S} p_sz^s \end{aligned}$$
(19)
$$\begin{aligned}& {{\mathrm{S.t.}}} \quad \sum _{s' \in S} p_{s'} \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^{s'}_{ijkm}\nonumber \\&\quad - \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{m \in K} c_{ijkm} x^s_{ijkm} - z^s \le 0 \quad {s \in S} \end{aligned}$$
(20)
$$\begin{aligned}&\sum _{m \in K, m\ne k} x^s_{ijmk} + \sum _{m \in K} x^s_{ijkm} \nonumber \\&\quad \le w^s_{ij} y^h_k \quad {i, j \in N, k \in K, s \in S} \end{aligned}$$
(21)
$$\begin{aligned}&\sum _{k \in K} \sum _{m \in K} x^s_{ijkm} = w^s_{ij} \quad i,j \in N, s \in S \end{aligned}$$
(22)
$$\begin{aligned}&x^s_{ijkm} \ge 0 \quad i,j \in N, k,m \in K, s \in S \end{aligned}$$
(23)
$$\begin{aligned}&y_k \in \{0, 1\} \quad k \in K \end{aligned}$$
(24)
$$\begin{aligned}&z^s \ge 0, \forall s \in S \end{aligned}$$
(25)

The dual problem is derived by associating the dual variables \(e^s, u^s_{ijk}, v^s_{ij}\) with the constraints (20)–(22), respectively. Thus, a dual SP is formulated as follows:

$$\begin{aligned}& {{\mathbf{max}}} \quad \sum _{i \in N} \sum _{j \in N} \sum _{s \in S} w^s_{ij} v^s_{ij} - \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{s \in S} u^s_{ijk} w^s_{ij} y^h_k \end{aligned}$$
(26)
$$\begin{aligned}& {{\mathrm{S.t.}}} \quad e_s\le 2\lambda p_s \quad s \in S \end{aligned}$$
(27)
$$\begin{aligned}&c_{ijkm}e_s - p_sc_{ijkm}\sum _{s \in S} e_s + v^s_{ij} - u^s_{ijk} - u^s_{ijm}\nonumber \\&\quad \le c_{ijkm}p_s \qquad {i, j \in N, k \ne m, k,m \in K, s \in S} i, j \in N, \end{aligned}$$
(28)
$$\begin{aligned}&\quad k \ne m, k,m \in K, s \in S\nonumber \\&c_{ijkk}e_s - p_sc_{ijkk}\sum _{s \in S} e_s + v^s_{ij} - u^s_{ijk}\nonumber \\&\quad \le c_{ijkk}p_s \quad {i, j \in N, k \in K, s \in S} \end{aligned}$$
(29)
$$\begin{aligned}&e_s \ge 0 \quad s \in S \end{aligned}$$
(30)
$$\begin{aligned}&v^s_{ij} \ge 0 \quad i,j \in N, s \in S \end{aligned}$$
(31)
$$\begin{aligned}&u^s_{ijk} \in R \quad i,j \in N, k \in K, s \in S \end{aligned}$$
(32)

The dual SP (26)–(32) is a linear problem. The objective function (26) participates in optimality Benders cuts construction with a combination of auxiliary continuous nonnegative variable \(\eta \) for estimation of the total expected flow transportation costs in sum with the expected deviation:

$$\begin{aligned} \eta + \sum _{s \in S} \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} u^{sh}_{ijk} w^s_{ij} y_k \ge \sum _{i \in N} \sum _{j \in N} \sum _{s \in S} w^s_{ij} v^{sh}_{ij}, \end{aligned}$$
(33)

where variables of the dual SP problem \(e^{sh}, u^{sh}_{ijk}, v^{sh}_{ij}\) are fixed by optimal values in the iteration h.

Master problem MP

The MP consists of binary variables \(y_k\) and \(\eta \), and most of original problem (5), (7)–(9), (16)–(18) constraints belong to the SP problem; therefore, we have the following MP:

$$\begin{aligned} {{\mathbf{min}}} \quad \sum _{k \in K} a_k y_k + \eta \end{aligned}$$
(34)

S.t. (33)

$$\begin{aligned}&\sum _{k \in K} y_k \ge 1 \end{aligned}$$
(35)
$$\begin{aligned}&y_k \in \{0, 1\} \quad k \in K \end{aligned}$$
(36)
$$\begin{aligned}&\eta \ge 0 \end{aligned}$$
(37)

where the (36) is added to assure the installation at least one hub; otherwise, the extreme ray generation is not excluded in Benders iterations. This constraint guarantees the feasibility of (26)–(32).

The basic benders algorithms

The basic Benders algorithm in UMAHLP application is discussed in de Camargo et al. (2008) and is illustrated in Algorithm 1, where \(\phi _{{{\mathrm{MP}}}}(y,\eta )\) and \(\phi _{{{\mathrm{SP}}}}(e,u,v)\) are the MP and dual SP objective functions optimal values.

figure a

Improved benders algorithm

The Benders decomposition algorithm’s efficiency depends on the number of iterations to reach the stop criterion, especially, it depends on the dual problem variables, i.e., the dual SP usually has several optimal solutions which derive the same optimal objective function. However, it has an effect on cuts quality and convergence.

A Pareto-optimality introduction into the Benders cuts generation helps to increase the quality of cuts, that is shown in De Camargo et al. (2011) and de Sá et al. (2013). We follow the Papadakos (2008) of Pareto-optimal cuts update scheme; therefore, the dual SP is modified:

$$\begin{aligned} {{\mathbf{max}}} \quad \sum _{i \in N} \sum _{j \in N} \sum _{s \in S} w^s_{ij} v^s_{ij} - \sum _{i \in N} \sum _{j \in N} \sum _{k \in K} \sum _{s \in S} u^s_{ijk} w^s_{ij} y^0_k \end{aligned}$$
(38)

S.t. (27)–(32)

where \(y^0_k\) is a start core point, a point which belongs to the relative interior of the convex hull of Y; however, as it is shown in Papadakos (2008) the Magnanti and Wong points (Magnanti and Wong 1981) can be used instead of the core points to derive Pareto-optimal cuts. Since there are not practical methods of the core points or Magnanti and Wong points evaluation according to Mercier et al. (2005), the results of De Camargo et al. (2011) and de Sá et al. (2013) are used for Magnanti and Wong points initialization (39) and points update algorithm (40):

$$\begin{aligned} y^0_k= & {} 1/2 \quad k \in K \end{aligned}$$
(39)
$$\begin{aligned} y^0_k= & {} (1- \gamma ) y^0_k + \gamma y^h_k \quad k \in K \end{aligned}$$
(40)

where \(0<\gamma <1\). The improved Benders decomposition algorithm is presented on Algorithm 2, where it is assumed to set \(\gamma = 1/2\) as the best empirically obtained value by Papadakos (2008) and Mercier et al. (2005).

figure b

Computational experiments

Here, the extensive computational experiments are described in order to demonstrate the absolute deviation effects on the resulting solutions under demand uncertainty. Besides, a comparison of the performance of Algorithms 1 and 2 is presented.

Calculations have been carried out using Civil Aeronautic Board (CAB) and Australian Post (AP) data sets from OR-Library (Beasley 1990). The data in CAB refers to 25 US cities, where distances between cities approximated by the Euclidean ones \(d_{ij}\) and the service demand between every pair of cities are provided. The demands are normalized for CAB and AP, i.e., total demand is equal to 1. Since the hub setup costs are omitted in CAB data set, the following procedure has been done to model missed data: (Alumur et al. 2012): \(a_k = 15 {{\mathrm{log}}} \sum _{j\in N} w_{kj},\)\(k \in K\). There are 25 and 40 nodes selected for analysis from CAB and AP data sets correspondingly, where all nodes are the candidates to be a hub.

Table 1 Calculations on Stochastic model from “Stochastic formulation of UMAHLP” section
Full size table

The stochastic formulation, in current work notions, assumes the set of scenarios for the demands uncertainty with certain probabilities. The scenarios generation algorithm is associated with procedures from Alumur et al. (2012), where the demands are realized from the interval \([0.01w_{ij}, 10w_{ij}]\) for CAB and AP. The interval is divided into two parts: \([0.01w_{ij}, 5w_{ij}]\) and \([5w_{ij}, 10w_{ij}]\), where the demand for i, j and each scenario s takes a random value with probability 2/3 from the first half and with probability 1/3 from the second one. This procedure is introduced to avoid the symmetry in scenarios.

Table 2 Robust results
Full size table

The instances designation is CAB and AP for appropriate data set where 5 and 3 scenarios are generated correspondingly. We consider two types of scenario occurrence probabilities: uniform distribution and decreasing probabilities, i.e., [1/3, 1/4, 1/6, 1/6, 1/12] and [1/2, 1/3, 1/6] probability sets for CAB and AP accordingly. The names of the instances are coded as CAB\(10\alpha \).d and AP\(10\alpha \).d, where \(10\alpha \) is \(\alpha \) discount factor multiplying by 10 and \(d \in \{U, C\}\), i.e., U uniform distribution, C decreasing probabilities. The \(\lambda \in \{0.5, 5\}\) are considered.

The solutions for every instance were obtained with GUROBI Optimizer 8.0.1 on the server with 4.2 GHz and 64 GB of RAM under Linux environment. The algorithms and LP/MIP models are implemented on PyCharm IDE by using Python 3.6.

In Tables 1 and 2, the “Time (s)” columns list the processor time of solving the problem, the “Installed hubs” list the numbers of hubs to be located, and the “Obj.” presents the value of the objective function. Table 2 also contains the results for each risk trade-off factor \(\lambda \).

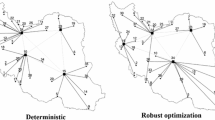
Table 1 presents the computational results obtained by the stochastic model described in “Stochastic formulation of UMAHLP” section. Table 2 is derived from the experiments with the problem in “Robust hub location problem concept” section. The “Obj. Stoch.” in Table 2 lists the values of the objective function without absolute deviation term with the purpose of the absolute deviation influence detection. The objective function values “Obj.” in Table 1 and “Obj. Stoch.” values for \(\lambda = 0.5\) in Table 2 are equal as well as the installed hubs for the corresponding instances; it is due to small weight of absolute deviation term in the objective function, where for CAB instances it constitutes 0.7% in average and for AP instances 0.3% from objective value. In case, when \(\lambda = 5\) the hub locations for \(\alpha \in \{0.6, 0.8\}\) in Table 2 differ from the described one in Table 1, the objectives in Table 1 and “Obj. Stoch.” differ from each other for all instances. The expected costs increase for 2% in the CAB instances and for 0.6% in the AP instances where the expected costs are the hub installation costs and the expected transportation costs.

The absolute deviation value is calculated by a formula “Obj.” minus “Obj. Stoch.” by using the columns in Table 2. This difference for \(\lambda =0.5\) is not equal to 0 for all considered instances; however, the 75% of the instances have the absolute deviation value equal to zero for \(\lambda =5\). Evidently, the solutions correspond to the concept of robustness that was described in the “Robust hub location problem concept” section because the zero absolute deviation means the same objective value for each scenario separately. The 25% of the instances with nonzero absolute deviation are the decreasingly distributed scenario cases (marked by “C”), and the scenarios with higher probability have the stronger influence on the solution than the lower one.

The trade-off factor \(\lambda \) is a control parameter of expected absolute deviation term influence, which in zero case reduces the proposed in the “Robust hub location problem concept” section problem to basic stochastic formulation. The large \(\lambda \) values in comparison with transportation and hub setup costs increase absolute deviation term impact on the objective function, as a consequence, the optimization of setup and transportation costs will be relegated to the background.

The second part of the experiments focuses on the algorithms in the “Benders decomposition” section performance. In Table 3, the computational results of Standard Benders cuts and Pareto-optimal cuts on the instances introduced above are obtained. The classical Benders decomposition shows the best results for all instances except CAB2.C in comparison with the improved Benders cuts (Pareto-optimal cuts) by processor time measure. From the other side, the Pareto-optimal cuts are designed to reduce the number of cuts: about 4 times less cuts in CAB and about 1.5 times less in the AP instances. It demonstrates us the cuts complexity grows if the cuts quality increases. Additionally, the “Time (s)” of Standard Benders cuts algorithm in Table 3 and GUROBI Optimizer with basic parameters in Table 2 vary by instances: GUROBI Optimizer about 4 times faster on CAB and 6.3 times more slowly in average on AP in comparison with classical Benders cuts. This effect manifests itself because CAB data set generates HLP which is easier to solve as compared with AP data set.

Table 3 Computational effort
Full size table

Conclusion

This work proposes a new decision robustness concept in hub location problem. The method is applied to stochastic formulation of UMAHLP under uncertainty in demand in scenario form. The absolute deviation of the expected transportation costs is added into the objective function of the problem to realize the basic idea: the solution is robust with respect to optimality if it is “close” to optimal for any scenario in the scenario set. It is shown that trade-off parameter λ has a significant influence on the result. For example, for the large λ = 5, several nodes are served by other hub in contrary to the simple stochastic case. That fact means that the decision maker has to think about addition investments for ensuring the robustness.

Moreover, the formulated problem is linearized and decomposed via Benders cuts. Two strategies of cuts generation for the linear formulation of the problem are performed: classical Benders cuts and Pareto-optimal cuts.

The extensive computational analysis of absolute deviation impact on the decision-making process and the decomposition algorithms performance in application to the CAB and AP data are obtained and discussed.