Bi-objective optimization of multi-server intermodal hub-location-allocation problem in congested systems: modeling and solution

Abstract

A new multi-objective intermodal hub-location-allocation problem is modeled in this paper in which both the origin and the destination hub facilities are modeled as an M/M/m queuing system. The problem is being formulated as a constrained bi-objective optimization model to minimize the total costs as well as minimizing the total system time. A small-size problem is solved on the GAMS software to validate the accuracy of the proposed model. As the problem becomes strictly NP-hard, an MOIWO algorithm with an efficient chromosome structure and a fuzzy dominance method is proposed to solve large-scale problems. Since there is no benchmark available in the literature, an NSGA-II and an NRGA are developed to validate the results obtained. The parameters of all algorithms are tuned using the Taguchi method and their performances are statistically compared in terms of some multi-objective metrics. Finally, the entropy-TOPSIS method is applied to show that MOIWO is the best in terms of simultaneous use of all the metrics.

Introduction and literature review

Aiming to minimize the total network cost (transportation and fixed cost) while the customer demand is met, the hub-location-allocation problem (HLAP) is generally stated to determine the locations of hub nodes from a set of potential hub nodes in a network and to allocate demand nodes to the selected hub nodes. HLAPs are classified into four major groups of problems including (1) capacitated and incapacitated HLAP, (2) P-hub-covering location problems, (3) P-hub center problems, and (4) P-hub median problems (Campbell 1994). In an incapacitated HLAP, the capacities of the hub nodes are not limited, while in a capacitated HLAP, it is limited and all the non-hub nodes may not be dedicated to their nearest hub nodes. In the P-hub-covering location problems, the number of hub nodes is limited. This constraint limits the areas covered by each hub node. The P-hub center problems are defined to find the best positions of the hubs in a network and to allocate non-hub nodes to them so that the maximum travel time (or distance) between any origin–destination pair is minimized. Finally, analogous to the P-median problem, the P-hub median problem is a hub location problem in which the number of hubs (P) is predetermined. The aim is to locate the hubs, to allocate the non-hubs to the hubs, and to determine the path for each origin–destination pair such that the total transportation cost for satisfying the demand of the customers, each supplied from its closest facility, is minimized.

Hub-location-allocation models were firstly developed by O’Kelly (1986, 1987), where a quadratic integer model for the hub location problem was presented and shown to belong to the class of NP-Hard problems. Campbell (1994) used some flow variables to present a new linear formulation for multiple-allocation P-hub problems. Lin et al. (2012) developed a mathematical formulation for the capacitated P-hub median problem. The objective of their model was to minimize the total costs consisting of the fixed costs of creating the hub facilities along with the transportation costs. They added some singular path constraints to the model in order to prevent storing commodities on hub facilities. García et al. (2012) presented a mixed-integer linear program for the incapacitated multiple-allocation P-hub median problem. Their model aimed to determine the optimal location of the hub facilities among some candidate sites so that the total transportation cost is minimized.

Ghodratnama et al. (2013) proposed a fuzzy possibilistic bi-objective nonlinear mixed-integer programming formulation for the hub-covering problem. They considered the major parameters of their mathematical formulation to be fuzzy in order to model the uncertainties involved. The first objective function of their formulation intended to minimize six major cost components comprising opening cost, reopening cost, transportation cost, covering cost, activating cost, and cost of purchasing transportation vehicles. The second objective function of their proposed model designed to minimize the transportation of the commodities from their origin nodes to their destination nodes using the hub facilities. They used a linearization method to convert the problem into a linear optimization problem, based on which they utilized four fuzzy approaches to solve the problem. Peiró et al. (2014) introduced a novel mixed-integer programming model for the P-hub median problem and extended it to an R-allocation P-hub median problem. Based on this extension, they assumed that every spoke node could be allocated to R of P chosen active hub nodes. Their model meant to minimize the total routing cost. They proposed a heuristic algorithm to solve the proposed problem. Habibzadeh Boukani et al. (2016) developed two mathematical models, one for a capacitated single, and the other for a capacitated multiple-allocation P-hub median problems. They used a robust optimization approach to consider uncertainties involved in the parameters of the models including the capacity of the hub nodes and the fixed costs of establishing the hub facilities. They showed that the consequences of considering the uncertainties were to reduce the total cost as well as to reduce delays in delivering the commodities to the customers. Parvaresh et al. (2014) proposed a mixed-integer programming formulation for the multiple-assignment P-hub median problem. They developed a bi-objective bi-level model to consider the occurrence of intentional disruptions on the hub facilities. The upper-level model aimed to optimize two different objectives of minimizing the total transportation costs in normal and worst cases. Meanwhile, the lower level aimed to minimize the maximum damage to the network. A bi-objective nonlinear binary programming model was presented by Zade et al. (2014) for the maximal hub-covering problem. The first objective function of their formulation intended to maximize the total utility of the hub network and the second objective was to maximize the safety of the network’s weakest path. They also considered uncertainties involved in transporting the commodities from their origins to their destinations via the hub nodes. Ghaffari-Nasab et al. (2015) developed two mixed- integer linear programming models for a single and a multiple-allocation capacitated hub location problem with stochastic demands. Their models aimed to minimize the total cost (fixed, transportation, and capacity acquisition costs). They employed a robust optimization approach to account for the uncertainties in the parameters and used a standard optimization package to solve the problems.

Various exact and heuristic methods were developed in the literature to solve hub location problems. O’kelly (1986, 1987) proposed an enumeration-based heuristic to solve the problem. Skorin-Kapov et al. (1996) proposed an exact method to solve P-hub median problem by using a tight linear relaxation method presented by Campbell (1992). A hybrid branch-and-bound and simulated annealing (SA)-based greedy interchange heuristic was proposed by Aykin (1995) to solve an HLP. Campbell (1996) introduced another heuristic based on the greedy interchange algorithm to solve a P-hub median problem. Puerto et al. (2011) presented a new branch-and-bound and cut method for the single-assignment P-hub median problem. They concluded that their proposed algorithm could find efficient solutions for small- and medium-sized problems. García et al. (2012) used a branch-and-cut algorithm to solve an incapacitated multiple-allocation P-hub median problem modeled by a mixed-integer linear programming formulation and showed that it performs well especially when it solves large-scale instances. Peiró et al. (2014) proposed a heuristic algorithm to solve a P-hub median problem modeled by a mixed-integer programming model.

Since the time O’Kelly (1987) proved that the hub-location-allocation problem is NP-hard, many meta-heuristic algorithms have been developed to find efficient feasible solutions. The genetic algorithms (GA) of Topcuoglu et al. (2005), Kratica et al. (2007), Cunha and Silva (2007), Takano and Arai (2009) and Lin et al. (2012); the Tabu search (TS) algorithms of Calık et al. (2009), Ishfaq and Sox (2010), Shahvari et al. (2012) and Shahvari and Logendran (2016); the evolutionary algorithm (EA) of Kratica et al. (2011); the ant colony optimization (ACO) algorithm of Ting and Chen (2013); the particle swarm optimization (PSO) algorithm of Yang et al. (2013); and the variable neighborhood search (VNS) algorithm of Ilić et al. (2010) are some examples among others to solve hub location problems. In multi-objective optimization of the hub-location-allocation problems, Parvaresh et al. (2014) utilized two multi-objective meta-heuristic algorithms called multi-objective simulated annealing (MOSA) and multi-objective Tabu search (MOTS) algorithms. Zade et al. (2014) used a non-dominated sorting genetic algorithm (NSGA-II) to solve a maximal hub-covering problem.

To the best of the authors’ knowledge, only a few researchers proposed hub location models that consider congestion. Marianov and Serra (2003) proposed a hub location model for an airline industry under congestion. They used an M/D/c queuing system to impose a probabilistic capacity constraint to the hub location problem first. Then, they turned the probabilistic capacity constraint into a linear form. Elhedhli and Hu (2005) presented a congestion-based hub-location-allocation model. Their model aimed to minimize the total cost of the hub network including congestion cost in the hub nodes along with the transportation cost. As their proposed cost function was nonlinear, they linearized the objective function and solved the linearized model using a Lagrange heuristic method. de Camargo et al. (2009) presented a model for a multiple-allocation hub location problem under congestion. Their objective function aimed to minimize the total cost (fixed, transportation, and congestion costs). The benders decomposition algorithm was utilized in their work to solve the problem. de Camargo et al. (2011) developed a model for a single-allocation hub-location-allocation problem with congestion. Their model aimed to minimize the total costs (congestion and transportation costs). They solved the problem utilizing a hybrid outer approximation method and Benders decomposition algorithm. Mohammadi et al. (2011) introduced an M/M/c queuing model for a hub-covering location problem under capacity constraint. They linearized the probabilistic capacity constraint using M/M/c queuing formulation. de Camargo and Miranda (2012) developed a single-allocation hub location model with congestion. They proposed a nonlinear mixed-integer programming model and considered congestion in the form of a convex cost function. Their model aimed to minimize the total cost (transportation and fixed costs) along with minimizing the maximum congestion effect. A Benders decomposition algorithm was used in their work to solve the problem. Seifbarghi and Mansouri (2016) presented a model to determine the locations of immobile service facilities congested by stochastic demands originated by nearby customer locations. Recently, Maghsoudlou et al. (2016) utilized the concept of congested systems to design a three-echelon multi-server supply chain network. This concept will also be used in this paper to propose a multi-server intermodal hub-location-allocation model.

The above literature review reveals that there is no research work performed on a multi-objective intermodal hub-location-allocation problem under a capacity constraint that causes congestion. Consequently, in order to fill the gap, a new stochastic multi-objective P-hub median multiple-location problem is formulated in this paper. In other words, the traditional intermodal hub location model is extended in this paper by considering M/M/c queuing systems in the hub nodes. The proposed multi-objective formulation includes two objectives. The first objective intends to minimize the total idle time of the servers located in the hub nodes along with the total waiting time of the customers arriving at the hub nodes. The second objective function involves minimizing the total network costs including transportation, fixed cost of locating the hub nodes, and the fixed cost of locating the servers in the hub nodes.

The rest of the paper is organized as follows. The problem is stated in “The problem and its formulation” section, where a bi-objective optimization model is proposed. A small-size problem is solved in “Model validation” section to validate the mathematical formulation and to show the NP-Hardness of the problem. “Solving methodologies” section is devoted to the meta-heuristic solution approaches. “Applications” section presents the validation and the application of the proposed methodology. Computational results and performance comparison of the solution methods are presented in “Computational results” section. Finally, conclusions are brought in “Conclusion and future research” section, where some topics are suggested for future research.

The problem and its formulation

This section is devoted to describing the problem along with its assumptions and mathematical formulation. To this aim, the problem and the assumptions are first stated in “Problem definition and assumptions” section. Then, the notation including the indices, the parameters, and the decision variables are given in “Notation” section. At the end, the model is derived in “The mathematical formulation” section.

Problem definition and assumptions

The problem being investigated in this paper is an intermodal congested multi-echelon hub-location-allocation problem. In this structure, servers are fixed at their locations in their origin and destination hubs, where commodities are dedicated to open origin–destination hub pairs to be shipped to their destinations. The aims are to determine the number of required hub facilities for each origin and destination layers, to obtain the number of servers in the hub nodes, and to allocate flows to the open hub facilities. Moreover, to bring the problem more applicable to real-world networks, two objectives are considered based on some real constraints such as the capacities of the hub nodes located at both origin and destination layers. The first objective function minimizes the total costs including transportation and fixed costs and the second minimizes the total system time (including waiting, service, and idle times) in both origin and destination hubs. The total system time is obtained using some formulations in M/M/c queuing systems. Both the origin and the destination hub layers can be mapped in many real-world transportation networks such as airports, rail, and road networks. In these systems, commodities arrive at their origin hub nodes based on a Poisson process with a specific rate and the service time to deliver the commodities to their destination follows an exponential distribution with a given mean. Moreover, it is assumed that all the servers located in a given hub node are similar and share a unique service rate, while the service rates of the servers located in the other hub nodes are different. The transportation process is performed in the context of an intermodal network so that the commodities can be shipped using either a rail or a road network. Furthermore, every origin–destination node pair can be assigned to more than one hub pair.

Notation

The notations including the indices, the parameters, and the decision variables are as follows.

Indices and sets

• $i$: An index for an origin node.

• $j$: An index for a destination node.

• $k$: An index for an origin hub node.

• $m$: An index for a destination hub node.

• $N$: The set of all nodes indexed by either $i$ or $j\,{\text{or}}\,k\, {\text{or}}\, m$; $N = \left\{ {1,2, \ldots , 2\left| C \right|} \right\}$.

• $C$: Set of all cities indexed by $c^{\prime}$, $C = \left\{ {1,2, \ldots ,\left| C \right|} \right\}$.

• $S$: The set of index to calculate $\pi_{0k}$; $S = \left\{ {1,2, \ldots ,u_{k} } \right\}$ and $\pi_{0m}$; $S = \left\{ {1,2, \ldots ,u_{m} } \right\}$.

Parameters

• $\lambda k_{k}$: The arrival rate of the commodities to origin hub node $k$.

• $\lambda m_{m}$: The arrival rate of the commodities to destination hub node $m$.

• $\mu k_{k}$: The service rate of the servers located at the to origin hub node $k$.

• $\mu m_{m}$: The service rate of the servers located at the destination hub node $m$.

• $uk_{k}$: The maximum number of servers that can be used in each origin hub node $k$.

• $um_{m}$: The maximum number of servers that can be used in each destination hub node $m$.

• $P1$: The number of hub facilities located at the origin layer.

• $P2$: The number of hub facilities located at the destination layer.

• $Ak_{k}$: The productivity factor of origin hub node $k$, $Ak_{k} = \frac{{\lambda k_{k} }}{{\mu k_{k} }}$.

• $Am_{m}$: The productivity factor of destination hub node $m$, $Am_{m} = \frac{{\lambda m_{m} }}{{\mu m_{m} }}$.

• $\alpha$: The cost discount factor.

• $C$: The number of all cities.

• $\nu k_{k}$: A multiplier for calculating fixed establishment costs of both types of road/train origin hub node $k$.

• $\nu m_{m}$: A multiplier for calculating fixed establishment costs of both types of road/train destination hub node $m$.

• $Fk_{k}$: The fixed cost of establishing a facility at a potential origin hub node $k$.

• $Fm_{m}$: The fixed cost of establishing a facility at a potential destination hub node $m$.

• $ck_{k}$: The unit staffing cost at the origin hub node $k$.

• $cm_{m}$: The unit staffing cost at the destination hub node $m$.

• $C1_{ik}$: The unit transportation cost from the origin node $i$ to the origin hub node $k$.

• $C2_{km}$: The unit transportation cost from the origin hub node $k$ to the destination hub node $m$.

• $C3_{mj}$: The unit transportation cost from the destination hub node $m$ to the destination node $j$

• $$f_{ij} = \left\{ {\begin{array}{*{20}l} {{\text{Flows}}\, {\text{from}}\, {\text{the}}\, {\text{origin}}\, {\text{node}}\, i\, {\text{to}}\, {\text{the}}\, {\text{destination}} \,{\text{node}} \,j;} \hfill & { \left\{ {i\, \ne \,j\;\; {\text{and}}\;\; i,j \, \le \,C} \right\}} \hfill \\ {0;} \hfill & { \left\{ {i\, = \,j\;\; {\text{or}}\;\; i > C,\;\; {\text{or}}\;\; j\, > \,C} \right\}} \hfill \\ \end{array} } \right.$$

Decision variables

$$yk_{k} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,{\text{node}}\,k\,{\text{is}}\,{\text{an}}\,{\text{origin}}\,{\text{hub}}\,{\text{node}}} \hfill \\ 0 \hfill & {\text{otherwise }} \hfill \\ \end{array} } \right.$$

$$ym _{m} = \left\{ {\begin{array}{*{20}l} 1 \hfill & { {\text{if}}\,{\text{node}}\,m\,{\text{is}}\,{\text{a}}\,{\text{destination}}\,{\text{hub }}\,{\text{node}}} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$

$$\it \it \it x_{ijkm} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,{\text{the}}\,{\text{shipments}}\,{\text{for}}\,{\text{the}}\,{\text{origin}}\,{\text{destination}}\,{\text{pair}}\,\left( {i,j} \right)\,{\text{are}}\,{\text{assigned}}\,{\text{to}}\,{\text{the}}\,{\text{hubs}}}\, k\,\text{and}\,m \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$

• $lk _{k}$: An integer variable indicating the number of required servers in the origin hub node $k$.

• $lm _{m}$: An integer variable indicating the number of required servers in the destination hub node $m$.

• $\pi k _{0,k}$: The idle probability of the open origin hub facility $k$.

• $\pi m _{0,m}$: The idle probability of the open destination hub facility $m$.

• $Wk _{k}$: The expected waiting time of the commodities at the open origin hub facility $k$.

• $Wm _{m}$: The expected waiting time of the commodities at the open destination hub facility $m$.

The mathematical formulation

A node identification method is applied in the proposed model to distinguish between rail and road nodes. In this method, while the road nodes are numbered from 1 to $C$, and the rail nodes are numbered from $C$ + 1 to $2C$, where $C$ is the number of all cities in the network under investigation. As the fixed cost of opening a rail hub node is more than that of a road hub node, a multiplier $\nu k_{k} ,vm_{m}$ is used to calculate the fixed establishment costs of both types of hub nodes. This multiplier takes the value of 1 for the road nodes and 1.5 for the intermodal nodes (Ishfaq and Sox 2010). Note that a single objective of minimizing the waiting times in both origin and destination hub layers will probably leads into an increased number of servers used in each hub node with higher fixed cost and higher idle time. Therefore, minimizing the cost is considered as another objective function. These objective functions are clearly in conflict with each other.

The mathematical formulation of the intermodal hub-location-allocation problem is as follows.

$$\text{Min}\, \, f_{1} = \sum\limits_{k}^{N} {\left[ {\lambda k_{k} \times \, Wk_{k} + \text{(}1 - Ak_{k} \text{)} \times \frac{{lk_{k} }}{{\mu k_{k} }}} \right]} + \sum\limits_{m}^{N} {\left[ {\lambda m_{m} \times \, Wm_{m} + \text{(}1 - Am_{m} \text{)} \times \frac{{lm_{m} }}{{\mu m_{m} }}} \right] \, }$$

(1)

$$\text{Min}\, \, f_{2} = \sum\limits_{i}^{N} {\sum\limits_{j}^{N} {\sum\limits_{k}^{N} {\sum\limits_{m}^{N} { \, f_{ij} \times x_{ijkm} \times \left( {C1_{ik} + \alpha \times C2_{km} + C3_{mj} } \right) + \sum\limits_{k}^{N} {\nu k_{k} } \times Fk_{k} \times yk_{k} + lk_{k} \times ck_{k} + \sum\limits_{m}^{N} {\nu m_{m} } \times Fm_{m} \times ym_{m} + lm_{m} \times cm_{m} } } } }$$

(2)

Subject to:

$$\pi k_{0k} = \frac{{yk_{k} }}{{\left( {\sum\nolimits_{s = 0}^{{lk_{k} - 1}} {\frac{{Ak_{k}^{s} }}{{s\text{!}}} + \left( {\frac{{Ak_{k}^{{lk_{k} }} }}{{lk_{k} \text{!}}} \times \frac{{lk_{k} }}{{\text{(}lk_{k} - Ak_{k} \text{)}}}} \right)} } \right)}};\quad \forall \;\; k \in N$$

(3)

$$\pi m_{0m} = \frac{{ym_{m} }}{{\left( {\sum\limits_{s = 0}^{{lm_{m} - 1}} {\frac{{Am_{m}^{s} }}{{s\text{!}}} + \left( {\frac{{Am_{m}^{{lm_{m} }} }}{{lm_{m} \text{!}}} \times \frac{{lm_{m} }}{{\text{(}lm_{m} - Am_{m} \text{)}}}} \right)} } \right)}}\text{;}\quad \forall \,\, m \in N$$

(4)

$$Wk_{k} = \frac{{Ak_{k}^{{lk_{k} }} \times \mu k_{k} \times lk_{k} \times \pi k_{0k} }}{{lk_{k} \text{;} \times \left( {\mu k_{k} \times lk_{k} - \lambda k_{k} } \right)^{2} }} + \frac{{yk_{k} }}{{\mu k_{k} }}\text{;}\quad \forall \;\; k \in N$$

(5)

$$Wm_{m} = \frac{{Am_{m}^{{lm_{m} }} \times \mu m_{m} \times lm_{m} \times \pi m_{0m} }}{{lm_{m} \text{!} \times \left( {\mu m_{m} \times lm_{m} - \lambda m_{m} } \right)^{2} }} + \frac{{ym_{m} }}{{\mu m_{m} }}\text{;}\quad \forall \;\; m \in N$$

(6)

$$\sum\limits_{k}^{N} {yk_{k} = P_{1} } \text{;}$$

(7)

$$\sum\limits_{m}^{N} {ym_{m} = P_{2} } \text{;}$$

(8)

$$\mathop{\mathop{\mathop{\mathop{\mathop{\mathop{\sum}\limits_{ k \ne i }}\limits_{ k \ne i - city }}\limits_{ k \ne i + city }}\limits_{ k \ne j }}\limits_{ k \ne j - city }}\limits_{ k \ne j + city }\limits^{N}\mathop{\mathop{\mathop{\mathop{\mathop{\mathop{\sum}\limits_{ m \ne i }}\limits_{ m \ne i - city }}\limits_{ m \ne i + city }}\limits_{ m \ne j }}\limits_{ m \ne j - city }}\limits_{ m \ne j + city{\text{ }}k \ne m }\limits^{N} {x_{{ijkm}} = 1};\quad \forall \;\; i \cdot j \in N\; {\text{and}}\,\, \left\{ {i \ne j \; \& \; i + \left| C \right| \ne j \; \& \; i - \left| C \right| \ne j} \right\}$$

(9)

$$\sum\limits_{m}^{N} { \, x_{ijkm} \le yk_{k} } \text{;}\quad \forall \,\, i \cdot j \cdot k \in N$$

(10)

$$\sum\limits_{k}^{N} { \, x_{ijkm} \le ym_{m} } \text{;}\quad \forall \,\, i \cdot j \cdot m \in N$$

(11)

$$yk_{k} + yk_{{k + \left| { \, C} \right|}} \le 1\text{;}\quad \forall \;\; k \in N\text{,}\;\;k \le \,\,|c|$$

(12)

$$ym_{m} + ym_{{m + \left| { \, C} \right|}} \le 1\text{;}\quad \forall \;\; m \in N\text{,}\;\;m \, \le \,|c|$$

(13)

$$yk_{i} + ym_{i} \le 1\text{;}\quad \forall \;\; i \in N$$

(14)

$$Ak_{k} \times \left( {\sum\limits_{i}^{N} {\sum\limits_{j}^{N} {\sum\limits_{m}^{N} { \, x_{ijkm} } } } } \right) \le lk_{k} \text{;}\quad \forall \;\; k \in N$$

(15)

$$Am_{m} \times \left( {\sum\limits_{i}^{N} {\sum\limits_{j}^{N} {\sum\limits_{k}^{N} { \, x_{ijkm} } } } } \right) \le lm_{m} \text{;}\quad \forall \;\; m \in N$$

(16)

$$lk_{k} \le \, uk_{k} \times yk_{k} \text{;}\quad \forall \;\; k \in N$$

(17)

$$lm_{m} \le \, um_{m} \times ym_{m} \text{;}\quad \forall \,\, m \in N$$

(18)

$$x_{ijkm} = 0;\quad \forall \,\, i \cdot j \cdot k \cdot m \in N\;\; {\text{and}}\,\, \left\{ {k = m } \right\}$$

(19)

$$x_{ijkm} = 0 ;\quad \forall \,\, i \cdot j \cdot k \cdot m \in N\,\, {\text{and}}\,\, \left\{ {i = j } \right\}$$

(20)

$$yk_{k} \in \left\{ {0.1} \right\};\quad \forall \,\, k \in N$$

(21)

$$ym_{m} \in \left\{ {0.1} \right\};\quad \forall \,\, m \in N$$

(22)

$$x_{ijkm} \in \left\{ {0.1} \right\} \text{;}\quad \forall \,\, i \cdot j \cdot k \cdot m \in N$$

(23)

$$lk_{k} \ge 0 \cdot {\text{integer }};\quad \forall \,\,k \in N$$

(24)

$$lm_{m} \ge 0 \cdot {\text{integer}};\quad \forall \,\, m \in N$$

(25)

$$\pi k _{0 k} \, \ge \,0 \cdot {\text{positive}};\quad \forall \,\, k \in N$$

(26)

$$\pi m _{0 m} \ge 0 \cdot {\text{positive}};\quad \forall \,\, m \in N$$

(27)

$$Wk _{k} \, \ge \,0 \cdot {\text{positive}};\quad \forall \,\, k \in N$$

(28)

$$Wm _{m} \, \ge \,0 \cdot {\text{positive}};\quad \forall \,\, m \in N$$

(29)

The first objective function in (1) minimizes the total waiting times of the commodities alongside the servers’ total idle times in both origin and destination layers. Some of the terms in this equation are obtained using the steady-state performance measures of M/M/c queuing systems discussed later in this paragraph. The second objective function in (2) minimizes the total transportation costs for all origin–destination flows along with the fixed costs of establishing hub nodes. The fixed cost of the hub nodes includes costs of establishing the hub nodes and the staffing costs. Constraints (3) and (4) calculate the idle probabilities of open origin and open destination hub facilities, respectively (Gross and Harris 1998). Constraints (5) and (6) calculate the waiting times of the commodities at the origin or destination hub facilities, respectively (Gross and Harris 1998). Constraints (7) and (8) ensure that exactly P₁ and P₂ hub facilities are used in origin and destination hub layers, respectively. Constraint (9) ensures that every origin–destination pair is assigned to the hub pairs. Constraints (10) and (11) guarantee that an origin–destination flow can be assigned to nodes k and m if the origin and destination hub facilities are located at nodes $k$ and $m$, respectively. Constraints (12) and (13) forces one node in each city $c^{\prime }$ to be selected as a hub origin or destination node. Constraint (14) forces each node to be selected as either one origin or one destination hub node. Constraints (15) and (16) imply that the servers’ service rates must be greater than the arrival rates of the commodities at all origin and destination hub facilities. Constraints (17) and (18) restrict the number of servers at every origin and destination hub node, respectively. Constraint (19) guarantees that hub pairs cannot be the same node. Constraint (20) guarantee that one node cannot be considered as both origin and destination node, indeed there is no loop. Constraints (21)–(29) define the types of the variables used in the proposed formulation.

Model validation

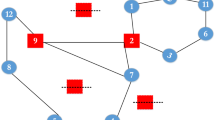
A small-size problem with eight cities and two road and train nodes is solved in this section to validate the accuracy of the mathematical formulation developed in “The problem and its formulation” section. This problem is solved using the GAMS software, where the optimal solution is shown in Table 1. In addition, the optimal locations of the hub nodes along with the spoke nodes connected to them are schematically shown in Fig. 1. It should be noted that the required computational time of solving this problem on a PC with core i5 CPU and 4 GB RAM was 19,052.31 s. This fact somehow shows that the intricacy degree of the problem at hand is too high so as its large instances cannot be solved using an exact solution algorithm in a reasonable computational time. As such, one needs to utilize a meta-heuristic to find near optimal solutions of the problems.

Table 1 Result of solving a small test problem on the GAMS software

Fig. 1

Schematic representation of the solution of a small-size problem on the GAMS software (solver 1 and 2)

Solving methodologies

As the multi-objective intermodal hub location-allocation problem modeled in “Model validation” section is strictly NP-hard, a population-based meta-heuristic optimization algorithm called multi-objective invasive weeds optimization (MOIWO) algorithm is utilized in this section to solve the problem. In addition, in order to evaluate the performance of the MOIWO, two other population-based multi-objective optimization algorithms including a non-dominated ranking genetic algorithm (NRGA) and a non-dominated sorting genetic algorithm (NSGA-II) are used.

The multi-objective invasive weeds optimization (MOIWO) algorithm

The MOIWO algorithm has been presented by Kundu et al. (2011). As an initial population in an IWO algorithm, a set of weeds are generated randomly. Each weed is a plant that grows globally in a specified region so that it cannot be controlled or removed by a human being. A popular claim about weed is that they always are a winner and the more farmers try, the more they grow on the land. The pruning system of the weeds is the base for the weed’s behavior to occupy soil and to generate new colony. Using this system, they initially find appropriate regions to attack, to invade and generate new colonies. Consequently, new plants are generated to use appropriate regions.

The invasive weeds optimization (IWO) algorithm simulates the colonizing behavior of the weeds. This behavior can be used as a method to search the solution space. In this method, the seeds that are scattered in a specified region will turn in weeds, where they grow better in a more fertile region and hence will have higher competency and will have more chance to survive. Thus, higher breeding is reached in the vicinity of these weeds. An important point is that as the number of iterations increases, the distance of the generated weeds from their parent weed will decrease remarkably. This process that is called competitive elimination will continue until better weeds are obtained.

The following steps are taken in the IWOA of this paper:

• Generate an initial random population and evaluate its fitness using the objective functions.

• Use a fuzzy sorting method (explained in the next section) to prioritize the population.

• Permit all members of the population to generate several seeds with better properties. The seeds will be produced based on Eq. (30).

  $${\text{seeds}}_{i} = {\text{floor}}\left( {S_{\hbox{min} } + \left( {S_{\hbox{max} } - S_{\hbox{min} } } \right) \times \left( {\frac{{np - {\text{rank}}_{i} }}{np}} \right)} \right),$$

  (30)

  where the grade of ith population member, the number of seeds generated by ith population member, the maximum number of seeds generated by a weed, the minimum number of seeds generated by every weed, and the population number are shown, respectively, by ${\text{rank}}_{i}$, ${\text{seeds}}_{i}$, $S_{\hbox{max} }$, $S_{\hbox{min} }$, and $np$.

• Breed based on the competency and the updated standard deviation. The corresponding value of the standard deviation is calculated by Eq. (31).

  $$\sigma_{\text{iter}} = \left( {{\text{iter}}_{\hbox{max} } - {\text{iter}}} \right)^{n} \times \frac{{\sigma_{\text{initial}} - \sigma_{\text{final}} }}{{\left( {{\text{iter}}_{\hbox{max} } } \right)^{n} }} + \sigma_{\text{final}} ,$$

  (31)

  where nonlinear modulation index, the standard deviation of the seeds in each iteration, the maximum number of iterations, initial, and final standard deviation are denoted, respectively, by $n$, $\sigma_{\text{iter}}$, ${\text{iter}}_{\hbox{max} }$, $\sigma_{\text{initial}}$ and $\sigma_{\text{final}}$.

• Competitive elimination.

• Control the stopping criterion.

The pseudocode of the proposed MOIWO algorithm is presented below:

• 1. Assess proportion of members of $np$ population.

• 2. Use the fuzzy sorting method to prioritize the population.

• 3. Let all members of the population make several seeds. More proportionate members of the population make a greater number of seeds in accordance with Eq. (30).

• 4. Seeds that have been produced are scattered on the search space using a normal random variable with mean zero and varying standard deviations. The corresponding value of the standard deviation is obtained using Eq. (31).

• 5. When the population size of the weeds becomes greater than the upper limit $(p_{\hbox{max} } )$, apply the fuzzy sorting method and keep $p_{\hbox{max} }$ seeds with better competencies.

• 6. Resume until the stopping criterion is met.

Fuzzy dominance-based sorting

In order to utilize the multi-objective version of the IWOA discussed in “The multi-objective invasive weeds optimization (MOIWO) algorithm” section, we start with an elementary phase of routine using the fuzzy dominance of the solutions in the population, based on which the solutions are first sorted in ascending order. Then, regarding the crowding distance, the diversity is obtained through sorted solutions. Obtaining the greatest n-dimensional hyper cube over objective space per solution enables the hypercube to find similar solutions. This is achieved using Eq. (32) (Kundu et al. 2011).

$$I\left( {\vec{v}} \right) = \mathop \sum \limits_{i = 1}^{n} \left( {y_{i} \left( {\vec{u}} \right) - y_{i} \left( {\vec{w}} \right)} \right)/\left( {\hbox{max} \left( {y_{i} } \right) - \hbox{min} \left( {y_{i} } \right)} \right).$$

(32)

In this equation, the neighboring solutions of $\vec{v}$ are demonstrated by $\vec{u}$ and $\overrightarrow { w}$, where the combined population is sorted in ascending order based on the ith objective function $y_{i}$. In Eq. (32), the dominator is used for normalization and the boundary solutions in the denominator include the extremes of the assigned values. Clearly, a higher value of $I\left( {\vec{v}} \right)$ indicates more dispersal over the solution space. The non-dominated solutions are placed in the archive alongside those solutions which were placed in sparser region.

The pseudocode of utilized MOIWA using the fuzzy dominance method for each solution is presented in Algorithm 1. In this algorithm, the membership degree of $i^{ih}$ population member’s domination to other weeds and membership degree of weed $i$ to weed $k$ are, respectively, denoted by $\mu \left( i \right)$ and $\mu_{i}^{\text{dom}} \left( {\overrightarrow {{x_{k} }} \prec \,_{i}^{F} \overrightarrow {{x_{i} }} } \right)$.

The coding method

To avoid generating infeasible solutions, a new structure is designed for a chromosome to assure satisfaction of all constraints all the times. This structure consists of six vectors. The lengths of these vectors represent the number of origin nodes, the number of destination nodes, the number of servers located in origin hub nodes, the number of servers located in destination hub nodes, the number of origin nodes allocated to origin hub nodes, and the number of destination nodes allocated to the destination hub nodes. An instance of this structure is shown in Fig. 2, where Vector 1 is a $1 \times 5$ vector of origin hub nodes demonstrating origin hub node’s assignment. Vector 2 is a $1 \times 5$ vector of destination hub nodes indicating destination hub node’s assignment. Vector 3 is a $1 \times 5$ vector of the servers located in the origin hub nodes. Vector 4 is a $1 \times 5$ vector of the servers located in destination hub nodes. Vector 5 is a $1 \times 5$ vector of origin nodes allocated to origin hub nodes, and Vector 6 is a $1 \times 5$ vector of destination nodes allocated to destination hub nodes. The elements of all the above vectors are random samples taken from a uniform distribution in $\left[ {0 , 1} \right]$.

Fig. 2

Representation of the chromosome structure

The decoding method

An example of the decoding method is demonstrated in this section to show the way the constraints are satisfied. Assuming the numbers of origin and destination nodes both are 5 and that the maximum number of origin and destination hub nodes is 2, the following procedure is used to generate feasible solutions with respect to Constraint (7). First, the elements of Vector 1 in Fig. 3 are sorted in ascending order. Then, the lowest two elements are considered as open (active) origin hub nodes. This method is shown in Fig. 4, in which the origin hubs 2 and 5 are chosen as the active origin hub nodes.

Fig. 3

Decoding active origin hub nodes

Fig. 4

Decoding active destination hub nodes

Similarly, the elements of Vector 2 are first sorted in ascending order. Then, the lowest two elements are chosen as open destination hub nodes in order to generate the solutions that satisfy Constraint (8). According to the procedure shown in Fig. 4, destination hub nodes 3 and 2 are selected as active destination hub facilities.

Vector 5 is used to satisfy Constraints (9) and (10) to determine the origin nodes that are allocated to origin hub nodes. As shown in Fig. 5, the elements of Vector 5 are first multiplied by $P_{1}$ and are added by 1, where the resulted values are rounded down. If the resulted number becomes 1, then the origin node will be assigned to the origin hub node 2, which is shown as an active origin hub node in Fig. 3. However, if the resulted number becomes 2, then the origin node will be assigned to the origin hub node 5, which is also shown as an active origin hub node in Fig. 3.

Fig. 5

Allocating origin nodes to origin hub nodes

Similarly, in order to generate solutions that satisfy Constraints (9) and (11) to determine the origin hub nodes allocated to destination hub nodes, the elements of Vector 6 are first multiplied by $P_{2}$ and then are added by 1, where resulted values are rounded down. If the resulted number becomes 1, then the origin hub node is assigned to destination hub node 3, which is shown as an active destination hub node in Fig. 4. However, if the resulted number becomes 2, then the origin hub node is assigned to destination hub node 3. This procedure is shown in Fig. 6.

Fig. 6

Allocating origin hub nodes to destination hub nodes

Vector 3 is used to determine the number of allocated servers to active hubs. As an obvious fact, servers can only be located in active origin hub nodes. Moreover, the lower and the upper bounds on the number of servers located in each active origin hub node can be obtained using Constraints (15) and (17). Hence, Eq. (33) is used to determine the exact number of the servers that should be located in each origin hub node

$$l_{k} = {\text{round}}\left( {{\text{LB}}_{k} + x_{k} \times \left( {{\text{UB}}_{k} - {\text{LB}}_{k} } \right)} \right),$$

(33)

where, ${\text{LB}}_{k}$ and ${\text{UB}}_{k}$ are the lower and upper bounds of the active number of servers located in origin hub $k$, $l_{k}$ is the number of servers located in origin hub $k$ and $x_{k}$ is the kth element of the Vector 3. The procedure used to determine the number of servers that are located in every open origin hub is presented schematically in Fig. 7.

Fig. 7

Encoding the number of servers located in active origin hub facilities

Similarly, Vector 4 is used to identify the number of the servers assigned to each active destination hub node. To do this, Constraints (16) and (18) are used to determine the lower and the upper bounds on the number of servers that should be located in each active destination hub node. The exact number of these servers is obtained using Eq. (34),

$$l_{m} = {\text{round}}\left( {{\text{LB}}_{m} + x_{m} \times \left( {{\text{UB}}_{m} - {\text{LB}}_{m} } \right)} \right),$$

(34)

where ${\text{LB}}_{m}$ and ${\text{UB}}_{m}$ represent the lower and the upper bounds on the number of active servers located in destination hub $m$, $l_{m}$ is the number of servers located in destination hub $m$, and $x_{m}$ is the mth element of Vector 4. The procedure of satisfying Constraints (16) and (18) and determining the number of servers assigned to each active destination hub node is depicted in Fig. 8.

Fig. 8

Encoding the number of servers located in active destination hub facilities

NRGA and NSGA-II

The chromosome structure of both NSGA-II (Deb et al. 2002) and NRGA (Al Jadaan et al. 2008) algorithms is the one proposed for the MOIWO algorithm. Moreover, both NSGA-II and NRGA algorithms use the same mutation and crossover operator. Their mutation operator is a combination of three operators; reversion, insertion, and swap mutations. Besides, in order to enhance the performances, a combination of three different crossover operators (single-point, double-point, and uniform crossover) is used in these two algorithms. However, as the main difference, NSGA-II employs the binary tournament selection, while NRGA uses the Rolette wheel selection strategy. The flowchart of NSGA-II and NRGA algorithms is shown in Fig. 9.

Fig. 9

Flowchart of the NSGA-II and NRGA

Applications

The implementation of the three utilized meta-heuristic algorithms called MOIWO, NSGA-II, and NRGA on 20 different test problems are discussed in this section. To do so, four different metrics called mean ideal distance (MID), the rate of achievement to two objectives simultaneously (RAS), the diversification matrix (DM), and the number of Pareto solutions (NPS) are used to evaluate the performances of the above algorithms. These metrics are:

• MID used to assess the closeness of the Pareto solutions obtained to an ideal point using Eq. (35) (Karimi et al. 2010).

  $${\text{MID}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \sqrt {\left( {\frac{{f1_{i} - f1_{\text{best}} }}{{f1_{\text{total}}^{ \hbox{max} } - f1_{\text{total}}^{\hbox{min} } }}} \right)^{2} + \, \left( {\frac{{f2_{i} - f2_{\text{best}} }}{{f2_{\text{total}}^{\hbox{max} } - f2_{\text{total}}^{\hbox{min} } }}} \right)^{2} } }}{n} ,$$

  (35)

  where, $f1_{\text{total}}^{\hbox{max} }$, $f2_{\text{total}}^{\hbox{min} }$ and $n$ denote, respectively, the smallest and the biggest values of the two fitness functions among all non-dominated solutions and the number of non-dominated solutions.

• RAS Eq. (36) is used to calculate the value of this metric (Asefi et al. 2014):

  $${\text{RAS}} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left[ {\left| {\frac{{f_{1i} \left( x \right) - f_{1i}^{\text{best}} \left( x \right)}}{{f_{1i}^{\text{best}} \left( x \right)}}} \right| + \left| {\frac{{f_{2i} \left( x \right) - f_{2i}^{\text{best}} \left( x \right)}}{{f_{2i}^{\text{best}} \left( x \right)}}} \right|} \right]}}{n}$$

  (36)

  where the value of the first and the second objective functions of the ith non-dominated solution and the number of non-dominated solutions are, respectively, denoted by $f_{1i} \left( x \right)$, $f_{2i} \left( x \right)$ and $n$.

• DM this metric is employed to obtain the diversity of the solutions in Pareto front using Eq. (37) (Mohammadi et al. 2013).

  $${\text{DM}} = \sqrt {\sum\nolimits_{i = 1}^{I} {\left( {{\text{Min }}\,f_{i} - {\text{Max}}\, f_{i} } \right)^{2} } }$$

  (37)

  where ${\text{Min}}\,f_{i}$ and ${\text{Max}}\,f_{i}$ are the minimum and the maximum values of the two fitness functions among all non-dominated solutions attained by the algorithm, respectively.

• NPS this metric is used to count the number of non-dominated solutions attained by each algorithm (Sarrafha et al. 2015).

Parameter setting

Since the performance of a meta-heuristic algorithm is significantly affected by the choice of its parameters, this section is dedicated for parameter calibration. To do this, some test problems are first generated in “Randomly generated test problems” section based on their parameters randomly. Then, the calibration process is explained in “Calibrating the parameters of the algorithms” section.

Randomly generated test problems

In this section, 20 test problems are generated randomly. These problems are categorized based on number of origin nodes ($I$), number of origin hub nodes ($K$), number of destination hub nodes ($M$), number of destination nodes ($J$), number of hub facilities located at origin layer ($P_{1}$) and number of hub facilities located at destination layer ($P_{2}$). The characteristics of these problems are presented in Table 2. Moreover, the following distributions are used to set the parameters of the test problems:

Table 2 General data of the test problems

• The demand for commodities from the origin node $i$ to the destination node $j$ follows a uniform distribution in $\left[ {100,1000} \right]$.

• Unit transportation costs from the origin node $i$ to the origin hub node $k$, from the origin hub node $k$ to the destination hub node $m$, and from the destination hub node $m$ to the destination node $j$ follow a uniform distribution in $\left[ {100,1000} \right]$.

• Unit staffing costs at the origin hub node $k$ and the destination hub node $m$ follow a uniform distribution in $\left[ {10,15} \right]$.

• Fixed establishment costs of a facility at the potential origin hub node $k$ and the potential destination hub node $m$ follow a uniform distribution in $\left[ {1000,10,000} \right]$.

• The discount factor is set to 0.3 for the costs.

• Maximum numbers of servers to be located in open origin hub node $k$ and open destination hub node $m$ are set to 4 and 5, respectively.

• Arrival rate of commodities to the origin hub node $k$ follows a uniform distribution in $\left[ {10,30} \right]$.

• Arrival rate of commodities to the destination hub node $m$ follows a uniform distribution in $\left[ {10,20} \right]$.

• Servers’ service rate at the origin hub node $k$ and the destination hub node $m$ follows a uniform distribution in $\left[ {20,25} \right]$.

Calibrating the parameters of the algorithms

In this section, the Taguchi method is utilized to tune the parameters of the three solution algorithms. This method has been proposed by Taguchi (1986) as an efficient alternative for the full-factorial experimental design. Taguchi method is aimed to investigate a group of decision variables using orthogonal arrays. As the main advantage, this method decreases the number of experiments required to calibrate the parameters. The main feature of these arrays is to set a family of experiences. These arrays should be designed and selected so that they can be considered as representative of all the possible arrays. Using this method, the performances of the algorithms are evaluated by a statistical measure called signal-to-noise ratio $\left( {S/N} \right)$. As multi-objective algorithms are evaluated based on multi-objective measures, the metric proposed by Rahmati et al. (2013) is employed in this paper as the response for the Taguchi method. This response that is shown in Eq. (38) considers two important features of meta-heuristic algorithms called diversity and convergence, simultaneously.

$$R = \frac{{{\text{MID}}}}{{{\text{DM}}}}$$

(38)

In Eq. (38), MID is used as the convergence metric and DM is used as the diversity metric. In addition, as both the objective functions of the mathematical formulation of the problem are of a minimization type, “the smaller is better” is employed to select the proper levels of the parameters.

As the first step of using the Taguchi method, the parameter levels of the algorithms are defined in Table 3. In this table, the low, the medium, and the high levels of the parameters are coded as “1”, “2”, and “3”, respectively.

Table 3 Parameters of the algorithm and their chosen levels

The experiments are designed in Minitab software. For the NRGA and NSGA-II, the L⁹ design is selected (Rahmati, et al. 2013), meanwhile, the L²⁷ design is chosen for the MOIWO algorithm (Maghsoudlou, et al. 2016). The resulted response values obtained by NSGA-II and NRGA when they are employed to solve the second problem (as an example) are shown in Table 4. Moreover, Table 5 contains the response values obtained by MOIWO. Using the Taguchi method, the levels with smaller values of $\left( {S/N} \right)$ are selected as the best levels of the parameters. The corresponding value of $\left( {S/N} \right)$ for each algorithm is illustrated in Fig. 10, based on which the best parameter levels are presented in bold in Table 3.

Table 4 Results to calibrate the parameters of NSGA-II and NRGA

Table 5 Results to tune the parameters of MOIWO

Fig. 10

Signal-to-noise ratios obtained by the algorithms

Computational results

The implementation results of the three parameter-tuned meta-heuristics on test problems with the general data in Table 2 are shown in Table 6. These algorithms were coded in MATLAB software and were executed on a PC with 2 GB RAM and Dual 2 GHz CPU. The problems are classified into three groups of small, medium, and large, based on which the test problems 1 to 6 are considered small, the test problems 7–14 are considered medium, and the rest are considered large-size problems. The average of each of the four metrics defined in “Applications” section for small-, medium-, and large-size problems are shown in the bottom three rows of this table. In addition, Fig. 11 shows the Pareto fronts obtained by each algorithm for small, medium and large problems. In order to compare the performances of the meta-heuristics in terms of the four metrics, the Fisher test is used. The p values of the Fisher statistics shown in Table 7 indicate that at a 95% confidence level, there are no significant differences among the algorithms in terms of all metrics, except MID. However, the box plots of the metrics in Fig. 12 show that MOIWO performs the best in term of MID, diversification (DM), and RAS metrics, while NRGA is the best in terms of the NPS metric.

Table 6 Implementation results

Fig. 11

Pareto fronts obtained by the solution algorithms

Table 7 Statistical comparisons of the algorithms

Fig. 12

Box plot of the four metrics obtained for the solution algorithms

Ranking the algorithms

As none of the three utilized parameter-calibrated algorithms is superior in terms of all of the four metrics, a hybrid multi-attribute decision-making (MADM) method called Entropy-TOPSIS is used to identify the best in terms of all metrics, simultaneously. In this method, the algorithms are considered as the alternatives and the metrics act as criteria. Moreover, the entropy method proposed by Hwang and Yoon (1981) is utilized to identify the weights of the criteria, meanwhile, the TOPSIS method presented by Hwang and Yoon (1981) is employed to identify the priority of the alternatives in solving the problems. The steps of the hybrid Entropy-TOPSIS method are:

• Create the decision matrices of the criteria for small-, medium-, and large-size problems

• Normalize the elements of the decision matrices using Eq. (39).

  $$p_{ij} = \frac{{a_{ij} }}{{\mathop \sum \nolimits_{i = 1}^{n} a_{ij} }},\quad \forall j,$$

  (39)

  where, $p_{ij}$ is the normalized element and $a_{ij}$ is an element of a decision matrix.

• Calculate the entropy of the jth criterion using Eq. (40).

  $$E_{j} = - \frac{1}{\ln m} \times \mathop \sum \limits_{i = 1}^{n} \left[ {p_{ij} \ln p_{ij} } \right]\quad \forall j$$

  (40)

• Compute the deviation or the uncertainty degree of a criterion using Eq. (41).

  $$d_{j} = 1 - E_{j} \quad \forall j$$

  (41)

• Obtain the weights of the criteria using Eq. (42).

  $$w_{j} = \frac{{d_{j} }}{{\mathop \sum \nolimits_{j = 1}^{n} d_{j} }}\quad \forall j$$

  (42)

• Calculate the normalized decision matrices, $r$, in the TOSIS method using (43).

  $$r_{ij} = \frac{{f_{ij} }}{{\sqrt {\mathop \sum \nolimits_{j = 1}^{n} f_{ij}^{2} } }}\quad \forall {\text{i}},$$

  (43)

  where $r_{ij}$, $f_{ij}$ and $n$ denote an element of the normalized decision matrix, an element of the decision matrix, and the number of alternatives, respectively.

• Obtain the weighted normalized decision matrices using Eq. (44):

  $$V = r*W_{n \times n} ,$$

  (44)

  where $V$ and $W_{n \times n}$ are the weighted normalized decision matrix and the diagonal weight matrix, respectively. Please note that the elements in the main diagonal of the weight matrix are the weights of the criteria calculated by the entropy approach.

• Compute the positive and the negative ideal solutions using Eqs. (45)–(46):

  $$v_{j}^{ + } = \left\{ {\begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{i} \left( {v_{ij} } \right)} \hfill & {{\text{for}}\,{\text{benefit}}\,{\text{criteria}}} \hfill \\ {\mathop {\hbox{min} }\limits_{i} (v_{ij} )} \hfill & {{\text{for}}\,{\text{cost}}\,{\text{criteria}}} \hfill \\ \end{array} } \right.$$

  (45)
  $$v_{j}^{ - } = \left\{ {\begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{i} \left( {v_{ij} } \right)} \hfill & {{\text{for}}\,{\text{benefit}}\,{\text{criteria}}} \hfill \\ {\mathop {\hbox{min} }\limits_{i} (v_{ij} )} \hfill & {{\text{for}}\,{\text{cost}}\,{\text{criteria}}} \hfill \\ \end{array} } \right.$$

  (46)

• Use Eqs. (47) and (48) to obtain the distances of the alternatives from the positive and the negative ideal solutions.

  $$d_{i}^{ + } = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {v_{ij} - v_{j}^{ + } } \right)^{2} } \quad i = 1, \ldots ,m$$

  (47)
  $$d_{i}^{ - } = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {v_{ij} - v_{j}^{ - } } \right)^{2} } \quad i = 1, \ldots ,m$$

  (48)

• Obtain the closeness of the alternatives using Eq. (49).

  $${\text{CL}}_{i} = \frac{{d_{i}^{ - } }}{{d_{i}^{ - } + d_{i}^{ + } }}\quad i = 1, \ldots ,m$$

  (49)

• Rank the alternatives based on their closeness. The best alternative (algorithm) is the one with the highest closeness.

A brief implementation of the above steps to rank the three meta-heuristics in terms of four metrics is shown in Tables 8, 9, 10, 11, 12, 13, 14, 15, and 16. According to the closeness of the alternatives obtained at the end, the MOIWO algorithm is the best to solve the problems.

Table 8 Decision and the normalized decision matrices (small-size problems)

Table 9 Weights of the criteria (small-size problems)

Table 10 Decision and the normalized decision matrices (medium-size problems)

Table 11 Weights of the criteria (medium-size problems)

Table 12 Decision and the normalized decision matrices (large-size problems)

Table 13 Weights of the criteria (large-size problems)

Table 14 Entropy-TOPSIS results (small-size problems)

Table 15 Entropy-TOPSIS results (medium-size problems)

Table 16 Entropy-TOPSIS results (large-size problems)

Conclusion and future research

In this paper, a new bi-objective intermodal hub-location-allocation problem within queuing framework was investigated. The developed model of this problem intended to simultaneously minimize the total network costs and the total time spent in the network. The solution of a small-size problem using the GAMS software was presented to show the accuracy of the developed formulation. As the problem belongs to the class of NP-Hard problems with conflicting objectives, an MOIWO algorithm with a new chromosome structure was utilized to solve the problem. Moreover, a fuzzy ranking method was used in MOIWO to prioritize the solutions obtained in each iteration. Since there was no available benchmark in literature, two other meta-heuristics called NSGA-II and NRGA with a unique chromosome structure were designed to qualify the solutions obtained by MOIWO. The parameters of the algorithms were tuned using the Taguchi method. The results obtained using these calibrated solution algorithms were compared statistically. The comparison results showed that the MOIWO algorithm acts better than the other two solution algorithms in terms of RAS, MID, and diversification metrics, while the NRGA algorithm is the best in term of the NPS metric. Finally, an Entropy-TOPSIS method was used to find the best algorithm in terms of all metrics. The results showed that the MOIWO algorithm was the best to solve all problems.

The following works can be recommended in future research:

• Formulating the uncertainties involved in the main parameters of the model using some other methods such as the robust optimization approach.

• Taking into consideration the failure probabilities of the origin and the destination hub facilities.

• Utilizing some other meta-heuristic solution algorithms to solve the problem.

• Employing a different approach to compare the performances of the solution algorithms.