Introduction

In a network with many origin–destination flows, hub facilities are used as interacting central points for different purposes such as better controlling on network flows and lower transportation cost. Hub networks are highly used in real-world problems such as freight and truck transport systems, postal network and telecommunications systems. In logistics application of hub network, aggregation of servicing demands in hub facilities creates economies of scale and discount factor is considered between hub-to-hub connections to take economies of scale into account.

The real-world problems have an uncertain nature. Accordingly, the hub location problem should be considered with uncertain parameters such as demand and transportation cost and, regarding the uncertainty, can describe real-world feature and can be more realistic. Marianov and Serra (2003) propose a model with chance constraints to control congestion in hub facility. They consider the network as an M/D/c queuing system where the arrival rate of demand to hub facilities is stochastic and c servers in hub facilities process the demand in a deterministic time. Mohammadi et al. (2011) extend that research by considering an M/M/c queuing system on the hub-covering model where processing time is stochastic. In both of these researches, a probabilistic constraint controls the congestion in the hub facilities.

Sim et al. (2009) consider p-center hub problem with service level constraints. They consider a stochastic travel time for each arc. The model determines location of hubs in the network which guarantees that the longest travel time through the network was satisfied with predefined service level.

Yang (2009) proposes a two-stage stochastic model to design hub network where parameters such as discount factor and demands are stochastic and described by a set of discrete scenarios. Adibi and Razmi apply a similar approach to design air transportation network in Iran. They consider transportation cost and demand as stochastic parameters (Adibi and Razmi 2015). Contreras et al. (2011) present three stochastic hub location models. They propose these models through the two-stage stochastic programming framework. The first model considers stochastic demand. The second one considers dependent stochastic transportation costs. Finally, the last one is associated with independent stochastic transportation costs. They prove that the first and second models are equivalent to the deterministic expected value one. However, the stochastic model was not equivalent to the deterministic expected value problem in the third model. They consider continuous distribution functions (normal and gamma distribution) to describe uncertain parameters and apply Monte-Carlo sampling-based techniques, sample average approximation (SAA), to approximate them by discrete set of scenarios. They implement Benders decomposition technique to tackle the large-scale optimization problem.

Alumur et al. (2012) consider different types of uncertainty in their research. Similar to previous research, they consider stochastic demands and propose two-stage stochastic models for single and multiple allocations. They reformulate the models to the extensive deterministic equivalent form. They regard uncertainty in the set up costs, which no probabilistic information is available. They model this uncertainty by minimax regrets approach. Finally, they propose a combined robust and stochastic model. Ghaderi and Rahmanian (2015) propose a robust stochastic single allocation hub location problem based on the p-robust concept. They use variable neighborhood search algorithm to solve the problem.

In addition to uncertainty of parameters, facilities in a network may fail due to random or intentional disruption. Kim and O’Kelly (2009) propose a reliable model for hub network where each link has a failure probability, and the model tries to locate hubs and allocate demand nodes to them so that the network has maximum reliability. Later, Kim (2012) proposes a protective model where a backup hub is considered after disruption of the primal link. Similar to the previous research, the protective hub location model aims to identify hub location and their allocation that maximize the total network reliability. Bashiri and Rezanezhad (2015) consider path reliability in the hub covering problem where both facility and covering reliability are considered in their proposed model. In addition to the maximizing network reliability, Snyder and Daskin (2005) propose a reliable model to minimize total transportation cost in normal and disruption situations. Generally, the random disruption can be modeled in two ways: implicit modeling and scenario-based modeling while the second one is more flexible against disruption (Snyder and Daskin 2007).

An et al. (2015) propose a quadratic implicit model of hub network where at most one hub in a path can be disrupted, and they propose its linearized formulation. To reach a proper network configuration, they propose Lagrangean relaxation and branch and bound solution approaches.

In addition to random failure, intentional disruption is considered in the hub network design in later studies. In the intentional disruption, r facilities from p unprotected facilities are disrupted by a potential attacker (called as r-interdiction). Recently, Parvaresh et al. (2013) have regarded intentional disruption in the hub network through a bi-level programming model. In their proposed model, hub network designer’s (leader) objective is minimization of expected transportation cost, including the lost-sales penalty. The attacker (follower) tries to maximize the total damage to the system. They propose simulated annealing algorithm to solve the bi-level model. In the other research, the same authors propose a multiple objective bi-level programming under intentional disruption (Parvaresh et al. 2014). The network designer objectives are to minimize network total transportation cost in usual condition and worst-case transportation costs after r-interdiction. The attacker’s objective is similar to the previous research. They propose simulated annealing and tabu search algorithms to solve the model.

To the best of our known, the scenario-based model for reliable hub location problem is not considered yet. In this study, a reliable hub location model as scenario-based one, which is more flexible than implicit models, is proposed and two-stage stochastic programming formulation is used to model reliable hub location problem. Moreover, benders decomposition is integrated with scenario reduction technique to solve the large-scale instances.

In the next section, a two-stage stochastic mathematical model and its deterministic equivalent form are presented. Moreover, the approximation methods are described in general. Sensitivity analysis and computational results are provided in Sect. 3. Finally, the conclusion is provided in the last section.

Problem definition

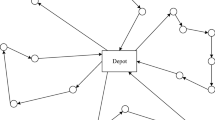
O’Kelly (1998) defined hub facility as special nodes in the network which is located to facilitate connectivity between interacting places. In this paper, it is considered that a disruption may occur at hub facilities and formulated as a two-stage stochastic problem. In the first stage, there are some candidate nodes to establish hub facilities (Fig. 1a) and the model determines location of hubs (p-hubs) from candidate nodes (Fig. 1b). After locating the hubs, in the second stage, the random parameter (a scenario) becomes known, and disruption may occur and some of the facilities may fail. In the second stage, demands are assigned to the remained hub facilities (Fig. 1c, d). The model objective is the minimization of expected transportation cost over all scenarios.

Fig. 1
figure 1

Reliable hub network structure design in two stages (a demand and potential hub nodes; b established hub facilities in the first stage; c, d two realizations of stochastic disruption in the network and their allocations)

Full size image

Model assumption

  • The capacities of the hub facilities are unlimited.

  • Disruption events can occur through the network independently.

  • There is a dummy hub which is never failed and an allocated flow to the dummy hub incur penalty (the flow is considered as an unserved one). This facility is used to keep model feasible for all scenarios.

  • The non-hub nodes can be assigned to several hubs (multiple allocation).

  • Each demand node is considered a candidate for establishment of hub.

  • A disrupted hub is considered as a demand node.

Parameters and decision variables

N :

Set of demand nodes;

DF:

Set of disrupted hub nodes;

d ij :

The distance to travel between nodes i (origin) and j (destination);

w ij :

Amount of flow between nodes i − j;

α :

Discount factor for inter hub connections;

c ijkm :

The cost per unit of flow between i and j, routed via k and m as first and second hubs, respectively, which is calculated according to c ijkm  = d ik  + αd km  + d mj ;

q i :

Shows failure probability of i th node;

p s :

Shows probability of ith scenario occurrence;

S :

Set of all scenarios;

S’ :

Subset of all scenarios generated in SAA procedure;

a i (ξ):

Random binary parameter that takes value 1 if ith node is being disrupted;

Ξ:

Support set of random variable;

a ik :

Binary parameter that takes value 1 if ith node is being disrupted in kth scenario;

x ijkm :

Continuous decision variable that shows amount of flow i − j that routed via hubs k and m;

\(x_{ijkm}^{s}\) :

Continuous decision variable that shows amount of flow i − j that routed via hubs k and m in scenario s;

z i :

Binary decision variable which takes value 1 if hub facility is established in ith node and 0 otherwise.

Each node in the network may fail or not and failures are independently and identically distributed according to the Bernoulli distribution. Therefore, in a realized scenario, the facilities can be divided into normal and disrupted facilities (DF). The occurrence probability of each scenario can be calculated as follows:

$$p_{s} = \prod\limits_{{j \in {\text{DF}}_{s} }} {q_{j} \prod\limits_{{j \in N\backslash {\text{DF}}_{s} }} {(1 - q_{j} )} }$$

and there are 2 |N|−1 scenarios.

Mathematical modeling

In the first stage, the location of hub is determined.

Stage 1:

$$\hbox{min} \, S1 = E[Q(x,\xi )]$$
(1)
$$\sum\limits_{i} {z_{i} = P}$$
(2)
$$z_{\text{dummy}} = 1$$
(3)
$${\text{subject to: }}z_{i} \in \{ 0,1\} ,\quad \forall i$$
(4)

One of the P established hubs is a dummy hub. The term \(Q(x,\xi )\), recourse function, is the optimal value of the second stage problem:

Stage 2:

$$Q(x,\xi ) = \hbox{min}\, S2 = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {\sum\limits_{m} {c_{ijkm} x_{ijkm} } } } }$$
(5)
$${\text{subject to:}}\;\sum\limits_{k} {\sum\limits_{m} {x_{ijkm} = w_{ij} \quad \forall i,j} }$$
(6)
$$\sum\limits_{m} {x_{ijkm} + \sum\limits_{m|m \ne k} {x_{ijkm} \le w_{ij} z_{k} (1 - a_{k} (\xi ))} } \quad \forall i,j,k,\quad m,\xi \in \varXi_{k}$$
(7)
$$x_{ijkm} \ge 0\quad \forall i,j,k,m$$
(8)

The objective function (1) contains the expected value of second stage objective function. Constraint (2) determines the number of hubs in the network. Constraint (3) assures that dummy hub should be established in the network. Constraint (4) imposes integrality requirement of location variables. The hubs location should be determined before observing the realization of uncertain binary parameters. The second stage objective is to minimize total transportation cost. Constraint (6) ensures that the flow i − j is routed through hubs. Constraint (7) guarantees that the flow i − j can be routed from node k if node k is selected as hub. Constraint (8) enforces the flow to be non-negative.

Simply, the above formulation can be considered as an extensive deterministic equivalent form as the following:

$$\hbox{min}\, E.F = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {\sum\limits_{m} {\sum\limits_{s \in S} {p_{s} } c_{ijkm} x_{ijkm}^{s} } } } }$$
(9)
$${\text{subject to:}}\;\sum\limits_{k} {\sum\limits_{m} {x_{ijkm}^{s} = w_{ij} } } ,\quad \forall i,j,\quad \forall s \in S$$
(10)
$$\sum\limits_{m} {x_{ijkm}^{s} + \sum\limits_{m,m \ne k} {x_{ijkm}^{s} \le w_{ij} z_{k} (1 - a_{ks} )} } \quad \forall i,j,k,m,\quad \forall s \in S$$
(11)
$$x_{ijkm}^{s} \ge 0\quad \forall i,j,k,m,\quad \forall s \in S;\quad z_{i} \in \{ 0,1\} ,\quad \forall i$$

As it is obvious in above formulation, the number of scenarios increases exponentially as the number of candidate nodes increases. The extensive deterministic equivalent form is difficult to solve directly since this form contains many scenario-dependent variables. Two common approaches can be applied in stochastic programming to tackle this drawback: decomposition techniques such as Benders decomposition, L-shaped methods and scenario approximation techniques such as SAA. In this paper, integrated solution approach is applied to overcome the computational difficulty.

Sample average approximation

Sample average approximation (SAA) is a Monte-Carlo-based approach that is used to solve two-stage stochastic programming. The SAA approximates the true optimal value by solving generated samples of stochastic parameters, and it is used in the reliable facility location problem with a large number of scenarios (Gade and Pohl 2009; Shen et al. 2011; Aydin and Murat 2013). The steps of SAA procedure are as follows (Kleywegt et al. 2001).

Step 1: Generate independent scenarios (S’) and solve the following SAA problem:

$$\hbox{min} \;{\text{S}} . {\text{P}} = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {\sum\limits_{m} {\sum\limits_{s \in S'} {\frac{1}{|S'|}} c_{ijkm} x_{ijkm}^{s} } } } }$$
(12)
$${\text{subject to:}}\;\sum\limits_{k} {\sum\limits_{m} {x_{ijkm}^{s} = w_{ij} \quad \forall i,j} } \in N,\quad \forall s \in S'$$
(13)
$$\sum\limits_{m} {x_{ijkm}^{s} + \sum\limits_{m,m \ne k} {x_{ijkm}^{s} \le w_{ij} z_{k} (1 - a_{ks} )} } \quad \forall i,j,k,m \in N,\quad \forall s \in S'$$
(14)
$$x_{ijkm}^{s} \ge 0\quad \forall i,j,k,m \in N,\quad \forall s \in S',\quad z_{i} \in \{ 0,1\} \forall i$$
(15)

Step 2: Repeat Step 1 M times and solve SAA problem and records (z *m, S.P*m) for m = 1…M.

Step 3: Calculate the statistical lower bound of true objective function according to (16):

$$Z_{\text{l}} = \frac{1}{M}\sum\limits_{m = 1}^{M} {{\text{S}} . {\text{P}}^{*m} }$$
(16)

The variance of the lower bound is calculated as follows:

$$\sigma_{{Z_{\text{l}} }}^{2} = \frac{1}{M(M - 1)}\sum\limits_{m = 1}^{M} {(z^{*m} - Z_{\text{l}} )^{2} }$$
(17)

Step 4: Generate N’ (\(|N'\left| \gg\right|S'|\)) of independent identically distributed random scenarios and solve the following problem where location variables are fixed and selected from one of the recorded solutions of Step 2. The extracted value is considered as the statistical upper bound of the true problem.

$$\hbox{min} Z_{\text{u}} = \sum\limits_{n \in N'}^{{}} {\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {\sum\limits_{m} {\frac{1}{|N'|}} } } } } c_{ijkm} x_{ijkm}^{n}$$
(18)

Z u estimates upper bound of the true objective function and its variance can be calculated according to the following:

$$\sigma_{{Z_{\text{u}} }}^{2} = \frac{1}{N'(N' - 1)}\sum\limits_{n \in N'}^{{}} {\left( {\sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {\sum\limits_{m} {c_{ijkm} x_{ijkm}^{n} } } } } - Z_{u} } \right)^{2} }$$
(19)

Step 5: Calculate the optimality gap by subtracting the lower bound from the upper bound:

$${\text{SAA}}_{\text{gap}} = Z_{\text{u}} - Z_{\text{l}}$$
(20)

and the variance of optimality gap is calculated as follows:

$$\sigma_{\text{gap}}^{ 2} = \sigma_{{Z_{\text{l}} }}^{2} + \sigma_{{Z_{\text{u}} }}^{2}$$
(21)

Multiple cuts Benders decomposition solution approach

The stochastic models are needed much more computational effort in comparison to deterministic one. Moreover, hub location problem is NP-hard. The proposed model contains these two complexity issues and an efficient algorithm is required. Therefore, stochastic decomposition-based approach is proposed to tackle with these complexities.

Van Slyke and Wets (1969) extended Benders decomposition method for mixed integer stochastic models. SAA can approximate the original two stochastic problem via sampling and reduce the number of scenarios. However, solving reliable hub location problem involving S’ scenarios is still difficult. Therefore, an integration of sampling approach and decomposition technique is applied to enhance computational performance.

Benders decomposition method decomposes the original stochastic problem into two main parts: the master problem and the slave problem. Generally, the master problem involves the first stage decision variables and slave problem contains second stage variables with considering fixed values for first stage variables. Due to block structure of the extensive form problem (Birge and Louveaux 1997), the slave problem can be decomposed into scenario subproblems. In following, the master and slave problem (22)–(25) is presented:

Slave Problem (for each scenario \(\forall s \in S\)):

$$\hbox{min} ({\text{SP}}) = \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {\sum\limits_{m} {c_{ijkm} x_{ijkm}^{{}} } } } }$$
(22)
$${\text{subject to:}}\;\sum\limits_{k} {\sum\limits_{m} {x_{ijkm} = w_{ij} \quad \forall i,j} }$$
(23)
$$\sum\limits_{m} {x_{ijkm} + \sum\limits_{m,m \ne k} {x_{ijkm} \le w_{ij} z_{k}^{\text{fixed}} (1 - a_{ks} )} } \quad \forall i,j,k,m$$
(24)
$$x_{ijkm}^{{}} \ge 0\quad \forall i,j,k,m$$
(25)

In the above formulation, slave problem is optimized by considering fixed location variables for each scenario. To generate optimality cut, dual variable associated with the slave problem is required. Therefore, the dual forms of the slave problems are stated as follows:

Dual of slave problem (for each scenario \(\forall s \in S\)):

$$\hbox{max} \sum\limits_{i} {\sum\limits_{j} {w_{ij} \tau_{ij} - \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {w_{ij} z_{k}^{\text{fixed}} (1 - a_{ks} )} } } } } \pi_{ijk}$$
(26)
$$\tau_{ij} - \pi_{ijk} - \pi_{ijm} \le C_{ijkm} \quad \forall i,j,k,m \in N,k \ne m$$
(27)
$$\tau_{ij} - \pi_{ijk} \le C_{ijkk} \quad \forall i,j,k$$
(28)
$$\pi_{ijk} \ge 0\quad \forall i,j,k;\quad \tau_{ij} \;{\text{is}}\;{\text{free}}.$$
(29)

For the proposed problem, we are facing the following master problem:

Master problem:

$$\hbox{min} ({\text{MP}}) = \sum\limits_{s \in S} {\theta_{s} }$$
(30)
$$\sum\limits_{i} {z_{i} = P}$$
(31)
$$z_{\text{dummy}} = 1$$
(32)
$$\theta_{s} + \sum\limits_{i} {\sum\limits_{j} {\sum\limits_{k} {p_{s} w_{ij} z_{k} (1 - a_{ks} )\pi_{ijk}^{iter} } } } \ge \sum\limits_{i} {\sum\limits_{j} {p_{s} w_{ij} \tau_{ij}^{\text{iter}} } \quad } \forall s \in S,\quad {\text{iter}} = 1, \ldots ,{\text{current}}\;{\text{Benders}}\;{\text{iteration}}$$
(33)
$$z_{i} \in \{ 0,1\} ,\quad \forall i \in I\quad \theta_{s} \ge 0$$
(34)

where Eq. (33) is set of optimality cuts generated in each iteration. It is worth noting that Eqs. (31) and (32) guarantee the feasibility of slave problems and there is no need to add Benders feasibility cuts to the master problem.

An aggregation of all dual information into one optimality cut leads to losing information in the single cut method (Trukhanov et al. 2010). Birge and Louveaux modified Benders decomposition method called multiple cuts Benders decomposition where the dual information of all scenarios is kept during algorithm execution. In the multiple cuts Benders decomposition method, optimality cuts are generated by each scenario in each iteration. In Algorithm 1, procedure of the multiple Benders decomposition method for proposed problem is demonstrated based on (Birge and Louveaux 1988).

The proposed solution approach is depicted in Algorithm 2.

Computational analysis

All the computational tests were carried out on the laptop computer with Intel Core i5 CPU with 2.5 GHz clock speed and 4 GB of RAM. The proposed models are solved by the GAMS (version 23.5.2) with CPLEX solver and CAB data set is used to do the computational tests.

Failure probability effect on the network

For sensitivity analysis of the proposed model, a 9-node problem (α = 0.5) from CAB dataset is generated. The number of established hubs varies from two to six in which one of them is a dummy hub. The penalty cost of flows used the dummy hub is considered as \(1.5 \times \mathop {\hbox{max} }\limits_{i,j} \{ c_{i,j} \}\). The computational results are depicted in Fig. 2. By considering Fig. 2, it can be concluded that

Fig. 2
figure 2

Sensitivity analysis of failure probability

Full size image

  • It is expected that when the number of hubs in the network increases, the total cost of network decreases,

  • Trend of proposed network toward classical hub network (q = 0) is observed as the failure probability decreases,

  • When failure probability increases, because of facilities unavailability, the total expected transportation cost increases.

  • The model is more sensitive (in objective function value aspect) to failure probability when the number of hubs reduces.

Sensitivity analysis of replication and sample size

Quality of SAA result depends on the proper selection of sample size and number of replications. From statistical point of view, increase in both sample size and the number of replications leads to better approximation. In contrast, from computational point of view, increasing these two parameters increases computational time. To determine the effect of sample size and number of replications, 10-node CAB data set (α = 0.5 and p = 3 and N′ = 1000) is used. The results are reported in Table 1 and Fig. 3. The result shows that the sample size is highly effective in quality of SAA procedure (in terms of optimality gap). However, as it is depicted in Fig. 4, the computational time increases by increasing the sample size.

Table 1 Optimality gap in different values of sample size and replication
Full size table
Fig. 3
figure 3

Trend of decreasing optimality gap by increasing the sample size

Full size image
Fig. 4
figure 4

Trend of increasing CPU time by increasing the sample size

Full size image

Multiple and single cut Benders decomposition

The performance of single and multiple cuts Benders decomposition in terms of computational time and number of iteration has been investigated in this subsection. To do so, four instances with different hub network parameters from the 26 nodes-CAB data set are considered. The algorithm terminates when the convergence criterion is reached (epsi is considered to be 1). In these cases, ten scenarios are generated randomly. The results show that multiple cuts method outperforms single cut method in both mentioned aspects (Table 2). The computational results demonstrate the superiority of the proposed multiple cuts method over the single one in terms of computational time and number of algorithm iterations.

Table 2 Comparison of multiple cut (MC) and single cut (SC) Benders decomposition for the reliable P-hub location problem
Full size table

SAA and multiple cut Benders decomposition

In this subsection, Benders decomposition is applied inside SAA procedure for instances with a large number of scenarios. To do so, 26 nodes-CAB data set is considered. It is clear that solving the reliable p-hub location problem with 225 scenarios is impossible even by Benders decomposition. Therefore, applying scenario reduction technique such as SAA seems to be necessary. In this section, SAA parameters are set to be |S′| = 15, M = 15 and N′ = 250.

The results are reported in Table 3. It is worth mentioning that without using the proposed algorithm, the same case cannot be solved. The results show that by considering the same failure probability and number of hubs in the network, as the discount factor is decreasing, the optimality gap increases. Moreover, by considering the fact that the uncertainty is concerned to strategic decisions, optimality gap is fairly good when the number of hubs in network increases. However, CPU time increases when number of hubs increases.

Table 3 Results of integrated SAA and multiple cut Benders decomposition
Full size table

Conclusions

In this paper, a two-stage stochastic programming problem is proposed to design multiple allocation hub network under disruption risk. The model tries to minimize the expected transportation cost. The two-stage stochastic model grows exponentially with the number of facility, and a scenario reduction technique is applied to tackle the issue of facing the large number of scenarios. In addition to the approximation scenarios by SAA, Benders decomposition approach is used inside the SAA to increase computational performance. Computational results show that the SAA can provide a good approximation in terms of optimality gap (especially in small instances). The results show that SAA performance is sensitive to the sample size. Two variants of benders decomposition are applied to solve large cases of reliable p-hub location problem. The comparison of the computational results obtained by these two approaches showed that the multiple cuts benders outperformed the classic one. Considering the arc failure probability in the reliable hub location problem using the mentioned algorithm can be considered as a future research direction.