Abstract
The buffer allocation problem is an NP-hard combinatorial optimization problem, and it is an important design problem in manufacturing systems. The research proposed in this paper concerns a product line consisting of n unreliable machines with n − 1 buffers and a preventive maintenance policy. The focus of the research is to obtain a better trade-off between the buffer level and the preventive maintenance actions. This paper proposes a dynamic control of the buffers’ level and the interval between two consecutive preventive actions. The set of the parameter of the proposed policy allows choosing the reduction in the costs or the increment of the throughput rate. A simulation model is developed to test the proposed model to the solution proposed in the literature. The proposed policy leads to better results in terms of total costs reduction keeping high production rate, while the design of a fixed level of buffer works better for lower production rates required.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
A production line is a manufacturing system where work centers are connected in series and separated with buffers. Each work center can consist of one or more identical machines in parallel. The introduction of buffers increases the throughput and customer service level of the production line by limiting the propagation of disruptions (as machine breakdowns, unbalance processing times, etc.). However, the introduction of buffers increases the work in process (additional working capital), space of the production line and, therefore, the capital investment. The design of the buffer storage size is crucial to improve the production rate with acceptable extra costs due to the buffers introduction to reduce the total manufacturing costs (Massim et al. 2010).
Chow (1987) highlighted two issues that cause difficulties to solve the buffer allocation problem: (1) an analytical relation between the performance of the production line and the storage capacities’ distribution between the work center of the line cannot be provided; (2) buffer sizing is an NP-hard combinatorial optimization problem.
Preventive maintenance is another method to increase the production rate (Patchong and Willaeys 2001; Northworthy and Abdul-Kader 2004; Yusuf 2014; Renna 2012).
The preventive maintenance actions increase the availability of the machines over the long term reducing sudden machine breakdowns (Gento and Redondo 2003).
The preventive maintenance plan with the introduction of buffers can improve the production rate to a higher level; a buffer can provide the parts for a downstream work center when the upstream work center performs preventive maintenance action.
The approaches proposed in the literature provide valuable information about how to allocate buffers ‘storage and plan the preventive maintenance actions. The practice of the proposed approaches in real industrial cases highlighted some difficulties due to industrial setting complexity, detail level of the model developed, extend to a different configuration of the production lines and different working conditions (Demir et al. 2014).
The aim of this paper is to develop a simulation model with higher detail to obtain a realistic evaluation of the manufacturing costs and production rate. Approaches proposed in the literature are used to show how a more detailed level leads to different performance evaluation. Then, it is proposed a dynamic policy for the buffers and preventive maintenance plan. The production line conditions are used to decide when performing preventive maintenance actions (with a dynamic period) and the storage levels allowed (dynamically over the planning period).
The remainder of the paper is organized as follows. In section two, the overview of the literature on buffer allocation problem and preventive maintenance policy is discussed. The research context is presented in the third section. The proposed dynamic policy is described in the forth section. The test case is presented in the fifth section, while the sixth section discusses the numerical results. Conclusions and future research paths are given in the seventh section.
Literature review
Several works have been proposed on the buffer allocation problem. Demir et al. (2014) presented a comprehensive survey on the buffer allocation problem in production systems. The survey grouped the studies into two categories: (1) Reliable production lines (2) Unreliable production lines.
In the field of unreliable production lines, Nahas et al. (2006, 2009) proposed a local search approach for solving the buffer allocation problem in unreliable production lines maximizing the average throughput. The degraded ceiling algorithm proposed was compared with a simulated annealing algorithm obtaining better results and reducing the time to get the optimum solution. The methods proposed analyzed only the productivity requirements.
Dolgui et al. (2007) considered the problem of buffer space allocation for a tandem production line with unreliable machines. The problem of buffer allocation is solved by the aggregation method combining the genetic and branch-and-bound approaches. The goal of the model is evaluated by a Markovian model aggregation technique considering only the production rate in a steady state condition.
Yuzukirmizi and Smith (2008) presented an optimal buffer allocation procedure for closed queueing networks with finite buffers. The objective is to maximize the production rate and minimize the cycle time. The main limitation of the method proposed is that only suboptimal solutions can be assured.
Shi and Gershwin (2009) proposed a nonlinear programming method for the design of the buffer storage to maximize the profits. The study includes the costs of buffer space, holding the part in the buffer with a production constraint rate. The numerical results are obtained for short and long production lines. The efficiency of the algorithm proposed is evaluated enough with production lines up to 30 machines.
Battini et al. (2009) presented a simulation study for the allocation of the buffer size in production lines to maximize the production rate. They proposed an experimental formula considering the machine availability in terms of MTTR and MTBF values. The objective of the study is to provide a rapid tool for designers and practitioners for the design of buffer size.
Massim et al. (2010, 2012) proposed an immune decomposition algorithm for the buffer allocation problem to maximize the production rate and minimize cost design of a series–parallel production system configuration. The numerical results are compared to a genetic algorithm to highlight the efficiency of the model proposed.
Srinivas et al. (2011) presented a simulation study to determine the buffer size for the layout obtained by the genetic algorithm in single- and multi-row flexible manufacturing systems. The main objectives of the study conducted were the minimization of buffer size and machines’ blocking state and to increase the machine utilization. The numerical results of the simulation can support the designers and practitioners for the design of the manufacturing system.
Staley and Kim (2012) presented a simulation study to understand buffer allocation in closed serial production lines. The main key findings are the following: Optimal buffer allocations in closed lines are less sensitive to bottleneck severity than in open production lines; buffer allocation decisions have more impact in closed reliable production lines than in closed unreliable production lines.
Amiri and Mohtashami (2012) proposed a multi-objective formulation of the buffer allocation problem in unreliable production lines. The objectives are to maximize the production rate and minimize the space due to the buffer allocation. The methodology used is the genetic algorithm to optimize the model and the queue network theory to evaluate the performance.
Tsarouhas (2015) proposed a mathematical model of the croissant production line using Markov process. The analysis provides a useful insight into the system’s behavior, helps to find design-inherent faults, and suggests optimal modifications to upgrade the system and improve its performance. Srinivasa Rao and Naikan (2014) proposed a hybrid approach called as Markov system dynamics (MSD) approach which combines the Markov approach with system dynamics simulation approach for reliability analysis and to study the dynamic behavior of systems.
The buffer allocation problem and preventive maintenance plan are studied together in few works.
Rezg et al. (2005) investigated the buffer allocation and preventive maintenance actions to minimize the average cost per time unit. The costs considered include the maintenance cost, the inventory holding cost, and the shortage cost. The proposed strategy is modeled by two approaches: a mathematical model and a combination of simulation, experimental design, and statistical analysis. The two approaches lead to the same results for a given set of parameters.
Zequeira et al. (2008) studied the optimal maintenance policy with the use of extra production capacity for the buffer inventory to satisfy the demand during the preventive maintenance action. The model developed includes the possibility of imperfect production. Then, it is determined the parameters of buffer level and time of preventive action to minimize the average cost rate.
Radhoui et al. (2009) proposed a joint quality control and preventive maintenance policy for a production system which produce non-conforming items due to the degradation of the machines. The introduction of the buffer reduces the perturbations due to the corrective and preventive maintenance. A mathematical model was proposed to determine the threshold level of the rate of non-conforming items (maintenance actions depends on this rate), and the size of the buffer stock in order to minimize the average total cost.
Nahas (2017) considered the problem to determine the optimal preventive maintenance policy and optimal buffer allocation that minimize the total system costs subject a throughput level. An analytical decomposition-type approximation is used to estimate the production line throughput. The optimal design problem is formulated as a combinatorial optimization one where the decision variables are buffer levels and times between preventive maintenance. To solve this problem, the extended great deluge algorithm is proposed.
Based on the above literature review, the following limitations can be drawn:
- a.
Mathematical approaches proposed in the literature are difficult to apply in general real industrial cases to obtain a decision support system for practitioners (several parameters to set, generalization, computational complexity, etc.).
- b.
Some of the past works used queue network model that has some limitations on the performance evaluation respect to real industrial cases. This approach over-estimates some performance measures.
- c.
The works on preventive maintenance policy and machine breakdowns are often simplified. For example, the time to perform the maintenance activities are assumed negligible, and the real utilization of the buffer storages is not considered because the costs are computed on the maximum level allowed.
The research proposed in this paper resulted in the above limitations in the following issues:
- a.
A simulation environment is developed with a higher level of detail to estimate the performance of the policy proposed compared to a methodology proposed in the literature. (For example, in some research, the time of preventive actions is negligible.)
- b.
The costs due to the buffer storage are evaluated considering the average utilization, and the time of preventive actions is introduced.
- c.
It is proposed a dynamic policy in terms of time between preventive actions, and buffer storage level set considering the manufacturing system conditions. This approach can be easily set and used to support the decision of practitioners in real industrial cases.
Research context
The production line considered is the same investigated in Nahas (2017). The production line consists of 10 work centers in series and 9 buffers between the work centers. It is assumed that the first machine is never starved and that the last machine is never blocked.
Each work center consists of one machine. Each part enters from the first machine, passes in order from all machines and the intermediate buffers, and exits the line from the last machine. The machines are considered unreliable. The processing times of the work centers are the same in order to obtain a balanced production line (Nahas (2017) considered only the production rate of the production line). The processing times assure the production rate required.
The operating time between failure and the time to repair a machine is supposed to be exponentially distributed with the meantime between failure (MTBF) and meantime to repair (MTTR), respectively.
The preventive maintenance activities proposed in Nahas (2017) are performed on each machine i at constant interval ti. The time of the preventive maintenance actions is identical for the work centers tpmi.
It is assumed that the increase in maintenance frequency increases the MTBFi of the machine i (Meller and Kim 1996) as shown in expression (1):
where MINi is the MTBFi with no preventive policy; MAXi is the maximum MTBFi with higher frequency of preventive maintenance actions; β shape factor for the asymptotic gain in preventive maintenance.
Moreover, the following notation is used:
Bimax is the buffer size of the machine i;
Ri number of preventive maintenance actions per hour (machine i);
Cr the cost of corrective maintenance action per hour ($/h);
Cp the cost of preventive maintenance action per hour ($/h);
Ch the cost of holding a unit of inventory per hour ($/(part * h))
Nahas (2017) determined the optimal preventive maintenance policy and the optimal buffer allocation to maximize the throughput level with buffer space constraint using the extended Great Deluge (EDG) algorithm. The better results obtained in Nahas (2017) are used as the benchmark of the proposed approach explained in “Dynamic policy” section.
Dynamic policy
The proposed policy consists of an adaptive preventive maintenance policy and buffer levels for each production stage. The preventive maintenance and buffer allocation policy is characterized by a dynamic decision on the time between the preventive actions, and a dynamic decision on the maximum level of the buffers’ storage allowed. The objective is to obtain a policy adaptable to the production line conditions reducing redesign activities.
Preventive maintenance decision
The first step of the proposed approach concerns the preventive maintenance policy. The preventive maintenance actions can be activated at constant interval IntTp to reduce the number of preventive actions.
The decision on the interval of periodic maintenance of each production stage uses some information of the production stage state. The main information used is the downstream buffer level and the time of the last maintenance action.
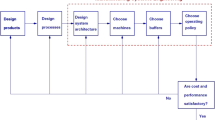
The controller of the production stage i checks the number of units in the downstream buffer i + 1. If the number of units is higher than a threshold thri + 1 and the time from the last preventive action is higher than intTp, then the preventive action can be performed. Figure 1 presents the flow chart of the decision algorithm.
This strategy allows to perform preventive actions when the downstream buffer contains an adequate level of units; then, the downstream production stage can process the units when the preventive action is activated and the machine is not available. In this way, the time between preventive maintenance actions is dynamic and depends on the manufacturing system conditions as the demand, the failures of the other machines, etc.
Dynamic buffer allocation
The second step of the approach proposed concerns the dynamic allocation of the buffers' level. The strategy proposed considers the idle percentage (IDLEi) of the machine in the production stage i. The upstream buffer level is as a function of the idle percentage of machine i. Each buffer level is computed as shown in expression (2):
where Lmin is the minimum level of buffer considered (in this research, equal for all machines); K is a coefficient to amplify the percentage idle of the machine (in this research, equal for all machines); Therefore, the maximum level of the buffer can be Lmin + K. The buffer storage oscillates between Lmin and Lmin + K in order to minimize the starving of the downstream machine.
Test case
The production line consists of 10 machines and 9 buffer positions, because the first machine works without buffer (the raw material is always available). The length of the simulation is 3000 h. The holding cost, PM action cost, and corrective maintenance cost are, respectively, Ch = 0.5 $/(parts * h), Cp = 5 $/action, and Cr = 15 $/action. Table 1 shows the data for this production line (Nahas 2017).
The best maintenance plans and the best buffer allocation solution obtained by Nahas (2017) are shown in Table 2. Seven cases with different production rates (P*) are considered to satisfy.
The benchmark (Nahas 2017) does not consider the processing time of the 10 machines, but only the throughput. The simulation model developed considers a production line balanced with processing time equal for the 10 machines. The raw materials are always available. The processing time of the machines depends on the throughput of the case evaluated.
In particular, the processing time is computed as shown in expression 3:
The production line is balanced and in ideal conditions can satisfy the production rate required.
The benchmark considers negligible the time of the preventive maintenance actions. In this research, the time of preventive maintenance actions is introduced. This time is considered equal for all machines different for each case evaluated as shown in expression (4).
Expression (4) means that the time of the maintenance actions is the half of the time between two preventive maintenance actions. The vector of the time of maintenance actions for the cases is the following [5,5,2,2.5,1.67,1.25,0.55]; these values are lower than the MTTR (see Table 1) proposed in the benchmark.
For each experiment class, a number of replications able to assure a 5% confidence interval and 95% of confidence level for each performance measure have been conducted.
Numerical results
The numerical results evaluated are the following:
P is the production rate of the production line;
CI is the total holding costs computed as the costs Ch per average number of parts in buffer storages;
CMP is the total costs of preventive maintenance costs computed as the cost Cp per number of preventive maintenance actions;
CMC is the total costs of corrective maintenance computed as the cost Cr per the number of corrective actions.
TC is the total costs computed as the sum of CI, CMP and CMC.
The first set of simulations is conducted with the best results of Nahas (2017); Table 3 reports the results comparison ((b)) denotes the results of the benchmark). This comparison is made considering negligible the preventive actions time in the simulation model.
In the case of no preventive actions (No PM), Nahas (2017) provided results only for the cases 1 and 2 (low production rate). The difference with the simulation results is relevant. The production rate is lower than the benchmark (over 70%) and the costs of the simulation results are lower than the benchmark.
The difference in the production rate with the benchmark reduces with the introduction of the preventive actions (PM). This difference is lower for the high production case (case 7) with a difference of about 14%. The total costs are very similar except for case 7. In case 7, Nahas (2017) considered a high level of buffer storage with a dramatic increase in holding costs.
From the above comparison, the following consideration can be drawn. The simulation model with a higher level of detail allows evaluating costs and production rate more realistic. This is relevant observing the production rate between the case with the PM and No PM. The simulation model allows evaluating the improvement in term of production rate introducing the preventive maintenance actions. Moreover, the simulation results highlight how the improvements in production rate lead to increase the total costs (the benchmark leads to reduction). The improvements in manufacturing performance cannot be free.
Then, it is evaluated the average utilization of the buffer storages. Table 4 reports the average percentage utilization of the buffer storages.
The cases with the high production rate (6 and 7) have an acceptable level of average utilization, while the cases with low production rate have some buffers underutilized. Therefore, the results of Nahas (2017) works better in cases of the high production rate.
Because in several cases the average utilization is very low the dynamic allocation of the buffer levels can reduce costs keeping the same level of throughput of the production line.
Figure 2 shows the improvement in production rate introducing first only PM, only buffer and PM with buffer.
The PM leads to higher improvements in the production rate than the introduction of the buffer. The combination of preventive maintenance and buffer increases the production rate to a higher level. These results are obtained in the cases that the time of preventive actions is negligible.
Further simulations are conducted introducing the time of preventive actions (see expression 4) evaluating the value added by the buffer and PM.
Figure 3 shows the value added by PM and buffer considering the time of preventive actions (the buffer leads to the same result of Fig. 2).
The difference between the preventive actions and buffer is reduced; however, the preventive actions lead to a better production rate than the buffer.
In this case, the cases lead to different improvements in the throughput. The cases 1 and 2 (lower throughput of the production line) have lower improvements, while the higher improvements are obtained when the production line is characterized by a higher level of the production rate.
Then, the simulations have been conducted to evaluate the proposed dynamic approach. The results are obtained for Lmin = 10 and K = 30 (see expression 2) and the values of threshold thri (see Fig. 1) equal for all machines of 0 (Thr1) and 1 (thr2).
Figure 4 shows the results of the dynamic approach considering only the dynamic time between preventive actions (Thr1 and Thr2) and the dynamic approach with PM and buffer storage level (Dyn) with the two levels of threshold.
The dynamic approach proposed with threshold 0 leads to better results of a production rate except for the cases 5 and 6. In all cases, the increment of the threshold from 0 to 1 reduces the improvements in the production rate because the preventive actions are reduced.
However, the proposed approach needs to be considering with the evaluation of the costs.
Table 5 reports the costs (/1000) for each combination and cases investigated. The costs reported concern the following cases:
NO B NO PM the simulation model without buffer and no preventive maintenance actions performed;
NO PM; the simulation model with buffer and no preventive maintenance actions performed;
NO B the simulation model without buffer and the introduction of preventive maintenance actions;
NO PM the simulation model with buffer and no preventive maintenance actions performed;
B PM the simulation model with buffer and the introduction of preventive maintenance actions;
Bench the results of Nahas (2017).
The other notations are the same used in Fig. 4.
The first consideration concerns the evaluation of the costs related to the increase in the production rate. Generally, the improvement in production rate is proportional to the investments in the buffer and preventive maintenance actions. The benefit of the PM is more relevant when the production rate required is higher (cases 5, 6 and 7). The dynamic allocation of the buffer storages works better when the production rate required is higher (case 7) reducing drastically the costs with the same level of the production rate of the other models tested. The cases of low production rate required (cases 1, 2, and 3) the fixed allocation of the buffer storages and dynamic PM actions lead to better results in terms of costs and production rate.
From the comparison of the simulation model with the benchmark, the following issues can be drawn:
The benchmark over-estimates the CMC and CI costs. The CI costs are over-estimated because the simulation models allow computing the real utilization of the buffers.
The performance of the production lines is over-estimated. The real throughput is lower than the benchmark model (modeled by queue network).
The map of the costs obtained with the simulation environment developed can be a decision support system to choose the best model evaluating the condition of production rate, preventive maintenance actions time required, and the buffer storages allocation.
Finally, a Design of Experiment is used to evaluate the effect of three parameters of the approaches proposed: Lmin, K and Thr.
Table 6 reports the eight combinations of the experimental classes and the results evaluated: CI, CMP, TC and P.
Figure 5 shows the evaluation of the effects as the percentage on the average value of the performance analyzed.
The effect on TC is due to the main effects of the three parameters. The TC depends mainly on the Lmin. The CI depends on the Lmin and K, while Thr affects the CMP (preventive maintenance). The interaction of the three parameters affects the CMP (over 20%).
The above results allow highlighting what is the parameter to modify to reduce a particular cost.
Moreover, it can be noticed that the throughput has a low dependency on the parameters of the approaches proposed. Therefore, the proposed dynamic approach allows keeping the same level of production rate controlling the cost components.
Conclusions and future development
In this paper, the buffer allocation problem with preventive maintenance policy in production lines is investigated. A simulation environment has been developed and compared to a benchmark proposed in the literature (Nahas 2017). The numerical results highlight the difference between the queue network and simulation in terms of performance evaluation. Moreover, a dynamic policy for buffer storage level and time between preventive maintenance actions is proposed. The numerical results show how the proposed policy leads to better results in terms of reduction of total costs and improvement of the production rate in case of high production rates required, while the design of fixed level of buffer storage works better for lower production rates required.
The proposed approach can be controlled by three parameters that have the main influence on the cost’ components: holding, preventive and corrective. Therefore, the practitioners can use the simulation environment developed and setting only three parameters to decide what costs to reduce keeping the same level of a production rate.
The managerial implications concern the suggestions to improve the production rate considering the set of the buffer level and preventive maintenance actions. The practitioners can use the proposed model to support the decision on the costs (due to the buffer level) and throughput rate to reach.
Moreover, the results highlight the main effects on the throughput rate to obtain a more robust production line behavior.
Future development research paths concern the following issues: the evaluation of the performance when the work center consists of parallel machines; the evaluation of the production rate fluctuates and when the processing times of the machines are different (unbalanced production lines).
References
Amiri M, Mohtashami A (2012) Buffer allocation in unreliable production lines based on design of experiments, simulation, and genetic algorithm. Int J Adv Manuf 62(1–4):371–383
Battini D, Persona A, Regattieri A (2009) Buffer size design linked to reliability performance: a simulative study. Comput Ind Eng 56(4):1633–1641
Chow W (1987) Buffer capacity analysis for sequential production lines with variable processing times. Int J Prod Res 25(8):1183–1196
Demir L, Tunali S, Eliiyi DT (2014) The state of the art on buffer allocation problem: a comprehensive survey. J Intell Manuf 25(3):1–22
Dolgui A, Eremeev A, Sigaev V (2007) HBBA: hybrid algorithm for buffer allocation in tandem production lines. J Intell Manuf 18:411–420
Gento AM, Redondo A (2003) Rough sets and maintenance in a production line. Expert Syst 20(5):271–279
Massim Y, Yalaouib F, Amodeob L, Chateletc E, Zeblaha A (2010) Efficient combined immune-decomposition algorithm for optimal buffer allocation in production lines for throughput and profit maximization. Comput Oper Res 37(4):611–620
Massim Y, Yalaoui F, Chatelet E, Yalaoui A, Zeblah A (2012) Efficient immune algorithm for optimal allocations in series-parallel continuous manufacturing systems. J Intell Manuf 23(5):1603–1619
Meller RD, Kim DS (1996) The impact of preventive maintenance on system cost and buffer size. Eur J Oper Res 95(3):577–591
Nahas N (2017) Buffer allocation and preventive maintenance optimization in unreliable production lines. Int J Intell Manuf. https://doi.org/10.1007/s10845-014-0963-y
Nahas N, Nourelfath M, Ait-Kadi D (2006) A new approach for buffer allocation in unreliable production lines. Int J Prod Econ 103(2):873–881
Nahas N, Nourelfath M, Ait-Kadi D (2009) Selecting machines and buffers in unreliable series-parallel production lines. Int J Prod Res 47:3741–3774
Northworthy S Abdul-Kader W (2004) Impact of preventive maintenance on serial production line performance: a simulation approach. In: ASAC 2004, Quebec city, Quebec
Patchong A, Willaeys D (2001) Modeling and analysis of an unreliable flow, line composed of parallel-machine stages. IIE Trans 33:559–568
Radhoui M, Rezg N, Chelbi A (2009) Integrated model of preventive maintenance, quality control and buffer sizing for unreliable and imperfect production systems. Int J Prod Res 47(2):389–402
Renna P (2012) Influence of maintenance policies on multi-stage manufacturing systems in dynamic conditions. Int J Prod Res 50(2):345–357
Rezg N, Chelbi A, Xie X (2005) Modeling and optimizing a joint inventory control and preventive maintenance strategy for a randomly failing production unit: analytical and simulation approaches. Int J Comput Integr Manuf 18(2–3):225–235
Shi C, Gershwin S (2009) An efficient buffer design algorithm for production line profitmaximization. Int J Prod Econ 122(2):725–740
Srinivas C, Satyanarayana B, Ramji K, Ravela N (2011) Determination of buffer size in single and multi row flexible manufacturing systems through simulation. Int J Eng Sci Technol 3(5):3889–3899
Srinivasa Rao M, Naikan VNA (2014) Reliability analysis of repairable systems using system dynamics modeling and simulation. J Ind Eng Int 10:69
Staley DR, Kim DS (2012) Experimental results for the allocation of buffers in closed serial production lines. Int J Prod Econ 137(2):284–291
Tsarouhas PH (2015) Performance evaluation of the croissant production line with reparable machines. J Ind Eng Int 11(1):101–110
Yusuf I (2014) Comparative analysis of profit between three dissimilar repairable redundant systems using supporting external device for operation. J Ind Eng Int 10:77
Yuzukirmizi M, Smith JM (2008) Optimal buffer allocation in finite closed networks with multiple servers. Comput Oper Res 35:2579–2598
Zequeira R, Valdes JE, Berenguer C (2008) Optimal buffer inventory and opportunistic preventive maintenance under random production capacity availability. Int J Prod Econ 111:686–696
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Renna, P. Adaptive policy of buffer allocation and preventive maintenance actions in unreliable production lines. J Ind Eng Int 15, 411–421 (2019). https://doi.org/10.1007/s40092-018-0301-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-018-0301-7