Introduction

The managing of inventories is one of the most significant tasks that every manager must do efficiently and effectively in any organization so that their organization can grow. Now, all the organizations are involved in a global competitive market and then these organizations are taking seriously the activities related to manage inventories. Thus, recently the practitioners and researchers have been increasing their interest in optimizing the inventory decisions in a holistic way. Thus, the manager tries to find out different ways through which the cost associated with inventory can reduce and the profit of the organization can increase. Recently, the business operations such as share marketing and trade credit financing have been a powerful tool to increase sales and profits. In practice, vendors allow a fixed period to settle the payment without penalty for their customers to increase sales and reduce on-hand inventory. In fact, a permissible delay in payment decreases the cost of inventory holding because this action decreases the amount of capital invested in inventory for the duration of the permissible period. Furthermore, for the period of the delay in payment, the retailer can accumulate revenue on sales and earn interest on that revenue via share marketing investment or banking business. This type of inventory problem is known as inventory problem with permissible delay in payments. In today’s severely competitive business environment, business men are increasingly using trade credit to stimulate the demand of the products and attract more customers. As a result, the trade credit financing plays an important role in modern business operations as a source of funds aside from banks and other financial institutions (Yang and Birge 2013). In India, the non-state-owned enterprises often obtain limited support from banks. Therefore, the trade credit policy is adopted as a very important short-term financing method. On the other hand, the policy of granting trade credit adds not only an additional cost but also an additional dimension of default risk (i.e., the event in which the buyer will be unable to payoff its debt obligations) to the retailer (Teng et al. 2005).

During the past few years, many articles dealing with a range of inventory models under trade credit have appeared in various journals. At the earliest, Goyal (1985) established a single-item inventory model under permissible delay in payments when selling price equals the purchase cost. Aggarwal and Jaggi (1995) extended Goyal (1985) model to consider the deteriorating items. Jamal et al. (1997) further generalized the model to allow for shortages. Teng (2002) amended Goyal (1985) model by considering the difference between selling price and purchasing cost, and found that it makes economic sense for a well-established retailer to order less quantity and take the benefits of payment delay more frequently. Chang et al. (2003) developed an EOQ model for deteriorating items under supplier credits linked to ordering quantity. Huang (2003) extended Goyal (1985) model to develop an EOQ model with up-stream and down-stream trade credits in which the length of down-stream trade credit period is less than or equal to the length of the up-stream trade credit period. Teng and Goyal (2007) complemented the shortcoming of Huang (2003) model and proposed a generalized formulation. Mahata and Goswami (2007) developed an inventory model to determine an optimal ordering policy for deteriorating items under two-level trade credit policy in the fuzzy sense. Huang (2007) incorporated Huang (2003) model to investigate the two-level trade credit policy in the EPQ frame work. Recently, Mahata (2012) proposed an EPQ model for deteriorating items with up-stream full trade credit and down-stream partial trade credit with a constant demand. Annadurai and Uthayakumar (2012) analyzed partial trade credit financing in a supply chain by EOQ-based model for decaying items with shortages. Taleizadeh et al. (2013) considered an EOQ problem under partial delayed payment and partial backordering. Chen et al. (2014) discussed the EPQ model under retailer partial trade policy. Taleizadeh and Nematollahi (2014) investigated the effects of time value of money and inflation on the optimal ordering policy in an inventory control system to manage a perishable item over the finite horizon planning under backordering and delayed payment. Ouyang et al. (2015) discussed the integrated inventory model with the order-size dependent trade credit and a constant demand. Lashgari et al. (2015) proposed a lot-sizing model with partial up-stream advanced payment and partial down-stream delayed payment in a three-level supply chain. Recently, Zia and Taleizadeh (2015) presented a lot-sizing model with backordering under hybrid linked-to-order multiple advance payments and delayed payment. Many related articles can be found in Chang and Teng (2004), Chung (2008), Chung and Liao (2004), Goyal et al. (2007), Huang and Hsu (2008), Mahata and Mahata (2011, 2014a, b), Lashgari et al. (2016) and their references.

All the Above researchers established their EOQ or EPQ inventory models under trade credit financing based on the assumption that the demand rate is constant over time. However, in practice, the market demand is always changing rapidly and is affected by several factors such as price, time, inventory level, and delayed payment period. From a product life cycle perspective, it is only in the maturity stage that demand is near constant. During the growth stage of a product life cycle (especially for high-tech products), the demand function increases with time. Moreover, the marginal influence of the credit period on sales is associated with the unrealized potential market demand. To obtain robust and generalized results, we extend the constant demand to a credit-sensitive and linear non-decreasing function of time.

Related to this context, few papers explore the optimal replenishment policies of the retailer under trade credit financing by considering demands that are sensitive to either time stock and/or credit period. Sarkar (2012), Teng et al. (2012) and Mahata and Mahata (2014b) build the economic order quantity model with trade credit financing for time-dependent demand. Mahata (2015a) discuss the inventory replenishment problems with up-stream full trade credit and down-stream partial trade credit financing by considering a price-sensitive demand. Soni (2013) developed the optimal replenishment policies under trade credit financing by considering price and stock-sensitive demand. Some studies focus on demand dependence on delayed payment time. The inventory model with the credit-linked demand are discussed by Jaggi et al. (2008), Jaggi et al. (2012). Thangam and Uthayakumar (2009) discuss trade credit financing for perishable items in a supply chain when demand depends on both selling price and credit period. Lou and Wang (2012) study optimal trade credit and order quantity by considering trade credit with a positive correlation of market sales, but are negatively correlated with credit risk. Giri and Maiti (2013) discuss the supply chain model with price and trade credit-sensitive demand with trade credit by considering the fact that a retailer shares a fraction of the profit earned during the credit period. Wu (2014) explore optimal credit period and lot size by considering demand dependence on delayed payment time with default risk for deteriorating items with expiration dates. Annadurai and Uthayakumar (2015) develop the decaying inventory model with stock-dependent demand and shortages under two-level trade credit. Dye and Yang (2015) discuss the sustainable trade credit and replenishment policy with credit-linked demand and credit risk considering the carbon emission constraints. Mahata (2015b) propose an EOQ model for the retailer to obtain his/her optimal credit period and cycle time under two-level trade credit by considering demand dependence on delayed payment time with default risk for deteriorating items.

In traditional supplier-retailer-buyer supply chain inventory models, the supplier frequently offers the retailer a trade credit of M periods, and the retailer in turn provides a trade credit of N periods to her/his buyer to stimulate sales and reduce inventory. From the seller’s perspective, granting trade credit increases sales and revenue but also increases opportunity cost (i.e., the capital opportunity loss during credit period) and default risk. Also, from a product life cycle perspective, it is only in the maturity stage that demand is near constant. During the growth stage of a product life cycle (especially for high-tech products), the demand function increases with time. To obtain robust and generalized results, we extend the constant demand to a linear non-decreasing demand function of time. As a result, the fundamental theoretical results obtained here are suitable for both the growth and maturity stages of a product life cycle. However, none of the paper discusses the optimal trade credit and order policy by considering demand to a credit-sensitive and linear non-decreasing function of time involving default risk. Therefore, in-depth research is required on the inventory policy that considers demand sensitive to time and credit period involving default risk to extend the traditional EOQ model. The main aspects of this paper is to develop an economic order quantity model for the retailer where: (1) the supplier provides an up-stream trade credit and the retailer also offers a down-stream trade credit, (2) the retailer’s down-stream trade credit to the buyer not only increases sales and revenue but also opportunity cost and default risk, and (3) the demand rate of which varies simultaneously with time and the length of credit period that is offered to the customers. We model the retailer’s inventory system under these conditions as a profit maximization problem. We then show that the retailer’s optimal credit period and cycle time not only exist but also are unique. Furthermore, we run some numerical examples to illustrate the problem and provide managerial insights.

Problem description and formulation

In this paper, we formulate a supplier-retailer-customer supply chain inventory model under two levels of trade credit policy with default risk consideration. The supplier frequently offers the retailer a trade credit of M periods, and the retailer in turn provides a trade credit of N periods to her/his buyer to stimulate sales and reduce inventory. From the seller’s perspective, granting trade credit increases sales and revenue but also increases default risk (i.e., the percentage that the buyer will not be able to pay off her/his debt obligations). Here, the demand is assumed to be credit-sensitive and increasing function of time. The aim of this paper is to maximize the retailer’s annual total profit in each cycle by making decisions regarding the credit period and lot size. The following notation is used to model the problem

  • A ordering cost per order for the retailer

  • h unit stock holding cost per item per year (excluding interest charges) for the retailer

  • c unit purchasing cost of the retailer

  • s unit selling price with \(s>c\)

  • \(I_{\rm{e}}\) interest earned per \( \$ \) per year by the retailer

  • \(I_{\rm{p}}\) interest charged per \( \$ \) in stocks per year to the retailer

  • M the retailer’s trade credit period offered by supplier in years

  • N the customer’s trade credit period offered by retailer in years

  • T replenishment time interval for the retailer, where \(T\ge 0\)

  • Q the order quantity for the retailer

  • I(t) the inventory level in units at time t

  • D(t, N) the market annual demand rate in units, which is a function of time t and the trade credit period.

  • \(T^*\) the optimal replenishment period for the retailer

  • \(N^*\) the optimal trade credit period offered to the customers by the retailer

  • \(\Pi (N,T)\) the profit per year for the retailer

Also, the mathematical model proposed in this paper are based on the following assumptions:

  1. 1.

    Time horizon is infinite.

  2. 2.

    Replenishment is instantaneous; shortage is not allowed.

  3. 3.

    The supplier provides the trade credit period M to the retailer, and the retailer offers its customers trade credit period N.

  4. 4.

    Demand rate D(t, N) is a function of time t and the credit period N. For simplicity, we assume that \(D(t,N)=a+bt+\lambda (N)\), where a and b are non-negative constants, and t is within a positive time frame, governing the linear trend of the demand with respect to time t as the demand rate in today’s high-tech products increases significantly during the growth stage; \(\lambda '(N)>0\) reflects the demand increasing with the credit period as trade credit attracts new buyers who consider it a type of price reduction.

  5. 5.

    When the credit period is longer, the default risk to the retailer is higher. For simplicity, the rate of the default risk given the credit period offered by the retailer is \(F(N)=1-{\rm{e}}^{-kN}\), where \(k>0\). This default risk pattern is used in some studies (Lou and Wang 2012; Zhang et al. 2014).

Given the above assumptions, it is possible to formulate a mathematical inventory EOQ model with trade credit financing.

Model formulation

The retailer orders and receives the order quantity Q units at time \(t=0\) of a single product from the supplier. Hence, the inventory starts with Q units at time \(t=0\), and gradually depletes in the interval [0, T] due to increasing demand from the customers. At time \(t=T\), the inventory level reaches zero. Hence, inventory level I(t) with respect to time is governed by the following differential equation:

$$\begin{aligned} \frac{{\rm{d}}I(t)}{{\rm{d}}t}=-D(t,N) =-[a+bt+ \lambda (N)]\quad 0\le t\le T, \end{aligned}$$
(1)

with the boundary condition \(I(T)=0\). By solving the differential equation (1), we can obtain

$$\begin{aligned} I(t)=\rho (T-t)+\frac{1}{2}b(T^2-t^2), \quad 0\le t\le T,\quad\text{ where }\quad \rho =a+\lambda (N). \end{aligned}$$
(2)

Consequently, the retailer’s order quantity is

$$\begin{aligned} Q=I(0)=\rho T+\frac{1}{2}bT^2. \end{aligned}$$
(3)

The retailer’s annual profit per cycle consists of the following elements: revenue, ordering cost, purchasing cost, holding cost, interest charged, and interest earned. The components are evaluated as follows.

  1. 1.

    Annual ordering cost per cycle is \(\frac{A}{T}\).

  2. 2.

    Annual purchasing cost per cycle is \(\frac{cQ}{T}=\frac{c}{T}\Big (\rho T+\frac{1}{2}bT^2\Big )\).

  3. 3.

    Annual holding cost excluding interest charges per cycle is

    $$\begin{aligned} \frac{h}{T}\int _0^TI(t){\rm{d}}t=\frac{h}{T}\Big (\frac{1}{2}\rho T^2 +\frac{1}{3}bT^3\Big ). \end{aligned}$$
  4. 4.

    The sales revenue considering default risk is

    $$\begin{aligned} \frac{se^{-kN}}{T}\int _0^TD(t){\rm{d}}t=\frac{se^{-kN}}{T}\Big (\rho T+\frac{1}{2}bT^2\Big ). \end{aligned}$$
  5. 5.

    The interest earned and interest charged is shown in Case 1 and 2 below.

The following two potential cases are obtained from the values of M and N: (1) \(N\le M\), and (2) \(N\ge M\). Let us discuss them separately.

Case 1

\(N\le M\) In this case, we have two possible sub-cases: (1) \(T+N\le M\) and (2) \(T+N \ge T+N\). Now, let us discuss the detailed formulation in each sub-case.

Sub-case 1.1

\(T+N\le M\) With \(T+N\le M\), the retailer receives the sales revenue at time \(T+N\) and is able to pay off the total purchasing cost at time M. Therefore, there is no interest charged. During the period \([N,T+N]\), the retailer can obtain the interest earned on the sales revenues received and on the full sales revenue during the period \([T+N,M]\). Therefore, the annual interest earned is

$$\begin{aligned} &\frac{sI_{\rm{e}}}{T}\left[\int _0^{T+N}\int _N^{t+N}D(u-N){\rm{d}}u{\rm{d}}t +(M-T-N)\int _0^T D(u){\rm{d}}u\right]\\ &\quad= \frac{sI_{\rm{e}}}{T}\left [\frac{1}{2}\rho T^2+\frac{1}{6}bT^3+(M-T-N)\Big (\rho T+\frac{1}{2}bT^2\Big )\right].\end{aligned}$$

Combining the above results, the retailer’s annual total profit can be expressed as follows.

$$\begin{aligned} \Pi _1(N,T) &= \text{ Net } \text{ revenue } \text{ after } \text{ default } \text{ risk } - \text{ annual } \text{ ordering } \text{ cost } - \text{ annual } \text{ purchasing } \text{ cost }\nonumber \\ &\quad- \text{ annual } \text{ holding } \text{ cost } + \text{ annual } \text{ interest } \text{ earned } - \text{ interest } \text{ charged }\nonumber \\ &= \frac{1}{T}\Bigg \{\Big [se^{-kN}-c+sI_{\rm{e}}(M-N)\Big ]\Big (\rho T+\frac{1}{2}bT^2\Big ) -(h+sI_{\rm{e}})\Big (\frac{1}{2}\rho T^2+\frac{1}{3} bT^3\Big ) -A\Bigg \}. \end{aligned}$$
(4)

Next, we discuss the other sub-case in which \(M\le T+N\).

Sub-case 1.2

\(M\le T+N\) During the interval \([M,T+N]\), the retailer must pay the interest for the items unsold. Therefore, we can have the interest charged in the following:

$$\begin{aligned}&\frac{cI_{\rm{p}}}{T}\int _M^{T+N}I(t-N){\rm{d}}t= \frac{cI_{\rm{p}}}{T}\int _{M-N}^TI(t){\rm{d}}t \\ = & {} \frac{cI_{\rm{{p}}}}{T}\left [\frac{1}{2} \rho \{T-(M-N)\}^2+ \frac{1}{2}bT^2 \{T-(M-N)\} -\frac{1}{6}b\{T^3-(M-N)^3\}\right ]. \end{aligned}$$

The retailer can earn interest from the delayed payment during period [N, M]. Therefore, we have the interest earned in the following:

$$\begin{aligned} \frac{sI_{\rm{e}}}{T}\int _N^M\int _N^{t+N}D(u-N){\rm{d}}u{\rm{d}}t= \frac{sI_{\rm{e}}}{T}\Big [\frac{1}{2}\rho (M-N)^2+\frac{1}{6}b(M-N)^3\Big ]. \end{aligned}$$

Hence, similar to (4), we know that the retailer’s annual total profit is

$$\begin{aligned} \Pi _2(N,T)= \,& {} \frac{1}{T}\Bigg \{\Big [se^{-kN}-c+cI_{\rm{p}}(M-N)\Big ]\Big (\rho T+\frac{1}{2}bT^2\Big )+(sI_{\rm{e}}-cI_{\rm{p}})\Big [ \frac{1}{2}\rho (M-N)^2 \nonumber \\ &+\frac{1}{6}b(M-N)^3\Big ]-(h+cI_{\rm{p}})\Big (\frac{1}{2}\rho T^2+\frac{1}{3} bT^3\Big ) -A\Bigg \}. \end{aligned}$$
(5)

Combining (4) and (5), we have \(\Pi _1(N,M-N)=\Pi _2(N,M-N)\). Then, we formulate the retailer’s annual total profit for the case of \(N\ge M\) below.

Case 2

\(N\ge M\) Since \(M\le N\), there is no interest earned. The retailer must finance all the purchasing cost from [M, N] and pay off the loan from \([N,T+N]\). Therefore, the interest charged per cycle is

$$\begin{aligned} \frac{cI_{\rm{p}}}{T}\Big [(N-M)Q+\int _{N}^{T+N}I(t-N){\rm{d}}t\Big ] =\frac{cI_{\rm{p}}}{T}\Big [\Big (\rho T+\frac{1}{2}bT^2\Big )(N-M)+\Big (\frac{1}{2} \rho T^2+\frac{1}{3}bT^3\Big )\Big ]. \end{aligned}$$

Consequently, the retailer’s annual total profit function per cycle can be expressed as

$$\begin{aligned} \Pi _3(N,T)= \,& {} \frac{1}{T}\Bigg \{\Big [se^{-kN}-c+cI_{\rm{p}}(M-N)\Big ]\Big (\rho T+\frac{1}{2}bT^2\Big ) -(h+cI_{\rm{p}})\Big (\frac{1}{2}\rho T^2+\frac{1}{3} bT^3\Big ) -A\Bigg \}. \end{aligned}$$
(6)

Therefore, the retailer’s objective is to determine the optimal credit period \(N^*\) and cycle time \(T^*\) such that the annual total profit \(\Pi _i(N,T)\) for \(i=1, 2,\) and 3 is maximized.

Theoretical results and optimal solutions

The main purpose of this paper is to determine the optimal replenishment and trade credit policies that correspond to maximizing the total profit per unit time. To achieve our purpose, in all cases, we first establish conditions where for any given N, the optimal solution of T not only exists but also is unique. Then, for any given value of T, there exists a unique N that maximizes the total profit per unit time.

Optimal solution for the case of \(N\le M\)

For any given N, to find the optimal replenishment policy \(T_1^*\), we take the first-order partial derivative of \(\Pi _1(T|N)\) with respect to T, we can obtain

$$\begin{aligned} \frac{\partial \Pi _1(T|N)}{\partial T}= \frac{1}{T^2} \left \{\frac{[se^{-kN} -c+ sI_{\rm{e}}(M-N)]b}{2}T^2 -(h+sI_{\rm{e}})\Big ( \frac{1}{2}\rho T^2+\frac{2}{3}bT^3\Big ) +A\right \}=0, \end{aligned}$$
(7)

which implies that

$$\begin{aligned} \frac{2}{3}(h+sI_{\rm{e}})bT^3- \frac{[se^{-kN}-c+sI_{\rm{e}}(M-N)]b -(h+sI_{\rm{e}})\rho }{2}T^2-A =0. \end{aligned}$$
(8)

By taking the second-order partial derivative of \(\Pi _1(T|N)\) with respect to T, we can obtain

$$\begin{aligned} \frac{\partial ^2 \Pi _1(T|N)}{\partial T^2}=-\frac{2A}{T^3}-\frac{2}{3} b(h+sI_{\rm{e}})<0. \end{aligned}$$
(9)

Hence, for any given N, \(\Pi _1(T|N)\) is strictly concave function of T. For simplicity, let’s define a discrimination term:

$$\begin{aligned} \Delta =\frac{[se^{-kN}-c+sI_{\rm{e}}(M-N)]b- (h+sI_{\rm{e}}) \rho }{2} (M-N)^2 -\frac{2}{3}(h+sI_{\rm{e}})b(M-N)^3 +A. \end{aligned}$$
(10)

Then, we have the following result.

Theorem 1

For any given N, the following theoretical results can be obtained for the profit function \(\Pi _1(T|N)\):

  1. (i)

    Equation (8) has only one positive solution.

  2. (ii)

    If the only positive solution \(T_1\) to Eq. (8) is less than or equal to \(M-N\), then \(T_1\) is the only optimal solution to \(\Pi _1(T|N)\) in Eq. (4).

  3. (iii)

    If \(\Delta <0\), then \(\Pi _1(T|N)\) has the unique optimal solution \(T_1\), which is less than \(M-N\). Otherwise, if \(\Delta \ge 0\), the optimal solution is \(T_1=M-N\).

Proof

See Appendix A. For any given \(T>0\), taking the first-order and second-order partial derivative of \(\Pi _(N|T)\) with respect to N, we can obtain

$$\begin{aligned}&\frac{\partial \Pi _1(N|T)}{\partial N} = (-k\rho -kbT/2+\rho ')se^{-kN}\nonumber \\ &-c\rho '-\frac{h\rho 'T}{2} +\frac{sI_{\rm{e}}}{2}[2(M-N)\rho '-(bT+2\rho )-\rho 'T] \end{aligned}$$
(11)
$$\begin{aligned}&\frac{\partial ^2 \Pi _1(N|T)}{\partial N^2} = [\rho ''-2k\rho '+k^2(\rho +bT/2)]se^{-kN}\nonumber \\ &-c\rho '' -\frac{h\rho ''T}{2}+ \frac{sI_{\rm{e}}}{2}[(2(M-N)-T)\rho ''-4\rho '], \end{aligned}$$
(12)

where \(\rho '=\lambda '(N)\) and \(\rho ''=\lambda ''(N)\). Finding \(\Pi _1(N|T)\) is a continuous function of N for \(N\in [0,\infty )\) is easy. Therefore, \(\Pi _1(N|T)\) has a maximum value for \(N\in [0,\infty )\). To identify whether N is 0 or positive, we define the following discrimination term:

$$\begin{aligned}&\Delta _{N_1}=\frac{\partial \Pi _(N|T)}{\partial N}|_{N=0}=(-k\rho -kbT/2+\rho ')s \nonumber \\ &-c\rho '-\frac{h\rho 'T}{2} +\frac{sI_{\rm{e}}}{2}[2(M-N)\rho '-(bT+2\rho )-\rho 'T]. \end{aligned}$$
(13)

If \(\frac{\partial ^2\Pi _1(N|T)}{\partial N^2}<0\), \(\Pi _1(N|T)\) is strictly concave function in N, hence exists a unique maximum solution \(\widehat{N}_1\). If \(\Delta _{N_1}\le 0\), then \(\Pi _1(N|T)\) is maximized at \(N_1^*=0\); if \(\Delta _{N_1}>0\), \(\Pi _1(N|T)\) is maximized with \(N_1^*=\widehat{N}_1>0\). Based on Eq. (12), it is easy to obtain if \([\rho ''-2k\rho '+k^2(\rho +bT/2)]s-(c+hT/2)\rho ''\le 0\) and \([2(M-N)-T]\rho ''-4\rho '\le 0\), \(\Pi _1(N|T)\) is strictly concave function in N. Hence, a unique maximum solution exists. If \(\frac{\partial ^2\Pi _1(N|T)}{\partial N^2}\ge 0\), then \(\Pi _1(N|T)\) is a convex function of N. Therefore, the optimal solution of \(\Pi _1(N|T)\) is at one of the two boundary points 0 or \(\infty\). Substituting \(\infty\) in Eq. (11), we have \(\lim _{N\rightarrow \infty }\frac{\partial \Pi _1(N|T)}{\partial N}<0\). Hence \(N=+\infty\) is not an optimal solution, which implies that the optimal solution is \(N_1^*=0\). Consequently, the following theoretical result can be derived. \(\square\)

Theorem 2

For any given \(T>0\), if \([\rho ''-2k\rho '+k^2(\rho +bT/2)]s-(c+hT/2)\rho ''\le 0\) and \([2(M-N)-T]\rho ''-4\rho '\le 0\), then

  1. (1)

    \(\Pi _1(N|T)\) is strictly concave function in N, hence exists a unique maximum solution.

  2. (2)

    If \(\Delta _{N_1}\le 0\), then \(\Pi _1(N|T)\) is maximizedat \(N_1^*=0\).

  3. (3)

    If \(\Delta _{N_1}>0\), then there exists a unique \(\widehat{N}_1>0\) such that \(\Pi _1(N|T)\) is maximized at \(N_1^*=\widehat{N}_1>0\).

Similarly, for any given N, to find the optimal replenishment policy \(T_2^*\), we take the first-order partial derivative of \(\Pi _2(T|N)\) with respect to T, we can obtain

$$\begin{aligned}\frac{\partial \Pi _2(T|N)}{\partial T} = &\frac{[se^{-kN}-c+ cI_{\rm{p}}(M-N)]b-(h+cI_c)\rho }{2} -\frac{2}{3}(h+cI_{\rm{p}})bT \nonumber \\ & - (sI_{\rm{e}}-cI_{\rm{p}})\Big (\frac{\rho (M-N)^2}{2T^2}+\frac{b(M-N)^3}{6T^2}\Big ) +\frac{A}{T^2}=0,\end{aligned}$$
(14)

which implies that

$$\begin{aligned}&\frac{2}{3}(h+cI_{\rm{p}})bT^3- \frac{[se^{-kN}-c+cI_{\rm{p}}(M-N)]b-(h+cI_{\rm{p}})\rho }{2}T^2 \nonumber \\ &-\Big [A-(sI_{\rm{e}}-cI_{\rm{p}})\Big (\frac{\rho (M-N)^2}{2T^2}+\frac{b(M-N)^3}{6T^2}\Big )=0. \end{aligned}$$
(15)

By taking the second-order partial derivative of \(\Pi _2(T|N)\) with respect to T, we can obtain

$$\begin{aligned} \frac{\partial ^2 \Pi _2(T|N)}{\partial T^2}=-\frac{2}{3} b(h+cI_{\rm{p}})+(sI_{\rm{e}}-cI_{\rm{p}})\Big (\frac{\rho (M-N)^2}{2T^2}+\frac{b(M-N)^3}{6T^2}\Big ) -\frac{2A}{T^3}. \end{aligned}$$
(16)

For simplicity, we set

$$\begin{aligned} Z=&\frac{1}{3}(h+cI_c)bT^3-(sI_{\rm{e}}-cI_{\rm{p}})\\& \Big [\frac{1}{2}\rho (M-N)^2 +\frac{1}{6}b(M-N)^3\Big ]+A. \end{aligned}$$
(17)

From Eq. (16) we know that if \(Z>0\), then \(\frac{\partial ^2\Pi _2(T|N)}{\partial T^2}<0\), and \(\Pi _2(T|N)\) is strictly concave in T. In this case, if the only positive solution \(T_2\) to Eq. (15) is greater than or equal to \(M-N\), then \(T_2\) is the only optimal solution to \(\Pi _2(T|N)\). On the other hand, if the only positive solution \(T_2\) to Eq.  (14) is less than \(M-N\), then \(\Pi _2(T|N)\) is a strictly decreasing function of T from \(M-N\) on. Hence, \(\Pi _2(T|N)<\Pi _2(M-N|N)\), for all \(T>M-N\). Consequently, the only optimal solution to \(\Pi _2(T|N)\) is \(T_2=M-N\). Next, we discuss the other case in which \(Z\le 0\). If \(Z\le 0\) then \(\frac{\partial ^2\Pi _2(T|N)}{\partial T^2}\ge 0\) and \(\Pi _2(T|N)\) is a convex function of T. Therefore, the optimal solution of \(\Pi _2(T|N)\) is at one of the two boundary points (i.e., \(T=M-N\) or \(T=+\infty\). Substituting \(Z\le 0\) into Eq. (14), we have

$$\begin{aligned}&\frac{\partial \Pi _2(T|N)}{\partial T} = \frac{[se^{-kN}-c+ cI_{\rm{p}}(M-N)]b-(h+cI_c)\rho }{2} +\frac{Z^3}{T^2} -(h+cI_{\rm{p}})bT\nonumber \\ < & {} \frac{[se^{-kN}-c+ cI_{\rm{p}}(M-N)]b-(h+cI_c)\rho }{2} -(h+cI_{\rm{p}})bT <0, \text{ if } T\rightarrow +\infty . \end{aligned}$$
(18)

Hence, \(T=+\infty\) is not an optimal solution, which implies that the optimal solution is \(T_2=M-N\). Consequently, the following theoretical results for \(\Pi _2(T|N)\) can be derived.

Theorem 3

For any given N, the following theoretical results can be obtained for the profit function \(\Pi _2(T|N)\):

  1. (i)

    Equation (15) has only one positive solution.

  2. (ii)

    If the only positive solution \(T_2\) to Eq. (15) is greater than or equal to \(M-N\), then \(T_2\) is the only optimal solution to \(\Pi _2(T|N)\) in Eq. (5). Otherwise, the only optimal solution to \(\Pi _2(T|N)\) is \(T_2=M-N\).

  3. (iii)

    If \(\Delta >0\), then \(\Pi _2(T|N)\) has the unique optimal solution \(T_2\), which is greater than \(M-N\). Otherwise, if \(\Delta \le 0\), the optimal solution is \(T_2=M-N\).

Proof

See Appendix B.

Based upon the above two Theorems 1 and 3, the following main theorem can be derived to determine the optimal solution \(T^*\) to be \(T_1\) or \(T_2\). \(\square\)

Theorem 4

For any given \(N\ge 0\),

  1. (1)

    If \(\Delta <0\), then \(\Pi (T^*|N) =\Pi _1(T_1|N)\). Hence \(T^*=T_1\), and \(T_1<M-N\).

  2. (2)

    If \(\Delta =0\), then \(\Pi (T^*|N) =\Pi _1(M-N|N)=\Pi _2(M-N|N)\). Hence \(T^*=M-N\).

  3. (3)

    If \(\Delta >0\), then \(\Pi (T^*|N) =\Pi _2(T_2|N)\). Hence \(T^*=T_2\), and \(T_2>M-N\).

Proof

See Appendix C. For any given T, taking the first-order and second-order partial derivative of \(\Pi _2(N|T)\) with respect to N, we can obtain

$$\begin{aligned}&\frac{\partial \Pi _2(N|T)}{\partial N} = [\rho '-k\rho -\frac{1}{2} kbT]se^{-kN}\nonumber \\ &-c\rho '-\frac{1}{2}h\rho ' T -\frac{cI_{\rm{p}}}{2T}\Big [(T-(M-N))^2\rho ' +2(T-(M-N))\rho \nonumber \\ &+b(T^2-(M-N)^2)\Big ] +\frac{sI_{\rm{e}}}{T}\Big [\rho '(M-N)^2 -2\rho (M-N)-b(M-N)^2\Big ] \end{aligned}$$
(19)
$$\begin{aligned}&\frac{\partial ^2 \Pi _2(N|T)}{\partial N^2} = [\rho ''-2k\rho ' +k^2(\rho +\frac{1}{2}bT]se^{-kN} -c\rho ''-\frac{1}{2}h\rho '' T \nonumber \\ &-\frac{cI_{\rm{p}}}{2T}\Big [(T-(M-N))^2\rho '' +4(T-(M-N))\rho ' +2\rho +2b(M-N)\Big ] \nonumber \\ &+\frac{sI_{\rm{e}}}{2T}\Big [\rho ''(M-N)^2 -4\rho '(M-N)+2\rho +2b(M-N)\Big ]. \end{aligned}$$
(20)

To identify whether \(N_2\) is 0 or positive, we define the following discrimination term:

$$\begin{aligned} \Delta _{N_2}= \frac{\partial \Pi _2(N|T)}{\partial N}|_{N=0}&= {} [\rho '-k\rho -\frac{1}{2} kbT]s-c\rho '-\frac{1}{2}h\rho ' T -\frac{cI_{\rm{p}}}{2T}\Big [(T-M)^2\rho ' +2(T-M)\rho \nonumber \\ &+b(T^2-M^2)\Big ] +\frac{sI_{\rm{e}}}{T}\Big [\rho 'M^2 -2\rho M-bM^2\Big ]. \end{aligned}$$
(21)

If \(\frac{\partial ^2 \Pi _2(N|T)}{\partial N^2}<0\), \(\Pi _2(N|T)\) is strictly concave function in N, a unique maximum solution \(\widehat{N}_2\) exists. If \(\Delta _{N_2}\le 0\), then \(\Pi _2(N|T)\) is maximized at \(N_2^*=0\); if \(\Delta _{N_2}>0\), then there exists a unique \(N_2^*=\widehat{N}_2>0\) solution, such that \(\Pi _2(N|T)\) is maximized. Based on Eq. (20), for any given T, if \([\rho ''-2k\rho '+k^2(\rho +bT/2)]s-(c+hT/2)\rho ''\le 0\) and \(\rho ''(M-N)^2 -4\rho '(M-N)+2\rho +2b(M-N)\le 0\), then \(\Pi _2(N|T)\) is strictly concave function in N, resulting to a unique maximum solution. If \(\frac{\partial ^2\Pi _2(N|T)}{\partial N^2}\ge 0\), then \(\Pi _2(N|T)\) is a convex function of N. Therefore, the optimal solution of \(\Pi _2(N|T)\) is at one of the two boundary points 0 or \(\infty\). Substituting \(\infty\) in Eq. (19), we have \(\lim _{N\rightarrow \infty }\frac{\partial \Pi _2(N|T)}{\partial N}<0\). Hence \(N=+\infty\) is not an optimal solution, which implies that the optimal solution is \(N_2^*=0\). Consequently, the following theoretical result can be derived based on the analysis above. \(\square\)

Theorem 5

For any given \(T>0\), if \([\rho ''-2k\rho '+k^2(\rho +bT/2)]s-(c+hT/2)\rho ''\le 0\) and \(\rho ''(M-N)^2 -4\rho '(M-N)+2\rho +2b(M-N)\le 0\), then

  1. (1)

    \(\Pi _2(N|T)\) is strictly concave function in N, hence exists a unique maximum solution.

  2. (2)

    If \(\Delta _{N_2}\le 0\), then \(\Pi _2(N|T)\) is maximized at \(N_2^*=0\).

  3. (3)

    If \(\Delta _{N_2}>0\), then there exists a unique \(\widehat{N}_2>0\) such that \(\Pi _2(N|T)\) is maximized at \(N_2^*=\widehat{N}_2>0\).

Optimal solution for the case of \(N>M\)

For any given N, to find the optimal replenishment policy \(T_3^*\), we take the first-order partial derivative of \(\Pi _3(T|N)\) with respect to T, we can obtain

$$\begin{aligned} \frac{\partial \Pi _3(T|N)}{\partial T}= \frac{1}{T^2}\Big \{\frac{[se^{-kN}-c+ cI_{\rm{p}}(M-N)]b}{2}T^2 -(h+cI_{\rm{p}})\Big ( \frac{1}{2}\rho T^2+\frac{2}{3}bT^3\Big ) +A\Big \}=0, \end{aligned}$$
(22)

By taking the second-order partial derivative of \(\Pi _3(T|N)\) with respect to T, we can obtain

$$\begin{aligned} \frac{\partial ^2 \Pi _3(T|N)}{\partial T^2}=-\frac{2A}{T^3}-\frac{2}{3} b(h+cI_{\rm{p}})<0. \end{aligned}$$
(23)

Hence, for any given N, \(\Pi _3(T|N)\) is strictly concave function of T. Thus, \(\widehat{T}_3\) does not only exist, but is also unique. Since \(\lim _{T\rightarrow 0^+} \frac{\partial \Pi _3(T|N)}{\partial T} =\Big \{\frac{[se^{-kN}-c+ cI_{\rm{p}}(M-N)]b}{2} -\frac{1}{2}\rho (h+cI_{\rm{p}})+\lim _{T\rightarrow 0^+}\frac{A}{T^2}\Big \}=+ \infty\), and \(\lim _{T\rightarrow +\infty } \frac{\partial \Pi _3(T|N)}{\partial T} =-\infty\). Therefore, the intermediate value theorem yields that \(\widehat{T}_3\) exists as the root of Eq. (22) for \(T\in (0,\infty )\). Based on the analysis above, it is easy to obtain Theorem 6.

Theorem 6

For any given N with \(M\le N\), \(\Pi _3(T|N)\) is a strictly concave function in T, which is a unique maximum solution \(\widehat{T}_3\) for \(T\in (0,\infty )\); the optimal value of \(T^*_3\) corresponds to \(\widehat{T}_3\). For any given T, taking the first-order and second-order partial derivative of \(\Pi _3(N|T)\) with respect to N, we can obtain

$$\begin{aligned} &\frac{\partial \Pi _3(N|T)}{\partial N} = (\rho '-k(\rho +bT/2))se^{-kN}\nonumber \\ &\quad -c\rho '-\frac{h\rho 'T}{2} -\frac{cI_{\rm{p}}}{2}[\rho '-2(M-N)\rho '+2\rho +bT]\end{aligned}$$
(24)
$$\begin{aligned}&\frac{\partial ^2 \Pi _1(N|T)}{\partial N^2} = (\rho ''-2k\rho '+k^2(\rho +bT/2))se^{-kN} \nonumber \\ &\quad-c\rho '' -\frac{h\rho ''T}{2}- \frac{cI_{\rm{p}}}{2}[(1+2(N-M))\rho ''+ 4\rho '].\end{aligned}$$
(25)

To identify whether \(N_3\) is M or \(N_3>M\), we define the following discrimination term:

$$\begin{aligned}&\Delta _{N_3}=\frac{\partial \Pi _(N|T)}{\partial N}|_{N=M}=(-k\rho +\rho ')se^{-kM} -c\rho ' \nonumber \\ &\quad -\frac{h\rho 'T}{2} +\frac{sI_{\rm{e}}}{2}[2(M-N)\rho '-(bT+2\rho )-\rho 'T].\end{aligned}$$
(26)

If \([\rho ''-2k\rho '+k^2(\rho +bT/2)]s-(c+hT/2)\rho ''<0\), then \(\frac{\partial ^2 \Pi _3(N|T)}{\partial N^2}<0\), and \(\Pi _3(N|T)\) is a strictly concave function in N. Hence, the retailer’s profit exists given the unique maximum solution \(\widehat{N}_3\). Otherwise, the optimal solution of \(\Pi _3(N|T)\) is at one of the two boundary points M or \(\infty\). Substituting \(\infty\) in Eq. (24), we have \(\lim _{N\rightarrow \infty }\frac{\partial \Pi _3(N|T)}{\partial N}<0\). Hence \(N=+\infty\) is not an optimal solution, which implies that the optimal solution is \(N_1^*=M\). Consequently, the following theoretical result can be derived.

Theorem 7

For any given \(T>0\), if \([\rho ''-2k\rho '+k^2(\rho +bT/2)]s -(c+hT/2)\rho '' \le 0\), then

  1. (1)

    \(\Pi _3(N|T)\) is strictly concave function in N, hence exists a unique maximum solution.

  2. (2)

    If \(\Delta _{N_3}\le 0\), then \(\Pi _3(N|T)\) is maximized at \(N_1^*=M\).

  3. (3)

    If \(\Delta _{N_3}>0\), then there exists a unique \(\widehat{N}_1>M\) such that \(\Pi _3(N|T)\) is maximized at \(N_1^*=\widehat{N}_3>M\).

Numerical analysis

In this section, we assume that \(\lambda (N)=de^{uN}\) (Teng et al. 2014; Wu 2014) to conduct the numerical analysis for illustrating the theoretical results and obtaining the optimal solutions using the software Mathematica 7.

Numerical examples

Example 1

Let us assume \(a=100\) units/year, \(b=0.2\)/year, \(d=1\)/year, \(u=0.1\)/year, \(s=\$20\)/unit, \(k=0.2\)/year, \(A=\$10\)/order, \(M=0.5\)/year, \(h=\$5\)/year, \(c=\$10\)/unit, \(I_{\rm{e}}=0.09\), \(I_{\rm{p}}=0.14\). Using software Mathematica 7.0, we have the optimal solution as follow:

$$\begin{aligned}&N_1^*=0 ~\text{ years },~~T_1^*=0.1735~ \text{ years }, ~~\text{ and } ~~ \Pi _1^*(N,T) =\$1094.54, \\ &N_2^*=0 ~\text{ years },~~T_2^*=0.5~ \text{ years }, ~~\text{ and } ~~ \Pi _2^*(N,T) =\$1043.25,\\ &N_3^*=0.5 ~\text{ years },~~T_3^*=0.1706~ \text{ years }, ~~\text{ and } ~~ \Pi _3^*(N,T) =\$810.23. \end{aligned}$$

Consequently, the retailer’s optimal solution is \(N^*=0 ~\text{years },~T^*=0.1735~\text{ years },~\text{ and }~\Pi ^*(N,T) =\$1094.54.\)

Example 2

The parameters are same as in Example 1, except \(d=5\)/year, \(u=5\)/year, \(s=\$30\)/unit, \(k=0.5\)/year. Similar to Example 1, we have the maximum solution to \(\Pi (N,T)\) in the following:

$$\begin{aligned}&N_1^*=0.4398 ~\text{ years },~~T_1^*=0.1989~ \text{ years }, ~~\text{ and } ~~ \Pi _1^*(N,T) =\$2268.82, \\ &N_2^*=0 ~\text{ years },~~T_2^*=0.5~ \text{ years }, ~~\text{ and } ~~ \Pi _2^*(N,T) =\$2098.35,\\ &N_3^*=1.5486 ~\text{ years },~~T_3^*=0.0256~ \text{ years }, ~~\text{ and } ~~ \Pi _3^*(N,T) =\$24867.26 \end{aligned}$$

Consequently, the retailer’s optimal solution is \(N^*=1.5486 ~\text{ years }, ~T^*=0.0256 ~\text{ years }, ~\text{ and }~\Pi ^*(N,T)=\$24867.26.\)

Sensitivity analysis and real usage of the model

We visited a Cement retailer shop and his corresponding Distributer (Supplier) on last January 2017 near Kolkata Airport, West Bengal, India. After careful study we have seen that the Cement distributer supply goods to a retailer offering some credit period under some conditions. If the retailer fails to pay the cost of the purchased Cement to the distributer within this credit period then he used to be charged some interest otherwise the retailer might earn some interest within this credit period over the unpaid cost of the purchased goods. Similarly, the retailer offers some credit period to his customers to increase the demand (sale of goods) so that he could get more profit from those goods. It is also noted that the retailer has a variable replenishment time which is decided by how much credit period he avails from the distributer and how much credit time he already have offered to his customers and how quick the goods have been exhausted through sale exclusively. Through the discussion with the retailer it is also found that though the commodities have normal linear demand with time but beyond that, as the offering credit period of the customer increases the demand rate of the commodity has increased alone. However, for the case of the retailer, a risk has been incurred (generally called default risk) from the customers’ side for non receiving of money of the sold goods in due time. Thus, the problem of the retailer gets more complex to make the final decision over replenishment time and order quantity under different scenarios of availed and offered credit period also. The different cost was as follows: \(a=150\) units/year, \(A=\$14\)/order, \(s=\$35\)/unit, \(c=\$11\)/unit, \(h=\$7\)/year, \(k=0.6\)/year, \(d=7\)/year, \(b=0.3\)/year and \(u=6\)/year. Using software Mathematica 7.0, we have the optimal solution as follow:

$$\begin{aligned}&N_1^*=0.4456 ~\text{ years },~~T_1^*=0.1997~ \text{ years }, ~~\text{ and } ~~ \Pi _1^*(N,T) =\$2199.98, \\ &N_2^*=0 ~\text{ years },~~T_2^*=0.5~ \text{ years }, ~~\text{ and } ~~ \Pi _2^*(N,T) =\$1998.74,\\ &N_3^*=1.5448 ~\text{ years },~~T_3^*=0.0257~ \text{ years }, ~~\text{ and } ~~ \Pi _3^*(N,T) =\$24947.58 \end{aligned}$$

Consequently, the retailer’s optimal solution is \(N^*=1.5448\) years, \(T^*=0.0257\) years, and \(\Pi ^*(N,T) =\$24947.58\)

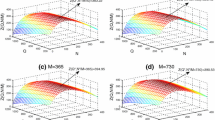
Now, we now study the effects of variations in the values of the system parameters A, a, b, h, c, k, s, d, and u on the optimal total profit. The sensitivity analysis is given by changing each of the parameter taking one parameter at a time and keeping the remaining parameters unchanged. The analysis is based on the parameter values of the inventory system are defined above. The computational results are shown in Table 1.

Table 1 Sensitivity analysis of the parameters
Full size table

The following managerial insights are derived from the obtained computational results:

  1. 1.

    If the value of A increases, then the optimal order cycle \(T^*\) increases while the values of \(N^*\) and the optimal profit \(\Pi ^*(N,T)\) decrease. When the ordering cost is higher, the retailer orders the products in the longer replenishment period to reduce the order frequency. Thus, he pays less ordering cost.

  2. 2.

    If the value of a increases, then the values of \(N^*\) and the optimal order cycle \(T^*\) decrease while the value of the optimal profit \(\Pi ^*(N,T)\) increases. When the initial market demand is greater, the retailer can make more profit.

  3. 3.

    If the value of b increases, then the values of \(N^*\) decrease, but the optimal order cycle \(T^*\) and the value of the optimal profit \(\Pi ^*(N,T)\) increase. When the market demand is more sensitive to time, the retailer provides shorter delayed payment time and longer order cycle to make more profit.

  4. 4.

    If the value of h increases, then the values of \(N^*\), the optimal order cycle \(T^*\), and the value of the optimal profit \(\Pi ^*(N,T)\) decreases. The retailer can adopt some measurements to reduce the holding cost to make more profit.

  5. 5.

    If the value of c or k increases, then the values of \(N^*\) and the optimal profit \(\Pi ^*(N,T)\) decrease while the value of the order cycle \(T^*\) increases. When the unit purchasing price of the retailer is higher, the retailer makes less profit. When the default risk of the customers is higher, the retailer should offer a shorter delayed payment time to his customers. The retailer can take some measurements to reduce the default risk of the customer, such as by adopting the partial delayed payment policy, to make more profit.

  6. 6.

    If the value of s, d, or u increases, then the values of \(N^*\) and the value of the optimal profit \(\Pi ^*(N,T)\) increase while the optimal order cycle \(T^*\) decreases. When the sales price is higher, the retailer offers a shorter delayed payment time and longer order cycle for his customers to make more profit. When the market demand is more sensitive to the trade credit, the retailer should provide a longer delayed payment time to make more profit.

Conclusions

Most of the existing inventory models under trade credit financing are assumed that the demand rate remains constant. However, in practice the market demand is always changing rapidly and is affected by several factors such as price, time, inventory level, and delayed payment period. In today’s high-tech products demand rate increases significantly during the growth stage. Moreover, the marginal influence of the credit period on sales is associated with the unrealized potential market demand. In this paper, we have developed an EOQ model under two-level trade credit financing involving default risk by considering demand to a credit-sensitive and linear non-decreasing function of time. The objective is to find optimal replenishment and trade credit policies while maximizing profit per unit time. For any given credit period, we first prove that the optimal replenishment policy not only exists, but is also unique in some conditions. Second, we show how the optimal credit period for any given replenishment cycle can be decided. Furthermore, we use the Mathematica 7.0 to obtain the optimal inventory policies for the proposed model. Sensitivity analysis is conducted to provide some managerial insights. To the authors’ knowledge, this type of model has not yet been considered by any of the researchers/scientists in inventory literature. Therefore, this model has a new managerial insight that helps a manufacturing system/industry to gain maximum profit. The model can be extended in several ways, for example, we may consider the deteriorating items with a constant deterioration rate. Also, we can extend the model to allow for shortages and partially backlogging. Finally, the effect of inflation rates on the economic order quantity can also be considered.