Introduction and literature review

Two-echelon supply chain consists of one or more manufactures or warehouses who wholesale their products to lower echelon (retailers) who retail them to end customers (Lau and Lau 2005). To maximize their profits, each echelon should make decisions about pricing and appropriate replenishment policy, including order quantity (Q) and reorder point (R) (Heydari 2014). The related literature on optimal pricing and (R, Q) in the supply chain regarding lead time and service level can be categorized into two groups: up-to-level policy (R, Q) and game theoretic pricing and ordering decisions. These models are briefly summarized to be compared with the proposed model.

The first group focuses on (R, Q) inventory when an order for Q is placed and the inventory level falls to R (Li et al. 2011). In optimization cost and profit of supply chain, it is common to assume that retailers and warehouses and even plant follow (R, Q) policy for replenishment. The interruption demand of lower level in a supply chain does not violate the assumption of (R, Q) replenishment policy (Forsberg 1997) and (Ganeshan 1999). Considering stochastic demand is the common assumption in this group (Tan and Weng 2013) (Alkhedher and Darwish 2013). For instance, Taleizadeh et al. (2011) proposed a multi-buyer multi-vendor supply chain and determined ordering policy, including reorder point and number of shipments as well as safety stock to minimize the total cost. Strijbosch and Moors (2006) considered single-stage supply chain with (R, Q) policy. By considering the demand with truncated normal distribution and taking into account the non-negative values, they derive ordering policy. While lead time demand has normal distribution, Chung et al. (2009) presented an accurate algorithm to determine the order quantity and the reorder point. Thangam and Uthayakumar (2008) derived optimal reorder points in two-echelon supply chain, while the number of backorders which are allowed during the lead time is limited. Isotupa and Samanta (2013) developed a cost function for (R, Q) and a lost sales inventory system with stochastic lead time and two types of customers with different priorities. Al-Rifai and Rossetti (2007) proposed a two-echelon inventory system with non-reparable spare parts and utilized a heuristic algorithm to drive ordering decisions. Although the proposed models considered different real-world situations on (R, Q) inventory systems, the interaction between each echelon of the supply chain, such as coordination, cooperation, or competition, has been ignored. Moreover, some researchers have applied metaheuristic methods for optimizing supply chain. Taleizadeh et al. (2010a) applied genetic algorithm to optimize multiproduct multiconstraint inventory control systems with stochastic replenishment intervals and discount. Taleizadeh et al. (2010b) used A particle swarm optimization approach for constraint joint single buyer-single vendor inventory problem with changeable lead time and (R, Q) policy in supply chain.

The second group of literature has been dedicated to the pricing and ordering decisions. These decisions in the supply chain would be also practical and efficient, because emphasis is placed the dynamic behavior of members by the game theory approach. Most papers present the non-cooperative game in the supply chain as the Stackelberg game. Taleizadeh and Noori-daryan (2016) optimized the total cost of the supply chain network by coordinating decision-making policy using Stackelberg–Nash equilibrium. The decision variables of their model were the supplier’s price, the producer’s price, and the number of shipments received by the supplier and producer. Taleizadeh et al. (2015) used Stackelberg game for optimizing prices and ordering decisions in a supply chain with imperfect quality items and inspection under the buyback of defective items. Heydari (2014) considered the coordination between a supplier and a retailer in the supply chain with respect to fixed amount of demand, and also the variation of lead time with complete information structure. Nevertheless, the optimal ordering and pricing policies are obtained in a seller–buyer supply chain with partial lost sale and stochastic demands as the seller-Stackelberg game (Cai et al. 2011). Ye and Xu (2010) presented a vendor–buyer model under buyer-Stackelberg and cooperative games. Taleizadeh et al. (2016) determined price and ordering decisions for two competing supply chains using a Stackelberg game approach. The heuristic algorithms have been used to obtain the optimal order quantity, length of lead time, the safety factor, and the number of products which are delivered to the buyer to minimize their costs. Moreover, many researchers have to make decisions in the supply chain using incomplete information. A supply chain model is proposed to obtain optimal order quantity and selling price, while the seller’s setup, purchase costs, and the demand are unknown (Esmaeili and Zeephongsekul 2010). Uncertain market demand is also considered in a duopoly market, where two separate firms offer complementary goods regarding the Stackelberg model (Mukhopadhyay et al. 2011). In addition, to obtain the optimal pricing policy in a supply chain, including a multi-channel manufacturer, a retailer uncertain demand is considered (Yan and Pei 2011). The model is analyzed with information sharing and non-information sharing. Later, the optimal pricing and collection policies for a manufacturer–retailer are obtained in a closed-loop supply chain with complete and incomplete information about customer’s demand (Wei et al. 2015). Hu et al. (2014) obtained optimal ordering and production policy in a two-echelon supply chain to maximize expected profit. They considered stochastic demand and production yield, while these factors, as well as price, are proposed to be common knowledge.

The features of this paper are classified in terms of decision policies, the main assumptions, and solution methods in comparison with those of the literature (Table 1). To the best of our knowledge, ordering size, safety factor, and pricing policies in a supply chain have not been studied regarding incomplete information of lead time and retailer’s service level in the literature. This paper considers a two-echelon supply chain that includes one warehouse and one retailer under incomplete information. Both the warehouse and the retailer apply (R, Q) replenishment policy with a continuous-review backorder inventory model and truncated normal demand. The warehouse’s order quantity is integer multiples of the retailer’s order quantity. The warehouse uses two transportation modes via a logistic service provider (LSP), the traditional, and the emergency ones, to deliver batches to the retailer. Whenever the warehouse is out of stock, orders are delivered with delay. The warehouse uses emergency transportation, such as air transportation, to keep high service level. Practical examples would be observed in the delivery of large-sized transactions in a supply chain for each industry, such as car, tire, and computer companies. For example, in Customs Administration or when there is a distance between the upstream (vendors) or downstream (sellers), there are some silos and warehouses at the Customs Administration. The existence of such silos and warehouses is required for exchanging, sending, and receiving cargo, shipment, products with, to, and from their retailers or buyers. Regarding the strategic location of warehouse or silos, a warehouse could be considered as a monopolist by different retailers or sellers. Therefore, the relationship between the retailer and the warehouse is investigated based on the warehouse–Stackelberg game with incomplete information. Moreover, the warehouse offers a fraction of its profit to the retailer, while the retailer offers more order quantities to reveal their private information. The optimal inventory and pricing policies are obtained using the algorithm based on BLPP. Numerical examples, including sensitivity analysis on the probability distribution of transportation mode (proposed by the retailer) and the retailer’s service-level mean and variance (estimated by the warehouse), will compare the results between the Stackelberg models. The results show that information sharing is more beneficial to the warehouse rather than the retailer.

Table 1 Features of the study
Full size table

The rest of this paper is organized as follows. In Sect. 2, the notations and assumptions of the proposed model under complete information are presented. In Sect. 3, a model regarding incomplete information is provided. The warehouse–Stackelberg game with incomplete information and incentive strategies to reveal the information is presented in Sect. 4. Computational results include the numerical example and sensitive analyses are considered to analyze the effect of parameters on the model in Sect. 5. Finally, conclusion and future suggestions are presented in Sect. 6.

Notation and problem formulation

This section introduces the notation, all decision variables, input parameters, assumptions, and details of the models which will be stated here:

Input parameters

\(h_{0}\)

The warehouse’s holding cost

\(h_{\text{r}}\)

The retailer’s holding cost

\(h_{\text{c}}\)

The retailer’s fixed holding cost

\(L_{\text{o}}\)

The warehouse’s lead time

\(L_{\text{r}}\)

The retailer’s lead time

\(D_{0}\)

Total demand from the warehouse (\(\mu_{0}^{ *}\), \(\sigma_{0}^{ *2}\))

\(D_{\text{r}}\)

Customers’ potential demand from the retailer (\(\mu_{\text{r}}^{ *}\), \(\sigma_{\text{r}}^{ *2}\))

\(R_{0}\)

The reorder point of the warehouse

\(R_{\text{r}}\)

The reorder point of the retailer

\({\text{SS}}_{0}\)

Safety stock of the warehouse

\({\text{SS}}_{\text{r}}\)

Safety stock of the retailer

\({\text{S}}_{0}\)

Backorder level of the warehouse

\(S_{\text{r}}\)

Backorder level of the retailer

\(w\)

Whole sale price charged by the warehouse

\(p_{0}\)

The warehouse’s selling price, including transportation cost

\(p_{i0}\)

The warehouse’s selling price

\(p_{\text{r}}\)

The retailer’s selling price

\(C_{0}\)

The warehouse’s ordering cost

\(C_{\text{r}}\)

The retailer’s ordering cost

\(\gamma_{0}\)

The warehouse’s shortage cost

\(\gamma_{\text{r}}\)

The retailer’s shortage cost

\(C_{\text{T1}}\)

Transportation cost (Type 1)

\(C_{\text{T2}}\)

Transportation cost (Type 2)

\(\delta_{\text{r}}\)

The retailer’s service level

\(\theta_{\text{r}}\)

The retailer’s service level proposed by the warehouse

\(\mu_{{\theta_{\text{r}} }}\)

The retailer’s service-level mean estimated by the warehouse

\(\sigma_{{\theta_{\text{r}} }}^{2}\)

The retailer’s service-level variance estimated by the warehouse

\(f\left( y \right)\)

The warehouse’s lead time demand probability density function

\((y\sim\) Truncated normal distribution \((\mu_{0}^{ *} L_{\text{o}} ,\sigma_{0}^{ *2} L_{\text{o}} ))\)

\(g\left( x \right)\)

The retailer’s lead time demand probability density function

\((x\sim\) truncated normal distribution \((\mu_{\text{r}}^{ *} L_{\text{r}} ,\sigma_{\text{r}}^{ *2} L_{\text{r}} ))\)

\(\varepsilon_{0}\)

The warehouse’s minimum service level

\(\varepsilon_{\text{r}}\)

The retailer’s minimum service level

\(\pi_{0}\)

The warehouse’s profit function

\(\pi_{\text{r}}\)

The retailer’s profit function

\(t_{a}\)

The time that there is not backorder

\(t_{b}\)

The time that there is backorder

\(i\)

Annual interest rate

Decision variables

\(Q_{\text{r}}\)

The retailer’s lot size

\(N\)

The integer multiples of the retailer’s lot size

(\(Q_{0}\) as the warehouse’s lot size,\(Q_{0} = NQ_{\text{r}}\))

\(k_{0}\)

The warehouse‘s safety factor

\(k_{\text{r}}\)

The retailer’s safety factor

\(d_{0}\)

A fraction of profit charged by the warehouse to the retailer

Assumptions

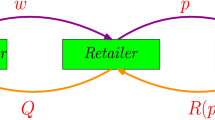
The following assumptions are considered for the warehouse and retailer’s models (Fig. 1):

Fig. 1
figure 1

Warehouse and the retailer’s inventory levels

Full size image
  1. 1.

    The planning horizon is infinite.

  2. 2.

    The warehouse and the retailer follow (R, Q) replenishment policy. An order for Q is placed when the inventory level falls to R. In optimization cost and profit of supply chain, it is common to assume that retailers and warehouses and even plant follow (R, Q) policy for replenishment (Forsberg 1997) and (Ganeshan 1999).

  3. 3.

    The warehouse’s lead time \(L_{\text{o}}\) is constant.

  4. 4.

    The unsatisfied demand is backordered.

  5. 5.

    The warehouse’s lot size is \(Q_{0} = NQ_{\text{r}}\) when \(N\) is integer multiples of retailer’s lot size.

  6. 6.

    The retailer’s demand from the warehouse, \(D_{0}\), is a function of final customers’ potential demand, \(D_{\text{r}}\), and the retailer’s service level, \(\theta_{\text{r}}\) [Eq. (1)]. Therefore,

    $$D_{0} = D_{\text{r}} \theta_{\text{r}}$$
    (1)
  7. 7.

    Retailer and the warehouse are unaware of \(L_{\text{r}}\) and \(\theta_{\text{r}}\), respectively.

  8. 8.

    Retailer’s holding cost is proportional to the unit price of \(h_{\text{r}} = h_{\text{c}} + ip_{\text{r}}\).

  9. 9.

    According to the strategic location of warehouse, a warehouse would be interacted by different retailers or sellers; therefore, the warehouse has greater power than the retailer or the seller.

  10. 10.

    Since negative demands are meaningless, the truncated normal distribution is considered for the customers’ and retailer’s demand.

Model description

In this section, the warehouse and the retailer’s models are introduced regarding complete information.

The warehouse model

The warehouse’s profit function is described as follows:

$$\begin{aligned} \pi_{0} \left( {N,k_{0} } \right) & = {\text{Total revenue}} - {\text{Total purchasing cost}} - {\text{Total ordering cost}} \\ & \, - {\text{Total holding cost}} - {\text{Total stock out cost}} .\\ \end{aligned}$$

Or, expressed as Eq. (2):

$$\pi_{0} \left( {N,k_{0} } \right) = \left( {p_{0} - w} \right)D_{0} - C_{0} \frac{{D_{0} }}{{Q_{0} }} - h_{0} \left( {\frac{{(Q_{0} - S_{0} )^{2} }}{{2Q_{0} }} + {\text{SS}}_{0} } \right) - \gamma_{0} \frac{{D_{0} S_{0} }}{{Q_{0} }},$$
(2)

where

$${\text{SS}}_{0} = R_{0} - \mu_{0}^{ *} L_{0} = k_{0} \sigma_{0}^{ *} \sqrt {L_{0} } ,$$
(3)
$$\begin{aligned} S_{0} & = \mathop \smallint \limits_{{R_{0} }}^{\infty } \left( {y - R_{0} } \right)f\left( y \right){\text{d}}y = \sigma_{0}^{ *} \sqrt {L_{0} } \mathop \smallint \limits_{{k_{0} }}^{\infty } \left( {z - k_{0} } \right)f\left( z \right){\text{d}}z \\ & = \sigma_{0}^{ *} \sqrt {L_{0} } (\phi \left( {k_{0} } \right) - k_{0} [1 - \phi (k_{0} )]), \\ \end{aligned}$$
(4)
$$p_{0} = \left( {\frac{{Q_{0} - S_{0} }}{{Q_{0} }}} \right)C_{\text{T1}} + \left( {\frac{{S_{0} }}{{Q_{0} }}} \right)C_{\text{T2}} + p_{i0} ,$$
(5)
$$\frac{{S_{0} }}{{Q_{0} }}\, \ge\, \varepsilon_{0} ,$$
(6)
$$Q_{0} = NQ_{\text{r}} ,$$
(7)
$$Q_{0} \ge 0.$$
(8)

Equation (3) describes the warehouse’s safety stock. \(S_{0}\) in Eq. (4) represents the warehouse’s stock out. Equation (5) indicates the expected selling price, including the price of goods and the expected transportation cost. The first term of Eq. (5) indicates the traditional transportation cost which is calculated as follows (Fig. 2):

Fig. 2
figure 2

Warehouse inventory and stock out graph

Full size image
$$\begin{aligned} {\text{Traditional transportation cost}} & = (1 - { \Pr }({\text{stock out}})) \times C_{\text{T1}} \\ & = \frac{{t_{a} }}{{t_{a} + t_{b} }} \times C_{\text{T1}} = \left( {\frac{{Q_{0} - S_{0} }}{{Q_{0} }}} \right)C_{\text{T1}} .\\ \end{aligned}$$

In addition, the second term explains the emergency transportation cost:

$$\begin{aligned} {\text{Emergency transportation cost}} & =\, { \Pr }({\text{stock out}}) \times C_{\text{T2}} \\ & = \,\frac{{t_{b} }}{{t_{a} + t_{b} }} \times C_{\text{T2}} = \left( {\frac{{S_{0} }}{{Q_{0} }}} \right)C_{\text{T2}} . \\ \end{aligned}$$

Equation (6) determines a lower bound for the warehouse’s service level. Equation (7) is written with respect to assumption (5).

According to assumption (10), total retailer’s demand from the warehouse has truncated normal distribution (modified normal distribution) with the following parameters:

$$\mu_{0}^{ *} = \mu_{\text{r}}^{ *} \theta_{\text{r}} ,$$
(9)
$$\sigma_{0}^{ *2} = \sigma_{\text{r}}^{ *2} \cdot \theta_{\text{r}}^{2} .$$
(10)

While

$$\mu_{0}^{*} = \sigma_{0} G\left( { - \frac{1}{v}} \right)\varPhi \left( {\frac{1}{v}} \right),$$
(11)
$$\sigma_{0}^{ *2} = \frac{{\sigma_{0}^{2} \left[ {\varPhi \left( {\frac{1}{v}} \right)H\left( { - \frac{1}{v}} \right) - G^{2} \left( { - \frac{1}{v}} \right)\varPhi \left( {\frac{1}{v}} \right)} \right]}}{{\varPhi \left( {\frac{1}{v}} \right)}},$$
(12)

where

$$G\left( { - \frac{1}{v}} \right) = \varphi \left( { - \frac{1}{v}} \right) - \frac{1}{v}\varPhi \left( {\frac{1}{v}} \right),$$
(13)
$$H\left( { - \frac{1}{v}} \right) = \left( { - \frac{1}{v}} \right)\varphi \left( { - \frac{1}{v}} \right) + \left( {\frac{1}{{v^{2} }} + 1} \right)\varPhi \left( {\frac{1}{v}} \right).$$
(14)

In the above equations, \(v = \frac{{\sigma_{0} }}{{\mu_{0} }}\), and \(\varphi ( \cdot )\) and \(\varPhi ( \cdot )\) are probability density and cumulative distribution functions of the standard normal distribution for safety factor (\(k_{0}\)), respectively. Moreover, the retailer’s service level proposed by the warehouse is considered to have a probability distribution over its value (\(\theta_{\text{r}} (\mu_{{\theta_{\text{r}} }} , \sigma_{{\theta_{\text{r}} }}^{2} )\)) regarding assumption (8).

The retailer’s model

To satisfy the final customers’ demand, the retailer places orders from the warehouse. Due to the competitive conditions, the retailer has no bargaining power and charges \(p_{0}\) per each item. The retailer’s profit function is described as follows:

$$\begin{aligned} \pi_{r} \left( {Q_{r} ,k_{r} } \right) & = {\text{Total revenue}} - {\text{Total purchasing cost}} \\ & \quad - {\text{Total ordering cost}} - {\text{Total holding cost}} - {\text{Total stock out cost}} .\\ \end{aligned}$$

Or mentioned as follows (Eq. (15)):

$$\pi_{\text{r}} \left( {Q_{\text{r}} ,k_{\text{r}} } \right) = \left( {p_{\text{r}} - p_{0} } \right)D_{\text{r}} - C_{\text{r}} \frac{{D_{\text{r}} }}{{Q_{\text{r}} }} - h_{\text{r}} \left( {\frac{{\left( {Q_{\text{r}} - S_{\text{r}} } \right)^{2} }}{{2Q_{\text{r}} }} + {\text{SS}}_{\text{r}} } \right) - \gamma_{\text{r}} \frac{{D_{\text{r}} S_{\text{r}} }}{{Q_{\text{r}} }},$$
(15)

where

$${\text{SS}}_{\text{r}} = R_{\text{r}} - \mu_{\text{r}}^{ *} \delta_{\text{r}} L_{\text{r}} = k_{\text{r}} \sigma_{\text{r}}^{ *} \delta_{\text{r}} \sqrt {L_{\text{r}} } ,$$
(16)
$$S_{\text{r}} = [\varphi \left( {k_{\text{r}} } \right) - k_{\text{r}} \left( {1 - \varPhi \left( {k_{\text{r}} } \right)} \right]\sigma_{\text{r}}^{ *} \delta_{\text{r}} \sqrt {L_{\text{r}} } ,$$
(17)
$$\frac{{S_{\text{r}} }}{{Q_{\text{r}} }} \ge \varepsilon_{\text{r}} ,$$
(18)
$$Q_{\text{r}} \ge 0.$$
(19)

In Eq. (15), \(p_{\text{r}}\) is the retailer’s selling price when \(p_{\text{r}} = ap_{0}\) (\(a \ge 1\)) and \(h_{\text{r}} = h_{\text{c}} + ip_{0}\). Equation (16) describes retailer’s safety stock. In Eq. (17), \(S_{\text{r}}\) indicates the retailer’s stock out. Equation (18) determines a lower bound for the retailer’s service level.

According to assumption (10), customer’s demand from the retailer has truncated normal distribution with the following parameters per unit time:

$$\mu_{\text{r}}^{ *} = \sigma_{\text{r}} G\left( { - \frac{1}{v}} \right)\varPhi \left( {\frac{1}{v}} \right),$$
(20)
$$\sigma_{\text{r}}^{ *2} = \frac{{\sigma_{\text{r}}^{2} \left[ {\varPhi \left( {\frac{1}{v}} \right)H\left( { - \frac{1}{v}} \right) - G^{2} \left( { - \frac{1}{v}} \right)\varPhi \left( {\frac{1}{v}} \right)} \right]}}{{\varPhi \left( {\frac{1}{v}} \right)}}.$$
(21)

In the above equations, \(v = \frac{{\sigma_{\text{r}} }}{{\mu_{\text{r}} }}\), \(G\left( { - \frac{1}{v}} \right)\), and \(H\left( { - \frac{1}{v}} \right)\) are calculated based on Eqs. (13) and (14).

The models regarding incomplete information

According to the uncertainty of transportations time and demand in the real world, the transportation time from the warehouse to the retailer and the retailer’s service level is considered unknown to the retailer and the warehouse. Therefore, the warehouse and the retailer’s models are presented under incomplete information.

The warehouse model

The warehouse is unaware of the retailer’s service level; therefore, the uncertainty of service level (\(\theta_{\text{r}}\)) is expressed by probability density function (pdf), \(g(\theta_{\text{r}} )\). The expected profit function of the warehouse, \(E\left( {\pi_{0} \left( {Q_{0} ,k_{0} } \right)} \right)\), is maximized with respect to order quantity, \(Q_{0}\), and safety factor \(k_{0}\), such that

$$\begin{aligned} & E(\pi_{0} (Q_{0} ,k_{0} )) & = \mathop \smallint \nolimits (p_{0} - w)\mu_{0}^{ *} \left( {\theta_{\text{r}} } \right) - C_{0} \frac{{\mu_{0}^{ *} (\theta_{\text{r}} )}}{{Q_{0} }} \\ \,\, & \, - h_{0} \left( {\frac{{(Q_{0} - S_{0} (\theta_{\text{r}} ))^{2} }}{{2Q_{0} }} + {\text{SS}}_{0} (\theta_{\text{r}} )} \right) - \gamma_{0} \frac{{\mu_{0}^{ *} \left( {\theta_{\text{r}} } \right)S_{0} \left( {\theta_{\text{r}} } \right)}}{{Q_{0} }}f\left( {\theta_{\text{r}} } \right){\text{d}}\theta_{\text{r}} . \\ \end{aligned}$$
(22)

Given that \(A_{0} = \sigma_{0}^{ *} \sqrt {L_{0} } (\phi \left( {k_{0} } \right) - k_{0} [1 - \varPhi (k_{0} )])\), we have

$$\begin{aligned} E\left( {\pi_{0} \left( {N,k_{0} } \right)} \right) & = \left( {\left( {\frac{{Q_{0} E\left( {\theta_{\text{r}} } \right) - A_{0} E\left( {\theta_{\text{r}}^{2} } \right)}}{{Q_{0} }}} \right)C_{\text{T1}} + \left( {\frac{{A_{0} E\left( {\theta_{\text{r}}^{2} } \right)}}{{Q_{0} }}} \right)C_{\text{T2}} + (P_{i0} - w)E\left( {\theta_{\text{r}} } \right) - C_{0} \frac{{E\left( {\theta_{\text{r}} } \right)}}{{Q_{0} }} - \gamma_{0} \frac{{A_{0} E\left( {\theta_{\text{r}}^{2} } \right)}}{{Q_{0} }}} \right)\mu_{\text{r}}^{*} \\ & \,\, - h_{0} \left( {\frac{{Q_{0}^{2} + A_{0}^{2} E\left( {\theta_{\text{r}}^{2} } \right) - 2A_{0} Q_{0} E\left( {\theta_{\text{r}} } \right)}}{{2Q_{0} }} + k_{0} \sigma_{0}^{*} \sqrt {L_{0} } E\left( {\theta_{\text{r}} } \right)} \right), \\ \end{aligned}$$
(23)

where

$$\frac{{A_{0} E\left( {\theta_{\text{r}} } \right)}}{{Q_{0} }} \ge \varepsilon_{0} ,$$
(24)
$$Q_{0} = NQ_{\text{r}} ,$$
(25)
$$Q_{0} \ge 0.$$
(26)

The retailer’s model

The transportation mode is shown with \(\xi\) with two types: traditional and emergency ones that are different. Since the retailer is unaware of the transportation time (lead time), therefore, the uncertainty of, \(L_{\text{r}}\), is expressed by probability distribution over its value \(L_{\text{r}} (\alpha ,1 - \alpha )\). Therefore, the expected annual profit function of the retailer, \(E\left( {\pi_{\text{r}} \left( {Q_{\text{r}} ,k_{\text{r}} } \right)} \right)\), is maximized with respect to order quantity,\(Q_{\text{r}}\), and safety factor \(k_{\text{r}}\), such that

$$\begin{aligned} E\left( {\pi_{\text{r}} \left( {Q_{\text{r}} ,k_{\text{r}} } \right)} \right) & = \mathop \smallint \nolimits \left( {p_{\text{r}} - p_{0} } \right)\mu_{\text{r}}^{ *} \delta_{\text{r}} - C_{\text{r}} \frac{{\mu_{\text{r}}^{ *} \delta_{\text{r}} }}{{Q_{\text{r}} }} \\ & \, - h_{\text{r}} \left( {\frac{{\left( {Q_{\text{r}} - S_{\text{r}} \left( \xi \right)} \right)^{2} }}{{2Q_{\text{r}} }} + {\text{SS}}_{\text{r}} \left( \xi \right)} \right) - \gamma_{\text{r}} \frac{{\mu_{\text{r}}^{ *} S_{\text{r}} \left( \xi \right)}}{{Q_{\text{r}} }}f\left( \xi \right){\text{d}}\xi . \\ \end{aligned}$$
(27)

Given that \(A_{\text{r}} = [\varphi \left( {k_{\text{r}} } \right) - k_{\text{r}} (1 - \varPhi (k_{\text{r}} )]\sigma_{\text{r}}^{ *} \delta_{\text{r}}\), we achieve

$$\begin{aligned} E\left( {\pi_{\text{r}} \left( {Q_{\text{r}} ,k_{\text{r}} } \right)} \right) & = (\alpha - 1)p_{0} \mu_{\text{r}}^{*} \delta_{\text{r}} - C_{\text{r}} \frac{{\mu_{\text{r}}^{*} \delta_{\text{r}} }}{{Q_{\text{r}} }} & \\ & - h_{\text{r}} \left( {\frac{{Q_{\text{r}}^{2} + A_{\text{r}}^{2} E\left( {L_{\text{r}} \left( \xi \right)} \right) - 2A_{\text{r}} Q_{\text{r}} E\left( {\sqrt {L_{\text{r}} \left( \xi \right)} } \right)}}{{2Q_{\text{r}} }} + k_{\text{r}} \sigma_{\text{r}}^{*} \delta_{\text{r}} E\left( {\sqrt {L_{\text{r}} \left( \xi \right)} } \right)} \right) \\ & \, - \gamma_{r} \frac{{\mu_{\text{r}}^{*} \delta_{\text{r}} A_{\text{r}} E(\sqrt {L_{\text{r}} (\xi )} )}}{{Q_{\text{r}} }}, \\ \end{aligned}$$
(28)

where

$$\frac{{E(S_{\text{r}} )}}{{Q_{\text{r}} }} \ge \varepsilon_{\text{r}} ,$$
(29)
$$Q_{\text{r}} \ge 0.$$
(30)

Warehouse–Stackelberg game

In Sects. 2 and 3, the warehouse and the retailer’s models under complete and incomplete information were considered separately. The warehouse–Stackelberg model with incomplete information and under information sharing regarding incentive strategy will be represented as follows:

The warehouse–Stackelberg game with incomplete information

According to assumption (9), considering the warehouse selling price, \(p_{0}\), the retailer (follower) obtains ordering policy, \(Q_{\text{r}}\) and \(R_{\text{r}}\), to maximize the profit. Then, the warehouse as a leader determines the optimal \(p_{0}\) and \(Q_{0}\) by maximizing the profit. The solutions to the retailers’ problem (follower) are exhibited by \((Q_{\text{r}}^{ *} ,R_{\text{r}}^{ *} )\). Given that \(A_{0} = \sigma_{0}^{ *} \sqrt {L_{0} } (\phi \left( {k_{0} } \right) - k_{0} [1 - \varPhi (k_{0} )])\) and \(A_{\text{r}} = [\varphi \left( {k_{\text{r}} } \right) - k_{\text{r}} (1 - \varPhi (k_{\text{r}} )]\sigma_{\text{r}}^{ *} \delta_{\text{r}}\), the following model is presented for the warehouse (leader):

$$\begin{aligned} {\text{Max}}E(\pi_{0} (N,k_{0} ,Q_{\text{r}}^{ *} ,k_{\text{r}}^{ *} )) \hfill \\ {\text{s}}.{\text{t}}: \hfill \\ \frac{{A_{0} E(\theta_{\text{r}} )}}{{NQ_{\text{r}} }} \ge \varepsilon_{0} , \hfill \\ \end{aligned}$$
(31)
$$N \ge 0,$$
(32)
$$\begin{aligned} {\text{Max}}E\left( {\pi_{\text{r}} \left( {Q_{\text{r}} ,k_{\text{r}} } \right)} \right) \hfill \\ {\text{s}}.{\text{t}}: \hfill \\ \frac{{A_{\text{r}} E(\sqrt {L_{\text{r}} (\xi )} )}}{{Q_{\text{r}} }} \ge \varepsilon_{\text{r}} , \hfill \\ \end{aligned}$$
(33)
$$Q_{\text{r}} \ge 0.$$
(34)

Due to the complexity of the model, the optimal solution could not be obtained as a closed-form solution. Therefore, the warehouse–Stackelberg is applied as a bi-level programming (BLPP). The retailer and the warehouse’s models are presented as the inner and outer levels, respectively. The optimal inventory and pricing policies are obtained using the algorithm based on BLPP (Gümüş and Floudas 2001) that guarantees the global optimality of solution. Their algorithm is as follows:

Step 1 Set the lower and upper bound of the outer level objective function (leader), \({\text{LB}} = - \infty\) and \({\text{UB}} = \infty\).

Step 2 Use KKT optimality conditions instead of the inner level optimization problem (follower), and consider them as the constraints of the outer level problem.

Step 3 Use the current problem from the second step to calculate the lower bound of the outer level objective function.

Step 4 Substitute the nonlinear equality constraints of the outer problem with two inequality constraints (greater than or smaller than).

Step 5 Determine the lower and upper bounds of the variables.

Step 6 To calculate the upper bound of the outer level objective function, first convert the inner level objective function problem to a convex shape and then use the KKT optimality conditions instead of the inner level problem.

Step 7 Substitute the complementarily conditions with their equivalent linear constraints to calculate the upper bound of outer level objective function.

Step 8 If the upper and the lower bounds of the outer level objective function converge, then stop, otherwise divide the interval of one of the variables into two or more sub-intervals, and then go back to step 2.

Revealing information regarding incentive strategies

In this case, both the warehouse and the retailer reveal their private information according to an incentive strategy. The warehouse shares transportation information, while the retailer promises to buy more rather than an incomplete pattern. On the other hand, the retailer shares an accurate service level and demand, while the warehouse offers the retailer a fraction of its profit by \(d_{0}\) percent. However, both the warehouse and the retailer’s objective functions should be at least the optimal value in the case of incomplete information.

Given that the warehouse’s selling price is (\(d_{0} p_{0}\)), the retailer (follower) obtains an optimal ordering policy. Proposing \(A_{0} = \sigma_{0}^{ *} \sqrt {L_{0} } (\phi \left( {k_{0} } \right) - k_{0} [1 - \varPhi (k_{0} )])\) and \(A_{\text{r}} = [\varphi \left( {k_{\text{r}} } \right) - k_{\text{r}} (1 - \varPhi (k_{\text{r}} )]\sigma_{\text{r}}^{ *} \delta_{\text{r}}\), the following model is presented for the retailer as a follower:

$$\begin{aligned} {\text{Max}}\pi_{\text{r}} \left( {Q_{\text{r}} ,k_{\text{r}} } \right) = \left( {p_{\text{r}} - p_{0} } \right)D_{\text{r}} - C_{\text{r}} \frac{{D_{\text{r}} }}{{Q_{\text{r}} }} - h_{\text{r}} \left( {\frac{{\left( {Q_{\text{r}} - S_{\text{r}} } \right)^{2} }}{{2Q_{\text{r}} }} + {\text{SS}}_{\text{r}} } \right) - \gamma_{\text{r}} \frac{{D_{\text{r}} S_{\text{r}} }}{{Q_{\text{r}} }} + d_{0} \pi_{0} \hfill \\ {\text{s}}.{\text{t}}: \hfill \\ \end{aligned}$$
(35)
$$\frac{{A_{\text{r}} \sqrt {L_{\text{r}} (\xi )} }}{{Q_{\text{r}} }} \ge \varepsilon_{\text{r}} ,$$
(36)
$$\pi_{\text{r}} \left( {Q_{\text{r}} ,k_{\text{r}} } \right) \ge \pi_{\text{r}}^{ *} ,$$
(37)
$$Q_{\text{r}} > Q_{\text{r}}^{ *} ,$$
(38)
$$Q_{\text{r}} \ge 0.$$
(39)

In addition, in the following model, the warehouse is considered as a leader:

$$\begin{aligned} {\text{Max}}\pi_{0} \left( {N,k_{0} ,d_{0} } \right) & & = (1 - d_{0} ) & \,\left( {\left( {p_{0} - w} \right)D_{0} - C_{0} \frac{{D_{0} }}{{Q_{0} }} - h_{0} \left( {\frac{{\left( {Q_{0} - S_{0} } \right)^{2} }}{{2Q_{0} }} + {\text{SS}}_{0} } \right) - \gamma_{0} \frac{{D_{0} S_{0} }}{{Q_{0} }}} \right) \\ {\text{s}} . {\text{t}}: \\ \end{aligned}$$
(40)
$$\frac{{A_{0} \theta_{\text{r}} }}{{NQ_{\text{r}} }} \ge \varepsilon_{0} ,$$
(41)
$$\pi_{0} \left( {N,k_{0} ,d_{0} } \right) \ge \pi_{0}^{ *} ,$$
(42)
$$0 \le d_{0} \le 1,$$
(43)
$$N \ge 0.$$
(44)

Due to the complexity of the model, the optimal solution could not be obtained as a closed-form solution. The optimal inventory and pricing policies are obtained using the algorithm based on BLPP (Gümüş and Floudas 2001) that guarantee the global optimality of solution.

Computational results

In this section, a numerical example is presented to illustrate the proposed models and also a sensitivity analysis is performed.

Numerical example

Suppose a supply chain consists of one central warehouse and a retailer. The retailer pays \(p_{0}\) per each item and sells it to the end customer by \((1 + a)p_{0} , 0 < a \le 1\). All parameters are known to both the warehouse and the retailer except \(L_{\text{r}}\) and \(\theta_{r}\). The parameters are presented in Table 2. The optimal solution of the warehouse–Stackelberg problem with incomplete information is shown in Table 3 using the algorithm in Sect. 4. Moreover, the Stackelberg game regarding information sharing as well as incomplete information is considered to compare the results. In this numerical problem, information sharing enables both the warehouse and the retailer to gain more compared with the incomplete structure.

Table 2 Warehouse–Stackelberg game numerical problem
Full size table
Table 3 Warehouse and the retailer’s optimal solutions and profit
Full size table

It is necessary to note that the warehouse’s reorder point can be obtained based on Eq. (45):

$$R_{0} = \mu_{0}^{ *} L_{0} + k_{0} \sigma_{0}^{ *} \sqrt {L_{0} } .$$
(45)

Similarly, the retailer’s reorder point can be calculated.

Sensitivity analysis

Sensitivity analysis is performed regarding the main parameters, including the probability of common transportation mode proposed by the retailer (\(\alpha\)) and the retailer’s service-level mean (\(\mu_{{\theta_{\text{r}} }}\)) and variance (\(\sigma_{{\theta_{\text{r}} }}\)) estimated by the warehouse.

As exhibited in Table 4 and Fig. 3, unlike the retailer, the warehouse’s decisions have been affected by changing the retailer’s service-level estimation (\(\mu_{{\theta_{\text{r}} }}\)). When \(\mu_{{\theta_{\text{r}} }}\) decreases, the warehouse’s payoff decreases as well. If the warehouse underestimates the retailer’s service level, less order quantity (\(Q_{0}\)) will be placed to satisfy the retailer’s demand. Therefore, the warehouse will keep fewer inventories and faces more stock out.

Table 4 Sensitivity analysis of the warehouse–Stackelberg model with respect to \(\mu_{{\theta_{\text{r}} }}\)
Full size table
Fig. 3
figure 3

Warehouse and the retailer’s payoff function versus the retailer’s service-level estimation

Full size image

As shown in Table 5 and Fig. 4, by increasing \(\sigma_{{\theta_{r} }}\), the warehouse’s payoff (\(\pi_{0}\)) decreases. However, the change in the retailer’s payoff can almost be ignored. Therefore, information sharing is more beneficial to the warehouse compared to the retailer. Thus, the warehouse should provide motivating options, such as price discount or service-level improvement to develop its relationship with the retailer (Table 5).

Fig. 4
figure 4

Warehouse and the retailer’s payoff function versus the retailer’s service-level variance

Full size image
Table 5 Sensitivity analysis of the warehouse–Stackelberg model with respect to \(\sigma_{{\theta_{\text{r}} }}\)
Full size table

By increasing the probability of common transportation type (\(\alpha\)), the lead time is overestimated by the retailer. Therefore, more order quantities should be placed to prevent stock out. Consequently, the warehouse places more order quantities to satisfy the retailer’s demand and prevent stock out. While keeping more inventory increases the warehouse’s holding cost, it also reduces the shortage cost. When the shortage cost is rather high, the warehouse’s profit increases accordingly. Similarly, keeping more inventories affects the retailer’s profit (Table 6; Fig. 5).

Table 6 Sensitivity analysis of the warehouse–Stackelberg model with respect to \(\alpha\)
Full size table
Fig. 5
figure 5

Warehouse and the retailer’s payoff function versus traditional transportation probability

Full size image

Conclusion

Inventory systems to analyze different real-world situations have received great interest in the literature. This paper considers a two-echelon supply chain that includes a warehouse and a retailer who are faced with the stochastic demand. The retailer’s service level and the transportation time from the warehouse to the retailer are private information for the retailer and the warehouse, respectively. Regarding incomplete information, the interaction between the warehouse and the retailer is considered by Stackelberg game. The optimal inventory and pricing policies are obtained using the algorithm based on BLPP. While the warehouse’s policy and profit are very sensitive to the estimation of parameters, the retailer’s decisions and profit change can almost be ignored. In this case study, the warehouse has more motivation to share information compared to the retailer to gain more benefit.

There are more scopes in extending the present work. For example, other types of inventory control policies could be considered regarding incomplete information. Moreover, other parameters of the model, such as the order quantity or different costs, could be presented as private information for both the warehouse and the retailer.