Introduction and literature review

Pricing and ordering decisions play crucial role in optimizing the costs of inventory systems. So, firms try to employ these optimal decision strategies to content their customers. Recently, many researches were performed in the area of supply chain by employing pricing and ordering decisions. For instance, Abad (2003) applied the optimal pricing ordering strategies with partial backordering shortage for a deteriorating item. Arcelus et al. (2005); Liu (2006) and Zhang and Bell (2007) considered pricing and ordering problem under various assumptions. Chao et al. (2008) discussed a distribution network design problem and utilized pricing and inventory policies under trade credits. Sajadieh and Akbari Jokar (2009) examined pricing, ordering and shipment policies in a two- echelon supply chain. Xiao et al. (2010) surveyed pricing, ordering and lead time policies in a three-echelon supply chain where demand is uncertain. Shao et al. (2011) employed pricing and inventory policies in a supply chain involving a supplier and multiple retailers for single product. Thangam (2012) studied pricing and lot-sizing decisions in a supply chain model for a deteriorating product where the supplier provides the retailer a full trade credit period for payments and the retailer offers the partial trade credit to end users. Noori-daryan et al. (2014) discussed pricing and inventory policies in a four-echelon supply chain composed of a supplier, a manufacturer, a distributor and multi- retailers under rework process. Taleizadeh and Noori-daryan (2015) determined pricing, manufacturing and ordering decisions in a three-echelon supply chain including a supplier, a producer and several retailers. Therefore, some authors as Sadjadi et al. (2015), Taleizadeh and Charmchi (2015), Esmaeilzadeh and Taleizadeh (2016), Vijayashree and Uthayakumar (2017) and Sundara Rajan and Uthayakumar (2017) surveyed optimal pricing and ordering policies under different settings.

Nowadays, owing to high competition, the companies combined some coordination mechanisms such as return policy with the optimal decision strategies such as pricing and ordering strategies. Under the return policy, customers can send back the defective items after inspecting them and the seller purchases the defective ones at a lower price. Therefore, the customers would be ordered more considering this agreement. Some researchers considered the coordination mechanisms in addition to pricing and ordering policies in their researches. For instance, Gurnani et al. (2010) surveyed the optimal return policy under three ways where demand is uncertain. Chen and Bell (2011) survey a return agreement in a decentralized supply chain where a manufacturer and a retailer are the members of chain. Zhu (2012) studied the joint pricing and inventory problem with return and expediting policy in a single-item periodic-review model so that the total profit is maximized. Hu and Xu (2012) proposed a customer return policy in a one-manufacturer-one-retailer supply chain where a distribution free approach to solve the centralized and decentralized decision model is applied. Sana (2013) employed several coordination mechanisms such as return, cost sharing and discount policies in a two-echelon supply chain contains a manufacturer and a retailer. Hu et al. (2014) considered a consignment contract with consumer return policy in a two echelons chain involving a vendor and a retailer. Additionally, Maleki Vishkaei et al. (2014) extended Hsu and Hsu (2012)’s research to determine the optimal ordering strategy considering a return agreement between a supplier and a retailer for defective items, stored in a warehouse to return to the supplier by receiving a new order. Moreover, some other related works can be found in Taleizadeh et al. (2008a, b, 2009, 2010a, b, 2011, 2013), Taleizadeh and Pentico (2013), and Taleizadeh (2014).

Based on the present literature review, none of the authors considered a return contract as the coordination decision policy in a three-echelon supply chain by employing pricing and ordering strategies. So, in this paper, we examine the optimal pricing and inventory decisions in a three-echelon supply chain under a return contract where the backordering shortage is permitted and a Nash-equilibrium approach is used to deal with the proposed problem. Moreover, a supplier, a manufacturer, a wholesaler are the members of this chain.

The contribution of this research is twofold. The first part examines a single-supplier–single-manufacturer–single-wholesaler supply chain where the upstream members of the chains (i.e., outside supplier and manufacturer) offer a coordinating strategy to downstream members (i.e., manufacturer and retailers). This research deals with a pricing and inventory models for single product in presence of two different scenarios to obtain optimal values of the decision variables, in closed-form solutions so that the total profits of the chains are maximized. In the second part, the concavity of the total profit functions is proven by employing theorems.

The rest of the paper arranged as follows. The problem is described in the next section. The mathematical model is formulated in the following section. The next section is shown the solution method and the following sections contain the numerical example and the conclusion, in turn.

Problem statement

In this paper, a decentralized supply chain involving a supplier, a manufacturer and a wholesaler under two-scenario is considered. Here, we assume that, as the first scenario, a return contract is concluded between the outside supplier and the supplier and also between the manufacturer and the wholesaler. In this chain, under the first scenario, the supplier receives the raw material and after inspecting them, send back the defective ones where those are purchased and the outside supplier purchase the defective raw material at a lower price. Then the supplier ships the healthy raw material to the manufacturer and the manufacturer transmutes them to the finished product to satisfy the wholesaler’s demand. In this stage of chain, the manufacturer employs a return policy to incentive the wholesaler’s orders where the manufacturer ships the products to the wholesaler and the wholesaler after receiving and inspecting items, returns the defective items to the manufacturer and fulfill the market demand with the health ones. Then the manufacturer purchases returned items at a lower price. In the second scenario, the return policy between the manufacturer and its wholesaler is not applied to examine the difference of the chain profit under both scenarios. Besides, backordering shortage is permitted and demand is price-sensitive.

The objective of the research is to determine the optimal values of the order quantity of supplier and the selling prices of manufacturer and wholesaler as the decision variables by applying the optimal pricing and inventory decision strategies such that the profit of the chain is optimized.

The notations used to formulate the mathematical model are as follows:

Parameters:

Is(t):

The inventory level of the supplier at time t,

Im(t):

The inventory level of the manufacturer at time t,

\(I_{\text{w}} (t)\) :

The inventory level of the wholesaler at time t,

B :

The inventory level of the wholesaler which is encountered shortage at time t,

h s :

The holding cost of the supplier per item per unit time,

h m :

The holding cost of the manufacturer per item per unit time, hm > hs

h w :

The holding cost of the wholesaler per item per unit time, hw > hm

O s :

The ordering cost of the supplier per order,

O m :

The ordering cost of the manufacturer per order,

O w :

The ordering cost of the wholesaler per order,

C r :

The purchasing price of raw material per item,

C is :

The inspection cost of the supplier per item,

p s :

The selling price of the supplier per item, ($)

r is :

The inspection rate of the supplier,

r p :

The production rate of the manufacturer,

C P :

The production cost of the manufacturer per item,

C iw :

The inspection cost of the wholesaler per item,

C bw :

The shortage cost of the wholesaler per item,

r iw :

The inspection rate of the wholesaler,

C ′r :

Buyback price of the returned items of the supplier per item, ($)

p ′m :

Buyback price of the returned items of the manufacturer per item, ($), p ′m  = fpm

p ′ w :

Buyback price of the returned items of the wholesaler per item, ($), p ′w  = gpw

d m :

The demand rate of the manufacturer, dm = a – bps

d w :

The demand rate of the wholesaler, dw = a − bpm

d b :

The demand rate of buyers, db = a − bpw

y :

The proportion of the defectives items of the supplier, 0 ≤ y < 1

x :

The proportion of the defectives items of the wholesaler, 0 ≤ x < 1

T s :

The cycle length of the supplier,

t pm :

The cycle length of the manufacturer for production,

t sm :

The cycle length of the manufacturer for selling,

T m :

The cycle length of the manufacturer,

t cw :

The cycle length of the wholesaler for collecting,

t sw :

The cycle length of the wholesaler for selling,

t bw :

The cycle length of the wholesaler facing shortage,

T w :

The cycle length of wholesaler,

π s j :

The total profit of the supplier for jth scenario per unit time,

π m j :

The total profit of the manufacturer for jth scenario per unit time,

π w j :

The total profit of the wholesaler for jth scenario per unit time,

π j :

The total profit of supply chain for jth scenario per unit time.

Decision variables:

Q :

The ordering lot size of the supplier,

p m :

The selling price of the manufacturer, ($)

p w :

The selling price of the wholesaler, ($).

The following assumptions employed to model the problem:

  1. 1.

    The model developed for single-item.

  2. 2.

    The chain contains one supplier, one manufacturer and one wholesaler.

  3. 3.

    A return contract is considered between the outside supplier and the supplier and also between the manufacturer and the wholesaler.

  4. 4.

    The costs of members at each level are different.

  5. 5.

    Demand is constant and price-sensitive.

  6. 6.

    Proportions of unhealthy items are constant.

  7. 7.

    The inspection rate of the supplier is larger than the production rate of the manufacturer. So, shortage is not permitted at the manufacturer’s stage.

  8. 8.

    Shortage is permitted at the wholesaler.

  9. 9.

    Lead time is negligible.

  10. 10.

    All the parameters of model are constant.

Model formulation

Here, an economic production and inventory problem in a three-echelon supply chain is developed under two scenarios where a supplier, a manufacturer and one wholesaler are the members of chain.

The first scenario with return policy

Supplier model

Raw materials are shipped to the supplier and the supplier inspects them. The defective ones are sent back to the outside supplier and he purchases the unhealthy items at a lower price. Then the supplier delivers the healthy items to the manufacturer at a rate of \(d_{\text{m}}\) (see Fig. 1). Since shortage is not permitted, the number of healthy items at the supplier is greater than or at least equal to the manufacturer’s demand, \((1 - y)Q \ge d_{\text{m}} T_{\text{s}}\). Hence, the differential equation of this level is:

$$\frac{{{\text{d}}I_{\text{s}} (t)}}{{{\text{d}}t}} = - d_{\text{m}} , \quad 0 \le t \le T_{\text{s}} .$$
(1)
Fig. 1
figure 1

The inventory levels of the chain members

Full size image

And we have \(I_{\text{s}} (0) = (1 - y)Q\) and \(I_{\text{s}} (T_{\text{s}} ) = 0\). So, his inventory level is:

$$I_{\text{s}} (t) = (1 - y)Q - d_{\text{m}} t, \quad 0 \le t \le T_{\text{s}} .$$
(2)

Additionally, we have:

$$I_{\text{s}} (T_{\text{s}} ) = 0 \Rightarrow T_{\text{s}} = \frac{(1 - y)Q}{{d_{\text{m}} }}.$$
(3)

The holding cost of the supplier is:

$$\frac{1}{{T_{\text{s}} }}\left[ {h_{\text{s}} \int_{0}^{{T_{\text{s}} }} {\left( {(1 - y)Q - d_{\text{m}} t} \right){\text{d}}t} } \right] = h_{\text{s}} \left[ {(1 - y)Q - \left( {\frac{{d_{\text{m}} T_{\text{s}} }}{2}} \right)} \right] = h_{\text{s}} \frac{(1 - y)Q}{2}.$$
(4)

And his annual ordering cost is:

$$\frac{{O_{\text{s}} }}{{T_{\text{s}} }} = \frac{{d_{\text{m}} O_{\text{s}} }}{(1 - y)Q}.$$
(5)

The inspection cost is:

$$\frac{{C_{\text{is}} Q}}{{T_{\text{w}} }} = \frac{{C_{\text{is}} }}{(1 - y)}d_{\text{m}} .$$
(6)

Then, the total profit of the supplier is:

$$\pi_{\text{s1}} (Q) = \left( {p_{\text{s}} + \frac{y}{(1 - y)}C^{\prime}_{\text{r}} } \right)d_{\text{m}} - \left( {\left( {C_{\text{r}} + C_{\text{is}} } \right)\frac{{d_{\text{m}} }}{(1 - y)} + h_{\text{s}} \frac{(1 - y)Q}{2} + \frac{{d_{\text{m}} O_{\text{s}} }}{(1 - y)Q}} \right).$$
(7)

Manufacturer model

In this stage, raw materials are sent to the manufacturer and he transforms them to the finished products to satisfy the wholesaler’s demand. To encourage the wholesaler to order more, the manufacturer offers the return policy to him such that the wholesaler can return the defective items to the manufacturer after inspection process. The inventory level of the manufacturer increases at a rate of \(r_{\text{p}} - d_{\text{w}}\) during \([0,t_{\text{m}}^{\text{p}} ]\) and then he starts consuming his inventory completely during \([t_{\text{m}}^{\text{p}} ,t_{\text{m}}^{\text{s}} ]\) (see Fig. 1). Here, it is assumed that to prevent shortage, \(r_{\text{p}}\) must be greater than or equal to the wholesale’s demand, \(r_{\text{p}} \ge d_{w}\).

Hence, the differential equations of this level are given by:

$$\frac{{{\text{d}}I_{\text{m}} (t)}}{{{\text{d}}t}} = r_{\text{p}} - d_{\text{w}} , \quad 0 \le t \le t_{\text{m}}^{\text{p}}$$
(8)
$$\frac{{{\text{d}}I_{\text{m}} (t)}}{{{\text{d}}t}} = - d_{\text{w}} , \quad t_{\text{m}}^{\text{p}} \le t \le T_{\text{m}} .$$
(9)

The cycle length of the manufacturer is \(T_{\text{m}} = t_{\text{m}}^{\text{p}} + t_{\text{m}}^{\text{s}}\) where:

$$t_{\text{m}}^{\text{p}} = \frac{(1 - y)Q}{{r_{\text{p}} }}$$
(10)
$$t_{\text{m}}^{\text{s}} = \frac{(1 - y)Q}{{d_{\text{w}} }}\left[ {1 - \frac{{d_{\text{w}} }}{{r_{\text{p}} }}} \right].$$
(11)

Therefore, we have:

$$T_{\text{m}} = \frac{(1 - y)Q}{{d_{\text{w}} }}.$$
(12)

Additionally, using Eqs. (10–12), the manufacturer’s inventory level where \(I_{\text{m}} (0) = 0\) and \(I_{\text{m}} (t_{\text{m}}^{\text{p}} + t_{\text{m}}^{\text{s}} ) = 0\) is:

$$I_{\text{m}} (t) = (r_{\text{p}} - d_{\text{w}} )t, \quad 0 \le t \le t_{\text{m}}^{\text{p}}$$
(13)
$$I_{\text{m}} (t) = d_{\text{w}} (T_{\text{m}} - t), \quad t_{\text{m}}^{\text{p}} \le t \le T_{\text{m}} .$$
(14)

Then, the total holding cost of manufacturer is:

$$\frac{1}{{T_{\text{m}} }}\left[ {h_{\text{m}} \left[ {\int_{0}^{{t_{\text{m}}^{\text{p}} }} {\left( {r_{\text{p}} - d_{\text{w}} } \right)t{\text{d}}t} + \int_{{t_{\text{m}}^{\text{p}} }}^{{T_{\text{m}} }} {d_{\text{w}} \left( {T_{\text{m}} - t} \right){\text{d}}t} } \right]} \right] = \frac{{h_{\text{m}} (1 - y)Q}}{2}\left[ {1 - \frac{{d_{\text{w}} }}{{r_{\text{p}} }}} \right].$$
(15)

And his annual ordering cost is:

$$\frac{{O_{\text{m}} }}{{T_{\text{m}} }} = \frac{{d_{\text{w}} O_{\text{m}} }}{(1 - y)Q}.$$
(16)

Hence, the total profit of manufacturer is:

$$\pi_{{{\text{m}}1}} (p_{\text{m}} ) = \left( {p_{\text{m}} - C_{\text{p}} - p_{\text{s}} - xp^{\prime}_{\text{m}} } \right)d_{\text{w}} - \left( {\frac{{h_{\text{m}} (1 - y)Q}}{2}\left[ {1 - \frac{{d_{\text{w}} }}{{r_{\text{p}} }}} \right] + \frac{{d_{\text{w}} O_{\text{m}} }}{(1 - y)Q}} \right).$$
(17)

Wholesaler model

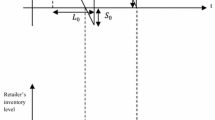
In this stage, the finished products are delivered to the wholesaler and he starts inspecting them. Then unhealthy items are returned to the manufacturer and he purchases the defective items at a lower price. The inventory level of the wholesaler increases at a rate of \((1 - x)d_{\text{w}} - d_{\text{b}}\) during \([0,t_{\text{w}}^{\text{c}} ]\) then start decreasing at the rate of \(d_{\text{b}}\) during the \([t_{\text{w}}^{\text{c}} ,t_{\text{w}}^{\text{s}} ]\). Moreover, we suppose the wholesaler confronts to the shortage which is the kind of backordering during \([t_{\text{w}}^{\text{s}} ,T_{\text{w}} ]\) (see Fig. 1). So, the differential equations of this level are given by:

$$\frac{{{\text{d}}I_{\text{w}} }}{{{\text{d}}t}} = (1 - x)d_{\text{w}} - d_{\text{b}} ,0 \le t \le t_{\text{w}}^{\text{c}}$$
(18)
$$\frac{{{\text{d}}I_{\text{w}} }}{{{\text{d}}t}} = - d_{\text{b}} , \quad t_{\text{w}}^{\text{c}} \le t \le t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}}$$
(19)
$$\frac{{{\text{d}}I_{\text{w}} }}{{{\text{d}}t}} = - d_{\text{b}} , \quad t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}} \le t \le T_{\text{w}} .$$
(20)

The cycle length of wholesaler is \(T_{\text{w}} = t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}} + t_{\text{w}}^{\text{b}}\) where:

$$t_{\text{w}}^{\text{c}} = \frac{(1 - y)Q - B}{{(1 - x)d_{\text{w}} }}$$
(21)
$$t_{\text{w}}^{\text{s}} = \frac{(1 - y)Q - B}{{d_{\text{b}} }}\left[ {1 - \frac{{d_{\text{b}} }}{{(1 - x)d_{\text{w}} }}} \right]$$
(22)
$$t_{\text{w}}^{\text{b}} = \frac{B}{{d_{\text{b}} }}.$$
(23)

And the cycle length of the wholesaler is:

$$T_{\text{w}} = \frac{(1 - y)Q}{{d_{\text{b}} }}.$$
(24)

The inventory level of wholesaler, using Eqs. (21–24), where \(I_{\text{w}} (0) = 0\) and \(I_{\text{w}} (t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}} ) = 0\) is:

$$I_{\text{w}} (t) = \left( {(1 - x)d_{\text{w}} - d_{\text{b}} } \right)t, \quad 0 \le t \le t_{\text{w}}^{\text{c}}$$
(25)
$$I_{\text{w}} (t) = d_{\text{b}} \left( {t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}} - t} \right), \quad t_{\text{w}}^{\text{c}} \le t \le t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}}$$
(26)
$$I_{\text{w}} (t) = - d_{\text{b}} \left( {t - t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}} } \right), \quad t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}} \le t \le T_{\text{w}} ,$$
(27)

Then, the total holding cost of the wholesaler is:

$$\frac{1}{{T_{\text{w}} }}\left[ {h_{\text{w}} \left[ {\int_{0}^{{t_{\text{w}}^{\text{c}} }} {\left( {(1 - x)d_{\text{w}} - d_{\text{b}} } \right)t{\text{d}}t} + \int_{{t_{\text{w}}^{\text{c}} }}^{{t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}} }} {d_{\text{b}} \left( {t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}} - t} \right){\text{d}}t} } \right]} \right] = \frac{{h_{\text{w}} \left( {(1 - y)Q - B} \right)^{2} }}{2(1 - y)Q}\left[ {1 - \frac{{d_{\text{b}} }}{{(1 - x)d_{\text{w}} }}} \right].$$
(28)

The ordering cost is:

$$\frac{{O_{\text{w}} }}{{T_{\text{w}} }} = \frac{{d_{\text{b}} O_{\text{w}} }}{(1 - y)Q}.$$
(29)

The inspection cost is:

$$\frac{{C_{\text{iw}} (1 - y)Q}}{{T_{\text{w}} }} = C_{\text{iw}} d_{\text{b}} .$$
(30)

The backordering shortage cost is:

$$- \int_{{t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}} }}^{{T_{\text{w}} }} {I_{\text{w}} (t){\text{d}}t} = - C_{\text{bw}} \int_{{t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}} }}^{{T_{\text{w}} }} {\left( { - d_{\text{b}} \left( {t - t_{\text{w}}^{\text{c}} + t_{\text{w}}^{\text{s}} } \right)} \right){\text{d}}t} = \frac{{C_{\text{bw}} B}}{{2d_{\text{b}} }}.$$
(31)

And the total profit of the wholesaler is:

$$\begin{aligned} & \pi_{{{\text{w}}1}} \left( {p_{\text{w}} } \right) = \left( {p_{\text{w}} + xp^{\prime}_{\text{w}} - p_{\text{m}} - C_{\text{iw}} } \right)d_{\text{b}} \\ & \quad - \left( {\frac{{h_{\text{w}} \left( {(1 - y)Q - B} \right)^{2} }}{2(1 - y)Q}\left[ {1 - \frac{{d_{\text{b}} }}{{\left( {(1 - x)d_{\text{w}} } \right)^{2} }}} \right] + \frac{{d_{\text{b}} O_{\text{w}} }}{(1 - y)Q} + \frac{{C_{\text{bw}} B}}{2(1 - y)Q}} \right). \end{aligned}$$
(32)

Finally, the total profit of the chain is:

$$\pi_{1} = \pi_{\text{s1}} + \pi_{\text{m1}} + \pi_{\text{w1}} .$$
(33)

The second scenario-without return policy between the manufacturer and the wholesaler

Supplier model

The total profit of the supplier does not change. So, we have:

$$\pi_{\text{s2}} = \pi_{\text{s1}} .$$
(34)

Manufacturer’s model

In this stage, the manufacturer does not offer the return policy to the wholesaler. So, the total profit of the manufacturer is changed to:

$$\pi_{m2} (p_{\text{m}} ) = \left( {p_{\text{m}} - C_{\text{p}} - p_{\text{s}} } \right)d_{\text{w}} - \left( {\frac{{h_{\text{m}} (1 - y)Q}}{2}\left[ {1 - \frac{{d_{\text{w}} }}{{r_{\text{p}} }}} \right] + \frac{{d_{\text{w}} O_{\text{m}} }}{(1 - y)Q}} \right).$$
(35)

Wholesaler model

The total profit of the wholesaler is changed. Hence, we have:

$$\pi_{\text{w2}} (p_{\text{w}} ) = \left( {p_{\text{w}} - p_{\text{m}} - C_{\text{iw}} } \right)d_{\text{b}} - \left( {\frac{{h_{\text{w}} \left( {(1 - y)Q - B} \right)^{2} }}{2(1 - y)Q}\left[ {1 - \frac{{d_{\text{b}} }}{{\left( {(1 - x)d_{\text{w}} } \right)^{2} }}} \right] + \frac{{d_{\text{b}} O_{\text{w}} }}{(1 - y)Q} + \frac{{C_{\text{bw}} B}}{2(1 - y)Q}} \right).$$
(36)

Eventually, the total profit of the chain is:

$$\pi_{2} = \pi_{\text{s2}} + \pi_{\text{m2}} + \pi_{\text{w2}} .$$
(37)

Solution method

Here, we assume the members of the chain compete with each other and they intend to determine their decision variables individually so that their total profits are optimized to attract own customers. Therefore, Nash-equilibrium approach is applied to solve the problem. Based on this method, the chain members make decision simultaneously about own decision variables where the order quantity of the supplier and the selling prices of the manufacturer and the wholesaler are their decision variables.

Since the total profit of the chain is acquired from the summation of the total profits of the chain partners, so the concavity of the partners’ profit functions under the first and second scenarios should be proven to optimize the chain profit of both scenarios.

Theorem 1

The supplier’s profit function is concave.

Proof

Concavity of the supplier’s profit function can be proven by taking the second derivative of \(\pi_{\text{s1}} (Q)\) respect to \(Q\) which is strictly negative.

$$\frac{{\partial^{2} \pi_{\text{s1}} (Q)}}{{\partial Q^{2} }} = - \frac{{2d_{\text{m}} O_{\text{s}} }}{{(1 - y)Q^{3} }} < 0$$
(38)

Besides, the first derivative of \(\pi_{\text{s1}} (Q)\) respect to \(Q\) is as follows:

$$\frac{{\partial \pi_{\text{s1}} (Q)}}{\partial Q} = - \frac{{h_{\text{s}} (1 - y)}}{2} + \frac{{d_{\text{m}} O_{\text{s}} }}{{(1 - y)Q^{2} }}.$$
(39)

Theorem 2

The manufacturer’s total profit function is concave.

Proof

Concavity of the manufacturer’s profit function can be proven by taking the second derivative of \(\pi_{\text{m1}} (p_{\text{m}} )\) respect to \(p_{\text{m}}\) which is strictly negative.

$$\frac{{\partial^{2} \pi_{\text{m1}} (p_{\text{m}} )}}{{\partial p_{\text{m}}^{2} }} = - 2b < 0$$
(40)

In addition, the first derivative of \(\pi_{\text{m1}} (p_{\text{m}} )\) respect to \(p_{\text{m}}\) is as follow:

$$\frac{{\partial \pi_{\text{m1}} (p_{\text{m}} )}}{{\partial p_{\text{m}} }} = a - 2bp_{\text{m}} + bC_{\text{P}} + bp_{\text{s}} + bxp^{\prime}_{\text{m}} - \frac{{bh_{\text{m}} (1 - y)Q\,}}{{2r_{\text{p}} }} + \frac{{bO_{\text{m}} }}{(1 - y)Q} = 0.$$
(41)

Theorem 3

The wholesaler’s total profit is concave.

Proof

Concavity of the wholesaler’s profit function can be proven by taking the second derivative of \(\pi_{\text{w1}} (p_{\text{w}} )\) respect to \(p_{\text{w}}\) which is strictly negative:

$$\frac{{\partial^{2} \pi_{\text{w1}} (p_{\text{d}} )}}{{\partial p_{\text{w}}^{2} }} = - 2b < 0$$
(42)

Moreover, the first derivative of \(\pi_{\text{w1}} (p_{\text{w}} )\) respect to \(p_{\text{w}}\) is as follows:

$$\frac{{\partial \pi_{\text{w1}} (p_{\text{w}} )}}{{\partial p_{\text{w}} }} = a - 2bp_{\text{w}} - bxp^{\prime}_{\text{m}} + bp_{\text{m}} + bC_{\text{iw}} + \frac{{bO_{\text{w}} }}{(1 - y)Q} - \frac{{bh_{\text{w}} \left( {(1 - y)Q - B} \right)^{2} }}{{2(1 - y)Q\left( {(1 - x)d_{\text{w}} } \right)^{2} }} = 0.$$
(43)

Theorem 4

Like the similar case in the first scenario, the manufacturer’s profit function under the second scenario is concave, but it’s the first derivative changes to:

$$\frac{{\partial \pi_{\text{m2}} (p_{\text{m}} )}}{{\partial p_{\text{m}} }} = a - 2bp_{\text{m}} + bC_{\text{P}} + bp_{\text{s}} - \frac{{bh_{\text{m}} (1 - y)Q\,}}{{2r_{\text{p}} }} + \frac{{bO_{\text{m}} }}{(1 - y)Q} = 0.$$
(44)

Theorem 5

Like the similar case in the first scenario, the wholesaler’s profit function under the second scenario is concave, but it’s the first derivative changes to:

$$\frac{{\partial \pi_{\text{w2}} (p_{\text{w}} )}}{{\partial p_{\text{w}} }} = a - 2bp_{\text{w}} + bp_{\text{m}} + bC_{\text{iw}} + \frac{{bO_{\text{w}} }}{(1 - y)Q} - \frac{{bh_{\text{w}} \left( {(1 - y)Q - B} \right)^{2} }}{{2(1 - y)Q\left( {(1 - x)d_{\text{w}} } \right)^{2} }} = 0.$$
(45)

So, the optimal values of the decision variables under the first and second scenarios, based on the Nash-equilibrium approach, will be obtained by solving Eqs. (39), (41), and (43) and (39), (44), and (45) at the same time, respectively, which all of them are global optimum and unique.

Numerical example

In this case, we propose a numerical example to clarify applicability of the introduced production and inventory model in a three echelons supply chain involving a supplier, a manufacturer and one wholesaler under two scenarios. So, the parameters used to solve the model are as follows.

$$\begin{aligned} &a = 10000, \;b = 45,\;p_{\text{s}} = 15,\;B = 50,\;h_{\text{s}} = 3,\;h_{\text{m}} = 5,\\ & \quad h_{\text{w}} = 6,\;O_{\text{s}} = 100,\;O_{\text{m}} = 150,\;O_{\text{w}} = 200,\;C_{\text{r}} = 8 \hfill \\ \quad &C^{\prime}_{\text{r}} = 5,\;r_{\text{is}} = 150,\;r_{\text{p}} = 100,\;C_{\text{P}} = 18,\;C_{\text{is}} = 3,\;\\ & \quad C_{\text{bw}} = 30,\;r_{\text{iw}} = 200,\;C_{\text{iw}} = 3,\;y = 0.3,\;x = 0.2,\;f = 0.5,\;g = 0.4. \hfill \\ \end{aligned}$$

The results, which are shown in Table 1, indicate that the total profit of the chain under the first scenario is more than the second scenario. Under the first scenario, the supplier and wholesaler order more. On the other hand, the demand of buyer increases because of the lower selling price of the wholesaler. In fact, the profit of the manufacturer decreases by employing the return policy but the selling price of the wholesaler decreases which is caused to attract customers. So, the manufacturer prefers to gain the less profit in order to incentive the wholesaler’s demand and also market demand.

Table 1 The results of example
Full size table

Conclusion

In this paper, a three-echelon supply chain under a return contract concluded between the outside supplier and the supplier and also between the manufacturer and the wholesaler is deemed where the manufacturer receives raw materials from its outside supplier, transforms it into finished products and then sells them to the wholesaler to satisfy buyers’ demands. The outside supplier and the manufacturer intend to incentive the supplier and the wholesaler’s orders, by applying a coordination mechanism as return policy. Here, demand is price-sensitive and shortage at the wholesaler is backordered.

This model is developed for single product under two scenarios that as the first one, we consider the return policy between the members of the chain and in the second one; we assume the return policy is not employed between the manufacturer and the wholesaler. Moreover, a Nash-equilibrium method is considered between the partners of the chain. Gradually, to show the practicality of the discussed model, a numerical example is presented which based on the results, we found that the profit of the chain under the first scenario is more profitable. It means that considering the return contract between the partners of the chain leads to increase the orders due to essence of possibility of return defective items especially for breakable/delicate items which the buyers are worried about their healthy. In turn, it is found that this coordinating contract is profitable and proper for items which the possibility of their deficiency is higher than the others. For the future researches, the model can be extended under demand uncertainty and also the other coordination mechanisms such as quantity discount, buyback, profit sharing and etc. In addition, readers can extend or develop the model considering delivery lead time or multiple competing manufacturers/wholesalers with cooperative or competitive games.