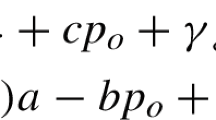1 Introduction

Inventory is the source of a large part of the costs of organizations which affects directly the pricing strategy. When products are purchased from an outside supplier it is also necessary to deal with the replenishment time for best optimal decisions. Decision-maker uses price as a decision variable which needs to be optimized and demand is also considered as price-sensitive [2, 4]. Hence pricing and inventory control are necessary to increase the ability of an organization to be competitive in the market and it is also very eminent when considered product deterioration. Deterioration of various products is a natural occurrence for production inventory which occurs due to damage, dryness, evaporation, spoilage, etc. It also reduces the quality and quantity of stored products. In recent studies of the inventory model, many researchers have investigated their models with deterioration of products [12, 18, 24]. To evaluate the pricing and inventory strategy, non-instantaneous deterioration of items was considered in an EOQ model under price and time-sensitive demand [15]. Food wastage was decreased through pricing strategy and maximize the profit under price-sensitive demand in [27]. An inventory mechanism with a price-dependent demand pattern evaluated the order amount, sales price, and cycle-length of deteriorating product [5]. Other factors like advertising play a key role in pricing decisions of deteriorating inventory model in [9].

In many earlier studies, the demand function is assumed to be constant. But for a variety of items like soft drinks, fruit juice, detergent, etc. this assumption is violated and demand is often assumed as iso-elastic [13] and infrequently depend on selling price. The exponential and negative power of the price form of demand curve was used to determine optimum cycle length, deteriorating length, and sales price of a deteriorating inventory model [17]. Optimum sales price, replenishment number, and full-cycle length for iso-elastic price-sensitive demand in a deteriorating EOQ model were discussed in [14]. An EOQ model for deteriorating items that specify the demand explicitly in the multivariate form of price, freshness, and display of stocks in [8]. Two different demand function with iso-elastic price-sensitive form and linear price- and stock-sensitive demand form has been discussed in [20] to study a deteriorating inventory model for different credit periods.

All of the above literature, various policies are determined for a single decision-maker to optimize its own performance. In today’s competitive market, organizations and businesses have enlarged their profitability by utilizing co-ordination strategy. Supply chain management is considered the most advantageous ways to enhance benefits for the organization. Today, rapid urbanization and competing global markets increase the importance of coordination between independent organizations. In a coordinated supply chain, various channel members work jointly to minimize system-related costs and get competitive advantages. An integrated inventory system for one supplier-one customer problem has been performed in for companies’ supply chain management mechanism [11]. The profit of a manufacturer-retailer supply chain was maximized with the level of inventory-dependent demand under discount contract [28]. Different supply chain policies containing a manufacturer and a retailer in which upstream member retailer inventory contains multiple costs for price and inventory-level-dependent demand [21]. An enmesh marketing and operations deal with information asymmetry and its profitability implications under rebates, as the trade incentive of interest in a two-stage supply chain has been discussed in [3, 19]. An integrated inventory model for a single manufacturer and multiple buyers under price-sensitive demand studied in [1].

Supply chain members manage their inventory level and faced deterioration of products during stock due to different geographical locations. Many studies such as [22, 26] analyze the pricing strategy and inventory decisions of deteriorated products through supply chain structure. To minimize the cost of deteriorating items, a two-layer supply chain mechanism has been established in [6] to evaluate replenishment time and total credit under constant demand. A two-stage supply chain mechanism considering the deterioration of product with linear price-sensitive demand was discussed in [7].

The decision-making process of an organization is characterized as centralized and decentralized. In a centralized structure, a central decision-maker controls the chain’s desired outcome such that all the members of the chain can gain together. This decision-making process is our present paper concern. In the decentralized structure, each channel member autonomously picks his techniques and therefore the general framework effectiveness may not necessarily be optimized. A decentralized structure of supply chain with linear selling price-dependent demand to optimize sales price, number of shipments, and cycle length for minimizing overall cost were studied in [23]. A manufacturer-retailer supply chain mechanism was illustrated under the linear and iso-elastic pattern of the price-sensitive demand function for both centralized and decentralized structures in [10]. A closed-loop supply chain model was addressed for re-manufactured products under price-sensitive for both centralized and decentralized cases in [16].

In Table 1, we have summarized some main assumptions and objectives of the recent literature to make it simpler for the readers to appreciate the contribution of our model. There are lot of researchers generalized different decision-making strategies for different demand patterns under a single decision-maker as well as multiple stages containing supply chain model but the purpose of this paper how both linear and iso-elastic price-sensitive demand pattern together effect on joint pricing and inventory policy of a two-echelon supply chain. We have designed a two-echelon supply chain model considering various assumptions like deterioration of the product, shortage with constant backlogging in-retailer inventory but neglect the inventory of the manufacturer. Also, we have seen from Table 1 that no work has previously done considering the effect of two different demand patterns in supply chain scenario. Our model is more prominent for the deteriorated products such as fruits, vegetables, sweets, etc. The demand for these products is mainly dependent on the sales price. These products sell through the retailer or directly to the customer and market decisions of the products are managed by the channel members together or individually as indicated by their significance, singular benefit, and connection. One of the practical examples of our proposed model is ice-cream factory. During any season, the demand for ice-cream increases linearly and nonlinearly with the selling price.

Our investigation contrasts from the earlier studies in the accompanying significant aspects. Firstly, we have considered the demand of the customers (1) linear function of selling price. (2) iso-elastic form of selling price. Secondly, under price-dependent demand, consideration of the deterioration of products plays an important role in pricing and inventory decisions to analyze the optimal profit of the supply chain. Thirdly, a shortage at the retailer warehouse is allowed with a constant backlogging rate of \(\delta\). Fourthly, we study the performance of our proposed manufacturer-retailer supply chain in a joint centralized structure. Lastly, a comparative study on linear and iso-elastic demand function on our proposed joint centralized supply chain strategy are examined.

Our work aims to compare joint pricing and replenishment strategies throughout the supply chain using two different types of demand patterns. The proposed analysis gives two aspects of a supply chain model (1) increasing profitability from the customer by optimizing sales price and order amount of a product under different demand scenario, (2) reducing cost of material flow between supply chain members. The results of considering all these demand functions greatly influence the total profit of business organizations and their decisions.

The paper is structured as follows. Section 2 is based on subsection “Notations and assumptions” of the model, “Mathematical Formulation” and the “Solution methodology” under centralized coordination with theoretical results of the model. In Sect. 3, theoretical results are demonstrated by a numerical example and a sensitivity analysis is conducted. Lastly, conclusion and future research direction are presented in Sect. 4.

Table 1 Summary of existing literature which are closely related to this model
Full size table

2 Model formulation and solution methodology

2.1 Notations and assumptions

2.1.1 Notations

The following notations are used to establish the model.

Notations

Descriptions

p

Selling price for the item (/unit )

\(T_1\)

Time length up to zero inventory level of the retailer

\(I_{1}(t)\)

Retailer inventory level at time t for the item, \(0< t < T_1\)

\(I_{2}(t)\)

Retailer inventory level at time t for the item, \(T_1< t < T\)

R(p)

Demand rate at time t for the item

Q

Total order quantity of the item (units)

q

Retailer on-hand inventory of the item (units)

S

Backlogging size (units) during \([T_1, T]\) of retailer

O

Retailer ordering cost of the item (/cycle )

T

The duration of the cycle

M

Manufacturing cost for the item ( /unit )

w

Wholesale price of the manufacturer ( /unit )

h

Retailer holding cost for the item (/unit/time unit )

d

Retailer deterioration cost for the item ( /unit /time unit)

s

Retailer shortage cost for the item ( /unit /time unit)

\(\theta\)

Deterioration rate for the item

\(TP_M\)

Total profit of the manufacturer

\(TP_R\)

Total profit of the retailer

TP

Total profit

2.1.2 Assumptions

The following assumptions are considered to develop the model.

  1. 1.

    The supply chain consists of one manufacturer and one retailer with a single-item inventory system.

  2. 2.

    Demand rates of the items are considered as (a) \(R(p)= a-bp\) with \(b> 0\), price elasticity and a basic demand, where \(a>>b\). (b) \(R(p)= d_0 p^{-k}\) where \(d_0 > 0\), is a scaling factor and \(k>1\) is the price elasticity parameter. This form of demand is known as iso-elastic demand.

  3. 3.

    The on-hand inventory of the products at the retailer warehouse deteriorates with a constant deterioration rate of \(\theta\), (\(0< \theta < 1\)). Also, it is presumed that deteriorated products are not replenished during [\(0, T_1\)].

  4. 4.

    The supply chain system operates for a prescribed period of T units (planning horizon). At time \(t=0\) the initial inventory of the retailer is q and \(t=T_1\) the inventory level of the retailer is zero. Then the shortage occurs up to next replenishment time T. Clearly, \(T>T_1.\)

  5. 5.

    Shortages are allowed and partially backlogged with a constant backlogging rate \(\delta\). The shortage period is \((T-T_1)\).

  6. 6.

    Lead time is negligible.

2.2 Mathematical formulation

In this paper, we consider a two-layered supply chain comprising of a manufacturer and a retailer. In Fig. 1, we see that the manufacturer delivers the product to the retailer at a wholesale price of w. Retailer ordering lot size from the manufacturer is Q. Some products are deteriorated at retailer inventory which is described elaborately in Sect. 2.2.1 and Fig. 2. The retailer faces a demand R(p) from the customer side and sells the products at a price p to the customer.

Fig. 1
figure 1

Supply chain structure

Full size image

2.2.1 Retailer profit function

The retailer inventory level follows the pattern presented in Fig. 2. At the beginning of the retailer inventory cycle, inventory starts with an on-hand inventory \(I_1(0)=q\) at time \(t=0\). This stock is reduced to meet the customers’ demand with deterioration of product and inventory level reaches zero at time \(t=T_1\). Then shortage at the retailer warehouse appears which is partially backlogged with a constant backlogging rate \(\delta\) at time-interval \([T_1, T]\). We mention the amount of backlogging is S. So, the total order quantity placed by the retailer to the manufacturer is \(q+S\).

Fig. 2
figure 2

Retailer’s inventory diagram

Full size image

During the time interval \([0,T_1]\), the retailer’s inventory follows the following differential equation:

$$\begin{aligned} \frac{\mathrm{d}I_1(t)}{\mathrm{d}t}+\theta I_1(t)=-R(p) \end{aligned}$$
(1)

with the initial condition \(I_1(0)=q\) and boundary condition \(I_1(T_1)=0\). By solving (1), it yields

$$\begin{aligned} I_1(t)=R(p) \Big [e^{\theta (T_1-t)}-1 \Big ] , \qquad t \in [0,T_1] \end{aligned}$$
(2)

Finally, in the interval \([T_1,T]\), the shortage occurs and demand is partially backlogged. Thus, the below differential equation represents the inventory status during the shortage

$$\begin{aligned} \frac{\mathrm{d}I_2(t)}{\mathrm{d}t}=-\delta R(p)=-\delta R(p) \end{aligned}$$
(3)

with the boundary condition \(I_2(T_1)=0\) the solution of (3) is

$$\begin{aligned} I_2(t)= \delta R(p)(T_1-t), \qquad t \in [T_1,T] \end{aligned}$$
(4)

If we put \(t=T\) into (4), the maximum amount of backlogging will be obtained as follows

$$\begin{aligned} S=-I_2(T)=- \delta R(p) (T_1-T) \end{aligned}$$
(5)

Then the total order quantity per cycle (Q) is the sum of q and S, i.e.,

$$\begin{aligned} Q=q+S=R(p) \Big [\frac{e^{\theta T_1}-1}{\theta }-\delta (T_1-T) \Big ] \end{aligned}$$
(6)

Now, we have calculated different inventory costs and sales revenue per unit time per cycle that consist of the following six components:

  1. 1.

    Ordering cost = \(\frac{O}{T}\)

  2. 2.

    Retailer’s purchasing cost = \(\frac{wQ}{T}\)

    $$\begin{aligned} =\frac{w R(p)}{T } \Big [\frac{e^{\theta T_1}-1}{\theta }-\delta (T_1-T) \Big ] \end{aligned}$$
    (7)
  3. 3.

    Holding cost = \(\frac{h}{T} \int _{0}^{T_1} I_1(t)\mathrm{d}t\)

    $$\begin{aligned} = \frac{h R(p)}{T\theta } \Big [\frac{e^{\theta T_1}}{\theta }-T_1-\frac{1}{\theta } \Big ] \end{aligned}$$
    (8)
  4. 4.

    Deterioration cost = \(\frac{d}{T} \Big [I_1(0)-\int _{0}^{T_1} R(p) \mathrm{d}t \Big ]\)

    $$\begin{aligned} = \frac{d R(p) }{T } \Big [\frac{e^{\theta T_1}-1}{\theta }-T_1 \Big ] \end{aligned}$$
    (9)
  5. 5.

    Shortage cost = \(\frac{s}{T} \int _{T_1}^{T} \Big [-I_2(t) \Big ] \mathrm{d}t\)

    $$\begin{aligned} = -\frac{s \delta R(p)}{T } \Big [TT_1-\frac{T_1^2}{2}-\frac{T^2}{2} \Big ] \end{aligned}$$
    (10)
  6. 6.

    Sales revenue = \(\frac{p}{T} \int _{0}^{T} R(p) \mathrm{d}t\)

    $$\begin{aligned} = p R(p) \end{aligned}$$
    (11)

Therefore, the total profit of the retailer per unit time per cycle (denoted by \(TP_R\)) is obtained by:

Total profit \(=\) Sales revenue − Ordering cost − Purchasing cost − Holding cost − Deterioration cost− Shortage cost.

$$\begin{aligned} TP_R &= \frac{p T R(p)}{T } - \frac{O}{T} - \frac{w R(p)}{T } \Big [\frac{e^{\theta T_1}-1}{\theta }-\delta (T_1-T) \Big ] \nonumber \\&- \frac{h R(p)}{T\theta } \Big [\frac{e^{\theta T_1}}{\theta }-T_1-\frac{1}{\theta } \Big ] - \frac{d R(p) }{T } \Big [\frac{e^{\theta T_1}-1}{\theta }-T_1 \Big ] \nonumber \\&+ \frac{s \delta R(p)}{T } \Big [TT_1-\frac{T_1^2}{2}-\frac{T^2}{2} \Big ] \end{aligned}$$
(12)

with \(p>w\), \(w>0\), p \(\in\) \(R^{+}\), \(T_1\) \(\in\) \(R^{+}\).

Rearranging Eq. (12) we get,

$$\begin{aligned} TP_R &= \frac{R(p)}{T} \Big [p -\Big (w+d+\frac{h}{\theta }\Big ) \Big (\frac{e^{\theta T_1}-1}{\theta } \Big )-w \delta T \nonumber \\&+ \Big (w \delta + s \delta +d+\frac{h}{\theta } \Big )T_1 -s \delta \Big (\frac{T_1^2}{2}+\frac{T^2}{2} \Big ) \Big ]-\frac{O}{T} \end{aligned}$$
(13)

with \(p>w\), \(w>0\), p \(\in\) \(R^{+}\), \(T_1\) \(\in\) \(R^{+}\).

2.2.2 Manufacturer profit function

There are no different individual cost of the manufacturer. The manufacturer makes the products and delivers them to the retailer with zero lead time. Products are stored for a short period at the manufacturer warehouse. So, we neglect deterioration cost, inventory cost and optimized the manufacturer overall profit(\(TP_M\)) per unit time.

$$\begin{aligned} TP_M &= (w-M)\frac{Q}{T} \nonumber \\ &= (w-M) \frac{R(p)}{T} \Big [\frac{e^{\theta T_1}-1}{\theta }-\delta (T_1-T) \Big ] \end{aligned}$$
(14)

with \(w>M\), w \(\in\) \(R^{+}\), \(T_1\) \(\in\) \(R^{+}\).

2.3 Solution methodology

The manufacturer and the retailer are both decision-makers and they jointly optimize the profit function for both the demand scenario. This strategy to solve the mathematical model is a centralized system. Let, \(TP(p, T_1)\) be the joint average profit function of the supply chain that is the sum of manufacturer’s and retailer’s average profit.

$$\begin{aligned} TP(p,T_1) &= TP_R + TP_M \nonumber \\ &= \frac{R(p)}{T} \Big [p -\Big (M+d+\frac{h}{\theta }\Big ) \Big (\frac{e^{\theta T_1}-1}{\theta } \Big ) \nonumber \\- & {} M \delta T + \Big (M \delta + s \delta +d+\frac{h}{\theta } \Big )T_1 \nonumber \\- & {} s \delta \Big (\frac{T_1^2}{2}+\frac{T^2}{2} \Big ) \Big ]-\frac{O}{T} \end{aligned}$$
(15)

with \(p>w>M>0\), \(T> T_1\), p \(\in\) \(R^{+}\), \(T_1\) \(\in\) \(R^{+}\).

The corresponding optimization problem for the overall supply chain can be written as

$$\begin{aligned}&\max \qquad \qquad TP(p,T_{1}) \nonumber \\&\text {such that:} \qquad p>w>M>0, \nonumber \\&\qquad \qquad \qquad T> T_{1}, p \in R^{+},T_{1} \in R^{+} \end{aligned}$$
(16)

2.3.1 Supply chain profit under linear price-sensitive demand

For \(R(p)=a-bp\), the joint average supply chain profit is

$$\begin{aligned} TP(p,T_1) &= \frac{(a-bp)}{T} \Big [p -\Big (M+d+\frac{h}{\theta }\Big ) \Big (\frac{e^{\theta T_1}-1}{\theta }\Big )\nonumber \\- & {} M \delta T + \Big (M \delta + s \delta +d+\frac{h}{\theta } \Big )T_1 \nonumber \\- & {} s \delta \Big (\frac{T_1^2}{2}+\frac{T^2}{2}\Big )\Big ]-\frac{O}{T} \end{aligned}$$
(17)

with \(p>w>M>0\), \(T> T_1\), p \(\in\) \(R^{+}\), \(T_1\) \(\in\) \(R^{+}\).

Proposition 1

For a fixed T, the joint supply chain profit \(TP(p,T_1)\) under linear price-sensitive demand is concave with respect to p and \(T_1\). For \(p>w>M\) and \(T> T_1\), the selling price p and inventory time \(T_1\) are obtained by solving the following system of equations:

  1. 1.
    $$\begin{aligned}&p= \frac{1}{\delta -1} \Big [ s \delta (T-T_1)-M(e^{\theta T_1 }-\delta ) \nonumber \\&-(d+h)(e^{\theta T_1}-1) \Big ] \end{aligned}$$
    (18)
  2. 2.
    $$\begin{aligned}&\Big [ a-\frac{2b}{\delta -1} \Big \{ s \delta (T-T_1)-M(e^{\theta T_1 }-\delta ) \nonumber \\&-(d+h)(e^{\theta T_1}-1)\Big \} \Big ] \times \Big \{T_1+(T-T_1)\delta \Big \} \nonumber \\&-b \Big [s\delta \Big (TT_1-\frac{T_1^2}{2}-\frac{T^2}{2} \Big ) \nonumber \\&-(h+d+M)\frac{e^{\theta T_1}}{\theta } +(h+d) \Big (T_1+\frac{1}{\theta } \Big ) \nonumber \\&+M \Big \{\frac{1}{\theta }-\delta (T-T_1) \Big \} \Big ]=0 \end{aligned}$$
    (19)

Proof

To find the optimality, differentiating \(TP(p,T_1)\) with respect to p and \(T_1\) we get the following,

$$\begin{aligned} \frac{\partial TP(p,T_1) }{\partial p} &= \frac{(a-2bp)}{T} \Big \{T_1+(T-T_1)\delta \Big \} \nonumber \\- & {} \frac{b}{T} \Big [ s\delta \Big (TT_1-\frac{T_1^2}{2}-\frac{T^2}{2} \Big ) \nonumber \\- & {} (h+d+M)\frac{e^{\theta T_1}}{\theta } +(h+d) \Big (T_1+\frac{1}{\theta } \Big ) \nonumber \\+ & {} M \Big \{\frac{1}{\theta }-\delta (T-T_1) \Big \} \Big ] \end{aligned}$$
(20)
$$\begin{aligned} \frac{\partial TP(p,T_1) }{\partial T_1} &= \frac{(a-bp)}{T} \Big [p(1-\delta )+s \delta (T-T_1) \nonumber \\- & {} M(e^{\theta T_1 }-\delta )-(d+h)(e^{\theta T_1}-1) \Big ] \end{aligned}$$
(21)

Equating \(\frac{\partial TP(p,T_1) }{\partial T_1} = 0\) and \(\frac{\partial TP(p,T_1) }{\partial p} =0\), we get (18) and (19). Due to the complexity of Eq. (19), it is difficult to show analytically the expression of time-length up to zero inventory \(T_1\). Using mathematical software, we easily derive \(T_1\) and shown it numerically.

Total profit (TP) is concave in retail price (p) and time-length up to zero inventory (\(T_1\)). The second-order derivative of the profit function is

$$\begin{aligned} \frac{\partial ^2 TP(p,T_1) }{\partial p^2} &= -\frac{2b}{T} \Big [T_1+(T-T_1)\delta \Big ] < 0 \end{aligned}$$
(22)
$$\begin{aligned} \frac{\partial ^2 TP(p,T_1) }{\partial T_1^2} &= -\frac{(a-2bp)}{T} \Big [s\delta +(d+h+M)\theta e^{\theta T_1} \Big ] < 0 \end{aligned}$$
(23)

if \(a>2bp\) holds, since \(a>>b\) and \(T> T_1\) assumed.

To verify the optimality of Eqs. (18) and (19), we calculate the Hessian matrix (H) of the corresponding profit function \(TP(p, T_1)\) is

$$\begin{aligned} \mathbf {H}=\left[ \begin{array}{cc} \frac{\partial ^2 TP(p,T_1) }{\partial p^2}&{}\frac{\partial ^2 TP (p,T_1)}{\partial p\partial T_1}\\ \frac{\partial ^2 TP(p,T_1) }{\partial T_1\partial p}&{}\frac{\partial ^2 TP (p,T_1)}{\partial T_1^2}\\ \end{array}\right] \end{aligned}$$

Here expressions

$$\begin{aligned} \frac{\partial ^2 TP(p,T_1) }{\partial p \partial T_1} &= \frac{\partial ^2 TP(p,T_1) }{\partial T_1 \partial p} \nonumber \\ &= \frac{(1-\delta )}{T}(a-bp)+\frac{b}{T} \Big [(d+h)(e^{\theta T_1}-1) \nonumber \\&\quad +M(e^{\theta T_1}-\delta ) -p(1-\delta )-s\delta (T-T_1) \Big ] \end{aligned}$$
(24)

To prove the concavity, we have to show that the Hessian matrix is negative definite, i.e., principal minors alternate their sign starting with a negative sign. Clearly, \(\Delta _1 =\frac{\partial ^2 TP (p,T_1)}{\partial p^2}<0\) as \(T> T_1\).

Since \(p>w>M\) and \(T> T_1\), \(\Delta _2 > 0\) holds (see “Appendix 1”, when Eq. (35) satisfy) then the solution set is optimal. \(\square\)

2.3.2 Supply chain profit under iso-elastic price-sensitive demand

For \(R(p)=\frac{d_0}{p^k}\), the joint supply chain profit is

$$\begin{aligned} TP(p,T_1) &= \frac{d_0}{T p^k} \Big [p - \Big (M+d+\frac{h}{\theta } \Big ) \Big (\frac{e^{\theta T_1}-1}{\theta } \Big ) \nonumber \\ &\quad -{} M \delta T + \Big (M \delta + s \delta +d+\frac{h}{\theta } \Big )T_1 \nonumber \\ &\quad - s \delta \Big (\frac{T_1^2}{2}+\frac{T^2}{2} \Big ) \Big ]-\frac{O}{T} \end{aligned}$$
(25)

with \(p>w>M>0\), \(T>T_1\), p \(\in\) \(R^{+}\), \(T_1\) \(\in\) \(R^{+}\).

Proposition 2

For a fixed T , the joint supply chain profit \(TP(p,T_1)\) under iso-elastic price-sensitive demand is concave with respect to p and \(T_1\) . For \(p>w>M\) and \(T> T_1\) , the selling price p and inventory time \(T_1\) are obtained by solving the following system of equations:

  1. 1.
    $$\begin{aligned}&p= \frac{1}{\delta -1} \Big [ s \delta (T-T_1)-M(e^{\theta T_1 }-\delta ) \nonumber \\&-\quad(d+h)(e^{\theta T_1}-1) \Big ] \end{aligned}$$
    (26)
  2. 2.
    $$\begin{aligned}&(1+k) \Big \{T_1+(T-T_1)\delta \Big \} \nonumber \\&\quad -\frac{k \delta (\delta -1) \Big (TT_1-\frac{T_1^2}{2}-\frac{T^2}{2} \Big ) }{\Big [ s \delta (T-T_1)-M(e^{\theta T_1 }-\delta )-(d+h)(e^{\theta T_1}-1) \Big ]} \nonumber \\&\quad -(h+d+M)\frac{e^{\theta T_1}}{\theta } +(h+d) \Big (T_1+\frac{1}{\theta } \Big ) \nonumber \\&\quad +M \Big \{\frac{1}{\theta }-\delta (T-T_1) \Big \} ]=0 \end{aligned}$$
    (27)

Proof

To find the optimality differentiating total profit \(TP(p,T_1)\) with respect to p and \(T_1\) we get the following,

$$\begin{aligned} \frac{\partial TP(p,T_1) }{\partial p} &= \frac{d_0 }{T p^k} \Big \{T_1+(T-T_1)\delta \Big \} \nonumber \\- & {} \frac{d_0 k }{T p^k} \Big [\delta \Big (TT_1-\frac{T_1^2}{2}-\frac{T^2}{2} \Big ) \nonumber \\- & {} (h+d+M)\frac{e^{\theta T_1}}{\theta } +(h+d) \Big (T_1+\frac{1}{\theta } \Big ) \nonumber \\+ & {} M \Big \{\frac{1}{\theta }-\delta (T-T_1) \Big \} \Big ] \end{aligned}$$
(28)
$$\begin{aligned} \frac{\partial TP(p,T_1) }{\partial T_1} &= \frac{d_0 p^k}{T} \Big [p(1-\delta )+s \delta (T-T_1) \nonumber \\- & {} M(e^{\theta T_1 }-\delta ) -(d+h)(e^{\theta T_1}-1) \Big ] \end{aligned}$$
(29)

Equating \(\frac{\partial TP(p,T_1)}{\partial T_1} = 0\) and \(\frac{\partial TP(p,T_1) }{\partial p} =0\), we get (26) and (27).

Again closed form of optimal solutions of \(T_1\) for iso-elastic demand could not be obtained due to complexity of Eq. (27). So, we derive it numerically in Sect. 3.

The supply chain profit function (TP) is concave in retail price (p) and time-length up to zero inventory (\(T_1\)). The second-order derivative under iso-elastic demand pattern are

$$\begin{aligned} \frac{\partial ^2 TP(p,T_1) }{\partial p^2} &= -\frac{2d_0 k}{T p^{k+1}} [T_1+\delta (T-T_1)] \nonumber \\+ & {} \frac{d_0 k (k+1)}{T p^{k+2}} \Big [s\delta \Big (TT_1-\frac{T_1^2}{2}-\frac{T^2}{2} \Big ) \nonumber \\+ & {} p \Big \{T_1+\delta (T-T_1) \Big \} +M \delta (T_1-T) \Big ] \nonumber \\- & {} (h+d+M) \Big (\frac{e^{\theta T_1}-1}{\theta } \Big )+(h+d)T_1 \nonumber \\&< 0 \end{aligned}$$
(30)

if

$$\begin{aligned}&\frac{2d_0 k}{T p^{k+1}} \Big [T_1+\delta (T-T_1) \Big ]+(h+d+M) \Big (\frac{e^{\theta T_1}-1}{\theta } \Big ) > \nonumber \\&\frac{d_0 k (k+1)}{T p^{k+2}} \Big [s\delta \Big (TT_1-\frac{T_1^2}{2}-\frac{T^2}{2} \Big )+ p \Big \{T_1+\delta (T-T_1)\Big \} \nonumber \\&+M \delta (T_1-T) \Big ]+(h+d)T_1 \end{aligned}$$
(31)

holds for \(p>w>M\), \(T> T_1\) and

$$\begin{aligned} \frac{\partial ^2 TP(p,T_1)}{\partial T_1^2}=-\frac{d_0}{T p^k} \Big [s\delta +(d+h+M)\theta e^{\theta T_1}\Big ] < 0. \end{aligned}$$
(32)

To verify the optimality of Eqs. (26) and (27), we calculate the Hessian matrix (H) of the corresponding profit function \(TP(p,T_1)\) is

$$\begin{aligned} \mathbf {H}=\left[ \begin{array}{cc} \frac{\partial ^2 TP(p,T_1) }{\partial p^2}&{}\frac{\partial ^2 TP (p,T_1)}{\partial p\partial T_1}\\ \frac{\partial ^2 TP(p,T_1) }{\partial T_1\partial p}&{}\frac{\partial ^2 TP (p,T_1)}{\partial T_1^2}\\ \end{array}\right] \end{aligned}$$

Here expressions

$$\begin{aligned} \frac{\partial ^2 TP(p,T_1) }{\partial p \partial T_1} &= \frac{\partial ^2 TP(p,T_1) }{\partial T_1 \partial p} \nonumber \\ &= \frac{d_0 (1-\delta )}{T p^k} -\frac{d_0 k}{T p^{k+1}}[(d+h)(e^{\theta T_1}-1) \nonumber \\&\quad+ {} M(e^{\theta T_1}-\delta ) - p(1-\delta )-s\delta (T-T_1) \Big ] \end{aligned}$$
(33)

To prove the concavity, we have to show that hessian matrix is negative definite, i.e., principal minors alternate their sign starting with a negative sign. Clearly, \(\Delta _1 =\frac{\partial ^2 TP (p,T_1)}{\partial p^2}<0\) if

$$\begin{aligned}&\frac{2d_0 k}{T p^{k+1}} \Big \{ T_1+\delta (T-T_1) \Big \} +(h+d+M) \Big (\frac{e^{\theta T_1}-1}{\theta } \Big ) > \nonumber \\&\frac{d_0 k (k+1)}{T p^{k+2}} \Big [s\delta \Big (TT_1-\frac{T_1^2}{2}-\frac{T^2}{2} \Big )+ p \Big \{T_1+\delta (T-T_1)\Big \} \nonumber \\&+M \delta (T_1-T) \Big ]+(h+d)T_1 \end{aligned}$$
(34)

for \(p>w>M>0\) and \(T> T_1\) .

Since \(p>w>M\) and \(T> T_1\), \(\Delta _2 > 0\) holds (see “Appendix 2”, when Eq. (36) satisfy) then the solution set is optimal. \(\square\)

3 Algorithm

  1. 1.

    Start

  2. 2.

    Find \(TP_R\) and \(TP_M\), calculating all inventory cost. Then find joint overall supply chain profit \(TP(p,T_1)\) under centralized structure.

  3. 3.

    Evaluate \(\frac{\partial TP(p,T_1)}{\partial p}\), \(\frac{\partial TP(p,T_1)}{\partial T_1}\) simultaneously.

  4. 4.

    Solve the nonlinear-dependent equations \(\frac{\partial TP(p,T_1)}{\partial p}=0\) and \(\frac{\partial TP(p,T_1)}{\partial T_1}=0\) by initializing the values of \(d_{0}\), k, a, b, M, h, s, d, \(\theta\), \(\delta\) and T.

  5. 5.

    Choose set of solutions from step 4.

  6. 6.

    Evaluate \(\frac{\partial ^2 TP(p,T_1) }{\partial ^2 p}\), \(\frac{\partial ^2 TP(p,T_1)}{\partial T_1^2}\) and \(\frac{\partial ^2 TP(p,T_1) }{\partial p \partial T_1}\).

  7. 7.

    If the principal minor of the Hessian matrix alternate there sign starting with negative, i.e., \((-1)^j\Delta _j>0\), here \(j=1,2\), then the solution is optimal.

  8. 8.

    Evaluate the selling price (p), time length up to zero inventory (\(T_1\)), and then order quantity (Q) as well as total profit of the retailer (TP).

  9. 9.

    End

4 Numerical results and discussion

Our mechanism is mainly applicable for the organizations which stored deteriorated items like fruits, vegetables, sweets, and so on. During any season, the demand for these products increases linearly dependent on selling price or sometimes negative power of selling price. One of the popular examples of our anticipated model is (ice-cream factory/Chocolate factory/bakery/vegetable or food supply chain etc.). Due to the linear and nonlinear behavior of demand, business organizations can adjust their pricing strategy by understanding the market situation and rapid globalization.

4.1 Numerical example

In this section, to illustrate the applicability of the proposed model, we study a numerical example considering the values of the input parameters \(M=\$20\), \(s=\$5\), \(T=10\) week are taken from [3], the value of deterioration rate \(\theta =0.08\) taken from [15] and some of the key parameters \(d_0=400000\), \(k=2.2\), \(a=250\), \(b=3.2\), \(\delta =0.7\), \(O=\$100\)/order, \(h=\$4\), \(d=\$3\) are logically chosen based on the assumptions presented in Sect. 2.1.

Customer demand for product move proportionately with the price changes. We have shown the sensitivity of the price-elasticity parameter of linear demand (a,b) in Table 5 and price elasticity parameter of iso-elastic demand (k) in Table 6 and discuss the managerial insights in Sect. 3.3.

4.2 Solution and discussion

By using software MATHEMATICA, we have evaluated the optimum solutions to maximize total profit \(TP(p, T_1)\) are listed in Table 2. The optimality of the proposed model has been performed considering the cycle length T=10 weeks and then analyze the changes of the optimal solutions under different T value for \(T=8\), 9, 11, 12 weeks (shown in Table 4). To illustrate the concavity of the objective function \(TP(p, T_1)\) the sufficient conditions of the profit function have been evaluated in Table 3. The numerical illustration may help to elucidate the comparisons between linear and nonlinear behavior of demand functions.

Comparing the results of the supply chain for two different demand strategies, we find that the retail price in a linear price-sensitive demand scenario is higher than that of the iso-elastic price-sensitive demand scenario. Meanwhile, the order quantity and time-length to stock out the products as well as the total profit under linear price-sensitive demand are greater than those of iso-elastic demand pattern.

Figure 3a shows the concavity of total profit \(TP(p,T_1)\) with respect to p and \(T_1\) under linear price-sensitive demand. Employing the suggested solution algorithm and the result of the proposed mechanism shown in Table 2, if the retailer sells the product at \(p=\$53.48\) then the stock out time of products in retailer’s inventory will be \(T_1=7.038\) weeks and the supply chain will achieve it’s highest profit \(\$1761.06\) employing the sufficient conditions of Table 3.

Similarly, Fig. 3b shows the concavity of total profit \(TP(p,T_1)\) under iso-elastic price-sensitive demand. From optimal Table 2, it is clear that if the retailer sells the product at \(p=\$52.47\) and able to sells the product at time \(T_1=6.771\) weeks, then the supply chain will achieve its highest profit \(\$1457.89\) employing the sufficient conditions of Table 3.

From Table 4, it is interesting to show the variation of cycle duration T on optimal profit under linear and iso-elastic price-sensitive demand scenario. Keeping order quantity as low as possible for a short duration of the cycle, save money on holding and other costs associated with the item. Also the retailer sells the product at a lower selling price as he invests less on inventory costs. But the shortened cycle duration is profitable for an organization’s supply chain model. An increase in cycle length sustained high-order quantity call for an increase in other costs associated with that item. So stock-outs of items are costly and they represent the lost sales and failure of supply chain coordination for both demand patterns.

Table 2 Optimal solution
Full size table
Table 3 Value of second-order derivative
Full size table
Fig. 3
figure 3

Concavity curve of profit function

Full size image

4.3 Sensitivity analysis

Tables 4, 5, 6, 7, 8, 9 and 10 and Figs. 4 and 5 show the impact of the percentage change of different cost parameters M, h, d, s on optimal selling price (p), optimal order quantity (Q), optimal time-length up to zero inventory(\(T_1\)) and total supply chain profit (TP). The analysis is conducted by changing the value of one of the parameters by \(-30\%\), \(-15\%\), \(+15\%\) and \(+30\%,\) respectively, keeping the other parameters constant.

Table 5 shows the impact of changes of a, b for linear demand and table 6 shows impact of changes of k for iso-elastic demand in total profit TP and decision variables. We change the initial value of some particular parameters (a, b, k) keeping other parametric values unchanged at that time.

Results of sensitivity analysis have revealed that there is a significant effect of change in the values of duration of cycle T and cost parameters M, h, d, s on the optimal Net Profit (TP) as well as on the optimal values of the decision variables which are shown in Figs. 4 and 5.

Table 4 Sensitivity analysis with respect to cycle duration T
Full size table
Table 5 Sensitivity analysis with respect to linear price elasticity a and b
Full size table
Table 6 Sensitivity analysis with respect to iso-elastic price elasticity k
Full size table
Table 7 Sensitivity analysis with respect to manufacturing cost M
Full size table
Table 8 Sensitivity analysis with respect to holding cost h
Full size table
Table 9 Sensitivity analysis with respect to deterioration cost d
Full size table
Table 10 Sensitivity analysis with respect to shortage cost s
Full size table

Based on Tables 4, 5, 6, 7, 8, 9 and 10 and Figs. 4 and 5, we have the following managerial insights according to change the behavior of different parameters.

  1. 1.

    As the manufacturing cost (M) increases, the selling price (p) of the retailer increases, ordering lot size (Q) of the manufacturer, time-length up to zero inventory (\(T_1\)) of retailer warehouse and the total profit (TP) of the supply chain decreases as shown in Table 7 and Figs. 4a, e and 5a. From an economic viewpoint, when manufacturing cost increases retailer prefers to raise its selling price to chase more benefits. But under both linear and nonlinear demand, the rate of change of selling price, ordering lot size is different. Increasing manufacturing cost leads to a very low demand under iso-elastic price-sensitive demand pattern compared to linear price-sensitive demand and fewer products have sold out at less time which prompts the retailer to increase its selling price at a higher rate in case of iso-elastic demand pattern, as a result, this affects a negative impact on total supply chain profit. The total profit for the iso-elastic demand form is very less compared to the linear demand for increasing manufacturing cost.

  2. 2.

    As the holding cost (h) increases, the retailer selling price (p) also increase, but the order quantity (Q), time length up to zero inventory (\(T_1\)) reduce so that that the total profit (TP) of the supply chain decrease as shown in Table 8 and Figs. 4b, f and 5b. Increasing holding cost keeps away the retailer to stock more amount and sells the product as soon as possible which shortened the time-length up to zero inventory. Also, retailer slightly increases its selling price for the hope of gain benefit. But contrary to retailer expectation, overall profit of the supply chain decreases simultaneously under both linear and nonlinear demand. The impact of the change of holding cost on optimal solutions is approximately the same for both linear and iso-elastic demand patterns. The physical phenomena implies that the retailer should balance their ordering quantity based on holding costs.

  3. 3.

    As the deterioration cost (d) increases, the overall profit (TP) of the supply chain decreases as shown in Table 9. From the business viewpoint, it is clear that due to increasing deterioration cost the retailer has to increase a minimum around on their selling price (p) and reduce order quantity (Q) at the optimum level. The changes of different optimality are also shown in Figs. 4c, g and 5c. Less stock is sold out at a shortened period. The impact of both linear and iso-elastic demand on the rate of change of optimal solutions is approximately the same for increasing deterioration cost.

  4. 4.

    As the shortage cost (s) increases as shown in Table 10 and Figs. 4d, h and 5c, selling price (p), inventory time (\(T_1\)) increases under both the demand pattern. But with the changes in shortage cost, order quantity (Q) will increase under the linear demand policy while it decreases under the iso-elastic demand policy. Moreover, increasing shortage cost (due to various phenomenon like a quantity discount, price discount, offering facility, an opportunity of delay in payment, etc.) always reduce supply chain profitability under both the demand analysis.

  5. 5.

    It is observed that when a increases in linear demand pattern, market demand will be increased. It indicates the instantaneous growth of ordering lot size. As a result, the time-length to stock out the product is lengthier and organizations sell the more product at more selling price and get higher profit shown in Table 5.

  6. 6.

    When price-elasticity parameters for both linear and iso-elastic demand (b, k) increases demand decreases. The organization will bring down the retail price and order amount. Fewer products are stock out at less time. Due to the fixed replenishment cycle, shortage period is lengthened. All these behavior of the price-elasticity parameter b, k decreases the total profit(TP) of the supply chain shown in Tables 5 and 6.

Fig. 4
figure 4

Changes of p and Q with respect to M, h, d and s

Full size image
Fig. 5
figure 5

Changes of Total profit (TP) with respect to M, h, d and s

Full size image

5 Conclusion

In this article, we have considered a two-echelon supply chain comprising of a manufacturer and a retailer for two different demand functions. The demand function of the customer is linearly dependent on selling price and iso-elastic form of the selling price. The manufacturer offers the product to the retailer and at retailer warehouse products are deteriorated at a constant deterioration rate. The shortage also occurs at the retailer warehouse which is partially backlogged with a backlogging rate \(\delta\). Under these circumstances, the joint profit function of the channel members of the supply chain is discussed. We have developed two models under two different patterns and compare the total profit under a joint centralized strategy. The key decision variables of our proposed model are the selling price of the retailer, optimal time-length up to zero inventory, total supply chain profit by which the organization can invest securely for different demand patterns. In our model, we assume the total duration of the cycle to be fixed and discuss the profitability of a coordinated organization by showing the impact of different time-length of the cycle in Table 4.

A numerical example has been solved to demonstrate the proposed algorithm. Through the comparison of two different demand scenarios, the retailer sells the product at a higher selling price for a fixed period in case of linear price-sensitive demand compared to the iso-elastic price-sensitive form. Moreover, higher selling price and more ordering lot size lead to more profit in linear price-sensitive demand.

Sensitivity of some key parameters has been analyzed which will give an option in contrast to given strategies in the area of supply chain management and construct the route for a more extensive application extent of the model. The result shows that the change of some input parameters has a significant impact on the optimal decisions of the supply chain system. Total profit of the supply chain decreases for increasing holding cost, deterioration cost, shortage cost and manufacturing cost. But,the decreasing rate of total profit is high for increasing manufacturing cost which indicates that a lower manufacturing cost is more beneficial for the joint supply chain system. In case of demand elasticity parameter, the increasing market potential is always beneficial for the supply chain system but increasing price-elasticity parameter value for both the demand pattern causes a loss for the system.

The new major contribution of this paper is a comparison of joint profit and optimal decisions under linear and iso-elastic demand form and also consideration of deterioration, shortage of product at retailer warehouse compared to the existing literature. This model is applicable for the deteriorated products like fruits, vegetables, etc. when the market decisions are taken together by both manufacturer/supplier and retailer.

In this paper, both the manufacturer and retailer are decision-makers and they jointly optimize their profit under different demand patterns but we have not discussed our model if any of the channel members may not accept to participate in the joint centralized model which is a limitation of our model. Different incentive plans could be considered including a decentralized decision model in the future direction. Another limitation is the constant deterioration rate which is very common in literature. We may extend our model considering time-dependent deterioration at the retailer warehouse and for a multi-stage supply chain.