Seismic performance of arch dams on non-homogeneous and discontinuous foundations (a case study: Karun 4 Dam)

Abstract

The present study set out to investigate the nonlinear seismic response of the dam–reservoir–rock foundation system, taking into consideration the effects of change in the material properties of discontinuous foundation. To this end, it is important to provide the proper modeling of truncated boundary conditions at the far-end of rock foundation and reservoir fluid domain and to correctly apply the in situ stresses for rock foundation. The nonlinear seismic response of an arch dam mainly depends on the opening and sliding of the dam body’s contraction joints and foundation discontinuities, failure of the jointed rock and concrete materials, etc. In this paper, a time domain dynamic analysis of the 3D dam–reservoir–foundation interaction problem was performed by developing a nonlinear Finite Element program. The results of the analysis of Karun-4 Dam revealed the essential role of modeling discontinuities and boundary conditions of rock foundation under seismic excitation.

Introduction

A large number of high arch dams in the world are built or to be built in the seismically active areas. Therefore, it is essential to carry out the seismic analysis of coupled dam–foundation system to ensure the safety and reliability of high arch dam structures. The structural strength of an arch dam under ground motion is mostly dependent on the stability and strength of its abutments. Actually, even high safety margins for unexpected ground motions do not guarantee the stability of dam if it is constructed on an uncertain foundation. In addition, due to the complex nature of rock foundation including non-homogeneous materials, the existence of joint sets and faults, etc., final judgment about the performance of dam will be difficult. Collapse of Malpasset Dam in France in 1959 is an apparent example of the lack of foundation strength.

During the past few years, extensive research has been done in the analysis and design of concrete dams, but the need for more accurate modeling of abutments in a coupling system with regard to the effects of mass, flexibility and non-homogeneity of discontinuous rock foundation are still felt. In the current study, a numerical program for 3D nonlinear dynamic analysis of concrete arch dams is developed in FORTRAN language and applies it to Karun 4 Dam. The study attempts to control two main features which directly affect the accuracy and precision of analytical results, i.e., correct in situ stresses for the bedrock and the choice of a proper boundary condition for the far-end of discontinuous rock foundation.

A review of research areas and solving methods

The main factors that influence significantly the three-dimensional nonlinear dynamic analysis of arch dams are identified: (1) dam–reservoir interaction and resulted distribution of hydrodynamic pressure, (2) reservoir–foundation interaction and the related effects of reservoir bottom sediments, (3) dam–foundation interaction and the role of non-homogeneity and discontinuities in bedrock, (4) non-uniform input of the free-field motions, (5) nonlinear behavior of the quasi-brittle material of concrete and jointed rock, and contact in the contraction and peripheral joints of dam body, and (6) boundary conditions.

Great effort has been made to develop the fundamentals and analytical methods of the above-mentioned subjects and a brief review of the main issues related to research are presented here.

Fluid–solid interaction is a very complicated problem which involves both structural and fluid dynamics. Several researchers have developed advanced numerical methods based on the finite element, boundary element or combination of them to model the dynamic dam–reservoir interactions. Two common approaches in fluid domain are Eulerian- and Lagrangian-based formulations (Bouaanani and Lu 2009). The former approach is known as pressure- or potential-based formulations where fluid pressure or velocity potential is selected as state variable. The Lagrangian approach in fluid domain is an extension of the solid finite element formulation with nodal displacements as degrees of freedom. As a result, the fluid domain is formulated using the same shape functions as structural elements and, in this way, compatibility at the fluid–structure interface is automatically fulfilled. In such cases, fluid elements are characterized by a volumetric elastic modulus equal to the fluid bulk modulus (or fluid compressibility); with a negligible shear resistance and Poisson constant being nearly 0.5 to simulate the fluid flow more reliable. The major disadvantage of Lagrangian approach is the generation of spurious circulation modes, due to the zero shear modulus. There are different methods for eliminating these zero energy modes that have been used by a large number of researchers (Chopra et al. 1969; Shugar and Katona 1975; Hamdi et al. 1978; Zienkiewicz and Bettess 1978; Akkaş et al. 1979; Wilson and Khalvati 1983; Olson and Bathe 1983; Doğangün et al. 1996; Doğangün and Livaoglu 2006, etc.). One approach is based on assuming that the shear modulus of the fluid is numerically very small. This approach has been adopted by this study. The partial absorption of pressure waves at sediment layers of reservoir bottom and its lateral sides may significantly affect the magnitude of hydrodynamic forces while the response of dam due to the ground motion is being investigated (Mirzabozorg et al. 2003). In the present study, the Lagrangian approach is used for modeling the fluid and sediment domain. Also, the interface elements with low shear stiffness are used to model the common surfaces of the fluid and solid elements.

Dam–foundation interaction is mainly related to the bedrock’s flexibility, changes of physical properties of rock foundation, existence of joints and faults in it, geometry of dam body, water leakage, uplift pressure, etc. It has been proven that in a nonlinear dynamic analysis including dam–foundation interaction, the foundation’s mass, flexibility and radiation damping are important (Tan and Chopra 1995). In addition, in order to model the behavior of jointed rock masses, their strength and deformability should be expressed as a function of joint orientation, joint size, and joint frequency. Moreover, it is not possible to represent every joint individually in a constitutive model. Therefore, it is necessary to use simple techniques such as equivalent continuum method which can capture reasonably the behavior of jointed rock mass. The finite element method developed in the present study applies for the foundation rock model both: nonlinear solid element for modeling the jointed rock as an equivalent continuum whose properties represent material properties of the jointed rock, and nonlinear interface element to account for the surface roughness of discontinuities.

The best way to determine the size of foundation model is based on the ratio of deformation modulus of foundation (E _f ) to the elastic modulus of concrete dam (E _c ). For a flexible rock foundation with E _f /E _c less than ½, the foundation model should extend at least twice the dam height in all directions (Federal Energy Regulatory Commission Division of Dam Safety and Inspections, Washington DC 1999).

The definition of suitable boundary conditions related to its surrounding domain is another important part of modeling procedure. In the present study, the governing equations and related boundary conditions consist of water free surface and far-end truncated boundaries of the reservoir and rock foundation. By neglecting the effects of gravity waves, a zero-pressure boundary condition is prescribed at the horizontal free surface water (assuming negligible surface tension). This simplification is a common assumption in the analysis of concrete dams, particularly for deep reservoirs. Also, several studies have been carried out into the improvement of the boundary condition at far-end of the reservoir and rock foundation in the dynamic analysis of coupling system. A radiation condition (such as, Sommerfeld’s and Sharan’s boundary conditions and Küçükarslan 2004) can be applied at the truncated boundary of the reservoir. A similar boundary for eliminating waves propagating outward from the foundation domain is Lysmer and Kuhlemeyer (1969) boundary. Boundary element method has also been widely used (Beer et al. 2008; Brebbia and Dominguez 1992). In this method, only the boundaries of the unbounded medium are discretized so that the spatial dimension is reduced by one and the radiation condition is satisfied automatically as a part of the fundamental solution (Estorff and Kausel 1989). Many researchers have successfully used infinite boundary elements to model wave propagation problems on far-end boundary (Valliappan and Zhao 1992, etc.). In this study, for the truncated boundary conditions of reservoir and rock foundation, interface elements have been used. Using these boundary conditions does not prevent the sliding at foundation discontinuities due to seismic loading, thus providing non-uniform excitation.

It has been recognized that for infrastructures with extended foundations such as concrete arch dams, the ground motion is non-uniform along the canyon due to the wave passage effects, coherency effects and site response effects (Der kiureghian 1996). Several researchers have studied on the response of concrete dams when the system was excited non-uniformly (Bayraktar et al. 1996; Mirzabozorg et al. 2007, etc.). Some studies indicate that the non-uniform seismic input can have an important role in the dam response (Alves and Hall 2006).

In addition, the nonlinear material properties of concrete dam and bedrock as well as the nonlinear effects of contraction joints of dam body and discontinuities in the dam foundation are modeled by appropriate methods which will be described later (Ahmadi and Razavi 1992; Ahmadi et al. 2001; Mojtahedi and Fenves 2000).

Description of the analysis procedure

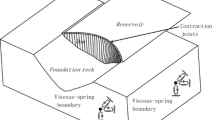
The schematic view of dam–reservoir–foundation system is shown in Fig. 1. The full system is modeled by an assemblage of solid and interface elements. The isoparametric 8-node solid elements with 2 × 2 × 2 Gauss integration are used for all domains including dam body, reservoir, sediment and rock abutments. Also, eight-node interface elements are used in common surfaces of domains, such as the contraction and perimetral joints in dam body and discontinuities of rock abutments. The finite element formulations support both geometric and material nonlinearity. Assuming that non-linearities are limited to the concrete dam, rock blocks, contraction joints of dam body and rock discontinuities, the stiffness of these elements needs to be updated at each iteration. Interface elements are placed between continuum (solid) elements, as shown in Fig. 2. A summary flow chart of the finite element program is shown in Fig. 3. In the programing, the capabilities of several open source programs that are developed for the analysis of concrete dams such as ADAP-88, EAGD-SLIDE, EACD-3D-96 (Mojtahedi et al. 1992; Chavez and Fenves 1994; Tan and Chopra 1996) were investigated and useful subroutines and subprograms of them were used (Smith and Griffiths 2004; Bathe 1996).

Fig. 1

Schematic view of dam–reservoir–foundation system

Fig. 2

Detailed view of solid-interface elements

Fig. 3

Flow chart of nonlinear finite element program

Nonlinear dynamic analysis

The governing equations of motion for 3D nonlinear dynamic analysis of coupling system (subjected to earthquake loads) were discretized using Newmark’s method. By adopting very large time increments, static nonlinear analysis can be accomplished as a special case of dynamic analysis. The discretized nonlinear dynamic equation of motion is given by (Bathe 1996; Zienkiewicz and Taylor 2005):

$$\begin{aligned} & \left[ {\left[ {K_{T} } \right] + \frac{\gamma }{\beta \Delta t}\left[ {C_{T} } \right] + \frac{1}{{\beta \Delta t^{2} }}\left[ M \right]} \right]\left\{ {\ddot{U}_{n + 1} } \right\} = \left\{ {R_{n + 1} } \right\}\, + \left[ C \right]\left\{ {\frac{\gamma }{\beta \Delta t}\left\{ {U_{n} } \right\} + \left( {\frac{\gamma }{\beta } - 1} \right)\left\{ {\dot{U}_{n} } \right\} + \Delta t\left( {\frac{\gamma }{2\beta } - 1} \right)\left\{ {\ddot{U}_{n} } \right\}} \right\} \\ & \quad + \left[ M \right]\left\{ {\frac{1}{{\beta \Delta t^{2} }}\left\{ {U_{n} } \right\} + \frac{1}{\beta \Delta t}\left\{ {\dot{U}_{n} } \right\} + \left( {\frac{1}{2\beta } - 1} \right)\left\{ {\ddot{U}_{n} } \right\}} \right\} \\ \end{aligned}$$

(1)

where [M] is the mass matrix, [C] is the damping matrix, [K] is the stiffness matrix and {R} is the nodal external forces. $\left\{ {\ddot{U}} \right\}$, $\left\{ {\dot{U}} \right\}$ and $\left\{ U \right\}$ are the acceleration, velocity and displacement vectors, respectively, at the (n + 1)th time step. Also, [K _T ] is the tangent stiffness matrix and [C _T ] is the updated damping matrix which changes at the same time as the stiffness reduces. The dynamic equilibrium of the system at time “n + 1” can be written in terms of the unknown node displacements U _n+1 by substitution of (Wilson 2002):

$$\ddot{U}_{n + 1} = b_{1} (U_{n + 1} - U_{n} ) + b_{2} \dot{U}_{n} + b_{3} \ddot{U}_{n}$$

(2)

$$\dot{U}_{n + 1} = b_{4} (U_{n + 1} - U_{n} ) + b_{5} \dot{U}_{n} + b_{6} \ddot{U}_{n}$$

(3)

where the constants b ₁ to b ₆ are defined: $b_{1} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\beta \Delta t^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\beta \Delta t^{2} }$}} ,\; b_{2} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\beta \Delta t }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\beta \Delta t }$}}, \;b_{3} = \beta - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}} , \;b_{4} = \gamma \Delta t b_{1} ,\;b_{5} = 1 + \gamma \Delta t b_{2} \;{\text{and}}\;b_{6} = \Delta t (1 + \gamma b_{3} - \gamma ).$

The damping matrix is determined based on the well-known Rayleigh damping:

$$\left[ C \right] = a\left[ K \right] + b\left[ M \right]$$

(4)

The parameters a and b are pre-defined constants and can be evaluated by the solution of a pair of simultaneous equations if the two damping ratios ($\xi_{i}$) associated with two specific frequencies $(\omega_{i} )$ are known:

$$2\omega_{i} \xi = a + b\omega_{i}^{2}$$

(5)

The full Newton–Raphson iteration scheme can be used to resolve the nonlinearity. The parameters β and γ determine the stability and accuracy characteristics of the algorithm. The constant acceleration method is obtained when β = 1/4 and γ = 1/2.

Nonlinear models for foundation rock and Dam body

Combinations of Mohr–Coulomb (1882–1900) yield function with a tension cut-off (i.e., The Modified Mohr–Coulomb model suggested by Paul in 1961) are used for both concrete and jointed rock materials. Crook et al. (2003) presented that the Modified Mohr–Coulomb model is able to effectively model both brittle-tensile or axial splitting fractures and shear features model. The Mohr–Coulomb criterion is based on Coulomb’s equation (1773). If $\sigma_{11} \ge \sigma_{22} \ge \sigma_{33}$ are the principal stresses, we can write this criterion as (Lubliner 1990):

$$\sigma_{11} - \sigma_{33} + (\sigma_{11} + \sigma_{33} ){ \sin }\phi - 2c({ \cos }\phi ) = 0$$

(6)

where $\phi$ and c are the internal friction angle and cohesion, respectively. The 3D failure surface of the Mohr–Coulomb criterion can be expressed in terms of stress invariants ($I_{1} = \sigma_{ii} = \sigma_{11} + \sigma_{22} + \sigma_{33}$, $J_{2} = \frac{1}{2}s_{ij} s_{ij} ,$ J ₃ = $\frac{1}{3}s_{ij} s_{jk} s_{ki}$ with $s_{ij} = \sigma_{ij} - \frac{1}{3} I_{1} \delta_{ij} ,$ “Kronecker delta $\delta_{ij}$”):

$$f_{1} (I_{1} ,J_{2} ,J_{3} ) = \frac{{I_{1} }}{3}\sin \phi + \sqrt {J_{2} } \sin \left( {\theta + \frac{\pi }{3}} \right) + \sqrt {\frac{{J_{2} }}{3}} \cos \left( {\theta + \frac{\pi }{3}} \right)\sin \phi - c({ \cos }\phi ) = 0\,$$

(7)

where the lode angle is: $\theta = \frac{1}{3}\cos^{ - 1} \left( {\frac{3\sqrt 3 }{2}\frac{{J_{3} }}{{J_{2}^{3/2} }}} \right)$.

For the tension cutoff yield function (Rankine crack model), we have

$$\sigma_{11} = f_{t}^{\prime } ,\quad \sigma_{22} = f_{t}^{\prime } ,\quad \sigma_{33} = f_{t}^{\prime }$$

(8)

where $f_{t}^{'}$ is tension strength. This criterion can be fully described by the following equation:

$$f_{2} (I_{1} ,J_{2} ,J_{3} ) = 2\sqrt {3J_{2} } \,\cos \theta + I_{1} - 3f_{t}^{\prime } = 0,\quad 0 \le \theta \le \pi /3$$

(9)

Reservoir modeling and simulation

The finite element formulation for fluid is based on Lagrangian approach in which the fluid strains are calculated from the linear strain–displacement equations. The pressure volume relationship for a linear fluid is expressed by

$$p = \lambda \varepsilon_{v}$$

(10)

where p, $\lambda$ and εv are pressure that is equal to the mean stress, the bulk modulus and the volumetric strains of the fluid, respectively. The volumetric strain can be expressed in terms of Cartesian displacement components as follows:

$$\varepsilon_{v} = \frac{{\partial u_{x} }}{\partial x} + \frac{{\partial u_{y} }}{\partial y} + \frac{{\partial u_{z} }}{\partial z}$$

(11)

where ux, uy and uz are displacement components related to axes x, y and z, respectively.

Nonlinear interface element

Different models have been developed to represent the contact between two surfaces. One is based on the cohesive law which can be expressed in a way that the local traction $({\mathbf{\mathfrak{t}}})$ across the interface is taken as a function of displacement jump $(\delta )$ across the cohesive surfaces. A formula worked out by Ortiz and Pandolfi (1999) accounts for the free energy density per unit undeformed area (Θ) so that the traction acting on the interface:

$$t = \frac{\partial \varTheta }{\partial \delta } = e\sigma_{c} \frac{\delta }{{\delta_{c} }}{ \exp }\left( { - \frac{\delta }{{\delta_{c} }}} \right)\quad {\text{if}}\;(\delta = \delta_{ \hbox{max} } \;{\text{and}}\;\dot{\delta } \ge 0)$$

(12)

where $\delta_{c}$ denotes the value of $\delta$ (Needleman 1990) at peak traction $({\mathbf{\mathfrak{t}}}_{ \hbox{max} } = \sigma_{c} )$:

$$\delta = \left\|\varvec{\delta}\right\| = \sqrt {\delta_{n}^{2} + \beta^{2} \delta_{s}^{2} } ,\quad \left( {\varvec{\delta}_{n} =\varvec{\delta}.\varvec{n}\;{\text{and}}\;\delta_{s} = \left\| {\varvec{\delta}- \delta_{n} \varvec{n}} \right\| = \sqrt {\delta_{s1}^{2} + \delta_{s2}^{2} } } \right)$$

(13)

$$\varvec{t} = \varvec{t}_{n} + \varvec{t}_{s} = \frac{\partial \varTheta }{{\partial \delta_{n} }}\varvec{n} + \frac{\partial \varTheta }{{\partial \delta_{s} }}\frac{{\partial \delta_{s} }}{{\partial \delta_{s} }} = \frac{t}{\delta }(\delta_{n} n + \beta^{2} \delta_{s} )$$

(14)

$$\varTheta = e\sigma_{c} \delta_{c} \left[ {1 - \left( {1 + \frac{\delta }{{\delta_{c} }}} \right)e^{{{\raise0.7ex\hbox{${ - \delta }$} \!\mathord{\left/ {\vphantom {{ - \delta } {\delta_{c} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\delta_{c} }$}}}} } \right],\quad (e = { \exp }(1))$$

(15)

Figure 4 illustrates the curve of loading and unloading responses of interface elements. When the contact surfaces undergo a combination of shear deformation and normal compression, the effective separation $(\delta )$ is computed only from the shear components. Also, under normal compression the cohesive material behaves like a linear spring. The weighting coefficient $(\beta )$ defines the ratio between critical shear and normal tractions (Ruiz et al. 2001).

Fig. 4

Loading and unloading traction–separation exponential curve for interface elements

The value of interface stiffness depends on the roughness of contact surfaces, as well as the relevant properties of filling material and its moisture. For an initially closed interface, the normal stiffness K _n and the tangential stiffness K _S are assumed to have large values. These values can be estimated from the lowest Young’s modulus and shear modulus of the adhesive domain around it, according to the following equations:

$$K_{n} = m_{1} \frac{{EA_{e} }}{{L_{e} }}\quad {\text{and}}\quad K_{s} = m_{2} \frac{{GA_{e} }}{{L_{e} }}$$

(16)

where $m_{i}\, (i = 1,2)$ is a factor that controls the contact properties (only in penetration), E and G are the smaller elastic and shear modulus when considering the contact between two different materials, $L_{e}$ is the characteristic thickness of the adjacent solid element perpendicular to the interface, and $A_{e}$ is the surface area of the interface element.

For a proper numerical modeling of the far-end boundaries of massed foundation and reservoir, the viscous boundary condition must be applied to prevent wave reflection from the artificial boundary of infinite media in finite element analysis (Ghaemian et al. 2005).

Combinations of viscous and spring boundaries were used as the basis for interface element to find a simple and efficient model. Therefore, interface elements are placed around the problem boundaries with equivalent stiffness of infinite media and related damping to absorb the energy of outgoing waves in the normal and tangential directions. To calculate the damping coefficient C ^tb for the elements of far-end boundaries, the following equations are used:

$$C_{n}^{tb} = A_{e} \rho_{f} V_{\text{P}} \quad {\text{and}}\quad C_{s,t}^{tb} = A_{e} \rho_{f} V_{\text{S}}$$

(17)

In which V _P and V _S are the primary and secondary wave propagation velocity within the foundation medium and are given as:

$$V_{\text{P}} = \sqrt {\frac{{E_{f} (1 - v_{f} )}}{{\rho_{f} (1 + v_{f} )(1 - 2v_{f} )}}} \quad {\text{and}}\quad V_{\text{s}} = \sqrt {\frac{{G_{f} }}{{\rho_{f} }}}$$

(18)

where subscript f indicates the parameters pertinent to the rock foundation. The radiation damping derived from Eq. (17) is applied on the far-end boundaries of the foundation which are added to the global damping matrix of the structure, [C]. Similarly, linear viscous elements can be inserted at the upstream boundary of the reservoir that will allow the wave to pass and the strain energy in the water to “radiate” away from the dam.

Verification example

To verify the accuracy and validity of the finite element modeling and developed computer code, the tallest monolith with unit width of well-known Pine Flat Dam, a concrete gravity dam in California, which is 122 m high, is selected. A water depth of 116 m is considered as the full reservoir condition. The geometry and FE model of the Pine Flat dam monolith with unit width is shown in Fig. 5 (Batta and Pekae 1996). The properties of applied material in the modeling are: E _c  = 22.75 GPa, $v = 0.2$ and $\rho = 25\;{\text{kN}}/{\text{m}}^{3} .$ For nonlinear analysis, the tensile strength of concrete is taken to be 3.36 MPa which is about 12% of its compressive strength. The dynamic tensile strength must be equivalent to the direct tensile strength multiplied by a factor of 1.50 (Raphael 1984). The analysis results consist of the weight of the dam, the static pressure of impounded water and the seismic response for earthquake excitation of horizontal-x component of Taft-1952 Lincoln California ground motion with scaling to a PGA = 0.4 g. The applied proportional damping of the dam provides a critical damping ratio of 5% in the fundamental vibration mode of it. Figure 6 shows the comparison between the obtained results for crest displacement of the first 15 s excitation from the program developed for the present study and commercially available ANSYS program for the case of linear material behavior. In addition, Fig. 7 shows the analysis results obtained from developed program by considering the effects of material nonlinearity and base sliding. For transient structural analysis in ANSYS, a corresponding 8-node 3-D concrete element SOLID65 is selected.

Fig. 5

FE model of Pine Flat dam on rigid base and subjected to Taft-1952 ground motion

Fig. 6

Comparison of displacement results of the Pine flat dam crest with ANSYS program results due to horizontal component of dam base displacement Taft-1952

Fig. 7

Comparison of horizontal displacement for the nonlinear behavior of materials and the possibility of slip at the base of dam

Results of case study analysis

Karun-4 Dam is a double curvature arch dam on Karun River in the province of Chaharmahal-e Bakhtiari, Iran. Its whole crest length is divided by 20 contraction joints. The geometric characteristics of the dam shape are listed in Table 1. The geometry and FE model of the Karun-4 Dam is shown in Figs. 8 and 9, respectively. The modulus of elasticity, Poisson’s ratio and unit weight of concrete are taken as 23.6 GPa, 0.2 and 24 kN/m³, respectively. The tensile strength of concrete is assumed to be 2.75 MPa. Dynamic magnification factors of 1.5, 1.3 and 1.25 are applied to its modulus of elasticity, tensile and compressive strengths, respectively. The damping ratio for the dam and its foundation was set 5%. Based on the geotechnical investigations of the dam site, the geomechanical parameters of most regions of bedrock are as follows (Mahab Ghodss Consulting Engineering Company 2003): unit weight = 25 kN/m³, deformation modulus = 11.0 GPa, Poison’s ratio = 0.25, friction angle = 42°, cohesion = 0.5 MPa and allowable bearing capacity: From 9 to 14 MPa (Used 12 MPa). Nonlinearity in the finite element analysis was incorporated in the form of material nonlinearity of equivalent rock with uniaxial compressive and tensile strength of 12 and 1.2 MPa, respectively. The developed FE model of foundation extends 2.5 times of dam height in all directions. Regarding the geometry of discontinuities in each abutment and based on the results of a preliminary analysis, “F4-a & F6-a” and “MJ67-c & MJ28” are defined as critical discontinuities on the left and right abutments, respectively. The characteristics of critical discontinuities are presented in Table 2. These plates cause six large blocks, as shown in Fig. 10.

Table 1 The geometric characteristics and dimensions of the dam shape

Fig. 8

General view of Karun 4 project area

Fig. 9

3D finite element model of the Karun 4 arch dam and interface elements of contraction and perimetral joints

Table 2 Geomechanical parameters of the critical discontinuities in the left abutment

Fig. 10

3D finite element model of the rock foundation is divided into six blocks

The water in the reservoir was assumed to have a constant depth of 155 m, mass density = 10 kN/m³, bulk modulus = 2131 MPa and Poisson’s ratio = 0.495 for nearly incompressible fluid. For the upstream/downstream sediments with the assumption of about 60/30 m depth: mass density ρ _s  = 13.6 kN/m³, and bulk modulus B _s  = ρ _s c ² _s  = 3312 MPa, where the sound speed profile is estimated through the physical sediment properties using Biot theory and assuming c _s  = 1560 m/s. The developed finite element mesh for the reservoir and sediments is shown in Fig. 11.

Fig. 11

Finite element mesh of the reservoir and sediment elements

Interface elements are used for the modeling of rock discontinuities, vertical joints between the cantilevers and the intersection of the dam with canyon rock, as well as the boundary between reservoir and surrounding domain with negligible shear stiffness. At the truncated boundaries of the reservoir and rock foundation (later called as “Moving B.C.”), the interface elements are available in the developed numerical program. The properties of several interface elements are presented in Table 3. The developed coupled model includes 11,764 nodes and 9348 elements. The position of interface elements is shown in Fig. 12.

Table 3 Interface elements parameters

Fig. 12

Finite element mesh of interface elements

The loads applied to the model consist of static and dynamic loading. Static loads are dead weight and the hydrostatic pressure of reservoir water at its normal level in addition to the sediment weight.

Information about the in situ stresses of the rock field is a fundamental parameter for the dam–foundation analysis and has a direct effect on dynamic design of such a coupled system. The in situ stress in a rock mass is simply equal to the weight of the overlying material; therefore, the discontinuities will control the magnitude and direction of this stress field. In this study, firstly the static load of discontinuous rock weight was applied to investigate the in situ stress. For this loading case, the dam body should remain free of stress because of canyon deformation. To overcome this problem, the numerical program has the ability to change the material properties in loading steps. Therefore, in a pre-loading step, Young’s modulus of dam body and a region of the rock abutments near the dam gradually decrease and Poisson’s ratio increases to 0.49. In the next dummy load step, material properties gradually change to real values.

The first 40 s of the three components of Taft Lincoln School records obtained from the 1952 earthquake happening in Kern County, California are used as input ground motion. The peak ground acceleration of x, y (horizontal components), and z (vertical component) directions are 0.156, 0.178 and 0.108g, respectively. For seismic hazard study of Karun 4 Dam site, the earthquake time histories are scaled to the maximum credible level at the middle height of canyon (PGA_hor = 0.49g, PGA_ver = 0.26g). A time step of 0.01 s is chosen for the analysis. The displacement time histories for the three components of Taft earthquake are shown in Fig. 13.

Fig. 13

Three displacement components of the Kern County, California earthquake of 21 July 1952 recorded at the Taft Lincoln School Tunnel

To present the effect of foundation interaction on the seismic response, several cases of massive foundation are chosen:

• C0 Continuous rock foundation—Moving B.C (without interface elements between the rock blocks and with interface elements on the truncated boundary);

• C1 Continuous rock foundation—Fixed B.C (without interface elements between the rock blocks and on the truncated boundary);

• C2 Discontinuous rock foundation—Moving B.C (called “Real Case”);

• C3 Condition “C1” with rigid and massless foundation;

• C4 Condition “C2” with applying a reduction factor of 10% for deformation modulus and allowable bearing capacity of the rock blocks RB1, RB2, RB3 and RB4 (demonstrated in Fig. 10);

• C5 Condition “C2” with applying a reduction factor of 10% for deformation modulus and allowable bearing capacity of rock blocks RB5 and RB6 (demonstrated in Fig. 10);

• C6 Condition “C6” with applying a reduction factor of 20%; and

• C7 Condition “C7” with applying a reduction factor of 20%.

Figures 14, 15, 16, 17 and 18 show the comparison of crest displacement of the crown cantilever (node number 64 in Fig. 9) in upstream–downstream direction for several cases. As can be seen, detailed modeling of foundation with high accuracy has a very important role in the coupled system analysis. Also, using the interface elements with appropriate characteristics on the far-end boundaries and major fault zones of the foundation changes the seismic response of dam significantly. It should also be noted that such boundary conditions and modeling of discontinuities in bedrock are critical for an actual response of dam as compared in Fig. 14. The foundation flexibility effects on dam response is also compared in Fig. 15.

Fig. 14

Comparison of upstream/downstream crest displacement of Karun 4 dam under Taft earthquake for C0, C1 and C2 cases

Fig. 15

Comparison of upstream/downstream crest displacement of Karun 4 dam under Taft earthquake for C1 and C3 (continuous, rigid and massless foundation) cases

Fig. 16

Comparison of upstream/downstream crest displacement of Karun 4 dam under Taft earthquake for different reduction factor of rock blocks

Fig. 17

Comparison of displacements time history between the three adjacent nodes of truncated boundary of rock foundation (demonstrated in Fig. 9) in normal direction (case C2)

Fig. 18

Comparison of crest and mid-height joint sliding at the crown cantilever (case C2)

The results of the analysis, as shown in Fig. 16, illustrate the importance of the effects of inhomogeneity and change in the material properties of discontinuous rock foundation on the seismic response of concrete dams. As can be seen, the foundation flexibility with a reduction factor of 10 and 20% for deformation modulus and allowable bearing capacity of domain parts has significantly affected the dam response. Figure 17 shows the difference between time history response of three adjacent nodes of the truncated boundary of foundation (belongs the three blocks RB1, RB2 and RB3). This is a result of non-uniform excitation of discontinuities foundation that has been composed of blocks with different mass, geometry and boundary conditions. To study the effect of contraction joint nonlinearity on the seismic response of dam, the time history comparison of joint sliding at the crown cantilever in crest and mid-height levels is considered as shown in Fig. 18. The maximum joint sliding is 10.1 cm at time 29.5 s for case C2. It should be noted that for the model with joint nonlinearity, there are two nodes at each point which are located on the interface elements. For example, nodes 64 and 53 at crest level and nodes 775 and 814 at the mid-height level are both on the crown cantilever at the same position (demonstrated in Fig. 9). Also, the contours of maximum and minimum principal stress obtained from nonlinear analysis for real case (Case C2) with a deformed scale of 20 at time 40 s are shown in Fig. 19a, b. A summary of the upstream–downstream and vertical displacements for all the analyses is provided for comparison in Table 4.

Fig. 19

a Maximum principal stress contours, and b minimum principal stress contours with deformed scale of 20 at time 40 s for the cases of C2 “Real Case” (upstream-right and downstream-left views) <unit: MPa>

Table 4 Upstream–downstream and vertical displacement comparison of crest at crown cantilever (node 64)

Conclusions

In this study, after conducting a survey of the literature on numerical methods for modeling of coupled concrete dam–reservoir water–foundation rock systems, a finite element computer program developed for the analysis and design of new dams and for the seismic safety evaluation of existing concrete dams.

For the purpose of the study, the highest arch dam in Iran, i.e., “Karun 4”is selected. To evaluate the seismic response of this arch dam more accurately, various effects of dam–foundation interaction in time domain including the effects of inertia and flexibility of non-homogeneous foundation rock as well as the proper exertion of in situ stresses have been taken into account.

As mentioned in the previous section, ten cases are considered: the linear model, and nine nonlinear models with flexibility, non-homogeneous and discontinuities effects of foundation rock and hydrodynamic effects of reservoir on dam response. In each case, the time history response of crest displacement of the crown cantilever in upstream–downstream direction is obtained.

The results demonstrate that the response of concrete arch dam–reservoir–foundation system is significantly affected by “concrete and rock material nonlinearity”, “the role of various discontinuities present in real system”, “flexibility of non-homogeneous foundation”, and “far-end boundary condition”. Also, the results show that the application of material non-homogeneity in foundation for dynamic analysis is a key factor for seismic response, but neglecting the foundation discontinuities and moving and viscous properties of far-end boundary condition leads to inappropriate results.