Numerical methods for hyperbolic SPDEs: a Wiener chaos approach

Abstract

In this paper we propose a novel numerical scheme based on the Wiener chaos expansion for solving hyperbolic stochastic partial differential equations (PDEs). Through the Wiener chaos expansion the stochastic PDE is reduced to an infinite hierarchy of deterministic PDEs which is then truncated to a finite system of PDEs, that can be addressed by standard techniques. A priori and a posteriori convergence results for the method are provided. The proposed method is applied to solve the stochastic wave equation with additive noise and the stochastic Klein–Gordon wave equation with multiplicative noise and the results are compared to those derived by the Monte Carlo method. The main advantages of the proposed scheme is that it provides almost identical results and is significantly faster than the Monte Carlo simulation method, providing a convenient way to compute numerically the statistical moments of the solution.

1 Introduction

In recent years there is a growing interest in developing numerical techniques for solving and simulating problems concerning stochastic partial differential equations (SPDEs). This interest is due to the fact that SPDEs are the most common method by which we model several phenomena in the natural sciences, engineering and economics. Many algorithms that are used for solving SDEs are extensions of existing methods for solving ODEs, such as the Euler–Maruyama and the Milstein method [15]. These methods approximate the true solution of a stochastic differential equation as a Markov Chain. However, the extension to the stochastic partial differential problems is a relatively new field and a lot of work needs to be done in this direction. The well known Monte Carlo (MC) method is still the most popular method for simulating SPDEs and dealing with the statistical characteristics of the solution, although it is a rather computationally expensive method.

In the current work we develop a numerical scheme for solving hyperbolic SPDEs, based on recent work concerning analytic results on solvability and well-posedness for such equations based on the Wiener chaos expansion [9]. This method is relatively new and inspired by the seminal relevant work on parabolic SPDEs as proposed by Lototsky and Rozovsky in [11, 12], and [13]. The basic idea of the method is to construct the solution as a generalized Fourier series that (depending on the type of equation and the data) may converge in appropriate weighted Wiener chaos spaces that contain important information on the statistical properties of the random fields generated by the SPDE. The random field is thus expressed in terms of an infinite sum of elements, which expresses randomness through a “generic” basis which is determined solely by the Wiener process. The deterministic amplitudes that multiply the elements of this generic stochastic basis, take values in appropriate function spaces, and are equation specific. The random field which is the solution of the SPDE is reconstructed as the random series, however it is important to note that important statistical features of the solution such as the moments can be reconstructed by knowledge of the deterministic amplitudes only.

These can be determined through the solution of an infinite hierarchy of deterministic evolution equations (called the propagator)—uniquely defined from the SPDE in question. The ability to recover statistical information only by the knowledge of the solution of the deterministic propagator equation allows us to avoid time consuming computations based on the Monte-Carlo method (see [8] and the references therein).

Therefore, the Wiener chaos expansion (WCE) may serve not only as an important analytical and theoretical tool to study existing and novel types of solutions of SPDEs, but may be used for the development of efficient numerical schemes for the treatment of these problems, that may serve as useful alternatives to Monte-Carlo type methods. Similar a priori results for finite element methods have been established for elliptic and parabolic problems (cf. [8, 10] and the references therein).

It is the aim of the current paper to explore this suggestion in detail, by developing a novel numerical method for the solution of hyperbolic SPDEs based on the Wiener chaos expansion. To this end, we develop the method, provide suggestions concerning the truncation of the random series as well as a priori and a posteriori error estimates for the approximate solution. The method is tested on the stochastic wave equation with additive noise and the stochastic Klein–Gordon equation with multiplicative noise and it is shown to be superior to Monte-Carlo based methods in terms of accuracy and time consumed.

2 Weighted Wiener chaos solutions: general framework

2.1 Weighted Wiener chaos spaces and solutions to hyperbolic SPDEs

Let us consider a countable collection of independent one dimensional Brownian motions $W=({w_k=w_k(t), 1 \le k , 0 \le t \le T})$, for fixed $\hbox {T}>0$ on a complete probability space $\mathbb {W}=(\varOmega ,\fancyscript{F}, (\fancyscript{F}_t)_{0 \le t \le T}, \mathbb {P})$, where $\fancyscript{F}_t$ is the $\sigma$ -algebra generated by the random variables $(w_k(s), 1 \le k , s \le t)$ and denote by $\mathbb {X}=L^2(\mathbb {W};X)= L^2(\varOmega ,\fancyscript{F}_T, \mathbb {P};X)$ the separable Hilbert space of $\fancyscript{F}_T$ measurable square integrable $X$-valued random variables, where $X$ is a Hilbert space.¹ Let also $m=\{m_i, \; i\ge 1 \}$ be a given orthonormal basis of $L^2([0,T])$, such that $m_i (\cdot ) \in L^\infty ([0,T])$ where $i=\{1,2,\ldots \}$, and define the independent standard Gaussian random variables $\xi _{ik}=\int _{0}^{T} m_i(s) dw_k (s)$. As we will in general consider $m_{i}$ as a Fourier basis, we may assume without loss of generality that $m_i\in W^{1,\infty }([0,T])$. Now, consider the countable set of multi-indices $\fancyscript{J}=\left\{ \alpha =(\alpha _i^k, i,k\ge 1), \, \alpha _i^k\in \{0,1,2,\ldots \} \right\}$ with length $\left| \alpha \right| :=\sum _{i,k}\alpha _i^k<\infty$, order $\varpi ({\alpha }):=\max \{i\ge 1 :\alpha _i^k>0\}$ and dimension $d({\alpha }):=\max \{k\ge 1 :\alpha _i^k>0 \}$. Define the collection $\varXi =\left\{ \xi _\alpha ,\alpha \in \fancyscript{J}\right\}$ of random variables so that $\xi _\alpha =\frac{1}{\sqrt{\alpha !}} \prod _{i,k}H_{\alpha _i^k}(\xi _{ik})$, where $H_{n}(x)=(-1)^ne^{\frac{x^2}{2}}\frac{d^n}{dx^n}e^{\frac{-x^2}{2}}$ is the Hermite polynomial of order n and $\alpha !=\prod _{i,k}\alpha _i^k!$. We will also use the notation $\alpha ^{\pm }(i,k)$ for the multi-index with the components

$$\begin{aligned} \alpha ^{\pm }(i,k)_j^l = {\left\{ \begin{array}{ll} max(\alpha _i^k\pm 1,0) &{}\quad \text { if } i=j \text { and } k=l \\ \alpha _{i}^{k} &{}\quad \text {otherwise} \end{array}\right. }. \end{aligned}$$

For details concerning these definitions see e.g. [11]. The following theorem is the classical result obtained by Cameron and Martin and generalized by Lototsky and Rozovsky for square integrable random variables taking values in a general Hilbert space $X$ (see [11] and [18]).

Theorem 1

([11, 16]) The collection $\Xi =\left\{ \xi _\alpha ,\alpha \in \fancyscript{J}\right\}$ is an orthonormal basis in $L^2(\mathbb {W})$. If $u \in L^2(\mathbb {W};X)$ and $u_\alpha =\mathbb {E}[u\xi _\alpha ]\in X$, then

$$\begin{aligned} u=\sum _{\alpha \in \fancyscript{J}}u_\alpha \xi _\alpha \quad \text {and} \quad \mathbb {E}[ \left\| u\right\| ^2_X]=\sum _{\alpha \in \fancyscript{J}}\left\| u_\alpha \right\| _X^2 \end{aligned}$$

The Cameron–Martin expansion can be considered as a Fourier expansion that separates the stochastic from the deterministic part of a random field $u$. One may also consider the converse procedure, i.e., choosing a set of deterministic functions $\{u_{\alpha } \, : \, \alpha \in \fancyscript{J}\}$ and constructing the random series $\sum _{\alpha \in \fancyscript{J}} u_{\alpha } \xi _{\alpha }$ as a formal object. In case this series does not converge in $L^2(\mathbb {W};X)$ we may consider its convergence in appropriately weighted Hilbert spaces called weighted Wiener chaos spaces. This leads to the construction of generalized random fields, which are very useful in the study of SPDEs since many important SPDE models do not admit square integrable solutions. For the definition of weighted Wiener chaos spaces, we need to consider the collection of positive numbers $\{r_\alpha \, : \,\alpha \in \fancyscript{J}\}$ and introduce the bounded linear operator $\fancyscript{R}$ on $L^2(\mathbb {W})$ defined by $(\fancyscript{R} \xi )_\alpha := r_\alpha \xi _\alpha$ for every $\alpha \in \fancyscript{J}$, and its extension on $L^2(\mathbb {W};X)$ (still denoted by $\fancyscript{R}$) defined as the unique element $\fancyscript{R}f$ of $L^2(\mathbb {W};X)$ such that for $g\in L^2(\mathbb {W})$,

$$\begin{aligned} \mathbb {E}[(\fancyscript{R}f,g)_X] = \sum _{\alpha \in \fancyscript{J}} r_\alpha \mathbb {E}[(\fancyscript{R}f,g)_X \xi _\alpha ], \end{aligned}$$

and then using the operator $\fancyscript{R}$ define the norm

$$\begin{aligned} \left\| u \right\| ^2_{\fancyscript{R} L^2(\mathbb {W};X)} := || \fancyscript{R} u||_{L^2(\mathbb {W};X)}^{2}. \end{aligned}$$

(2.1)

The weighted Wiener chaos space is then defined as follows:

Definition 1

(Weighted Wiener chaos space) Given a collection $\left\{ r_\alpha , \alpha \in \fancyscript{J}\right\}$ of positive numbers, the weighted Wiener chaos space $\fancyscript{R} L^2(\mathbb {W};X)$, corresponding to this set of weights, is the closure of $L^2(\mathbb {W};X)$ with respect to the norm $|| \cdot ||_{\fancyscript{R} L^2(\mathbb {W};X)}$ defined in (2.1), or equivalently the space of random elements of the form $\sum _{\alpha \in \mathcal{J}} u_{\alpha } \, \xi _{\alpha }$, with coefficients $u_{\alpha } \in X$ such that $\sum _{\alpha \in \fancyscript{J}}{ r_\alpha ^2 \left\| u _\alpha \right\| ^2_X}< \infty$.

Weighted Wiener chaos spaces are Hilbert spaces. We may further introduce the dual space of $\fancyscript{R} L^2(\mathbb {W};X)$, relative to the inner product in the space $L^2(\mathbb {W};X)$ , which is described through the inverse operator $\fancyscript{R}^{-1}$ by

$$\begin{aligned} \fancyscript{R}^{-1} L^2(\mathbb {W};X) = \{ g \in L^2(\mathbb {W};X) : \fancyscript{R}^{-1} g \in L^2(\mathbb {W};X) \}. \end{aligned}$$

Weighted Wiener chaos spaces provide a rich and convenient functional framework within which we may consider a variety of random fields (and thus allow us to construct solutions of various SPDEs) as the following list of examples indicate:

• If the weights $r_{\alpha }=1$ for all $\alpha \in \fancyscript{J}$, then the weighted Wiener chaos space coincides with the standard Wiener chaos space $L^2(\mathbb {W};X)$.

• An interesting class of weighted Wiener spaces² are those for which the weighting functions are chosen of the special form $r_\alpha =\prod _{i,k} q_{k}^{\alpha _{i}^{k}}$ for all $\alpha \in \fancyscript{J}$ and a suitable sequence of positive numbers $\{q_k, k\ge 1\}$. If the sequence $\{q_k, k\ge 1\}$ is chosen so that $r_{\alpha } >1$ for all $\alpha \in \fancyscript{J}$ then the weighted Wiener chaos space generated is a subset of $L^2(\mathbb {W};X)$ and for the proper choice of the sequence the random elements of the corresponding weighted space are not only square integrable but also smooth (differentiable) in the Malliavin sense. On the other hand if the sequence $\{q_k, k\ge 1\}$ is chosen so that $r_{\alpha } <1$ for all $\alpha \in \fancyscript{J}$ then the random elements of the corresponding weighted space are not square integrable and are generalized random fields.

2.2 Stochastic linear evolution equations and the Wiener chaos expansion

Denote by $(V,H,V')$ a normal (Gel’fand) triple of Hilbert spaces, such that $V \!\subset \! H \subset V'$, with both embeddings continuous and dense. We denote by $V'$ the topological dual of $V$ and by $\left\langle v',v \right\rangle$, $v' \!\in \! V'$, $v \!\in \! V$, the duality pairing between $V$ and $V'$ relative to the inner product in $H$. For a complete presentation of the normal (or Gel’fand triple) see e.g. [3]. We will also use the notation: $\fancyscript{V}\!=\!L^2((0,T);V)$, $\fancyscript{H}\!=\!L^2((0,T);H)$ and $\fancyscript{V}\!'\!=L^2((0,T);V')$, for $T\!<\!\infty$. Consider now the linear stochastic evolution equation

$$\begin{aligned} u(t)&= u_0 + \int \limits _{0}^{t}{\bigl (\fancyscript{A}(s)u(s) +f(s)\bigr )ds}\nonumber \\&+ \int \limits _0^t\sum _{k \ge 1}(\fancyscript{M}_k(s)u(s)+g_k(s))dw_k(s), \; \; 0\le t\le T \end{aligned}$$

(2.2)

where the solution $u(\cdot )$ is considered as a Hilbert space valued stochastic process (typically for each $t$, $u(t) \in H$, and since we consider the case of SPDEs each $u(t)$ is to be understood as a function of a spatial variable $x \in U \subset {\mathbb R}^{n}$ i.e. $u(t)=u(t,x)$). The families of deterministic linear operators $\{\fancyscript{A}(t)\}_{t\in [0,T]}$ and $\{ \fancyscript{M}_k(t)\}_{t \in [0,T]}$ are assumed to be such that for each $t \in [0,T]$ the operators $\fancyscript{A}(t), \fancyscript{M}_k(t): V \rightarrow V'$ are linear and bounded and thus, there exists a constant $C_M$ such that $\left\| \fancyscript{M}_k v \right\| _{\fancyscript{V}'} \le C_M \left\| v \right\| _{\fancyscript{V}}$ for all $v \in \fancyscript{V}$. Moreover, for each $t$, the operators $\fancyscript{M}_k(t)$ are such that for every sequence $u_n$ such that $u_n\rightharpoonup u$ in $\fancyscript{V}$ and $u'_n\rightharpoonup u{'}$ in $\fancyscript{V}^{'}$, (primes denote differentiation with respect to time) it follows that $\fancyscript{M}_k(t) u'_n(t)\rightharpoonup \fancyscript{M}_k(t) u'(t)$. It is worth mentioning that the assumptions considered above are standard. An example is the case where $H=L^{2}(U)$ and $V=H_{0}^{1}(U)$, where $U \subset {\mathbb R}^{n}$ is an open and bounded domain with sufficiently smooth boundary, the operator $\fancyscript{A}$ is a first or second-order linear differential operator and the operator $\fancyscript{M}_k$ is a multiplicative operator, in the same functional setting. Assume also that $f, \; g_k \in \fancyscript{R}L^2(\mathbb {W};\fancyscript{V})$ are generalized random processes and $u(0)= u_0 \in L^2(\mathbb {W};V)$ is the initial condition.

A generalized solution $u \in \fancyscript{H}$ of (2.2) in the Wiener chaos expansion framework is constructed as an element of the weighted Wiener chaos space, such that the generalized Fourier coefficients satisfy a system of deterministic evolution equations, known as the propagator. The propagator is uniquely determined by the stochastic problem (2.2) and was introduced by Mikulevicius and Rozovsky in [14], and studied extensively by Lototsky and Rozovsky in [11]. This solution is called Wiener chaos solution and is a strong solution in the probabilistic sense, belonging to the class of variational solutions. In the special case where $r_{\alpha }=1$ for every $\alpha \in \mathcal{J}$, the Wiener chaos solution coincides with the standard square integrable solution. In this paper we focus on hyperbolic SPDEs. To this end we consider the stochastic evolution equation (2.2) as a hyperbolic system of $m$ first order equations in $[0,T] \times \mathbb {R}^n$ and the unknown is a random field consisting of random variables such that each realization $\omega$ consists of a vector field $u : [0,T] \times \mathbb {R}^n\rightarrow {\mathbb R}^m$. We will consider the case $\{\fancyscript{A}(t)\}_{t \in [0,T]}=\{\fancyscript{A}_h(t)\}_{t \in [0,T]}$ where $\{\fancyscript{A}_h(t)\}_{t \in [0,T]}$ is the family of first-order partial differential operators defined by $\fancyscript{A}_h(t) u(t)=-\sum _{j=1}^n \mathbf {B}_j(t)u_{x_j}(t)$, where the matrices $\mathbf {B}_j(t,x) \in C^2(\left[ 0,T\right] \times \mathbb {R}^n;\mathbb {M}^{m \times m})$, $(j=1,\dots ,n)$ are symmetric, satisfy the conditions $\sup _{[0,T] \times \mathbb {R}^n} (\left| \mathbf {B}_j\right| ,$ $\left| D^2_{t,x} \mathbf {B}_j\right| ,\left| D_{t,x} \mathbf {B}_j\right| )<\infty$. Furthermore, they satisfy the hyperbolicity condition, i.e., the matrix $\mathbf {B}(t,x;y):=\sum _{j=1}^{n}y_{j} \mathbf {B}_{j}(t,x)$, is diagonizable for every $x,y \in \mathbb {R}^n$, $t\in [0,T]$. A convenient functional setting is to choose $H=L^{2}({\mathbb R}^{n};{\mathbb R}^{m})$ and $V=H^{1}({\mathbb R}^{n};{\mathbb R}^{m})$. Boundary conditions can also be easily implemented by minor variations of the functional setting. An analytical treatment of hyperbolic SPDEs based on the Wiener chaos expansion has been proposed in [9], where well posedness of such equations in weighted Wiener chaos spaces has been proved. The treatment was constructive in nature, and was based on the study of the propagator

$$\begin{aligned} u_\alpha (t)&= u_{0,\alpha } + \int \limits _{0}^{t} {\bigl (\fancyscript{A}_h(s) u(s)+ f(s) \bigr )_\alpha } ds \nonumber \\&\quad + \int \limits _{0}^{t} {\sum _{i,k}\sqrt{\alpha _i^k} \bigl (\fancyscript{M}_k(s) u(s)+ g_k(s)\bigr )_{\alpha ^-(i,k)} m_i(s)ds}, \quad \alpha \in \fancyscript{J} \end{aligned}$$

(2.3)

where the subscript $\alpha$ denotes the deterministic amplitude of the corresponding random element, in terms of the chaos expansion, for example, $u_{0}=\sum _{\alpha \in \fancyscript{J}}u_{0,\alpha }\xi _{\alpha }$ with $u_{0,\alpha } \in V$ and similarly for the other random fields. Clearly, the propagator (2.3) is a lower diagonal infinite hierarchy of deterministic evolution equations. As it is the goal of this paper to explore the possibility of its use for numerical analysis of such systems, in the sequel we briefly recall the main results which will be used in the current work.

Theorem 2

(Existence and uniqueness of weak solution of the propagator [9]) For data such that $u_{0,\alpha }\in V$, $f_\alpha , \, g_{k,\alpha } \in \fancyscript{V}$, there exists a unique solution $u_\alpha$ of the propagator (2.3) such that $u_\alpha \in \fancyscript{V} \cap C([0,T];H)$ and $u'_\alpha \in \fancyscript{H}$ (where primes denote derivatives with respect to time) satisfying, for every $|\alpha |=n$, the energy estimates

$$\begin{aligned} \max _{0 \le t \le T} \left\| u_{\alpha } (t) \right\| _V + \left\| u'_{\alpha } \right\| _\fancyscript{H}&\le C(\fancyscript{A},\fancyscript{M},T) \sum _{|\alpha |\le n} \Bigg ( \left\| u_{0,\alpha } \right\| _V+ \left\| f_\alpha \right\| _\fancyscript{V} + \left\| f'_{\alpha } \right\| _\fancyscript{H} \\&\quad +\sum _{i,k\ge 1} \left( \sqrt{\alpha _i^k}\bigl \Vert g_{k,\alpha ^-(i,k)} \bigr \Vert _\fancyscript{V} + \left\| g'_{k,\alpha ^-(i,k)} \right\| _\fancyscript{H} \right) \Bigg ) \end{aligned}$$

and the constant $C(\fancyscript{A},\fancyscript{M},T)$ depends only on $T$ and the operators $\fancyscript{A}$ and $\fancyscript{M}_k$ and $\alpha \in \fancyscript{J}$.

Solutions of the hyperbolic SPDE are then constructed using the solutions of the propagator equation in terms of the expansion $u(t)=\sum _{\alpha \in \fancyscript{J}} u_{\alpha }(t) \xi _{\alpha }$. It is shown that this expansion converges in the appropriate weighted Wiener chaos space and that it is indeed the solution of the original SPDE.

Theorem 3

(Existence Theorem [9]) Let $u_0\in \fancyscript{R}L^{2}(\mathbb {W};{V})$ and $f,g_k\!\in \!\fancyscript{R}L^{2}(\mathbb {W};\fancyscript{V})$ for a suitably chosen weighted Wiener chaos space. Then there exists a variational solution $u \in \fancyscript{R}L^{2}(\mathbb {W};\fancyscript{V})$ of the hyperbolic SPDE (2.2). This solution admits a Wiener chaos expansion with respect to the Cameron–Martin basis, as $u= \sum _{\alpha \in \fancyscript{J}}{ u _\alpha \xi _\alpha }$ where $\{ u_{\alpha } \}_{\alpha \in {\fancyscript{J}}}$ is the solution of the propagator (2.3).

In case the data of the problem allow us to choose the operator $\fancyscript{R}=I$, the identity operator, the solution of the hyperbolic SPDE belongs to $L^{2}(\mathbb {W};\fancyscript{V})$, and coincides with the standard square integrable solution. Then the first and second moments are provided solely in terms of the solution of the propagator as

$$\begin{aligned} \mathbb {E}[u]=u_{(0)}, \,\,\, \mathbb {E}[||u||_{H}^2]=\sum _{\alpha \in \fancyscript{J}} ||u_\alpha ||_{H}^2, \end{aligned}$$

respectively and similar formulae can be derived for higher order moments, in case these exist (see e.g., [8]). For other choices of weights, the sum $\sum _{\alpha \in \fancyscript{J}} r_{\alpha }^{2} ||u_\alpha ||_{H}^2$ provides “generalized” moments. For example if the data allow us to choose $r_{\alpha }=\sqrt{a_{i}^{k}}$ the generalized moment corresponds to the norm of the first Malliavin derivative of the random field. Other choices leading to smoother or weaker random fields are of course possible.

3 A numerical scheme for hyperbolic SPDEs based on the Wiener chaos expansion

In this section we propose a numerical scheme, based on the Wiener chaos expansion. In summary, we treat the expansion $\sum _{\alpha \in \mathcal{J}}u_{\alpha }(t)\xi _{\alpha }$ as a stochastic Galerkin expansion and approximate this expression by finite dimensional random elements. For the convenience of the reader we summarize the steps of algorithm:

• Step 1 Choose a two-way truncation of the stochastic basis $\{\xi _{\alpha } \,:\, \alpha \in \fancyscript{J}\}$: Use a finite dimensional approximation of the infinite dimensional Wiener process and truncate the random series to a finite random sum.

• Step 2 For the chosen truncation of the stochastic basis solve the deterministic lower-triangular truncated propagator using any chosen algorithm for the deterministic system (e.g. Upwind or Lax–Wendroff).

• Step 3 From the solution of the deterministic propagator reconstruct the moments of the random field.

We note that implementation of the proposed numerical method does not require generation of the random variables $\xi _\alpha$ for the computation of the statistical moments of the solution to the SPDE (2.2). We also emphasize that the proposed deterministic algorithm for the computation of moments does not introduce any statistical error. In addition to the computation of the moments, using the proposed Wiener chaos algorithm and with one more step we can also reconstruct the solution of the stochastic PDE (2.2) as follows:

• Step 4 Generate the Gaussian random variables $\xi _\alpha$ and use the propagator components to compute the approximate solution of the stochastic equation (2.2).

Remark 1

In order to reconstruct the actual random field rather than just the moments we may use the following approach. Since the Gaussian random variables $\xi _{\alpha }$ are independent of the equation to be solved, one may use the Monte Carlo method to generate draws from the distribution of $\xi _{\alpha }$ that may be stored offline. Then, the reconstruction of the random field for a particular equation, can be performed simply by using the solution of the propagator.

Let us now pass to a detailed study of the above steps:

3.1 Truncation of the stochastic basis and the truncated propagator

It has been shown that the solution of the SPDE (2.2) can be expressed as the random series $u(t)=\sum _{\alpha \in \fancyscript{J}}u_{\alpha }(t) \xi _{\alpha }$. To make any use of this series as a numerical scheme for the calculation of the solution, we need to truncate it into a finite sum. This means truncating the full stochastic basis $\{ \xi _{\alpha }\,:\, \alpha \in \fancyscript{J}\}$ into a finite set $\{ \xi _{\alpha } \, : \, \alpha \in \fancyscript{J}_{f}\}$ where $\fancyscript{J}_{f} \subset \fancyscript{J}$ and finite. This is equivalent to truncating the propagator equation into a finite set of deterministic PDEs, i.e., working with the finite set of deterministic functions $\{u_{\alpha } \, : \, \alpha \in \fancyscript{J}_{f}\}$ in lieu of the original infinite set $\{ u_{\alpha }\,:\, \alpha \in \fancyscript{J}\}$. Our main goal in this section is to propose a scheme for choosing the finite index set $\fancyscript{J}_{f}$. To do this, note first that the sum over $\alpha \in \fancyscript{J}$ is a doubly-infinite sum, meaning that for each $N\ge 1$ there are infinitely many multi-indices such that $\left| \alpha \right| =N$. Note that if $\varpi (\alpha )\le n$ and $d(\alpha )\le r$, there exist at most $(nr)^N$ multi-indices $\alpha$ with length $|\alpha | =N$. Now, we introduce the truncated set of multi-indices

$$\begin{aligned} \fancyscript{J}_{N}^{n,r}:=\left\{ \alpha \in \fancyscript{J}: \, \left| \alpha \right| \le N, \, \varpi (\alpha ) \le n, \, d(\alpha ) \le r \right\} . \end{aligned}$$

The set $\fancyscript{J}_{N}^{n,r}$ is finite, and an upper bound of the number of elements is $[(nr)^{N+1}-1]/(nr-1)$ (cf. [6]).

In Table 1 we summarize the exact number of elements in the set $\fancyscript{J}_{N}^{n,r}$ for several values of the parameters $N$, $n$ and $r$.

Table 1 Exact number of elements in the truncated set $\fancyscript{J}_{N}^{n,r}$ for $n\cdot r =\{5,10,15,20\}$ and $N=\{1,2,3\}$

The exact number of elements in each case is equivalent to the dimension of the lower-triangular deterministic propagator system of equations to be solved.

The choice of $N,\, n,\, r$ affects the accuracy of the approximation and can be chosen so that the norm of the difference $\sum _{\alpha \in \fancyscript{J}{\setminus }\fancyscript{J}_{f}} u_{\alpha } \xi _{\alpha }$, where $\fancyscript{J}_{f}={\fancyscript{J}}_{N}^{n,r}$, is smaller than a prespecified acceptable error (see Sect. 4 for detailed estimates). Having chosen a convenient combination of $N,\, n,\, r$ we obtain the truncated propagator

$$\begin{aligned} u_\alpha (t)&= u_{0,\alpha } + \int \limits _{0}^{t} {\bigl (\fancyscript{A}_h(s) u(s)+ f(s) \bigr )_\alpha } ds \nonumber \\&\quad + \int \limits _{0}^{t} {\sum _{i,k}\sqrt{\alpha _i^k} \bigl (\fancyscript{M}_k(s) u(s)+ g_k(s)\bigr )_{\alpha ^-(i,k)} m_i(s)ds}, \quad \alpha \in \fancyscript{J}_{N}^{n,r}.\qquad \quad \end{aligned}$$

(3.1)

The truncated solution will be denoted by ${u}^{N,n,r}: =\sum _{\alpha \in \fancyscript{J}_{N}^{n,r}} u_{\alpha }\xi _\alpha$, to distinguish from the solution of the full stochastic equation (2.2). The sequence ${u}^{N,n,r}$ is a universal and flexible approximation of the solution to the stochastic problem (2.2), but it requires the solution of the deterministic propagator system of equations $u_\alpha , \; \alpha \in \fancyscript{J}_{N}^{n,r}$. While several well-known numerical methods can be implemented for the solution of the propagator, in the next section we briefly discuss two representative methods appropriate for solving deterministic hyperbolic PDEs.

It is worth noting that the Wiener chaos expansion $u=\sum _{\alpha \in \fancyscript{J}} u_\alpha \xi _\alpha$ converges rather fast. As shown in Sect. 5, even small values of $N$ (e.g. $N=1$) may lead to very accurate approximation of the random field $u$. Similar results are also produced by [19] for the stochastic advection-diffusion equation.

3.2 Numerical solution of the truncated propagator

The truncated propagator (3.1) is a finite set of deterministic hyperbolic PDEs but is still an infinite dimensional system. In order to approximate this system numerically we need to use a discretization scheme in space and/or time using an appropriate Finite Difference Scheme. In particular, we need to apply an effective numerical scheme to solve the propagator system of equations (3.1). However, the choice of the suitable scheme is not obvious. The order of accuracy along with the stability and the consistency are the main criteria used to determine the efficiency of a numerical scheme. Details on finite difference schemes in partial differential equations can be found in [17]. In our analysis we use the Upwind scheme and the Lax–Wendroff scheme, as representatives of first-order monotone and second-order central finite difference schemes respectively, which can be used for the implementation of the proposed numerical algorithm in the solution of the stochastic hyperbolic equation with either additive or multiplicative noise. However, the Upwind scheme for the stochastic wave and Klein–Gordon equation, seems to be an unsatisfactory alternative to the Lax–Wendroff method, as it shows an apparently unstable behavior for almost all values of the constant $c$ of the problem.

Note also that the Lax–Wendroff scheme can be interpreted as a vanishing viscosity limit of the solution to the original hyperbolic equation, including an artificial viscosity term of the form $\varepsilon \varDelta u$ for different values of the viscosity coefficient $\varepsilon$. The introduction of an artificial viscosity term is widely used also as an analytical tool for the study of well posedness and regularity of solutions of hyperbolic systems, typically by adding a perturbation of the form $\varepsilon \varDelta u$ where $\varDelta$ is the Laplacian, to the original hyperbolic equation, then treating the solution $u^{\varepsilon }$ of the resulting parabolic problem and going to the limit as $\varepsilon \rightarrow 0$ to obtain solutions of the original hyperbolic system (see e.g. [5]). This approach has been adopted in [9] and led to the solvability results for the hyperbolic SPDE (2.2). Thus, when employing the Lax–Wendroff scheme, the analytic results of [9] can be used to study the well-posedness of the scheme. Thus, one may refer to the analytic results on the convergence of the vanishing viscosity method for the propagator system (see [9]) in order to obtain existence and uniqueness results along with a prior bounds for the convergence of the Lax–Wendroff approximation of the propagator system.

Before proceeding with the implementation of the finite difference schemes, let us define a grid of points in the $(t,x) \in [0,T]\times U$ plane, where $U\subset \mathbb {R}^n$ and $x=(x^1,\cdots ,x^n)$. We also denote by $\fancyscript{G}:=\{t_\mathsf{i},x_\mathsf{j}\}$ where $\varDelta t$, $\varDelta x$ are positive numbers and $\mathsf{i},\mathsf{j}$ positive integers such that $t_\mathsf{i}=\mathsf{i}\varDelta t$ and $x_\mathsf{j}=\mathsf{j}(\varDelta x^1,\cdots ,\varDelta x^n)$. Then we denote by $u_\mathsf {j}^\mathsf {i}=u(t_\mathsf {i},x_\mathsf {j})$. Let us also introduce the function $h:=h(\varDelta x,\varDelta t)$ as a function of order $\fancyscript{O}(\varDelta x^p + \varDelta t^p)$, where $p=1$ corresponds to the Upwind scheme and $p=2$ corresponds to the Lax–Wendroff scheme.³

When the expansion $u=\sum _{\alpha \in \fancyscript{J}}u_\alpha \xi _\alpha$ is used, the computation of statistical moments can be obtained through knowledge of the deterministic components $u_\alpha$ only, without need of any statistical computation.

3.2.1 Numerical algorithm

As we have already completed the construction of the proposed numerical method and presented the error bounds of the scheme, we summarize the required steps for the implementation of the numerical scheme for the solution of the hyperbolic SPDE (2.2). Note that the random field ${u}_{\varDelta }^{N,n,r}:= \sum _{\alpha \in \fancyscript{J}_{N}^{n,r}} u_{\varDelta ,\alpha }\xi _\alpha$, where the process $u_{\varDelta ,\alpha }$ satisfies the discretized propagator (3.1).

4 A priori and a posteriori estimates of approximation errors

We summarize our approach so far; from the hyperbolic SPDE (2.2), we formulate the propagator system (2.3) (called ${P}$), which is then truncated using the truncated set of multi-indices $\fancyscript{J}_{N}^{n,r}$, thus forming a finite system of deterministic PDEs (3.1), hereafter called ${ P}^{N,n,r}$. We then approximate the truncated propagator ${ P}^{N,n,r}$ using either a space-discrete (or semi-discrete) finite difference scheme and obtain a finite dimensional system ${ P}_{\delta }^{N,n,r}$ or a fully-discrete finite difference scheme and obtain system ${ P}_{\varDelta }^{N,n,r}$. Each of these operators include some approximation error. It is the aim of this section to assess the overall error, i.e. the error induced when approximating the solution (2.2) as composed using the propagator ${P})$ with the random field obtained when recomposing the discretized truncated propagator ${ P}_{\varDelta }^{N,n,r}$. We adopt the convection of using the same subscripts and superscripts as employed above to denote the random fields or amplitudes rendering to the solution of the corresponding problems.

4.1 A priori error estimates

The error estimates due to the application of the proposed numerical scheme to the propagator system of equations (2.3) are provided in the following theorem.

Theorem 4

Under the assumptions of Theorem 2, the error due to the approximation of the solution $u=\sum _{\alpha \in \fancyscript{J}} u_\alpha \xi _\alpha \in \fancyscript{R}L^2(\mathbb {W};\fancyscript{V})$ of Eq. (2.2) by the solution ${u}_{\varDelta }^{N,n,r}=\sum _{\alpha \in \fancyscript{J}_{N}^{n,r}} u_{\varDelta ,\alpha }\xi _\alpha$, where the process $u_{\varDelta ,\alpha }$ is the discretized solution of the truncated equation (3.1) (produced through the finite difference method), satisfies the a priori bound

$$\begin{aligned} \left\| u-{u}_{\varDelta }^{N,n,r} \right\| _{\fancyscript{R}L^2(\mathbb {W};\fancyscript{V})}^2 \le I_1 + I_2 \end{aligned}$$

where the error term $I_1$ is given by

$$\begin{aligned} \begin{aligned} I_1:=&\, C \sum _{\alpha \in \fancyscript{J}{\setminus }\fancyscript{J}_N^{n,r}} r_\alpha ^2 \Biggl [\left\| u_{0,\alpha }\right\| _{V}+\left\| f_\alpha \right\| _{\fancyscript{V}} +\left\| f_\alpha '\right\| _{\fancyscript{H}} \\&+ {\left| \alpha \right| }^{1/2} \sum _{i,k} \left( \left\| g_{\alpha ^-(i,k)}\right\| _\fancyscript{V} + \left\| g'_{ \alpha ^-(i,k)} \right\| _\fancyscript{H} \right) \Biggr ]^2 \end{aligned} \end{aligned}$$

and the error term $I_2$ is given by $I_2:= \mathfrak {C}^2 (\fancyscript{M}_k,N,n,r) \left| h \right| ^2$ with the constant

$$\begin{aligned} \mathfrak {C}^2 (\fancyscript{M}_k,N,n,r) = \sum _{\alpha \in \fancyscript{J}_N^{n,r}} r_\alpha ^2 \left[ 1+ \sum _{p=1}^{N} {C_M}^{N-p+1} \prod _{|\beta |= p}^{N} |\beta | (nr)^{|\beta |-1} \right] ^2 \end{aligned}$$

depending only on the operator $\fancyscript{M}_k$, the order of the truncation and the weights $r_\alpha$.

It follows from the error estimates of Theorem 4 that the global error of the proposed numerical scheme depends on the order of the truncation of the propagator system of equations and the space-time discretization step, i.e. the error of the approximation of the propagator ${P}$ using the truncated propagator ${ P}_{\varDelta }^{N,n,r}$. If the random fields involved in the data are such that a high order Wiener chaos is required (large $N$, meaning slow convergence of the Wiener chaos expansion $u=\sum _{\alpha \in \fancyscript{J}}u_\alpha \xi _\alpha )$ then one may choose the discretization step $h$ small enough to compensate for the overall error. Note however that the choice of $h$ needed for the convergence of the discretization scheme for the Proposition is not (in principle) dependent on the choice of $N$ (unless the behaviour of the components of the expansion of the data of the problem $f_\alpha$ etc. for such $|\alpha |<N$ is requiring a specific attention as far as $h$ is concerned, e.g. high frequency oscillations etc.

The proof of the theorem (given at the end of this section) is based on estimates of (a) the error induced by the truncation of the stochastic basis and (b) the error induced by the discretization of the deterministic propagator system. Since these estimates are of interest in their own right, we choose to present them separately in two propositions, which are then combined at the end of this section to complete the proof of Theorem 4.

Proposition 1

(Error generated by the truncation of the Wiener chaos expansion and the Wiener process.) The random field ${u}^{N,n,r}=\sum _{\alpha \in \fancyscript{J}_{N}^{n,r}} u_\alpha \xi _\alpha \in \fancyscript{R}L^2(\mathbb {W},\fancyscript{V})$ produces an approximation to the solution $u$ of the stochastic evolution equation (2.2) and it satisfies the following a priori bound:

$$\begin{aligned} \left\| u-u_N^{n,r}\right\| _{\fancyscript{R}L^2\left( {\mathbb {W};\fancyscript{V}}\right) }^2 \le I_1 \end{aligned}$$

where the error coefficient $I_1$ is the error due to the truncation of the propagator on the set $\fancyscript{J}_{N}^{n,r}$, i.e. due to the elimination of the elements of the Wiener chaos expansion, along with the truncation of the infinite dimensional Wiener process, defined by

$$\begin{aligned} \begin{aligned} I_1:=&\,C \sum _{\alpha \in \fancyscript{J}{\setminus }\fancyscript{J}_N^{n,r}} r_\alpha ^2 \Biggl [\left\| u_{0,\alpha }\right\| _{V}+\left\| f_\alpha \right\| _{\fancyscript{V}} +\left\| f_\alpha '\right\| _{\fancyscript{H}} \\&+ {\left| \alpha \right| }^{1/2} \sum _{i,k} \left( \left\| g_{\alpha ^-(i,k)}\right\| _\fancyscript{V} + \left\| g'_{ \alpha ^-(i,k)} \right\| _\fancyscript{H} \right) \Biggr ]^2 \end{aligned} \end{aligned}$$

with the constant $C$ depending only on $T$, the operators $\fancyscript{A}$ and $\fancyscript{M}_k$ and $\alpha \in \fancyscript{J}$.

Proof

Let the Wiener chaos expansion of the solution $u$ and the truncated solution ${u}^{N,n,r}$ of the stochastic equation (2.2) be:

$$\begin{aligned} u=\sum _{\alpha \in \fancyscript{J}} u_\alpha \xi _\alpha \quad \text { and } \quad {u}^{N,n,r}=\sum _{\alpha \in \fancyscript{J}_{N}^{n,r}} u_\alpha \xi _\alpha , \end{aligned}$$

where $u_\alpha$ satisfies the propagator system of equations (2.3). Then, the approximation error due to the elimination of the higher order components of the Wiener chaos expansion and the truncation of the infinite dimensional Brownian motion is given by

$$\begin{aligned} u- {u}^{N,n,r}=\sum _{\alpha \in \fancyscript{J}} u_\alpha \xi _\alpha -\sum _{\alpha \in \fancyscript{J}_{N}^{n,r}} u_\alpha \xi _\alpha . \end{aligned}$$

Now, by using Parseval’s identity and from the triangle inequality we obtain:

$$\begin{aligned} \left\| u-u_N^{n,r}\right\| ^2_{\fancyscript{R}L^2\left( {\mathbb {W};\fancyscript{V}}\right) } \le \sum _{{\alpha \in \fancyscript{J}{\setminus }{\fancyscript{J}_N^{n,r}}}} r_\alpha ^2\left\| {u_\alpha }\right\| ^2_\fancyscript{V} = I_1^\star \end{aligned}$$

Applying the results of Theorem 2 to the error term $I_1^\star$ yields that

$$\begin{aligned} \begin{aligned} I_1^\star \le&\, C \sum _{\alpha \in \fancyscript{J}{\setminus }\fancyscript{J}_N^{n,r}} r_\alpha ^2 \Biggl [\left\| u_{0,\alpha }\right\| _{V}+\left\| f_\alpha \right\| _{\fancyscript{V}} +\left\| f_\alpha '\right\| _{\fancyscript{H}} \\&+ {\left| \alpha \right| }^{1/2} \sum _{i,k} \left( \left\| g_{\alpha ^-(i,k)}\right\| _\fancyscript{V} + \left\| g'_{ \alpha ^-(i,k)} \right\| _\fancyscript{H} \right) \Biggr ]^2 =: I_1 \end{aligned} \end{aligned}$$

and this completes the proof.

Remark 2

Note that this error term is related to the tail of the Wiener Chaos expansion of the data of the problem and can be recognized through Parseval’s identity (due to the orthonormality of the Cameron–Martin basis) as the tail of the numerical series defining moments of random fields involved with the data.

Remark 3

Note that the error term $I_1$ corresponds to the truncation of the components of the infinite-dimensional propagator system of equations and the infinite-dimensional Brownian motion. The constant $C$, for each $\alpha \in \fancyscript{J}_{N}^{n,r}$, depends only on the operators $\fancyscript{A}$ and $\fancyscript{M}_k$ and on $T$. From the analytical expression of the bound of the error term $I_1$, it is straightforward that the addition of the terms to the Wiener chaos expansion leads to the reduction of the error due to the truncation. Moreover, it reveals the dependence of the error on the structure of the weighted Wiener chaos space as if, for example, the weights $r_\alpha =1$, the contribution of each truncated component of the Wiener chaos expansion is equivalent.

The estimates provided by Proposition 1 would be satisfactory as long as we have the exact solution of the truncated propagator ${ P}^{N,n,r}$. However, this is a PDE system and must be approximated by a finite difference (or finite element) procedure, i.e. by an approximation system ${ P}_{\varDelta }^{N,n,r}$.

Proposition 2

(Discretization error) The random field ${u}_{\varDelta }^{N,n,r}= \sum _{\alpha \in \fancyscript{J}_{N}^{n,r}} u_{\varDelta ,\alpha } \xi _\alpha \in \fancyscript{R}L^2(\mathbb {W}; \fancyscript{V})$ produces an approximation to the solution ${u}^{N,n,r}=\sum _{\alpha \in \fancyscript{J}_{N}^{n,r}} u_{\alpha } \xi _\alpha$, where the process ${u_\alpha , \alpha \in \fancyscript{J}_{N}^{n,r}}$ is the solution of the truncated propagator (3.1) and it satisfies the following a priori bound:

$$\begin{aligned} \left\| {u}^{N,n,r}-{u}_{\varDelta }^{N,n,r}\right\| _{\fancyscript{R}L^2\left( {\mathbb {W};\fancyscript{V}}\right) }^2 \le I_2 \end{aligned}$$

where $I_2:= \mathfrak {C}^2 (\fancyscript{M}_k,N,n,r) \left| h \right| ^2$ with the constant

$$\begin{aligned} \mathfrak {C}(\fancyscript{M}_k,N,n,r) = \left\{ \sum _{\alpha \in \fancyscript{J}_N^{n,r}} r_\alpha ^2 \left[ 1+ \sum _{p=1}^{N} {C_M}^{N-p+1} \prod _{|\beta |= p}^{N} |\beta | (nr)^{|\beta |-1} \right] ^2 \right\} ^{1/2} \end{aligned}$$

depending only on the operator $\fancyscript{M}_k$, the order of the truncation and the weights $r_\alpha$.

Proof

Since the propagator is a lower triangular system, the proof is made by induction on $|\alpha |$. For $\alpha =(0)$, or equivalently, $\left| \alpha \right| =0$, equation (3.1) reduces to

$$\begin{aligned} u_{(0)} (t) = u_{0,{(0)}} + \int \limits _{0}^{t} {\bigl (\fancyscript{A}_h (s) u(s)+ f(s) \bigr )_{(0)}} ds \end{aligned}$$

and the error due to discretization can be directly derived by the Taylor’s theorem and equals to

$$\begin{aligned} \left\| u_{(0)}-u_{\varDelta ,(0)}\right\| _{\fancyscript{V}} \le \left| h \right| \end{aligned}$$

Consider now the case $|\alpha |=1$. This corresponds to a family of multi-indices which correspond to matrices, with only one nonzero element, the $(i,k)$ element, equal to $1$. For this index, equation (3.1) implies that

$$\begin{aligned} u_{(1)} (t) = u_{0,{(1)}} + \int \limits _{0}^{t} {\bigl (\fancyscript{A}_h(s) u(s)+ f(s) \bigr )_{(1)}} ds \\ + \int \limits _{0}^{t} {\bigl (\fancyscript{M}_k(s) u(s)+ g_k(s)\bigr )_{(0)} m_i(s)ds} \end{aligned}$$

Then, by subtracting the discretized truncated solution $u_{\varDelta , (1)}$ from the truncated solution $u_{(1)}$ of the propagator and from the previous level we obtain:

$$\begin{aligned} \left\| u_{(1)}-u_{\varDelta , (1)}\right\| _{\fancyscript{V}} \le \left| h \right| \left( 1+C_M \right) \end{aligned}$$

where the constant $C_M$ depends only on the operator $\fancyscript{M}_k$. Assume now that for $|\alpha |=N$, the discretized error is bounded by:

$$\begin{aligned} \left\| u_{(N)}-u_{\varDelta ,(N)}\right\| _{\fancyscript{V}} \le \left| h \right| \left[ 1+ \sum _{p=1}^{N} {C_M}^{N-p+1}\prod _{|\beta |= p}^{N} |\beta | (nr)^{|\beta |-1}\right] \end{aligned}$$

(4.1)

Therefore, for $|\alpha |=N+1$ and by using the induction hypothesis that inequality (4.1) holds, we obtain that

$$\begin{aligned}&\left\| u_{(N+1)}-u_{\varDelta ,(N+1)}\right\| _{\fancyscript{V}}\\&\quad \le \left| h \right| \left\{ 1+ C_M \left| N+1\right| (nr)^N \left[ 1+ C_M^N \sum _{p=1}^{N} C_M^{N-p+1} \prod _{|\beta |=p}^N |\beta | (nr)^{|\beta |-1} \right] \right\} \end{aligned}$$

or equivalently

$$\begin{aligned} \left\| u_{(N+1)}-u_{\varDelta ,(N+1)}\right\| _{\fancyscript{V}} \le \left| h \right| \left\{ 1+ C_M^{N+1} \left[ 1+ \sum _{p=1}^{N+1} \prod _{|\beta |=p}^{N+1} |\beta | (nr)^{|\beta |-1} \right] \right\} \end{aligned}$$

Thus, the error due to the discretization of the propagator system of equations (2.3) is bounded from above by:

$$\begin{aligned} \left\| u_\alpha -u_{\varDelta ,\alpha }\right\| _{\fancyscript{V}} \le \left| h \right| \left[ 1+ \sum _{p=1}^{\left| \alpha \right| } {C_M}^{\left| \alpha \right| -p+1}\prod _{|\beta |= p}^{\left| \alpha \right| } |\beta | (nr)^{|\beta |-1}\right] \end{aligned}$$

(4.2)

for all $\alpha \in \fancyscript{J}_{N}^{n,r}$. Now adding over all $\alpha \in \fancyscript{J}_{N}^{n,r}$ and using Parseval’s identity, yields that

$$\begin{aligned} \left\| {u}^{N,n,r}\!-\!{u}_{\varDelta }^{N,n,r}\right\| _{\fancyscript{R}L^2(\mathbb {W};\fancyscript{V})}^2 \!\le \! \sum _{\alpha \in \fancyscript{J}_N^{n,r}} r_\alpha ^2 \left| h \right| ^2 \left[ \!1\!+\! \sum _{p=1}^{\left| \alpha \right| } {C_M}^{\left| \alpha \right| -p+1}\prod _{|\beta |= p}^{\left| \alpha \right| } |\beta | (nr)^{|\beta |-1}\!\right] ^2 \end{aligned}$$

or equivalently

$$\begin{aligned} \left\| {u}^{N,n,r}-{u}_{\varDelta }^{N,n,r}\right\| _{\fancyscript{R}L^2(\mathbb {W};\fancyscript{V})}^2 \le {\mathfrak {C}^2(\fancyscript{M}_k,N,n,r) }\left| h \right| ^2 \end{aligned}$$

(4.3)

for the constant

$$\begin{aligned} \mathfrak {C}(\fancyscript{M}_k,N,n,r) = \left\{ \sum _{\alpha \in \fancyscript{J}_N^{n,r}} r_\alpha ^2 \left[ 1+ \sum _{p=1}^{\left| \alpha \right| } {C_M}^{\left| \alpha \right| -p+1}\prod _{|\beta |= p}^{\left| \alpha \right| } |\beta | (nr)^{|\beta |-1}\right] ^2 \right\} ^{1/2} \end{aligned}$$

and this completes the proof.

Remark 4

Note that the error bound (4.3) involves the product of the constant $\mathfrak {C}$ (which depends on the truncation of the Wiener chaos expansion) with $h$, which depends on the “fineness” of the grid. This is important, since $\mathfrak {C}$ may increase considerably when choosing larger values of $N,\, n$ and $r$. However, by choosing a finer grid $h$, we may compromise the overall error.

The following corollary provides a tradeoff between the number of “modes” employed in the Wiener chaos expansion and the discretization parameter $h$ of the deterministic propagator.

Corollary 1

Consider Eq. (3.1) and let the operator $\fancyscript{M}_k=0$ and the weighting function $r_\alpha =1$, $\forall \alpha$. Then, the discretized solution ${u}_{\varDelta }^{N,n,r}=\sum _{\alpha \in \fancyscript{J}_N^{n,r}} u_{\varDelta ,\alpha }\xi _\alpha$ of the stochastic equation (2.2), satisfies the following a priori bound:

$$\begin{aligned} \left\| {u}^{N,n,r}-{u}_{\varDelta }^{N,n,r}\right\| _{\fancyscript{R}L^2\left( {\mathbb {W};\fancyscript{V}}\right) } \le \left| h \right| \sqrt{\frac{(nr)^{N+1}-1}{nr-1}}. \end{aligned}$$

Proof

Recall that the set $\fancyscript{J}_{N}^{n,r}$ is finite with at most ${[(nr)^{N+1}-1]}/{(nr-1)}$ elements (cf. Sect. 3.1). Then, the proof is an immediate consequence of Proposition 2.

We are now ready to provide the proof of Theorem 4.

Proof

The approximation error can be decomposed in terms of the Wiener chaos expansion as:

$$\begin{aligned} u-{u}_{\varDelta }^{N,n,r} \!=\! \sum _{\alpha \in \fancyscript{J}}u_\alpha \xi _\alpha \!-\!\sum _{\alpha \in \fancyscript{J}_N^{n,r}} u_{\varDelta ,\alpha }\xi _\alpha \!=\! \sum _{\alpha \in \fancyscript{J}_N^{n,r}} \left( {u_\alpha \!-\! u_{\varDelta ,\alpha }}\right) \xi _\alpha \!+\!\sum _{{\alpha \in \fancyscript{J}{\setminus }{\fancyscript{J}_N^{n,r}}}}{u_\alpha } \xi _\alpha . \end{aligned}$$

By applying Parseval’s identity and the triangle inequality we obtain:

$$\begin{aligned} \left\| u-{u}_{\varDelta }^{N,n,r}\right\| ^2_{\fancyscript{R}L^2\left( {\mathbb {W};\fancyscript{V}}\right) } \le \sum _{\alpha \in \fancyscript{J}_N^{n,r}} {r_\alpha ^2\left\| u_\alpha - u_{\varDelta ,\alpha }\right\| }^2_\fancyscript{V} + \sum _{\alpha \in \fancyscript{J}{\setminus }{\fancyscript{J}_N^{n,r}}} r_\alpha ^2\left\| {u_\alpha }\right\| ^2_\fancyscript{V} \end{aligned}$$

or equivalently

$$\begin{aligned} \left\| u-{u}_{\varDelta }^{N,n,r}\right\| ^2_{\fancyscript{R}L^2\left( {\mathbb {W};\fancyscript{V}}\right) } \le I_1+I_2 \end{aligned}$$

Hence, the proof is an immediate consequence of Propositions 1 and 2.

4.2 A posteriori error estimates

At this point, we derive a posteriori error estimates for the error between the solution $u$ of the hyperbolic stochastic partial differential equation (2.2) and the solution of the corresponding space-discretized stochastic equation.

To perform our a posteriori analysis, we follow the construction proposed by [7], properly adapted for a lower triangular system of PDEs. At each level $\alpha \in \fancyscript{J}_{N}^{n,r}$ we consider the $L^2$- orthogonal projection operator $\Pi :H \rightarrow V_h$, where $H:=L^2(U)$ and with $V_h$ we denote the space-discretized space for $U \subset {\mathbb R}^{n}$. We also define the elliptic reconstruction $w_\alpha :=w_\alpha (t)\in V:=H_0^1(U)$, $t\in [0,T]$ of the discretized solution $u_{\delta ,\alpha }$, satisfying the elliptic problem $\mathsf {a}(w_\alpha ,v)=\langle z_\alpha ,v \rangle$, for all $v\in V$, where $z_\alpha :=\mathsf {A}v-\Pi \fancyscript{Z}_\alpha +\fancyscript{Z}_\alpha$ with $\fancyscript{Z}_{\alpha }=f_\alpha + \sum _{i,k}\sqrt{\alpha _i^k} \left( {\fancyscript{M}_ku+g_k}\right) _{\alpha ^-(i,k) }m_i(t)$ and $\mathsf{{A}}:V_h\rightarrow V_h$ be the discrete elliptic operator defined by: $\langle \mathsf{{A}}q,x \rangle =\mathsf{{a}}(q,x)$ for all $q,x\in V_h$. Moreover, we denote by $\langle \cdot ,\cdot \rangle$ the standard inner product of the $L^2$ space.

We also decompose the error of the approximation as:

$$\begin{aligned} e_\alpha :=u_{\delta ,\alpha }-u_\alpha \quad \varepsilon _\alpha :=w_\alpha - u_{\delta ,\alpha }\; \text { and } \; \rho _\alpha :=w_\alpha -u_\alpha \end{aligned}$$

Then, the following relation holds ([7]):

$$\begin{aligned} \langle {{e_\alpha }_{tt},v}\rangle +a(\rho _\alpha ,v)= 0, \qquad v\in V \end{aligned}$$

(4.4)

In order to construct an a posteriori error estimate for the solution of the stochastic hyperbolic PDE (2.2), we first introduce the a posteriori bound for the solution of the corresponding hyperbolic propagator ${ P}_{\delta }^{N,n,r}$.

At this point, we state the a posteriori error bound proposed by Lakkis et al. [7], with several modifications that are necessary for it to hold under the regularity assumptions of the proposed Wiener chaos solution, imposed by the deterministic propagator ${ P}_{\delta }^{N,n,r}$.

Before dealing with the general case, we first provide a result concerning the special case $M_{k} \equiv 0$.

Proposition 3

(A posteriori error estimate for the propagator) [7] The following a posteriori error estimate hold between the solution of the hyperbolic propagator ${P}$ and the semi-discrete propagator ${ P}_{\delta }^{N,n,r}$

$$\begin{aligned} \begin{aligned} \left\| \varepsilon _\alpha \right\| _\fancyscript{H} \le C \Big ( \left\| u_{\delta ,\alpha ,tt} \right\| _\fancyscript{H} +|h| + \left\| \varepsilon _{0,\alpha } \right\| _V +\left\| \varepsilon _{t,0,\alpha } \right\| _H \Bigr ) \end{aligned} \end{aligned}$$

(4.5)

where the constant $C$ depends on the order of the truncation $\alpha$, the domain $U$, the time $T$, the operator $\fancyscript{A}$ and the constant of the Poincare-Friedrichs inequality.

Proof

The proof is divided in two parts. In the first part, we sketch the main points of the proof of the a posteriori error bound, proposed by Lakkis [7], with minor modifications on the regularity of the estimates. In the second part, we impose the energy estimates for the wave equation in order to mitigate the dependence of the a posteriori bound on the auxiliary process $w_\alpha$.

(a) Let $\tilde{v}:=\int _t^\mathsf{T} \rho _\alpha (s,\cdot ) ds\in V$, where $t,\mathsf{T} \in [0,T]$ and $\rho _\alpha \in V$. Now, by setting $v=\tilde{v}$ in (4.4) and integrating by parts, we obtain:

$$\begin{aligned} -\int \limits _0^\mathsf{T} \langle e _{\alpha ,t},\tilde{v}_t \rangle +\langle e _{\alpha ,t} (\mathsf{T}),\tilde{v}(\mathsf{T}) \rangle -\langle e _{\alpha ,t} (0),\tilde{v}(0) \rangle + \int \limits _0^\mathsf{T} a(\rho _\alpha ,\tilde{v}) =0 \end{aligned}$$

or equivalently

$$\begin{aligned} \frac{1}{2}\left\| \rho _\alpha (\mathsf{T})\right\| ^2 -\frac{1}{2}\left\| \rho _\alpha (0)\right\| ^2 +\frac{1}{2} a(\tilde{v}(0),\tilde{v}(0)) = \int \limits _0^\mathsf{T} \langle {{e_\alpha }_t,\rho _\alpha }\rangle + \langle {e_{\alpha ,t}(0),\tilde{v}_t}(0)\rangle \end{aligned}$$

Due to the Cauchy-Schwartz inequality along with standard calculus results, we deduce that

$$\begin{aligned} \begin{aligned} \left\| u_\alpha \!-\!u_{\delta ,\alpha }\right\| _\fancyscript{H} \le&\,C \left( \left\| w_\alpha \!-\!u_{\delta ,\alpha }\right\| _\fancyscript{V} \!+\! \left\| u_{0,\alpha }\!-\!u_{\delta ,0,\alpha } \right\| _{H} \!+\!\left\| w_{0,\alpha }\!-\!u_{\delta ,0,\alpha } \right\| _{H}\right. \\&\left. + \int \limits _0^T \left\| (w_\alpha -u_{\delta ,\alpha })_t \right\| _H+\left\| (u_{t,0,\alpha }-u_{t,0,\delta ,\alpha }) \right\| _H \right) \end{aligned} \end{aligned}$$

(4.6)

(b) In order to mitigate the dependence of the a posteriori error bound on the auxiliary process $w_\alpha$, we use the auxiliary function $\varepsilon _\alpha :=w_\alpha -u_{\delta ,\alpha }$. Now for all $\alpha \in \fancyscript{J}_{N}^{n,r}$, the process $\varepsilon _\alpha$ satisfies the differential equation:

$$\begin{aligned} \begin{aligned} \varepsilon _{\alpha ,tt} - c\varepsilon _{\alpha ,xx} = Au_{\delta ,\alpha }- 2\Pi \fancyscript{Z}_{\alpha } +\fancyscript{Z}_{\alpha } \end{aligned} \end{aligned}$$

(4.7)

where $\fancyscript{Z}_{\alpha }=f_\alpha + \sum _{i,k}\sqrt{\alpha _i^k} g_{k,\alpha ^-(i,k) }m_i(t)$.

Thus, for the process $\varepsilon _\alpha$ due to the triangle inequality we have the energy estimate⁴:

$$\begin{aligned} \left\| \varepsilon _\alpha \right\| _\fancyscript{V} + \left\| \varepsilon _{\alpha ,t} \right\| _\fancyscript{H}&\le C\Big ( \left\| Au_{\delta ,\alpha }- \Pi \fancyscript{Z}_{\alpha } \right\| _\fancyscript{H}+ \left\| \Pi \fancyscript{Z}_\alpha - \fancyscript{Z}_{\alpha } \right\| _\fancyscript{H}\nonumber \\&+\left\| \varepsilon _{0,\alpha } \right\| _V +\left\| \varepsilon _{t,0,\alpha } \right\| _H\Big ) \end{aligned}$$

(4.8)

or equivalently

$$\begin{aligned} \begin{aligned} \left\| \varepsilon _\alpha \right\| _\fancyscript{V} + \left\| \varepsilon _{\alpha ,t} \right\| _\fancyscript{H} \le&C\Big ( \left\| u_{\delta ,\alpha ,tt}\right\| _\fancyscript{H} +|h| + \left\| \varepsilon _{0,\alpha } \right\| _V +\left\| \varepsilon _{t,0,\alpha } \right\| _H\Big ) \end{aligned} \end{aligned}$$

(4.9)

and this completes the proof.

Now assume that $\fancyscript{M}_k \ne 0$.

Proposition 4

(A posteriori error estimate for the propagator: general case) The following a posteriori error estimate hold between the solution of the hyperbolic propagator ${P}$ and the semi-discrete propagator ${ P}_{\delta }^{N,n,r}$

$$\begin{aligned} \begin{aligned} \left\| e_\alpha \right\| _\fancyscript{H} \le&\, C\left( \left\| u_{\delta ,\alpha ,tt} \right\| _\fancyscript{H} +|h| +\sum _{n=0}^{|\alpha |-1}\left\| \varepsilon _{n} \right\| _\fancyscript{H} + \left\| \varepsilon _{0,\alpha } \right\| _V +\left\| \varepsilon _{t,0,\alpha } \right\| _H \right) \qquad \quad \end{aligned} \end{aligned}$$

(4.10)

where the constant $C$ depends on the order of the truncation $\alpha$, the domain $U$, the time $T$, the operators $\fancyscript{A}$ and $\fancyscript{M}_k$ and the constant of the Poincare-Friedrichs inequality.

Proof

Since the propagator is a lower triangular system, the proof is made by induction on $|\alpha |$. For $\alpha =(0)$, or equivalently, $\left| \alpha \right| =0$, Eq. (3.1) reduces to

$$\begin{aligned} u_{(0)}(t) = u_{0,(0)}+ \int \limits _{0}^{t} {\bigl (\fancyscript{A} u(s)} + f(x,s) \bigr )_{(0)} ds \end{aligned}$$

and Proposition 3 holds. Thus, from Proposition 3, the a posteriori error bound becomes

$$\begin{aligned} \begin{aligned} \left\| e_{(0)} \right\| _\fancyscript{H} \le&\, C\Big ( \left\| u_{\delta ,(0),tt} \right\| _\fancyscript{H} +|h| + \left\| \varepsilon _{0,(0)} \right\| _V +\left\| \varepsilon _{t,0,(0)} \right\| _H \Bigr ) \end{aligned} \end{aligned}$$

(4.11)

where the constant $C$ depends on the order of the truncation $\alpha$, the domain $U$, the time $T$, the operators $\fancyscript{A}$ and the constant of the Poincare-Friedrichs inequality.

Consider now $\left| \alpha \right| =1$. This case corresponds to the multi-indices $\alpha$ with only one non-zero element $\alpha _i^k=1$. For this index, Eq. (3.1) implies that

$$\begin{aligned} u^{'}_{(1)} (t)&= {\bigl (\fancyscript{A}(t)u(t)+ f(x,t) \bigr )_{(1)}} + {\bigl ( \fancyscript{M}_k u+g_k\bigr )_{(0)}(t) \, m_i(t)},\nonumber \\ u_{(1)} (0)&= u_{0,(1)}. \end{aligned}$$

(4.12)

Then, for $(|\alpha |=1)$, the right hand side of Eq. (4.12) is fully determined by knowledge of $u_{(0)}$, which in turn is fully specified by the previous level. Thus, the process $\varepsilon _\alpha$, for $|\alpha |=1$ satisfies the differential equation:

$$\begin{aligned} \begin{aligned} \varepsilon _{ik,tt} - c\varepsilon _{ik,xx} = Au_{\delta ,(1)} - 2\Pi \fancyscript{Z}_{(1)} +\fancyscript{Z}_{(1)} \end{aligned} \end{aligned}$$

(4.13)

where $\fancyscript{Z}_{(1)}=f_{(1)} + ({\fancyscript{M}_k u +g_k})_{(0) } m_i(t)$. By applying the triangle inequality to the energy estimates (4.8) and due to the boundedness of the operator $\fancyscript{M}_k$, yields that

$$\begin{aligned} \left\| \varepsilon _{(1)} \right\| _\fancyscript{V} \!+\! \left\| \varepsilon _{(1),t} \right\| _\fancyscript{H}&\le C\Big ( \left\| A u_{\delta ,(1)}\!-\! \Pi \fancyscript{Z}_{(1)} \right\| _\fancyscript{H} \!+\!\left\| \Pi (f_{(1)} \!+\! g_{k,(0) })\!-\!(f_{(1)} \!+\! g_{k,(0)})\right\| _\fancyscript{H}\nonumber \\&\!+\!\left\| \Pi \fancyscript{M}_k u_{(0)}\!-\! \fancyscript{M}_k u_{(0)})\right\| _\fancyscript{H} \!+\! \left\| \varepsilon _{0,(1)} \right\| _V \!+\!\left\| \varepsilon _{t,0,(1)} \right\| _H\Big )\qquad \qquad \end{aligned}$$

(4.14)

or equivalently

$$\begin{aligned} \left\| \varepsilon _{(1)} \right\| _\fancyscript{V} \!+\! \left\| \varepsilon _{(1),t} \right\| _\fancyscript{H} \!\le \! C\Big ( \left\| u_{\delta ,(1),tt}\right\| _\fancyscript{H} \!+\!|h| \!+\! \left\| \varepsilon _{(0)}\right\| _\fancyscript{H} \!+\! \left\| \varepsilon _{0,(1)} \right\| _V \!+\!\left\| \varepsilon _{t,0,(1)} \right\| _H\Big )\nonumber \\ \end{aligned}$$

(4.15)

Continuing in this way, and by induction on $\left| \alpha \right|$ it follows that for every $\alpha \in \fancyscript{J}$, the process $u_\alpha$ satisfies the a posteriori bound

$$\begin{aligned} \left\| e_\alpha \right\| _\fancyscript{H} \le C\left( \left\| u_{\delta ,\alpha ,tt} \right\| _\fancyscript{H} +|h| +\sum _{n=0}^{|\alpha |-1}\left\| \varepsilon _{n} \right\| _\fancyscript{H} + \left\| \varepsilon _{0,\alpha } \right\| _V +\left\| \varepsilon _{t,0,\alpha } \right\| _H \right) \qquad \qquad \end{aligned}$$

(4.16)

with $|\alpha |=n$. However, from the definition of the multi-indices $\alpha$, each $\alpha$ has only finite nonnegative integer elements $\alpha _i^k$. As a result, the error bound (4.16) is bounded for all $\alpha \in \fancyscript{J}_{N}^{n,r}$ and this completes the proof.

In Theorem 5 we establish a global a posteriori error estimate for the solution of the hyperbolic SPDE (2.2).

Theorem 5

(A posteriori error estimate for hyperbolic SPDEs) The difference between the solution $u$ of the stochastic hyperbolic partial differential equation (2.2) and the solution ${u}_{\delta }^{N,n,r}$ of the corresponding semi-discretized equation satisfies the a posteriori error bound:

$$\begin{aligned} \left\| u-{u}_{\delta }^{N,n,r} \right\| _{\fancyscript{R}L^2(\mathbb {W};\fancyscript{H})}^2 \le I_1 +I_3 \end{aligned}$$

(4.17)

where the quantity

$$\begin{aligned} I_3&= C\Big ( \left\| u_{\delta ,tt} \right\| _{\fancyscript{R}L^2(\mathbb {W};\fancyscript{H})}^2 +|h|^2 +\left\| \varepsilon \right\| _{\fancyscript{R}L^2(\mathbb {W};\fancyscript{H})}^2 + \left\| \varepsilon _{0} \right\| _{\fancyscript{R}L^2(\mathbb {W};V)}^2\\&+\left\| \varepsilon _{t,0} \right\| _{\fancyscript{R}L^2(\mathbb {W};\fancyscript{H})}^2\Bigr ) \end{aligned}$$

Proof

Based on the Wiener chaos expansion of the random fields $u=\sum _{\alpha \in \fancyscript{J}} u_\alpha \xi _\alpha$ and $u_{\delta }=\sum _{\alpha \in \fancyscript{J}_{N}^{n,r}} u_{\delta ,\alpha }\xi _\alpha$, the approximation error can be decomposed as

$$\begin{aligned} u-u_\delta = \sum _{\alpha \in \fancyscript{J}_{N}^{n,r}} (u_\alpha -u_{\delta ,\alpha }) \xi _\alpha +\sum _{\alpha \in \fancyscript{J}{\setminus }\fancyscript{J}_{N}^{n,r}} u_\alpha \xi _\alpha . \end{aligned}$$

(4.18)

Then, triangle inequality and Parseval’s identity yields that

$$\begin{aligned} \Vert u-u_\delta \Vert ^2_{\fancyscript{R}L^2(\mathbb {W};\fancyscript{H})}&\le \sum _{\alpha \in \fancyscript{J}_{N}^{n,r}} \Vert u_\alpha -u_{\delta ,\alpha }\Vert ^2_{\fancyscript{R}L^2(\mathbb {W};\fancyscript{H})}\nonumber \\&+\,C \sum _{\alpha \in \fancyscript{J}{\setminus }\fancyscript{J}_{N}^{n,r}} \Vert u_\alpha \Vert _{\fancyscript{R}L^2(\mathbb {W};\fancyscript{V})}^2:=I_3^\star +I_1\qquad \end{aligned}$$

(4.19)

for some positive constant $C$, due to embedding theorems of $L^2$ space.

We now look at the term $I_3$. From Proposition 4, triangle inequality and Parseval’s identity, we obtain

$$\begin{aligned} I_3^\star&\le C\Big ( \left\| u_{\delta ,tt} \right\| _{\fancyscript{R}L^2(\mathbb {W};\fancyscript{H})}^2 +|h|^2 +\left\| \varepsilon \right\| _{\fancyscript{R}L^2(\mathbb {W};\fancyscript{H})}^2 + \left\| \varepsilon _{0} \right\| _{\fancyscript{R}L^2(\mathbb {W};V)}^2\nonumber \\&+\left\| \varepsilon _{t,0} \right\| _{\fancyscript{R}L^2(\mathbb {W};\fancyscript{H})}^2 \Bigr ):=I_3 \end{aligned}$$

(4.20)

Note that the a posteriori error estimate for the discretized propagator ${ P}_{\delta }^{N,n,r}$ at each step of the expansion is fully determined by the data of the problem and the previous steps.

The proof of Theorem 5 is directly derived from Parseval’s identity, triangle inequality, Theorem 2 and Proposition 4. Similar results can be derived for the fully discretized propagator, but it is beyond the scope of the current work.

5 Numerical results

In this section, we apply the general theory of the Wiener chaos expansion to the stochastic wave equation and the stochastic Klein–Gordon equation and provide numerical results for both equations, based on the proposed numerical scheme. In these experiments we compare the computational accuracy and the efficiency of the Wiener chaos expansion to the popular Monte Carlo method. For both the stochastic wave equation and the Klein–Gordon equation we use $N=1$ and $n=4$. Our numerical results show that the proposed Wiener chaos method is significantly faster than the corresponding Monte Carlo method, and the overall error is still small, compared to either the true solution or the Monte Carlo simulated solution for the Wave or the Klein–Gordon equation respectively.

5.1 Stochastic wave equation in 1D

The wave equation driven by Brownian motion has been a very active research field during the last decades, as it is a fundamental stochastic equation in physics relativistic quantum mechanics and oceanography (e.g. [3] and the references therein). In this section, we consider the following 1D stochastic wave equation:

$$\begin{aligned} \begin{aligned} \frac{\partial ^2 u}{\partial t^2}+\fancyscript{A}u&=\sum _{k=1}^d \sigma _k dW_t \\ u(0,x)&=u_0(x) \end{aligned} \end{aligned}$$

(5.1)

where $\fancyscript{A}=-c^2 \varDelta$ for a real constant $c$ and $W(t)=\{W_k(t)\}_{1\le k \le d}$ is a d-dimensional Brownian motion. For simplicity, we consider that the initial condition is deterministic. Under the proposed setting, Eq. (5.1) admits a unique square-integrable solution and thus, it has a Wiener chaos solution. In the sequel, we present the corresponding propagator system of equation for the current problem.

The moments of the solution $u$ of Eq. (5.1) can be derived directly from the stochastic equation using Itō calculus. For example, the first moment satisfies:

$$\begin{aligned} \frac{\partial ^2 u}{\partial t^2}+\fancyscript{A}u=0 \; \text { with } \; u(0,x)=u_0(x) \end{aligned}$$

(5.2)

Similar expressions hold for higher order moments.

5.1.1 Propagator system for the 1D wave equation

Using formula (2.3), we obtain the corresponding propagator system for the Wiener chaos expansion of the wave equation (5.1):

$$\begin{aligned} \begin{aligned} U_{t,\alpha }+\fancyscript{A}U_{\alpha }&=F_\alpha \\ U_\alpha (0,x)&=U_0(x) \mathbf {1}_{(|\alpha |=0) } \end{aligned} \end{aligned}$$

(5.3)

where $\fancyscript{A}=\begin{pmatrix} 0 &{}\quad -c\frac{\partial }{\partial x} \\ -c\frac{\partial }{\partial x} &{}\quad 0 \end{pmatrix} \quad \text {and} \quad F_\alpha =\begin{pmatrix} 0 \\ \sum _{k=1}^d \sigma _k \mathbf {1}_{(|\alpha |=1) } m_i(t) \end{pmatrix}$. As mentioned above, the propagator is a deterministic system of equations and the stochasticity of the solution is represented by the elements comprising the $L^2$ basis functions $\{m_i(t)\}_{i\ge 1}$. Note also that the first equation in the Wiener chaos expansion (5.3) coincides with the mean of the stochastic solution. In the sequel we demonstrate the efficiency and accuracy of the proposed Wiener chaos expansion based scheme.

5.1.2 Numerical results for the 1D wave equation

In our numerical experiments, we consider the following initial condition:

$$\begin{aligned} u_0(x)=2+x \mathbf {1}_{x\le 1}+(2-x) \mathbf {1}_{x\ge 1}, \quad x\in [0,2]. \end{aligned}$$

(5.4)

with $c=1$ and $\sigma =(2,\, 1)$. We also divide the space interval $[0,2]$ into $50$ points and the time interval $[0,1]$ into $200$ points. As we do not have an explicit analytical solution for Eq. (5.1), we formulate and solve the equations of the first four moments analytically. These solutions will hereafter be considered as the true solutions of the moment equations.

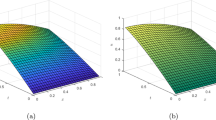
In Fig. 1 we present the first four statistical moments of the solution of equation (5.1) computed by the Wiener chaos expansion and compare them to the moments based on the Monte Carlo method with $10^5$ realizations.⁵ The numerical results obtained through the Wiener chaos expansion are almost identical to those obtained through the Monte Carlo method, with $10^5$ realizations. However, the computational time required for the Wiener chaos is only 0.0048 s as opposed to 397 s required for the Monte Carlo simulation.

Fig. 1

The first four moments of the Wiener chaos expansion compared to the Monte Carlo simulation with $10^5$ realizations for the wave equation (5.1)

Moreover, in Table 2, we provide numerical results concerning the $L^2$ error of the Wiener chaos expansion compared to the true solution for the moments. The relative error for the mean based on the Wiener chaos is given by ${\left\| E(u^{WCE})-E(u^{true})\right\| _{L^2}}/{\left\| E(u^{true})\right\| _{L^2}}$ and similar formulas hold for the higher-order moments.⁶

Table 2 Relative error of the first four moments of the Wiener chaos expansion compared to the true solution of the moments, for the one dimensional wave equation (5.1)

5.2 Numerical results for the rate of convergence of the Wiener chaos expansion

In the following numerical experiment we demonstrate the rate of convergence of the Wiener chaos solution of the stochastic evolution equation (5.5) with respect to the length of the truncation $N$.

Consider the 1D stochastic wave equation with random initial condition

$$\begin{aligned} \begin{aligned}&\frac{\partial ^2 u}{\partial t^2}+\fancyscript{A}u=\sum _{k=1}^d \sigma _k dW_t\qquad (t,x)\in (0,1]\times [0,2] \\&u(0,x)=sin(\pi x) + 0.5\sum _{N\ge 0} {\xi _N}/{{N!}} \qquad \{t=0\}\times x\in [0,2] \end{aligned} \end{aligned}$$

(5.5)

where $\xi _N \sim N(0,1)$. The initial condition $u_0(x)$ admits a Wiener chaos expansion, with $u_0(x)=sin(\pi x)+ \sum _{n>0}\sum _{|\alpha |=n}u_{0,\alpha } \xi _\alpha$ and by Theorem, 3 there exists a unique Wiener chaos solution $u=\sum _{\alpha \in \fancyscript{J}}u_\alpha \xi _\alpha$ to the stochastic evolution equation (5.5).

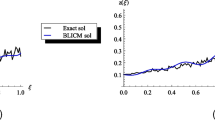
In Fig. 2, we demonstrate the convergence of the $L^2$ norm of the error due to truncation of the Wiener chaos expansion, with respect to the length of the truncation $N$. In particular, we compute the relative error of the second moment

$$\begin{aligned} \left\| E( u^{2}_{WC})-E(u^{2}_{MC})\right\| _{L^2} / \left\| E(u^{2}_{MC}) \right\| _{L^2} \end{aligned}$$

of the stochastic evolution equation (5.5) solved using the Wiener chaos expansion with $n=5,\, r=1$ and $1\le N \le 100$. As an analytical solution is not available, we consider the Monte Carlo solution with $10^5$ realizations as the “true solution” for the computation of the moments.

From Fig. 2, we conclude that the expansion converges fast with respect to $N$, even in the case of the stochastic initial condition. We also note that we obtain accurate results for $N>1$ and further addition of terms to the expansion does not improve the accuracy of the approximation.

Fig. 2

Convergence of the $L^2$ norm of the error due to the truncation of the Wiener chaos expansion, with respect to the length of the truncation $N$

5.3 Stochastic Klein–Gordon equation in 2D

In this section we apply our results to the stochastic Klein–Gordon equation in two space dimensions. This stochastic equation is the most frequently used wave equation for the description of particle dynamics in relativistic quantum mechanics (see e.g. [2, 4] and the references therein). In this section, we consider the following 2D Klein–Gordon equation with multiplicative noise:

$$\begin{aligned} \begin{aligned}&u_t+\fancyscript{A}u=u \sum _{k=1}^d \sigma _k dW_t \\&u(0,x,y)=u_0(x,y), \qquad (x,y)\in [0,2]^2 \end{aligned} \end{aligned}$$

(5.6)

where $\fancyscript{A}=-c^2 \left( \frac{\partial }{\partial x^2}+\frac{\partial }{\partial y^2}\right)$ and $W(t)=\{W_k(t)\}_{1\le k\le d}$ is a Brownian motion vector with $d$ independent components. Now, let us consider the deterministic initial condition $u_0(x,y)=sin(\pi x) \cdot sin(\pi y)$, with $c=0.5$ and $\sigma =(0.5,\, 0.2)$. Moreover, we divide the space interval into $50\times 50$ points and the time interval into $150$ points. As in the 1D case, Eq. (5.6) admits a Wiener chaos expansion, because it has a unique square-integrable solution. The corresponding propagator system of equation for the current problem satisfies the following system of equations:

$$\begin{aligned} \begin{aligned}&U_{t,\alpha }+\fancyscript{A}U_{\alpha }=0 \\&U_\alpha (0,x)=U_0(x) \mathbf {1}_{(|\alpha |=0) } \end{aligned} \end{aligned}$$

(5.7)

where

$$\begin{aligned} U=\begin{pmatrix} u_1\\ u_2 \\ u_3\\ u_4\end{pmatrix} \quad \text {and} \quad \fancyscript{A}=\begin{pmatrix}0&{}\quad 0 &{}\quad -c\frac{\partial }{\partial x} &{}\quad 0 \\ 0 &{}\quad 0&{}\quad -c\frac{\partial }{\partial x} &{}\quad 0 \\ -c\frac{\partial }{\partial x} &{}\quad -c\frac{\partial }{\partial y} &{}\quad 0 &{}\quad -\sum _{k=1}^d \sigma _k \mathbf {1}_{(|\alpha |=1) }m_i(t)\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -1\end{pmatrix}\nonumber \\ \end{aligned}$$

(5.8)

In contrast to the additive noise case, the higher moments of the Klein–Gordon equation of order higher that one cannot be computed analytically. For that reason, we compute only the first moment analytically and the higher order moments numerically, using the Monte Carlo simulation. In this case, we refer to the true solution as the best possible Monte Carlo estimator available, taking into account computational limitations and convergence results of the MC method (in terms of variance of the estimator). For the problem at hand, with volatility $\sigma =(0.5,0.2)$, we employ the MC method with $10^3$ realizations, which is sufficient as it produces an error for the mean of order $\fancyscript{O}(10^{-4})$, compared to the analytical solution.

In the following Table 3 we present the relative error of the first four moments computed using the proposed numerical Wiener chaos scheme, and those computed through the Monte Carlo simulation, with $10^3$ realizations.

Table 3 Relative error of the first four moments of the Wiener chaos compared to the Monte Carlo simulation, for the Klein–Gordon wave equation (5.6)

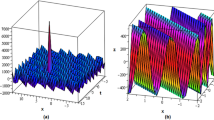
In Fig. 3 we compare the first two statistical moments of the solution of Klein–Gordon wave equation (5.6) computed by the Wiener chaos expansion to the moments based on the Monte Carlo method with $10^3$ realizations. As in the one-dimensional case, the numerical results obtained through the Wiener chaos expansion are almost identical to those obtained through the Monte Carlo method. In this case, the computational time required for the Wiener chaos expansion is only 0.3687 s as opposed to 536 s required for the Monte Carlo simulation.

Fig. 3

Comparison between the first two moments of the Wiener chaos and the Monte Carlo simulation for the Klein–Gordon wave equation (5.6). Left column first and second moment of the true solution, computed by the Monte Carlo simulation method. Right column difference between the first and the second moment computed by the Monte Carlo simulation and the corresponding moments computed using the Wiener chaos expansion

Concluding, we see that the proposed numerical algorithm based on the Wiener chaos expansion for the moments almost coincides with the Monte Carlo method with $10^3$ realizations, but is significantly faster. It is also evaluated numerically that the artificial viscosity term, introduced analytically in Sect. 3, is necessary, as it provides numerical stability in the solution of the wave equation in one and two space dimensions. All the computations ran on an Intel Core 2 3.06 GHz processor under Windows 7.

6 Conclusions and extensions

In the current work we proposed an efficient and accurate method for solving a large class of hyperbolic stochastic evolution equations, through the Wiener chaos expansion. The infinite dimensional stochastic evolution equation is projected on a finite dimensional space, and the solution is determined through the Wiener chaos expansion, as introduced by Lototsky and Rozovsky in [11] and further studied in [9]. The coefficients of the expansion satisfy a lower triangular system of deterministic hyperbolic partial differential equations, known as the Propagator. We then provided both analytical and numerical results for the rate of convergence of the expansion with respect to the norm. In particular, a priori error bounds for the error due to the truncation of the stochastic equation is provided, along with and a posteriori error estimates for the discretization are provided.

In hyperbolic PDEs, the smoothness of the solution depends on the smoothness of the initial and boundary conditions. For instance, if there is a jump in the data at the start or at the boundaries, then the jump will propagate as a shock in the solution. In order to provide smooth solutions for the hyperbolic stochastic model, and motivated by the Lax-Wendroff scheme, we employ the results derived in [9] concerning the convergence of solution of the hyperbolic equations to solutions of approximate parabolic equations as a vanishing viscosity limit. In this case, we use the Lax-Wendroff finite numerical scheme for the parabolic approximation along with the Upwind finite difference scheme for the purely hyperbolic problem. Then, it is evaluated numerically that only the parabolic approximation of the solution, derived through the vanishing viscosity limit, converges to the solution of the stochastic hyperbolic equation.

The Wiener chaos algorithm is significantly faster than the Monte Carlo method, while the numerical results derived through the proposed method are very accurate and almost identical to the Monte Carlo solution. As the theoretical basis of the Wiener chaos method is independent of the number of spatial dimensions, the computational gain of the implementation of the proposed numerical method will be definitely increased in higher spatial dimensions. Comparing the performance of the two different numerical approaches proposed in this paper, we conclude that the Upwind method produces apparently diffusive and unstable results. Thus, we conclude that the use of the Lax-Wendroff scheme, which is equivalent to the use of the vanishing viscosity limit, provides us with stable solutions that depend smoothly upon the data of the problem.

Concluding, the main advantage of the Wiener chaos expansion is the fast convergence due to the structure of the propagator of the Wiener chaos expansion, as a lower triangular system of deterministic equations. Another great advantage is the efficiency due to the orthogonality of the Hermite polynomials that generate the stochastic basis. The proposed method is general and can be easily extended to a broad family of hyperbolic stochastic partial differential equations. The use of the Wiener chaos expansion for the study of hyperbolic SPDEs is not necessarily restricted to the calculation of statistical moments. Through the proper modification of Markov type inequalities or formulae such as the Rice formula [1] one may use the deterministic propagator to approximate the level sets of the random field generated by the solution of the SPDE. This is beyond the scope of the present work and is under active consideration.