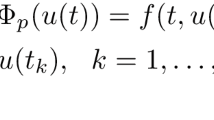1 Introduction

Mechanical systems with impact, heart beats, blood flows, population dynamics, industrial robotics, biotechnology, economics, etc are real world and applied science phenomena which are abruptly changed in their states at some time instants due to short time perturbations whose duration is negligible in comparison with the duration of these phenomena. They are called impulsive phenomena. A natural framework for mathematical simulation of such phenomena are impulsive differential equations or impulsive partial differential equations when more factors are taking into account.

Whereas impulsive differential equations are well studied, see for example the books [4, 8, 39, 42] and the references therein, the literature concerning impulsive partial differential equations does not seem to be very rich. The history of impulsive partial differential equations starts at the end of the 20th century with the pioneering work [15], in which, impulsive partial differential systems have been showed to be a natural framework for the mathematical modeling of processes in ecology and biology, like population growth, see also [10]. We can find studies of first order partial differential equations with impulses in [5, 21, 30, 40]. Higher-order linear and nonlinear impulsive partial parabolic equations were considered in [19]. An initial boundary value problem for a nonlinear parabolic partial differential equation was discussed in [9]. The approximate controllability of an impulsive semilinear heat equation was proved in [1]. A class of impulsive wave equations was investigated in [18]. In [27] a class of impulsive semilinear evolution equations with delays is investigated for existence and uniqueness of solutions. The investigations in [27] includes several important partial differential equations such as the Burgers equation and the Benjamin–Bona–Mahony equation with impulses, delays and nonlocal conditions. A class of semilinear neutral evolution equations with impulses and nonlocal conditions in a Banach space is investigated in [2] for existence and uniqueness of solutions. To prove the main results in [2] the authors use a Karakostas fixed point theorem. In [2] an example involving Burger’s equation is provided to illustrate the application of the main results. Some studies concerning impulsive Burgers equation can be found in [14, 25, 33].

Many classical methods have been successfully applied for solving impulsive partial differential equations. By using variational method, the existence of solutions for a fourth-order impulsive partial differential equations with periodic boundary conditions was obtained in [28]. The Krasnoselskii theorem is used to prove existence and uniqueness of solutions for impulsive Hamilton–Jacobi equation in [34]. Some other references on impulsive partial differential equations are: [3, 7, 11, 16, 17, 22,23,24, 26, 32, 35, 38, 41].

In this paper, we investigate the following class of nonlinear impulsive evolution partial differential equations

$$\begin{aligned} u_t+\left( \psi (u)\right) _x= & {} 0,\quad t\in J\backslash \{t_1, \ldots , t_k\}, \nonumber \\{} & {} J=[0, T],\quad x\in {\mathbb {R}}, \nonumber \\ u(t_j^+, x)= & {} u(t_j^-, x)+ I_j(x, u(t_j, x)),\quad j\in \{1, \ldots , k\}, \nonumber \\ {}{} & {} x\in {\mathbb {R}}, \nonumber \\ u(0, x)= & {} u_0(x),\quad x\in {\mathbb {R}}, \end{aligned}$$
(1.1)

where

$$\begin{aligned} u(t_j^+, x)=\lim _{t\rightarrow t_j^+} u(t, x),\quad u(t_j^-, x)=\lim _{t\rightarrow t_j^-} u(t, x)\quad x\in {\mathbb {R}},\quad j\in \{1, \ldots , k\}. \end{aligned}$$

Note that for \(\psi (u)=\frac{1}{2}u^{2},\) we get impulsive Burgers equations. Assume that

(A1):

\(0=t_0<t_1<\cdots< t_k<t_{k+1}=T\), \(u_0\in {\mathcal {C}}^1({\mathbb {R}})\), \(0< u_0\le B\) on \({\mathbb {R}}\) for some positive constant B,

(A2):

\(\psi \in {\mathcal {C}}^1({\mathbb {R}})\), and

$$\begin{aligned} |\psi ^{\prime }(u(t, x)))|\le b_1(t, x)+ b_2(t, x) |u(t, x)|^l, \end{aligned}$$

\((t, x)\in J\times {\mathbb {R}}\), \(b_1, b_2 \in {\mathcal {C}}(J\times {\mathbb {R}})\), \(0\le b_1, b_2\le B\) on \(J\times {\mathbb {R}}\), \(l\ge 0\),

(A3):

\(I_j \in {\mathcal {C}}({\mathbb {R}}^{2})\), \(|I_j(x, v)|\le a_j(x) |v|^{p_j}\), \(x\in {\mathbb {R}}\), \(v\in {\mathbb {R}}\), \(a_j\in {\mathcal {C}}({\mathbb {R}})\), \(0\le a_j(x)\le B\), \(x\in {\mathbb {R}}\), \(p_j\ge 0\), \(j\in \{1, 2, \ldots , k\}\),

(A4):

there exist a positive constant A and a function \(g\in {\mathcal {C}}(J\times {\mathbb {R}})\) such that \(g>0\) on \((0, T]\times \left( {\mathbb {R}}\backslash \{x=0\}\right) \) and

$$\begin{aligned} g(0, x)= & {} g(t, 0)= 0,\quad t\in [0, T],\quad x\in {\mathbb {R}}, \end{aligned}$$

and

$$\begin{aligned} 2(1+t)\left( 1+|x|\right) \int _0^t \left| \int _0^x g(t_1, s) \textrm{d}s\right| \textrm{d}t_1\le A,\quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$

In the last section, we will give an example for a function g that satisfies (A4). Assume that the constants B and A which appear in the conditions (A1) and (A4), respectively, satisfy the following inequalities:

(A5):

\(AB_1<B,\) where \(B_1=2B+T\left( B^{2}+ B^{2+l}\right) +\sum _{j=1}^k B^{1+p_j},\) and

(A6):

\(AB_1<\frac{L}{5},\) where \(B_1=2B+T\left( B^{2}+ B^{2+l}\right) +\sum _{j=1}^k B^{1+p_j}\) and L is a positive constant that satisfies the following conditions:

$$\begin{aligned} r< L<R_1\le B,\quad R_1+\frac{A}{m} B_1>\left( \frac{1}{5m}+1\right) L, \end{aligned}$$

with r and \(R_1\) are positive constants and m is the constant which appear in (A6).

Our aim in this paper is to investigate the problem (1.1) for existence of classical solutions. Let \(J_0=J\backslash \{t_j\}_{j=1}^k\) and define the spaces \(PC(J),\;PC^1(J)\) and \(PC^1(J, {\mathcal {C}}^1({\mathbb {R}}^n))\) by

$$\begin{aligned} PC(J)= & {} \{ g: g\in {\mathcal {C}}(J_0),\quad \exists g(t_j^+),\; g(t_j^-)\; \text {and}\; g(t_j^-)=g(t_j),\; j\in \{1, \ldots , k\}\},\\ PC^1(J)= & {} \{g: g\in PC(J)\cap {\mathcal {C}}^1(J_0),\; \exists g^{\prime }(t_j^-),\; g^{\prime }(t_j^+)\;\text {and}\; g^{\prime }(t_j^-)=g^{\prime }(t_j),\; j\in \{1, \ldots , k\}\} \end{aligned}$$

and

$$\begin{aligned} PC^1(J, {\mathcal {C}}^1({\mathbb {R}}))=\{u: J\times {\mathbb {R}}\rightarrow {\mathbb {R}}:u(\cdot , x)\in PC^1(J),\; x\in {\mathbb {R}}\; \text {and}\; u(t, \cdot )\in {\mathcal {C}}^1({\mathbb {R}}),\; t\in J\}. \end{aligned}$$
(1.2)

Our main results are as follows.

Theorem 1.1

Under the hypotheses (A1), (A2), (A3), (A4) and (A5), problem (1.1) has at least one solution in \(PC^1(J, {\mathcal {C}}^1({\mathbb {R}})).\)

Theorem 1.2

Assume that the hypotheses (A1), (A2), (A3), (A4) and (A6) are satisfied. Then the problem (1.1) has at least two nonnegative solutions in \(PC^1(J, {\mathcal {C}}^1({\mathbb {R}})).\)

Our work is motivated by the interest of researchers for many mathematical questions related to impulsive partial differential equations. In fact, some important applied problems reduce to the study of such equations, see for example, [6, 13, 20, 23, 29, 36, 43]. Some applications of the impulsive PDEs in the quantum mechanics can be found in [36]. The asymptotical synchronization of coupled nonlinear impulsive partial differential systems in complex networks was considered in [43]. Applications are given to models in ecology in [20]. Applications to the population dynamics are given in [6, 13, 23]. A cell population model described by impulsive PDEs was studied in [29].

This paper is organized as follows. In the next section, we give some existence and multiplicity results about fixed points of the sum of two operators. Then in Sect. 3, we prove our main results. First, we give an integral representation and a priori estimates related to solutions of problem (1.1). Then, we use these estimates to prove Theorems 1.1 and 1.2 by using the results on the sum of operators recalled in Sect. 2. Finally, in Sect. 4, we illustrate our main results by an application to an impulsive Burgers equation.

2 Fixed points for the sum of two operators

The following theorem concerns the existence of fixed points for the sum of two operators. Its proof can be found in [18].

Theorem 2.1

Let E be a Banach space and

$$\begin{aligned} E_{1}=\{x\in E: \Vert x\Vert \le R\}, \end{aligned}$$

with \(R>0.\) Consider two operators T and S,  where

$$\begin{aligned} Tx=-\epsilon x,\;x\in E_{1}, \end{aligned}$$

with \(\epsilon >0\) and \(S: E_{1}\rightarrow E\) be continuous and such that

  1. (i)

    \((I-S)(E_{1})\) resides in a compact subset of E and

  2. (ii)

    \(\{x\in E: x=\lambda (I-S)x,\quad \Vert x\Vert =R\}=\emptyset ,\; \text{ for } \text{ any } \; \lambda \in \left( 0, \frac{1}{\epsilon }\right) .\)

Then there exists \(x^*\in E_{1}\) such that

$$\begin{aligned} Tx^*+Sx^*=x^*. \end{aligned}$$

In the sequel, E is a real Banach space.

Definition 2.2

A closed, convex set \({\mathcal {P}}\) in E is said to be cone if

  1. (i)

    \(\alpha x\in {\mathcal {P}}\) for any \(\alpha \ge 0\) and for any \(x\in {\mathcal {P}}\),

  2. (ii)

    \(x, -x\in {\mathcal {P}}\) implies \(x=0\).

Definition 2.3

A mapping \(K: E\rightarrow E\) is said to be completely continuous if it is continuous and maps bounded sets into relatively compact sets.

Definition 2.4

Let X and Y be real Banach spaces. A mapping \(K: X\rightarrow Y\) is said to be expansive if there exists a constant \(h>1\) such that

$$\begin{aligned} \Vert Kx-Ky\Vert _Y \ge h\Vert x-y\Vert _X \end{aligned}$$

for any \(x, y\in X\).

The following theorem concerns the existence of nonnegative fixed points for the sum of two operators. The details of its proof can be found in [12] and [31].

Theorem 2.5

Let \({\mathcal {P}}\) be a cone of a Banach space E; \(\Omega \) a subset of \({\mathcal {P}}\) and \(U_1, U_2 \text{ and } U_3\) three open bounded subsets of \({\mathcal {P}}\) such that \({\overline{U}}_1\subset {\overline{U}}_2\subset U_3\) and \(0\in U_1.\) Assume that \(T: \Omega \rightarrow {\mathcal {P}}\) is an expansive mapping, \(S: {\overline{U}}_3\rightarrow E\) is a completely continuous and \(S({\overline{U}}_3)\subset (I-T)(\Omega ).\) Suppose that \(({U}_2{\setminus }{\overline{U}}_1)\cap \Omega \ne \emptyset ,\, ({U}_3{\setminus } {\overline{U}}_2)\cap \Omega \ne \emptyset ,\) and there exists \(w_{0}\in {\mathcal {P}}\backslash \{0\}\) such that the following conditions hold:

  1. (i)

    \(Sx\ne (I-T)(x-\lambda w_{0}),\;\) for all \(\lambda >0\) and \(x\in \partial U_1\cap (\Omega +\lambda w_0),\)

  2. (ii)

    there exists \(\varepsilon > 0\) such that \(Sx\ne (I-T)(\lambda x), \;\) for all \(\,\lambda \ge 1+\varepsilon , \, x\in \partial U_2\) and \(\lambda x\in \Omega \),

  3. (iii)

    \(Sx\ne (I-T)(x-\lambda w_{0}),\;\) for all \(\lambda >0\) and \(x\in \partial U_3\cap (\Omega +\lambda w_0).\)

Then \(T+S\) has at least two non-zero fixed points \(x_1, x_2\in {\mathcal {P}}\) such that

$$\begin{aligned} x_1\in \partial U_2\cap \Omega \text{ and } x_2\in ({\overline{U}}_3{\setminus } {\overline{U}}_2)\cap \Omega \end{aligned}$$

or

$$\begin{aligned} x_1\in (U_2{\setminus }{U}_1)\cap \Omega \text{ and } x_2\in ({\overline{U}}_3{\setminus } {\overline{U}}_2)\cap \Omega . \end{aligned}$$

3 Proof of the main results

3.1 Integral representation and a priori estimates related to solutions of problem (1.1)

In the sequel, we will denote the space \(PC^1(J, {\mathcal {C}}^1({\mathbb {R}}))\) defined in (1.2) by X and it will be endowed by the following norm:

$$\begin{aligned} \Vert u\Vert= & {} \sup \Bigg \{ \sup _{(t, x)\in [t_j, t_{j+1}]\times {\mathbb {R}}}|u(t, x)|, \quad \sup _{(t, x)\in [t_j, t_{j+1}]\times {\mathbb {R}}}|u_{x}(t, x)|,\\ \\{} & {} \sup _{(t, x)\in [t_j, t_{j+1}]\times {\mathbb {R}}}|u_{t}(t, x)|,\quad j\in \{1, \ldots , k\},\quad i\in \{1, \ldots , n\}\Bigg \}, \end{aligned}$$

provided it exists.

Lemma 3.1

Under hypothesis (A2) (respectively, (A3)) and for \(u\in X\) with \(\Vert u\Vert \le B\), the following estimate holds:

$$\begin{aligned} |\psi ^{\prime }(u(t, x))|\le & {} B(1+B^l), \end{aligned}$$

respectively,

$$\begin{aligned} |I_j(x, u(t, x))|\le & {} B^{p_j+1},\quad j\in \{1, \ldots , k\},\\ \\ \left| \sum \limits _{j=1}^kI_j(x, u(t, x))\right|\le & {} \sum \limits _{j=1}^k B^{p_j+1},\quad (t, x)\in J\times {\mathbb {R}}). \end{aligned}$$

Proof

  1. (i)

    The estimation of \(|\psi ^{\prime }(u(t, x))|,\; (t, x)\in J\times {\mathbb {R}}:\)

    $$\begin{aligned} |\psi ^{\prime }(u(t, x))|\le & {} b_1(t, x)+b_2(t, x)|u(t, x)|^l\\\le & {} B+B^{l+1}\\= & {} B(1+B^l). \end{aligned}$$
  2. (ii)

    The estimation of \(|I_j(x, u(t, x))|,\; (t, x)\in J\times {\mathbb {R}},\;j\in \{1, \ldots , k\}:\)

    $$\begin{aligned} |I_j(x, u(t, x))|\le & {} a_j(x)|u(t, x)|^{p_j}\\\le & {} B^{p_j+1}. \end{aligned}$$
  3. (iii)

    The estimation of \(\left| \sum \nolimits _{j=1}^k I_j(x, u(t, x))\right| ,\; (t, x) \in J\times {\mathbb {R}}:\)

    $$\begin{aligned} \left| \sum \limits _{j=1}^k I_j(x, u(t, x))\right|\le & {} \sum \limits _{j=1}^k |I_j(x, u(t, x))|\\\le & {} \sum \limits _{j=1}^k B^{p_j+1}. \end{aligned}$$

This completes the proof. \(\square \)

For \(u\in X\), define the operator

$$\begin{aligned} S_1u(t, x)= & {} u(t, x) +\int _0^t \psi ^{\prime }(u(s, x))u_x(s, x)\textrm{d}s\\\ \\{} & {} -u_0(x) -\sum _{0<t_k<t} I_k(x, u(t_k, x)),\quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$

Lemma 3.2

Suppose (A1)–(A3). If \(u\in X\) satisfies the equation

$$\begin{aligned} S_1u(t, x)=0,\quad (t, x)\in J\times {\mathbb {R}}, \end{aligned}$$
(3.1)

then it is a solution to the IVP (1.1).

Proof

We have

$$\begin{aligned} 0= & {} S_1u(t, x)\\= & {} u(t, x) +\int _0^t \psi ^{\prime }(u(s, x)) u_x(s, x)\textrm{d}s\\{} & {} -u_0(x) -\sum _{0<t_k<t} I_k(x, u(t_k, x)),\quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$

Hence,

$$\begin{aligned} u(t, x)= & {} -\int _0^t\psi ^{\prime }(u(s, x)) u_x(s, x)\textrm{d}s \nonumber \\{} & {} \quad + u_0(x) +\sum \limits _{0<t_k<t} I_k(x, u(t_k, x)),\quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$
(3.2)

We differentiate (3.2) with respect to t and we find

$$\begin{aligned} u_t(t, x)=-\psi ^{\prime }(u(t, x)) u_x(t, x),\quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$

We put \(t=0\) in (3.2) and we get

$$\begin{aligned} u(0, x)=u_0(x),\quad x\in {\mathbb {R}}. \end{aligned}$$

Now, by (3.2), we obtain

$$\begin{aligned} u(t_j^+, x)= & {} -\int _0^{t_j} \psi ^{\prime }(u(s, x)) u_x(s, x)\textrm{d}s\\{} & {} \quad + u_0(x) +\sum _{0<t_k<t_j^+} I_k(x, u(t_k, x)),\quad x\in {\mathbb {R}}, \end{aligned}$$

\(j\in \{1, \ldots , k\}\), and

$$\begin{aligned} u(t_j^-, x)= & {} -\int _0^{t_j}\psi ^{\prime }(u(s, x)) u_x(s, x)\textrm{d}s\\{} & {} +u_0(x) +\sum _{0<t_k<t_j^-} I_k(x, u(t_k, x)),\quad x\in {\mathbb {R}}, \end{aligned}$$

\(j\in \{1, \ldots , k\}\), whereupon

$$\begin{aligned} u\left( t_j^+, x\right) -u\left( t_j^-, x\right) = I_j(x, u(t_j, x)),\quad x\in {\mathbb {R}},\quad j\in \{1, \ldots , k\}. \end{aligned}$$

This completes the proof. \(\square \)

Lemma 3.3

Suppose (A1)–(A3). If \(u\in X\), \(\Vert u\Vert \le B\), then

$$\begin{aligned} |S_1u(t, x)|\le & {} B_1,\quad (t, x)\in J\times {\mathbb {R}}, \end{aligned}$$

where \(B_1=2B+T\left( B^2+ B^{2+l}\right) +\sum _{j=1}^k B^{1+p_j}.\)

Proof

We apply Lemma 3.1 and we get

$$\begin{aligned} |S_1u(t, x)|= & {} \bigg | u(t, x) +\int _0^t \psi ^{\prime }(u(s, x)) u_x(s, x)\textrm{d}s\\{} & {} -u_0(x) -\sum _{0<t_k<t} I_k(x, u(t_k, x))\bigg |\\\le & {} |u(t, x)| +\int _0^t |\psi ^{\prime }(u(s, x))| |u_x(s, x)|\textrm{d}s\\{} & {} +|u_0(x)| +\sum _{0<t_k<t} |I_k(x, u(t_k, x))|\\\le & {} 2B+T\left( B^2+ B^{2+l}\right) +\sum _{j=1}^k B^{1+p_j}\\= & {} B_1,\quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$

This completes the proof. \(\square \)

For \(u\in X\), define the operator

$$\begin{aligned} S_2u(t, x)= \int _0^t \int _0^x(t-\tau ) (x-s) g(\tau , s) S_1u(\tau , s) \textrm{d}s \textrm{d}\tau ,\;(t, x)\in J\times {\mathbb {R}}, \end{aligned}$$
(3.3)

with g is the function which appears in the condition (A4).

Lemma 3.4

Suppose (A1)–(A4). If \(u\in X\) and \(\Vert u\Vert \le B\), then

$$\begin{aligned} \Vert S_2 u\Vert \le AB_1, \end{aligned}$$

where \(B_1=2B+T\left( B^2+ B^{2+l}\right) +\sum _{j=1}^k B^{1+p_j}.\)

Proof

We have

$$\begin{aligned} |S_2u(t, x)|= & {} \bigg |\int _0^t \int _0^x(t-t_1) (x-s) g(t_1, s) S_1u(t_1, s) \textrm{d}s \textrm{d}t_1\bigg |\\\le & {} \int _0^t \bigg |\int _0^x(t-t_1) |x-s| g(t_1, s) |S_1u(t_1, s)| \textrm{d}s\bigg | \textrm{d}t_1\\\le & {} B_1t 2 |x|\int _0^t \bigg |\int _0^x g(t_1, s) \textrm{d}s \bigg |\textrm{d}t_1\\\le & {} B_1 2 (1+t) (1+|x|)\int _0^t \bigg | \int _0^x g(t_1, s)\textrm{d}s\bigg | \textrm{d}t_1\\\le & {} AB_1,\quad (t, x)\in J\times {\mathbb {R}}, \end{aligned}$$

and

$$\begin{aligned} \bigg |\frac{\partial }{\partial t}S_2u(t, x)\bigg |= & {} \bigg |\int _0^t \int _0^x (x-s) g(t_1, s) S_1u(t_1, s) \textrm{d}s \textrm{d}t_1\bigg |\\\le & {} \int _0^t \bigg |\int _0^x |x-s| g(t_1, s) |S_1u(t_1, s)| \textrm{d}s\bigg | \textrm{d}t_1\\\le & {} B_1 2 |x|\int _0^t \bigg |\int _0^x g(t_1, s) \textrm{d}s \bigg |\textrm{d}t_1\\\le & {} B_1 2 (1+t) (1+|x|)\int _0^t \bigg | \int _0^x g(t_1, s)\textrm{d}s\bigg | \textrm{d}t_1\\\le & {} AB_1,\quad (t, x)\in J\times {\mathbb {R}}, \end{aligned}$$

and

$$\begin{aligned} \bigg |\frac{\partial }{\partial x}S_2u(t, x)\bigg |= & {} \bigg |\int _0^t \int _0^x(t-t_1) g(t_1, s) S_1u(t_1, s) \textrm{d}s \textrm{d}t_1\bigg |\\\le & {} \int _0^t \bigg |\int _0^x(t-t_1) g(t_1, s) |S_1u(t_1, s)| \textrm{d}s\bigg | \textrm{d}t_1\\\le & {} B_1t \int _0^t \bigg |\int _0^x g(t_1, s) \textrm{d}s \bigg |\textrm{d}t_1\\\le & {} B_1 (1+t)\int _0^t \bigg | \int _0^x g(t_1, s)\textrm{d}s\bigg | \textrm{d}t_1\\\le & {} AB_1,\quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$

Thus, \(\Vert S_2u\Vert \le B\). This completes the proof. \(\square \)

Lemma 3.5

Suppose (A1)–(A4). If \(u\in X\) satisfies the equation

$$\begin{aligned} S_2u(t, x)=0,\quad (t, x)\in J\times {\mathbb {R}}, \end{aligned}$$
(3.4)

then u is a solution to the IVP (1.1).

Proof

We differentiate two times with respect to t and two times with respect to x the Eq. (3.4) and we find

$$\begin{aligned} g(t, x) S_1u(t, x)=0,\quad (t, x)\in J\times {\mathbb {R}}, \end{aligned}$$

whereupon

$$\begin{aligned} S_1u(t, x)=0,\quad (t, x)\in (0, T]\times \left( {\mathbb {R}}\backslash \{x=0\}\right) . \end{aligned}$$

Since \(S_1u(\cdot , \cdot )\in {\mathcal {C}}(J\times {\mathbb {R}})\), we get

$$\begin{aligned} 0= & {} \lim \limits _{t\rightarrow 0} S_1u(t, x)\\= & {} S_1u(0, x)\\= & {} \lim \limits _{x\rightarrow 0}S_1u(t, x)\\= & {} S_1u(t, 0),\quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$

Thus,

$$\begin{aligned} S_1u(t, x)=0,\quad (t, x)\in [0, T]\times {\mathbb {R}}. \end{aligned}$$

Hence and Lemma 3.2, we conclude that u is a solution to the IVP (1.1). This completes the proof. \(\square \)

3.2 Proof of Theorem 1.1

Suppose that the constants B,  A and \(B_1\) are those which appear in the conditions (A1), (A4) and (A5), respectively. Choose \(\epsilon \in (0, 1),\) such that \(\epsilon B_1(1+A)<B.\) Let \(\widetilde{\widetilde{{\widetilde{Y}}}}\) denotes the set of all equi-continuous families in \(X=PC^1(J, {\mathcal {C}}^1({\mathbb {R}}))\) with respect to the norm \(\Vert \cdot \Vert \). Let also, \({\widetilde{{\widetilde{Y}}}}=\overline{\widetilde{\widetilde{{\widetilde{Y}}}}}\) be the closure of \({\widetilde{{\widetilde{{\widetilde{Y}}}}}}\), \({\widetilde{Y}}=\widetilde{{\widetilde{Y}}}\cup \{u_0\}\),

$$\begin{aligned} Y=\{u\in {\widetilde{Y}}: \Vert u\Vert \le B\}. \end{aligned}$$

By the Ascoli–Arzelà theorem, it follows that Y is a compact set in X. For \(u\in X\), define the operators

$$\begin{aligned} Tu(t, x)= & {} -\epsilon u(t, x),\\ Su(t, x)= & {} u(t, x)+\epsilon u(t, x)+ \epsilon S_2u(t, x), \quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$

where \(S_2\) is the operator defined by formula (3.3). For \(u\in Y\), using Lemma 3.4, we have

$$\begin{aligned} \Vert (I-S)u\Vert= & {} \Vert -\epsilon u-\epsilon S_2 u\Vert \\\le & {} \epsilon \Vert u\Vert +\epsilon \Vert S_2 u\Vert \\\le & {} \epsilon B_1+\epsilon AB_1\\= & {} \epsilon B_1(1+A)\\< & {} B. \end{aligned}$$

Thus, \(S: Y\rightarrow X\) is continuous and \((I-S)(Y)\) resides in a compact subset of X. Now, suppose that there is \(u\in E\) so that \(\Vert u\Vert =B\) and

$$\begin{aligned} u=\lambda (I-S)u \end{aligned}$$

or

$$\begin{aligned} \frac{1}{\lambda }u= (I-S)u=-\epsilon u -\epsilon S_2u, \end{aligned}$$

or

$$\begin{aligned} \left( \frac{1}{\lambda }+\epsilon \right) u=-\epsilon S_2u \end{aligned}$$

for some \(\lambda \in \left( 0, \frac{1}{\epsilon }\right) \). Hence, \(\Vert S_2u\Vert \le AB_1<B\),

$$\begin{aligned} \epsilon B<\left( \frac{1}{\lambda }+\epsilon \right) B=\left( \frac{1}{\lambda }+\epsilon \right) \Vert u\Vert =\epsilon \Vert S_2u\Vert <\epsilon B, \end{aligned}$$

which is a contradiction. Hence and Theorem 2.1, it follows that the operator \(T+S\) has a fixed point \(u^*\in Y\). Therefore

$$\begin{aligned} u^*(t, x)= & {} T u^*(t, x)+ Su^*(t, x)\\= & {} -\epsilon u^*(t, x)+u^*(t, x)+\epsilon u^*(t, x)+ \epsilon S_2 u^*(t, x),\quad (t, x)\in J\times {\mathbb {R}}, \end{aligned}$$

whereupon

$$\begin{aligned} 0=S_2 u^*(t, x),\quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$

From here and from Lemma 3.5, it follows that u is a solution to the problem (1.1). This completes the proof.

3.3 Proof of Theorem 1.2

Let \(X=PC^1(J, {\mathcal {C}}^1({\mathbb {R}}))\) and

$$\begin{aligned} {\widetilde{P}}=\{u\in X: u\ge 0\quad \text {on}\quad J\times {\mathbb {R}}\}. \end{aligned}$$

With \({\mathcal {P}}\) we will denote the set of all equi-continuous families in \({\widetilde{P}}\). For \(v\in X\), define the operators

$$\begin{aligned} T_1v(t, x)= & {} (1+m \epsilon ) v(t, x) -\epsilon \frac{L}{10},\\ S_3v(t, x)= & {} -\epsilon S_2v(t, x)-m\epsilon v(t, x) -\epsilon \frac{L}{10},\;(t, x)\in J\times {\mathbb {R}}, \end{aligned}$$

where \(\epsilon \) is a positive constant, \(m>0\) is the constant which appear in (A6) and the operator \(S_2\) is given by formula (3.3). Note that any fixed point \(v\in X\) of the operator \(T_1+S_3\) is a solution to the IVP (1.1). Now, let us define

$$\begin{aligned} U_1= & {} {\mathcal {P}}_{r}= \{v\in {\mathcal {P}}: \Vert v\Vert<r\},\\ U_2= & {} {\mathcal {P}}_{L}= \{v\in {\mathcal {P}}: \Vert v\Vert<L\},\\ U_3= & {} {\mathcal {P}}_{R_1}= \{v\in {\mathcal {P}}: \Vert v\Vert <R_1\},\\ \Omega= & {} \overline{{\mathcal {P}}_{R_2}}=\{v\in {\mathcal {P}}: \Vert v\Vert \le R_2\},\; \text {with}\;R_2= R_1+\frac{A}{m} B_1+\frac{L}{5m}, \end{aligned}$$

where \(r, L, R_1, A, B_1\) are the constants which appear in condition (A6).

  1. 1.

    For \(v_1, v_2\in \Omega \), we have

    $$\begin{aligned} \Vert T_1v_1-T_1v_2\Vert = (1+m\epsilon ) \Vert v_1-v_2\Vert , \end{aligned}$$

    whereupon \(T_1: \Omega \rightarrow X\) is an expansive operator with a constant \(h=1+m\epsilon >1\).

  2. 2.

    For \(v\in \overline{{\mathcal {P}}_{R_1}}\), we get

    $$\begin{aligned} \Vert S_3v\Vert\le & {} \epsilon \Vert S_2v\Vert +m\epsilon \Vert v\Vert +\epsilon \frac{L}{10}\\\le & {} \epsilon \bigg (AB_1+mR_1 +\frac{L}{10}\bigg ). \end{aligned}$$

    Therefore \(S_3(\overline{{\mathcal {P}}_{R_1}})\) is uniformly bounded. Since \(S_3: \overline{{\mathcal {P}}_{R_1}}\rightarrow X\) is continuous, we have that \(S_3(\overline{{\mathcal {P}}_{R_1}})\) is equi-continuous. Consequently \(S_3: \overline{{\mathcal {P}}_{R_1}}\rightarrow X\) is completely continuous.

  3. 3.

    Let \(v_1\in \overline{{\mathcal {P}}_{R_1}}\). Set

    $$\begin{aligned} v_2= v_1+ \frac{1}{m} S_2v_1+\frac{L}{5m}. \end{aligned}$$

    Note that \( S_2v_1+ \frac{L}{5}\ge 0\) on \(J\times {\mathbb {R}}\). We have \(v_2\ge 0\) on \(J\times {\mathbb {R}}\) and

    $$\begin{aligned} \Vert v_2\Vert\le & {} \Vert v_1\Vert +\frac{1}{m}\Vert S_2v_1\Vert +\frac{L}{5m}\\\le & {} R_1+ \frac{A}{m}B_1+\frac{L}{5m}\\= & {} R_2. \end{aligned}$$

    Therefore \(v_2\in \Omega \) and

    $$\begin{aligned} -\epsilon m v_2= -\epsilon m v_1 -\epsilon S_2v_1-\epsilon \frac{L}{10}-\epsilon \frac{L}{10} \end{aligned}$$

    or

    $$\begin{aligned} (I-T_1) v_2= & {} -\epsilon mv_2 +\epsilon \frac{L}{10}\\ \\= & {} S_3v_1. \end{aligned}$$

    Consequently \( S_3(\overline{{\mathcal {P}}_{R_1}})\subset (I-T_1)(\Omega )\).

  4. 4.

    Assume that for any \(v_0\in {\mathcal {P}}^*={\mathcal {P}}{\setminus }\{0\}\) there exist \(\lambda > 0\) and \(v\in \partial {\mathcal {P}}_{r}\cap (\Omega +\lambda v_0)\) or \(v\in \partial {\mathcal {P}}_{R_1}\cap (\Omega +\lambda v_0)\) such that

    $$\begin{aligned} S_3v=(I-T_1)(v-\lambda v_0). \end{aligned}$$

    Then

    $$\begin{aligned} -\epsilon S_2v-m\epsilon v-\epsilon \frac{L}{10}=-m\epsilon (v-\lambda v_0)+\epsilon \frac{L}{10} \end{aligned}$$

    or

    $$\begin{aligned} -S_2v= \lambda mv_0+\frac{L}{5}. \end{aligned}$$

    Hence,

    $$\begin{aligned} \Vert S_2v\Vert =\left\| \lambda m v_0+\frac{L}{5}\right\| >\frac{L}{5}. \end{aligned}$$

    This is a contradiction.

  5. 5.

    Let \(\varepsilon _1=\frac{2}{5m}.\) Assume that there exist \(w\in \partial {\mathcal {P}}_{L}\) and \(\lambda _1\ge 1+\varepsilon _1\) such that \(\lambda _1w\in \overline{{\mathcal {P}}_{R_2}}\) and

    $$\begin{aligned} S_3w= (I-T_1)(\lambda _1w). \end{aligned}$$

    Since \(w\in \partial {\mathcal {P}}_{L}\) and \(\lambda _1w\in \overline{{\mathcal {P}}_{R_2}}\), it follows that

    $$\begin{aligned} \left( \frac{2}{5m}+1\right) L<\lambda _1L=\lambda _1\Vert w\Vert \le R_1+\frac{A}{m} B_1+\frac{L}{5m}. \end{aligned}$$

    Moreover,

    $$\begin{aligned} -\epsilon S_2w-m\epsilon w-\epsilon \frac{L}{10}=-\lambda _1m\epsilon w+\epsilon \frac{L}{10}, \end{aligned}$$

    or

    $$\begin{aligned} S_2w+\frac{L}{5}=(\lambda _1-1)mw. \end{aligned}$$

    From here,

    $$\begin{aligned} 2\frac{L}{5}> \left\| S_2w+\frac{L}{5}\right\| =(\lambda _1-1)m \Vert w\Vert =(\lambda _1-1) m L \end{aligned}$$

    and

    $$\begin{aligned} \frac{2}{5m}+1> \lambda _1, \end{aligned}$$

    which is a contradiction.

Therefore all conditions of Theorem 2.5 hold. Hence, the problem (1.1) has at least two solutions \(u_1\) and \(u_2\) so that

$$\begin{aligned} \Vert u_1\Vert =L< \Vert u_2\Vert \le R_1 \end{aligned}$$

or

$$\begin{aligned} r\le \Vert u_1\Vert<L< \Vert u_2\Vert \le R_1. \end{aligned}$$

4 An Example

Below, we will illustrate our main results. Let \(k=2\),

$$\begin{aligned} T=B=1,\quad t_1=\frac{1}{4},\quad t_2=\frac{1}{2},\quad p_1=2,\quad p_2=3. \end{aligned}$$

and

$$\begin{aligned} R_1=10,\quad L=5,\quad r=4,\quad m=10^{50},\quad A=\frac{1}{10B_1},\quad \epsilon = \frac{1}{5B_1(1+A)}. \end{aligned}$$

Then

$$\begin{aligned} B_1= & {} 2+2+2=6 \end{aligned}$$

and

$$\begin{aligned} AB_1=\frac{1}{10}<B,\quad \epsilon B_1(1+A)<1, \end{aligned}$$

i.e., (A5) holds. Next,

$$\begin{aligned} r<L<R_1,\quad \epsilon>0,\quad R_1+\frac{A}{m} B_1>\left( \frac{1}{5m}+1\right) L,\quad AB_1<\frac{L}{5}. \end{aligned}$$

i.e., (A6) holds. Take

$$\begin{aligned} h(s)= \ln \frac{1+s^{11}\sqrt{2}+s^{22}}{1-s^{11}\sqrt{2}+s^{22}},\quad l(s)= \arctan \frac{s^{11}\sqrt{2}}{1-s^{22}},\quad s\in \mathbb {R},\quad s\ne \pm 1. \end{aligned}$$

Then

$$\begin{aligned} h^{\prime }(s)= & {} \frac{22\sqrt{2}s^{10}(1-s^{22})}{(1-s^{11}\sqrt{2}+s^{22})(1+s^{11}\sqrt{2}+s^{22})},\\ l^{\prime }(s)= & {} \frac{11 \sqrt{2}s^{10}(1+s^{22})}{1+s^{44}},\quad s\in \mathbb {R},\quad s\ne \pm 1. \end{aligned}$$

Therefore

$$\begin{aligned} -\infty< & {} \lim _{s\rightarrow \pm \infty }(1+s+s^2)^3h(s)<\infty ,\\ -\infty< & {} \lim _{s\rightarrow \pm \infty }(1+s+s^2)^3l(s)<\infty . \end{aligned}$$

Hence, there exists a positive constant \(C_1\) so that

$$\begin{aligned} \begin{array}{lll} (1+s+s^2)^3\left( \frac{1}{44\sqrt{2}}\ln \frac{1+s^{11}\sqrt{2}+s^{22}}{1-s^{11}\sqrt{2}+s^{22}}+\frac{1}{22\sqrt{2}}\arctan \frac{s^{11}\sqrt{2}}{1-s^{22}}\right)\le & {} C_1, \end{array} \end{aligned}$$

\(s\in {\mathbb {R}}\). Note that \(\lim \limits _{s\rightarrow \pm 1} l(s)=\frac{\pi }{2}\) and by [37, pp. 707, Integral 79], we have

$$\begin{aligned} \int \frac{\textrm{d}z}{1+z^4}= \frac{1}{4\sqrt{2}}\ln \frac{1+z\sqrt{2}+z^2}{1-z\sqrt{2}+z^2}+\frac{1}{2\sqrt{2}}\arctan \frac{z\sqrt{2}}{1-z^2}. \end{aligned}$$

Let

$$\begin{aligned} Q(s)= \frac{s^{10}}{(1+s^{44})(1+s+s^2)^2},\quad s\in {\mathbb {R}}, \end{aligned}$$

and

$$\begin{aligned} g_1(t, x)= Q(t) Q(x),\quad t\in J,\quad x\in {\mathbb {R}}. \end{aligned}$$

Then there exists a constant \(C>0\) such that

$$\begin{aligned} 2(1+t) \left( 1+|x|\right) \int _0^t \Bigg | \int _0^x g_1(\tau , z)\textrm{d}z\Bigg | \textrm{d}\tau \le C,\quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$

Let

$$\begin{aligned} g(t, x)= \frac{A}{C}g_1(t, x),\quad (t, x)\in J\times {\mathbb {R}}. \end{aligned}$$

Then

$$\begin{aligned} 2 (1+t)\left( 1+|x|\right) \int _0^t \Bigg | \int _0^x g(\tau , z)\textrm{d}z\Bigg | \textrm{d}\tau \le A,\quad (t, x)\in J\times {\mathbb {R}}, \end{aligned}$$

i.e., (A4) holds. Therefore for the problem

$$\begin{aligned} \begin{array}{lll} u_t+uu_{x}&{}=&{}0,\quad t\in [0, 1],\quad x\in {\mathbb {R}},\\ u(t_1^+, x)&{}=&{} u(t_1^-, x)+\frac{(u(t_1, x))^2}{1+x^{10}},\quad x\in {\mathbb {R}},\\ u(t_2^+, x)&{}=&{} u(t_2^-, x)+\frac{(u(t_2, x))^3}{1+x^{18}},\quad x\in {\mathbb {R}},\\ u(0, x)&{}=&{} \frac{1}{1+x^4},\quad x\in {\mathbb {R}}, \end{array} \end{aligned}$$

are fulfilled all conditions of Theorems 1.1 and 1.2.