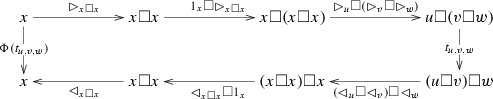Coherence and strictification for self-similarity

Abstract

This paper studies questions of coherence and strictification related to self-similarity—the identity $S\cong S\otimes S$ in a semi-monoidal category. Based on Saavedra’s theory of units, we first demonstrate that strict self-similarity cannot simultaneously occur with strict associativity—i.e. no monoid may have a strictly associative (semi-) monoidal tensor, although many monoids have a semi-monoidal tensor associative up to isomorphism. We then give a simple coherence result for the arrows exhibiting self-similarity and use this to describe a ‘strictification procedure’ that gives a semi-monoidal equivalence of categories relating strict and non-strict self-similarity, and hence monoid analogues of many categorical properties. Using this, we characterise a class of diagrams (built from the canonical isomorphisms for the relevant tensors, together with the isomorphisms exhibiting the self-similarity) that are guaranteed to commute, and give a simple intuitive interpretation of this characterisation.

1 Introduction

An object S in a semi-monoidal category $(\mathcal C,\otimes )$ is self-similar when it satisfies the identity $S\cong S\otimes S$. In a 1-categorical sense, self-similar objects are simply (pseudo-)idempotents and thus share many categorical properties with unit objects as characterised by Saavedra (see Sect. 2.1); they also provide particularly well-behaved examples of split idempotents (see Sect. 3.1). The most familiar non-unit example of a self-similar object is undoubtedly the natural numbers in the monoidal categories $(\mathbf{Set},\times )$ and $(\mathbf{Set},\uplus )$, as illustrated by Hilbert’s parable of the ’Grand Hotel’ (see [40] for a good exposition in a general context). Topologically, self-similarity is clearly seen in the Cantor set and other fractals [14, 32]; algebraically, it is very closely connected with Thompson’s groups (see Sect. 5), the polycyclic monoids [14, 15, 30], and finds applications to algebraic models of tilings [25].

In computer science, self-similarity plays a key role in categorical models of untyped systems such as the C-monoids of [29] (single-object Cartesian closed categories without unit objects modelling untyped lambda calculus—see [12] for a survey). It is particularly heavily used in Girard’s Geometry of Interaction program [10, 11] where, as well as being a key feature of the ‘dynamical algebra’ it is implicitly used together with compact closure to construct monoids isomorphic to their own endomorphism monoid [1, 14, 15]. More recently, it has found applications in linguistic and grammatical models [18] and categorical models of quantum mechanics [20]. Self-similarity also has a very close connection with Thompson’s group $\mathcal F$ (see Sect. 5), and thus is relevant to cryptography and cryptanalysis [21, 39], and homotopy idempotents [6].

This paper gives a strictification procedure for self-similarity and coherence results relating the isomorphisms exhibiting self-similarity with canonical isomorphisms for the relevant (semi-)monoidal structures. The motivation for this is the observation (Theorem 5), based on Saavedra’s theory of units (See Sect. 2.1), that strict self-similarity and strict associativity are mutually exclusive—either one or the other of these properties must be up to non-trivial isomorphism.

2 Categorical preliminaries

We refer to [33] for the theory of monoidal categories. We work with a slight generalisation that satisfies all the axioms for a monoidal category except for the existence of a unit object; following [28], we refer to these as semi-monoidal.

Definition 1

A semi-monoidal category is a category ${\mathcal C}$ with a functor $\_\otimes \_:{\mathcal C}\times {\mathcal C}\rightarrow {\mathcal C}$ that is associative up to an object-indexed family of natural isomorphisms $\tau _{X,Y,Z}:X\otimes (Y\otimes Z)\rightarrow (X\otimes Y)\otimes Z$ satisfying MacLane’s pentagon condition

$$\begin{aligned} ( \ \tau _{W,X,Y}\otimes 1_Z) \ \tau _{W,X\otimes Y,Z} \ (1_W \otimes \ \tau _{X,Y,Z}) \ = \ \ \tau _{W\otimes X,Y,Z} \ \tau _{W,X,Y\otimes Z} \end{aligned}$$

A functor between semi-monoidal categories that (strictly) preserves the tensor is a (strict) semi-monoidal functor. We assume the obvious definition of semi-monoidal equivalence of categories.

(The above definition differs from that of [28] in that we do not assume strict associativity—see Theorem 5 for the motivation for this). When we do consider unit objects, we will use Saavedra’s characterisation, rather than MacLane and Kelly’s original definition—see Sect. 2.1 below.

Remark 1

Any category $\mathcal C$ may be given a (degenerate) semi-monoidal tensor by fixing some object $X\in Ob({\mathcal C})$, and and defining $A\otimes B=X$, $f\otimes g=1_X$ for all objects $A,B\in Ob({\mathcal C})$ and arrows $f,g\in Arr({\mathcal C})$. Standing assumptions such as well-pointedness or monoidal well-pointedness are commonly used to exclude such pathologies (see, for example [2], for definitions and applications of monoidal well-pointedness). As we will consider semi-monoidal monoids where the unique object is frequently neither terminal, nor a unit object, we will instead use the related assumption of ‘faithful objects’ given below.

Definition 2

We say that an object A of a semi-monoidal category $(C,\otimes )$ is faithful when the functors $A\otimes \_, \_ \otimes A :{\mathcal C}\rightarrow {\mathcal C}$ are faithful.

Convention 1

Objects of semi-monoidal categories are faithful We make the standing assumption of faithful objects as a replacement for the notions of well -pointedness or monoidal well-pointedness, and instead indicate when an object of a semi-monoidal category is not faithful.

2.1 Saavedra’s theory of units

MacLane’s original presentation of the theory of coherence for monoidal categories gave a single coherence condition for associativity (the Pentagon condition) and four coherence conditions for the units isomorphisms. Three of these four axioms were shown to be redundant in [26], leaving a single coherence condition expressing the relationship between the units isomorphisms, and associativity. In [38] an alternative characterisation of units objects was given that required no additional coherence conditions—albeit at the expense of replacing the single coherence condition with a conditional statement about the category as a whole (see [28] for a comprehensive study of this, and [23] for extensions of this theory). We follow this approach because of the close connection with the theory of self-similarity. Definition 3 and Theorem 2 below are taken from [23, 28].

Definition 3

A (Saavedra) unit in a semi-monoidal category $({\mathcal C},\otimes , \tau )$ is a cancellable pseudo-idempotent, i.e. an object $U\in Ob({\mathcal C})$ equipped with an isomorphism $\alpha : U \otimes U \rightarrow U$, where the functors $(U\otimes \_ ), (\_ \otimes U) : {\mathcal C}\rightarrow {\mathcal C}$ are fully faithful.

We also refer to [28] for the following key results:

Theorem 2

• 1. Saavedra units are units in the sense of MacLane / Kelly, and thus a semi-monoidal category with a (Saavedra) unit is a monoidal category.

• 2. Saavedra units are idempotents; i.e. $\alpha \otimes I_U \ = \ 1_U \otimes \alpha$

• 3. The functors $U\otimes \_$ and $\_ \otimes U$ are equivalences of categories.

Remark 2

The (equivalent) definitions of a unit object due to MacLane/Kelly, and Saavedra/Kock are very different in approach; we do not present one as more fundamental than the other, but instead take a purely pragmatic viewpoint. Abstractly, the MacLane/Kelly definition offers finitary conditions that are close in character to the treatment of associativity; however, the Saavedra/Kock definition provides us with a neat way of characterising when a ‘collapse to the unit object’ occurs (e.g. Theorem 5).

3 Self-similar objects and structures

The theory of self-similarity is precisely the theory of pseudo-idempotents in (semi-)monoidal categories. The difference in terminology arises for historical reasons—in particular, differing conventions in computer science, mathematics, and pure category theory.

Definition 4

An object S in a semi-monoidal category $({\mathcal C},\otimes )$ is called self-similar when $S\cong S\otimes S$. Making the isomorphism exhibiting this self-similarity explicit, a self-similar structure is a tuple $(S,\lhd )$ consisting of an object $S\in Ob({\mathcal C})$, and an isomorphism $\lhd :S\otimes S \rightarrow S$ called the code isomorphism. We denote its inverse by $\lhd ^{-1}=\rhd : S\rightarrow S\otimes S$ and refer to this as the decode isomorphism.

A strictly self-similar object is an object S such that $(S,1_S)$ is a self-similar structure. The endomorphism monoid of a strictly self-similar object is thus itself a semi-monoidal category with a single object—i.e. it is a semi-monoidal monoid.

Examples 3

Examples of non-strict self-similarity are discussed in Sect. 1. Strict examples include Thompson’s group F (see [5] for the semi-monoidal tensor and associativity isomorphism of this group, and Sect. 5 for the explicit connection with strict self-similarity), and the group of bijections on the natural numbers, with the semi-monoidal tensor given by

$$\begin{aligned} (f\star g) (n) \ = \ \left\{ \begin{array}{l@{\quad }l} 2.f\left( \frac{n}{2}\right) &{} n \text{ even, } \\ 2.g\left( \frac{n-1}{2}\right) + 1 &{} n \text{ odd, } \end{array} \right. \end{aligned}$$

and canonical associativity and symmetry isomorphisms respectively given by

$$\begin{aligned} \tau (n) =\left\{ \begin{array}{l@{\quad }l} 2n &{}n\ (mod \ 2)=0, \\ n+1 &{}n\ (mod \ 4)=1, \\ \frac{n-3}{2} &{}n\ (mod \ 4)=3. \\ \end{array}\right. \ \ \ , \ \ \ \sigma (n) \ = \ \left\{ \begin{array}{ll} n+1 &{}\quad n \text{ even, } \\ n-1 &{}\quad n \text{ odd. } \end{array} \right. \end{aligned}$$

An elementary arithmetic proof that the above data specifies a semi-monoidal monoid is given in [17]. More generally, it arises from a special case of a large class of representations of Girard’s dynamical algebra (viewed as the closure of the two-generator polycyclic monoid [34] under the natural partial order of an inverse semigroup) as partial functions, given in [14, 30]. Readers familiar with the Geometry of Interaction program will recognise the $(\_ \star \_)$ operation as Girard’s model (up to Barr’s $l_2:\mathbf{pInj}\rightarrow \mathbf{Hilb}$ functor—see [3, 13]) of the (identified) multiplicative conjunction & disjunction of [10, 11].

3.1 Self-similarity as idempotent splitting

Self-similar structures are a special case of idempotent splittings. We refer to [9, 29, 36, 37] for the general theory and reprise some basic properties below:

Definition 5

An idempotent $e^2=e\in {\mathcal C}(A,A)$ splits when there exists some $B\in Ob({\mathcal C})$ together with arrows $f\in {\mathcal C}(A,B)$, $g\in {\mathcal C}(B,A)$ such that $e=gf$ and $fg=1_B$. We refer to the pair (f, g) as a splitting of the idempotent $e^2=e$.

Remark 3

We may characterise self-similar structures in terms of splittings of identities: a self-similar structure $(S,\lhd )$ uniquely determines, and is uniquely determined by, an isomorphism $\lhd$ such that $(\lhd ,\rhd )$ is a splitting of $1_S$ and $(\rhd ,\lhd )$ is a splitting of $1_{S\otimes S}$.

This characterisation allows us to use standard results on idempotent splittings, such as their uniqueness up to unique isomorphism:

Lemma 1

Given an idempotent $e^2=e\in {\mathcal C}(A,A)$ together with a pair of splittings $(f\in {\mathcal C}(A,B), g\in {\mathcal C}(B,A))$ and $(f'\in {\mathcal C}(A,B'),g'\in {\mathcal C}(B',A))$, then there exists a unique isomorphism $\phi :B\rightarrow B'$ such that the following diagram commutes:

Proof

This is a standard result of the theory of idempotent splittings. See, for example, [36]. $\square$

Corollary 4

Self-similar structures at a given self-similar object are unique up to unique isomorphism

Proof

The proof of this is somewhat simpler than the general case, as the splittings have both left and right inverses. Given a self-similar structure $(S,\lhd )$, and an isomorphism $U:S\rightarrow S$, then $(S,U\lhd )$ is also a self-similar structure. Conversely, let $(S,\lhd ')$ be a self-similar structure, and define $U=\lhd '\rhd$. Then $(S,U\lhd ) = (S,\lhd ')$ and $U=\lhd '\rhd$ is the unique isomorphism satisfying this condition. $\square$

Remark 4

Uniqueness of self-similar structures Corollary 4 provides an illustration of the distinction between ‘unique up to unique isomorphism’, and ‘actually unique’. If a self-similar structure at some object $S\in Ob({\mathcal C})$ is actually unique, then the only isomorphism from S to itself is the identity. Theorem 5 below then shows that S must be the unit object for the tensor given in Theorem 9.

4 Strict self-similarity and strict associativity

Unit objects are special cases of self-similar objects—the distinction being that for an arbitrary self-similar object S, the functors $S\otimes \_$ and $\_ \otimes S$ need not be fully faithful. We now describe how Saavedra’s characterisation relates strictness for both associativity and self-similarity.

Lemma 2

Let $({\mathcal M},\star )$ be semi-monoidal monoid. The endomorphisms $(\_ \star 1)$ and $(1 \star \_)$ are injective, and are isomorphisms precisely when the unique object of M is the unit.

Proof

Functoriality implies that $\_ \star 1$ and $1 \star \_$ are monoid homomorphisms, and injectivity follows from the assumption (Convention 1) of faithful objects. These homomorphisms are isomorphisms precisely when they are fully faithful, in which case the unique object of ${\mathcal M}$ satisfies Saavedra’s characterisation of a unit object. $\square$

Theorem 5

Let $({\mathcal M},\star , \tau )$ be a semi-monoidal monoid. Then $\_ \star \_$ is strictly associative if and only if the unique object of M is the unit for $\_\star \_$.

Proof

$(\Rightarrow )$ From Lemma 2 above, and strict associativity, $1 \star (\_ \star 1) ,(1 \star \_) \star 1 : {\mathcal M}\rightarrow {\mathcal M}$ are identical injective monoid homomorphisms. Let us denote this monoid embedding by $\eta : {\mathcal M}\hookrightarrow {\mathcal M}$. By injectivity, for every arrow $F\in \eta ({\mathcal M})$, there exists a unique arrow $f\in M$ satisfying $F=1\star f \star 1$.

Define a (strict) semi-monoidal tensor $(\_ \odot \_ ) : \eta ({\mathcal M}) \times \eta ({\mathcal M}) \rightarrow \eta ({\mathcal M})$ by $F \odot G = 1 \star (f\star g) \star 1$, for all $F=1\star f \star 1, G = 1 \star g \star 1$. It is immediate that this is well-defined, and a semi-monoidal tensor. By definition, $\eta (f\star g) = \eta (f) \odot \eta (g)$, so $({\mathcal M},\star ) \cong (\eta ({\mathcal M}),\odot )$.

Finally $(1\odot F) = 1 \star (1\star f) \star 1 = 1\star 1 \star f \star 1 = 1\star f \star 1 = F$, for arbitrary $F=1\star f \star 1$, and hence $1\odot \_ : \eta ({\mathcal M})\rightarrow \eta ({\mathcal M})$ is the identity isomorphism. Similarly, $\_ \odot 1= Id_{\eta ({\mathcal M})}$, and thus by Lemma 2, the unique object of $({\mathcal M},\star ) \cong (\eta ({\mathcal M}),\odot )$ is the unit object.

$(\Leftarrow )$ It is a standard result of monoidal categories that the endomorphism monoid of a unit object is an abelian monoid, and the tensor at this object coincides (up to isomorphism) with this strictly associative composition. $\square$

Remark 5

No simultaneous strictification This paper is about strictification and coherence for self-similarity and its interaction with associativity. From Theorem 5, strictifying the associativity of a semi-monoidal monoid will result in non-strict self-similarity; conversely, strictifying self-similarity in a strictly associative setting will give a monoid with a non-strict semi-monoidal tensor (Proposition 3).

Examples 6

Finite and infinite matrices An illustrative example is given by infinitary matrix categories. Countable matrices over a 0-monoid R enriched with a suitable (partial, infinitary) summation¹ $\mathcal R$ form a category $\mathbf Mat_\mathcal R$, with $Ob(Mat_\mathcal R)=\mathbb N \cup \{ \infty \}$. Hom-sets $\mathbf {Mat_\mathcal R} (a,b)$ are subsets² of the set of functions $\mathbf{Fun}([0,b)\times [0,a), \mathcal R)$, and composition is given by the Cauchy product.

Assuming technical conditions on summation are satisfied, the subcategory of finite matrices has a strictly associative monoidal tensor, denoted $\_ \oplus \_$. On objects it is simply addition; given arrows, $m\in Mat_R(a,b)$, $n\in Mat_R(p,q)$, with $a,b,p,q<\infty$, it is given by the familiar block diagonal formula,

$$\begin{aligned} \left( m\oplus n\right) (x,y) = \left\{ \begin{array}{lr} m(x,y) &{} x<a \ , \ y<b \\ n(x-a,y-b) &{} x\ge a \ , \ y\ge b \\ 0 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

Although this definition cannot be extended to infinite matrices, the endomorphism monoid $\mathbf{Mat_\mathcal R}(\infty , \infty )$ can be given a non-strict semi-monoidal tensor (again, assuming technicalities on summation), such as

$$\begin{aligned} (A\oplus _c B)(x,y) = \left\{ \begin{array}{ll} A\left( \frac{x}{2},\frac{y}{2}\right) &{}\quad x,y \ \text{ even, } \\ B\left( \frac{x-1}{2},\frac{y-1}{2}\right) &{}\quad x,y \ \text{ odd, } \\ 0 &{}\quad \text{ otherwise. } \end{array}\right. \end{aligned}$$

This is the familiar ‘interleaving’ of infinite matrices, determined by the Cantor pairing $c:\mathbb N \uplus \mathbb N\rightarrow \mathbb N$ given by $c(n,i)=2n+i$, and used to great effect in modelling the structural rules (as opposed to logical rules) of linear logic [10, 11]. Any such isomorphism $\lhd : \mathbb N \uplus \mathbb N \rightarrow \mathbb N$ will determine a (non-strict) semi-monoidal tensor on this monoid. However, by Theorem 5, no strict semi-monoidal tensor on $\mathbf{Mat}_{\mathcal {{\mathbf {R}}}} (\infty ,\infty )$ may exist.

5 The group of canonical isomorphisms

In a semi-monoidal monoid, the isomorphisms canonical for associativity are closed under composition, tensor, and inverses, and thus form a group with a semi-monoidal tensor. As demonstrated in [8], in the free case this group is the well-known Thompson group $\mathcal F$ (see [7] for a non-categorical survey). An algebraic connection between this group and associativity laws is well-established (see [4] for a more categorical perspective), and the tensor was given in [5]—although not in categorical terms. An explicit connection with semi-monoidal monoids was observed in [31] where $\mathcal F$ is given in terms of canonical isomorphisms and single-object analogues of projection / injection arrows for the tensor.

An interesting connection between Thomson’s group $\mathcal F$ and the theory of idempotent splittings is given in [6], in the context of (connected, pointed) CW complexes. The unsplittable homotopy idempotents of a CW complex K are characterised by the fact that they give rise to a copy of $\mathcal F$ in $\pi _1(K)$. The categorical interpretation of this is unfortunately beyond the scope of this paper.

6 A simple coherence result for self-similarity

We now give a simple result that guarantees commutativity for a class of diagrams built inductively from the code/decode isomorphisms of a self-similar structure, and the relevant semi-monoidal tensor. This is modelled very closely indeed on MacLane’s original presentation of his coherence theorem for associativity (briefly summarised in Sect. 6.1), in order to describe the interaction of self-similarity and associativity.

6.1 Coherence for associativity—the unitless setting

We first briefly reprise some basic definitions and results on coherence for associativity, taken from MacLane’s original presentation [33], in the semi-monoidal setting. This is partly to fix notation and terminology, and partly to ensure that the absence of a unit object does not lead to any substantial difference in theory. We also restrict ourselves to the monogenic case, as this suffices to describe the interaction of associativity and self-similarity.

More structural approaches to coherence may be found in [24, 27, 35]—these motivate the approach taken in Sect. 7 onwards.

Definition 6

The set Tree of free non-empty binary trees over some symbol x is is inductively defined by: $x\in Tree$, and for all $u,v\in Tree$ then $(u\Box v)\in Tree$. The rank of a tree $t\in Tree$ is the number of occurrences of the symbol x in t, or equivalently, the number of leaves of t.

We denote (the unitless version of) MacLane’s monogenic monoidal category by $({\mathcal W},\Box )$. This is defined by: $Ob({\mathcal W})=Tree$ and there exists a unique arrow $(t\leftarrow s)\in \mathcal {\mathcal W}(s,t)$ iff $rank(s)=rank(t)$. Composition is determined by uniqueness. Given $p,q\in Ob({\mathcal W})$, their semi-monoidal tensor is $p\Box q$; the tensor of arrows is again determined by uniqueness.

Remark 6

MacLane’s definition [33] included the empty tree as a unit object, giving a monoidal, rather than semi-monoidal, category. Applying the common technique of adjoining a strict unit to a semi-monoidal category will recover MacLane’s original definition, and MacLane’s original theory in the exposition below.

Definition 7

Given a semi-monoidal category $({\mathcal C},\otimes , \tau _{\_,\_,\_})$, and some $A\in Ob({\mathcal C})$, MacLane’s associativity substitution functor ${\mathcal W}Sub_{A} :({\mathcal W},\Box ) \rightarrow ({\mathcal C},\otimes )$ is defined inductively below. When the context is clear, we elide the subscript on ${\mathcal W}Sub_\_$.

• (Objects) For all $u,v\in Ob({\mathcal W})$,

  • ${\mathcal W}Sub(u\Box v) = {\mathcal W}Sub(u) \otimes {\mathcal W}Sub(v)$

  • ${\mathcal W}Sub(x) =A\in Ob({\mathcal C})$.

• (Arrows) Given $a,b,c,u,v\in Tree$, where $rank(u)=rank(v)$,

  • ${\mathcal W}Sub(a\leftarrow a) = 1_{{\mathcal W}Sub(a)} \in {\mathcal C}({\mathcal W}Sub(a),{\mathcal W}Sub(a))$.

  • ${\mathcal W}Sub((a\Box b)\Box c\leftarrow a\Box (b\Box c))= \ \tau _{{\mathcal W}Sub(a),{\mathcal W}Sub(b),{\mathcal W}Sub(c)}$

  • ${\mathcal W}Sub(a\Box v \leftarrow a\Box u)=1_{{\mathcal W}Sub(a)} \otimes {\mathcal W}Sub(v\leftarrow u)$

  • ${\mathcal W}Sub(b\Box u \leftarrow a\Box u)={\mathcal W}Sub(b\leftarrow a) \otimes 1_{{\mathcal W}Sub(u)}$

Remark 7

It is non-trivial that ${\mathcal W}Sub:({\mathcal W},\Box )\rightarrow ({\mathcal C}_A,\otimes )$ is a semi-monoidal functor. This is a consequence of MacLane’s Pentagon condition [33].

Remark 8

As ${\mathcal W}$ is posetal, all diagrams over ${\mathcal W}$ commute, so all (canonical) diagrams in ${\mathcal C}$ that are the image of a diagram in ${\mathcal W}$ are guaranteed to commute. Naturality and substitution are then used [33] to extend this to the general setting.

6.2 A preliminary coherence result for self-similarity

We now exhibit a class of diagrams based on identities, tensors, and the code / decode maps for a self-similar structure that are guaranteed to commute. This is based on a substitution functor from a posetal monoidal category that contains MacLane’s $({\mathcal W}, \Box )$ as a semi-monoidal subcategory.

Definition 8

The monogenic self-similar category $({\mathcal X},\Box )$ was defined in [14] as follows:

• Objects $Ob({\mathcal X})=Tree$

• Arrows There exists unique $(b \leftarrow a)\in {\mathcal X}(a,b)$ for all $a,b\in Ob({\mathcal X})$.

• Composition This is determined by uniqueness.

• Tensor Given $u,v\in Ob({\mathcal X})$, their tensor is the binary tree $u\Box v$. The definition on arrows again follows from uniqueness.

• Unit object All objects $e\in Ob({\mathcal X})$ are unit objects; by definition, the unique arrow $(e\leftarrow e\Box e)$ is an isomorphism, and the functors $(e\Box \_),(\_ \Box e):{\mathcal X}\rightarrow {\mathcal X}$ are fully faithful.

Remark 9

Abstractly, $({\mathcal X},\Box )$ may be characterised as the free monogenic indiscrete monoidal category. Thus, it is monoidally equivalent to the terminal monoidal category—in the semi-monoidal setting, it is more interesting.

Definition 9

Let $(S,\lhd )$ be a self-similar structure of a semi-monoidal category $({\mathcal C},\otimes )$. We define ${\mathcal X}Sub_{\lhd \rhd }: (X,\Box ) \rightarrow ({\mathcal C},\otimes )$, the self-similarity substitution functor, inductively by, for all $u,v,p,q\in Ob({\mathcal X})$:

• ${\mathcal X}Sub(x)=S$, and ${\mathcal X}Sub(u\Box v) = {\mathcal X}Sub(u) \otimes {\mathcal X}Sub(v)$.

• ${\mathcal X}Sub(x\leftarrow u\Box v) = \lhd ( {\mathcal X}Sub(x\leftarrow u) \otimes {\mathcal X}Sub(x \leftarrow v))$

• ${\mathcal X}Sub(u\Box v\leftarrow x) = \rhd ({\mathcal X}Sub(u \leftarrow x) \otimes {\mathcal X}Sub(v \leftarrow x))$

• ${\mathcal X}Sub(u\Box v \leftarrow p\Box q) = {\mathcal X}Sub(u\Box v \leftarrow x) {\mathcal X}Sub(x \leftarrow p \Box q)$

(We again omit the subscript when the context is clear).

Remark 10

In stark contrast to MacLane’s substitution functor, it is immediate that ${\mathcal X}Sub : (X,\Box ) \rightarrow ({\mathcal C},\otimes )$ is a strict semi-monoidal functor—no coherence conditions are needed to ensure functoriality.

We may now give a preliminary coherence result on self-similarity.

Lemma 3

Let $(S,\lhd )$ be a self-similar structure of a semi-monoidal category $({\mathcal C},\otimes )$, and let ${\mathcal X}Sub: (X,\Box )\rightarrow ({\mathcal C},\otimes )$ be as above. Then every diagram over $\mathcal C$ of the form ${\mathcal X}Sub (\mathfrak D)$, for some diagram $\mathfrak D$ over ${\mathcal X}$, is guaranteed to commute.

Proof

As $({\mathcal X},\Box )$ is posetal, $\mathfrak D$ commutes; by functoriality so does ${\mathcal X}Sub(\mathfrak D)$. $\square$

Remark 11

The diagrams predicted to commute by Lemma 3 are ‘canonical for self-similarity’, with arrows built from code / decode isomorphisms, identities, and the tensor. The more important question is about diagrams that are ‘canonical for self-similarity and associativity’—when may these be guaranteed to commute? This follows as a special case of a more general result (Sect. 8).

Remark 12

Does ${\mathcal W}Sub$ factor through ${\mathcal X}Sub$? There is an immediate semi-monoidal embedding $\iota : ({\mathcal W},\Box ) \rightarrow ({\mathcal X},\Box )$. An obvious question is whether, or under what circumstances, the above substitution functors will factor through this embedding—i.e. when does the diagram of Fig. 1 commute?

It is immediate that this can only commute under very special conditions. Functoriality of ${\mathcal W}Sub$ requires coherence conditions (i.e. MacLane’s pentagon), whereas none are required for the functoriality of ${\mathcal X}Sub$. Further, commutativity of this diagram would give a decomposition of canonical (for associativity) isomorphisms of $({\mathcal C},\otimes )$ into ‘more primitive’ operations built from $\{ \lhd , \rhd , \otimes \}$; in particular, $\tau _{S,S,S} = (\rhd \otimes 1_S)(1_S \otimes \lhd )$. A slight generalisation of Isbell’s argument on the skeletal category of sets [33] would show that when $({\mathcal C},\otimes )$ admits projections, S is the terminal object. Instead of giving a direct proof of this, we will give a more general result in Corollary 13.

Fig. 1

Under what circumstances does the following diagram commute?

7 Strictification for self-similarity

We first describe a strictification procedure for self-similarity that gives a semi-monoidal equivalence between a monoid and a monogenic category, then use this to give a coherence theorem that answers the question posed in Remark 11 in a more general setting. This strictification procedure generalises the ‘untyping’ construction of [14, 15] (and indeed corrects it in certain cases—see Remark 15).

Definition 10

Given a semi-monoidal category $(C,\otimes ,\tau _{\_,\_,\_})$ and arbitrary $S\in Ob({\mathcal C})$, the semi-monoidal category freely generated by S , denoted $\mathcal F_{S}$, is defined analogously to the usual monoidal definition. The assignment $Inst:Tree\rightarrow Ob({\mathcal C})$ is defined inductively by $Inst(x)=S\in Ob({\mathcal C})$, and $Inst(p\Box q) = Inst(p) \otimes Inst(q)$ and based on this, objects and arrows are given by $Ob({\mathcal F}_S)=Tree$, and ${\mathcal F}_S(u,v)= {\mathcal C}(Inst(u),Inst(v))$.

Composition is inherited in the natural way from ${\mathcal C}$, as is the tensor: on objects this is simply the formal pairing $\_ \Box \_$, and given arrows $f\in {\mathcal F}_S(u,v)$, $g\in {\mathcal F}_S(x,y)$ we have

$$\begin{aligned} f\Box g = f\otimes g\in {\mathcal F}_S(u\Box x, v\Box y) = {\mathcal C}(Inst(u)\otimes Inst(x) ,Inst(v)\otimes Inst(y)) . \end{aligned}$$

The assignment $Inst:Tree\rightarrow Ob({\mathcal C})$ extends in a natural way to a strict semi-monoidal functor; using computer science terminology, we call this the instantiation functor $Inst_S: ({\mathcal F}_S,\Box )\rightarrow ({\mathcal C},\otimes )$. It is as above on objects, and the identity on hom-sets, as ${\mathcal F}_S(u,v) = {\mathcal C}(Inst(u),Inst(v))$. It is immediate that this epic strict semi-monoidal functor is a semi-monoidal equivalence of categories. When the object is clear from the context, we simply write $Inst: ({\mathcal F}_S,\Box )\rightarrow ({\mathcal C},\otimes )$

The image of $Inst_S$ is the full semi-monoidal subcategory of ${\mathcal C}$ inductively generated by the object S, together with the tensor $\_ \otimes \_$. We refer to this as the semi-monoidal category generated by S within $({\mathcal C},\otimes )$, denoted $({\mathcal C}_S,\otimes )$.

Based on the above definitions, the following are immediate:

Lemma 4

Let $(S,\lhd )$ be a self-similar structure of a semi-monoidal category $({\mathcal C},\otimes )$. Then the small semi-monoidal categories $({\mathcal W},\Box )$, $({\mathcal X},\Box )$ and $({\mathcal F}_S,\Box )$ have the same set of objects, and

• 1. The tuple $(x,\lhd )$ is a self-similar structure of $({\mathcal F}_S,\Box )$.

• 2. The functors ${\mathcal X}Sub:(X,\Box )\rightarrow ({\mathcal F}_S,\Box )$ and ${\mathcal W}Sub(W,\Box ) \rightarrow (F_S,\Box )$ are monic.

• 3. The following diagram commutes:

  

Remark 13

The commutativity of the left hand triangle in the above diagram is well-established, and part of a standard approach to coherence for associativity and other properties. In particular, Joyal and Street phrased MacLane’s theorem as an equivalence between the free monoidal category on a category and the free strict monoidal category on a category (see [24] for details and extensions of this approach).

7.1 Functors from categories to monoids

The monic functor ${\mathcal X}Sub:(X,\Box )\rightarrow ({\mathcal F}_S,\Box )$ specifies a distinguished wide semi-monoidal subcategory of $({\mathcal F}_S,\Box )$; we use the following notation and terminology for its arrows:

Definition 11

Given a self-similar structure $(S,\lhd )$ of a semi-monoidal category, we define an object-indexed family of arrows, the generalised code isomorphisms, by $\{ \lhd _u = {\mathcal X}Sub(x\leftarrow u) \in {\mathcal F}_S(u,x)\}_{u\in Ob({\mathcal F}_S)}$. We refer to their inverses, $\{ \rhd _u= {\mathcal X}Sub(u\leftarrow x) \in {\mathcal F}_S(x,u) \}_{u\in Ob ({\mathcal F}_S)}$ as the generalised decode isomorphisms.

Remark 14

As observed in Remark 16 below, the above object-indexed families of arrows are the components of a natural transformation. An alternative perspective is that $(\lhd _u,\rhd _u)$ is a splitting of $1_u$, and $(\rhd _u,\lhd _u)$ is a splitting of $1_x$. The unique isomorphism ${\mathcal X}Sub(v\leftarrow u)=\rhd _v\lhd _u\in {\mathcal F}_S(u,v)$ is then the isomorphism exhibiting the uniqueness up to isomorphism of idempotent splittings described in Corollary 4.

Remark 15

As $({\mathcal F}_S,\Box )$ is freely generated, we may give an inductive characterisation of the generalised code arrows by:

• $\lhd _x=1_S\in {\mathcal C}(S,S)={\mathcal F}_S(x,x)$.

• $\lhd _{x\Box x} = \lhd \in {\mathcal C}(S\otimes S,S)= {\mathcal F}_S(x\Box x,x)$

• $\lhd _{u\Box v} = \lhd _{x\Box x}(\lhd _u\Box \lhd _v)\in {\mathcal F}_S(x,u\Box v)$.

and similarly for the generalised decode arrows. This is used as a definition in [15], where it is (incorrectly) assumed that $(C_S,\otimes ) \cong ({\mathcal F}_S,\Box )$ in every case—an assumption holds for the particular examples considered there, but not more generally.

These generalised code/decode arrows allow us to define a fully faithful functor from ${\mathcal F}_S$ to the endomorphism monoid ${\mathcal F}_S(x,x)$, considered as a single-object category.

Definition 12

Let $(S,\lhd )$ be a self-similar object of a semi-monoidal category $({\mathcal C},\otimes )$. We denote the endomorphism monoid ${\mathcal F}_S(x,x)$, considered as a single-object category, by End(x), and define the generalised convolution functor $\Phi _{\lhd } : {\mathcal F}_S\rightarrow End(x)$ by

• Objects $\Phi _{\lhd } (A)=x$, for all $A\in Ob({\mathcal F}_S)$.

• Arrows Given $f\in {\mathcal F}_S(A,B)$, then $\Phi _{\lhd } (f)= \lhd _Bf\rhd _A$, where $\lhd _\_$ and $\rhd _\_$ are as in definition 11.

When the self-similar structure in question is apparent from the context, we will omit the subscript and write $\Phi : {\mathcal F}_S\rightarrow End(x)$.

Proposition 1

The generalised convolution functor given above is indeed a fully faithful functor.

Proof

For all $a\in Ob({\mathcal F}_S)$, $\Phi (1_a) = 1_x$. Given $f\in {\mathcal F}_S(a,b)$, $g\in {\mathcal F}_S(b,c)$, then $\Phi (gf)= \lhd _c gf \rhd _a = \lhd _c g \rhd _b\lhd _b f \rhd _a = \Phi (g) \Phi (f)$, and thus $\Phi$ is a functor. For all $h\in {\mathcal F}_S(x,x)$, $\Phi (h)=h\in End(x)= {\mathcal F}_S(x,x)$, and thus $\Phi$ is full. Finally, given $f,f'\in {\mathcal F}_S(a,b)$, then

$$\begin{aligned} \Phi (f)= & {} \Phi (f') \ \Leftrightarrow \ \lhd _bf\rhd _a=\rhd _b f'\lhd _a \ \Leftrightarrow \ \rhd _b\lhd _b f \rhd _a\lhd _a\\= & {} \rhd _b\lhd _b f' \rhd _a\lhd _a \ \Leftrightarrow \ f=f' \end{aligned}$$

and thus $\Phi :{\mathcal F}_S \rightarrow End(x)$ is faithful. $\square$

A simple corollary is that the category freely generated by a self-similar object, and the endomorphism monoid of that object (considered a a single-object category) are equivalent:

Corollary 7

Let $(S,\lhd )$ be a self-similar object of a semi-monoidal category $({\mathcal C},\otimes )$. Then the categories ${\mathcal F}_S$ and End(x) are equivalent.

Proof

Since $\Phi$ is fully faithful, it simply remains to prove that it is isomorphism-dense. For arbitrary $u\in Ob({\mathcal F}_S)$, the generalised code/decode arrows $\lhd _u\in {\mathcal F}_S(u,x)$ and $\rhd _u=\lhd _u^{-1}\in {\mathcal F}_S(x,u)$ exhibit the required isomorphism $End(x)\cong {\mathcal F}_S(x,x) \cong {\mathcal F}_S(u,u)$. $\square$

In Definition 13 below, we give a semi-monoidal tensor on End(x) that makes the above equivalence a semi-monoidal equivalence of categories.

Remark 16

Corollary 7 guarantees the existence of suitable functors exhibiting this equivalence of categories; more explicitly, let us denote the obvious inclusion by $\iota :End(x)\hookrightarrow {\mathcal F}_S$. Then $\Phi \iota =Id_{End(x)}$, and there is a natural transformation from $\iota \Phi$ to $Id_{{\mathcal F}_S}$ whose components are the generalised decode isomorphisms of Definition 11:

It is also almost immediate that a diagram over ${\mathcal F}_S$ commutes iff its image under $\Phi$ commutes; due to the issues mentioned in Remark 15, we prove this explicitly in order to illustrate how this relies on uniqueness of generalised code / decode arrows:

Corollary 8

Let $(S,\lhd )$ be a self-similar object of a semi-monoidal category $({\mathcal C},\otimes )$. Then a diagram $\mathfrak D$ over ${\mathcal F}_S$ commutes iff $\Phi (\mathfrak D)$ commutes.

Proof

$(\Rightarrow )$ This is a simple, well-known consequence of functoriality.

$(\Leftarrow )$ Let $\mathfrak D$ be an arbitrary diagram over $({\mathcal F}_S,\Box )$. Up to the obvious inclusion $\iota :End(x)\hookrightarrow {\mathcal F}_S$, $\mathfrak D$ and $\Phi (\mathfrak D)$ are diagrams in the same category; we treat their disjoint union $\mathfrak D \uplus \Phi _(\mathfrak D)$ as a single diagram. We then add edges to $\mathfrak D \uplus \Phi (\mathfrak D)$ by linking each node n with its image using the unique generalised code/decode arrows. This is illustrated in Fig. 2.

Each additional polygon added to $\mathfrak D \uplus \Phi (\mathfrak D)$ commutes by definition of $\Phi$. Thus the entire diagram commutes iff $\mathfrak D$ commutes iff $\Phi (\mathfrak D)$ commutes. $\square$

Fig. 2

$\mathfrak D$ and $\Phi (\mathfrak D)$ as a single diagram

7.2 Semi-monoidal tensors on monoids

We now exhibit a semi-monoidal tensor on the endomorphism monoid of a self-similar object such that the equivalence of Corollary 7 becomes a semi-monoidal equivalence.

Lemma 5

Let $(S,\lhd )$ be a self-similar structure of a semi-monoidal category and let $({\mathcal F}_S,\Box ,t_{\_,\_,\_})$ be the semi-monoidal category freely generated by S. Then, up to the inclusion $End(x)\hookrightarrow {\mathcal F}_S$,

• 1. $\Phi (f\Box g) = \Phi \left( \Phi (f) \Box \Phi (g) \right)$.

• 2. $\Phi (t_{u,v,w})=\Phi (t_{x,x,x})$, for all $u,v,w\in Ob({\mathcal F}_S)$.

Proof

• 1. Given $f\in {\mathcal F}_S(a,b)$ and $g\in {\mathcal F}_S(u,v)$, then $\Phi (f\Box g) = \lhd _{b\Box v}(f\Box g)\rhd _{a\Box u} =$

  $$\begin{aligned}&\lhd _{x\Box x}(\lhd _b\Box \lhd _v)((f\Box g) (\rhd _a\Box \rhd _u)\rhd _{x\Box x} = \lhd _{x\Box x} ( \lhd _bf\rhd _a \Box \lhd _v g \rhd _u ) \rhd _{x\Box x}\\&\quad = \lhd _{x\Box x} \left( \Phi (f) \Box \Phi (g) \right) \rhd _{x\Box x} = \Phi \left( \Phi (f) \Box \Phi (g) \right) \end{aligned}$$

• 2. By definition, $\Phi (t_{u,v,w})= \lhd _{(u\Box v)\Box v} t_{u,v,w} \rhd _{u\Box (v\Box w)}$, and by Remark 15, the following diagram commutes:

  

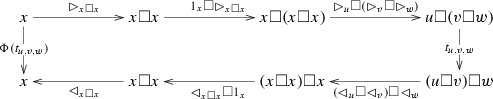
  By naturality of associativity isomorphisms, $\Phi (t_{u,v,w})=$

  $$\begin{aligned} \begin{array}{l} \ \ \ \lhd _{x\Box x}(\lhd _{x\Box x}\Box 1_x) ((\lhd _u \Box \lhd _v) \Box \lhd _w) ((\rhd _u \Box \rhd _v) \Box \rhd _w) t_{x,x,x} (1_x \Box \rhd _{x\Box x}) \rhd _{x\Box x} \\ \qquad = \lhd _{x \Box x}(\lhd _{x\Box x} \Box 1_x) t_{x,x,x} (1_x \Box \rhd _{x\Box x} ) \rhd _{x\Box x} \\ \qquad = \Phi (t_{x,x,x}) \\ \end{array} \end{aligned}$$

  as required.$\square$

Based on the above lemma, we give a semi-monoidal tensor on the endomorphism monoid of a self-similar object.

Definition 13

Let $(S,\lhd )$ be a self-similar object of a semi-monoidal category. We define the semi-monoidal tensor induced by $(S,\lhd )$ to be the monoid homomorphism $\_ \star _\lhd \_ : End(x)\times End(x)\rightarrow End(x)$ given by

$$\begin{aligned} f \star _\lhd g \ \mathop {=}\limits ^{def.} \ \Phi (f\Box g) \ =\ \lhd _{x\Box x} (f\Box g)\rhd _{x\Box x} \end{aligned}$$

When the self-similar structure is clear from the context, we elide the subscript, and write $\_ \star \_ : End(x)\times End(x)\rightarrow End(x)$

Theorem 9

The operation $\_ \star \_$ defined above is a semi-monoidal tensor, and thus $(End(x), \_ \star \_)$ is a semi-monoidal monoid.

Proof

Functoriality of $\Phi$ gives $1\star 1 =\Phi (1_{x}\Box 1_{x})=\Phi (1_{x\Box x})=1$, and

$$\begin{aligned} (f\star g)(h\star k) = \Phi (f\Box g)\Phi (h\Box k)=\Phi ((f\Box g)(h\Box k))=\Phi (fh\Box gk)=fh\star gk \end{aligned}$$

Let us define $\alpha =\Phi (t_{x,x,x})$. From Part 2. of Lemma 5, $\Phi (t_{u,v,w})=\alpha$, for arbitrary $u,v,w\in Ob({\mathcal F}_S)$. From Part 1. of Lemma 5, and Corollary 8,

$$\begin{aligned} \alpha (f\star (g\star h)) = ((f\star g)\star h)\alpha \quad \ \ \forall f,g,h\in End(x) \end{aligned}$$

and $\alpha ^2 = (\alpha \star 1)\alpha (1\star \alpha )$. Thus both naturality and MacLane’s pentagon condition are also satisfied. $\square$

Corollary 10

The functor $\Phi :{\mathcal F}_S\rightarrow End(x)$ satisfies $\Phi (f\Box g )= \Phi (f) \star \Phi (g)$, and thus is a strict semi-monoidal functor $\Phi :({\mathcal F}_S,\Box )\rightarrow ({\mathcal C}_S,\otimes )$.

Proof

This follows from Theorems 5 and 9. $\square$

At a given self-similar object $S\in Ob ({\mathcal C})$, the semi-monoidal tensor is determined by the choice of isomorphism $\lhd \in {\mathcal C}(S\otimes S,S)$; however, these are related by conjugation in the obvious way, and thus $\_ \star \_$ is unique up to unique isomorphism.

Proposition 2

Let (S, c) and $(S,\lhd )$ be self-similar structures at a given self-similar object. Then $f \star _{\lhd } g = \lhd c^{-1} (f\star _c g) c \rhd$ for all $f,g\in End(x)$.

Proof

This follows by direct calculation on Definition 13; alternatively, and more structurally, it follows from the uniqueness up to unique isomorphism of idempotent splittings, and hence self-similar structures (Corollary 4). $\square$

Remark 17

The above Proposition does not imply that all semi-monoidal tensors on a given monoid are related by conjugation. As a counterexample, the monoid of functions on $\mathbb N$ has distinct semi-monoidal tensors, arising from the fact that it is a self-similar object in both $(Fun, \times )$ and $(Fun,\uplus )$, that are clearly not related in this way (the relationship between the two is highly non-trivial and a key part of Girard’s Geometry of Interaction program [10, 11], the details of which are beyond the scope of this paper—see [19] for details).

From Theorem 5, $(End(x), \_ \star \_)$ can only be strictly associative when x is the unit object for $\_ \star \_$. When $(S,\lhd )$ is a self-similar structure of a strictly associative semi-monoidal category (e.g. the rings isomorphic to their matrix rings characterised in [22]), the associativity isomorphism for $\_ \star \_$ has the following neat form:

Proposition 3

Let $(S,\lhd )$ be a self-similar object of a strictly associative semi-monoidal category $(C,\otimes )$. Then the associativity isomorphism for $(End(x),\star )$ is given by $\alpha =\lhd (\lhd \otimes 1_S)(1_S\otimes \rhd )\rhd \in End(x)\cong {\mathcal C}(S,S)$.

Proof

This follows by direct calculation on Part 2. of Lemma 5. $\square$

7.3 The strictly self-similar form of a monogenic category

The following is now immediate:

Theorem 11

Let $(S,\lhd )$ be a self-similar structure of a semi-monoidal category $({\mathcal C},\otimes )$. Then $({\mathcal C}_S,\otimes )$, $({\mathcal F}_S,\Box )$ and $(End(x),\star )$ are semi-monoidally equivalent.

Proof

The semi-monoidal equivalence between $({\mathcal F}_S,\Box )$ and $({\mathcal C}_S,\otimes )$ is given by the semi-monoidal functor of Definition 10. From Corollary 10, the equivalence of categories between ${\mathcal F}_S$ and End(x) gives a semi-monoidal equivalence between $({\mathcal F}_S,\Box )$ and $(End(x),\star )$. $\square$

Corollary 12

Every monogenic semi-monoidal category with a self-similar generating object is semi-monoidally equivalent to a semi-monoidal monoid. This justifies the description of $(End(x),\star )$ as the self-similarity strictification of $({\mathcal C}_S,\otimes )$.

Remark 18

A general principle is that ‘categorical structures’ are preserved by equivalences of categories. For example, if ${\mathcal C}_S$ is closed, then so is End(x); this is used implicitly in [29] to construct single-object analogues of Cartesian closed categories, and in [14, 15] to construct single-object analogues of compact closure. Similarly, when $(C_S,\otimes )$ admits projections / injections, $(End(x),\star )$ contains a copy of Girard’s dynamical algebra [14, 15, 30] and under relatively light additional assumptions, admits a matrix calculus [20]. In general, we may find single-object (i.e. monoid) analogues of a range of categorical properties. This is particularly relevant to the ‘objects as types’ paradigm of some branches of theoretical computer science, where ‘untyped’ systems are more properly thought of as ‘single-type’ systems.

We may now answer the question posed in Remark 12.

Corollary 13

The diagram of Fig. 1 commutes precisely when the self-similar object in question is the unit object.

Proof

In the self-similarity strictification of $({\mathcal C}_S,\otimes )$, the self-similarity is exhibited by identity arrows. Commutativity of the diagram of Fig. 1 implies that $(End(x),\star )$ has a strictly associative semi-monoidal tensor, so by Theorem 5, the unique object of End(x) is the unit object for $\_ \star \_$. The equivalences of Theorem 11 then imply that S is the unit object for $({\mathcal C}_S,\otimes )$. $\square$

Self-similarity strictification also illustrates a close connection between the generalised convolution and instantiation functors; informally, generalised convolution is simply instantiation in an isomorphic category:

Proposition 4

Let $(S,\lhd )$ be a self-similar object of a semi-monoidal category $({\mathcal C},\otimes )$, and denote by $({\mathcal F}_S,\Box )$ and $({\mathcal F}_x,\Diamond )$ the semi-monoidal categories freely generated by S, and the unique object of $(End(x),\star )$, respectively. Then there exists a semi-monoidal isomorphism $K: (F_S,\Box )\rightarrow ({\mathcal F}_x,\Diamond )$ such that the following diagram of semi-monoidal categories commutes:

Proof

We define the semi-monoidal functor $K:({\mathcal F}_S,\Box )\rightarrow ({\mathcal F}_x,\Diamond )$ as follows:

• The small categories $({\mathcal F}_x,\Diamond )$ and $({\mathcal F}_S,\Box )$ have the same underlying set of objects; we take K to be the identity on objects.

• Given $f\in {\mathcal F}_S(u,v)$ we define $K(f)=\lhd _v f \rhd _u \in {\mathcal F}_S(x,x)={\mathcal F}_x(u,v)$.

The inverse is immediate, as is the (strict) preservation of the semi-monoidal tensor. The commutativity of the above diagram follows by expanding out the definitions of $\Phi$ and Inst. $\square$

8 General coherence for self-similarity

We now consider coherence in the general case. Let us fix a a self-similar structure $(S,\lhd )$ of a semi-monoidal category $({\mathcal C},\otimes ,\tau _{\_,\_,\_})$. We will abuse notation slightly; based on the monoid isomorphism $End(x)\cong {\mathcal C}(S,S)$, we treat the semi-monoidal tensor $\_ \star _\lhd \_$ equally as an operation on ${\mathcal C}(S,S)={\mathcal F}_S(x,x)$ and denote the (unique) associativity isomorphism for $\_\star \_$ as $\alpha \in {\mathcal C}(S,S)$.

The question we address is the following:

Given a diagram over $\mathcal C_S$ with arrows built inductively from

$$\begin{aligned} \{ \ \_ \otimes \_ \ , \tau _{\_,\_,\_} \ ,\ \lhd \ , \ \_\star \_ \ ,\ \ \alpha \ ,\ ( \ )^{-1} \ \}, \end{aligned}$$

when may it be guaranteed to commute?

We first fix some terminology.

Notation 14

Given a category ${\mathcal C}$ and a class $\Gamma$ of operations and arrows of ${\mathcal C}$, we say that a diagram is canonical for $\Gamma$ when its edges are built inductively from members of $\Gamma$. For example, in a semi-monoidal category $({\mathcal C},\_ \otimes \_ , \tau _{\_,\_,\_})$, a diagram canonical for $\{ \_ \otimes \_ , \tau _{\_,\_,\_} , (\ )^{-1} \}$ is a diagram canonical for associativity, as usually understood.

The following demonstrates that a simple appeal to freeness is not sufficient:

Proposition 5

Let $({\mathcal F}_S,\Box , t_{\_,\_,\_} )$ be the semi-monoidal category freely generated by S. Then, over ${\mathcal F}_S$

• 1. All diagrams canonical for $\{ \_ \Box \_ , t_{\_,\_\_ ,\_ } , (\ )^{-1} \}$ commute.

• 2. All diagrams canonical for $\{ \_ \Box \_ , \lhd _\_ , (\ )^{-1} \}$ commute.

• 3. All diagrams canonical for $\{ \_ \Box \_ , t_{\_,\_\_ ,\_ } , \lhd _\_ , (\ )^{-1} \}$ commute iff S is a unit object for $({\mathcal C}_S,\otimes )$.

Proof

1. is well-established, and follows from the monic-epic decomposition of MacLane’s substitution functor described in Lemma 4 and (in the monoidal case) is commonly used [24] to study coherence. 2. follows similarly from Lemma 4. For 3., the following diagram is canonical for self-similarity and associativity:

Applying $\Phi :(F_S,\Box )\rightarrow (End(x),\star )$ to this diagram gives the associativity isomorphism for $(End(x),\star )$ as $\alpha =1_x$, so by Theorem 5 the unique object of End(x) is the unit object for $\_ \star \_$. Appealing to the semi-monoidal equivalences of Theorem 11 gives that $S\in Ob({\mathcal C}_S)$ is the unit object for $\_ \otimes \_$. $\square$

We now introduce an equivalence relation on diagrams over ${\mathcal F}_S$ that allows us to answer this question in the free case:

Definition 14

As $\mathcal F_S$ is a small category, we may treat a diagram $\mathfrak D$ over ${\mathcal F}_S$, with underlying directed graph $G=(V,E)$, as a pair of functions $\mathfrak D_V:V\rightarrow Ob ({\mathcal F}_S)$ and $\mathfrak D_E:E\rightarrow Arr({\mathcal F}_S)$ satisfying

$$\begin{aligned} \mathfrak D_E(e) \in {\mathcal F}_S(\mathfrak D_V(v),\mathfrak D_V(w)) \ \ \text{ for } \text{ all } \text{ edges } \ \ v\mathop {\longrightarrow }\limits ^{e} w \ \in E \end{aligned}$$

We will omit the subscripts on $\mathfrak D_V$ and $\mathfrak D_E$ when the context is clear.

Given diagrams $\mathfrak T,\mathfrak U$ with underlying graphs $G=(V,E)$ and $G'=(V',E')$ respectively, we say they are self-similarity equivalent, written $\mathfrak T \sim _{\lhd \rhd }\mathfrak U$ when there exists a graph isomorphism $\eta :G\rightarrow G'$ such that, for all edges $s\mathop {\longrightarrow }\limits ^{e} t$ of G, the following diagram commutes:

(An intuitive description is illustrated by example in Fig. 3). This is an equivalence relation, since the object-indexed isomorphisms $\lhd _\_$ and $\rhd _\_$ specify a wide posetal subcategory of ${\mathcal F}_S$. We denote the corresponding equivalence classes by $[\_ ]_{\lhd \rhd }$.

Fig. 3

$\mathfrak T \sim _{\lhd \rhd }\mathfrak U$ when all ‘vertical’ squares commute in the rhs diagram

Lemma 6

Given $\mathfrak T \sim _{\lhd \rhd }\mathfrak U$ over ${\mathcal F}_S$, then $\mathfrak T$ commutes iff $\mathfrak U$ commutes.

Proof

This is immediate from the definition, and a slight generalisation of the reasoning in the proof of Theorem 8. $\square$

We may now demonstrate commutativity for a class of diagrams in the free setting:

Theorem 15

Let $(S,\lhd )$ be a self-similar structure of a semi-monoidal category $({\mathcal C},\otimes )$, and let $\mathfrak D$ be a diagram over $({\mathcal F}_S,\Box )$ canonical for $\{ \Box , t_{\_,\_,\_} , \lhd _\_ ,\star , \alpha , (\ )^{-1} \}$. The following two conditions are equivalent, and characterise a class of diagrams guaranteed to commute:

• 1. $[ \mathfrak D]_{\lhd \rhd }$ contains a diagram canonical for $\{ \Box , t_{\_,\_,\_} , (\ )^{-1} \}$.

• 2. $\Phi (\mathfrak D)$, which is canonical for $\{ \star ,\alpha , (\ )^{-1} \}$, is guaranteed to commute by MacLane’s coherence theorem for associativity.

Proof

Somewhat redundantly, we give separate proofs that both these conditions characterise a class of commuting diagrams:

• 1. From the basic theory of coherence for associativity (see Lemma 4), in $({\mathcal F}_S,\Box )$, all diagrams canonical for $\{ \Box , t_{\_,\_,\_} , (\ )^{-1} \}$ are guaranteed to commute by MacLane’s theorem; our result then follows from Lemma 6.

• 2. By construction, $\Phi (\lhd _\_) = 1_x$ and $\Phi (f\Box g)=\Phi (f)\star \Phi (g)$ for all arrows f, g. Thus $\Phi (\mathfrak D)$ is indeed canonical for $\{ \star ,\alpha , (\ )^{-1} \}$. From Corollary 8, $\Phi (\mathfrak D)$ commutes iff $\mathfrak D$ commutes. Thus when MacLane’s theorem predicts $\Phi (\mathfrak D)$ to commute, $\mathfrak D$ also commutes.

We now show that they characterise the same class of commuting diagrams:

$(1.\Rightarrow 2.)$ Let $\mathfrak R \in [\mathfrak D]_{\lhd \rhd }$ be canonical for $\{ \_ \Box \_ ,t, (\ )^{-1} \}$. As the functor $K:({\mathcal F}_S,\Box , t_{\_,\_,\_})\rightarrow ({\mathcal F}_x,\Diamond ,t'_{\_,\_,\_})$ of Proposition 4 is semi-monoidal, $K(\mathfrak R)$ is canonical for $\{ \Diamond , t'_{\_,\_,\_}, ( \ )^{-1} \}$ and thus $Inst (K(\mathfrak R)) = \Phi (\mathfrak R)$ is predicted to commute by MacLane’s theorem. However, up to isomorphism of the underlying graph, $\Phi (\mathfrak R)$ is identical to $\Phi (\mathfrak D)$.

$(2.\Rightarrow 1.)$ As $\Phi (\mathfrak D)$ is predicted to commute by MacLane’s theorem, there exists some diagram $\mathfrak P$ over $({\mathcal F}_x,\Diamond , t'_{\_,\_,\_})$ that is canonical for $\{ \Diamond , t'_{\_,\_,\_} , (\ )^{-1} \}$ satisfying $Inst(\mathfrak P) = \Phi (\mathfrak D)$. As the isomorphism $K:({\mathcal F}_S,\Box , t_{\_,\_,\_})\rightarrow ({\mathcal F}_x,\Diamond ,t'_{\_,\_,\_})$ of Proposition 4 is semi-monoidal, $K^{-1}(\mathfrak P)$ is canonical for $\{ \Box , t_{\_,\_,\_}, (\ )^{-1} \}$ and by construction $K^{-1}(\mathfrak P) \sim _{\lhd \rhd }\mathfrak D$. Thus our result follows. $\square$

The above theorem answers the question posed at the start of this section in the ‘formal’ setting $({\mathcal F}_S,\Box )$. To map this free setting to the concrete setting, we apply the $Inst:({\mathcal F}_S,\Box )\rightarrow ({\mathcal C}_S,\otimes )$ functor, giving the following corollary:

Corollary 16

Given a diagram $\mathfrak E$ over ${\mathcal C}_S$ canonical for $\{ \otimes , \tau _{\_,\_,\_} , \lhd , \star , \alpha , ( \ )^{-1} \}$, then $\mathfrak E$ is guaranteed to commute when there exists a diagram $\mathfrak D$ over ${\mathcal F}_S$ that is canonical for $\{ \Box , t_{\_,\_,\_} , \lhd _\_ ,\star , \alpha , (\ )^{-1} \}$ satisfying

• 1. $\mathfrak D$ is guaranteed to commute by Theorem 15 above.

• 2. $Inst(\mathfrak D)=\mathfrak E$.

The identification of generalised convolution as the instantiation functor of a semi-monoidally isomorphic category (Proposition 4) then translates the above into the following intuitive characterisation of such diagrams:

Corollary 17

Let $\mathfrak E$ be a diagram over ${\mathcal C}_S$ canonical for $\{ \otimes , \tau _{\_,\_,\_} , \lhd , \star , \alpha , ( \ )^{-1} \}$. Let us form a new diagram $\mathfrak E^\flat$ over C(S, S) by the following procedure:

• Replace every object in $\mathfrak E$ by S.

• Replace every occurrence of $\otimes$ by $\star$.

• Replace every occurrence of $\tau _{\_,\_,\_}$ by $\alpha$.

• Replace every occurrence of $\lhd$ by $1_S$.

Then $\mathfrak E^\flat$, which is canonical for $\{ \_ \star \_ , \alpha , (\ )^{-1} \}$, is guaranteed to commute by MacLane’s coherence theorem for associativity iff $\mathfrak E$ is guaranteed to commute by Corollary 16.