Introduction

Rivers are a major source of drinking water and are also used for irrigation and industrial purposes; therefore, the prevention and management of river water pollution is crucial. Globally, climate change has led to a reduction in water resources, which is compounded by the increasing demand for water because of rising urbanization (Haque et al. 2014; Karakuş 2019). The increase in demand for water resources and the imbalance in availability can pose a threat to human sustainable development. For this reason, each country is evaluating the water footprint for water resource management; this is a concept that includes all water required from product consumption to disposal, considering the entire process of material production and service provision (Park et al. 2020). In Korea, the life cycle assessment (LCA) method was used to calculate the water footprint and evaluation data of the rainwater exclusion system in consideration of the environment. (Ahn et al. 2019). LCA is a tool to implement an environmental management system, and it is a technique to evaluate potential environmental impacts that may occur in the manufacturing process of a product (Chen et al. 2020). To achieve common performance for the circular economy from the management point of view of scarce water resources, a strategy to increase economic advantage and reduce environmental water loss by performing LCA is needed (Silvestri et al. 2021).

Reliable water quality data are required to prevent and manage water pollution in rivers, and continuous water quality assessment must be conducted to monitor pollutants and water resource management based on spatial-scale water quality analyses (Wu et al. 2018). To assess water quality, several researchers have used methods, such as classification, correlation analysis, and time-series numerical analysis of measured data (Singh et al. 2008; Sharma et al. 2012). These methods have the advantage of not requiring expert knowledge about water quality or the environment. However, water quality assessment by time-series numerical analysis on long-term measured data requires a cumbersome and time-consuming data arrangement process.

Principle component analysis (PCA), used in regional assessment to analyze major water quality variables, enables an in-depth analysis of river characteristics through complex data matrix analysis (Tripathi et al. 2019). This method provides a quick solution for the proper management of water resources (Singh et al. 2004; Liu et al. 2011). Barakat et al. (2016) evaluated water quality variability of the Oum Er Rbia and El Abid rivers in Morocco according to spatial (cluster) classification by using PCA and cluster analysis (CA). These techniques are valuable for water resource management as they can identify and help investigate the origin of critical factors affecting rivers (Barakat et al. 2016; Varol 2020). Multivariate statistical analysis techniques, such as PCA and CA, reflect temporal and spatial changes in water quality and are used widely when evaluating water quality for river management by assisting in the selection of components that affect river water quality (Gamble and Babbar-sebens 2012; Bora and Goswami 2016).

The combined impact of many different factors that characterize the water quality is complex; and so are the challenges of classifying the significant parameters used to measure the status of water resources quantitatively. Therefore, the water quality index (WQI) is considered a mathematical tool that significantly simplifies these data sets and provides a single classifying value that describes the water quality status of water bodies or degree of pollution (Naseem et al. 2021). WQI is a performance measurement that combines information from significant physical, chemical, and biological parameters into a functional form, reducing large amounts of data to a single number (Gradilla-Hernández et al. 2019).

Using WQI, water quality is converted into a single score for comprehensive assessment, helping the public and policy makers to understand water quality (Terrado et al. 2010; Upadhyay et al. 2011; Gupta et al. 2017). In WQI, a water body is allocated a number between 0 and 100, which indicates its drinking water quality (Gradilla-Hernández et al. 2019). The WQI is the most effective way to express the suitability of a water body, such as a river, as a water source for human use (Ewaid et al. 2017; Khangembam et al. 2019). Further, WQI is used as a policy-making tool for water quality assessment by environmental monitoring organizations (Bharti and Katyal 2011), as the public can easily obtain and understand the relevant in-depth information (Naseem et al. 2021).

When performing water quality evaluation of the survey site using WQI, the same water quality variables were applied to each stream in the previous studies (Shin et al. 2018; Cho et al. 2021), whereas in this study, the water quality evaluation method that more quickly reflected the characteristics of rivers using major water quality variables for each stream was used. The applicability and feasibility of the results of this study were evaluated by selecting major variables reflecting the quality of rivers using statistical techniques. We also compared the WQI calculated in this study with the WQI currently presented by the domestic Ministry of Environment. These results may serve as basis for simplifying the number of variables for water quality evaluation of rivers in the future and for efficiently derive pollutants that need to be preferentially managed. In addition, this study may be used by policy makers for water quality improvement by region or by river.

Materials and methods

Study progress flow

Figure 1 shows  the series of analysis procedures performed in this study. It was divided into three stages. First, cluster analysis by survey sites, and major water quality variables were selected through multivariate statistical analysis. Second, the WQI (according to the difference in the application of water quality variables) was calculated and compared with RT-WQI. Third, water quality evaluation was performed using the WQI calculation method proposed in this study.

Fig. 1
figure 1

Flowchart to illustrate how this study

Full size image

Survey point and item

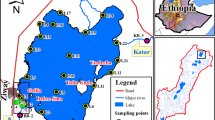
The Nam River is located in the southwest of South Korea. It has a total flow length of 144.59 km and a basin area of 3 467.5 km2. From the upper stream to the lower stream, the major tributaries of the Nam River include the Namgang, Ram, Obong, and Im streams, the Dongcheon River, Sindeung, Yang, and Migok streams, Youngcheon River, and the Euiryung and Haman streams. The survey points and variables of this study are shown in Table 1 and Fig. 2. The survey points include the 13 water quality measurement points at the main tributaries of the Nam River operated by the Ministry of Environment. Water quality data (2012–2020) obtained from the Water Environment Information System (http://water.nier.go.kr) were used. From the acquired data, nine variables used in the RT-WQI were selected. In 2012, an artificial structure called a weir was installed in the Nakdong River, changing the water environment (Jo et al. 2022). Therefore, in this study, the monitoring results collected from 2012 to 2020, after the artificial structures were installed, were applied to the water quality evaluation.

Table 1 Survey point status and survey items
Full size table
Fig. 2
figure 2

Nam River watershed with 13 water quality measurement points. The first letter of all the words in the name of the measurement locations has been capitalized in this study

Full size image

Statistical analysis

CA and PCA were applied for the spatial classification of the measured data and selection of major water quality variables. Therefore, various rivers can be classified according to their characteristics, and the main water quality variables representing the water quality characteristics of the river could be determined (Pekey et al. 2004). CA and PCA were standardized to z-scores to prevent errors between data owing to different units of measurement. An statistical software (IBM SPSS 24.0 Inc.) was used for data analysis.

Cluster analysis

In this study, CA was performed for the spatial classification of nine water quality variables (water temperature [WT], dissolved oxygen [DO], electrical conductivity [EC], pH, biochemical oxygen demand [BOD], total organic carbon [TOC], chemical oxygen demand [COD], suspended Solid [SS], total nitrogen [TN], and total phosphorus [TP]) of the 13 tributaries of the Nam River (Fig. 2). For that, we used monthly survey results from 2012 to 2020.

CA collects and classifies variables with similar characteristics among multiple variables; it is a statistical analysis method that can identify the structure of data by grouping them according to the homogeneous properties of the variables. It classifies the data into clusters by using the distance or the similarity between the variables of the population, and it can be classified as a hierarchical or a non-hierarchical method, according to the method used to analyze the clusters. To classify the clusters as temporally and spatially homogeneous based on the correlation of the data (Vega et al. 1998), hierarchical CA, in which sequential clustering occurs, is used and is represented by a dendrogram (McKenna 2003). The hierarchical clustering method is used for classification; the Euclidean distance (Otto et al. 1998) is used for measuring the distance between clustered variables; and Ward’s method (Fan et al. 2010), which can minimize information loss between clusters, is used for merging.

Principal component analysis

PCA is used to find the direction of scattered data, re-express the data to facilitate understanding of the information in the data, and reduce the variability of variables. In other words, it is a statistical analysis method to find a new variable (principal component), expressed as a linear combination of variables by using the correlation between multiple variables (Sârbu and Pop 2005; Barakat et al. 2016). In PCA, the eigenvalue represents the magnitude of the variance that can be explained by the principal component. If the eigenvalue is greater than 1.0, it means that one principal component can explain more than one variable. Therefore, the principal component is extracted based on principal components with an eigenvalue of 1.0 or greater (Varol et al. 2012; Park et al. 2019).

In this study, PCA was performed to select the main water quality variables (WT, EC, DO, pH, BOD, COD, TOC, TN, and TP) by CA that could represent the characteristics of each stream and PCA was used to extract the components that could have the most significant influence on the water quality characteristics of the basin surveyed. Based on the CA results, PCA was performed on the water quality components of each cluster. The eigenvalue represents the magnitude of the variance that can be explained by the principal component, and as mentioned, an eigenvalue greater than 1.0 means that one principal component (PC) could explain more than one variable. We used the only PC with an eigenvalue of 1 in our analyses. With regard to the components of the ten water quality variables, the eigenvalue obviously represents the eigenvalue, and variability (%) is the ratio that explains the variability of the PC with respect to the original variable. Cumulative (%) is the cumulative ratio used to explain the PC.

Water quality index

WQI converts important water quality variables into a single index, which can be used as an easy-to-understand scale when evaluating the water quality of a target stream. Many researchers have used multivariate statistical techniques, such as PCA and CA, for selecting key variables for calculating WQI (Sutadian et al. 2016, 2018; Tripathi and Singal 2019; Gradilla-Hernández et al. 2019). With regard to the assessment criteria for the calculated WQI, we used five grades suggested by the Ministry of Environment (Table 2). The five grades were Excellent (80 to 100), Good (60 to 79), Poor (40 to 59), Very Poor (20 to 39), and Unsuitable for Drinking Use and Fish Culture (0 to 19). With regard to the water quality variables for calculating WQI, the water quality data (WT, EC, DO, pH, BOD, COD, TOC, TN, and TP) measured at 13 measurement points from the Water Environment Information System (http://water.nier.go.kr), were used.

Table 2 WQI assessment criteria provided by the Korean Ministry of Environment
Full size table

For quality assessment of the water of the Namgang inflow tributaries, we calculated the annual WQI from 2012 to 2020. The WQI was calculated as in Eq. 1 (Seo et al. 2021a, b) for seven factors, including WT, pH, DO, EC, TOC, TN, and TP, and by varying the main water quality variable for each group. The main water quality variables applied in the calculation of WQI for each cluster were selected by PCA.

$${\text{WQI}} = 100 - \surd \left[ {\left( {F_{1}^{2} + \, F_{2}^{2} + \, F_{3}^{2} } \right)/3} \right]$$
(1)

where F1 is the fraction of the number of water quality variables that violate the criteria, F2 is the fraction of the total number of times the criterion is violated in all water quality variable, and F3 is calculated by the sum of the values obtained by fractionating the degree of violation of the criteria for the water quality variable. Details are available from the Real-time Water Quality Information System (http://www.koreawqi.go.kr). The assessment for each survey point was conducted by varying the WQI calculation factors.

The water quality index calculated using the RT-WQI provided by the Ministry of Environment was compared with the index calculated based on the method proposed in this study using the PCs for each Cluster (Table 3 and Fig. 3). Seven water quality variables were applied to the RT-WQI analysis provided by the Ministry of Environment, including WT, pH, DO, EC, TOC, TN, and TP. However, the water quality variables used in our method of calculating the WQI (i.e., using the principal variables of each Cluster) were four in Cluster 1 (COD, TOC, TN, and TP), four in Cluster 2 (WT, DO, COD, and TOC), and five in Cluster 3 (WT, DO, EC, COD, and TOC).

Table 3 WQI scores of the stations in the Nam River watershed during the study period
Full size table
Fig. 3
figure 3

Comparison of the assessment results for each method used to calculate the water quality index. Point S5 is not shown because the assessment results are the same

Full size image

Results and discussion

Results of water quality analysis according to spatial classification

CA was performed based on the area according to the land-use type in the river basin for the classification of the water quality concentration and spatial characteristics of the 13 survey points (Fig. 2). The CA results were classified into three clusters, and the survey points for each cluster were Cluster 1 (S1 to S5), Cluster 2 (S6 to S11), and Cluster 3 (S12 and S13). The analyses result of the characteristics of the basin for each survey point indicated that the clusters were formed by the influence of urbanization and human activities (Fig. 4). In terms of the land-use ratio, the average urbanization/drying ratio was 2.2% for Cluster 1, 3.6% for Cluster 2, and 5.7% for Cluster 3. The average ratio of agricultural land was 11.7% for Cluster 1, 17.9% for Cluster 2 17.9%, and 18.4% for Cluster 3, demonstrating a trend similar to the urbanization/drying ratio. As the ratio of the forests in the basin (Cluster 1: 78.8%, Cluster 2: 68.3%, and Cluster 3: 63.8%) that represented the natural characteristics of the basin showed an opposite trend from the previous results, apparently urbanization and human activities were the crucial factors defining the characteristics of the water basin. Seo et al. (2021a) identified water quality variables that affect the spatial difference and concentration of water quality by river through a study on the effect of spatial variability by river basin on the water quality of the Nakdong River in Korea.

Fig. 4
figure 4

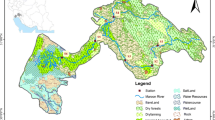
Ratio of the land-use area in the basin to which the river belongs. The upper right table shows the ratio of area according to land use in the watershed at the survey sites, with the results being expressed using the cluster analysis. The land-use types include urbanization/drying land, agricultural land, forest, grassland, wetland, bare land, and fresh water

Full size image

The water quality characteristics were explained by dividing the water quality variables into clusters and expressing the average and range of concentrations for each variable (Table 4 and Fig. 5). Interquartile range (IQR) was calculated by subtracting the third quartile by the first quartile, and the text (A, B, and C) on the box plot was used to characterize the homogeneity of the Scheffe test (analysis of variance, ANOVA; p < 0.05).

Table 4 Average concentration and concentration range of each water quality variable at survey points
Full size table
Fig. 5
figure 5

Boxplot of the water quality measurement data from 2012 to 2020 for each group, confirming homogeneity according to spatial classification

Full size image

In the results shown in the box plots for each group, ANOVA results according to the Scheffe method also appeared to confirm the homogeneity between the groups. The WT was analyzed as 16.4 °C and 16.9 °C on average for Clusters 1 and 3, and 14.4 °C on average for Cluster 2. Among the investigated water quality variables, the mean concentration, and the range of change in concentration of electrical conductivity (EC), BOD, COD, TOC, TN and TP were the highest in Cluster 3 with a wide range, followed by Clusters 2 and 1 (Fig. 6). With regard to DO, Clusters 1 and 2 had similar mean values (11.0, 11.1 mg/L, respectively) and ranges (6.7 to 17.0 mg/L, 5.7 to 17.5 mg/L, respectively), whereas Cluster 3 had a lower mean concentration (10.1 mg/L). With regard to pH, similar concentrations and trends were observed for all clusters. With regard to the classification of the basin area by land use as shown in Fig. 4, the results show that the water quality characteristics of each watershed to which a stream belongs can be distinguished by the influence of human activities, such as urbanization and agriculture, similar to the results of CA. Compared with the other clusters, the water quality concentration of the basins in Cluster 1 was superior because of its strong natural characteristics, whereas the water quality concentration of the basins in Cluster 3 was inferior because of more urbanized and agricultural lands. Other studies have suggested that human activities affecting agricultural and urbanization of land have a significant positive correlation with water quality variables of rivers (Giri and Qiu 2016; Lintern et al. 2018). The results of analyzing clusters and water quality characteristics appeared to suggest the need for the differentiation of the method and target item for water quality assessment according to the land-use characteristics of the basin.

Fig. 6
figure 6

Comparison of key water quality variables according to the cluster analysis. The larger the factor-loading value of the component, the closer it is to the circle, thereby indicating a stronger influence that could explain all variables (WT, pH, EC, DO, BOD, COD, TOC, SS, TN, and TP)

Full size image

Results of principal component analysis

The results of the PCA indicated the cumulative explanatory power of Clusters 1 and 2 as 70% and 65%, respectively, with only three principal components, and the cumulative explanatory power of Cluster 3 as 82%, which could be reduced to two principal components. As the number of variables decreases, the efficiency of PCA increases, indicating the value of the method proposed in this study, i.e., reducing a total of ten components to 3 and 4 PCs per Cluster (Table 5 and Fig. 6).

Table 5 Results of analyses to determine variability and eigenvalue of principal components (PC) by cluster
Full size table

With regard to PCA, the factor-loading value for each component was considered “strong” when it exceeded 0.7, “moderate” when it was between 0.7 and 0.5, and “weak” when it was < 0.5. The results of PCA for each cluster and component are shown in Table 6. To select the principal component, the component corresponding to “strong” was selected among the factor-loading values of PC1 and PC2, which had the highest explanatory power.

Table 6 Principal component analysis by cluster
Full size table

Among the PC1 variables of Cluster 1, COD (0.864), TOC (0.794), and TP (0.718) were selected as the factor-loading values corresponding to “strong”, that is, which have the strongest influence in evaluating the water quality characteristics of the Cluster. In the case of PC2, TN (0.852) was selected. For PC1 of Cluster 2, WT (0.794), DO (0.756), COD (0.854), and TOC (0.732) were selected, and there was no variable corresponding to “strong” in PC2. For PC1 of Cluster 3, EC (0.889), COD (0.895), and TOC (0.882) were selected; for PC2, WT (0.790) and DO (0.849) were selected as principal variables. Cho et al. (2021) selected four out of ten major water quality variables using PCA to identify major variables contributing to the water quality fluctuation characteristics of the South Han River in Korea. Kim et al. (2007) reported that in determining the number of major water quality variables, the determined variable was sufficient to explain the whole when the cumulative % was 60% to 80% or more.

The selected principal components representing the water quality variables at the survey points selected after performing PCA included COD, TOC, TN, and TP for Cluster 1; WT, DO, COD, and TOC for Cluster 2; and WT, DO, EC, COD, and TOC for Cluster 3.

Results of water quality index assessment

After comparing the calculated WQIs (Table 3, Fig. 3), we obtained similar results for most sites despite the differences in the assessment factors. However, the results for S1, S2, and S4 differed. The river water quality using the existing RT-WQI for S1 was evaluated as “Excellent” every year from 2013 to 2016. However, the WQI calculation results applying the principal variables were evaluated differently by year (Very Poor, in 2013; Good, in 2014 and 2015; and Poor, in 2016).

The concentration of each water quality variable in the same year as the WQI assessment is shown in Fig. 7. From 2013 to 2016, which showed a large difference in the WQI assessment, the differences in concentration by year were identified clearly, and the same differences as in the previous results were observed from 2018 to 2019. As the index is calculated based on factors applicable to all the basins in South Korea for RT-WQI, it will be difficult to reflect the detailed characteristics of a specific basin. For S2 and S4, the WQI calculation results were analyzed differently depending on whether principal variables were applied. As a result of comparing the water quality concentration change by year and the calculation result (Fig. 7), it was determined that calculating the WQI by selecting the main variables for each river would reflect the characteristics of the target river in more detail. When the change in water quality by year and the WQI calculation result were compared, the concentration of water quality variables showed (BOD 0.5–1.5 mg/L, COD 2.4–3.0 mg/L, TN 1.647–2.162 mg/L, TP 0.020–0.065 mg/L, and TOC 1.3–2.3 mg/L) a change according to the surveyed year. However, the RT-WQI calculation result for the same year was analyzed as Good, indicating no change in water quality by year. Conversely, the WQI results of this study showed a similar trend from Excellent to Good according to the annual concentration change of water quality variables. Kang et al., (2019a) analyzed the long-term measurement data of the Nam River in Korea. The authors suggested that monthly river water quality variability is large. In addition, a study that evaluated the water quality grade for Namgang reported that the yearly and seasonal evaluation results showed similar trends to water quality variability (Kang et al. 2019b). According to Pejman et al. (2009), when water quality is evaluated in a watershed, the principal water quality variables reportedly appear different depending on the types of rivers distributed in the watershed. For some rivers (S1–S3), the assessment results were analyzed differently depending on the selection conditions of the water quality variables; however, when compared with the concentration of the water quality variables by year, the assessment results by the WQI applied in this study reflect the water quality.

Fig. 7
figure 7

Comparison of the water quality index assessment results and the annual average water quality at point S1. The difference between the existing method used for calculating the water quality index (RT-WQI) and the calculation method proposed in this study was analyzed

Full size image

The results of the annual water quality assessment from 2016 to 2020 for each river or stream were incorporated and compared with the nine-year average of water quality assessment for the water quality variables proposed in this study, as shown in Fig. 8. For survey points classified as Cluster 1 (S1, S2, S3, S4, and S5), the average and annual assessment results at the S3 and S5 points were Excellent. The average assessment result was Good at S1, but the annual assessment result was Poor in 2019 and 2020 compared with that in 2016, indicating that the water quality was deteriorating. The assessment result at S4 was the worst (Very Poor) of all the survey points. At S2, upstream of S4, the assessment result was Poor on average, but the water quality improved to Excellent in 2020, indicating that the water quality at S4 could have been affected partially by the upstream environment, but the extent of this influence was not absolute. Based on these results, the pollutants dispersed across the basin at S4 must be monitored to enhance the water quality. With regard to the survey points classified as Cluster 2 (S6, S7, S8, S9, S10, and S11), the water quality was assessed as Good or Excellent, except for that of S9. At S9, the water quality deteriorated from Good in 2018 to Poor in 2020. With regard to the survey points classified as Cluster 3 (S12 and S13), the water quality was assessed as Good on average; however, the WQI assessment indicated a value in the boundary between Poor and Good. This result points to the need for continuous water quality management in the future.

Fig. 8
figure 8

Water quality assessment results for each river basin and analyses of the change patterns in the river basin compared to the results of the water quality assessment over the last five years. The assessment results over the last five years are grouped into previously analyzed clusters

Full size image

Conclusion

In this study, statistical techniques were used to select the main water quality variables of streams, and the WQI was calculated by applying the same water quality variables to streams with the same spatial classification. By comparing the results obtained using the RT-WQI and those obtained by the WQI calculation method proposed in this study, the main water quality variables (COD, TOC, TN and TP for Cluster 1; WT, DO, COD and TOC for Cluster 2; WT, DO, EC, COD, and TOC for Cluster 3) for each river were selected to assess water quality. The selected major variables can be used as representative items to evaluate the characteristics of each river. As a result of the assessment, WQI grade was assessment as S1 Good (63.0), S2 Poor (53.3), S3 Excellent (98.4), S4 Poor (48.4), S5 (Excellent (100.0), S6 Good (77.6), S7 Good (76.2), S8 Good (76.5), S9 Good (69.9), S10 Excellent (81.5), S11 Good (71.2), S12 Good (63.1), and S13 Good (63.5). The water quality of a river is highly dependent on the land-use status of the basin, implying that the level of pollution would be high in the basin subjected to extensive human activity. Accordingly, such variables should preferably be considered in the assessment of water quality reflecting the of rivers and basins.

The limitation of the current study is that it only included the rivers with the water quality measurement points operated by the Ministry of Environment. For more accurate analyses than those of this study, a higher number of rivers should be included, and an additional review of ionic substances would be required for the selection of water quality parameters. And in the case of the current analysis result, the method of this study can be applied even to rivers that have undergone the same water quality evaluation as the existing RT-WQI. However, efforts to increase applicability through diverse case studies are needed for rivers that show differences in some evaluation results.

The existing water quality improvement management plan uses a single standard for all rivers and basins in South Korea, implying several limitations in terms of space, time, and expense. River management policies should be established in a direction that can improve the water quality of rivers distributed throughout the country (bottom-up method) by establishing a management plan reflecting the characteristics of the target rivers by watershed and improving the water quality. As can be seen from the results of this study, it is necessary to simplify the variables statistically and scientifically for water quality evaluation and to establish water quality evaluation methods according to land-use and river characteristics. Therefore, in the future, calculating and assessing WQI based on the characteristics of each river will enable priority management of rivers that are more vulnerable to pollution by establishing the direction of water quality and basin management for rivers.