Abstract
Key message
New genotypes of hybrid poplars from the Aigeiros and Tacamahaca sections have great potential for increasing genetic gain from selection. The most promising traits are associated with productivity and resistance to Sphaerulina musiva -induced canker while wood density can be selected for secondarily. A minimum age of 8 years is reliable to select fast-growing resistant clones in northern climates.
Context
Productivity, wood density, and disease resistance of hybrid poplar clones are important traits when selecting for cultivation at an industrial scale.
Aims
We studied 1978 hybrid poplar clones from 63 families, bred from poplars native (Populus balsamifera and Populus deltoides) and non-native to Canada from the Aigeiros and Tacamahaca sections, to improve economically important traits for plantations in northern Alberta.
Methods
Genetic parameters for diameter at breast height (DBH), height, resistance to Sphaerulina musiva-induced canker, and wood density were determined up to age 10.
Results
A mean annual increment of 16.5 m3 ha−1 year−1 was achieved at age 10 in the best-performing clones. The potential genetic gain for DBH, height, and canker resistance, 37%, 26%, and ~ 13%, respectively, was achieved when selecting the top 10% of the tested clones. The genetic effect for wood density was weak. The age-age genetic correlations identified age eight as a reliable selection age.
Conclusion
The new hybrid poplar clones tested exhibited great potential for tree improvement. The next phase of selection should test a reduced number of clones on different site types, identifying stable clones for productivity and resistance, while wood density can be selected for secondarily. In northern regions, a minimum age of 8 years is reliable to select fast-growing resistant clones for commercial deployment.
Similar content being viewed by others
1 Introduction
The application of tree improvement in breeding programmes allows, in a broad sense, an increase in yields and value of plantations, while helping to meet the rising demand for forest products, and in some regions of the world, thereby reducing the pressure on natural forests. Generally, such programmes aim at developing genetically improved varieties in an economically efficient manner by maximizing genetic gain per unit time at the lowest possible cost (White et al. 2007). Poplars (Populus spp.), provide an excellent opportunity for tree improvement to maximize selection and production of fast-growing plantations, through exploitation of the vast natural genetic variation which exists over very broad natural ranges and ecological conditions, combined with the ease with which both intra- and interspecific hybridization is possible (Stettler et al. 1996). Hybridization in poplars enables tree breeders to combine the desirable traits of different species together, capitalizing on hybrid vigour (heterosis). Hybrid vigour constitutes a multi-genetic complex trait and can be generalized as the sum of multiple physiological and phenotypic traits including the magnitude and rate of growth, flowering time, yield, and resistance to biotic and abiotic environmental factors (Baranwal et al. 2012; Lippman and Zamir 2007).
The genetic resources of poplars are commonly managed as a source of fibre in the pulp and paper industry, and more recently in biomass and biofuel production, carbon sequestration, and phytoremediation (Balatinecz and Kretschmann 2001; Zalesny Jr. et al. 2016). For these reasons, tree improvement programmes using hybrid poplars have been developed in several countries in North America and Europe. For most of these programmes, traits of economic importance constitute quantitative polygenic traits such as growth, productivity, and wood quality as well as survival and disease resistance (Stanton et al. 2014). Such traits are influenced by many gene loci and by environmental effects. To distinguish environmental effects from genetic differences, genotypes are tested in common garden trials where the environmental component is controlled as much as possible. Such an experimental design allows for partitioning of the genetic variation from the overall phenotypic variation (Gylander et al. 2012). Consequently, the heritability, which represents the proportion of the total variance in a phenotypic trait that is controlled by these genes, can be calculated (Falconer and Mackay 1996). On that basis, with a high selection intensity, genetic gain in the traits of interest in a tree breeding programme can be determined. When measurements carried out on genotypes are repeated over multiple years, additional information can be obtained by estimating the age-age correlation for the same trait. The development of these correlations can be used to support decisions regarding the youngest age possible at which to make the selection for a given trait (White et al. 2007).
Information about the genetic effects related to singular polygenic traits is generally available (Pliura et al. 2007; Pliura et al. 2014; Rae et al. 2004; Yáñez et al. 2019). Depending on the tree age and site conditions, the weak/moderate to strong genetic control of diameter (heritability, 0.49–0.91) and height (heritability, 0.18–0.87) of trees has been reported from various common garden poplar trials (Pliura et al. 2007; Pliura et al. 2014; Yáñez et al. 2019; Yu et al. 2001; Yu and Pulkkinen 2003). However, the knowledge regarding the genetic effect of resistance to major fungal diseases and wood density, in combination with growth traits at an area of future utilization, is much less frequent.
Disease resistance plays a universal role of singular importance in defining the long-term sustainability of Populus cultivars (Stanton et al. 2014). Canker (on stems and branches), caused by the fungus Sphaerulina musiva (Peck) Quaedv., Verkley and Crous (syn. Septoria musiva Peck), is the most economically important disease and the major limiting factor to the production of Populus spp. as a commercial crop in North America (Dunnell and LeBoldus 2017; Feau et al. 2010; Newcombe and Ostry 2001; Ostry et al. 2014; Ostry and Mcnabb Jr. 1985). Due to the invasiveness of Sphaerulina musiva, it is also regarded as a high-priority quarantine pathogen for Europe. The only way to prevent the spread of Sphaerulina musiva is to plant resistant hybrid poplars. The results of controlled inoculation experiments have indicated that poplar genotype is a prominent factor in disease development and resistance to Sphaerulina musiva (Dunnell et al. 2016; LeBoldus et al. 2007; LeBoldus et al. 2008; Qin and LeBoldus 2014), which implies a possible increase in resistance by appropriate selection of clones.
Wood density, on the other hand, affects the production process and quality of pulp and paper as well as solid products (Downes et al. 1997; Haygreen and Bowyer 1996; Valente et al. 1992). As high-density wood produces more pulp per unit of wood volume than low-density wood, an increase in wood density has an important effect in the efficiency of pulp production (Downes et al. 1997; Foelkel 1997; Zobel and van Buijtenen 1989). Many studies that have been carried out on wood density in poplar species, hybrids, and clones (Farmer Jr. and Wilcox 1968; Farmer Jr. 1970; Hernandez et al. 1998; Ivkovich 1996; Koubaa et al. 1998; Mutibarić 1971; Nepveu et al. 1978; Olson et al. 1985; Pliura et al. 2007; Walters and Bruckmann 1965; Yanchuk et al. 1983; 1984; Yu et al. 2001) showed a moderate to large genetic effect for wood density. Interestingly, however, there is still no clear evidence indicating how growth rate affects wood density in a specific environment. When a negative relationship between growth traits and wood density occurs, then the beneficial impact of selecting for a faster growth rate may be decreased if wood density is to be maintained or maximized. For this reason, the relationships between growth rate and wood density have been studied extensively, resulting in variable and often ambiguous results. In some studies, significant negative correlations between faster growth and wood density have been reported for poplars and their hybrids (Beaudoin et al. 1992; Farmer Jr. and Wilcox 1968; Kennedy and Smith 1959; Olson et al. 1985; Hernandez et al. 1998; Pliura et al. 2005; Yanchuk et al. 1984), while other research proved little to no relationship between growth rate and wood density (Ilstedt and Gullberg 1993; Zhang 1995; Zhang et al. 2003).
The gaps in knowledge regarding the relationship between multiple effects, combining wood density with growth and/or resistance to major fungal diseases, in areas of future utilization, can be fulfilled by recently developed more advanced non-parametric methods such as generalized additive models (GAM). Such modelling techniques allow us to overcome the limitations of traditionally used linear models, connected with a non-linear course of variables and a non-constant variance distribution, and/or when explanatory variables show collinearity, leading to a large fraction of the unexplained variation (Aertsen et al. 2010). A better understanding of the nature of the relationship between economically important polygenic traits on the basis of a better statistical model fit may support tree breeders in selecting a critical set of characteristics depending on the desired manufacturing products for the fibre.
The application of tree improvement programmes requires the breeding and selection of multiple hybrids and clones for screening and testing (Pliura et al. 2007). In the current study, we focused on using a broad genetic base of hybrids developed from hybridizing of native Canadian Populus balsamifera L. (s. Tacamahaca) and Populus deltoides Marshall (s. Aigeiros) with/and non-native Populus spp. from the Tacamahaca and Aigeiros sections resulting in nearly 2000 new clones (first time being tested) in a common garden genetics trial to improve economically important polygenic traits for plantations in northern climates (Alberta, Canada). The specific objectives were to (1) quantify the clonal variation in growth, wood density, and resistance to Sphaerulina musiva-induced canker; (2) investigate the relationship between wood density and other economically important traits, providing the background information for better understanding the nature of such a relationship to support selection decisions; (3) calculate the broad-sense heritability of selected traits and expected genetic gains possible across traits; and (4) assess the clonal stability of growth traits across time and minimum age required for clonal selection.
2 Materials and methods
2.1 Experimental design and materials
A large experimental genetics trial was established at the Alberta-Pacific Forest Industries Inc. (Al-Pac) pulp mill site in Athabasca, Alberta, Canada (54° 53′ 21′′ N, 112° 51′ 33′′ W, 575 m a.s.l.) in spring 2008. The site experiences a humid continental climate (Köppen climate classification Dfb) that borders on a subarctic climate (Köppen Dfc). The long-term average (since 1961) January and July temperatures are − 14.4 °C and 16.3 °C, respectively. The average annual temperature for the last 10 years (2008–2018) was 2.2 °C with a mean annual precipitation of 432 mm (https://agriculture.alberta.ca/acis).
The trial represents 1978 hybrid poplar clones from 63 families. The hybrid poplar genotypes were bred in Quebec (Table 1) and include interspecific crosses between Populus deltoides (D), Populus nigra (N), Populus balsamifera (B), P. maximowiczii (M), and P. × petrowskyana (P. laurifolia × P. nigra). Two related poplar clones, widely planted across the Canadian Prairies, the female clone ‘Walker’ (Populus deltoides × (P. laurifolia × P. nigra)) (Lindquist et al. 1977) and male progeny clone ‘Okanese’ (‘Walker’ × (P. laurifolia × P. nigra)) (Schroeder et al. 2013) were used as reference clones. Both clones are of economic importance in shelterbelts and, more recently, in short rotation intensive crop (SRIC) plantations (Goehing et al. 2017). In spring 2008, over-winter dormant stock that had been rooted the previous summer in a commercial greenhouse was planted following a randomized complete block design, with one ramet per clone in each of four blocks. All families and clones were represented in each block, although the number of clones per family was unbalanced. Tree spacing was 2.5 m × 2.5 m with a single tree buffer row established around the trial.
2.2 Growth parameters
Measurements of diameter at breast height (DBH; measured at a height of 1.3 m) and the height of all trees were taken after 3, 8, and 10 years of growth at the plantation. For the measurements carried out on 8- and 10-year-old trees, the tree volume was calculated using the following equation (Boysen and Strobl 1991):
where V represents an individual tree stem volume, H is tree height (m), and DBH (cm) is the diameter at breast height.
Individual tree volumes were used for calculating tree volume per hectare (1600 stems per ha) and the mean annual increment (MAI, m3 ha−1 year−1) for each clone at a given age. The survival rate was assessed based on the number of living trees.
2.3 Assessment of canker severity
Assessment of canker severity, caused by the fungus Sphaerulina musiva, was carried out twice: at the age of 8 and 10, by visual observations of stems and branches on all trees in the plantation. A four-degree scale code was used, whereby 0 = no canker present, 1 = canker on branch, 2 = canker on the main stem but healed or healing, and 3 = canker on main stem and determined that the top could break off or was already a broken top.
2.4 Wood density measurements (resistograph measurements)
Wood density of trees was assessed at age 10. Because of the destructive nature of wood density measurement and potential for future damage to the trees, the wood density measurements were carried out on a subset of selected trees. We selected a total of nine families from the range of growth performance to measure and analyse wood density. The families selected belonged to one of three groups, high, average, or low volume. The selected subset included five clones of each family. The clones Walker and Okanese were included as reference clones. Wood density measurements were carried out indirectly by drilling resistance (DR). The trees were drilled using a resistograph (series 6 Rinntech e.K. DE / Germany). Two bark-to-bark measurements—N-S and E-W—were taken from each selected tree at breast height (1.3 m). The profiles stored in the resistograph memory were transferred to a PC, and the data produced by resistograph were evaluated using Decom™ Scientific software. The borders of the profile, representing a small piece of the resistogram which marked the changing environment for the drilling tip, were removed prior to further assessment and the profiles were divided into two separate sections: (1) from bark to pith and (2) from pith to bark. Because we noticed a statistically significant increase in drilling resistance between the two sections (t = 14.05, p < 0.001), for further analysis, we only used data from the first half of the profile (from bark to pith) (Gao et al. 2017).
In order to calibrate the drilling resistance to specific wood density, 5-mm increment cores were also taken from 10 trees. Trees were drilled approximately 5 cm above the 3-mm hole made by the resistograph pin to reduce variation between the two measurements. Wood density of the increment cores was assessed by the gravimetric method (Krzysik 1974). The volume was calculated by the displacement method, where the volume of a sample was measured by the weight of the displaced water, when the sample was submerged. The oven-dry weight of samples was obtained by drying them at 70 °C until constant weight. The wood density, in absolute units, obtained by the gravimetric method was used to calibrate values on a relative scale from the same trees obtained from the drilling resistance. After removing outlier measurements, the estimated Pearson correlation was r = 0.987 and the linear regression coefficients fitted are as follows: WD = 221.0372 + 0.7770 × DR.
2.5 Statistical analysis
Prior to statistical analysis, all data were examined with box plots and line plots to identify errors in measurements. On this base, we removed outlier measurements (± 3 SD). In total, three measurements from the set of growth traits were removed.
Spearman rank correlation between canker symptoms and survival rate or growth parameters was carried out. Moreover, all productivity parameters measured (DBH, H, and MAI) and canker resistance were inputted into a principal component analysis (PCA) to investigate the correlations among the key traits defining the best performance of the clones.
A generalized additive model (GAM) was used to predict wood density as a function of growth traits and canker severity. GAM, as a non-parametric extension of the multiple linear regression, uses transformation techniques that are independent for each predictor variable, which are counted together to calculate the response variable (Guisan and Zimmermann 2000). An identity link function was specified for the normally distributed response data. The criterion of the model performance was the coefficient of determination (R2). The general formula was as follows:
where E(WD) is the expected value of the dependent variable; (Xi), the predictor variables; (G), identity link function; f1, f2, … fn, the smoothing spline functions estimated from the data; and β, the regression coefficient. The above statistical analyses were performed using STATISTICA 13 software (Dell Inc., 2016).
A linear mixed model was used to test the effect of clones and clonal variation within families separately for each age as follows:
where yijkl is the response measured by the kth ramet of the jth clone within the ith family for a given age A = l, μ is the overall mean, fi is the random effect of the family i at a given age l, cij is the random effect of clone j nested in family i at a given age l, Bk is the fixed effect of block k at a given age l, Iik is the random interaction effect of family i with block k at a given age l, and eijkl is the random error in block k on clone j within family i at a given age l. Z tests were carried out to determine where random effects were significantly different from zero. The significance of fixed effects was tested with F tests, followed by their p values.
The variance components were estimated for each trait at different ages according to model 3. In particular, the genetic variance was partitioned by the following variance-covariance components:
where we assumed a constant covariance (\( {\sigma}_{ee^{\prime }} \)) between residuals from different blocks (common microenvironmental effect related to the block), by using a compound symmetry (CS) covariance structure. The broad-sense heritability (repeatability) H2 was calculated using the function developed by Zamudio et al. (2008):
where VG is genetic variance; VP, phenotypic variance; \( {\sigma}_f^2 \), variance of family effects; \( {\sigma}_c^2 \), variance of clonal within family effects; \( {\sigma}_l^2 \), variance of family-by-block interaction effects; \( {\sigma}_e^2 \), variance of residual effects; and \( {\sigma}_{ee^{\prime }} \), covariance between residuals of the same clone in different blocks. Approximate standard errors of heritability and variance-covariance estimates were calculated using the asymptotic large-sample dispersion matrix associated with the restricted maximum likelihood procedure (REML) method (Searle et al. 1992; Zamudio et al. 2008) in Proc Mixed of SAS (SAS/STAT rel. 14.3 statistical package (Cary, NC, USA)).
The expected genetic gain (∆G) in clonal selection was estimated using the following equation:
where σp contributes to the SD of the phenotypic distribution and i is the intensity of selection based on selection of n clones from N clones tested. We assumed that i = 1.7537 which corresponds to 10% selection intensity.
The genetic correlations (age-age correlation) between the same growth traits expressed at two different ages were estimated in accordance with Yáñez et al. (2019):
where \( {\sigma}_{c\left(l,{l}^{\prime}\right)} \) is the clonal genetic covariance for a given trait assessed between age l and age l′ and σc(l) \( and\ {\sigma}_{c\left({l}^{\prime}\right)} \) are the clonal genetic standard errors at age l and age l′, respectively.
3 Results
3.1 General characteristics
The survival rate for all clones was high and decreased only slightly over time, with 97% at age 3, 95% at age 8, and 89% at age 10. The reference clone Walker had a lower-than-average recorded survival rate of 20% at age 10 and the most severe canker symptoms (mean rank = 3). Overall, the canker had a significant impact on the survival of clones, which was reflected in the Spearman rank correlation (RS = − 0.523, p < 0.001). The mean value for canker symptoms for all trees on the plantation was 1.6 and 1.7 for ages 8 and 10, respectively. The most resistant crosses were the D × B (mean rank = 1.26), B × B (1.29), and DP × P (=Okanese at 1.35) while the most severe canker symptom was recorded for D × P (=Walker) and the? × B hybrid cross (Appendix, Fig. 4). At the family and clonal level, the variance between genotypes was much greater. In general, three families were characterized by a lack of canker symptoms on the main stem (mean rank values below 1 (all three families belong to the B × M cross type), while among clones, 73 showed no canker evidence at all (at age 8)).
The growth parameters varied significantly among clones within families and crosses, and differences increased with tree age. There was no particular cross type which distinguished itself from the others in growth parameters.
By age 10, the overall mean for DBH was 9.8 cm (range from 2.2 to 17.4 cm) and 9.9 m for height (range from 3.4 to 13.6 m). In terms of tree diameter at age 10, the reference clones Walker and Okanese ranked 1756 and 1055, respectively, out of all 1976 clones, whereas for height, they ranked 1582 and 932, respectively (see Niemczyk and Thomas 2020). While the ranks for clones were changing over time, the results of the Spearman rank correlation between growth parameters and canker severity score showed no relationship to DBH (RS = 0.01, p = 0.731, at age 8 and RS = − 0.013, p = 0.302, at age 10) and a weak statistically significant (α = 0.05) negative relationship for height (RS = − 0.119, p < 0.001, at age 8; RS = − 0.146, p < 0.001, at age 10).
During the studied period, clones showed an increasing MAI that progressed from 4.04 m3 ha−1 year−1 on average at age 8 to 6.16 m3 ha−1 year−1 at age 10. In general, however, there were large differences in MAI between clones ranging from 0.24 to 16.5 m3 ha−1 year−1 for individual clones at age 10 (see Niemczyk and Thomas 2020). The overall results of traits measured in the plantation in different years are shown in the Appendix (Fig. 4).
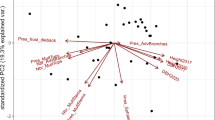
All of the variables mentioned above (DBH, H, MAI, canker severity) were considered in a principal component analysis (PCA). Results of the PCA showed strong dominance by the first principal component (PC1), which explained 70.6% of the variance and was associated with productivity traits (H, MAI, DBH), and all productivity traits were strongly correlated with each other. The second principal component (PC2) was associated with canker resistance and explained a further 25% of the variance. Clones were differentiated along PC1, showing different productivity levels. The reference clone Okanese was classified as an average (in the middle) clone, while Walker (on the left above) was a poor performer and showed a strong susceptibility to canker (overall score of Walker − 1.5 SD; Fig. 1). The two principal components identify a set of desirable clones for selection in northern climates. These clones are on the right, partway down the biplot (Fig. 1) and represent simultaneously both extraordinary productivity (+ 2 SD) and below-average canker susceptibility.
Principal component analysis of four traits, height—H [m], mean annual increment—MAI [m3 ha−1 year−1], diameter at breast height—DBH [cm], and canker severity caused by Sphaerulina musiva. The first principal component explains 70.6% of the total variation and is mainly associated with productivity traits (H, DBH, MAI). Clones placed on the right side of the biplot along the first principal component (PC1) characterize above-average productivity. Clones located below the dotted horizontal line, along PC2, characterize below-average susceptibility to canker. Both better performing and Sphaerulina musiva-resistant clones are identified by their family-clone number as are the reference clones (Walker and Okanese). The light blue colour area surrounding the center of the biplot identifies ± 1.0 SD (standard deviation), while the blue line indicates ± 1.5 SD
3.2 Modelling wood density
The average wood density for the selected clones tested in the plantation was 333 kg m−3. The highest wood density was recorded for Walker (366 kg m−3), while the lowest was for a (DN)B × B cross at 325 kg m−3 (Fig. 2).
The wood density was modelled as a function of all available traits (DBH, H, and canker severity) in the GAM analysis. The model explained 36.4% of the variation in drilling resistance wood density. DBH was the only variable that significantly affected wood density (p value for DBH = 0.006 while for H = 0.309 and canker = 0.569). Effects of the investigated variables on wood density were estimated from the spline function presented in Fig. 3. DBH negatively affected wood density, and the strongest negative effect in the dependent variable, at about 7.5 kg m−3 per 1 cm, was exhibited in the DBH range of 4–8 cm. The effect of DBH was weaker in the average-diameter classes, and wood density decreased to about 3 kg m−3 per 1 cm in the range of 8–11 cm, while in the thicker-diameter classes (12–16 cm), there was no visible effect of DBH on wood density.
3.3 Clonal variation, heritability, and genetic gain
The mixed-model analysis showed a significant impact of family, clone within family, and microenvironment (block effect) for DBH, H, and canker at all ages (Table 2). In most cases, the family × microenvironment interaction was also statistically significant (p ≤ 0.05). There was, however, no significant effect of family or clone within family for wood density. The results of GLMM were reflected by the variance components for this trait, which reached only 14% and 4% for family and clone within family, respectively, while the residual effect accounted for 81%.
The genetic effects were stronger, and clonal variance components were much higher for growth traits than for wood density. The variance components of tree diameter at different ages varied from 12% for family and 26% for clone at age 3 to 26% for family and 34% for clone within family at age 8. For tree height, variance components were slightly higher, varying from 15% for family and 30% for clone within family at age 3 to 25% for family and 34% for clone within family at age 8. The variance components were at similar levels for growth traits for ages 8 and 10. Although the mixed-model analysis showed a significant effect for family and clone within family for the susceptibility to Sphaerulina musiva-induced canker, the genetic effect was much lower than for growth traits. The family effect represented only 4% (for 8- and 10-year-old trees) of the total variance, while clone within family represented total variance for both ages (eight and 10) (Table 3).
Broad-sense heritability (H2) of growth traits ranged from 0.37 (age 3) to 0.64 (age 8) for DBH and from 0.46 (age 3) to 0.65 (age 8) for tree height while the heritabilities for the susceptibility to Sphaerulina musiva-induced canker and wood density were much lower at 0.10 for canker and 0.19 for wood density (Table 3).
The highest expected genetic gain (ΔG) based on 10% selection intensity was obtained for DBH followed by height, while moderate to weak gain can be expected for resistance to canker and wood density. The expected gains from various combinations of ages and traits are presented in Table 3.
3.4 Age-age genetic correlations
The age-age genetic correlations for growth traits indicated a weak positive correlation between age 3 versus eight or 10, and stronger clonal stability between age 8 versus 10 (0.86 for H and 0.92 for DBH). The correlations for growth traits at age 3 had higher standard errors than correlations calculated for older ages. Table 4 summarizes the age-age correlations between the studied ages for the same traits along with their standard errors.
4 Discussion
The results obtained from a large-scale genetics trial in northern Alberta indicate the relatively poor performance of the two reference clones, Walker and Okanese, in their growth parameter rankings in particular and susceptibility to canker in the case of Walker. Overall, the performance results together with large variation in growth parameters, production, and resistance to Sphaerulina musiva-induced canker, show that through selection, considerably higher genetic gain is possible with higher yielding and more resistant clones than those currently used in this region (see PCA results; Fig. 1).
In terms of parental species of hybrid poplars tested in this study, crosses with P. balsamifera—a native species of northern (boreal) environments—performed best. The second-best-performing parental species was P. maximowiczii, which aligns with previous research findings that P. maximowiczii hybridized with P. balsamifera demonstrates good performance in cooler Canadian climates (Pliura et al. 2014). Interestingly, however, some clones of P. balsamifera and P. maximowiczii were also among the lowest-performing clones in the genetics trial. This suggests that the focus should be placed on families and clones rather than on poplar hybrid types and parental species alone.
The growth parameters (DBH and H) differed among both families and clones within families, and these traits were also under moderate (at age 3) to strong genetic control (age 8, 10). In general, these results correspond to other studies of genetic effects for growth traits with poplar and aspen hybrids (Pliura et al. 2007; Pliura et al. 2014; Yáñez et al. 2019; Yu and Pulkkinen 2003). The relatively high heritabilities for growth traits together with the large number of families and clones included in this genetics trial resulted in capturing a wide range in variation, which translated into a 37% genetic gain for DBH and close to 27% for H with a 10% selection intensity. The expected selection effectiveness may, however, be reduced due to statistically significant genotype × microenvironment interaction across the four blocks, which implies that genotypes (families) revealed different relative performance on different microenvironments. Thus, the next stage of this tree improvement programme in northern Alberta should be to select a reduced number of clones and continue testing on several sites with contrasting conditions to further identify the potential ramifications of a potentially strong genotype-by-environment interaction influence on performance and allow for selection of stable clones for volume trials.
In a similar manner to the growth traits, canker resistance was not directly related to any particular hybrid type, which is often a subject of discussion in the literature (Dunnell et al. 2016; Dunnell and LeBoldus 2017; Feau et al. 2010; LeBoldus et al. 2009; Lo et al. 1995). In this case, our results are in line with previous findings by Ward and Ostry (2005) and LeBoldus et al. (2009). Our study also showed that canker infections negatively affected height growth and were associated with an increase in mortality among clones. These findings correspond to previous research, showing that canker is a significant factor influencing productivity and survival of hybrid poplar clones in managed plantations in North America (Dunnell et al. 2016; Lo et al. 1995). According to Lo et al. (1995), annual biomass losses due to Sphaerulina musiva infection can be as high as 63% of the total yield, while the mortality of highly susceptible clones affected by cankers can reach 100% within 5–10 years after the establishment of the plantation (Mottet et al. 2007). The relatively high number of Sphaerulina musiva infections in the experimental plantation in the current study, taken on combination with the large unexplained variation associated with the residual effect for canker severity, suggests that there are additional factors which play a role in the development of infections in the plantation. These factors should be taken into consideration in further analysis and field tests. Several studies carried out in controlled environment conditions have revealed, however, that the poplar clone genotype has a stronger impact on disease severity than the Sphaerulina musiva genotype itself and other abiotic factors (LeBoldus et al. 2007; LeBoldus et al. 2009). In addition, controlled inoculation experiments have shown that pathogen isolates and clone × isolate interaction effects were found to be lower than poplar clone genotype effects (Dunnell et al. 2016; LeBoldus et al. 2008) which suggests that Populus spp. clones should be subject to resistance screening under both controlled greenhouse conditions (LeBoldus et al. 2009) in addition to field testing.
Wood density, as a vitally important trait in developing Populus cultivars (Downes et al. 1997; Haygreen and Bowyer 1996; Valente et al. 1992), was assessed in the current research by the drilling resistance measurements taken on selected families and clones within families. The results obtained for wood density correspond to those reported previously for hybrid poplar clones of the Aigeiros–Tacamahaca sections (Beaudoin et al. 1992; Hernandez et al. 1998; Pliura et al. 2005; Pliura et al. 2007). Apart from the values of wood density obtained from the researched clones, attention was also given to the relationship between growth rate and how it affects wood density, in order to provide the background information for better understanding the nature of such a relationship to support selection decisions. In our study, growth parameters (DBH and H) and canker severity, taken together, explained only 36.4% of the total variability in wood density and the DBH was the only significant predictor in GAM that had a negative effect on wood density. Considering the low effects of explanatory variables on wood density, the results of GAM analysis suggest that selection of the best-performing clones made on the basis of growth parameters and height in particular may not necessarily mean a decrease in wood density.
Furthermore, contrary to previous research (Hernandez et al. 1998; Pliura et al. 2007), results of the linear mixed model used in the present study showed no statistically significant genetic effect on wood density, while microenvironment (block effect) was the only significant factor. These results suggest that further selection should be focused on more heritable growth traits and resistance to Sphaerulina musiva-induced canker as the crucial factors for sustainability of a plantation. Ultimately, desirable wood density could be selected secondarily, depending on the expected purpose of the fibre for manufacturing.
Given the importance of growth traits in the selection process and their significant genetic effect, as well as repeated measurements taken at three ages, the age-age genetic correlations were possible to calculate. Although this approach has been questioned on theoretical grounds, due to autocorrelation between ages (diameter at breast height at the older age is a function of diameter at the younger age, Riemenschneider 1988), it is still of value to calculate age-age correlations. Such correlations have important implications for selecting trees, by applying the gain-per-unit-time concept, instead of the gain per breeding cycle. The results showed that age-age genetic relationships for DBH and H were always positive and much weaker for the traits studied at age 3 versus 8 or 10, than for the same trait between ages 8 versus 10. The trend of having considerably lower values for genetic correlations at age 3 suggests that at this very young age, a different set of gene loci influence DBH and H growth than at older ages. Similar to our results, several authors observed smaller correlations between ages 1, 2, or 3 years with older ages (Isik et al. 2010; Lambeth 1980; Riemenschneider 1988). Therefore, in northern regions, where harvest ages (or rotation length) for hybrid poplars generally range from 20 to 25 years (Rytter et al. 2016), it may be necessary to wait until trees have reached a minimum age of 8 years, as shown in our study by the larger correlation coefficients between ages 8 and 10, when growth parameters have stabilized and clones can be reliably selected for commercial deployment.
5 Conclusions
This study revealed great potential for tree improvement based on an extensive genetics trial of new hybrid poplar clones tested for deployment in northern climates. Large variability among previously untested hybrid poplar clones and high heritability estimated for growth traits, and to a lesser extent for the resistance to Sphaerulina musiva-induced canker, allow considerable genetic gain to be achievable. These traits taken together play a crucial role in increasing the productivity and sustainability of plantations in the boreal region of western Canada, which may readily translate into economic benefits resulting from the cultivation of improved genotypes of hybrid poplars compared to those currently used in this region. Traits associated with wood quality, such as wood density, can be selected for secondarily depending on the desired manufacturing products.
Future research should focus on the best-performing set of clones identified and test on several sites to further identify the potential for genotype-by-environment interactions, allowing for selection of stable clones for operational deployment. In addition to field testing, controlled inoculation experiments are recommended to more clearly determine the resistance of these hybrid poplar clones and to establish if other potentially important factors play a role in infections of Sphaerulina musiva. Waiting until trees have reached a minimum age of 8 years (stable growth parameters) may be required for reliable selection of fast-growing resistant clones for commercial deployment in northern climates.
Data availability
The datasets generated during and/or analysed during the current study are available in a public repository (Niemczyk and Thomas 2020) which can be accessed online (https://doi.org/10.5281/zenodo.3627992).
References
Aertsen W, Kint V, van Orshoven J, Özkan K, Muys B (2010) Comparison and ranking of different modelling techniques for prediction of site index in Mediterranean mountain forests. Ecol Model 221:1119–1130
Balatinecz JJ, Kretschmann DE (2001) Properties and utilization of poplar wood. In: Dickmann DI, Isebrands JG, Eckenwalder JE, Richardson J (eds) Poplar culture in North America. NRC Research Press, Ottawa, pp 277–291
Baranwal VK, Mikkilineni V, Zehr UB, Tyagi AK, Kapoor S (2012) Heterosis: emerging ideas about hybrid vigour. J Exp Bot 63:6309–6314
Beaudoin M, Hernandez RE, Koubaa A, Poliquin J (1992) Interclonal, intraclonal and within-tree variation in wood density of poplar hybrid clones. Wood Fiber Sci 24:147–153
Boysen B, Strobl S (1991) A grower’s guide to hybrid poplar Ministry of Natural Resources. Ontario, Forest Resources Development Agreement
Downes G, Hudson I, Raymond C, Dean G, Michell A, Schmileck L, Evans R, Muneri A (1997) Sampling plantation eucalyptus for wood and fiber properties. CSIRO, Canberra, p 132
Dunnell KL, LeBoldus JM (2017) The correlation between Septoria leaf spot and stem canker resistance in hybrid poplar. Plant Dis 101:464–469. https://doi.org/10.1094/PDIS-06-16-0903-RE
Dunnell KL, Berguson B, McMahon B, LeBoldus JM (2016) Variation in resistance of Populus nigra to Sphaerulina musiva in the north-central United States. Plant Dis 100:287–291. https://doi.org/10.1094/PDIS-05-15-0516-RE
Falconer DS, Mackay FC (1996) Introduction to quantitative genetics, 4th edn. Longman Group Ltd, Burnt Mill, Harlow, Essex, England
Farmer RE Jr (1970) Variation and inheritance of eastern cottonwood growth and properties under two soil moisture regimes. Silvae Genet 19:5–8
Farmer RE Jr, Wilcox JR (1968) Preliminary testing of eastern cottonwood clones. Theor Appl Genet 38:197–201
Feau N, Mottet MJ, Périnet P, Hamelin RC, Bernier L (2010) Recent advances related to poplar leaf spot and canker caused by Septoria musiva. Can J Plant Pathol 32:122–134
Foelkel C (1997) Eucalyptus wood quality to comply with the pulp and paper market requirement. Proceedings of the IUFRO Conference on Silviculture and Improvement of Eucalypts. Salvador, Brazil, 24–29 August 1997. pp: 15–22
Gao S, Wang X, Wiemann MC, Brashaw BK, Ross RJ, Wang L (2017) A critical analysis of methods for rapid and nondestructive determination of wood density in standing trees. Ann For Sci 74. https://doi.org/10.1007/s13595-017-0623-4
Goehing J, Thomas BR, Macdonald SE, Bork EW (2017) Effects of alternative establishment systems on resource availability, understory composition and tree performance in juvenile hybrid poplar plantations. Forestry 90:515–529. https://doi.org/10.1093/forestry/cpx005
Guisan A, Zimmermann NE (2000) Predictive habitat distribution models in ecology. Ecol Model 135:147–186
Gylander T, Hamann A, Brouard JS, Thomas BR (2012) The potential of aspen clonal forestry in Alberta: breeding regions and estimates of genetic gain from selection. PLoS One 7. https://doi.org/10.1371/journal.pone.0044303
Haygreen J, Bowyer J (1996) Forest products and wood science, 3rd edn. Iowa State University Press, Ames, p 484
Hernandez RE, Koubaa A, Beaudoin M, Fortin Y (1998) Selected mechanical properties of fast-growing poplar hybrid clones. Wood Fiber Sci 30:138–147
Ilstedt B, Gullberg U (1993) Genetic variation in a 26-year old hybrid aspen trial in southern Sweden. Scand J For Res 8:185–192
Isik K, Kleinschmit J, Steiner W (2010) Age-age correlations and early selection for height in a clonal genetic test of Norway spruce. For Sci 56:212–221
Ivkovich M (1996) Genetic variation of wood properties in balsam poplar (Populus balsamifera L.). Silvae Genet 45:119–124
Kennedy RW, Smith JG (1959) The effect of some genetic and environmental factors on wood quality in poplar. Pulp Pap Mag Can 59:37–38
Koubaa A, Hernandez RE, Beaudoin M (1998) Shrinkage of fast-growing hybrid poplar clones. Forest Products J 48:82–87
Krzysik F (1974) Nauka o drewnie. PWN, Warszawa
Lambeth CC (1980) Juvenile–mature correlations in Pinaceae and implications for early selection. For Sci 26:571–580
Leboldus JM, Blenis PV, Thomas BR (2007) Evaluating the interaction between genotype and water stress in the hybrid poplar – Septoria musiva pathosystem. Can J Bot 85:1098–1102
Leboldus JM, Blenis PV, Thomas BR (2008) Clone by isolate interaction in the hybrid poplar–Septoria musiva pathosystem. Can J For Res 38:1888–1896
LeBoldus JM, Blenis PV, Thomas BR, Feau N, Bernier L (2009) Susceptibility of Populus balsamifera to Septoria musiva: a field study and greenhouse experiment. Plant Dis 93:1146–1150
Lindquist CH, Cram WH, Howe JAG (1977) Walker Poplar. Can J Plant Sci 57:1019
Lippman ZB, Zamir D (2007) Heterosis: revisiting the magic. Trends Genet 23:60–66
Lo MH, Abrahamson LP, White EH, Manion PD (1995) Early measures of basal area and canker disease predict growth potential of some hybrid poplar clones. Can J Res 25:1113–1118
Mottet MJ, Lamontagne D, Caron F, Fauchon A, Perinet P (2007) Risk management of Septoria canker in Quebec hybrid poplar plantation. In: Conference handbook – Annual Meeting of the Poplar Council of Canada, 16–21 Septembre 2007 p. 59
Mutibarić J (1971) Comparative qualitative relationships of wood properties of Euramerican poplars. Silvae Genet 20:199–204
Nepveu G, Keller R, Tessier du Cross E (1978) Selection juvenile pour la qualite du bois chez certains peupliers noirs. Ann Sci Forest 35:69–92
Newcombe G, Ostry ME (2001) Recessive resistance to Septoria stem canker of hybrid poplar. Phytopathology 91:1081–1084
Niemczyk M, Thomas BR (2020). Growth parameters and resistance to Sphaerulina musiva induced canker are more important than wood density for increasing genetic gain from selection of Populus spp. hybrids for northern climates. V1. Zenodo. [dataset]. https://zenodo.org/record/3627992#.Xk-jMWhKiF4
Olson JR, Jourdain CR, Rousseau RJ (1985) Selection for cellulose content, specific gravity and volume in young Populus deltoides clones. Can J For Res 15:393–396
Ostry ME, Mcnabb HS Jr (1985) Susceptibility of Populus species and hybrids to disease in the North Central United States. Plant Dis 69:755–757
Ostry M, Ramstedt M, Newcombe G, Steenackers M (2014) Diseases of poplars and willows. In: Isebrands JG, Richardson J (eds) Poplars and willows: trees for society and the environment. CABI International, Wallingford, pp 443–458
Pliura A, Yu Q, Zhang SY, MacKay J, Perinet P, Bousquet J (2005) Variation in wood density and shrinkage and their relationship to growth of selected poplar hybrid crosses. For Sci 51:472–482
Pliura A, Zhang SY, MacKay J, Bousquet J (2007) Genotypic variation in wood density and growth traits of poplar hybrids at four clonal trials. For Ecol Manag 238:92–106. https://doi.org/10.1016/j.foreco.2006.09.082
Pliura A, Suchockas V, Sarsekova D, Gudynaite V (2014) Genotypic variation and heritability of growth and adaptive traits, and adaptation of young poplar hybrids at northern margins of natural distribution of Populus nigra in Europe. Biomass Bioenergy 70:513–529. https://doi.org/10.1016/j.biombioe.2014.09.011
Qin R, LeBoldus JM (2014) The infection biology of Sphaerulina musiva: clues to understanding a forest pathogen. PLoS One 9. https://doi.org/10.1371/journal.pone.0103477
Rae AM, Robinson KM, Street NR, Taylor G (2004) Morphological and physiological traits influencing biomass productivity in short-rotation coppice poplar. Can J For Res 34:1488–1498. https://doi.org/10.1139/x04-033
Riemenschneider DE (1988) Heritability, age-age correlations, and inferences regarding juvenile selection in jack pine. Forest Sci 34(4):1076–1082. https://doi.org/10.1093/forestscience/34.4.1076
Rytter L, Kilpeläinen A, Muiste P, Torssonen P, Lazdina D, Löf M, Madsen P, Muiste P, Stener LG (2016) Increased forest biomass production in the Nordic and Baltic countries – a review on current and future opportunities. Silva Fenn:50. https://doi.org/10.14214/sf.1660
Schroeder W, Soolanayakanahally R, Lindquist C (2013) Okanese poplar. Can J For Res 93:1281–1283
Searle SR, Casella G, McCulloch CE (1992) Variance components. Wiley, New York, p 501
Stanton BJ, Serapiglia MJ, Smart LB (2014) In: Isebrands JG, Richardson J (eds) The domestication and conservation of Populus and Salix genetic resources. Poplars and willows: trees for society and the environment. CABI international, Wallingford, pp 124–199
Stettler R, Bradshaw T, Heilman P, Hinckley T (eds) (1996) Biology of Populus and its implications for management and conservation. NRC Research Press
Valente CA, de Sousa M, Furtado F, de Carvalho AP (1992) Improvement program for Eucalyptus globulus at Portucell: technological component. Appita J 45:403–407
Walters CS, Bruckmann B (1965) Variation in specific gravity of cotton- wood: as affected by tree sex and stand location. J For 63:182–185
Ward KT, Ostry ME (2005) Variation in Septoria musiva and implications for disease resistance screening of poplars. Plant Dis 89:1077–1082
White TL, Adams WT, Neale DB (ed) (2007) Forest genetics. Cabi
Yanchuk AD, Dancik BP, Micko MM (1983) Intraclonal variation in wood density of trembling aspen in Alberta. Wood Fiber Sci 15:387–394
Yanchuk AD, Dancik BP, Micko MM (1984) Variation and heritability of wood density and fiber length of trembling aspen in Alberta, Canada. Silvae Genet 33:11–16
Yáñez MA, Zamudio F, Espinoza S, Ivković M, Guerra F, Espinosa C, Baettig RM (2019) Genetic variation and growth stability of hybrid poplars in high-density short-rotation coppice stands in central Chile. Biomass Bioenergy 120:84–90
Yu Q, Pulkkinen P (2003) Genotype-environment interaction and stability in growth of aspen hybrid clones. For Ecol Manag 173:25–35. https://doi.org/10.1016/S0378-1127(01)00819-2
Yu Q, Pulkkinen P, Rautio M, Haapanen M, Alen R, Stener LG, Beuker E, Tigerstedt PMA (2001) Genetic control of wood physiochemical properties, growth and phenology in hybrid aspen clones. Can J For Res 31:1348–1356
Zalesny RS Jr, Stanturf JA, Gardiner ES, Perdue JH, Young TM, Coyle DR, Headlee WL, Banuelos GS, Hass A (2016) Ecosystem services of woody crop production systems. BioEnergy Research 9:465–491. https://doi.org/10.1007/s12155-016-9737-z
Zamudio F, Wolfinger R, Stanton B, Guerra F (2008) The use of linear mixed model theory for the genetic analysis of repeated measures from clonal tests of forest trees. I. A focus on spatially repeated data. Tree Genet Genomes 4:299–313. https://doi.org/10.1007/s11295-007-0110-4
Zhang SY (1995) Effect of growth rate on wood specific gravity and selected mechanical properties in individual species from distinct wood categories. Wood Sci Technol 29:451–465
Zhang SY, Yu Q, Chauret G, Koubaa A (2003) Selection for both growth and wood properties in hybrid poplar clones. For Sci 49:901–908
Zobel B, van Buijtenen J (1989) Wood variation, its causes and control. Springer, Berlin, Heidelberg, New York, p 363
Acknowledgements
We are thankful to Dr. Erwin Dreyer and anonymous reviewers for providing us with valuable comments on improving the quality of this manuscript. We also wish to express our gratitude to Pierre Périnet (QC) who conducted the breeding, Bobby (Yue) Hu (University of Alberta) and David Kamelchuk (Alberta-Pacific Forest Industries Inc.) for their contributions to field data collection, and Marek Karwański (Warsaw University of Life Sciences) for fruitful conversations bringing useful insights into the use of mixed models.
Funding
This manuscript was developed under a scholarship grant to Marzena Niemczyk within a Scholarship Fund of the Forest Research Institute, pursuant to the decision of the Head of the Institute dated 20 October 2017 (based on an agreement concluded on 23 October 2017 with a further Annex no. 1 of 2, May 2018) and start-up funds of Barb R. Thomas. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Handling Editor: Ricardo Alia
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contribution of the co-authors Conceptualization: Barb R. Thomas and Marzena Niemczyk; formal analysis: Marzena Niemczyk; funding acquisition: Marzena Niemczyk and Barb R. Thomas; investigation: Marzena Niemczyk; methodology: Marzena Niemczyk and Barb R. Thomas; resources: Barb R. Thomas; writing—original draft preparation: Marzena Niemczyk; writing—review and editing: Barb R. Thomas and Marzena Niemczyk.
Appendix
Appendix
Diameter at breast height (DBH), height (H), mean annual increment (MAI), and canker severity over time for cross-types (left panel) and families (right panel). The horizontal dotted lines indicate mean values at a given age for all trees on plantation. Mean values for control clones Walker and Okanese shown with their standard errors (vertical bars)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Niemczyk, M., Thomas, B.R. Growth parameters and resistance to Sphaerulina musiva-induced canker are more important than wood density for increasing genetic gain from selection of Populus spp. hybrids for northern climates. Annals of Forest Science 77, 26 (2020). https://doi.org/10.1007/s13595-020-0931-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13595-020-0931-y