Introduction

With increasing climatic events affecting forest trees (e.g., Benomar et al. 2022; Kirilenko and Sedjo 2007) and arrival of new forest pests further north (Frankel et al. 2012), the study of presence and intensity of a potential trade-off between growth and response to biotic and abiotic stresses is becoming crucial for tree survival. Although some authors suggest the existence of a trade-off between growth and pest resistance (e.g., de la Mata et al. 2017; Herms and Mattson 1992), others find that trees showing vigorous growth show better resilience to environmental stress (e.g., Laverdière et al. 2022; Lenz et al. 2020b; Porth et al. 2012). Since breeding programs have an economic goal (White et al. 2007), growth traits and survival have been widely selected by tree breeders as they are directly linked to commercial tree plantations. While total height growth represents the general response of a tree to its past and actual environments, now it seems essential to also add some direct adaptive traits in breeding objectives. Indeed, that will allow parent trees and their progeny to cope with current and future conditions and, as a result, ensure long-term plantation productivity and resilience.

Poplars are one of the fastest-growing trees in Canada. Their economic contribution is non-negligible as they represented 66% of hardwood trees harvested in 2017 (Kort and Schroeder 2020). Hybridization in poplars allows breeders to take advantage of the positive heterosis, commonly known as hybrid vigor, which is well recognized to improve growth (e.g., Rood et al. 2017). Besides growth, hybridization allows combination of favorable traits (e.g., disease and insect resistance, adaptation medium fertility soil, etc.) (Riemenschneider et al. 2001). In North America, poplar breeders have been focusing on increasing the resistance of hybrids to Sphaerulina musiva (Peck) Quaedv., Verkley, and Crous (syn. Septoria musiva Peck) a native ascomycete responsible for leaf spot and canker disease on poplar trees (e.g., Mottet et al. 1991). The native species Populus deltoides Marsh. and Populus balsamifera L. have been naturally in contact with the pathogen and are more resistant compared to Populus maximowiczii A. Henry and Populus trichocarpa Torr. & Gray (Muchero et al. 2018; Newcombe et al. 2001). As a result, most hybrids in the Quebec breeding program have one of P. deltoides or P. balsamifera as a parent as they show good adaptation and are often associated with more resistance to this disease (Mottet et al. 1991). But the disease continues to be one of the most important factors limiting the hybrid poplar production (Feau et al. 2010; Rousseau et al. 2022) and is spreading to new regions now reaching some with naive host (Callan et al. 2007). This situation amplifies the need for identifying resistant clones as deployment of resistant clones is one of the best ways to cope with this pathogen (Feau et al. 2010; Mottet et al. 2007). Moderate estimates of the broad-sense heritability of resistance to Sphaerulina musiva have been obtained on P. trichocarpa (Muchero et al. 2018) while low estimates were obtained on crosses between native and non-native poplars in common gardens (Niemczyk and Thomas 2020). This indicated that variation in resistance could be partially attributed to genetic factors. Moreover, Niemczyk and Thomas (2020) also suggest that genetic gain on resistance should be achievable without compromising growth gains. On the other hand, while having clones showing good resistance and growth is already appreciable, several other traits such as the apical dominance, stem form, branching habit or adaptive traits such as frost resistance (or cold hardiness) and phenology have shown good potential for selection with moderate to high broad-sense heritability estimates (Adler et al. 2021; Karacic et al. 2021; Pliura et al. 2014) and should therefore also be considered in clonal deployment. Accordingly, these traits could also be included in multi-trait selection (Riemenschneider et al. 1992).

Poplar breeding programs are generally considering two timelines, where the long-term strategy is to maintain a diverse genetic pool into the intraspecific populations, and the short-term strategy is to select clonal varieties for operational use (Stettler 1996). Usually, clonal selection is based on many individual hybrids which are being tested on multiple sites up to the selection of the best clones for operational deployment. However, as to plan selection strategies, and many others breeding program activities to improve the breeding populations, tree breeders must also obtain an estimation of genetic parameters such as the heritability of traits of interest or the general combining ability (GCA). The latter represents the result of additive effect of genes, as well as their interaction and, as a result, allows a good evaluation of the parents of a breeding population. One of the strategies that allow the evaluation the GCA is a polycross design. As stated by Lenz et al. (2020a), by using a common mix of pollen from the male trees, which is assumed to be equal in regard of fertilization effectiveness (Fowler 1987), to pollinate a female tree, this design has the advantage to give a large number of parental combinations (Lambeth et al. 2001). Such design is simple to implement while giving good estimates of potential genetic gains but, on the other hand, only allows to evaluate the breeding values of the mothers where each of her progenies are considerate half-sibs. Otherwise, one needs to identify fathers with molecular markers to allow full-sib analysis, father GCA estimation and specific combining ability (SCA) (e.g., Lambeth et al. 2001; Lenz et al. 2020a).

This paper focus on two non-native poplars species in Quebec, P. maximowiczii and P. trichocarpa, which are known to produce hybrids progenies that have vigorous growth and being well suited for biomass production but lack coevolutionary background with the pathogen Sphaerulina musiva.

This study aims to (1) estimate the genetics parameters, such as heritability, genetic correlations and breeding values for growth traits (total height and diameter), quality (adventitious branches, multiple stems, multiple tops) and adaptive traits (cold hardiness), (2) to characterize the susceptibility and resistance against Sphaerulina musiva canker in non-native hybrids, and (3) to evaluate the effect of including spatial variability on model fit.

Material and methods

Genetic material, sites, and field design

Parental material was composed of Populus maximowiczii and Populus trichocarpa, hereafter referred as M and T, respectively. M of this study is from the island of Hokkaido, in Japan, and represent two regions, one around Sapporo and one in the central part of the island represented by three different altitudes (475 m, 580 m and 920 m). Our T material is in majority from different parts of Oregon, USA and completed with some material from the south of British Columbia, Canada, ranging between 44.3° and 50.6° of latitude. All parental material was already tested in 2 clonal trials in the province of Quebec, in areas with the presence of Sphaerulina musiva. The selected parents were considered well adapted as they showed some resistance and according to their survival and good performance in those environments.

In 2012, interspecific crosses were conducted between those two parental breeding populations, using a polymix crossing scheme with 24 males (11 T and 13 M) and 18 females (8 T and 10 M). A total of 34 families (25 M × T and 9 T × M) represented by a maximum of 40 individuals each was obtained. The seeds were planted during the spring of 2013 at the Grandes-Piles nursery. To plant identical biological material on two contrasting sites (Table 1), two cuttings of 25 cm on each individual were taken during autumn 2014 and planted on both sites during the spring of 2015. On each site, a randomized complete block design with 20 blocks was established. Each block contained from two to four single tree plots per family for a total of 1290 trees per site.

Table 1 Location and climatic dataa of the two sites
Full size table

Each site was about 1.1 ha including buffer trees, with an initial spacing between trees of 2 m × 3.25 m and characterized by a well-drained loamy soil. The first two years (2015–2016), herbicide as well as mouse traps, were used to limit vegetation competition and herbivory damage. In 2017, the first thinning was done by removing approximately one tree out of three to keep between 25 and 30 trees per family on each site.

Data collection

After the first growing season on planting sites, all the trees were measured for total height (TH), in cm, using a graduated rule. A second measurement campaign was done during spring 2018 (3 years after planting) where each tree was measured for TH, using a vertex on Grande-Piles site and a graduated rule on Normandin site, for diameter at breast height (DBH), in mm, using a caliper and the length of frost dieback during the winter of 2016–2017 (second year after planting), using a graduated rule. Presence/absence observations were also noted to evaluate adventitious branches, multiple stems, and multiple tops in addition to the number for each of these traits. Finally, a third measurement campaign was done during autumn 2020 (6 years after planting) where each tree was measured for TH, using a vertex and DBH, using a caliper. Categorical observations of Sphaerulina musiva susceptibility and resistance traits were also noted as follows:

$$Pres\_ SphaerulinaCanker=\left\{\ \begin{array}{cc}0& if\ absence\ of\ active\ canker\ on\ main\ stem\\ {}1& if\ at\ least\ on e\ active\ canker\ on\ main\ stem\end{array}\right.$$
$$Resistance=\left\{\begin{array}{ll} Not\ resistant\kern3em & if\ cankers\ are\ active, top\ could\ or\ is\ broken\ up\kern1.5em \\ {}Moderatly\ resistant& if\ cankers\ are\ healing, with\ stem\ deformation\\ {} Resistant\kern5em & if\ cankers\ are\ healing, with out\ stem\ deformation\end{array}\right.$$
$$Non\_ Resistant=\left\{\kern0.5em \begin{array}{ll}0& if\ cankers\ are\ healing, with\ or\ without\ stem\ deformation\\ {}1& if\ cankers\ are\ active, top\ could\ or\ is\ broken\ up\kern5.75em \end{array}\right.$$

Note that the last two variables related to resistance to Sphaerulina musiva canker are defined only for trees with at least one canker observation at 6 years old since the goal is to measure the response of trees to attacks.

Statistical analyses

Models

Analyses were done separately for variables measured in 2017 and 2020. The model used for the growth variables included sites as fixed-effect factor, while the blocks nested in the sites, the families, as well as the interaction between them and the sites, were considered as random-effect factors.

$${Y}_{ijkl}=\mu +{S}_i+B{(S)}_{j(i)}+{F}_k+{\left(S\times F\right)}_{ik}+{\varepsilon}_{l(ijk)}$$

where

Yijkl:

measured trait value for the tree l of family k located in block j of site i

μ:

overall mean

S i:

site effect i(i = GPI, NOR)

B(S)j(i):

:block effect j of site i( j = 1, …, 20), \(B{(S)}_{j(i)}\sim \kern0.5em N\left(0,{\sigma}_{B(S)}^2\right)\)

F k:

family effect k(k = 1, ..., 34), \({F}_k\sim \kern0.5em N\left(0,{\sigma}_F^2\right)\)

(S × F)ik:

interaction effect between site i and family k, \({\left(S\times F\right)}_{ik}\sim \kern0.5em N\left(0,{\sigma}_{S\times F}^2\right)\)

ε l(ijk):

experimental error, \({\varepsilon}_{l(ijk)}\sim \kern0.5em N\left(0,{\sigma}_{\varepsilon}^2\right)\)

For the three variables related to Sphaerulina canker, the sites, as well as the interaction between the family and the sites, were removed from the model since only the data from the Normandin site were analyzed.

Other models were tested, one considering a different residual variance for each site \(({\sigma}_{\varepsilon \_ NOR}^2\ and\ {\sigma}_{\varepsilon \_ GPI}^2\Big)\), and some spatial models, in which the residuals were modeled as ε = ξ + η where ξ is a vector of spatially dependent residuals and η is the vector of spatially independent residuals. A separable first-order autoregressive process (AR1 ⊗ AR1) was used to model covariance structure of ξ (Costa e Silva et al. 2001; Dutkowski et al. 2002). The R matrix was given by \(\boldsymbol{R}={\sigma}_{\xi}^2\ \left[ AR1\left({\rho}_{col}\right)\otimes AR1\left({\rho}_{row}\right)\right]+{\sigma}_{\eta}^2\ \boldsymbol{I}\) where \({\sigma}_{\xi}^2\)and \({\sigma}_{\eta}^2\) are respectively the spatial and non-spatial residual variances, AR1(ρcol) and AR1(ρrow) represent first-order autoregressive correlation matrices for columns and rows, respectively, I is the identity matrix, and ⊗ is the Kronecker product. The base and spatial models were compared using Akaike Information Criterion (AIC, Akaike 1974) and Schwarz’s Bayesian Information Criterion (BIC, Schwarz 1978) values. Better model fits are represented by smaller values for AIC and BIC.

All analyses were carried out using ASReml Stand-alone software (version 4.1, Gilmour et al. 2014) which provided REML or Pseudo-REML estimates of variance components for random effects and effect predictions for sites and families used to calculate predicted breeding values of the families with R Statistical Software (v4.0.3; R Core Team 2021). To determine whether the variance estimates were significantly greater than 0, likelihood ratio tests were conducted using ASReml for continuous variables (the model with and without the term to be tested) and the COVTEST statement of the SAS GLIMMIX procedure (SAS statistical software version 9.4, SAS Institute Inc., Cary, North Carolina, USA) for qualitative variables.

Heritabilities and type-B genetic correlation

For continuous traits, heritabilities were calculated using the following equations:

One site models:

$${h}_{ind}^2=\kern0.5em \frac{4\ {\sigma}_F^2}{\left({\sigma}_F^2+{\sigma}_{\varepsilon}^2\right)}$$
$${h}_{fam}^2=\kern0.5em \frac{\sigma_F^2}{\left({\sigma}_F^2+\frac{\sigma_{\varepsilon}^2}{n_{hbl}\bullet {n}_{hpe}}\right)}$$

Multi-sites models:

$${h}_{ind}^2=\kern0.5em \frac{4\ {\sigma}_F^2}{\left({\sigma}_F^2+{\sigma}_{S\times F}^2+{\sigma}_{\varepsilon}^2\right)}$$
$${h}_{fam}^2=\kern0.5em \frac{\sigma_F^2}{\left({\sigma}_F^2+\frac{\sigma_{S\times F}^2}{n_s}+\frac{\sigma_{\varepsilon}^2}{n_s\bullet {n}_{hbl}\bullet {n}_{hpe}}\right)}$$

where \({\sigma}_F^2\), \({\sigma}_{S\times F}^2\), and \({\sigma}_{\varepsilon}^2\) represent the variance associated with family, site × family interaction and residual variance, respectively. The terms ns, nhbl, and nhpe represent the number of sites, the harmonic mean of the number of blocks per site, and the harmonic mean of the number of trees per block-progeny, respectively.

When a different residual variance was estimated for each site (heterogeneous residual error variances), the mean value of the residual variances was used in \({h}_{ind}^2\), so \({\sigma}_{\varepsilon}^2\) was therefore replaced by\({\overline{\sigma}}_{\varepsilon}^2\), where \({\overline{\sigma}}_{\varepsilon}^2\)corresponds to \(\left({\sigma}_{\varepsilon \_ GPI}^2+{\sigma}_{\varepsilon \_ NOR}^2\right)/2\), whereas \({h}_{fam}^2\) included a weighted average of within-environment variances, the part related to \({\sigma}_{\varepsilon}^2\) in the denominator being replaced by \(\kern0.5em \frac{1}{2}\times \left(\frac{\sigma_{\varepsilon \_ GPI}^2}{n_s\bullet {n}_{hbl\_ GPI}\bullet {n}_{hpe\_ GPI}}+\frac{\sigma_{\varepsilon \_ NOR}^2}{n_s\bullet {n}_{hbl\_ NOR}\bullet {n}_{hpe\_ NOR}}\right)\) (Isik et al. 2017).

Spatial models:

For spatial models, a better fit to the data is generally obtained, but with a larger residual variance. Since the calculations use only the variance components and ignore the correlations between the residual effects, if the residual variance increases, the estimates of the heritabilities will decrease. To properly account for correlated residuals, the equation used to calculate the adjusted family heritability is as follows (Cullis et al. 2006; Isik et al. 2017; Piepho and Möhring 2007) :

$${h}_{fam\_C}^2=1-\frac{{\overline{V}}_{BLUP\_ difference}}{2\ {\sigma}_F^2}$$

where \({\overline{V}}_{BLUP\_ difference}\) is the mean variance of the difference between two families.

For qualitative traits such as binary traits (presence/absence), binary distribution and logit linkage function were considered. Using the variance of the standard logistic distribution ( π2/3 = 3.29) as an estimate of residual variance on the logit scale (De Silva et al. 2014; Isik 2011; Nakagawa and Schielzeth 2010), heritabilities were calculated as follows:

$${h}_{ind}^2=\kern0.5em \frac{4\ {\sigma}_F^2}{\left({\sigma}_F^2+{\sigma}_{S\times F}^2+\frac{\pi^2}{3}\right)}$$
$${h}_{fam}^2=\kern0.5em \frac{\sigma_F^2}{\left({\sigma}_F^2+\frac{\sigma_{S\times F}^2}{n_s}+\frac{\pi^2/3}{n_s\bullet {n}_{hbl}\bullet {n}_{hpe}}\right)}$$

Whereas for the multinomial categorical trait related to Sphaerulina canker, a multinomial distribution and logit linkage function were considered, and heritabilities were calculated as follow:

$${h}_{ind}^2=\kern0.5em \frac{4\ {\sigma}_F^2}{\left({\sigma}_F^2+\frac{\pi^2}{3}\right)}$$
$${h}_{fam}^2=\frac{\sigma_F^2}{\left({\sigma}_F^2+\frac{\pi^2/3}{n_{hbl}\bullet {n}_{hpe}}\right)}$$

For traits corresponding to a count (number of tops/stems/branches), the Poisson distribution and the log link function were used, and the heritabilities were calculated based on the link function (Nakagawa and Schielzeth 2010):

$${h}_{ind}^2=\kern0.5em \frac{4\ {\sigma}_F^2}{\left({\sigma}_F^2+{\sigma}_{S\times F}^2+\varphi \ln \left({\lambda}^{-1}+1\right)\right)}$$
$${h}_{fam}^2=\frac{\sigma_F^2}{\left({\sigma}_F^2+\frac{\sigma_{S\times F}^2}{n_s}+\frac{\varphi\ \ln \left({\lambda}^{-1}+1\right)}{n_s\bullet {n}_{hbl}\bullet {n}_{hpe}}\right)}$$

where λ is the mean of the response variable, and φ is the dispersion parameter, taking the value of 1 if it has not been included in the model. A dispersion parameter was added when the variance of the Pearson residuals was not close to the value of 1 to address the over or under dispersion problem.

Type-B genetic correlation:

For all traits, the type-B genetic correlation was obtained using the following equation:

$${r}_B=\frac{\sigma_F^2}{\sigma_F^2+{\sigma}_{S\times F}^2}$$

Age-age correlation and phenotypic correlations

Age-age correlations, corresponding to type A genetic correlations, and phenotypic correlations were calculated for TH and DBH between the 2 years of measurement, i.e., 3 (2017) and 6 years (2020). The randomized block model in a bivariate analysis was used with the inclusion of the year (3 and 6 years) as a fixed-effect factor and its interaction with the site factor. The unstructured covariance matrix was used to estimate variance and covariance components of the growth trait measured at 3 and 6 years for genotypic, genotype × environment, and experimental error. All measurements of living trees at 6 years old were retained for the analyses. The following formulas were used:

$${r}_{A\_3-6}=\frac{{\sigma_F}_{3-6}}{\sqrt{\sigma_{F\_3}^2+{\sigma}_{F\_6}^2}}$$

where

rA _ 3 − 6:

type A genetic correlation between the trait measured at 3 and 6 years

σ F3 − 6:

family covariance between the trait measured at 3 and 6 years

\({\sigma}_{F\_3}^2\):

family variance at 3 years

\({\sigma}_{F\_6}^2\):

family variance at 6 years

$${r}_{p\_3-6}=\frac{{\sigma_F}_{3-6}+{\sigma_{S\times F}}_{3-6}+{\sigma_{\varepsilon}}_{3-6}}{\sqrt{\left({\sigma}_{F\_3}^2+{\sigma}_{S\times F\_3}^2+{\sigma}_{\varepsilon \_3}^2\ \right)\bullet \left({\sigma}_{F\_6}^2+{\sigma}_{S\times F\_6}^2+{\sigma}_{\varepsilon \_6}^2\ \right)}}$$

where

rp _ 3 − 6:

phenotypic correlation between the trait measured at 3 and 6 years

σ F3 − 6:

family covariance between the trait measured at 3 and 6 years

σ S × F3 − 6:

covariance of site × family interaction between the trait measured at 3 and 6 years

σ ε3 − 6:

family variance at 3 years

\({\sigma}_{F\_3}^2\):

variance of site × family interaction at 3 years

\({\sigma}_{S\times F\_3}^2\):

experimental error variance at 3 years

\({\sigma}_{\varepsilon \_3}^2\):

family variance at 6 years

\({\sigma}_{F\_6}^2\):

variance of site × family interaction at 6 years

\({\sigma}_{S\times F\_6}^2\):

experimental error variance at 6 years

\({\sigma}_{\varepsilon \_6}^2\):

Standard errors of estimated genetic parameters were calculated using the delta method based on a Taylor series expansion.

Breeding values

Family breeding values (BV) are obtained by doubling the predicted values obtained for each family, which correspond to the general combining ability (GCA). The adjusted values ( BVadj) are obtained by adding the overall mean of the measured trait, in the original scale (μ) or in the logit (μ_logit) or log (μ_log) scale, and by applying the inverse of the link function for categorical traits:

$${BV}_{adj}=\left\{\begin{array}{l}2\ GCA+\mu \kern0.5em for\ quantitative\ traits\\ {}\begin{array}{cc}\frac{e^{\left(2\ GCA+\mu \_ logit\right)}}{1+{e}^{\left(2\ GCA+\mu \_ logit\right)}}& for\ binary\ traits\end{array}\\ {}\begin{array}{cc}{e}^{\left(2\ GCA+\mu \_\mathit{\log}\right)}& for\ number\ of\ tops, stems, branches\end{array}\end{array}\right.$$

Genetic gain

The theoretical calculation of expected gain (∆G = i × h2 × CV where i = 1.755 is the intensity of selection based on top 10% families, h2 corresponds to the individual or family heritability, and CV is the coefficient of variation, calculated as the phenotypic standard deviation divided by the mean of the measured trait) was calculated for each trait and compared to the empirical genetic gain corresponding to the average of the breeding values of the selected families (top 10% families).

Results and discussion

Polycross performance

A moderately good success rate was observed for the different crosses. The number of seedlings produced ranged from 28 to 126 seedlings per family while the germination rate was between 12% and 50%. In general, the M × T families had a better germination rate (on average 39%) than the T × M families (on average 24%).

The germination rate was lower than what we normally observe when sowing poplar seeds from previous control crosses (above 90%, data not shown). This could be explained by temperature control problems in the greenhouses in 2012 during seed maturation. For consecutive days, temperatures between 30 and 40 °C were often reached. This might have caused thermal stress which had a negative impact on seed maturation and delayed embryonic development, as observed with binoculars. The negative effect of thermal stress during seed maturation had already been formally observed for Populus nigra (Dewan et al. 2018). This embryonic delay was more present for T × M than for M × T, which could, at least partially, explain the lower germination success for these crosses. According to these preliminary results, it seemed that T mothers are more sensitive than M mothers during seed maturation, but a more structured experiment is required to document this observation.

General observations on tree establishment and performance

Tree survival was very good on both sites, being 97% 1 year after planting and 96% 3 years after planting. These high survival rates show good establishment and that trees were well adapted to their environments.

Morphological traits, such as multiple tops (291 trees; 12%), adventitious branches (144 trees; 6%), multiple stems (147 trees; 6%), and frost dieback (283 trees; 12%), were observed in low proportions on both sites and in a similar manner (± 1%) except for the presence of frost dieback which is greater at Grandes-Piles (182 trees; 15%) than at Normandin (101 trees; 9%). This could be because most of the traits measured in this experiment are weakly regulated by the environment, unlike frost dieback. Effectively, this latter trait can be related to cold hardiness (Lazdiņa et al. 2016) and that could explain different responses in the two planting sites. Frost dieback was also more severe on affected trees at Grandes-Piles (122.6 ± 4.8 cm), the southernmost site, than at Normandin (96.0 ± 5.3 cm). This could be explained by a later budset, which have been correlated with longer day length and higher temperature (Rohde et al. 2011a). While this can benefit growth, later budset could also cause frost damage caused by early or late frost events during the fall and the spring (Howe et al. 2000). Frost damage such as frost dieback can have negative impact on growth, especially when observed in consecutive years, as well as on stem quality (Zalasky 1976). As these events are expected to increase with climate change, more observations and monitoring seems essential to include adaptive traits, such as frost resistance, in breeding programs to ensure plantation performance.

As expected, growth after 6 years was better at Grandes-Piles (1492.8 ± 8.3 cm in TH and 140.3 ± 1.2 mm in DBH—within the sugar maple-yellow birch bioclimatic domain) as compared to Normandin (901.4 ± 5.9 cm in TH and 90.4 ± 0.8 mm in DBH—within the balsam fir-yellow birch bioclimatic domain). Some families stand out in terms of growth in height and diameter, both positively and negatively and differences seem to increase with time, based on values averaged on both sites. Nevertheless, longer term monitoring would be needed to ensure that these observations are maintained until maturity.

Sphaerulina musiva canker was observed in greater proportion at the Normandin site (351 attacked trees; 33%) compared to Grandes-Piles (25 attacked trees; 2%), but most trees remain unattacked. The occurrence per family ranged from 0 to 68% attacked trees. Most observed cankers were still considered active as trees were not yet showing the ability to repel the canker. Only 29 trees (8%), from 21 different families, showed the ability to repel the canker and to heal but more should be observed as the infection phase was still at a young stage.

Model selection and variation on genetic parameters

As observed in many forest genetic trials (e.g., Dutkowski et al. 2006; Ye and Jayawickrama 2008; Zas Arregui 2006), for growth traits the spatial model showed the best fit to the data according to the log likelihood value (Log L),and the AIC and BIC criteria. However, convergence difficulties with spatial models were observed for most qualitative traits. The best model for each variable, based on AIC and BIC criteria, is identified in bold in Online Resource 1 and their genetic parameters are reported in Tables 2, 3 and 4. The results of the analyses of qualitative variables show that although models can be estimated for binary and multinomial variables, enough occurrence is important to obtain reliable results (Isik 2011). As expected, it is also observed that the estimated individual heritability from spatial analysis is generally lower than the estimated heritability with the classical block method since the spatial autocorrelation effect tends to increase the residual variance and thus decrease the heritability value as previously stated. However, the family heritability and adjusted family heritability show very little variation from one model to another and as expected, the adjusted family heritability is higher than the unadjusted one with the best model. As compared to observation of Ye and Jayawickrama (2008), our estimated adjusted family heritabilities were not really better with the best model; we observed very small variation for growth traits and qualitative traits. We also observed very low variation of type-B genetic correlation according to various models tested. The best spatial model led to higher or lower type-B correlations, as compared to Belaber et al. (2019), who observed higher type-B correlation for spatial models.

Table 2 Means, variance components, and genetic parametersa for growth traits on both trials according to the best model
Full size table
Table 3 Means, variance components, and genetic parametersa for morphological traits on both trials according to the best model
Full size table
Table 4 Means, variance components, and genetic parametersa for adaptive traits according to the best model
Full size table

Genetics parameters for growth and morphology

The family variance for growth traits accounted for a significant proportion of the total variance (between 10.22 and 13.99%; Table 2). Tree age did not seem to affect this proportion, at least within the range used (at 3 and 6 years after planting). This shows that genetic variation exists between half-sib families for these traits and that those traits could be interesting for selection. For morphological traits, family variance is present but in smaller proportions (between 0.76 and 5.13%; Table 3). This makes these traits less interesting for selection purpose.

Individual narrow sense heritabilities at 3 and 6 years old for TH and DBH indicate moderate to high genetic control while family narrow sense heritabilities show high genetic control (Table 2). The interaction between genetic and environment is weak, as demonstrated by the high type-B correlation. These values are higher than those reported by Ding et al. (2020) on aspen (Populus tremuloides Michx; ranging from 0.03 to 0.54) and by Berguson et al. (2017) for basal area on different Populus species (P. deltoides, P. maximowiczii, P. nigra) and their hybrids (ranging from 0.487 to 0.893). In our case, being on nursery grounds, little difference in the microenvironment on the two sites and between sites was observed. This has probably reduced the effect of environmental variation, resulting in very high heritability values as well as high type-B correlation. However, the fast growth of poplar trees probably increased the variation between trees and families as observed by large standard errors for tree height and as compared to other taxa such as Picea (e.g., Mottet et al. 2015), and Pinus (e.g., Belaber et al. 2019). The small number of families could have had an impact on the estimation, although it has been suggested that smaller number of sampled families usually underestimates heritability values and that the impact on average values is usually little (Perron et al. 2013). The number of trees per family seems to have a more important impact and Perron et al. (2013) results agree with the optimum open-family size formula suggested by Robertson (1959; n=4/h2i). In the present study, the 40 individuals per family is largely over the optimum family size for all traits measured, which suggests that our estimates should be reliable although it should be kept in mind that the confidence intervals could be larger than expected due to the small number of families (Perron et al. 2013).

Morphological traits linked to trunk quality (multiple tops, adventitious branches and multiple stems) show low to moderate individual heritabilities and family heritabilities (Table 3) and are lower than those reported by Karacic et al. (2021) on other morphological traits for poplar. Heritability estimates are generally showing large standard errors, as expected due to low occurrence. Type-B correlations range from low to moderate with the highest value for multiple stems at 0.77. This is probably due once again to low occurrence on both sites. Most of the qualitative traits measured at a young age appear to be marginal in the population, which probably explains the problems of model convergence, except for the block model (Online resource 1). It would be interesting to continue monitoring these populations and test whether other qualitative morphological traits on older trees, such as trunk straightness, the presence of forks or the presence of large branches, might be more interesting for genetic selection in hybrid poplar (Karacic et al. 2021).

Genetics parameters of adaptive variables for frost dieback and Sphaerulina musiva susceptibility and resistance

The family variance for both susceptibilities to frost damage (presence/absence of frost dieback) and the presence/absence of Sphaerulina musiva, which is associated with the susceptibility to attacks, accounted for a significant proportion of the total variance (13.57% and 8.77% respectively; Table 4). This indicates that genetic variation exists between families for these traits and that they could be interesting for selection.

The presence/absence of frost dieback the second year after planting shows high individual and family heritabilities. This suggests that gain is possible by selecting parents less susceptible to frost damage. The high type B correlation also indicates that the interaction between genetics and environment is low, indicating that the best families are the same regardless of the site. These heritabilities are higher than those estimated by Howe et al. (2000) (H2 of 0.27), who assessed frost damage according to different scores. Several studies have shown that frost tolerance is strongly correlated with phenology and timing of budburst and budset (e.g., Menon et al. 2015; Pliura et al. 2014; Vitasse et al. 2014). In our population, it is interesting to note that T×M crosses seemed more sensitive to frost than M×T. Furthermore, within the M×T crosses, families with mothers from higher altitudes seemed less susceptible to frost dieback, which could indicate a potential relationship with phenology (data not shown). This relationship seems less clear for T×M crosses. Given that phenology traits are known to have moderate to high heritability estimates in poplar (e.g., Adler et al. 2021; Howe et al. 2000; Pliura et al. 2014; Rohde et al. 2011b), it would be advisable to evaluate it in the future to see if we could have greater genetic control over those traits within our population, especially since M×T crossing seems particularly sensitive to cold (Gudynaitė-Franckevičienė et al. 2020; Šēnhofa et al. 2021). Furthermore, it would be important to assess the relationships between growth, frost damage, and phenology, given that measuring phenology is more complex and demanding than assessing frost damage and that the relationship between growth and phenology is generally significant (Howe et al. 2000; Lazdiņa et al. 2016; Pliura et al. 2014; Šēnhofa et al. 2021; Stener and Westin 2017) but not always (Pliura et al. 2014; Schreiber et al. 2013a; Schreiber et al. 2013b).

The presence/absence of canker variable 6 years after planting shows moderate individual heritability but high family heritability (Table 4). These results show that family gains are possible, even by crossing two species that did not coevolve with the fungus to develop a higher natural resistance. The moderate to high heritabilities show that part of the variation in susceptibility is due to genetics, even if this trait was observed only on one site. This suggests that the selection of certain parents for crosses could reduce the susceptibility of their offspring to be attacked by the fungus. This analysis does not, however, take into account the response of the trees to the attack, which would be consistent with the evaluation of resistance. Longer term monitoring will be interesting to see if heritability values for susceptibility are maintained over time and if there is a correlation with resistance.

Although some models converged for the resistance to Sphaerulina musiva canker (results not presented), there was not enough trees in each category (even with the resistance binary variable). Since the variance associated with the families was very close to 0, and the standard error was not estimable, heritabilities were also close to 0. The almost zero variance associated with the families shows that selection based on resistance traits are of low interest for those populations and taxa, at least at that young age. However, other authors have shown that resistance in hybrid poplars is a trait partially controlled by genetics and that gains are possible without sacrificing growth, as the broad sense heritability for this trait was about 0.1 (Niemczyk and Thomas 2020). The use of greenhouse screening methods (e.g., Qin et al. 2014) would be interesting to integrate to see if there is a correlation with our results and to allow us to obtain results on resistance in less time. The combination of parental GCA and heritability as well as the integration of new screening methods appears to us as an interesting avenue for the long-term poplar breeding program to decrease susceptibility and increase resistance in breeding populations and for the deployment of resistant clones.

Age-age correlation and phenotypic correlations

The age-age genetic correlations for growth traits show highly positive correlation between 3 and 6 years old (Table 5). Type A genetic correlations are high and similar for height and DBH while phenotypic correlations show lower values, where DBH is higher than the height one. Those results were expected since the low difference in age, but are higher than those found by Niemczyk and Thomas (2020). As pointed out by the authors, their results as well as other studies found it to be lower between 3 years old and older age (e.g., Isik et al. 2010) which suggests that longer term monitoring should be carried out to see if those high correlations are maintained over time. Selection as early as 3 years old after planting would be a huge gain of time for the selection cycle and eventually for the deployment of new clones.

Table 5 Age-age correlation (type_A genetic correlations) and phenotypic correlations between 3 and 6 years old for height and diameter at breast height (standard error in brackets)
Full size table

Expected genetic gain and breeding values

The theoretical and empirical method showed similar results but considering the limited number of families, we decided to use the theoretical method.

As already stated, expected genetic gain was calculated with a 10% selection. The highest expected gain was found for the presence of Sphaerulina musiva, followed by DBH, height and number of adventitious branches (Tables 2, 3, and 4). However, these results should be taken with caution, since a 10% selection would represent only 3 families in our study. The gains presented here are potentially amplified by the small number of families selected and the potential presence of extremes among the bests. Some of the binary variables have no expected gain because the average percentage of occurrence was less than 20% or greater than 80%, which is associated with too much environmental variance (Isik 2011).

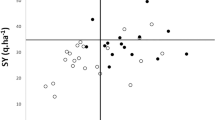
Family breeding values were also calculated for each variable (Online Resource 2). In order to determine if a family selection can result in genetic gain on more than one variable, family breeding values for variables showing possible genetic gain were considered in a principal component analysis (PCA). The first principal component (PC1), which explained 50.7% of the variance, is related to growth variables (height and DBH), morphological variables (adventitious branches and multiple tops) as well as the presence of frost dieback whereas the second principal component (PC2) is associated with presence of canker and multiple stems and explained 19.3% of the variance (Fig. 1). The most interesting observation is that frost dieback is negatively correlated with growth variables, suggesting that the best growing families are also the best adapted in our study and that they are less likely to suffer from frost dieback. These preliminary results differ from those of others (e.g., Howe et al. 2000; Riemenschneider et al. 1992) who suggested that selection for height growth could lead to later budset in selected individuals, and hence to more frost vulnerability. Based on the preliminary observation that M×T families from a high-altitude mother seem less likely to suffer from frost dieback, it would be important to investigate this issue further in the coming years by including phenological data to verify this relationship between growth and phenology in our selections.

Fig. 1
figure 1

Principal component analysis for traits showing possible genetic gain on multiple traits

Full size image

The resulting graph also shows a weak to moderate correlation between the presence of Sphaerulina musiva canker and growth traits. DBH in 2020 seems to have a stronger correlation with the presence of the canker, and this is confirmed by looking at the breeding values presented in the Online Resources 2, where a positive relationship between the BV of these two variables can be observed. These results are similar to those of Zamudio et al. (2022), who suggest that the larger surface area and thinner bark of larger trees could facilitate pathogen entry. To better consider this relationship in the canker susceptibility analysis, a model including DBH2020 as a covariate was tested, but even if the covariate was highly significant, the results did not show significantly different variance estimates from those obtained with the model without the covariate (data not shown). This positive relationship could be an issue for selection of individuals with superior growth as well as lower susceptibility to Sphaerulina musiva canker. On the other hand, some families show the possibility to obtain a genetic gain on multiple variables, including susceptibility to Sphaerulina musiva canker as well as growth (Fig. 1). Therefore, a selection index could also be established to optimize the weights associated with each desired variable for multi-trait selection (Riemenschneider et al. 1992). The use of breeding values or GCA allowed us to identify the best mothers to enhance certain traits in our population and will be useful in future crosses to obtain new clones demonstrating, for instance, good growth and low susceptibility to Sphaerulina musiva.

Conclusion

Growth, cold tolerance, and susceptibility to the pathogen Sphaerulina musiva are under strong genetic control, while morphological traits are under weak to moderate genetic control. Some half-sib families show gains in all these traits, showing that cold tolerance and susceptibility to the pathogen Sphaerulina musiva can be improved without affecting growth, even when using non-native material. This suggests that poplar family selection could be carried out using a selection index to increase the proportion of traits of interest in breeding populations. These results will guide future improvement strategies in hybrid poplar breeding programs and will contribute to the selection of interesting individuals for clonal deployment. Furthermore, multi-trait top-ranked parents will be beneficial for genetic gains in the next breeding population.